求锐角三角函数值的经典题型+方法归纳(超级经典好用)
锐角三角函数的题型及解题技巧
锐角三角函数的题型及解题技巧锐角三角函数是三角函数的基础，它应用广泛，解题技巧性强，下面归纳出锐角三角函数的常见题型，并结合例题介绍一些解题技巧。
一、 化简或求值例1 （1）已知tan 2cot 1a a -=，且a 是锐角，求22tan cot 2a a +-的值。
（2）化简()()22sin cos cos sin a b a b a a a a ++-。
分析分析 （1）由已知可以求出tan a 的值，化简22tan cot 2a a +-可用1tan cot a a =×；（2）先把平方展开，再利用22sin cos 1a a +=化简。
化简。
解 （1）由tan 2cot 1a a -=得2tan 2tan a a -=，解关于tan a 的方程得tan 2a =或tan 1a =-。
又a 是锐角，∴tan 2a =。
∴22tan cot 2a a +-＝22tan 2tan cot cot a a a a -×+＝2(tan cot )a a -＝tan cot a a -。
由tan 2a =，得1cot 2a =，∴22tan cot 2a a +-＝tan cot a a -＝13222-=。
（2）()()22sin cos cos sin a b a b a a a a ++-＝2222sin 2sin cos cos a ab b a a a a +××+＋2222cos 2cos sin sin a ab b a a a a -××+＝()()222222sin cos sin cos a b a a a a +++＝22a b +。
说明说明 在化简或求值问题中，经常用到“1”的代换，即22sin cos 1a a +=，tan cot 1a a ×=等。
等。
二、已知三角函数值，求角例2 在△ABC 中，若223cos sin 022A B æö-+-=ç÷ç÷èø(),A B ÐÐ均为锐角，求C Ð的度数。
初三锐角三角函数知识点总结、典型例题附带部分答案、练习(精选)
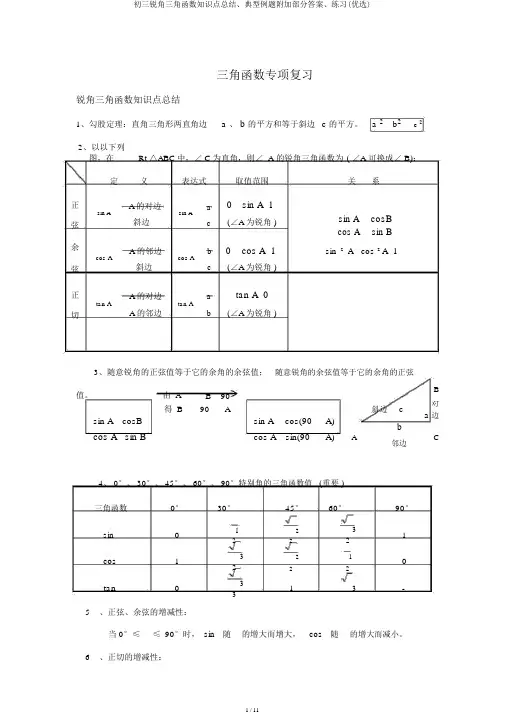
三角函数专项复习锐角三角函数知识点总结1、勾股定理：直角三角形两直角边 a 、 b 的平方和等于斜边 c 的平方。
a 2 b 2c 22、以以下列图，在Rt △ABC 中，∠ C 为直角，则∠ A 的锐角三角函数为 ( ∠A 可换成∠ B)：定 义 表达式取值范围关系正A 的对边 a 0 sin A 1sin A 斜边sin A(∠A 为锐角 )sin A cosB 弦ccos Asin B余A 的邻边 b 0 cos A 1sin 2 A cos 2 A 1cos A 斜边cos A(∠A 为锐角 )弦c正A 的对边atan A 0tan Atan A(∠A 为锐角 )切A 的邻边b3、随意锐角的正弦值等于它的余角的余弦值； 随意锐角的余弦值等于它的余角的正弦值。
由 A B 90 B得 B90A斜边c对a 边sin A cosBsin Acos(90A)bcos A sin Bcos A sin(90A)AC邻边4、 0°、 30°、 45°、 60°、 90°特别角的三角函数值 (重要 )三角函数0° 30°45°60°90°sin0 1 2 3 1 222cos13 2 1 02 22tan0 3 13-35 、正弦、余弦的增减性：当 0°≤≤ 90°时， sin 随 的增大而增大， cos 随的增大而减小。
6 、正切的增减性：当 0° < <90°时， tan随的增大而增大，7、解直角三角形的定义：已知边和角（两个，此中必有一边）→全部未知的边和角。
依照：①边的关系：a2b2c2；②角的关系：A+B=90°；③边角关系：三角函数的定义。
( 注意：尽量防范使用中间数据和除法)8、应用举例：(1)仰角：视野在水平线上方的角；俯角：视野在水平线下方的角。
初三下学期锐角三角函数知识点总结及经典例题20202011
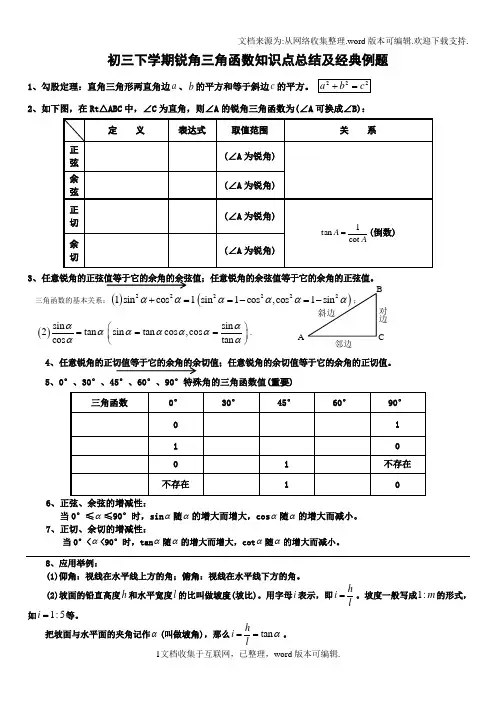
初三下学期锐角三角函数知识点总结及经典例题1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。
三角函数的基本关系：()221sin cos 1αα+=(222sin 1cos ,cos ααα=-()sin 2tan cos ααα=sin sin tan cos ,cos tan αααααα⎛⎫== ⎪⎝⎭．4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)6、正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。
7、正切、余切的增减性：当0°<α<90°时，tan α随α的增大而增大，cot α随α的增大而减小。
8、应用举例：(1)仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示，即hi l=。
坡度一般写成1:m 的形式，如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。
对边邻边3、从某点的指北方向按顺时针转到目标方向的水平角，叫做方位角。
如图3，OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°。
4、指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是：北偏东30°（东北方向） ， 南偏东45°（东南方向）， 南偏西60°（西南方向）， 北偏西60°（西北方向）。
专题01 求直角三角形锐角三角函数的方法(解析版)
九年级数学下册解法技巧思维培优专题01 求直角三角形锐角三角函数的方法题型一 直接运用定义求锐角三角函数值【典例1】（2019•金堂校级期末）如图，Rt △ABC 中，∠C ＝90°，且AC ＝1，BC ＝2，则sin ∠A ＝2√55．【点拨】根据勾股定理先得出AB ，再根据正弦的定义得出答案即可．【解析】解：∵∠C ＝90°， ∴AC 2+BC 2＝AB 2， ∵AC ＝1，BC ＝2， ∴AB =√5；∴sin ∠A =BC AB =5=2√55， 故答案为2√55． 【典例2】（2019•镇海区一模）如图，直线y =34x +3与x 、y 轴分别交于A 、B 两点，则cos ∠BAO 的值是（ ）A ．45B ．35C ．43D ．54【点拨】根据一次函数图象上点的坐标特征求出点A 、B 的坐标，得到OA 、OB 的长，根据勾股定理求出AB ，根据余弦的定义解答即可． 【解析】解：当x ＝0时，y ＝3， 当y ＝0时，x ＝﹣4，∴直线y =34x +3与x 、y 轴的交点A 的坐标（﹣4，0）、B （0，3）， ∴OA ＝4，OB ＝3， 由勾股定理得，AB ＝5，则cos ∠BAO =OAAB =45， 故选：A ．【典例3】（2019•咸宁模拟）如图，P （12，a ）在反比例函数y =60x图象上，PH ⊥x 轴于H ，则tan ∠POH 的值为512．【点拨】利用锐角三角函数的定义求解，tan ∠POH 为∠POH 的对边比邻边，求出即可．【解析】解：∵P （12，a ）在反比例函数y =60x 图象上， ∴a =6012=5， ∵PH ⊥x 轴于H ，∴PH＝5，OH＝12，∴tan∠POH=5 12，故答案为：512．【典例4】（2019•成都月考）如图，在正方形ABCD中，M是AD的中点，BE＝3AE，试求sin∠ECM的值．【点拨】依题意设AE＝x，则BE＝3x，BC＝4x，AM＝2x，CD＝4x，先证明△CEM是直角三角形，再利用三角函数的定义求解．【解析】解：设AE＝x，则BE＝3x，BC＝4x，AM＝2x，CD＝4x，∴EC=√(3x)2+(4x)2=5x，EM=√x2+(2x)2=√5x，CM=2+(4x)2=2√5x，∴EM2+CM2＝CE2，∴△CEM是直角三角形，∴sin∠ECM=EMCE=√55．题型二利用等角转换求锐角三角函数值【典例5】（2019•雁塔区校级月考）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，BC＝3，AC＝4，则cos ∠DCB 的值为（ ）A ．35B ．45C ．34D ．43【点拨】先利用勾股定理计算出AB ＝5，再利用等角的余角得到∠A ＝∠DCB ，然后根据余弦的定义求出cos A 即可．【解析】解：在Rt △ABC 中，AB =√BC 2+AC 2=√32+42=5， ∵CD ⊥AB ，∴∠DCB +∠B ＝90°， 而∠A +∠B ＝90°， ∴∠A ＝∠DCB ，而cos A =ACAB =45， ∴cos ∠DCB =45．故选：B ．【典例6】（2019•兰州模拟）如图，CD 是平面镜，光线从A 点出发经过CD 上点E 反射后照到B 点，若入射角为α（入射角等于反射角），AC ⊥CD ，BD ⊥CD ，垂足分别为C ，D ，且AC ＝3，BD ＝4，CD ＝11，则tan α的值为（ ）A．311B．711C．113D．117【点拨】根据反射的性质，可得β，根据余角的性质，可得∠1与∠2的关系，根据相似三角形的判定与性质，可得CE的长，根据正切函数，可得答案．【解析】解：设CE的长为x，如图，，由入射角等于反射角，得∠β＝∠α，由余角的性质，得∠1＝∠2．由AC⊥CD，BD⊥CD，得∠ACE＝∠BDE，△ACE∽△BDE，AC BD =CEDE，即3x=411−x，解得x=33 7由题意，得∠A＝∠α．tanα＝tan∠A=CEAC=3373=117，故选：D．【典例7】（2019•太仓市期末）如图，在△ABC 中，AB ＝AC ＝5，BC ＝8．若∠BPC =12∠BAC ，则sin ∠BPC ＝45．【点拨】先过点A 作AE ⊥BC 于点E ，求得∠BAE =12∠BAC ，故∠BPC ＝∠BAE ．再在Rt △BAE 中，利用锐角三角函数的定义，求得sin ∠BPC ＝sin ∠BAE =BE AB ． 【解析】解：过点A 作AE ⊥BC 于点E ，∵AB ＝AC ＝5，∴BE =12BC =12×8＝4，∠BAE =12∠BAC ， ∵∠BPC =12∠BAC ，∴∠BPC ＝∠BAE ． 在Rt △BAE 中，∴sin ∠BPC ＝sin ∠BAE =BEAB =45． 故答案为：45．【典例8】（2019•望江校级月考）如图，在Rt△ABC中，∠C＝90°，M是直角边AC上一点，MN⊥AB 于点N，AN＝3，AM＝4，求cos B的值．【点拨】根据AA可证△AMN∽△ABC，根据相似三角形的性质得到ACAB =ANAM=34，设AC＝3x，AB＝4x，由勾股定理得：BC=√7x，在Rt△ABC中，根据三角函数可求cos B．【解析】解：∵∠C＝90°，MN⊥AB，∴∠C＝∠ANM＝90°，又∵∠A＝∠A，∴△AMN∽△ABC，∴ACAB =ANAM=34，设AC＝3x，AB＝4x，由勾股定理得：BC=√AB2−AC2=√7x，在Rt△ABC中，cos B=BCAB=√7x4x=√74．题型三设参数求锐角三角函数值【典例9】（2019•沙坪坝区校级月考）如图，在菱形ABCD中，DE⊥AB于点E，cos A=35，BE＝4，则tan ∠DBE的值是（）A ．43B ．34C ．2D ．12【点拨】在直角三角形ADE 中，cos A =35，求得AD ，AE ．再求得DE ，即可得到tan ∠DBE =DEBE ． 【解析】解：设菱形ABCD 边长为x ， ∵BE ＝4， ∴AE ＝x ﹣4，∵cos A =35，∴AE AD=x−4x=35，∴x ＝10， ∴AE ＝10﹣4＝6， ∴DE =√AD 2−AE 2=8， ∴tan ∠DBE =DE BE =84=2． 故选：C ．【典例10】（2019•湘西州）如图，在△ABC 中，∠C ＝90°，AC ＝12，AB 的垂直平分线EF 交AC 于点D ，连接BD ，若cos ∠BDC =57，则BC 的长是（ ）A ．10B ．8C ．4√3D ．2√6【点拨】设CD ＝5x ，BD ＝7x ，则BC ＝2√6x ，由AC ＝12即可求x ，进而求出BC ；【解析】解：∵∠C ＝90°，cos ∠BDC =57， 设CD ＝5x ，BD ＝7x ， ∴BC ＝2√6x ，∵AB 的垂直平分线EF 交AC 于点D ， ∴AD ＝BD ＝7x ， ∴AC ＝12x ， ∵AC ＝12， ∴x ＝1， ∴BC ＝2√6； 故选：D ．【典例11】（2019•南山区一模）如图，延长Rt △ABC 的斜边AB 到点D ，使BD ＝AB ，连接CD ，若tan ∠BCD =13，则tan ∠A 的值是（ ）A ．1B ．23C ．9D ．32【点拨】若想利用tan ∠BCD 的值，应把∠BCD 放在直角三角形中，为此，过B 作BE ∥AC 交CD 于E ，得到△ACD 的中位线，可分别得到所求的角的正切值相关的线段的比．【解析】解：如图，过B作BE∥AC交CD于E．∵AC⊥BC，∴BE⊥BC，∠CBE＝90°，∴BE∥AC．∵AB＝BD，∴AC＝2BE．又∵tan∠BCD=13，设BE＝x，则BC＝3x，AC＝2x，∴tan A=BCAC=3x2x=32．故选：D．【典例12】（2019•杨浦区模拟）如图，在Rt△ABC中，∠C＝90°，点D在BC边上，∠ADC＝45°，BD＝2，tan B=3 4（1）求AC和AB的长；（2）求sin∠BAD的值．【点拨】（1）由tan B=ACBC=34设AC＝3x、BC＝4x，据此得DC＝4x﹣2，根据∠ADC＝45°得AC＝DC，即3x＝4x﹣2，解之得出x的值，继而可得答案；（2）作DE⊥AB，设DE＝3a、BE＝4a，根据DE2+BE2＝BD2可求得a的值，继而根据正弦函数的定义可得答案．【解析】解：（1）如图，在Rt△ABC中，∵tan B=ACBC=34，∴设AC＝3x、BC＝4x，∵BD＝2，∴DC＝BC﹣BD＝4x﹣2，∵∠ADC＝45°，∴AC＝DC，即4x﹣2＝3x，解得：x＝2，则AC＝6、BC＝8，∴AB=√AC2+BC2=10；（2）作DE⊥AB于点E，由tan B=DEBE=34可设DE＝3a，则BE＝4a，∵DE2+BE2＝BD2，且BD＝2，∴（3a）2+（4a）2＝22，解得：a=25（负值舍去），∴DE ＝3a =65，∵AD =√AC 2+DC 2=6√2，∴sin ∠BAD =DE AD =√210． 题型四 构造直角三角形求锐角三角函数值【典例13】（2019•玉环模拟）如图，△ABC 的各个顶点都在正方形的格点上，则sin A 的值为 √55．【点拨】利用图形构造直角三角形，进而利用sin A =BE AB求出即可． 【解析】解：如图所示：延长AC 交网格于点E ，连接BE ，∵AE ＝2√5，BE =√5，AB ＝5，∴AE 2+BE 2＝AB 2，∴△ABE 是直角三角形，∴SinA =BE AB =√55．故答案为：√55．【典例14】（2019•吴江区期末）如图，在锐角△ABC中，AB＝10，BC＝11，S△ABC＝33，求tan C的值．【点拨】过A作AD⊥BC于点D，利用面积公式求出高AD的长，从而求出BD、CD的长，此时再求tan C 的值就不那么难了．【解析】解：过A作AD⊥BC于点D．∵S△ABC=12BC•AD＝33，∴12×11×AD＝33，∴AD＝6．又∵AB＝10，∴BD=√AB2−AD2=√102−62=8．∴CD＝11﹣8＝3．在Rt△ADC中，∴tanC=ADDC=63=2．【典例15】（2019•京山期中）如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝3，点D在边AC上，且AD＝2CD，DE⊥AB，垂足为点E，连CE，求：（1）线段BE的长；（2）线段CE的长．【点拨】（1）证明△ADE是等腰直角三角形，求出AE即可解决问题．（2）作EF⊥AC于F．求出EF，CF即可解决问题．【解析】解：（1）∵CA＝CB＝3，∠ACB＝90°，∴∠A＝45°，AB=√2AC＝3√2，∵DE⊥AE，∴△ADE是等腰直角三角形，∵AC＝BC＝3，AD＝2CD，∴AD＝2，CD＝1，∴AE＝DE=√2，∴BE＝AB﹣AE＝2√2．（2）作EF⊥AC于F．∵EF⊥AD，△ADE是等腰直角三角形，∴EF＝AF＝DF＝1，∴CF＝2，在Rt△EFC中，EC=√EF2+CF2=√12+22=√5．巩固练习1．（2019•雁塔区校级模拟）直线y＝3x与x轴正半轴的夹角的锐角为α，那么下列结论正确的是（）A．tanα＝3B．tanα=13C．sinα＝3D．cosα＝3【点拨】根据题意结合一次函数图象上点的坐标性质得出AB，OB的长，再利用锐角三角函数关系得出答案．【解析】解：如图所示：AB⊥x轴于点B，∵y＝3x，A点在y＝3x的图象上，∴设BO＝x，则AB＝3x，故tanα=ABOB=3x x=3．故选：A．2．（2019•雁塔区校级模拟）如图，在菱形ABCD中，DE⊥AB，cos A=35，BE＝2，则BD的值（）A．2B．√5C．2√5D．5【点拨】直接利用菱形的性质结合锐角三角函数关系得出AD，AE的长，进而利用勾股定理得出BD的长．【解析】解：∵四边形ABCD是菱形，∴AD＝AB，∵DE⊥AB，cos A=3 5，∴设AE＝3x，则AD＝5x，故BE＝2x，∵BE＝2，∴x＝1，故AB＝AD＝5，则DE＝4，故BD=√DE2+BE2=2√5．故选：C．3．（2019•儋州期末）已知：如图，某学生想利用标杆测量一棵大树的高度，如果标杆EC的高为1.6m，并测得BC＝2.2m，CA＝0.8m，那么树DB的高度是（）A ．6mB ．5.6mC ．5.4mD ．4.4m【点拨】先根据相似三角形的判定定理得出Rt △ACE ∽Rt △ABD ，再根据相似三角形的对应边成比例即可求出BD 的长．【解析】解：∵EC ∥AB ，BD ⊥AB ，∴EC ∥BD ，∠ACE ＝∠ABD ＝90°，在Rt △ACE ∽Rt △ABD 中，∠A ＝∠A ，∠ACE ＝∠ABD ＝90°，∴Rt △ACE ∽Rt △ABD ，∴EC BD =CA CA+BC ，即1.6BD =0.80.8+2.2，解得BD ＝6m ．故选：A ．4．（2019•富平期末）如图，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于点D ，BC ＝3，AC ＝4，tan ∠BCD 的值为（ ）A ．34B ．43C ．45D ．54 【点拨】根据直角三角形的性质、同角的余角相等得到∠BCD ＝∠A ，根据正切的定义计算即可．【解析】解：∵∠ACB ＝90°，∴∠A +∠B ＝90°，∵CD ⊥AB ，∴∠BCD +∠B ＝90°，∴∠BCD ＝∠A ，∴tan ∠BCD ＝tan ∠A =BC AC =34，故选：A ．5．（2019•宽城区期末）如图，点A 、B 、C 均在小正方形的顶点上，且每个小正方形的边长均为1，则cos ∠BAC 的值为（ ）A ．12B ．√22C ．1D ．√2【点拨】根据题目中的数据和勾股定理，可以求得AB 、BC 、AC 的长，然后根据勾股定理逆定理可以判断△ABC 的形状，从而可以求得cos ∠BAC 的值．【解析】解：连接BC ，∵每个小正方形的边长均为1，∴AB =√5，BC =√5，AC =√10，∵(√5)2+(√5)2=(√10)2，∴△ABC 是直角三角形，∴cos ∠BAC =AB AC =√510=√22， 故选：B ．6．（2019•西湖区校级月考）如图所示，在△ABC中，∠C＝90°，AB＝8，CD是AB边上的中线，作CD 的中垂线与CD交于点E，与BC交于点F．若CF＝x，tan A＝y，则x与y之间满足（）A．4y2+4=x2B．4y2−4=x2C．8y2−8=x2D．8y2+8=x2【点拨】由直角三角形斜边上的中线性质得出CD=12AB＝AD＝4，由等腰三角形的性质得出∠A＝∠ACD，得出tan∠ACD=GECE=tan A＝y，证明△CEG∽△FEC，得出GECE=CEFE，得出y=2FE，求出y2=4FE2，得出4y2=FE2，再由勾股定理得出FE2＝CF2﹣CE2＝x2﹣4，即可得出答案．【解析】解：如图所示：∵在△ABC中，∠C＝90°，AB＝8，CD是AB边上的中线，∴CD=12AB＝AD＝4，∴∠A＝∠ACD，∵EF垂直平分CD，∴CE=12CD＝2，∠CEF＝∠CEG＝90°，∴tan∠ACD=GECE=tan A＝y，∵∠ACD+∠FCE＝∠CFE+∠FCE＝90°，∴∠ACD＝∠FCE，∴△CEG∽△FEC，∴GE CE =CE FE ，∴y =2FE， ∴y 2=4FE 2， ∴4y =FE 2，∵FE 2＝CF 2﹣CE 2＝x 2﹣4，∴4y 2=x 2﹣4， ∴4y +4＝x 2，故选：A ．7．（2020•闵行区一模）在△ABC 中，若∠C ＝90°，AB ＝10，sin A =25，则BC ＝ 4【点拨】根据锐角三角函数的定义得出sin A =25=BC AB ，代入求出即可．【解析】解：∵sin A =25=BC AB ，SB ＝10，∴BC ＝4，故答案为：4．8．（2019•黄浦区一模）在等腰△ABC 中，AB ＝AC ，如果cos C =14，那么tan A ＝√157． 【点拨】过点A 作AE ⊥BC 于点E ，过点B 作BD ⊥AC 于点D ，由于cos C =14，所以CD BC=14，CE AC=14，设CD ＝x ，BC ＝4x ，根据勾股定理以及锐角三角函数的定义可求出BD 与AD 的长度． 【解析】解：过点A 作AE ⊥BC 于点E ，过点B 作BD ⊥AC 于点D ，∵cos C =14， ∴CD BC=14，CEAC=14，设CD ＝x ，BC ＝4x ， 由于AB ＝AC ， ∴CE ＝2x ， ∴AC ＝8x ，∴AD ＝AC ﹣CD ＝7x ，∴由勾股定理可知：BD =√15x ， ∴AB ＝AC ＝8x ，∴tan ∠BAC =BDAD =√157， 故答案为：√157．9．（2019•百色期末）在△ABC 中，∠C ＝90°，AB ＝10，BC ＝8，则cos A ＝35．【点拨】根据勾股定理求出AC ，根据锐角三角函数定义求出即可．【解析】解：由勾股定理得：AC =√AB 2−BC 2=√102−82=6，cos A =ACAB =610=35， 故答案为：35．10．（2019•宽城区校级月考）如图，△ABC 的顶点在正方形网格的格点处，则tan B 的值为 1 ．【点拨】根据在直角三角形中，锐角的正切为对边比邻边，可得答案．【解析】解：如图：，由正切函数的定义，得tan B =AD BD =33=1． 故答案为：1．11．（2019•相山区四模）如图，在△ABC 中，∠B 为锐角，AB ＝3√2，AC ＝5，sin C =35，求BC 的长．【点拨】作AD⊥BC，在△ACD中求得AD＝AC sin C＝3、CD=√AC2−AD2=4，再在△ABD中根据AB＝3√2、AD＝3求得BD＝3，继而根据BC＝BD+CD可得答案．【解析】解：作AD⊥BC于点D，∴∠ADB＝∠ADC＝90°．∵AC＝5，sinC=3 5，∴AD＝AC•sin C＝3．∴在Rt△ACD中，CD=√AC2−AD2=4．∵AB=3√2，∴在Rt△ABD中，BD=√AB2−AD2=3．∴BC＝BD+CD＝7．12．（2019•奉化市模拟）2019年3月29日，宁波市第十二届山地户外运动挑战赛在奉化市大堰镇举行，比赛全程42公里，共有20支队伍参加，其中三支外国队．划皮艇横渡柏坑水库是其中一个项目，横渡直线距离900米．在实际比赛中，甲队皮艇的划行路线偏离了最短路线约5°，但甲队还是以15分钟12秒的成绩摘得冠军．问：（1）在这次比赛中，甲队皮艇的平均速度为多少？（精确到0.01米/秒）（2）若甲队划皮艇的平均速度不变且在比赛中沿最短路线划行，则可比实际比赛提前几秒到达终点？（精确到0.1秒）（参考数据：sin5°＝0.0872；cos5°＝0.9962；tan5°＝0.0875）【点拨】（1）先根据锐角三角函数的定义求出AC的长度，由速度=路程时间即可得出甲队划皮艇的平均速度；（2）由甲队划皮艇的时间减去沿最短路线划行的时间即可．【解析】解：（1）由图可知，在△ABC中，∠ABC＝90°，∠BAC＝5°，AB＝900，∴AC=ABcos∠BAC=9000.9962，∵15分钟12秒＝912秒，9000.9962÷912≈0.99（米/秒）．答：甲队划皮艇平均速度为0.99米/秒；（2）912﹣900÷（9000.9962÷912）≈3.5（秒）．答：甲队可比实际比赛提前3.5秒到达终点．13．（2019•芙蓉区校级期末）如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝3√2，点D在边AC上，且AD＝2CD，DE⊥AB，垂足为点E．求：线段BE的长．【点拨】证明△ADE是等腰直角三角形，求出AB，AE即可解决问题．【解析】解：∵AC＝BC＝3√2，∠ACB＝90°，∴∠A＝45°，AB=√2AC＝6，∵DE⊥AB，∴∠AED＝90°，∴△ADE是等腰直角三角形，∵AD＝2CD，∴AD＝2√2，∵AE＝DE＝2，∴BE＝AB﹣AE＝6﹣2＝4．14．（2019•宁夏）已知点E为正方形ABCD的边AD上一点，连接BE，过点C作CN⊥BE，垂足为M，交AB于点N．（1）求证：△ABE≌△BCN；（2）若N为AB的中点，求tan∠ABE．【点拨】（1）根据正方形的性质和全等三角形的判定证明即可； （2）根据全等三角形的性质和三角函数解答即可．【解析】（1）证明：∵四边形ABCD 为正方形∴AB ＝BC ，∠A ＝∠CBN ＝90°，∠1+∠2＝90° ∵CM ⊥BE ， ∴∠2+∠3＝90° ∴∠1＝∠3在△ABE 和△BCN 中{∠A =∠CBN AB =BC ∠1=∠3∴△ABE ≌△BCN （ASA ）； （2）∵N 为AB 中点，∴BN =12AB又∵△ABE ≌△BCN ，∴AE ＝BN =12AB在Rt△ABE中，tan∠ABE═AEAB=AE2AE=12．15．（2019•崇明期中）如图，在△ABC中，∠C＝90°，点D在BC上，AD＝BC＝5，cos∠ADC=35，求：sin B的值．【点拨】先由AD＝BC＝5，cos∠ADC=35及勾股定理求出AC及AB的长，再由锐角三角函数的定义即可求解．【解析】解：∵AD＝BC＝5，cos∠ADC=35，∴CD＝3，在Rt△ACD中，∵AD＝5，CD＝3，∴AC=√AD2−CD2=√52−32=4，在Rt△ACB中，∵AC＝4，BC＝5，∴AB=√AC2+BC2=√42+52=√41，∴sin B=ACAB=41=4√4141．。
初三锐角三角函数题型及解题方法
初三锐角三角函数题型及解题方法初三数学中，锐角三角函数是一个非常重要的内容。
学习锐角三角函数，不仅需要掌握其概念和公式，还需要掌握一些常见的题型及解题方法。
本文将介绍一些常见的锐角三角函数题型及解题方法，帮助初三学生更好地掌握这一内容。
一、求三角函数值求三角函数值是锐角三角函数中最基本的题型。
一般来说，题目都会给出三角函数的角度，要求求出其对应的正弦、余弦、正切等函数值。
解题方法：对于这类题目，我们需要掌握三角函数的定义和公式。
例如，正弦函数的定义是：在直角三角形中，对于一个锐角角度A，其对边长度与斜边长度的比值称为正弦值sinA。
因此，我们只需要根据这个定义和公式进行计算即可。
举个例子，题目给出角度A=30度，要求求出其正弦值sinA。
根据正弦函数的定义和公式，我们得到：sinA=对边长度/斜边长度=sqrt(3)/2因此，sinA=√3/2。
二、三角函数的基本关系式三角函数的基本关系式指的是三角函数之间的基本等式。
例如，正切函数的基本关系式是tanA=sinA/cosA。
这类题目一般要求将一个三角函数用另外一个三角函数表示出来，或者将两个三角函数相互表示。
解题方法：对于这类题目，我们需要掌握三角函数之间的基本关系式。
例如，正切函数的基本关系式是：tanA=sinA/cosA因此，如果题目给出sinA的值，要求求出tanA的值，我们只需要将sinA/cosA代入上式，即可得到：tanA=sinA/cosA=√3/3三、三角函数值的范围三角函数值的范围是指，每个三角函数的取值范围。
例如，正弦函数的取值范围是[-1,1]，余弦函数的取值范围也是[-1,1]。
解题方法：对于这类题目，我们需要掌握每个三角函数的取值范围。
例如，正弦函数的取值范围是[-1,1]，因此，如果题目给出sinA=-0.5，我们就可以知道sinA的值在[-1,1]范围之内。
四、三角函数的性质三角函数的性质指的是，它们在不同象限中的正负性和大小关系。
求锐角三角函数的四种方法.docx
求锐角三角函数的四种方法＞方法一运用定义求锐角三角函数值1 •如图 6-ZT-1，在 Rt/XABC 中，ZC = 90° ，BC=3，AC=4，那么 sinA 的值等于图 6-ZT-12 •如图6-ZT-2，在心ZXABC 中，CD 是斜边AB 上的中线.若CD = 5，AC=6，则 tanB 的值是（）A 5 C 4 33 • a ，b ，c 是AABC 中ZA ，ZB ，ZC 的对边，且 a ： b ： c=l ：迈：萌，则 cosB 的 值为（）A •普B.普C.芈D 逹4 •如图6-ZT-3，AABC 的顶点都在小正方形组成的网格的格点上，则cosC 的值为 （） 厂湖 ::a~~\图 6-ZT-3D •呼5 ・如图 6-ZT-4，在厶 ABC 中，ZC = 90° ，BC = 3，AB=5，求 sinA > cos A ，tanA 的值.6 •如图6-ZT-5，在正方形ABCD 中，M 是AD 的中点，BE=3AE ，试求sinZECM 的值.4-5 D 3-5 c4-3 B. 3-4 A＞方法二利用互余两角三角函数的关系求锐角三角函数值7•在AABC 中，cosA=^j，则血(90° -ZA)的值为( )512 8 小5A l3 C l3 D l28• [2017-福建]小明在某次作业屮得到如下结果: sin2!0 +朋83。
^0.122+0.992=0.9945，sin 22° +朋68。
^0.372+ 0.932= 1.0018，朋29。
+ 朋61。
^0.482+ 0.872= 0.9873，s卅3丁+sin5r ^0.602+0.802= 1.0000 »sitT45 ° +C45° =（¥）? +（¥）2据此，小明猜想：对于任意锐角a，均有曲2 a +加2(90°— a )=1.⑴当a=30°时，说明sin a +5m2(90°—a)=l是否成立；(2)小明的猜想是否成立？若成立，请给予证明；若不成立，请举出一个反例.A 方法三利用等角求锐角三角函数值9 •如图6-ZT-6，己知h 〃b 〃13，相邻两条平行直线间的距离相等.若等腰直角三角 形ABC 的三个顶点分别在这三条平行直线上，则sin a 的值是（）10 •如图 6-ZT-7，在 AABC 屮，AB=AC=5，8。
用锐角三角函数概念解题的常见方法(含答案页)
用锐角三角函数概念解题的常见方法(含答案11页)用锐角三角函数概念解题的常见方法1．锐角三角函数（1）锐角三角函数的定义我们规定：sinA=abab，cosA=，tanA=，cotA=．ccba锐角的正弦、余弦、正切、余切统称为锐角的三角函数．（2）用计算器由已知角求三角函数值或由已知三角函数值求角度对于特殊角的三角函数值我们很容易计算，甚至可以背诵下来，但是对于一般的锐角又怎样求它的三角函数值呢？用计算器可以帮我们解决大问题．①已知角求三角函数值；②已知三角函数值求锐角．2直角三角形中，30°的锐角所对的直角边等于斜边的一半．3．锐角三角函数的性质（1）0<sinα<1，o<cosα<1（0°<α<90°）1（2）tanα·cotα=1或tanα=（3）tanα=1；cot?sin?cos?，cotα=．cos?sin?（4）sinα=cos（90°-α），tanα=cot（90°-α）．有关锐角三角函数的问题，常用下面几种方法：一、设参数例1. 在?ABC中，?C?90?，如果tanA?5，那么sinB的值等于（）12D.12 5A.513B.1213C.512解析：如图1，要求sinB的值，就是求AC5的值，而已知的tanA?，也就是AB12BC5? AC12可设BC?5k，AC?12k则AB?(5k)2?(12k)2?13k?sinB?12k12?，选B 13k13二、巧代换例2. 已知tan??3，求sin??2cos?的值。
5sin??cos?解析：已知是正切值，而所求的是有关正弦、余弦的值，我们可以利用关系式sin??3，作代换sin??3cos?，代入即可达到约分的目的，也可以把所求的cos?分式的分子、分母都除以cos?。
tan??2sin??2sin??2cos? ?cos?sin5sin??cos?5?1cos?再把sin?1?3代入，得：原式? cos?16三、妙估计例3. 若太阳光与地面成37?角，一棵树的影长为10m，则树高h的范围是（取?1.7）A. 3?h?5B. 5?h?10C. 10?h?15D. h?15 解析：如图2，树高h?10tan37?，要确定h的范围，可根据正切函数是增函数，估计tan30??tan37??tan45?即10tan30??10tan37??10tan45??10??h?10 3?5?h?10，故选B四、善转化例4. 在?ABC中，1?A?30?，tanB?BC?，求AB的长。
小专题(八) 求锐角的三角函数值的常用方法
方法 4 构造直角三角形
若要求的三角函数值的角不在直角三角形中，则需要根据 已知条件构造直角三角形来解决．
9．如图，在△ABC 中，AE⊥BC 于点 E，D 为 AB 边上一点．如
果 BD＝2AD，CD＝10，sin∠BCD＝35，那么 AE 的长为
(D)
A．3
B．6
C．7.2
D．9
10．(合肥市庐阳区期末)如图，网格中的每一个正方形的边长
∴BC＝ AB2－AC2＝ 9m2－4m2＝ 5m.
ห้องสมุดไป่ตู้∴在
Rt△ABC
中，tanB＝ABCC＝
2m ＝ 5m
2 5.
在 Rt△EFB 中，EF＝BF·tanB＝2m5，
∴CE＝EF＝2m5.
2m
∴在
Rt△ACE
中，tan∠CAE＝ACEC＝2m5＝
5 5.
方法 3 等角转换
当一个锐角的某个三角函数不容易求解时，可以借助与其 相等的一个角进行转化，进而求出其三角函数值．
解：(1)在 Rt△ABD 中，∵BD＝DC＝9，AD＝6，
∴AB＝ BD2＋AD2＝ 92＋62＝3 13.
∴sinB＝AADB＝3
6 ＝2 13
1313.
(2)∵EF∥AD，BE＝2AE， ∴AEDF＝BBDF＝BBAE＝23.∴E6F＝B9F＝23. ∴EF＝4，BF＝6.∴DF＝3. 在 Rt△DEF 中，DE＝ EF2＋DF2＝ 42＋32＝5.
在 Rt△ADC 中，tanA＝32， 设 AC＝2a，CD＝3a(a>0)，∴DE＝a. 在 Rt△CDE 中，由勾股定理，得 CE＝ CD2＋DE2＝ （3a）2＋a2＝ 10a. ∴cos∠BCD＝CCDE＝ 31a0a＝130 10.
求锐角三角函数常用方法
求锐角三角函数常用方法锐角三角函数是三角函数中的一部分，它们是正弦函数、余弦函数和正切函数的定义域在锐角范围内的部分。
在数学中，常用的锐角三角函数常见方法有：单位圆法、加法公式、倍角公式和倒数关系等。
1.单位圆法：单位圆法是研究锐角三角函数最基本的方法之一、单位圆法的基本思想是，把一个角落在标准位置的角看做单位圆上的一条弧，角的顶点作为圆心，角的边所在的直线成为弧的切线。
这样可以通过单位圆上的坐标来表示角的边上的函数值。
以正弦函数为例，假设角为A，边所在的线段与单位圆交于点P(x,y)。
可以得到如下关系：sin(A) = y2.加法公式：加法公式是指锐角三角函数在角度A和角度B的和角度(A+B)时，对应的函数值之间的关系。
常用的加法公式如下：sin(A + B) = sin(A)cos(B) + cos(A)sin(B)cos(A + B) = cos(A)cos(B) - sin(A)sin(B)tan(A + B) = (tan(A) + tan(B))/(1 - tan(A)tan(B))3.倍角公式：倍角公式是指锐角三角函数在角度A的两倍角度2A时，对应的函数值之间的关系。
常用的倍角公式如下：sin(2A) = 2sin(A)cos(A)cos(2A) = cos^2(A) - sin^2(A)tan(2A) = 2tan(A)/(1 - tan^2(A))4.倒数关系：倒数关系是指锐角三角函数之间的倒数关系。
常用的倒数关系如下：cosec(A) = 1/sin(A)sec(A) = 1/cos(A)cot(A) = 1/tan(A)5.三角函数的特殊值：在锐角三角函数中，特殊的角度对应的函数值是常用的。
常见的特殊角度包括：- sin(0) = 0- cos(0) = 1- tan(0) = 0- sin(30°) = 1/2- cos(30°) = √3/2- tan(30°) = √3/3- sin(45°) = √2/2- cos(45°) = √2/2- tan(45°) = 1除了以上常见的方法外，还有其他一些方法也能在特定的问题中应用。
锐角三角函数的题型及解题技巧
锐角三角函数的题型及解题技巧锐角三角函数是三角函数的基础，它应用广泛，解题技巧性强，下面归纳出锐角三角函数的常见题型，并结合例题介绍一些解题技巧。
一、 化简或求值例1 （1）已知tan 2cot 1αα-=，且α是锐角，的值。
（2）化简()()22sin cos cos sin a b a b αααα++-。
分析 （1）由已知可以求出tan α1tan cot αα=⋅；（2）先把平方展开，再利用22sin cos 1αα+=化简。
解 （1）由tan 2cot 1αα-=得2tan 2tan αα-=，解关于tan α的方程得tan 2α=或tan 1α=-。
又α是锐角，∴tan 2α=＝tan cot αα-。
由tan 2α=，得1cot 2α=＝tan cot αα-＝13222-=。
（2）()()22sin cos cos sin a b a b αααα++-＝2222sin 2sin cos cos a ab b αααα+⋅⋅+＋2222cos 2cos sin sin a ab b αααα-⋅⋅+＝()()222222sin cos sin cos a b αααα+++＝22a b +。
说明 在化简或求值问题中，经常用到“1”的代换，即22sin cos 1αα+=，tan cot 1αα⋅=等。
二、已知三角函数值，求角例2 在△ABC 中，若2cos sin 02A B ⎛--= ⎝⎭(),A B ∠∠均为锐角，求C ∠的度数。
分析 几个非负数的和为0，则这几个数均为0。
由此可得cos A 和sin B 的值，进而求出,A B ∠∠的值，然后就可求出C ∠的值。
解由题意得cos 0,2sin 0.A B ⎧-=⎪⎪-=解得cos 2sin 3A B ⎧=⎪⎪⎨⎪=⎪⎩又∵,A B ∠∠均为锐角，∴45A ∠=,60B ∠=。
∴18075C A B ∠=-∠-∠=.说明 解这类问题首先要熟记特殊角的三角函数值，还要掌握一些化简的技巧。
2024年北师大版九年级全一册数学微专题10方法技巧 锐角三角函数求值的常用方法
微专题10 方法技巧 锐角三角函数求值的常用方法【类型一】定义法求锐角三角函数值前提 具体步骤锐角在直角三角形中 1.计算对边、邻边或斜边的长; 2.根据定义,计算锐角三角函数值; 3.化简针对训练1.在Rt △ABC 中,∠C =90°,AB =3,AC =2,那么cos A 的值是 (B) A .13B .23C .√53D .√522.如图源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为α,则cos α的值为(D)A .34B .43C .35D .453.已知:如图,矩形ABCD 的对角线AC ,BD 相交于点O ,∠BOC =120°,AB =2. (1)求矩形对角线的长;(2)过O 作OE ⊥AD 于点E ,连接BE.记∠ABE =α,求tan α的值.【解析】(1)∵∠BOC =120°, ∴∠AOB =60°, ∵四边形ABCD 是矩形,∴∠BAD =90°,AC =BD ,AO =OC ,BO =DO , ∴AO =BO ,∴△AOB 是等边三角形, ∴AB =AO =BO , ∵AB =2,∴BO =2, ∴BD =2BO =4,∴矩形对角线的长为4;(2)由勾股定理得:AD =√BD 2-AB 2=√42-22=2√3, ∵OA =OD ,OE ⊥AD 于点E , ∴AE =DE =12AD =√3,∴tan α=AE AB =√32.【类型二】公式法求锐角三角函数值公式 条件 作用sin 2A +cos 2A =1 0°<∠A <90° 易计算sin A 或cos A 的值sin A =cos B ∠A +∠B =90° 易计算∠A 或∠B 和sin A 或cos B 的值 tan A =sinAcosA 0°<∠A <90° 在sin A ,cos A 和tan A 中知二求一 tan B ·tan A =1 ∠A +∠B =90°易计算∠A 或∠B 和tan A 或tan B 的值针对训练4.在Rt △ABC 中,∠C =90°,若tan A =23,则tan B = (C) A .√133B .√132C .32D .√525.若α为锐角,sin α=13,则cos α= 2√23.6.α是锐角,若sin α=cos 15°,则α= 75 °.【类型三】参数法求锐角三角函数值前提具体步骤已知两条边的比值或关系 1.参数表示边的长;2.代入锐角三角函数定义,得到等式;3.计算边的比值针对训练7.如图,在Rt △ABC 中,∠C =90°,BC =3AC ,则sin B = (C)A .13B .3C .√1010 D .3√10108.在Rt △ABC 中,∠C =90°,已知∠A 的正弦值是23,那么∠B 的正弦值是 √53.【类型四】等角转化法求锐角三角函数值前提具体步骤不能直接求出锐角三角函数值1.找出相等的角;2.计算等角的三角函数值;3.利用“等角的三角函数值相等”解答针对训练9.如图,在△ABC 中,∠ACB =90°,AC =4,BC =3,CD 是△ABC 的高,则tan ∠BCD 的值是 (B)A .43B .34C .35D .4510.如图,在Rt △ABC 中,∠C =90°,D 是AC 边的中点,过D 作DE ⊥AB ,垂足为点E ,如果AD =2,AB =6,那么cos ∠ADE =√53.11.如图,AD ,BE 分别是△ABC 中BC ,AC 边上的高,AD =4,AC =6,则sin ∠EBC =√53.【类型五】构造直角三角形求锐角三角函数值前提具体步骤锐角不在直角三角形中1.添加辅助线构造直角三角形;2.在直角三角形中计算锐角三角函数值针对训练12.如图,△ABC的顶点都在正方形网格的格点上,则tan B的值为23.13.如图,△ABC中,∠A=30°,E为AC上一点,且AE∶EC=3∶1,EF⊥AB,F为垂足,连接FC,则tan∠CFB的值等于4√33.14.如图,E为正方形ABCD边AB的中点,以BE为边作正方形BEFG,连接BD,DF,则sin∠BDF=√55.。
(完整版)求锐角三角函数值的经典题型+方法归纳(超级经典好用)
求锐角三角函数值的几种常用方法一、定义法当已知直角三角形的两条边，可直接运用锐角三角函数的定义求锐角三角函数的值． 例1 如图1，在△ABC 中，∠C =90°，AB =13，BC =5，则sin A 的值是( )(A )513 (B )1213 (C )512 (D )135 对应训练：1．在Rt △ABC 中，∠ C ＝90°，若BC ＝1，AB =5，则tan A 的值为( )A ．5 B ．25 C ．12D ．2 二、参数（方程思想）法锐角三角函数值实质是直角三角形两边的比值，所以解题中有时需将三角函数转化为线段比，通过设定一个参数，并用含该参数的代数式表示出直角三角形各边的长，然后结合相关条件解决问题． 例2 在△ABC 中，∠C =90°，如果tan A =512，那么sin B 的值是 ． 对应训练：1．在△ABC 中，∠C =90°，sin A=53，那么tan A 的值等于（ ）. A ．35 B . 45 C . 34 D . 432．已知△ABC 中，ο90=∠C ，3cosB=2， AC=52 ，则AB= ．3．已知Rt △ABC 中，,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B ．4．已知：如图，⊙O 的半径OA ＝16cm ，OC ⊥AB 于C 点，⋅=∠43sin AOC求：AB 及OC 的长．D C B A Oyx第8题图AD ECBF三、等角代换法当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时，可将此角通过等 角转换到能够求出三角函数值的直角三角形中，利用“两锐角相等，则三角函数值也相等” 来解决．例3 在Rt △ABC 中，∠BCA =90°，CD 是AB 边上的中线，BC =5，CD =4，则cos ∠ACD 的值为 ． 对应训练1.如图，O ⊙是ABC △的外接圆，AD 是O ⊙的直径，若O ⊙的半径为32，2AC =，则sin B 的值是（ ）A ．23 B ．32 C ．34 D ．432. 如图4，沿AE 折叠矩形纸片ABCD ，使点D 落在BC 边的点F 处．已知8AB =，10BC =，AB=8,则tan EFC ∠的值为 ( )Ａ．34 Ｂ．43 Ｃ．35 Ｄ．453. 如图6，在等腰直角三角形ABC ∆中，90C ∠=︒，6AC =，D 为AC 上一点，若1tan 5DBA ∠= ，则AD 的长为( )A ．2B ．2C ．1D ．224． 如图，直径为10的⊙A 经过点(05)C ，和点(00)O ，，与x 轴的正半轴交于点D ，B 是y 轴右侧圆弧上一点，则cos ∠OBC 的值为（ ）A ．12 B ．32 C ．35D ．455.如图，角α的顶点为O ，它的一边在x 轴的正半轴上，另一边OA 上有一点P （3，4），则sin α= ．6.（庆阳中考）如图，菱形ABCD 的边长为10cm ，DE ⊥AB ，3sin 5A =，则这个菱形的面积= cm 2．7. 如图6，在Rt △ABC 中，∠C =90°，AC =8，∠A 的平分线AD =3316求 ∠B 的度数及边BC 、AB 的长.DABCCBA四、构造（直接三角形）法直角三角形是求解或运用三角函数的前提条件，故当题目中已知条件并非直角三角 形时，需通过添加辅助线构造直角三角形，然后求解，即化斜三角形为直角三角形． （1）化斜三角形为直角三角形例4 在△ABC 中，∠A =120°，AB =4，AC =2，则sinB 的值是( )(A )5714 (B )35 (C )217 (D )2114对应训练：1．已知：如图，△ABC 中，AB ＝9，BC ＝6，△ABC 的面积等于9，求sin B ．2．（重庆）如图，在Rt △ABC 中，∠BAC=90°，点D 在BC 边上，且△ABD 是等边三角形．若AB=2，求△ABC 的周长．（结果保留根号）（2）利用网格构造直角三角形例5 如图所示，△ABC 的顶点是正方形网格的格点，则sinA 的值为（ ）A ．12 B ．55 C ．1010D ．255 1．如图，△ABC 的顶点都在方格纸的格点上，则sin A =_______. 2．如图，A 、B 、C 三点在正方形网络线的交点处，若将ABC ∆绕着点A 逆时针旋转得到''B AC ∆，则'tan B 的值为（ ）A.41B.31C.21D.13．正方形网格中，AOB∠如图放置，则tan AOB∠的值是（）Ａ．5Ｂ．25Ｃ．12Ｄ．24. 如图，在边长为1的小正方形组成的网格中，ABC△的三个顶点在格点上，请按要求完成下列各题：（1）用签字笔．．．画AD∥BC（D为格点），连接CD；（2）线段CD的长为；（3）请你在ACD△的三个内角中任选一个锐角．．，若你所选的锐角是，则它所对应的正弦函数值是．（4）若E为BC中点，则tan∠CAE的值是 .三角函数与四边形：1．如图，四边形ABCD中，∠BAD=135°，∠BCD=90°，AB=BC=2，tan∠BDC=63．(1) 求BD的长；(2) 求AD的长．2．如图，在平行四边形ABCD中，过点A分别作AE⊥BC于点E，AF⊥CD于点F．（1）求证：∠BAE=∠DAF；（2）若AE=4，AF=245，3sin5BAE∠=，求CF的长．三角函数与圆：3.如图，DE是⊙O的直径，CE与⊙O相切，E为切点.连接CD交⊙O于点B，在EC上取一个点F，使EF=BF. （1）求证:BF是⊙O的切线;（2）若54Ccos=, DE=9，求BF的长．ABO。
三法教你求锐角三角函数值
三法教你求锐角三角函数值要求锐角的三角函数值，我们需要使用三角函数的定义和性质。
以下是三个法则，可以帮助我们求解锐角的三角函数值。
对于特殊的角度，我们可以通过直接代入角度值来求解三角函数值。
下面是一些常见的特殊角度及其对应的正弦、余弦和正切值：角度正弦值余弦值正切值0°01030°1/2√3/2√3/345°1/√21/√2160°√3/21/2√390°10无穷大法则二：半角公式通过半角公式，我们可以将求解锐角的三角函数值问题转化为求解特殊角的问题。
半角公式如下：sin(x/2) = ±√[(1 - cos(x)) / 2]cos(x/2) = ±√[(1 + cos(x)) / 2]tan(x/2) = sin(x) / (1 + cos(x))通过半角公式，我们可以将一个锐角x转化为一个特殊角度x/2，然后使用法则一中的特殊角度的三角函数值来求解。
法则三：倍角公式倍角公式可以将求解锐角的三角函数值问题转化为两倍角度或半角度的问题。
倍角公式如下：sin(2x) = 2sin(x)cos(x)cos(2x) = cos^2(x) - sin^2(x)tan(2x) = 2tan(x) / (1 - tan^2(x))通过倍角公式，我们可以将一个锐角x转化为两倍角度2x或者半角度x/2的问题，然后使用法则一中的特殊角度的三角函数值来求解。
举例：现在我们来求解一个锐角的三角函数值，假设锐角为45°。
根据法则一，我们知道sin(45°) = 1/√2，cos(45°) = 1/√2，tan(45°) = 1根据法则二，将角度45° 转化为半角度22.5°。
根据半角公式，我们可以得到sin(22.5°) = ±√[(1 - cos(45°))/2] = ±√[(1 - 1/√2)/2] ≈ ±0.382，cos(22.5°) = ±√[(1 + cos(45°))/2] =±√[(1 + 1/√2)/2] ≈ ±0.924，tan(22.5°) = sin(45°) / (1 + cos(45°)) = (1/√2) / (1 + 1/√2) ≈ 0.414根据倍角公式，将角度45° 转化为两倍角度90° 或者半角度22.5°。
(完整)锐角三角函数题型分类总结,推荐文档
锐角=角函数∙知识点一：钦角三角国数的≡x≡ 一、 锐角三角函数定义：在 RiAABC 中，ZC=9O 0, ZAS ZBX ZC 的对边分别为 a 、b 、c, 则ZA 的正弦可表示为；S ilLX= _________ JZA 的余弦可表示为CoSA= _________厶的正切:Tan-A= ________ ,它们弦称为ZA 的锐角三角函数2、取値范围—<¾inA< Co i⅛< __________ tanA>______1例如图所示，在RlA^C 中〉乙C=9Q° .例2.锐角三角函数束值；在 RtΔ,45C 中，ZC= 90° ,若 σ=9, B= 12,则 C= ___________SilL a l — _______ , COSU I f- __________ 9 taiL -l — __________ SSin^= _____ ； CQ ∖B= ____ ； tan.例3∙已知；如图，RI0∙∖M r 中，Z∏I ∖r =90o …⑷丄ZV 于出点，Zy=4, Hv=3• 求：SinZ732KxCOSZrVC?、tanZ∏IK .典型m ：类型一：直角三角形求值31 .已知 RtQUBC 中丿 ZC≡90Q 5 taπJ= ,5C≡1⅞ 求.4C ∖∙3 和 8田・② CoSJ = ® tan.4∙=第1题團① sin J( ) 软边 an 5【an 方=ZB 旳对边( )2. 如朗 OO 的半径θA = 16cm, OC 丄貝B 于C 点，an ΛAOC =-.求肋及OC 的长•3. 已知：0。
中，OC 丄朋于 C 点；J5= 16cm ； dnZA0C (1) 求OQ 的半径OA 的长及弦心距& (2) 求 COSz4 OC 及 ta∏ZJθC∙g4. 已知ZJ 是锐角，SitIW=—；求COSA > tan J 的值17对应ill 练二1. 在RtA^C 中7 ZC=90C 7 若5C=1, .15-√5 ；则Ianj 的值为5B.巫5C.丄 2D. 22.在ABC 中，ZC=90o ,S inA=- >那么tanA 的值等于( ).53G 4 C 3 c 4 A.-5 B.— 5 C. 一4D. 一 3类型二利用角度转化求值,2. 如團，直径为10的CU 经过点C(Oo)和点O(Qo)；与X 轴的正半釉交于点D, B 是》轴右侧圆弧上一点〉则C O SZ^C 的值为〈)C.-D-I1.已知；如图，RtZUBC 中，ZC= 90o ∙ Q 是Je 边上一点'DE 丄曲于E 点.^≡s⅛E3.如图，角α的顶点为0,它的一边在工轴的正半轴上J另一边Od上有一点Pd 4）,则3丄如團，菱形九5CD的边长为IQCm,DE1AB, SinJ =-,则遗个菱形的面积二.5.如國06＞是^iBC的外接圆,AD杲©O的直径，AC = I,则sin5的值是（7 \A. -B.-3 26.如图6,沿川E折蠡矩形纸片曲CQ ,c.£⅞□-4B=8, BC =10, AB=⅛ 则tan NEFC 的值为（A.- C.-57.如图7,在等腰直角三角形C中'ZC =90o , JC = 6, Z）为AC±—点，若tan ZDA.! = -,则-Q 的长为（）5A・近B・2 C・1 D・2√21 ^rIS.如图S,在RtA-LffC 中，Z090°,AOS, Ad的平分线/D=」一求ZB的度数及边BC. AB的长.类型三化斜三角形为直角三角形例1 如图，在A ABC中，Z A=30C,Z B=45% AC=2√3、求AB 的长.Cn T •353.正方形网格中, ZHoB 如團放乱则tanZJ （95的值是（√L例 2∙已知：如團，在 AABC 中，ZBAC=I 20° , ∠S=10, AC=5 .对应岷1.如图，在RlAABC 中,ZBAC=90=,点D 在BC 边上，且AABD 是等边三甬形.若.43=2, 求AABC 的周长•〈结果保留根号）2. 已知：如虱 AABC 中「3=9, BC=G,厶4恥的面枳尊于9丿求血^3. ABC 中,乙4=60° …4方=6 Cm , AC=4 Clrb 则A-45C 的面积是求:siik^ABC 的值..4 羽 CnrDllcm 2类型四；利用 构造直角三角形例1如图所示，AABC 的顶点杲正方形网格的格点，则SinA 的值为＜对应练习：1. ________________________________________________ 如图，AABC 的顶点都在方格纸的格点上，则Sir I A= ____________ .点厘逆吋针旋转得到AC8,则tanF 的值为D∙ 110D.IR特殊角的三角函数值锐角C30s45060。
求锐角三角函数的方法归类
求锐角三角函数的方法归类锐角三角函数是沟通代数与几何知识的桥梁，一直是中考命题的热点之一，从题型上看，选择题、填空题、解答题、综合题、压轴题，型型皆有，然面课本上的例题又比较少，使我们在求锐角三角函数值时无从下手，现将求锐角三角函数值常用的方法做个归纳：一、直接用锐角三角函数的定义例.如图,在△ABC中,AD⊥BC,垂足为点D.已知BC=14,AD=12，tan∠BAD=,求sinC的值,分析：已知条件中的tan∠BAD==,由AD=12，可得BD的值，问题中的sinC=,而AD=12是已知条件，所以我们只需求AD的值就可解了，这道题就是直接利用正弦值的定义求值。
解：∵在直角△ABD中，，∴BD=AD•tan∠BAD=12× =9. ∴CD=BC-BD=14-9=5.∴.∴．如果直接找不到边的值，该怎么办？在格点图形中，经常采用适当的方法求边例：如图,△ABC的三个顶点都在正方形网格的格点上,求sin∠ACB的值分析根据勾股定理，可得BC、AC的长，采用补全图形求出△ABC的面积，求出高AN，解直角三角形求出即可．解：由勾股定理可得：BC==5,AC==,∵∴∴AN=1二、巧用参数求锐角三角函数若已知两边的比值或一个三角函数值，而不能直接求出三角函数相应边的长，则可采用设参数的方法，先用参数表示出三角函数相应边的长，再根据三角函数公式计算它们的比值，即可得出三角函数值.例：已知a、b、c是的三边，且a、b、c满足,若5b-4c=0,求sinA+sinB的值。
分析：这是一道中档题，已知条件没有直接说明三角形的形状，所以先从入手，由勾股定理的逆定理判断出三角形为直角三角形，且斜边为c，再由5b-4c=0得出b,c之间的数量关系，此时用设参数的方法可以轻松得到三边之间的关系，问题就迎刃而解了。
三，用同角三角函数间的关系例.如图，在正方形网格中，求∠AOB的正切值.分析：连接AB，就可以根据勾股定理求出OA，OB，AB的长度，根据余弦定理就可以求出cos∠AOB，根据同角三角函数的关系，就可以求出，∠AOB的正切值．解：方法一：连接AB，根据勾股定理可以得到OA=OB=，AB=根据余弦定理可以得到：OA2+OB2-2OA•OB•cos∠AOB=AB2即：10+10-20cos∠AOB=8，解得cos∠AOB=．∴∠AOB的正切值．方法二：根据勾股定理可以得到OA=OB=，AB=过点A作AC⊥OB于C,=4=,可得AC=, sin∠AOB=,∴∠AOB的正切值．四、用等角来替代当直接用三角函数的定义求某锐角的三角函数值较为困难时，可通过相等角进行转换求值，这是一个非常重要的解题技巧。
专题 求锐角三角函数值的常用方法
专题 求锐角三角函数值的常用方法题型一 定义法直接根据定义求三角函数值,首先求出相应边的长度﹐然后代入三角函数公式计算即可. 类型1 直接定义法例1、如图，在Rt △ABC 中，∠C =90°，AC =12,BC =5 (1)求AB 的长.(2)求sinA ,cosA ,tanA ,sinB , cosB , tanB 的值.巩固练习1、如图,在△ABC 中,AB =15,AC =13,AD 上BC 于点D .CD =5时,求tan C 的值;2、如图,在Rt △ABC 中,∠C =90°,AB =4,AC =3,则cos B 的值为 。
类型2、网格中的三角函数例2、如图,在4×8的矩形网格中,每个小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上，则tan ∠ACB 的值为巩固练习1、正方形网格中，∠AOB 如图放置,则cos ∠AOB 的值为2、如图所示，∠AOB 是放置在正方形网格中的一个角，则cos ∠AOB ＝3、如图,在5×5的正方形网格中,每个小正方形的边长均为1,点A 、B 、C 都在格点上,则 cos ∠BAC 的值为 。
类型3、构造直角三角形例3、如图,在△ABC 中,AB =AC =13,BC =10, 则tan ∠BDE 的值等于巩固练习1、如图,在四边形ABCD 中,E ,F 分别是AB ,AD 的中点,若EF =2,BC =5,CD =3,则sinC 等于2、如图,在 Rt △ABC 中,∠C =90°,∠ABC =45° ,D 是AC 的中点,则sin ∠DBA =3、如图,在 Rt △BAD 中,延长斜边BD 到点C ,使DC =13BD ,连接AC ,若tanB =74,则tan ∠CAD 的值为 。
题型二 参数法若已知两边的比值或一个三角函数值,而不能直接求出三角函数相应边的长,则可采用设参数的方法﹐先用参数表示出三角函数相应边的长,再根据三角函数公式计算它们的比值,即可得出三角函数值.例3、在Rt △ABC 中,∠C =90°,AC =6，cosA =23 求 BC 的长，sinA ,tanA巩固练习1、在△ABC 中,∠C =90 , BC :CA =8:15,那么 sinA 等于 。
锐角三角函数 知识点总结+典型例题
AB= BC = 5，
sin A
4 5
，求
B
解：作BD⊥AC于点D， ∵ sin A 4
∴ BD AB sin A 5 4 4，
5
5
AD AB2 BD2 52 42 3.
，
5 A
5
C D
又∵ △ABC 为等腰三角形, BD⊥AC, ∴ AC=2AD=6，
∴S△ABC=AC×BD÷2=12.
斜边c
B ∠A的对边a
sin A=∠A斜的边对边 cos A=∠A斜的边邻边
A ∠A的邻边b C
tan A=∠∠AA的的对邻边边
锐角A的正弦、余弦、和正切统称∠A的锐角三角函数.
已知直角三角形两边求锐角三角函数的值
例 如图，在 Rt△ABC 中，∠C=90°，AB=10， BC=6，求sinA，cosA，tanA的值.
解：由勾股定理,得
B
因此 sin A BC = 6 = 3，
AB 10 5
10
6
A
C
cos A AC 8 4 , tan A BC = 6 = 3 .
AB 10 5
AC 8 4
已知一边及一锐角三角函数值求函数值
如图,在Rt△ABC中,∠C=90°,
求sinB的值.
sin A 5, AC=12.
13
B
解:在Rt △ABC中,
13 5
设AB=13x，BC=5x,;122=(13x)2.
C 12
解得x=1.所以AB=13，BC=5.
因此 sin B AC 12. AB 13
如图，在 △ABC中， △ABC 的面积.
正弦:
sin
A
A的对边 斜边
专题13 巧求锐角三角函数值（含答案）
第三章三角函数专题13 巧求锐角三角函数值知识解读在Rt△ABC中，∠C=90°，∠A的正弦sinA=错误!未找到引用源。
，∠A的余弦cos A=错误!未找到引用源。
，∠A的正切tanA=错误!未找到引用源。
，∠A的正弦、余弦、正切都是∠A的锐角三角函数.求锐角三角函数值的方法较多，常用的方法有：定义法、参数法、等角代换法、等比代换法、构造法.典例示范一、定义法当已知直角三角形的两条边时，可直接应用锐角三角函数的定义求锐角三角函数的值.例1 如图3-13-1，在Rt△ABC中，∠C=90°，AB=13，BC=5，则sinA的值为 .图3-13-1ABC【提示】题目中已知∠A的对边和斜边长，可直接应用正弦的定义求解.跟踪训练在Rt△ABC中，∠C=90°，BC=3，AC=4，那么cosA的值等于 .二、参数法锐角三角函数值实质上是直角三角形两边的比值，所以解题中有时需将三角函数转化为线段比，通过设定一个参数，并用含该参数的代数式表示出直角三角形各边的长，然后结合相关条件解决问题.例2在Rt△ABC中，∠C=90°，若tanA=错误!未找到引用源。
，则sinB的值为 .【提示】根据题意作出Rt△ABC，然后根据tanA=错误!未找到引用源。
，设一条直角边BC为5x，另一条直角边AC为12x，根据勾股定理求出另一条边AB的长度，然后根据三角函数的定义可求出sinB.跟踪训练1.在Rt△ABC中，∠C=90°，sinA=错误!未找到引用源。
，则tanB的值为( )A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
2.已知∠A=2，求错误!未找到引用源。
的值.【解答】3.求tan15°的值.【解答】三、等角代换法当一个锐角的三角函数不能直接求解或者锐角不在直角三角形中，可将该角通过等角转换到能够求出三角函数值的直角三角形中，利用“若两锐角相等，则此两角的三角函数值也相等”来求解.例3如图3-13-2，已知Rt △ABC 中，∠ACB =90°，CD 是斜边AB 上的中线，过点A 作AE ⊥CD ，AE 分别与CD ，CB 相交于点H ，E ，AH =2CH ，则sinB 的 .图3-13-2HABCDE【提示】根据∠ACB =90°，CD 是斜边AB 上的中线，可得出CD =BD ，则∠B =∠BCD ，再由AE ⊥CD ，可证明∠B =∠CAH ，由AH =2CH ，可得出CH :AC =1：错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
求锐角三角函数值的几种常用方法
一、定义法
当已知直角三角形的两条边，可直接运用锐角三角函数的定义求锐角三角函数的值． 例1 如图1，在△ABC 中，∠C =90°，AB =13，BC =5，则sin A 的值是( )
(A )
513 (B )1213 (C )512 (D )13
5 对应训练：
1．在Rt △ABC 中，∠ C ＝90°，若BC ＝1，AB =5，则tan A 的值为( )
A ．
55 B ．255 C ．1
2
D ．2 二、参数（方程思想）法
锐角三角函数值实质是直角三角形两边的比值，所以解题中有时需将三角函数转化为线
段比，通过设定一个参数，并用含该参数的代数式表示出直角三角形各边的长，然后结合相关条件解决问题． 例2 在△ABC 中，∠C =90°，如果tan A =
5
12
，那么sin B 的值是 ． 对应训练：
1．在△ABC 中，∠C =90°，sin A=
5
3
，那么tan A 的值等于（ ）. A ．35 B . 45 C . 34 D . 43
2．已知△ABC 中，
90=∠C ，3cosB=2， AC=52 ，则AB= ．
3．已知Rt △ABC 中，,12,4
3tan ,90==︒=∠BC A C 求AC 、AB 和cos B ．
4．已知：如图，⊙O 的半径OA ＝16cm ，OC ⊥AB 于C 点，⋅=∠4
3sin AOC
求：AB 及OC 的长．
D C B A O
y
x
第8题图
A
D E
C
B
F
三、等角代换法
当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时，可将此角通过等 角转换到能够求出三角函数值的直角三角形中，利用“两锐角相等，则三角函数值也相等” 来解决．
例3 在Rt △ABC 中，∠BCA =90°，CD 是AB 边上的中线，BC =5，CD =4，则cos ∠ACD 的值为 ． 对应训练
1.如图，O ⊙是ABC △的外接圆，AD 是O ⊙的直径，若O ⊙的半径为
3
2
，2AC =，则sin B 的值是（ ）A ．23 B ．32 C ．34 D ．4
3
2. 如图4，沿AE 折叠矩形纸片ABCD ，使点D 落在BC 边的点F 处．已知8AB =，10BC =，
AB=8,则tan EFC ∠的值为 ( )Ａ．34 Ｂ．43 Ｃ．35 Ｄ．45
3. 如图6，在等腰直角三角形ABC ∆中，90C ∠=︒，6AC =，D 为AC 上一点，若
1tan 5
DBA ∠= ，则AD 的长为( )
A ．2
B ．2
C ．1
D ．22
4． 如图，直径为10的⊙A 经过点(05)C ，和点(00)O ，，与x 轴的正半轴交于点D ，B 是y 轴右侧
圆弧上一点，则cos ∠OBC 的值为（ ）A ．
12 B ．32 C ．35
D ．45
5.如图，角α的顶点为O ，它的一边在x 轴的正半轴上，另一边OA 上有一点P （3，4），则
sin α= ．
6.（庆阳中考）如图，菱形ABCD 的边长为10cm ，DE ⊥AB ，3sin 5
A =，则这个菱形的面积= cm 2
．
7. 如图6，在Rt △ABC 中，∠C =90°，AC =8，∠A 的平分线
AD =
3
3
16求 ∠B 的度数及边BC 、AB 的长.
D
A
B
C
C
B
A
四、构造（直接三角形）法
直角三角形是求解或运用三角函数的前提条件，故当题目中已知条件并非直角三角 形时，需通过添加辅助线构造直角三角形，然后求解，即化斜三角形为直角三角形． （1）化斜三角形为直角三角形
例4 在△ABC 中，∠A =120°，AB =4，AC =2，则sinB 的值是( )
(A )
5714 (B )35 (C )217 (D )21
14
对应训练：
1．已知：如图，△ABC 中，AB ＝9，BC ＝6，△ABC 的面积等于9，求sin B ．
2．（重庆）如图，在Rt △ABC 中，∠BAC=90°，点D 在BC 边上，且△ABD 是等边三角形．若AB=2，求△ABC 的周长．（结果保留根号）
（2）利用网格构造直角三角形
例5 如图所示，△ABC 的顶点是正方形网格的格点，则sinA 的值为（ ）
A ．
12 B ．55 C ．1010
D ．25
5 对应练习：
1．如图，△ABC 的顶点都在方格纸的格点上，则sin A =_______. 2．如图，A 、B 、C 三点在正方形网络线的交点处，若将ABC ∆绕着点A 逆
时针旋转得到''B AC ∆，则'tan B 的值为（ ）
A.
41 B. 31 C.2
1 D. 1
3．正方形网格中，AOB ∠如图放置，则tan AOB ∠的值是（ ）
Ａ．
55 Ｂ．255
Ｃ．12 Ｄ．2
4. 如图，在边长为1的小正方形组成的网格中，ABC △的三个顶点在格点上，
请按要求完成下列各题：
（1） 用签字笔．．．画AD ∥BC （D 为格点），连接CD ；（2）线段CD 的长为 ； （3）请你在ACD △的三个内角中任选一个锐角．．，若你所选的锐角是 ，则它所对应的正弦函数值是 ．（4） 若E 为BC 中点，则tan ∠CAE 的值是 .
三角函数与四边形：
1．如图，四边形ABCD 中，∠BAD=135°，∠BCD=90°，AB=BC=2，
tan ∠BDC= 6
3． (1) 求BD 的长；(2) 求AD 的长．
2．如图，在平行四边形ABCD 中，过点A 分别作AE ⊥BC 于点E ，AF ⊥CD 于点F ． （1）求证：∠BAE =∠DAF ；（2）若AE =4，AF =
245，3
sin 5
BAE ∠=，求CF 的长．
三角函数与圆：
3.如图，DE 是⊙O 的直径，CE 与⊙O 相切，E 为切点.连接CD 交⊙O 于点B ，在EC 上取一个点F ，使EF=BF.
（1）求证:BF 是⊙O 的切线; （2）若5
4
C cos =
, DE =9，求BF 的长． A
B
O。