函数周期性公式大总结
函数的对称性与周期性(归纳总结)

函数的对称性与周期性(归纳总结)一、函数对称性:1.2.3.4.5.6.7.8.f(a+x)=f(a-x)==>f(x)关于x=a对称f(a+x)=f(b-x)==>f(x)关于x=(a+b)/2对称f(a+x)=-f(a-x)==>f(x)关于点(a,0)对称f(a+x)=-f(a-x)+2b==>f(x)关于点(a,b)对称f(a+x)=-f(b-x)+c==>f(x)关于点[(a+b)/2,c/2]对称y=f(x)与y=f(-x)关于x=0对称y=f(x)与y=-f(x)关于y=0对称y=f(x)与y=-f(-x)关于点(0,0)对称例1:证明函数y=f(a+x)与y=f(b-x)关于x=(b-a)/2对称。
【解析】求两个不同函数的对称轴,用设点和对称原理作解。
证明:假设任意一点P(m,n)在函数y=f(a+x)上,令关于x=t的对称点Q(2tm,n),那么n=f(a+m)=f[b(2tm)] ∴b2t=a,==>t=(b-a)/2,即证得对称轴为x=(b-a)/2.例2:证明函数y=f(a-x)与y=f(xb)关于x=(a+b)/2对称。
证明:假设任意一点P(m,n)在函数y=f(a-x)上,令关于x=t的对称点Q(2tm,n),那么n=f(a-m)=f[(2tm)b] ∴2t-b=a,==>t=(a+b)/2,即证得对称轴为x=(a+b)/2.二、函数的周期性令a,b均不为零,若:1、函数y=f(x)存在f(x)=f(x+a)==>函数最小正周期T=|a|2、函数y=f(x)存在f(a+x)=f(b+x)==>函数最小正周期T=|b-a|3、函数y=f(x)存在f(x)=-f(x+a)==>函数最小正周期T=|2a|4、函数y=f(x)存在f(x+a)=1/f(x)==>函数最小正周期T=|2a|5、函数y=f(x)存在f(x+a)=[f(x)+1]/[1f(x)]==>函数最小正周期T=|4a|这里只对第2~5点进行解析。
函数周期性结论总结

函数周期性结论总结函数周期性是数学中的一个重要概念,它在解决各种实际问题中起到了重要的作用。
在本文中,我将对函数周期性的结论做一个总结,以便对读者有更清晰的认识。
以下是我对函数周期性的总结:1. 周期性定义在数学中,一个函数被称为具有周期性,当且仅当存在一个正数T,使得对于每一个x值都有f(x+T) = f(x)成立。
其中,T被称为函数的周期。
2. 常见函数的周期性2.1 三角函数的周期性三角函数是一类具有周期性的函数。
常见的三角函数有正弦函数和余弦函数。
正弦函数的周期为2π,即sin(x+2π) = sin(x);余弦函数的周期也为2π,即cos(x+2π) = cos(x)。
这意味着在一个周期内,正弦函数和余弦函数的值会周期性地重复。
2.2 指数函数的周期性指数函数也具有周期性。
以自然对数为底的指数函数具有周期为2πi的形式,即e^(x+2πi) = e^x。
其中,i是虚数单位。
这意味着在一个周期内,指数函数的值也会周期性地重复。
3. 周期性性质3.1 零点的周期性如果一个函数的周期为T,那么对于任意一个零点x0,它的周期性可以表示为x0 + Tn,其中n为任意整数。
这意味着函数的零点也具有周期性,每隔一个周期就会出现一个零点。
3.2 值域的周期性如果一个函数具有周期T,那么对于函数值f(x)来说,它的周期性可以表示为f(x+T) = f(x)。
这意味着函数的值域也具有周期性,每隔一个周期就会重复一次。
4. 应用举例函数周期性在各个领域都有广泛的应用。
举几个例子来说明:4.1 电力系统在电力系统中,交流电的变化是具有周期性的。
电压和电流随着时间呈周期性变化,周期性的特点使得电力系统能够稳定地运行。
4.2 信号处理在信号处理领域,周期性信号的分析和处理是很重要的。
通过对周期信号的分析,可以准确地获取信号的频率和振幅等信息。
4.3 声音与音乐声音和音乐是具有周期性的。
乐器的音调是具有周期性的,音乐也是以一定的节拍和律动来展现周期性。
周期性函数
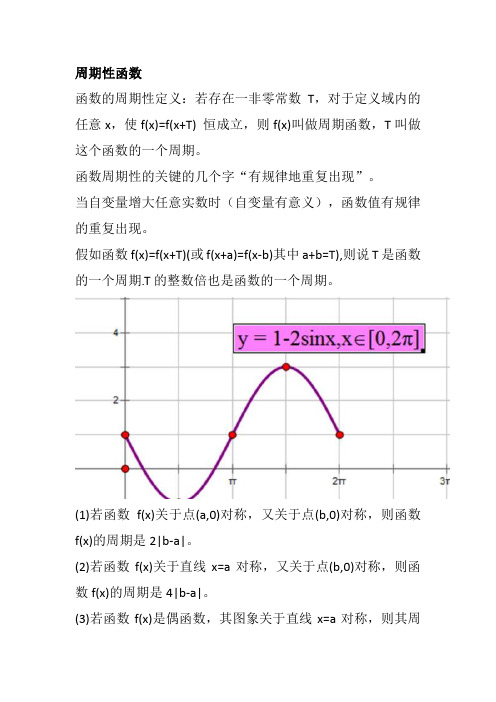
周期性函数函数的周期性定义:若存在一非零常数T,对于定义域内的任意x,使f(x)=f(x+T) 恒成立,则f(x)叫做周期函数,T叫做这个函数的一个周期。
函数周期性的关键的几个字“有规律地重复出现”。
当自变量增大任意实数时(自变量有意义),函数值有规律的重复出现。
假如函数f(x)=f(x+T)(或f(x+a)=f(x-b)其中a+b=T),则说T是函数的一个周期.T的整数倍也是函数的一个周期。
(1)若函数f(x)关于点(a,0)对称,又关于点(b,0)对称,则函数f(x)的周期是2|b-a|。
(2)若函数f(x)关于直线x=a对称,又关于点(b,0)对称,则函数f(x)的周期是4|b-a|。
(3)若函数f(x)是偶函数,其图象关于直线x=a对称,则其周期为2a。
(4)若函数f(x)是奇函数,其图象关于直线x=a对称,则其周期为4a。
根据函数的周期性,可以由函数局部的性质得到函数的整体性质,即周期性与奇偶性都具有将未知区间上的问题转化到已知区间的功能.在解决具体问题时,要注意结论:若T是函数的周期,则kT(k∈Z且k≠0)也是函数的周期。
函数周期性公式大总结:f(x+a)=-f(x)。
那么f(x+2a)=f=-f(x+a)=-[-f(x)]=f(x)。
所以f(x)是以2a为周期的周期函数。
f(x+a)=1/f(x)。
那么f(x+2a)=f=1/f(x+a)=1/[1/f(x)]=f(x)。
所以f(x)是以2a为周期的周期函数。
f(x+a)=-1/f(x)。
那么f(x+2a)=f=-1/f(x+a)=1/[-1/f(x)]=f(x)。
所以f(x)是以2a为周期的周期函数。
周期公式sinx的函数周期公式T=2π,sinx是正弦函数,周期是2π。
cosx的函数周期公式T=2π,cosx是余弦函数,周期2π。
tanx和cotx的函数周期公式T=π,tanx和cotx分别是正切和余切。
secx和cscx的函数周期公式T=2π,secx和cscx是正割和余割。
函数周期性公式大总结

函数周期性公式大总结首先,我们将讨论三角函数的周期性公式。
三角函数是周期函数的重要例子,其中最常见的是正弦函数和余弦函数。
正弦函数的周期为2π,可以表示为sin(x+2πn),其中n为整数。
同样,余弦函数的周期也为2π,可以表示为cos(x+2πn)。
因此,正弦函数和余弦函数都以2π的周期性在函数图像上循环。
接下来,我们来讨论其他函数的周期性公式。
一些常见的周期函数包括矩形波、方波和三角波函数。
矩形波函数的周期为T,可以表示为rect(x/T),其中rect为矩形波函数。
方波函数的周期也为T,可以表示为square(x/T)。
而三角波函数的周期为2T,可以表示为sawtooth(x/2T)。
除了这些常见的周期函数外,我们还可以通过对函数进行平移、伸缩和反转等操作来获得不同的周期性函数。
通过平移操作,我们可以将函数沿x轴平移k个单位,从而改变其周期。
例如,对于函数f(x),如果我们将其平移k个单位,则新的函数可以表示为f(x+k)。
同样地,通过伸缩操作,我们可以改变函数的周期。
对于函数f(x),如果我们将其沿x轴伸缩比例为a,则新的函数可以表示为f(ax)。
最后,通过反转操作,我们可以改变函数的周期。
对于函数f(x),如果我们反转它的原点,则新的函数可以表示为f(-x)。
此外,还有一些特殊的周期函数,例如斜坡函数和周期单位脉冲函数。
斜坡函数的周期为T,可以表示为ramp(x/T)。
周期单位脉冲函数是由一系列重复的单位脉冲构成的周期函数,可以表示为p(x/T),其中p为单位脉冲函数。
最后,我们需要注意的是,在实际应用中,函数的周期性可能不仅仅是简单的周期函数或方法所能描述的。
一些函数可能具有复杂的周期性,例如混沌函数和周期分形函数等。
这些函数的周期特性往往需要使用更高级的方法来进行分析。
总结起来,函数周期性公式是数学中非常重要的概念。
在本文中,我们总结了一些常见的函数周期性公式,包括三角函数的周期性、其他周期函数的周期性以及函数的平移、伸缩和反转等操作。
函数周期知识点总结

函数周期知识点总结一、函数的周期性函数的周期性是指函数在特定区间内具有重复性的性质。
如果函数在一个区间内满足f(x+T)=f(x),其中T为正数,则称函数f(x)在该区间上有周期T,T称为函数f(x)的周期。
函数的周期性是函数中非常重要的一种性质,对于周期函数而言,其周期性是其定义的本质。
二、周期函数的性质1. 周期函数的定义周期函数是指函数的取值在每个周期内具有重复性。
周期函数的周期是指函数在一个区间内具有重复性。
设f(x)是定义在一定区间上的函数,如果存在正数T,使得任意x∈[a,a+T],都有f(x+T)=f(x),则称函数f(x)为周期函数,T为周期。
周期函数的周期一般是不唯一的。
2. 周期函数的图像特点周期函数的图像表现出在一个周期内具有重复性的特点。
周期函数的图像通常是具有规律的波动,在一定周期内呈现出反复的形状。
3. 周期函数的基本性质周期函数在一个周期内具有相同的性质,包括最大值、最小值、零点等。
周期函数还具有周期平移、镜像对称等性质。
周期函数的和、差、积、商也是周期函数。
4. 周期函数的分类周期函数根据周期的不同可以分为正弦函数、余弦函数、正切函数、余切函数等等。
根据周期的形式还可以分为奇函数和偶函数。
5. 周期函数的应用周期函数在自然界和各种科学领域有着非常广泛的应用,如物理学、工程学、生物学等等。
周期函数的研究对于理解自然规律和解决实际问题具有重要的意义。
三、常见周期函数1. 正弦函数正弦函数是最基本的周期函数之一。
其函数表达式为y=Asin(Bx+C)+D,其中A,B,C,D为常数,A为振幅,B为角频率,C为相位差,D为垂直位移。
正弦函数的图像是一条连续的曲线,具有周期性。
2. 余弦函数余弦函数也是最基本的周期函数之一。
其函数表达式为y=Acos(Bx+C)+D,其中A,B,C,D为常数,A为振幅,B为角频率,C为相位差,D为垂直位移。
3. 正切函数正切函数的函数表达式为y=A tan(Bx+C)+D,其中A,B,C,D为常数,A为振幅,B为角频率,C为相位差,D为垂直位移。
周期函数公式大全推导

周期函数公式大全推导2019-11-25 16:56:26文/张敏函数周期性公式及推导:f(x+a)=-f(x)周期为2a。
证明过程:因为f(x+a)=-f(x),且f(x)=-f(x-a),所以f(x+a)=f(x-a),即f(x+2a)=f(x),所以周期是2a。
公式及推导f(x+a)=-f(x)那么f(x+2a)=f[(x+a)+a]=-f(x+a)=-[-f(x)]=f(x)所以f(x)是以2a为周期的周期函数。
f(x+a)=1/f(x)那么f(x+2a)=f[(x+a)+a]=1/f(x+a)=1/[1/f(x)]=f(x)所以f(x)是以2a为周期的周期函数。
f(x+a)=-1/f(x)那么f(x+2a)=f[(x+a)+a]=-1/f(x+a)=1/[-1/f(x)]=f(x)所以f(x)是以2a为周期的周期函数。
所以得到这三个结论。
函数的周期性设函数f(x)在区间X上有定义,若存在一一个与x无关的正数T,使对于任一x∈X,恒有f(x+T)=f(x)则称f(x)是以T为周期的周期函数,把满足上式的最小正数T称为函数f(x)的周期。
二、周期函数的运算性质:①若T为f(x)的周期,则f(ax+b)的周期为T/al。
②若f(x),g(x)均是以T为周期的函数,则f(X)+g(X)也是以T为周期的函数。
③若f(x),g(x)分别是以T1,T2,T1≠T2为周期的函数,则f(x)+g(x)是以T1,T2的最小公倍数为周期的函数。
周期公式sinx的函数周期公式T=2π,sinx是正弦函数,周期是2πcosx的函数周期公式T=2π,cosx是余弦函数,周期2π。
tanx和cotx的函数周期公式T=π,tanx和cotx分别是正切和余切。
secx和cscx的函数周期公式T=2π,secx和cscx是正割和余割。
函数的周期、对称公式大总结

函数的周期、对称公式一、函数的周期性(识别方法:看括号里面的x 系数相同为周期)()()()..1a b x f b x f a x f -+=+的周期为,则若 ()()().2.2a x f x f a x f 的周期为,则若-=+ ()()().21.3a x f x f a x f 的周期为,则若=+()()().21.4a x f x f a x f 的周期为,则若-=+()()()().211.5a x f x f x f a x f 的周期为,则若+-=+()()()().411.6a x f x f x f a x f 的周期为,则若-+=+()()()().62.7a x f x f a x f a x f 的周期为,则若-+=+二、函数的轴对称(识别方法:看括号里面的x 系数相反为对称,若f()外的系数相同则为轴对称,简称对称轴)()()()()()()()()()()()()()().2.4.2.3..2.22.1对称的图象关于直线对称的图象关于直线对称的图象关于直线对称图象关于直线若a x x f y x a f x f a x x f y x a f x f a x x f y x a f x a f b a x b x a x x f y x b f x a f ==⇔+=-==⇔-===⇔-=++=-++==⇔-=+三、函数的点对称(识别方法:看括号里面的x 系数相反为对称,若f()外的系数相反则为点对称,简称对称中心)()()()()()()()()()()()()()()()()()()().0,.5.,22.4.,22.3.,2.2.,22.1对称的图象关于点对称的图象关于点对称的图象关于点对称的图象关于点对称图象关于点若a x f y x a f x a f b a x f y b x a f x f b a x f y b x a f x f b a x f y b x a f x a f c b a x f y c x b f x a f =⇔--=+=⇔=++-=⇔=-+=⇔=-++⎪⎭⎫⎝⎛+=⇔=-++四、奇偶性的拓展()().)0,()()(,.2;.1对称关于件是是奇函数的充分必要条对于任意对称关于件是是偶函数的充分必要条,对于任意a x f y a x f x a x x f y a x f x =+==+五、对称与周期的关系()()().2.1a b x f b x a x x f -==的周期为对称,则、关于直线若函数两线对称型()()()()().20,0,.2a b x f b a x f -的周期为对称,则、点关于点若函数两点对称型()()()().40,.3a b x f b a x x f -=的周期为对称,则及点关于直线若函数一线一点对称型六、对称与周期常用的小结论.2)()()(.1对称还关于对称,那么关于直线,且的周期为若Ta x x f a x x f T x f ±==().02)(0,)()(.2对称,还关于对称,那么关于点,且的周期为若⎪⎭⎫ ⎝⎛±T a x f a x f T x f(在已有的对称轴,对称中心上加减半个周期即可得到新的对称轴与对称中心)七、三种关系的转化(已知其一必写其二,总有一个能用于解题)()()()为偶函数对称关于直线已知a x f x a f x a f a x x f +⇔-=+⇔=)(.1。
函数周期性公式大总结

(1)F(x + a)=-f(x)周期为2A。
在本文中,我们证明(F + x)= 2a-f(x)= F-X(F-X)。
(2)SiNx的功能周期公式为t = 2π。
SiNx是正弦函数,周期为2π(3)cosx的函数周期公式为t = 2π,cosx为余弦函数,周期为2π。
(4)TaNx和Cotx的周期公式为t =π,TaNx和Cotx分别为切线和Cotx(5)secx和CSCX的周期公式为t = 2π,secx和CSCX为secx和余割。
扩展数据:以下方法分为几个步骤(1)确定F(x)的域是否有界;(2)根据函数周期的定义,我们可以知道非零实数T在关系f (x + T)= f(x)中与X无关,因此可以求解方程f(x)-f(x)= 0,如果我们可以求解独立于X的非零常数t,则可以得出结论:函数f(x)是周期函数,如果不存在t,则f (x)是非周期性函数。
(3)通常用相反的证明方法证明。
(如果f(x)是周期函数,则推论矛盾,因此f(x)是非周期函数。
示例:证明f(x)= ax + B(a≠0)是一个非周期函数。
证明如果f(x)= ax + B是周期函数,则存在t(≠0),使其成立。
A(x + T)+ B = ax + Bax +在AX = 0,在at = 0且a≠0,t = 0与t≠0矛盾的情况下,﹤f(x)是一个非周期函数。
示例:证明f(x)= ax + B是一个非周期函数。
证明:如果f(x)是周期函数,则必须有一个t(≠0)对,并且必须有(x + T)= f(x)。
当x = 0时,f(x)= 0,但是x + T≠0,νf(x + T)= 1,νf(x + T)≠f(x)且f(x + T)= f (x)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
竭诚为您提供优质文档/双击可除函数周期性公式大总结
篇一:函数周期性结论总结
函数周期性结论总结
①f(x+a)=-f(x)T=2a
②f(x+a)=±1T=2af(x)
③f(x+a)=f(x+b)T=|a-b|证明:令x=x-b得
f(x-b+a)=f(x-b+b)f(x-b+a)=f(x)根据公式
f(x)=f(x+T)=f(x+nT)得T=-b+a即a-b
④f(x)为偶函数,且关于直线x=a对称,T=2a
证明:f(x+2a)=f(-x)=f(x)
证明:因为偶函数,所以f(-x)=f(x)因为关于x=a对称所以f(a+x)=f(a-x)(对称性质)设x=x+a所以
f(x+2a)=f(x)所以周期T=2a)⑤f(x)为奇函数,且关于直线x=a对称,T=4a
证明:f(x+2a)=f(-x)=-f(x)根据①可知T=2·2a=4a
证明:由于图像关于直线x=a对称、所以f(a+x)=f(a-x)令x=x+a得:f(x+2a)=f(-x)又f(x)=-f(-x)故f(x)=-f(x+2a)代换x=x+2a得:
f(x+2a)=-f(x+4a)即得f(x)=f(x+4a)于是函数f(x)的周期为4a
⑥f(x)=f(x+a)+f(x-a)有三层函数,用递推的方法来证明。
f(x+a)=f(x+2a)+f(x)
f(x+2a)=-f(x-a)换元:令x-a=t那么x=a+t
f(t+3a)=-f(t)根据①可知T=6a
⑦f(x)关于直线x=a,直线x=b对称,T=2|a-b|
证明:f(a+x)=f(a-x)
f(b+x)=f(b-x)
f(2b-x)=f(x)假设
a>b(当然假设a<b也可以同理证明出)
T=2(a-b)
现在只需证明f(x+2a-2b)=f(x)即可
⑧f(x)的图像关于(a,0)(b,0)对称,T=2a-2b(a>
b)f(x+2a-2b)=f[a+(x+a-2b)]关于直线x=a对称
=f[a-(x+a-2b)]关于直线x=b对称=f(2b-x)=f(x) 证明:根据奇函数对称中心可知:f(a+x)=-f(a-x)
f(2b-x)=-f(x)f(x+2a-2b)
=f[a+(x+a-2b)]
=-f[a-(x+a-2b)]
=-f(2b-x)
=f(x)
篇二:函数周期公式
主要知识:
1.周期函数:对于f(x)定义域内的每一个x,都存在
非零常数T,使得f(x?T)?f(x)恒成立,则称函数f(x)具有
周期性,T叫做f(x)的一个周期,则kT(k?Z,k?0)也是f(x)的周期,所有周期中的最小正数叫f(x)的最小正周期.2.几种特殊的抽象函数:具有周期性的抽象函数:
函数y?f?x?满足对定义域内任一实数x(其中a为常数),
(1)f?x??f?x?a?,则y?f?x?是以T?a为周期的周期函数;
(2)f?x?af?x?,则f?x?是以T?2a为周期的周期函数;
(3)f?x?a1,则f?x?是以T?2a为周期的周期函数;
fx(4)f?x?a??f?x?b?,则f?x?是以T?a?b为周期的周期函数;
以上(1)-(4)比较常见,其余几种题目中出现频率
不如前四种高,并且经常以数形结合的方式求解。
(5)函数y?f(x)满足f(a?x)?f(a?x)(a?0),若f(x)为
奇函数,则其周期为T?4a,若f(x)为偶函数,则其周期为T?2a.
(6)函数y?f(x)?x?R?的图象关于直线x?a和x?b?a?b?
都对称,则函数f(x)是以2?b?a?为周期的周期函数;
(7)函数y?f(x)?x?R?的图象关于两点A?a,0?、
b?b,0??a?b?都对称,则函数f(x)是以2?b?a?为周期的周期函数;
(8)函数y?f(x)?x?R?的图象关于A?a,0?和直线x?b?a?b?都对称,则函数f(x)是以4?b?a?为周期的周期函数;
(9)有些题目中可能用到构造,类似于常数列。
(二)主要方法:
1.判断一个函数是否是周期函数要抓住两点:
一是对定义域中任意的x恒有f(x?T)?f(x);
二是能找到适合这一等式的非零常数T,
2.解决周期函数问题时,要注意灵活运用以上结论,同时要重视数形结合思想方法的运用,还要注意根据所要解决的问题的特征来进行赋值.
证明举例:若函数f(x)有一条对称轴x=a和一个对称中心(b,0)
(a ?f(x)?f(2a?x)??f[2b?(2a?x)]??f[2(b?a)?x] ??f[2a?2(b?a)?x]??f[2(2a?b)?x]
?f[2b?2(2a?b)?x]?f[4(b?a)?x],周期为4(b?a).
举例:y=sinx,等.
篇三:函数的周期性
抽象函数的周期类型
抽象函数的周期没有具体公式,它需要掌握一定的规律,记住一些抽象函数的格式。
本文列出几种常见的抽象函数的周期类型,供大家参考(以下x取定义域内的任意值且a、b、T为非零常数,a≠b)。
1.f(x)?f(x?T)型
f(x)的周期为T。
释义:对x取定义域内的每一个值时,都有f(x?T)?f(x),则
f(x)为周期
函数,T叫函数f(x)的周期。
2.f(x?a)?f(x?b)型
f(x)的周期为|b?a|。
释义:
f(x?a)?f(x?b)?f(x)?f(x?b?a)。
3.f(x?a)??f(x)型f(x)的周期为2a。
释义:
f(x?2a)?f[(x?a)?a]??f(x?a)??[?f(x)]
?f(x)
例.设f(x)是R上的奇函数,f(x?2)??f(x),当0?x?1时,f(x)?x,则
f(20XX5.)等于()
A.0.5
b.-0.5
c.1.5
D.-1.5
.)=解:此题符合f(x?a)??f(x)型,所以f(x)是以4
为周期的函数。
f(20XX5
f(15.?501×
4)?f(15.)?f(?05.?2)??f(?05.)?f(05.)?05.,选A。
4.f(x?a)??
1
型f(x)
f(x)的周期为2a。
释义:f(x?2a)?f[(x?a)?a]??
1
??
f(x?a)
1
?f(x)。
1?
f(x)
5.f(x?a)?
1
型f(x)
f(x)的周期为2a。
释义:f(x?2a)?f[(x?a)?a]?
1
?
f(x?a)
1
?f(x)。
f(x)
6.f(x?a)?
1?f(x)
型
1?f(x)
f(x)的周期为4a。
释义:f(x?2a)?f[(x?a)?a]? 1?f(x?a)
1?f(x?a)
1?1?
?
1?1?
1?f(x)
1f(x)??,f(x)f(x)
1
??
f(x?2a)
1
?f(x)。
1?
f(x)
∴f(x?4a)?f[(x?2a)?2a]??。
