广东省部分地区2020届高三上学期考试数学理试题分类汇编：圆锥曲线

合集下载

广东省部分地区2020届高三上学期考试数学理试题分类汇编：三角函数

C.
D.
2
2
2
2
12 、（深圳市宝安区 2020 届高三上学期调研考试）已知 sin(θ − π ) = 1 ，且 θ ∈ (0, π ) ，则
62
2
cos(θ − π ) = ( ) 3
A．0
B． 1 2
C．1
D． 3 2
13、（湛江市 2020 届高三上学期调研考试）将函数 g（x）＝cos2x 一 sin 2x 图象上的所有点的横坐
f
(
x
)
在
0,
2π 15
上单调递增
C.
若
f
(
x
)
在
[0,
2π]
有且仅有
4
个零点，则
ω
的范围是
15 8
,
19 8
D.
若
f
( x) 图像关于 x
=
π 4
对称，且在
π 18
,
5π 36
单调，则
ω
的最大值为 9
15、（珠海市
2020
届高三上学期期末考试）已知
x
∈ ( 0,
π ] ，关于
x
的方程
2 sin
（1）若 a = 2 3 ，求 B ；（2）若 a = 2c ，求 ∆ABC 的面积。
2、（东莞市 2020 届高三上学期调研考试）如图 1，在 ∆ABC 中，内角 A, B, C 所对的边分别为 a, b, c ，且 2a cosC − c =2b ．
（1）求角 A 的大小；（2）若 ∠ABC = π ， AC 边上的中线 BD 的长为 7 ，求 ∆ABC 的面积．

2020高考—圆锥曲线(解答+答案)

2020年高考——圆锥曲线1.(20全国Ⅰ文21)（12分）已知A 、B 分别为椭圆E ：2221x y a+=（a >1）的左、右顶点，G 为E 的上顶点，8AG GB ⋅=，P 为直线x =6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点.2.(20全国Ⅰ理20)（12分）已知A 、B 分别为椭圆E ：2221x y a+=（a >1）的左、右顶点，G 为E 的上顶点，8AG GB ⋅=，P 为直线x =6上的动点，PA 与E 的另一交点为C ，PB 与E 的另一交点为D ．（1）求E 的方程；（2）证明：直线CD 过定点.3.（20全国Ⅱ文19）(12 分)已知椭圆C 1：22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴重直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |．（1）求C 1的离心率；（2）若C 1的四个顶点到C 2的准线距离之和为12，求C 1与C 2的标准方程．4.（20全国Ⅱ理19）（12分）已知椭圆C 1：22221x y a b+=(a >b >0)的右焦点F 与抛物线C 2的焦点重合，C 1的中心与C 2的顶点重合．过F 且与x 轴垂直的直线交C 1于A ，B 两点，交C 2于C ，D 两点，且|CD |=43|AB |．（1）求C 1的离心率；（2）设M 是C 1与C 2的公共点，若|MF |=5，求C 1与C 2的标准方程．5.（20全国Ⅲ文21）（12分）已知椭圆222:1(05)25x y C m m +=<<，A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线6x =上，且||||BP BQ =，BP BQ ⊥，求APQ △的面积．6.（20全国Ⅲ理20）（12分）已知椭圆222:1(05)25x y C m m+=<<，A ，B 分别为C 的左、右顶点．（1）求C 的方程；（2）若点P 在C 上，点Q 在直线6x =上，且||||BP BQ =，BP BQ ⊥，求APQ △的面积．7.（20新高考Ⅰ22）（12分）已知椭圆C ：22221(0)x y a b a b +=>>的离心率为2，且过点A （2，1）．（1）求C 的方程：（2）点M ，N 在C 上，且AM ⊥AN ，AD ⊥MN ，D 为垂足．证明：存在定点Q ，使得|DQ |为定值．8.(20天津18)（本小题满分15分）已知椭圆22221(0)x y a b a b+=>>的一个顶点为(0,3)A -，右焦点为F ，且||||OA OF =，其中O 为原点．（Ⅰ）求椭圆的方程；（Ⅱ）已知点C 满足3OC OF =，点B 在椭圆上（B 异于椭圆的顶点），直线AB 与以C 为圆心的圆相切于点P ，且P 为线段AB 的中点．求直线AB 的方程．9.(20浙江21)（本题满分15分）如图，已知椭圆221:12x C y +=，抛物线22:2(0)C y px p =>，点A 是椭圆1C 与抛物线2C 的交点，过点A 的直线l 交椭圆1C 于点B ，交抛物线2C 于点M （B ，M 不同于A ）．（Ⅰ）若116p =，求抛物线2C 的焦点坐标；（Ⅱ）若存在不过原点的直线l 使M 为线段AB 的中点，求p 的最大值．10.（20江苏18）（本小题满分16分）在平面直角坐标系xOy 中，已知椭圆22:143x y E +=的左、右焦点分别为F 1，F 2，点A在椭圆E 上且在第一象限内，AF 2⊥F 1F 2，直线AF 1与椭圆E 相交于另一点B ．（1）求12AF F △的周长；（2）在x 轴上任取一点P ，直线AP 与椭圆E 的右准线相交于点Q ，求OP QP ⋅的最小值；（3）设点M 在椭圆E 上，记OAB △与MAB △的面积分别为S 1，S 2，若213S S =，求点M 的坐标．11.(20北京20)（本小题15分）已知椭圆2222:1x y C a b+=过点(2,1)A --，且2a b =．（Ⅰ）求椭圆C 的方程：（Ⅱ）过点(4,0)B -的直线l 交椭圆C 于点,M N ,直线,MA NA 分别交直线4x =-于点,P Q ．求||||PB BQ 的值．参考答案：1．解：（1）由题设得(,0),(,0),(0,1)A a B a G -．则(,1)AG a =，(,1)GB a =-．由8AG GB ⋅=得218a -=，即3a =．所以E 的方程为2219x y +=．（2）设1122(,),(,),(6,)C x y D x y P t ．若0t ≠，设直线CD 的方程为x my n =+，由题意可知33n -<<．由于直线PA 的方程为(3)9t y x =+，所以11(3)9ty x =+．直线PB 的方程为(3)3t y x =-，所以22(3)3ty x =-．可得12213(3)(3)y x y x -=+．由于222219x y +=，故2222(3)(3)9x x y +-=-，可得121227(3)(3)y y x x =-++，即221212(27)(3)()(3)0m y y m n y y n ++++++=．①将x my n =+代入2219xy +=得222(9)290m y mny n +++-=．所以212122229,99mn n y y y y m m -+=-=-++．代入①式得2222(27)(9)2(3)(3)(9)0m n m n mn n m +--++++=．解得3n =-（舍去），32n =．故直线CD 的方程为32x my =+，即直线CD 过定点3(,0)2．若0t =，则直线CD 的方程为0y =，过点3(,0)2．综上，直线CD 过定点3(,0)2．2．解：（1）由题设得A （–a ，0），B （a ，0），G （0，1）.则(,1)AG a =，GB =（a ，–1）.由AG GB ⋅=8得a 2–1=8，即a =3.所以E 的方程为29x +y 2=1．（2）设C （x 1，y 1），D （x 2，y 2），P （6，t ）.若t ≠0，设直线CD 的方程为x =my +n ，由题意可知–3<n <3. 由于直线PA 的方程为y =9t （x +3），所以y 1=9t （x 1+3）.直线PB 的方程为y =3t （x –3），所以y 2=3t（x 2–3）.可得3y 1（x 2–3）=y 2（x 1+3）.由于222219x y +=，故2222(3)(3)9x x y +-=-，可得121227(3)(3)y y x x =-++，即221212(27)(3)()(3)0.m y y m n y y n ++++++=①将x my n =+代入2219xy +=得222(9)290.m y mny n +++-=所以12229mn y y m +=-+，212299n y y m -=+．代入①式得2222(27)(9)2(3)(3)(9)0.m n m n mn n m +--++++= 解得n =–3（含去），n =32.故直线CD 的方程为3=2x my +，即直线CD 过定点（32，0）．若t =0，则直线CD 的方程为y =0，过点（32，0）.综上，直线CD 过定点（32，0）.3．解：（1）由已知可设2C 的方程为24y cx =，其中c =不妨设,A C 在第一象限，由题设得,A B 的纵坐标分别为2b a ，2b a -；,C D 的纵坐标分别为2c ，2c -，故22||b AB a=，||4CD c =.由4||||3CD AB =得2843b c a=，即2322()c c a a ⨯=-，解得2c a =-（舍去），12c a =.所以1C 的离心率为12.（2）由（1）知2a c =，b =，故22122:143x y C c c+=，所以1C 的四个顶点坐标分别为(2,0)c ，(2,0)c -，)，(0,)，2C 的准线为x c =-. 由已知得312c c c c +++=，即2c =.所以1C 的标准方程为2211612x y +=，2C 的标准方程为28y x =.4．解：（1）由已知可设2C 的方程为24y cx =，其中c =不妨设,A C 在第一象限，由题设得,A B 的纵坐标分别为2b a ，2b a -；,C D 的纵坐标分别为2c ，2c -，故22||b AB a=，||4CD c =.由4||||3CD AB =得2843b c a=，即2322()c c a a ⨯=-，解得2c a =-（舍去），12c a =.所以1C 的离心率为12.（2）由（1）知2a c =，b =，故22122:143x y C c c+=，设00(,)M x y ，则220022143x y c c +=，2004y cx =，故20024143x x c c+=.①由于2C 的准线为x c =-，所以0||MF x c =+，而||5MF =，故05x c =-，代入①得22(5)4(5)143c c c c --+=，即2230c c --=，解得1c =-（舍去），3c =. 所以1C 的标准方程为2213627x y +=，2C 的标准方程为212y x =.5．解：（1）由题设可得54=，得22516m =，所以C 的方程为221252516x y +=. （2）设(,),(6,)P P Q P x y Q y ，根据对称性可设0Q y >，由题意知0P y >，由已知可得(5,0)B ，直线BP 的方程为1(5)Qy x y =--，所以||BP y =，||BQ =，因为||||BP BQ =，所以1P y =，将1P y =代入C 的方程，解得3P x =或3-. 由直线BP 的方程得2Q y =或8.所以点,P Q 的坐标分别为1122(3,1),(6,2);(3,1),(6,8)P Q P Q -.11||PQ 11PQ 的方程为13y x =，点(5,0)A -到直线11PQ，故11APQ △的面积为1522=. 22||PQ =22P Q 的方程为71093y x =+，点A 到直线22P Q的距离为26，故22AP Q △的面积为152262⨯=. 综上，APQ △的面积为52.6．解：（1）由题设可得54=，得22516m =，所以C 的方程为221252516x y +=. （2）设(,),(6,)P P Q P x y Q y ，根据对称性可设0Q y >，由题意知0P y >，由已知可得(5,0)B ，直线BP 的方程为1(5)Qy x y =--，所以||BP y =，||BQ =，因为||||BP BQ =，所以1P y =，将1P y =代入C 的方程，解得3P x =或3-. 由直线BP 的方程得2Q y =或8.所以点,P Q 的坐标分别为1122(3,1),(6,2);(3,1),(6,8)P Q P Q -.11||PQ 11PQ 的方程为13y x =，点(5,0)A -到直线11PQ 的距离为2，故11APQ △的面积为1522=.22||PQ =22P Q 的方程为71093y x =+，点A 到直线22P Q故22AP Q △的面积为1522=. 综上，APQ △的面积为52.7．解：（1）由题设得22411a b +=，22212a b a -=，解得26a =，23b =．所以C 的方程为22163x y +=．（2）设11(,)M x y ，22(,)N x y ．若直线MN 与x 轴不垂直，设直线MN 的方程为y kx m =+，代入22163x y +=得222(12)4260k x kmx m +++-=．于是2121222426,1212km m x x x x k k -+=-=++．①由AM AN ⊥知0AM AN ⋅=，故1212(2)(2)(1)(1)0x x y y --+--=，可得221212(1)(2)()(1)40k x x km k x x m ++--++-+=．将①代入上式可得22222264(1)(2)(1)401212m kmk km k m k k-+---+-+=++．整理得(231)(21)0k m k m +++-=．因为(2,1)A 不在直线MN 上，所以210k m +-≠，故2310k m ++=，1k ≠．于是MN 的方程为21()(1)33y k x k =--≠. 所以直线MN 过点21(,)33P -. 若直线MN 与x 轴垂直，可得11(,)N x y -.由0AM AN ⋅=得1111(2)(2)(1)(1)0x x y y --+---=. 又2211163x y +=，可得2113840x x -+=.解得12x =（舍去），123x =. 此时直线MN 过点21(,)33P -. 令Q 为AP 的中点，即41(,)33Q . 若D 与P 不重合，则由题设知AP 是Rt ADP △的斜边，故1||||2DQ AP ==. 若D 与P 重合，则1||||2DQ AP =. 综上，存在点41(,)33Q ，使得||DQ 为定值.8．（Ⅰ）解：由已知可得3b =．记半焦距为c ，由||||OF OA =可得3c b ==．又由222a b c =+，可得218a =．所以，椭圆的方程为221189x y +=．（Ⅱ）解：因为直线AB 与以C 为圆心的圆相切于点P ，所以AB CP ⊥．依题意，直线AB 和直线CP 的斜率均存在．设直线AB 的方程为3y kx =-．由方程组223,1,189y kx x y =-⎧⎪⎨+=⎪⎩消去y ，可得()2221120k x kx +-=，解得0x =，或21221k x k =+.依题意，可得点B 的坐标为2221263,2121k k k k ⎛⎫- ⎪++⎝⎭．因为P 为线段AB 的中点，点A 的坐标为(0,3)-，所以点P 的坐标为2263,2121k k k -⎛⎫ ⎪++⎝⎭．由3OC OF =，得点C 的坐标为(1,0)，故直线CP 的斜率为2230216121k k k --+-+，即23261k k -+．又因为AB CP ⊥，所以231261k k k ⋅=--+，整理得22310k k -+=，解得12k =，或1k =．所以，直线AB 的方程为132y x =-，或3y x =-．9.（Ⅰ）由116p =得2C 的焦点坐标是1(,0)32．（Ⅱ）由题意可设直线:(0,0)l x my t m t =+≠≠，点00(,)A x y ．将直线l 的方程代入椭圆221:12x C y +=得222(2)220m y mty t +++-=，所以点M 的纵坐标22M mt y m =-+．将直线l 的方程代入抛物线22:2C y px =得2220y pmy pt --=，所以02M y y pt =-，解得202(2)p m y m+=，因此22022(2)p m x m+=．由220012x y +=得2421224()2()160m m p m m =+++≥，所以当m，t =时，p．10.解：（1）椭圆22:143x y E +=的长轴长为2a ，短轴长为2b ，焦距为2c ，则2224,3,1a b c ===.所以12AF F △的周长为226a c +=.（2）椭圆E 的右准线为4x =.设(,0),(4,)P x Q y ，则(,0),(4,)OP x QP x y ==--，2(4)(2)44,OP QP x x x ⋅=-=--≥-在2x =时取等号.所以OP QP ⋅的最小值为4-.（3）因为椭圆22:143x y E +=的左、右焦点分别为12,F F ，点A 在椭圆E 上且在第一象限内，212AF F F ⊥，则123(1,0),(1,0),(1,)2F F A -. 所以直线:3430.AB x y -+= 设(,)M x y ，因为213S S =，所以点M 到直线AB 距离等于点O 到直线AB 距离的3倍. 由此得|343||30403|355x y -+⨯-⨯+=⨯，则34120x y -+=或3460x y --=. 由2234120,143x y x y -+=⎧⎪⎨+=⎪⎩得2724320x x ++=，此方程无解；由223460,143x y x y --=⎧⎪⎨+=⎪⎩得271240x x --=，所以2x =或27x =-. 代入直线:3460l x y --=，对应分别得0y =或127y =-. 因此点M 的坐标为(2,0)或212(,)77--.11.。

广东省13大市2020届高中数学上学期期末试题分类汇编立体几何文

广东省 13大市 2020届高三上期末考数学文试题分类汇编立体几何一、选择题1、（潮州市 2020 届高三上学期期末）对于平面和共面的两直线、，下列命题中是真命题的为A .若，，贝U B.若，，贝U C.若，，则D.若，，，，则答案： C2、（东莞市2020届高三上学期期末）点 M N 分别是正方体的棱、中点，用过 A 、M N 和 D N 的两个截面截去正方体的两个角后得到的几何体如右图，则该几何体的正视图、侧视图（左视图）、俯视图依次为A .①、②、③B .②、③、④C .①、③、④D .②、④、③答案： B3、（佛山市 2020 届高三上学期期末）一个长方体被一个平面截去一部分后所剩几何体的正视图和俯视图如图所示，则该几何体的侧视图可以为4、（广州市 2020 届高三上学期期末）设是两条不同的直线，是三个不同的平面，下列命题正确的是A .B .C .答案： D 5、（惠州市 2020 届高三上学期期末）已知是两条不同直线，是三个不同平面，下列命题中正确的有（）A. ；B. ；C. ；D. .答案： D6、（江门市 2020 届高三上学期期末）图 1，将一个正三棱柱截去一个三棱锥，得到几何体，则该几何体的正视图（或称主视图）是A ．B ．C ．D ．答案： C7、（茂名市 2020届高三上学期期末）若某一几何体的正视图与侧视图均为边长是 1 的正方形，且其体积为，则该几何体的俯视图可以是（）A .答案： BB .C .D .D .答案：C8、（汕头市2020 届高三上学期期末）如图正四棱锥（底面是正方形，顶点在底面的射影是底面的中心）P-ABCD的底面边长为6cm,侧棱长为5cm,则它的侧视图的周长等于（）.A.17cmB.C.16cmD.14cm答案：D9、（增城市2020 届高三上学期期末）给出三个命题：（1）若两直线和第三条直线所成的角相等，则这两直线互相平行.（2）若两直线和第三条直线垂直，则这两直线互相平行.（3）若两直线和第三条直线平行，则这两直线互相平行. 其中正确命题的个数是A. 0B. 1C. 2D. 3答案：B10、（湛江市2020届高三上学期期末）一个几何体的三视图如图所示，其中主视图和左视图都是边长为2 的正三角形，俯视图为圆，那么该几何体的表面积为A、6 B 、4 C、3 D、2答案：C11、（肇庆市2020 届高三上学期期末）某三棱锥的三视图如图2 所示，该三棱锥的体积是为（）A. B. C. D.答案：D解析：从图中可知，三棱锥的底为两直角边分别为和5 的直角三角形，高为4 体积为12、（中山市2020 届高三上学期期末）如图，在透明塑料制成的长方体容器内灌进一些水，将容器底面一边固定于地面上，再将容器倾斜，随着倾斜度的不同，有下列四个说法：①水的部分始终呈棱柱状；②水面四边形的面积不改变；③棱始终与水面平行；④当时，是定值其中所有正确的命题的序号是（）答案：D13、（珠海市2020届高三上学期期末）已知直线I , m和平面a ,则下列命题正确的是A．若I// m ma ,贝U I/aB．若I// a,n a,则1/mC．若I 丄m，I丄a,则m/aD．若I丄a,n a,则11丄m 答案：D二、填空题1、（潮州市2020 届高三上学期期末）若一个正三棱柱的三视图如下图所示，则这个正三棱柱的体积为___________________答案：由左视图知正三棱柱的高，设正三棱柱的底面边长，则，故，底面积，故．三、解答题1、（潮州市2020 届高三上学期期末）已知梯形中，，，、分别是、上的点，，．沿将梯形翻折，使平面丄平面（如图）•是的中点.（1）当时，求证：丄；2）当变化时，求三棱锥的体积的函数式．（1 ）证明：作，垂足，连结，，……2分•••平面平面，交线，平面，•••平面，又平面，故. …… 4分•四边形为正方形，故．又、平面，且，故平面．A.①②③B.①③C.②④D.①③④又平面，故．8分(2 )解：T,平面平面，交线，平面.•••面•又由(1)平面，故，……10分•••四边形是矩形，，故以、、、为顶点的三棱锥的高. ........ 11分又. ........ 1 2分•三棱锥的体积............... 14分19.解：( 1 )由，得；由，得.•，解得，故；………… 4 分2)当时，.由于也适合. ……… 8 分•；……… 9 分3). ……… 10 分•数列的前项和. ……… 14 分2、(东莞市2020届高三上学期期末)在等腰梯形PDCB见图a)中，DC//PB, PB=3DC=3,PD=, 垂足为A,将沿AD折起，使得，得到四棱锥P-ABCD(见图b).在图b 中完成下面问题：(I) 证明：平面平面PCD;(2) 点M在棱PB上，平面AMC把四棱锥P-ABCD分成两个几何体(如图b)，当这两个几何体的体积之比时，求的值；(3) 在⑵ 的条件下，证明：PDII平面AMC.证明：(1)因为在图a的等腰梯形中，，所以在四棱锥中, ,. ………… 1 分又，且，所以，，………… 2分而平面，平面，，所以平面. ………… 3分因为平面，所以平面平面. ………… 4 分解：(2) 因为，且所以平面，又平面，所以平面平面.如图，过作, 垂足为,在等腰梯形中，，则平面. 5分所以，，•......... 6分设，则............ 7分. ......... 8分因为，所以，解得• ......... 9分在中，, 所以,.所以• ....... 10分（3）在梯形中，连结、交于点，连结.易知s,所以. ........ 11分又，所以，........ 12分所以在平面中，有. ....... 13分又因为平面,平面,所以平面•........ 14分3、（佛山市2020 届高三上学期期末）如图所示,已知圆的直径长度为4,点为线段上一点,且,点为圆上一点, 且．点在圆所在平面上的正投影为点,．八、、5 •（1 ）求证：平面；（2）求点到平面的距离．解析：（I）法1:连接，由知，点为的中点，又•••为圆的直径，•••，由知,, •为等边三角形,从而．------------ 3 分•••点在圆所在平面上的正投影为点，•平面,又平面,•, ------------- 5 分由得,平面．---------------- 6 分（注：证明平面时,也可以由平面平面得到,酌情给分．）法2: •••为圆的直径，•，•••在中，，•••由，得，，，，•••,则，.•.,即. --------------- 3分•••点在圆所在平面上的正投影为点，•平面，又平面，.• --------------- 5 分由得，平面. ----------------- 6 分法3: •••为圆的直径，•，在中由得，，T,由得，，，由余弦定理得，，即. --------------- 3分•••点在圆所在平面上的正投影为点，•平面，又平面，5 由得，平面.--(n)法1:由(注：在第(I)------ 10 又，，，•••为等腰三角分6(I)可知，，问中使用方法分则. 12 设点到平面的距离为，由得，，解得. ---------- 14 分法2:由(I)可知，，过点作，垂足为，连接，再过点作, •••平面，又平面，•又，•平面，又平面，•又，•平面，故为点到平面的距离.在中，，，在中，，即点到平面的距离为.分——7 分1时，此处需要求出线段的长度，酌情给分.) 垂足为.10144、(广州市2020届高三上学期期末)已知四棱锥的正视图是一个底边长为、腰长为的等腰C三角形，图4、图5分别是四棱锥的侧视图和俯视图(1 )求证：；(2 )求四棱锥的侧面的面积.PAEFD（1）证明：依题意，可知点在平面上的正射影是线段的中点，连接，则平面•.......... 2分•••平面，.•• • ................ 3 分•••,平面，平面，•••平面• .......... 5分•••平面，•- . ................ 6 分（2）解：依题意，在等腰三角形中，，，在Rt△中，，............. 7分过作，垂足为，连接，•••平面，平面，•. ................ 8 分•••平面，平面，，•平面• .......... 9分•••平面，•. ................ 10 分依题意得•........... 11分在Rt△中，，.......... 12分•△的面积为••••四棱锥的侧面的面积为•.......... 14分5、（惠州市2020 届高三上学期期末）如图所示，在棱长为2 的正方体中，、分别为、的中点．八、、•（1 ）求证：// 平面；（2 ）求证：；（3）求三棱锥的体积．解：（1）连结，在中，、分别为，的中点，则•/ EF为中位线....... 2分而面，面面......... 4分（2）等腰直角三角形BCD中, F为BD中点①...... 5分正方体②...... 7分综合①②，且，而，9分(3 )由(2)可知即CF 为高， ........... 10分••• 即••• ............. 12 分 = ............... 14 分6、(江门市2020届高三上学期期末)如图平面，、分别是、的中点.⑴求证：平面；⑵记，表示四棱锥的体积，求的表达式(不必讨论的取值范围).证明与求解：⑴取的中点，连接、，^叽•… 因为，所以平面平面 4分，平面，所以平面…… 6分. ⑵，丄平面，所以丄平面…… 8分,平面，……9分，，所以……10分，由⑴知……11分，所以 .... 13分， .......14分.7、 (茂名市2020届高三上学期期末)在如图所示的多面体ABCD 冲，平面ACD 平面ACD,,,AD=DE=2 G 为 AD 的中点。

(广东版第01期)2020届高三数学试题分省分项汇编专题09 圆锥曲线理(无答案)

广东版（第01期）-2020届高三数学（理）试题分省分项汇编：专题09 圆锥曲线一．基础题组1.【广东省惠州市2020届高三第一次模拟考试（理）】设抛物线的顶点在原点,准线方程为-2,x =则抛物线的方程是( )A.28y x = B. 28y x =- C. 24y x =- D. 24y x =2.【广东省汕头四中2020届高三第一次月考（理）】双曲线的焦点在x 轴上，实轴长为4，离心率为3，则该双曲线的标准方程为，渐近线方程为．3.【广东省韶关市2020届高三摸底考试（理）】若抛物线22y px =的焦点与双曲线22163x y -=的右焦点重合，则p 的值为． 4.【广东省东莞市2020届高三模拟考试一（理）】已知抛物线24x y =上一点P 到焦点F 的距离是5，则点P 的横坐标是_____．5.【广东省珠海一中等六校2020届高三第一次联考（理）】已知双曲线C 的焦点、实轴端点恰好是椭圆2212516x y +=的长轴端点、焦点，则双曲线C 的渐近线方程是____________________. 二．能力题组1.【广东省佛山市南海区2020届高三8月质检（理）】已知抛物线22y px =的焦点F 与双曲线22179x y -=的右焦点重合，抛物线的准线与x 轴的交点为K ，点A 在抛物线上且|||AK AF ，则△AFK 的面积为（）A.4B.8C.16D.323.【广东省珠海一中等六校2020届高三第一次联考（理）】若动圆的圆心在抛物线212x y =上，且与直线30y +=相切，则此圆恒过定点（）A.(0,2)B.(0,3)-C.(0,3)D.(0,6)三．拔高题组1.【广东省汕头四中2020届高三第一次月考（理）】在平面直角坐标系xOy 中，动点P 到两点(30)，-，(30)，的距离之和等于4，设点P 的轨迹为曲线C ，直线l 过点(1,0)E -且与曲线C 交于A ，B 两点．（1）求曲线C 的轨迹方程；（2）是否存在△AOB 面积的最大值，若存在，求出△AOB 的面积；若不存在，说明理由. 2.【广东省惠州市2020届高三第一次模拟考试（理）】已知中心在原点O ，焦点在x 轴上，离心率为3的椭圆过点（2，2）．（1）求椭圆的方程；（2）设不过原点O 的直线l 与该椭圆交于P 、Q 两点，满足直线OP ，PQ ，OQ 的斜率依次成等比数列，求OPQ ∆面积的取值范围．3.【广东省韶关市2020届高三摸底考试（理）】在平面直角坐标系xOy 中，已知点(2,0)A ，2,0)B ，E 为动点，且直线EA 与直线EB 的斜率之积为12-. （1）求动点E 的轨迹C 的方程；（2）设过点(1,0)F 的直线l 与曲线C 相交于不同的两点M ，N .若点P 在y 轴上，且PM PN =，求点P 的纵坐标的取值范围.4.【广东省十校2020届高三第一次联考（理）】如图，已知椭圆C ：22221(0)x y a b a b+=>>的离心率为32，以椭圆C 的左顶点T 为圆心作圆T ：222(2)(0)x y r r ++=>，设圆T 与椭圆C 交于点M 与点N ．（1）求椭圆C 的方程；（2）求TM TN ⋅u u u r u u u r的最小值，并求此时圆T 的方程；（3）设点P 是椭圆C 上异于M ,N 的任意一点，且直线,MP NP 分别与x 轴交于点,R S ，O 为坐标原点，求证：OR OS ⋅为定值．5.【广东省珠海市2020届高三9月摸底考试（理）】已知点A B 、的坐标分别是(0,1)-、(0,1)，直线AM BM 、相交于点M ，且它们的斜率之积为12-．（1）求点M 轨迹C 的方程；（2）若过点(0,2)D 的直线l 与(1)中的轨迹C 交于不同的两点E F 、，试求OEF ∆面积的取值范围（O 为坐标原点）．6.【广东省广州市越秀区2020届高三入学摸底考试（理）】已知椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1(1,0)F -、2(1,0)F ，P 为椭圆C 上任意一点，且12cos F PF ∠的最小值为13. （1）求椭圆C 的方程；（2）动圆22223)x y t t +=<<与椭圆C 相交于A 、B 、C 、D 四点，当t 为何值时，矩形ABCD 的面积取得最大值？并求出其最大面积.7.【广东省东莞市2020届高三模拟考试一（理）】设椭圆22221(0)x y a b a b+=>>的左右顶点分别为()2,0A -，(2,0)B ，离心率32e =．过该椭圆上任一点P 作PQ x ⊥轴，垂足为Q ，点C 在QP 的延长线上，且||||QP PC =．（1）求椭圆的方程；（2）求动点C 的轨迹E 的方程；（3）设直线AC （C 点不同于,A B ）与直线2x =交于点R ，D 为线段RB 的中点，试判断直线CD 与曲线E 的位置关系，并证明你的结论．8.【广东省珠海一中等六校2020届高三第一次联考（理）】如图，椭圆22:13620x y C +=的左顶点、右焦点分别为,A F ，直线的方程为9x =，N 为上一点，且在x 轴的上方，AN 与椭圆交于M 点.（1）若M 是AN 的中点，求证：MF MA ⊥.（2）过,,A F N 三点的圆与y 轴交于,P Q 两点，求||PQ 的范围.9.【广东省汕头市金山中学2020届高三摸底考试（理）】已知1F 、2F 是双曲线115:22=-y x C 的两个焦点，若离心率等于54的椭圆E 与双曲线C 的焦点相同.（1）求椭圆E 的方程；（2）如果动点),(n m P 满足1021=+PF PF ，曲线M 的方程为: 12222=+y x .判断直线1:=+ny mx l 与曲线M 的公共点的个数，并说明理由；当直线l 与曲线M 相交时，求直线1:=+ny mx l 截曲线M 所得弦长的最大值.10.【广东省惠州市2020届高三第一次调研考试（理）】在平面直角坐标系x o y 中，点(,)(0)P a b a b >>为动点，12,F F 分别为椭圆22221x y a b+=的左右焦点．已知△12F P F 为等腰三角形．（1）求椭圆的离心率e ；（2）设直线2P F 与椭圆相交于,A B 两点，M 是直线2P F 上的点，满足2A MB M =-u u u u r u u u u rg ，求点M 的轨迹方程．。

广东省部分地区2020届高三上学期考试数学文试题分类汇编：平面向量

广东省部分地区2020届高三上学期考试数学文试题分类汇编平面向量一、填空、选择题1、（东莞市2020届高三上学期调研）已知向量,a b r r 满足||1,||2,a b ==r r 且a r 与b r的夹角为60o ，则||a b +=r rA. 7B. 3C. 5D. 222、（佛山市南海区2020届高三摸底考试）如图所示，△ABC 中，2BD DC =u u u r u u u r ，点E 是线段AD 的中点，则（）A 、3142AC AD BE =+u u u r u u u r u u u rB 、34AC AD BE =+u u u r u u u r u u u rC ．5142AC AD BE =+u u u r u u u r u u u r D 、54AC AD BE=+u u u r u u u r u u u r3、（广州市2020届高三12月调研）设 a ，b 是单位向量，a 与b 的夹角是60°，则c =a +3b 的模为（） A. 13 B.13 C. 16 D. 44、（广州市天河区2020年高考一模）已知向量(3,2)a =-r，(,1)b m =r ．若向量(2)//a b b -r r r ，则m = ． 5、（广州市增城区2020届高三调研测试（一））已知向量a ，b 满足2=a ，1=b ，且+223=a b 则a 与b 的夹角为 A.π6 B.π3 C. 2π3 D. 5π66、（华附、省实、深中、广雅2020届高三四校期末联考）若向量a r ，b r 满足12a b ==r r ，，且3a b -r r a r ，b r的夹角为A ．30°B ．60°C ．120°D ．150°7、（华南师大附中2020届高三月考（二））已知向量(1,2)=-r a ，(2,)b m =r ，且//a b r r，则a b =r rg ______.8、（惠州市2020届高三第二次调研）已知向量(12,)a k =r ，(2,14)b k =+r，若a b ⊥r r ，则实数k =__________．9、（惠州市2020届高三第三次调研）ABC ∆中，1=3AD DC u u u r u u u r，P 是直线BD 上的一点，若12AP mAB AC =+u u u r u u u r u u u r，则m =（）． A. 4- B. 1- C ．1 D ．4 10、（广东省六校2020届高三第二次联考）设平面向量()2,1a =-r ，(),2b λ=r ，若a r 与b r 的夹角为锐角，则λ的取值范围是（） A ．()(),44,1-∞--U B ．()1,22,2⎛⎫-+∞ ⎪⎝⎭U C ．()1,+∞ D ．(),1-∞ 11、（茂名市2020届五校联盟高三级第一次联考）已知两个向量a b rr ，满足23a ab a b b π-==r rr r r r =1，与的夹角为，则( )A. 1B. 3C.D. 12、（梅州市2020届高三上学期第一次质量检测）在边长为3的等边ABC ∆中，点M 满足2BM MA =u u u u r u u u r，则CM CA ⋅=u u u u r u u u r（）．A B ． C ．6 D ．15213、（湛江市2020届高三上学期调研）在直角△ABC 中，点E 是斜边BC 的中点，且AB ＝2，则AB AEu u u r u u u rg ＝14、（肇庆市2020届高三第二次统测）已知向量()()()1,2,2,2,1,a b c λ==-=r r r ，若()2c a b ⊥+r r r 则=λ .15、（珠海市2020届高三上学期期末）已知b a ρρ，满足32=a ρ，3=b ρ，6a b ⋅=-r r ,则a ρ在b r 上的投影为A ．2-B ．1-C ．3-D ．216、（佛山市南海区2020届高三摸底考试）在△ABC 中，a ＝5，b ＝8，C ＝60°，则BC CA u u u r u u u rg的值为．17、（广东省六校2020届高三第二次联考）a r 为单位向量，0b ≠r r ，若a b ⊥r r且32a b -=r r ，则b =r________.二、解答题 1、（茂名市2020届五校联盟高三级第一次联考）已知向量1(cos ,sin ),(cos )()2m x x n x x f x m n →→→→===⋅-，函数（1）求函数()f x 的最小正周期（2）若3()cos2625f ππααα∈=（，），，求的值参考答案：1、A2、C3、B4、32- 5、B6、B7、108、－12139、B 10、A 11、B 12、D 13、2 14、－2 15、A16、－20 17参考答案：1、解析：（1）21()cos cos 2f x x x x =-…………………………………………1分1cos21222x x +=-……………………………………2分12cos22x x =+……………………………3分 sin(2)6x π=+……………………………4分2()2f x T ππ∴==函数的最小正周期……………………………5分（2）3()sin(2)65f παα=+=7262266ππππααπ<<∴<+<Q ……………………………6分4cos(2)65πα∴+=-……………………………7分cos 2cos (266ππαα⎡⎤=+-⎢⎥⎣⎦）……………………………8分=cos(2)cos sin(2)sin 6666ππππαα+++……………………………9分431=552-+⨯分。

【2020届】高考数学圆锥曲线专题复习：圆锥曲线综合题

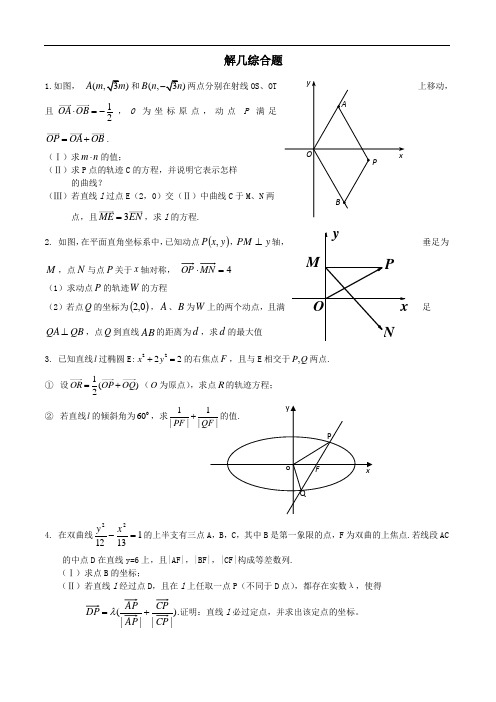
解几综合题1.如图，()A m 和(,)B n 两点分别在射线OS 、OT 上移动，且12OA OB ⋅=-，O 为坐标原点，动点P 满足OP OA OB =+.（Ⅰ）求m n ⋅的值；（Ⅱ）求P 点的轨迹C 的方程，并说明它表示怎样的曲线？（Ⅲ）若直线l 过点E （2，0）交（Ⅱ）中曲线C 于M 、N 两点，且3ME EN =，求l 的方程.2. 如图，在平面直角坐标系中，已知动点()y x P ,，y PM ⊥轴，垂足为M ，点N 与点P 关于x 轴对称， 4=⋅MN OP（1）求动点P 的轨迹W 的方程（2）若点Q 的坐标为()0,2，A 、B 为W 上的两个动点，且满足QB QA ⊥，点Q 到直线AB 的距离为d ，求d 的最大值3. 已知直线l 过椭圆E:2222x y +=的右焦点F ，且与E 相交于,P Q 两点. ① 设1()2OR OP OQ =+（O 为原点），求点R 的轨迹方程；② 若直线l 的倾斜角为060，求1||PF4. 在双曲线1131222=-x y 的上半支有三点A ，B ，C ，其中B 是第一象限的点，F 为双曲的上焦点.若线段AC 的中点D 在直线y=6上，且|AF|，|BF|，|CF|构成等差数列. （Ⅰ）求点B 的坐标；（Ⅱ）若直线l 经过点D ，且在l 上任取一点P （不同于D 点），都存在实数λ，使得 ||||(CP AP +=λ证明：直线l 必过定点，并求出该定点的坐标。

5. 如图，椭圆两焦点F 1、F 2与短轴两端B 1、B 2正好是正方形的四个顶点，且焦点到椭圆上一点最近距离为.12-（I ）求椭圆的标准方程；（II ）过D(0，2)的直线与椭圆交于不同的两点M 、N ，且M 在D 、N 之间，设λ=||DN DM ，求λ的取值范围.6. 已知F 1、F 2分别是椭圆)0,0(12222>>=+b a by a x 的左、右焦点，其左准线与x 轴相交于点N ，并且满足，.2||,221121==F F NF F F （1）求此椭圆的方程；（2）设A 、B 是这个椭圆上的两点，并且满足]31,51[,∈=λλ当NB NA 时，求直线AB 的斜率的取值范围.7. 已知O 为坐标原点，点E 、F 的坐标分别为（-1，0）、（1，0），动点A 、M 、N 满足||||AE m EF =（1m >），0MN AF =⋅，1()2ON OA OF =+，//AM ME ．（Ⅰ）求点M 的轨迹W 的方程；（Ⅱ）点0(,)2mP y 在轨迹W 上，直线PF 交轨迹W 于点Q ，且PF FQ λ=，若12λ≤≤，求实数m 的范围．8. 已知点A （－1，0），B （1，－1）和抛物线.x y C 4:2=，O 为坐标原点，过点A 的动直线l 交抛物线C 于M 、P ，直线MB 交抛物线C 于另一点Q ，如图.（I ）若△POM 的面积为25，求向量OM 与OP 的夹角；（II ）试探求点O 到直线PQ 的距离是否存在最大值？若存在，求出这个最大值；若不存在，说明理由.9. 设不等式组⎩⎨⎧x ＋y >0，x －y >0表示的平面区域为D ．区域D 内的动点P 到直线x ＋y ＝0和直线x －y ＝0的距离之积为1．记点P 的轨迹为曲线C ．（Ⅰ）求曲线C 的方程；（Ⅱ）过点F (2，0)的直线与曲线C 交于A ，B 两点．若以线段AB 为直径的圆与y 轴相切，求线段AB 的长．10. 如图，在△OSF 中，c OF a OS OSF ==︒=∠,,90（c a ,均为正常数），E 、P 是平面OSF内的动点，且满足0=⋅OF SE ，),(R ∈=λλ向量PE c PF a +与PE c PF a -垂直。

2020届广东省高三上学期期末数学(理)试题及答案

2020届广东省高三上学期期末数学（理）试题及答案一、单选题1．已知集合{}ln 0A x x =>，{}240B x x =-≤，则AB =（）A ．()1,2B ．(]1,2C ．(]0,2D ．()1,+∞【答案】B【解析】解出集合A 、B ，利用交集的定义可得出集合A B .【详解】{}()ln 01,A x x =>=+∞，{}[]2402,2B x x =-≤=-，因此，(]1,2A B =.故选：B. 【点睛】本题考查交集的计算，同时也考查了对数不等式和一元二次不等式的求解，考查计算能力，属于基础题. 2．复数121z i z i =+=，，其中i 为虚数单位，则12z z 的虚部为（） A ．1- B ．1 C ．i D ．i -【答案】A【解析】根据复数共轭的概念得到__1z ，再由复数的除法运算得到结果即可. 【详解】11211,1,z iz i i z i-=-==-- 虚部为-1，故选A. 【点睛】本题考查了复数的运算法则、复数的共轭复数等，考查了推理能力与计算能力，属于基础题,复数问题高考必考，常见考点有：点坐标和复数的对应关系，点的象限和复数的对应关系，复数的加减乘除运算，复数的模长的计算.3．已知函数()2f x x bx c =++，b 、R c ∈，则“0c <”是“函数()f x 有零点”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】A【解析】利用>0∆推出充分条件成立，取特殊值推出必要条件不成立，从而得出结论. 【详解】若0c <，则240b c ∆=->，此时，函数()f x 有零点，则“0c <”⇒“函数()f x 有零点”；取2b =，1c =，则()()22211f x x x x =++=+，此时，函数()f x 有零点，但0c >.则“函数()f x 有零点”⇒“0c <”.因此，“0c <”是“函数()f x 有零点”的充分而不必要条件. 故选：A. 【点睛】本题考查充分不必要条件的判断，同时也考查了二次函数的零点，考查推理能力，属于中等题.4．一个几何体是由若干个边长为1的正方体组成的，其主视图和左视图如图所示，且使得组成几何体的正方体个数最多，则该几何体的表面积为（）A．13B．28C．38D．46【答案】D【解析】根据题意作出组成几何体的正方体个数最多时几何体的实物图，然后计算出其表面积即可.【详解】当组成几何体的正方体个数最多时，几何体的实物图如下图所示：小正方体每个面的面积为211=，由实物图可知，该几何体的表面积为2341355446+⨯⨯++⨯=. 故选：D.【点睛】本题考查组合体表面积的计算，解题的关键就是结合三视图作出几何体的实物图，考查空间想象能力与计算能力，属于中等题.5．已知{}n a是各项都为正数的等比数列，n S是它的前n项和，若46S =，818S =，则12S =（） A ．24 B ．30 C ．42 D ．48【答案】C【解析】利用等比数列片断和的性质可得知4S 、84S S -、128S S -成等比数列，由此可计算出12S 的值.【详解】由题意可知，4S 、84S S -、128S S -成等比数列，即()()2844128S S S S S -=-，即()21212618S =⨯-，解得1242S =.故选：C. 【点睛】本题考查等比数列基本性质的应用，考查计算能力，属于基础题.6．如图，若在矩形OABC 中随机撒一粒豆子，则豆子落在图中阴影部分的概率为（）A ．21π-B ．2πC ．22πD ．221π-【答案】A【解析】分别求出矩形和阴影部分的面积，即可求出豆子落在图中阴影部分的概率. 【详解】1S ππ=⨯=矩形，又()00sin cos |cos cos02dx x πππ=-=--=⎰，2S π∴=-阴影，∴豆子落在图中阴影部分的概率为221πππ-=-.故选A. 【点睛】本题考查几何概率的求解，属于基础题，难度不大，正确求面积是关键.7．已知椭圆22221(0)x y a b a b +=>>的右焦点为F，离心率2，过点F 的直线l 交椭圆于,A B 两点，若AB 中点为(1,1)，则直线l 的斜率为（） A ．2 B ．2- C ．12-D ．12【答案】C【解析】先根据已知得到222a b =，再利用点差法求出直线的斜率. 【详解】由题得222222242,4()2,22c c a a b a a b a =∴=∴-=∴=. 设1122(,),(,)A x y B x y ，由题得1212+=2+=2x x y y ，，所以2222221122222222b x a y a b b x a y a b ⎧+=⎨+=⎩，两式相减得2212121212()()a ()()0b x x x x y y y y +-++-=，所以2212122()2a ()0b x x y y -+-=，所以221212()240()y y b b x x -+=-，所以1120,2k k +=∴=-. 故选C 【点睛】本题主要考查椭圆离心率的计算，考查直线和椭圆的位置关系和点差法，意在考查学生对这些知识的理解掌握水平，属于中档题.8．如果执行如图所示的程序框图，则输出的数S 不可能是（）A ．0.4B ．0.5C ．0.75D ．0.9【答案】A【解析】由题意可知，输出的S 值为数列()11n n ⎧⎫⎪⎪⎨⎬+⎪⎪⎩⎭的前n 项和，然后赋值可得出结果. 【详解】第一次循环，011i =+=，112S =⨯，1n ≥不成立；第二次循环，112i =+=，111223S =+⨯⨯，2n ≥不成立；依次类推，()11i n n =-+=，()11112231S n n =+++⨯⨯+，n n ≥成立. 输出()1111111111112231223111n S n n n n n n ⎛⎫⎛⎫⎛⎫=+++=-+-++-=-= ⎪ ⎪ ⎪⨯⨯++++⎝⎭⎝⎭⎝⎭.当1n =时，1=0.52S =；当3n =时，30.754S ==；当9n =时，90.910S ==. 令215n S n ==+，解得23n N *=∉.因此，输出的S 的值不可能是0.4. 故选：A. 【点睛】本题考查利用算法程序框图计算输出的结果，同时也考查了裂项求和法，考查推理能力与计算能力，属于中等题. 9．已知0x >，0y >，0z >，且911y z x+=+，则x y z ++的最小值为（） A ．8 B ．9 C ．12 D ．16【答案】D【解析】将代数式x y z ++与91y z x++相乘，展开后利用基本不等式可求出x y z ++的最小值. 【详解】0x，0y >，0z >，0x y ∴+>且911y z x+=+，所以，()19991010216x y z x y zx y z x y z x y z y z x y z x ⎛⎫++++=+++=++≥+⋅=⎡⎤ ⎪⎣⎦+++⎝⎭，当且仅当9x y zy z x+=+时，即当3y z x +=时，等号成立，因此，x y z ++的最小值为16. 故选：D. 【点睛】本题考查利用基本不等式求和的最小值，同时也考查了1的妙用，考查计算能力，属于基础题.10．太极图被称为“中华第一图”．从孔庙大成殿梁柱，到楼观台、三茅宫标记物；从道袍、卦摊、中医、气功、武术到韩国国旗⋯⋯，太极图无不跃居其上．这种广为人知的太极图，其形状如阴阳两鱼互抱在一起，因而被称为“阴阳鱼太极图”.在如图所示的阴阳鱼图案中，阴影部分可表示为()()()2222224,11110x y A x y x y x y x ⎧⎫⎧+≤⎪⎪⎪⎪⎪⎪=+-≤++≥⎨⎨⎬⎪⎪⎪≤⎪⎪⎪⎩⎩⎭或，设点(),x y ，则2z x y =+的最大值与最小值之差是（）A ．25B ．225+C ．235+D ．245+【答案】C【解析】平移直线2z x y =+，当直线2z x y =+与圆224x y +=切于第三象限的点B 时，该直线在x 轴上的截距最小，当直线2z x y =+与圆()2211x y +-=相切于第一象限的点A 时，该直线在x 轴上的截距最大，利用圆心到直线的距离等于圆的半径求出对应的z 值，即可得出所求结果. 【详解】如下图所示：当直线2z x y =+与圆224x y +=切于第三象限的点B 时，该直线在x 轴上的截距最小，此时0z <，22212z =+，解得25z =-，此时min 25z =- 当直线2z x y =+与圆()2211x y +-=相切于第一象限的点A 时，该直线在x 轴上的截距最大，此时0z>，由题意可得222112z -=+，解得25z =+max 25z =.因此，2z x y =+的最大值与最小值之差是(2525235-=+故选：C. 【点睛】本题考查非线性规划中线性目标函数的最值问题，同时也考查了直线与圆相切问题的处理，考查数形结合思想的应用，属于中等题.11．定义在R 上的函数()f x 满足'()()2(x f x f x e e -<为自然对数的底数），其中'()f x 为()f x 的导函数，若2(2)4f e =，则()2x f x xe >的解集为（）A ．(),1-∞B ．()1,+∞C ．(),2-∞D ．()2,+∞【答案】C 【解析】由()2x f x xe ＞，以及()()2xf x f x e -'＜，联想到构造函数()()2x f x g x x e =-，所以()2x f x xe ＞等价为()(2)g x g >，通过导数求()g x 的单调性，由单调性定义即可得出结果。

广东省13市高三上学期期末考试数学理试题分类汇编：圆锥曲线

广东省13市高三上学期期末考试数学理试题分类汇编圆锥曲线一、选择、填空题1、（潮州市2017届高三上学期期末）已知抛物线y 2=2p （p ＞0）的焦点成F ，过点F 且倾斜角为45°的直线l 与抛物线在第一、第四象限分别交于A 、B ，则等于（）A ．3B ．7+4C ．3+D ．22、（珠海市2017届高三上学期期末）已知双曲线221C 1164x y =：－，双曲线22222C 1(00)x y a b a b=>>：－，的左、右焦点分别为F 1，F 2，M 是双曲线C 2 一条渐近线上的点，且OM ⊥MF 2，若△OMF 2的面积为 16，且双曲线C 1，C 2的离心率相同，则双曲线C 2的实轴长为A ．4B ．8C ．16D ．323、（佛山市2017届高三教学质量检测（一））已知双曲线)0(1:2222>>=-a b by a x C 的右焦点为F ，O 为坐标原点，若存在直线l 过点F 交双曲线C 的右支于B A ,两点，使0=⋅OB OA ，则双曲线离心率的取值范围是________4、（广州市2017届高三12月模拟）已知双曲线：C 12222=-bx a y （0,0>>b a ）的渐近线方程为x y 21±=, 则双曲线C 的离心率为 (A)25(B) 5 (C)26(D) 65、（惠州市2017届高三第三次调研）设直线l 过双曲线C 的一个焦点，且与C 的一条对称轴垂直，l 与C 交于A ，B 两点，|AB |为C 的实轴长的2倍，则C 的离心率为( ) （A ） 3 （B ） 2 （C ）2 （D ）3 6、（江门市2017届高三12月调研）过抛物线（）焦点的直线与抛物线交于两点，以为直径的圆的方程为，则A ．B ．C ．D ．7、（揭阳市2017届高三上学期期末）设椭圆22221(0)x y a b a b+=>>的两焦点与短轴一端点组成一正三角形三个顶点，若焦点到椭圆上点的最大距离为则分别以,a b 为实半轴长和虚半轴长，焦点在y 轴上的双曲线标准方程为 .8、（茂名市2017届高三第一次综合测试）过双曲线()0,012222>>=-b a by a x 的右焦点2(,0)F c 作圆222a y x =+的切线，切点为M ，延长2M F 交抛物线24y cx =-于点,P 其中O 为坐标原点，若21()2OM OF OP =+，则双曲线的离心率为（） A ．7224- B ．7224+C ．231+D ．251+9、（清远市清城区2017届高三上学期期末）已知双曲线c ：，以右焦点F 为圆心，|OF|为半径的圆交双曲线两渐近线于点M 、N （异于原点O ），若|MN|=，则双曲线C 的离心率是（）A B C ．2 D 110、（汕头市2017届高三上学期期末）圆0138222=+--+y x y x 的圆心到直线01=-+y ax 的距离为1，则=a （） A ．34-B ．43- C ．3 D ．2 11、（韶关市2017届高三1月调研）已知点A 是双曲线)0,0(12222>>=-b a by a x 右支上一点，F是右焦点,若AOF ∆(O 是坐标原点)是等边三角形，则该双曲线离心率e 为(A)(B)(C) 1+ (D) 1+二、解答题1、（潮州市2017届高三上学期期末）已知点A 、B 分别是左焦点为（﹣4，0）的椭圆C ：22221(0)x y a b a b+=>>的左、右顶点，且椭圆C 过点P （，）．（1）求椭圆C 的方程；（2）已知F 是椭圆C 的右焦点，以AF 为直径的圆记为圆M ，过P 点能否引圆M 的切线？若能，求出这条切线与轴及圆M 的弦PF 所对的劣弧围成的图形面积；若不能，说明理由．2、（珠海市2017届高三上学期期末）在平面直角坐标系Oy 中，椭圆G 的中心为坐标原点，左焦点为F 1(－1，0)，离心率e ＝2. (1)求椭圆G 的标准方程；(2)已知直线l 1： y ＝+m 1与椭圆G 交于 A ，B 两点，直线l 2： y ＝+m 2（m 1≠m 2）与椭圆G 交于C ，D 两点，且| AB |＝|CD |，如图所示.①证明：m 1+m 2 ＝0；②求四边形ABCD 的面积S 的最大值.3、（佛山市2017届高三教学质量检测（一））已知椭圆)0(1:2222>>=+b a by a x C 过点)1,2(M ，且离心率为23（Ⅰ）求椭圆C 的方程；（Ⅱ）设)1,0(-A ，直线l 与椭圆C 交于Q P ,两点，且AQ AP =，当OPQ ∆（O 为坐标原点）的面积S 最大时，求直线l 的方程4、（广州市2017届高三12月模拟）已知动圆P 与圆221:(2)49F x y ++=相切，且与圆1)2(:222=+-y x F 相内切，记圆心P 的轨迹为曲线C .（Ⅰ）求曲线C 的方程；（Ⅱ）设Q 为曲线C 上的一个不在x 轴上的动点，O 为坐标原点，过点2F 作OQ 的平行线交曲线C 于,M N 两个不同的点, 求△QMN 面积的最大值．5、（惠州市2017届高三第三次调研）已知椭圆()2222:10x y C a b a b +=>>的左、右焦点分别为()()121,0,1,0F F -，点1,2A ⎛⎫⎪ ⎪⎝⎭在椭圆C 上．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）是否存在斜率为2的直线，使得当直线与椭圆C 有两个不同交点M N 、时，能在直线53y =上找到一点P ，在椭圆C 上找到一点Q ，满足PM NQ =？若存在，求出直线的方程；若不存在，说明理由．6、（江门市2017届高三12月调研）在平面直角坐标系中，椭圆：()的离心率为, 椭圆的顶点四边形的面积为．（Ⅰ）求椭圆的方程；（Ⅱ）过椭圆的顶点的直线交椭圆于另一点，交轴于点，若、、成等比数列，求直线的方程．7、（揭阳市2017届高三上学期期末）在平面直角坐标系xOy 中，已知点A （-1, 0）、B （1, 0）、C （0, -1），N 为y 轴上的点，MN 垂直于y 轴，且点M 满足AM BM ON CM ⋅=⋅（O 为坐标原点），点M 的轨迹为曲线T ． (Ⅰ)求曲线T 的方程；(Ⅱ)设点P （P 不在y 轴上）是曲线T 上任意一点，曲线T 在点P 处的切线l 与直线54y =-交于点Q ，试探究以PQ 为直径的圆是否过一定点？若过定点，求出该定点的坐标，若不过定点，说明理由．8、（茂名市2017届高三第一次综合测试）,x y R ∈，向量,i j 分别为直角坐标平面内,x y 轴正方向上的单位向量，若向量(3)a x i y j =++, (3)b x i y j =-+,且||||4a b +=．（Ⅰ）求点(,)M x y 的轨迹C 的方程；（Ⅱ）设椭圆22:1164x y E +=，P 为曲线C 上一点，过点P 作曲线C 的切线=+y kx m 交椭圆E 于A 、B 两点，试证：∆OAB 的面积为定值.9、（清远市清城区2017届高三上学期期末）以椭圆()222:11x M y a a +=>的四个顶点为顶点的四边形的四条边与O ：221x y +=共有6个交点，且这6个点恰好把圆周六等分. （Ⅰ）求椭圆M 的方程；（Ⅱ）若直线l 与O 相切，且与椭圆M 相交于P ，Q 两点，求PQ 的最大值.10、（汕头市2017届高三上学期期末）如图，在平面直角坐标系xOy 中，已知以M 为圆心的圆22:1214600M x y x y +--+=及其上一点(2,4)A（1）设圆N 与x 轴相切，与圆M 外切，且圆心N 在直线6x =上，求圆N 的标准方程；（2）设平行于OA 的直线l 与圆M 相交于,B C 两点，且BC OA =,求直线l 的方程；（3）设点(,0)T t 满足：存在圆M 上的两点P 和Q ,使得,TA TP TQ +=求实数t 的取值范围.11、（韶关市2017届高三1月调研）设椭圆2222:1(0)x y C a b a b+=>>，椭圆C 短轴的一个端点与长轴的一个端点的连线与圆O ：2243x y +=相切，且抛物线2y =-的准线恰好过椭圆C 的一个焦点. （Ⅰ）求椭圆C 的方程；（Ⅱ）过圆O 上任意一点P 作圆的切线l 与椭圆C 交于,A B 两点，连接PO 并延长交圆O 于点Q ，求ABQ ∆面积的取值范围.参考答案一、选择、填空题1、【解答】解：直线l 的方程为y=﹣，代入y 2=2p ，整理得42﹣12p +p 2=0，解得=p ，∴==3+2．故选C ．2、C3、4、B5、【解析】设双曲线的标准方程为x 2a 2－y 2b2＝1(a >0，b >0)，由于直线l 过双曲线的焦点且与对称轴垂直，因此直线l 的方程为：＝c 或＝－c ，代入x 2a 2－y 2b 2＝1得y 2＝b 2(c 2a 2－1)＝b 4a 2，∴y ＝±b 2a，故|AB |＝2b 2a ，依题意2b 2a ＝4a ，∴b 2a 2＝2，∴c 2－a 2a 2＝e 2－1＝2，∴e ＝ 3. 6、B7、221129y x -= 8、 D 解：如图9，∵21M (OP)2O OF =+，∴M 是2F P 的中点.设抛物线的焦点为F 1，则F 1为（- c ，0），也是双曲线的焦点. 连接PF 1，OM .∵O 、M 分别是12F F 和2PF 的中点，∴OM 为 △PF 2F 1的中位线.∵OM=a ，∴|PF 1|=2 a.∵OM ⊥2PF ，∴2PF ⊥PF 1，于是可得|2PF 2b =，设P （，y ），则 c - =2a ，于是有=c-2a ， y 2=4c （c 2 a ），过点2F 作轴的垂线，点P 到该垂线的距离为2a. 由勾股定理得 y 2+4a 2=4b 2，即4c(c-2a)+4 a 2=4(c 2- a 2)，变形可得c 2-a 2=ac ，两边同除以a 2有 210e e --=, 所以e = ,负值已经舍去. 故选D . 9、C 10、A11、【解析】依题意及三角函数定义,点(cos,sin )33B c c ππ⋅ ,即1(,)22B c c ，代入双曲线方程 22222234b c a c a b -=，又222c a b =+，得24e =+ e =1,故选D另解，设左焦点为1F , 可题意及双曲线几何性质可得190F AF ∠=,1AF = 所以212c e a ===二、解答题1、【解答】解：（1）由题意a 2=b 2+16，+=1，解得b 2=20或b 2=﹣15（舍），由此得a 2=36，所以，所求椭圆C 的标准方程为=1．（2）由（1）知A （﹣6，0），F （4，0），又（，），则得=（，），=（﹣，）．所以=0，即∠APF=90°，△APF 是Rt △，所以，以AF 为直径的圆M 必过点P ，因此，过P 点能引出该圆M 的切线，设切线为PQ ，交轴于Q 点，又AF 的中点为M （﹣1，0），则显然PQ ⊥PM ，而PM =，所以PQ 的斜率为﹣，因此，过P 点引圆M 的切线方程为：y ﹣=﹣（﹣），即+y ﹣9=0．令y=0，则=9，∴Q （9，0），又M （﹣1，0），所以S 扇形MPF ==，因此，所求的图形面积是S=S △PQM ﹣S 扇形MPF =．2、3、4、解：（Ⅰ）设圆P 的半径为R , 圆心P 的坐标为(,)x y ，由于动圆P 与圆221:(2)49F x y ++=相切，且与圆1)2(:222=+-y x F 相内切，所以动圆P 与圆1F 只能内切. …………………………………1分所以127,1.PF R PF R ⎧=-⎪⎨=-⎪⎩ …………………………………2分则4||6||||2121=>=+F F PF PF . …………………………………3分所以圆心P 的轨迹是以点12,F F 为焦点的椭圆,且3,2a c ==, 则2225b a c =-=.所以曲线C 的方程为15922=+y x . …………………………………4分（Ⅱ）设112233(,), (,), (,)M x y N x y Q x y ，直线MN 的方程为2x my =+，由222,1,95x my x y ì=+ïïïíï+=ïïî可得225920250m y my ++-=（），则1212222025,5959m y y y y m m +=-=-++. …………………………………5分所以MN =…………………………………6分=()22301.59m m +=+ …………………………………7分因为//MN OQ ，所以△QMN 的面积等于△OMN 的面积. …………………8分点O 到直线2:+=myx MN 的距离d =. ……………………………9分所以△QMN的面积221130(1)2259m S MN dm +=?创=+.…………………………………10分t ，则221m t =-(1)t ≥ ，()223030304545195t t S t t t t===+-++. 设()()451f t t t t =+?，则()2224545t f t t t -¢=-=. 因为1t ³, 所以()22540.t f t t-¢=> 所以()45f t t t=+在[)1,+?上单调递增. 所以当1t =时, ()f t 取得最小值, 其值为9. …………………………………11分所以△QMN 的面积的最大值为309. …………………………………12分说明 △QMN 的面积21212S OF yy =?=5、解（Ⅰ）设椭圆C 的焦距为2c ，则1c =，因为1,2A ⎛⎫ ⎪ ⎪⎝⎭在椭圆C上，所以122a AF AF =+=， (2)分因此2221a b a c ==-=，故椭圆C 的方程为2212x y +=．．．．．．5分（Ⅱ）椭圆C 上不存在这样的点Q ，证明如下：设直线的方程为2y x t =+，设()11,M x y ，()()223445,,,,,3N x y P x Q x y ⎛⎫ ⎪⎝⎭，MN 的中点为()00,D x y ，由22212y x t x y =+⎧⎪⎨+=⎪⎩消去，得229280y ty t -+-=， ……………6分所以1229t y y +=，且()2243680t t ∆=-->，故12029y y ty +==且33t -<<．．．．．．．．．．．．．．．．．．8分由PM NQ =得),()35,(2424131y y x x y x x --=-- ．．．．．．．．．9分所以有24135y y y -=-，=-+=35214y y y 3592-t ．．．．．．．．．．．．10分 (也可由PM NQ =知四边形PMQN 为平行四边形，而D 为线段MN 的中点，因此，也D 为线段PQ 的中点，所以405329yt y +==，可得42159t y -=)，又33t -<<，所以4713y -<<-，与椭圆上点的纵坐标的取值范围[]1,1-矛盾。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

求证△OPQ 的面积为定值，并求此定值·
11、（肇庆市
2020
届高三第二次统测）已知椭圆
x2 a2
+
y
2
=
b2
1 (a > b > 0) 的短半轴长为
2 ，离心率
为 2． 2
（1）求椭圆的方程；
（2）设 A, B 是椭圆上关于坐标原点对称的两点，且点 A 在第一象限， AE ⊥ x 轴，垂足为 E ，连接 BE 并延长交椭圆于点 D ，证明： ∆ABD 是直角三角形．
2 ，过点 F 的直线 l 交椭圆于 A, B 两点，若 AB 中点为 (1,1) ，则直线 l 的斜率为 2
A. 2
B. −2
1
C.
D. − 1
2
2
16、（惠州市 2020
届高三第三次调研）已知双曲线 C1 :
x2 － y2 a2 b2
=1(a
> 0，b
> 0) 的离心率 e
>
2，
左、右焦点分别为 F1、F2 ，其中 F2 也是抛物线 C= 2 : y2 2 px ( p > 0) 的焦点， C1 与 C2 在第一
=
1(a > b > 0) 的左焦点为 F ，上
顶点为 B ，右顶点为 A ，过点 F 作 x 轴垂线，该垂线与直线 AB 交点为 M ，若 AM = 3BM 且
△AFM 的面积为 9 3 ，则 C 的标准方程为 2
A． x2 + y2 = 1 B． x2 + y2 = 1
43
86
C． x2 + y2 = 1 2
12、（珠海市 2020 届高三上学期期末考试）已知 F 为抛物线 C= : y2 2 px( p > 0) 的焦点，过 F 垂直于 x 轴的直线被 C 截得的弦长为 4 ．（1）求抛物线 C 的方程；（2）过点 (m, 0) ，且斜率为1的直线被抛物线 C 截得的弦为 AB ，若点 F 在以 AB 为直径的圆内，求 m 的取值范围．
C : x2 + y2 = 1 交于不同的两点
，
，其中
.
4
的直线 l 与椭圆
（1）若
，求
的面积；
（2）在 x 轴上是否存在定点 T，使得直线 TA、TB 与 y 轴围成的三角形始终为等腰三角形。
8、（梅州市 2020 届高三上学期第一次质量检测）已知 F 为抛物线 T : x2 = 4 y 的焦点，直线 l : y = kx + 2 与T 相交于 A, B 两点. （1）若 k = 1，求 FA + FB 的值；（2）点 C(−3,−2) ，若 ∠CFA = ∠CFB ，求直线 l 的方程.
平行四边形 OAEB 的顶点 E 的轨迹方程.
10、（湛江市
2020
届高三上学期调研考试）已知椭圆
C：
x2 a2
+
y2 b2
=
1(a > b > 0) 的两个焦点与其中
一个顶点构成一个斜边长为 4 的等腰直角三角形． (1)求椭圆 C 的标准方程．
b2 (2)设动直线 l 交椭圆 C 于 P，Q 两点，直线 OP，OQ 的斜率分别为 k，k'，若 kk'＝一 a2 ，
9、（深圳市宝安区 2020 届高三上学期调研考试）P 是圆 x2 + y2 = 4 上的动点，P 点在 x 轴上的射影是 D，点 M 满足 DM = 1 DP . 2
（1）求动点 M 的轨迹 C 的方程，并说明轨迹是什么图形；（2）过点 N(3，0)的直线 l 与动点 M 的轨迹 C 交于不同的两点 A，B，求以 OA，OB 为邻边的
Ω 的另一个交点为 N ，当| AB | 取得最小值时，求 ∆ABN 的面积。
2、（佛山市 2020 届高三教学质量检测（一））已知椭圆
C
:
x2 a2
+ y2 b2
= 1(a > b > 0) 的离心率为 1 ， 2
点
A (1,
3) 在椭圆 2
C
上，直线 l1 过椭圆
C
的有交点与上顶点，动直线 l2
C
:
x2 a2
+
y2 b2
= 1（ a > b > 0 ）的离心率 e =
3
，
2
且椭圆 C 的短轴长为 2．（1）求椭圆 C 的方程；
（2）设直线 l
过点
D
0,
−
1 2
，且与椭圆
C
相交于
M
，
N
两点，又点
P
是椭圆 C
的上顶点，
求△ PMN 面积的最大值．
6、（惠州市 2020 届高三第二次调研）已知抛物线 C : y2 = 2x 的焦点为 F ，直线 l 与 C 交于 A, B 两
F2 ( 6,0) 且与 x 轴不重合，l 交圆 F1 于 C, D 两点，过 F2 作 F1C 的平行线，交 F1D 于点 E ，设 E 的轨迹为 Ω. （1）求 Ω 的方程；（2）直线 l1 与 Ω 相切于点 M ，l1 与两坐标轴的交点为 A 与 B ，直线 l2 经过点 M 且与 l1 垂直，l1 与
）
2
23
10
A．
B．2
C．3
D．
3
3
5、（广州市增城区 2020
届高三调研（一））已知双曲线 C :
x2 a2
−
y2 4
= 1 的焦距为 4
3 ，则 C 的离心
率为
A． 3 2
B． 2 33 11
C． 6 2
2 39
D．
13
6、（广州市增城区
2020
届高三调研（一））已知椭圆 C
:
x2 a2
+
y2 b2
广东省部分地区 2020 届高三上学期考试数学理试题分类汇编
圆锥曲线
一、填空、选择题
1、（广东省 2020
届高三调研考试 I）过双曲线 C :
x2 a2
−
y2 b2
= 1(a
>
0, b
>
0) 的右焦点 F
作双曲线 C
的一条弦 AB ，且 FA + FB = 0 ，若以 AB 为直径的圆经过双曲线 C 的左顶点，则双曲线的离心率
D． x2 + y2 = 1 42
7、（惠州市 2020 届高三第二次调研）我们把焦点相同，且离心率互为倒数的椭圆和双曲线称为一对
“相关曲线”，已知 F1、F2 是一对相关曲线的焦点， P 是椭圆和双曲线在第一象限的交点，当
∠F1PF2 = 60° 时，这一对相关曲线中双曲线的离心率是（
）
A． 3
B． 2
> 0)的右焦点F到左顶点的距离为3.
（1）求椭圆C的方程；（2）设O是坐标原点，过点F的直线与椭圆C交于A,B两点（A,B不在x轴上），若
OE = OA + OB ,延长AO交椭圆与点G，求四边形AGBE的面积S的最大值.
4、（广州市增城区 2020 届高三调研（一））已知动圆 E 经过点 F（1 , 0），且与直线 x = − 1 相切.
1
1
A.
B.
C.1
D.2
4
2
11、（深圳市宝安区
2020
届高三上学期调研考试）已知双曲线
C
:
x2 a2
−
y2 b2
= 1(a
> 0,b > 0) ，直线
y
=b
与 C 的两条渐近线的交点分别为 M ， N ，O 为坐标原点．若 ∆OMN 为直角三角形，则 C 的离心
率为( )
A． 2
B． 3
C．2
D． 5
C． 2 3 3
D．2
8、（惠州市
2020
届高三第二次调研）已知椭圆
x2 a2
+
y2 b2
=
1(a > b > 0) 的短轴长为 2，上顶点为 A ，
左顶点为 B ，左、右焦点分别是 F1,
F2
，且
△F1
AB
的面积为
2
− 2
3 ，点 P 为椭圆上任意一点，则
1 + 1 的取值范围是
．
PF1 PF2
9、（惠州市 2020 届高三第三次调研）已知 F 为抛物线
=
a
与双曲线 C 的两条渐近线交于 A, B 两点，若△OAB 是边长为 2 的等边三角形，则双曲线 C 的方程为
（）
4、（广州市 2020 届高三上学期调研考试）
已知F为双曲线
x2 a2
−
y2 b2
= 1 的右焦点，过 F做C的渐近线的垂线 FD，垂足为 D，且满足
FD = 1 OF （O为坐标原点），则双曲线的离心率为（
2
2
设圆心 E 的轨迹为 C .
（1）求 C 的方程；
（2）设动直线 l : =y kx + m 与曲线 C 相切于点 P ，点 Q 是直线 l 上异于点 P 的一点，若以 PQ 为
直径的圆恒过 x 轴上一定点 M ，求点 Q 的横坐标 x0 ．
5、（华南师大附中
2020
届高三月考（二））如图，椭圆
所以方程①为 k 2 x2 − x + m2 =0 ，解得 x = 2m2 ，不妨取点 P 的坐标为 (2m2 , 2m) . ……8 分
点 Q 的坐标为 (x0 , kx0 + m) ，设点 M 的坐标为 (r, 0) . ……9 分
= MP (2m2 − r, 2m) ， MQ =(x0 − r, kx0 + m) ， MP ⋅ MQ= (2m2 − r)(x0 − r) + 2kmx0 + = 2m2 2m2 (x0 − r +1) + x0 − rx0 = + r2 0