抛物线的简单几何性质导学案
3.3.2第1课时 抛物线的简单几何性质 导学案答案

3.3.2 抛物线的简单几何性质 第1课时 抛物线的简单几何性质【课前预习】知识点一向右 向左 向上 向下 x ≥0,y ∈R x ≤0,y ∈R y ≥0,x ∈R y ≤0,x ∈R x 轴 y 轴 (0,0) e=1 诊断分析(1)× (2)√ (3)√ [解析] (1)抛物线不关于原点对称. (2)抛物线只有一个焦点、一条对称轴,抛物线没有对称中心. (3)抛物线的离心率均为1.知识点二1.(2)焦点弦 x 0+p2 p2-x 0 y 0+p2 p2-y 0 2.2p 诊断分析(1)√ (2)× (3)× [解析] (1)抛物线x 2=4y ,y 2=4x 的焦点到准线的距离都是2,是相同的,离心率都是1,也相同. (2)过抛物线的焦点且垂直于对称轴的弦长是2p. (3)抛物线y 2=2px (p>0)的焦半径长|PF|=x 1+p2. 【课中探究】探究点一例1 解:(1)由y 2=8x ,得p=4,变量x 的范围为x ≥0,∴该抛物线的顶点、焦点、准线、对称轴分别为(0,0),(2,0),直线x=-2,x 轴.(2)椭圆的方程可化为x 24+y 29=1,其短轴在x 轴上,∴抛物线的对称轴为x 轴,∴设抛物线的方程为y 2=2px 或y 2=-2px ,其中p>0.∵抛物线的焦点到顶点的距离为3,即p2=3,∴p=6,∴抛物线的标准方程为y 2=12x 或y 2=-12x ,其准线方程为x=-3或x=3.变式 解:(1)设AB 与x 轴交于点E ,则由|AB|=2得E (√3,0),∴A (√3,1).设抛物线的方程为y 2=2px (p>0),则1=2p ·√3,∴2p=√33,∴抛物线的方程为y 2=√33x.(2)由(1)知2p=√33,∴p 2=√312,∴抛物线的焦点坐标为(√312,0),准线方程为x=-√312,离心率e=1.探究点二例2 解:(1)因为直线l 的倾斜角为60°,所以其斜率k=tan 60°=√3,又F (32,0),所以直线l 的方程为y=√3(x -32).由{y 2=6x ,y =√3(x -32),消去y 得x 2-5x+94=0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=5,而|AB|=|AF|+|BF|=x 1+p2+x 2+p2=x 1+x 2+p , 所以|AB|=5+3=8.(2)结合(1)知|AB|=|AF|+|BF|=x 1+p2+x 2+p2=x 1+x 2+p=x 1+x 2+3=9,所以x 1+x 2=6,于是线段AB 的中点M 的横坐标是3,又准线方程是x=-32,所以点M 到准线的距离为3+32=92.变式 AD [解析] 设直线AB 的方程为x=ty+p 2,将x=ty+p2代入y 2=2px ,得y 2-2pty-p 2=0,则y 1+y 2=2pt ,y 1y 2=-p 2,x 1+x 2=t (y 1+y 1)+p=2pt 2+p ,x 1x 2=y 12y 224p2=p24.当直线AB 与x 轴垂直时,t=0,|AB|最小,故A 中说法正确;1|AF |+1|BF |=1x 1+p 2+1x 2+p 2=x 1+x 2+px 1x 2+p 2(x 1+x 2)+p 24=2p,故B 中说法错误;以弦AB 为直径的圆的圆心为(x 1+x 22,y 1+y 22),半径为12|AB|=12(x 1+x 2+p )=pt 2+p ,圆心到准线的距离d=12(x 1+x 2)+12p=pt 2+p=12|AB|,所以圆与准线x=-p 2相切,故C 中说法错误;y 1y 2=-p 2,故D 中说法正确.故选AD .探究点三例3 (1)A (2)2√2 [解析] (1)依据抛物线的对称性,以及等边三角形的一个顶点位于原点,另外两个顶点在抛物线y 2=4x 上,可设另外两个顶点的坐标分别为(m 24,m),(m 24,-m)(m>0),∴tan 30°=√33=mm 24,解得m=4√3,故这个等边三角形的边长为2m=8√3.故选A .(2)因为抛物线C 的方程为y 2=4√2x ,所以2p=4√2,可得p2=√2,所以焦点为F (√2,0),准线方程为x=-√2,又P 为抛物线C 上一点,且|PF|=3√2,所以点P 到准线x=-√2的距离为3√2,所以x P =3√2-√2=2√2,所以y P 2=4√2×2√2=16,所以|y P |=4,所以S △POF =12×|OF|×|y P |=12×√2×4=2√2.变式 (1)B [解析] 根据题意,可得F (1,0),准线方程为x=-1.不妨设A (x ,y )(y>0),∵|AQ|=43,∴x+1=43,∴x=13,∴A (13,2√33),∴直线AF 的方程为2√33-0=x -113-1,即y=-√3(x-1).将x=-1代入y=-√3(x-1)中,可得y=2√3,∴B (-1,2√3).将y=2√3代入y 2=4x 中,可得x=3,∴P (3,2√3).△PBF 的周长C △PBF =|FB|+|PF|+|PB|,又|FB|=√22+(2√3)2=4,|PF|=|PB|=4,∴C △PBF =12.故选B .(2)解:设点A (x 0,y 0)(x 0>0),由题意可知点B (x 0,-y 0).∵抛物线的焦点F (p2,0)是△AOB 的垂心,∴AF ⊥OB ,∴k AF ·k OB =-1,即y 0x 0-p2·(-y 0x 0)=-1,∴y 02=x 0(x 0-p 2).又y 02=2px 0,∴x 0=2p+p 2=5p2, ∴直线AB 的方程为x=5p2.。
学案1:3.3.2 第1课时 抛物线的简单几何性质
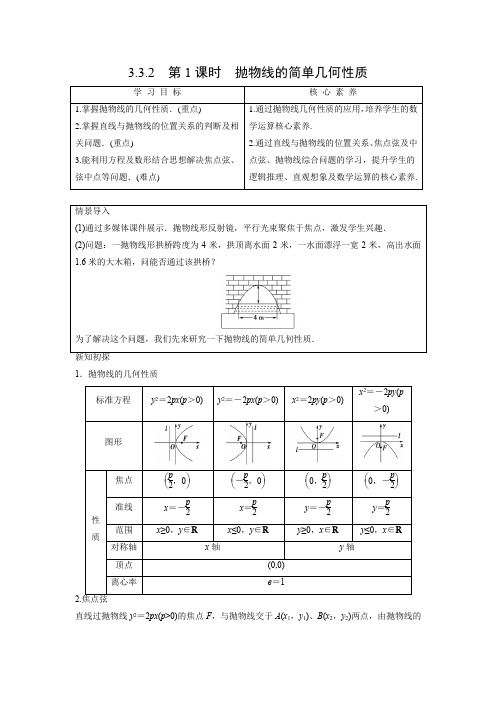
3.3.2第1课时抛物线的简单几何性质学习目标核心素养1.掌握抛物线的几何性质.(重点)2.掌握直线与抛物线的位置关系的判断及相关问题.(重点)3.能利用方程及数形结合思想解决焦点弦、弦中点等问题.(难点) 1.通过抛物线几何性质的应用,培养学生的数学运算核心素养.2.通过直线与抛物线的位置关系、焦点弦及中点弦、抛物线综合问题的学习,提升学生的逻辑推理、直观想象及数学运算的核心素养.情景导入(1)通过多媒体课件展示.抛物线形反射镜,平行光束聚焦于焦点,激发学生兴趣.(2)问题:一抛物线形拱桥跨度为4米,拱顶离水面2米,一水面漂浮一宽2米,高出水面1.6米的大木箱,问能否通过该拱桥?为了解决这个问题,我们先来研究一下抛物线的简单几何性质.新知初探1.抛物线的几何性质标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)图形性质焦点⎝⎛⎭⎫p2,0⎝⎛⎭⎫-p2,0⎝⎛⎭⎫0,p2⎝⎛⎭⎫0,-p2准线x=-p2x=p2y=-p2y=p2范围x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R 对称轴x轴y轴顶点(0,0)离心率e=12.直线过抛物线y2=2px(p>0)的焦点F,与抛物线交于A(x1,y1)、B(x2,y2)两点,由抛物线的定义知,|AF |=x 1+p 2,|BF |=x 2+p2,故|AB |= .3.直线与抛物线的位置关系直线与抛物线有三种位置关系:相离、相切和相交.设直线y =kx +m 与抛物线y 2=2px (p >0)相交于A (x 1,y 1),B (x 2,y 2)两点,将y =kx +m 代入y 2=2px ,消去y 并化简,得k 2x 2+2(mk -p )x +m 2=0. ①k =0时,直线与抛物线只有 交点;②k ≠0时,Δ>0⇔直线与抛物线 ⇔有 个公共点. Δ=0⇔直线与抛物线 ⇔只有 公共点. Δ<0⇔直线与抛物线 ⇔ 公共点.思考:直线与抛物线只有一个公共点,那么直线与抛物线一定相切吗? 初试身手1.思考辨析(正确的打“√”,错误的打“×”) (1)抛物线是无中心的圆锥曲线.( ) (2)抛物线y 2=2px 过焦点且垂直于对称轴的弦长是2p . ( ) (3)抛物线y =-18x 2的准线方程为x =132.( )2.顶点在原点,对称轴为y 轴,顶点到准线的距离为4的抛物线的标准方程是( ) A .x 2=16y B .x 2=8y C .x 2=±8yD .x 2=±16y3.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,若x 1+x 2=6,则|AB |=( ) A .10 B .8 C .6D .44.若双曲线x 23-16y 2p 2=1(p >0)的左焦点在抛物线y 2=2px 的准线上,则p =________.合作探究类型1 抛物线性质的应用例1 (1)已知抛物线的顶点在坐标原点,对称轴为x 轴且与圆x 2+y 2=4相交的公共弦长等于23,则抛物线的方程为________.(2)如图,过抛物线y 2=2px (p >0)的焦点F 的直线依次交抛物线及准线于点A ,B ,C ,若|BC |=2|BF |,且|AF |=4,求抛物线的方程.规律方法用待定系数法求抛物线方程的步骤提醒:求抛物线的方程时要注意抛物线的焦点位置,不同的焦点设出不同的方程.跟踪训练1.若直线x=m与抛物线y2=43x交于A、B两点,F是其焦点,若△ABF为等边三角形,求m的值.类型2 直线与抛物线的位置关系例2 (1)过定点P (0,1)作与抛物线y 2=2x 只有一个公共点的直线有几条?(2)若直线l :y =(a +1)x -1与曲线C :y 2=ax (a ≠0)恰好有一个公共点,试求实数a 的取值集合. 规律方法直线与抛物线交点问题的解题思路(1)判断直线与抛物线的交点个数时,一般是将直线与抛物线的方程联立消元,转化为形如一元二次方程的形式,注意讨论二次项系数是否为0.若该方程为一元二次方程,则利用判别式判断方程解的个数.(2)直线与抛物线有一个公共点时有两种情形:(1)直线与抛物线的对称轴重合或平行;(2)直线与抛物线相切. 跟踪训练2.若抛物线y 2=4x 与直线y =x -4相交于不同的两点A ,B ,求证OA ⊥OB .证明:由⎩⎪⎨⎪⎧y 2=4x ,y =x -4,消去y ,得x 2-12x +16=0.∵直线y =x -4与抛物线相交于不同两点A ,B , ∴可设A (x 1,y 1),B (x 2,y 2), 则有x 1+x 2=12,x 1x 2=16.∵OA →·OB →=x 1x 2+y 1y 2=x 1x 2+(x 1-4)(x 2-4)=x 1x 2+x 1x 2-4(x 1+x 2)+16=16+16-4×12+16=0,∴OA →⊥OB →,即OA ⊥OB . 类型3 中点弦及弦长公式例3 过点Q (4,1)作抛物线y 2=8x 的弦AB ,恰被点Q 所平分,求AB 所在直线的方程. 规律方法“中点弦”问题解题方法跟踪训练3.已知抛物线的顶点在原点,x 轴为对称轴,经过焦点且倾斜角为π4的直线l 被抛物线所截得的弦长为6,求抛物线的标准方程.类型4 抛物线的综合应用 [探究问题]1.若两条直线的斜率存在且倾斜角互补时,两条直线的斜率有什么关系?2.如何对待圆锥曲线中的定点、定值问题?例4 如图所示,抛物线关于x 轴对称,它的顶点为坐标原点,点P (1,2),A (x 1,y 1),B (x 2,y 2)均在抛物线上.(1)求抛物线的方程及其准线方程;(2)当P A 与PB 的斜率存在且倾斜角互补时,证明:直线AB 的斜率为定值. 母题探究1.若本例题改为:如图所示,已知直线l :y =2x -4交抛物线y 2=4x 于A ,B 两点,试在抛物线AOB 这段曲线上求一点P ,使△P AB 的面积最大,并求出这个最大面积.如何求解?2.若本例改为“抛物线方程为y2=x,且过点P(3,-1)的直线与抛物线C交于M,N两个不同的点(均与点A(1,1)不重合),设直线AM,AN的斜率分别为k1,k2”,求证:k1·k2为定值.应用抛物线性质解题的常用技巧(1)抛物线的中点弦问题用点差法较简便.(2)轴对称问题,一是抓住对称两点的中点在对称轴上,二是抓住两点连线的斜率与对称轴所在直线斜率的关系.(3)在直线和抛物线的综合题中,经常遇到求定值、过定点问题.解决这类问题的方法很多,如斜率法、方程法、向量法、参数法等.解决这些问题的关键是代换和转化.(4)圆锥曲线中的定点、定值问题,常选择一参数来表示要研究问题中的几何量,通过运算找到定点、定值,说明与参数无关,也常用特值探路法找定点、定值.课堂小结1.抛物线的性质可以总结为五个“1”,即:一个顶点,一个焦点,一条准线,一条对称轴,离心率为1的无心圆锥曲线.2.抛物线中常见的几个结论:已知AB 是抛物线y 2=2px (p >0)的焦点弦,且A (x 1,y 1),B (x 2,y 2).点F 是抛物线的焦点(如图).则有(1)y 1y 2=-p 2,x 1x 2=p 24. (2)|AB |=x 1+x 2+p .(3)以过焦点的弦为直径的圆与准线相切. (4)以焦半径为直径的圆与y 轴相切. 课堂检测1.若抛物线y 2=2x 上有两点A 、B 且AB 垂直于x 轴,若|AB |=22,则抛物线的焦点到直线AB 的距离为( ) A .12B .14C .16D .182.在抛物线y 2=16x 上到顶点与到焦点距离相等的点的坐标为( ) A .(42,±2) B .(±42,2) C .(±2,42)D .(2,±42)3.设O 为坐标原点,F 为抛物线y 2=4x 的焦点,A 是抛物线上一点,若OA →·AF →=-4, 则点A 的坐标是( ) A .(2,±22) B .(1,±2) C .(1,2)D .(2,22)4.已知AB 是过抛物线2x 2=y 的焦点的弦,若|AB |=4,则AB 的中点的纵坐标是________. 5.已知点P (1,m )是抛物线C :y 2=2px 上的点,F 为抛物线的焦点,且|PF |=2,直线l :y =k (x -1)与抛物线C 相交于不同的两点A ,B . (1)求抛物线C 的方程;(2)若|AB |=8,求k 的值.参考答案新知初探 2.x 1+x 2+p . 3.①一个 ②相交 两相切 一 相离 没有思考: [提示] 可能相切,也可能相交,当直线与抛物线的对称轴平行或重合时,直线与抛物线相交且只有一个公共点. 初试身手1.[提示] (1)√ (2)√ (3)× 2.【答案】D【解析】顶点到准线的距离为p 2,则p2=4.解得p =8,又因对称轴为y 轴,则抛物线方程为x 2=±16y . 3.【答案】B【解析】|AB |=x 1+x 2+p =6+2=8. 4.【答案】4【解析】双曲线的左焦点为(-3+p 216,0),由条件可知,-p2=-3+p 216,解得p =4. 合作探究类型1 抛物线性质的应用例1 (1)【答案】y 2=3x 或y 2=-3x【解析】根据抛物线和圆的对称性知,其交点纵坐标为±3,交点横坐标为±1,则抛物线过点(1,3)或(-1,3),设抛物线方程为y 2=2px 或y 2=-2px (p >0), 则2p =3,从而抛物线方程为y 2=3x 或y 2=-3x .(2)解:如图,分别过点A ,B 作准线的垂线,分别交准线于点E ,D ,设|BF |=a ,则由已知得:|BC |=2a , 由定义得:|BD |=a ,故∠BCD =30°, 在Rt △ACE 中,∵|AF |=4,|AC |=4+3a ,∴2|AE |=|AC |,∴4+3a =8,从而得a =43,∵BD ∥FG ,∴43p =23,p =2.因此抛物线的方程是y 2=4x . 跟踪训练1.解:根据题意△ABF 为等边三角形,则tan 60°=|m -3|43m ,m >0,解得m =73±12.类型2 直线与抛物线的位置关系例2 解:(1)当直线的斜率不存在时,直线x =0,符合题意.当直线的斜率存在时,设过点P 的直线方程为y =kx +1,当k =0时,直线l 的方程为y =1,满足直线与抛物线y 2=2x 仅有一个公共点;当k ≠0时,将直线方程y =kx +1代入y 2=2x ,消去y 得k 2x 2+2(k -1)x +1=0.由Δ=0,得k =12,直线方程为y =12x +1.故满足条件的直线有三条. (2)因为直线l 与曲线C 恰好有一个公共点,所以方程组⎩⎪⎨⎪⎧y =(a +1)x -1,y 2=ax只有一组实数解,消去y ,得[(a +1)x -1]2=ax ,即(a +1)2x 2-(3a +2)x +1=0 ①.(ⅰ)当a +1=0,即a =-1时,方程①是关于x 的一元一次方程,解得x =-1,这时,原方程组有唯一解⎩⎪⎨⎪⎧x =-1,y =-1.(ⅱ)当a +1≠0,即a ≠-1时,方程①是关于x 的一元二次方程. 令Δ=(3a +2)2-4(a +1)2=a (5a +4)=0,解得a =0(舍去)或a =-45.所以原方程组有唯一解⎩⎪⎨⎪⎧x =-5,y =-2.综上,实数a 的取值集合是⎩⎨⎧⎭⎬⎫-1,-45.跟踪训练2.证明:由⎩⎪⎨⎪⎧y 2=4x ,y =x -4,消去y ,得x 2-12x +16=0.∵直线y =x -4与抛物线相交于不同两点A ,B , ∴可设A (x 1,y 1),B (x 2,y 2), 则有x 1+x 2=12,x 1x 2=16.∵OA →·OB →=x 1x 2+y 1y 2=x 1x 2+(x 1-4)(x 2-4)=x 1x 2+x 1x 2-4(x 1+x 2)+16=16+16-4×12+16=0,∴OA →⊥OB →,即OA ⊥OB . 类型3 中点弦及弦长公式例3 解:法一:(点差法)设以Q 为中点的弦AB 的端点坐标为A (x 1,y 1),B (x 2,y 2),则有y 21=8x 1,y 22=8x 2,∴(y 1+y 2)(y 1-y 2)=8(x 1-x 2).又y 1+y 2=2,∴y 1-y 2=4(x 1-x 2), 即y 1-y 2x 1-x 2=4,∴k AB =4. ∴AB 所在直线的方程为y -1=4(x -4),即4x -y -15=0. 法二:由题意知AB 所在直线斜率存在,设A (x 1,y 1),B (x 2,y 2), 弦AB 所在直线的方程为y =k (x -4)+1.联立⎩⎪⎨⎪⎧y 2=8x ,y =k (x -4)+1,消去x ,得ky 2-8y -32k +8=0,此方程的两根就是线段端点A ,B 两点的纵坐标. 由根与系数的关系得y 1+y 2=8k .又y 1+y 2=2,∴k =4.∴AB 所在直线的方程为4x -y -15=0. 跟踪训练3.解:当抛物线焦点在x 轴正半轴上时,可设抛物线标准方程为y 2=2px (p >0),则焦点F ⎝⎛⎭⎫p 2,0,直线l 的方程为y =x -p 2.设直线l 与抛物线的交点为A (x 1,y 1),B (x 2,y 2),过点A ,B 向抛物线的准线作垂线,垂足分别为点A 1,点B 1,则|AB |=|AF |+|BF |=|AA 1|+|BB 1|=⎝⎛⎭⎫x 1+p2+⎝⎛⎭⎫x 2+p2=x 1+x 2+p =6, ∴x 1+x 2=6-p .①由⎩⎪⎨⎪⎧y =x -p 2,y 2=2px消去y ,得⎝⎛⎭⎫x -p 22=2px ,即x 2-3px +p 24=0.∴x 1+x 2=3p ,代入①式得3p =6-p ,∴p =32.∴所求抛物线的标准方程是y 2=3x .当抛物线焦点在x 轴负半轴上时,用同样的方法可求出抛物线的标准方程是y 2=-3x . 类型4 抛物线的综合应用 [探究问题]1.[提示] 两条直线的斜率互为相反数.2.[提示] 常选择一个参数来表示要研究问题中的几何量,通过运算说明与参数无关,进而找到定点、定值.也常用特值法找定点、定值.例4 解:(1)由题意可设抛物线的方程为y 2=2px (p >0),则由点P (1,2)在抛物线上,得22=2p ×1,解得p =2,故所求抛物线的方程是y 2=4x ,准线方程是x =-1.(2)证明:因为P A 与PB 的斜率存在且倾斜角互补,所以k P A =-k PB ,即y 1-2x 1-1=-y 2-2x 2-1. 又A (x 1,y 1),B (x 2,y 2)均在抛物线上,所以x 1=y 214,x 2=y 224,从而有y 1-2y 214-1=-y 2-2y 224-1,即4y 1+2=-4y 2+2,得y 1+y 2=-4,故直线AB 的斜率k AB =y 1-y 2x 1-x 2=4y 1+y 2=-1.1.【答案】A【解析】线段AB 所在的直线方程为x =1,抛物线的焦点坐标为⎝⎛⎭⎫12,0,则焦点到直线AB 的距离为1-12=12. 2.【答案】D【解析】抛物线y 2=16x 的顶点O (0,0),焦点F (4,0),设P (x ,y )符合题意,则有⎩⎪⎨⎪⎧ y 2=16x ,x 2+y 2=(x -4)2+y 2⇒⎩⎪⎨⎪⎧ y 2=16x ,x =2⇒⎩⎨⎧x =2,y =±4 2. 所以符合题意的点为(2,±42).]3.【答案】B【解析】由题意知F (1,0),设A ⎝⎛⎭⎫y 204,y 0,则OA →=⎝⎛⎭⎫y 204,y 0,AF →=⎝⎛⎭⎫1-y 204,-y 0, 由OA →·AF →=-4得y 0=±2,∴点A 的坐标为(1,±2),故选B.4.【答案】158【解析】设A (x 1,y 1),B (x 2,y 2),由抛物线2x 2=y ,可得p =14. ∵|AB |=y 1+y 2+p =4,∴y 1+y 2=4-14=154,故AB 的中点的纵坐标是y 1+y 22=158. 5.解:(1)抛物线C :y 2=2px 的准线为x =-p 2, 由|PF |=2得:1+p 2=2,得p =2. 所以抛物线的方程为y 2=4x .(2)设A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧ y =k x -1,y 2=4x ,可得k 2x 2-(2k 2+4)x +k 2=0,Δ=16k 2+16>0,∴x 1+x 2=2k 2+4k2. ∵直线l 经过抛物线C 的焦点F ,∴|AB |=x 1+x 2+p =2k 2+4k2+2=8, 解得k =±1,所以k 的值为1或-1.。
3.3.2第1课时 抛物线的简单几何性质 导学案正文

3.3.2抛物线的简单几何性质第1课时抛物线的简单几何性质【学习目标】能类比椭圆、双曲线几何性质的研究方法得到抛物线的范围、对称性、顶点、离心率等几何性质及其代数表达.◆知识点一抛物线的几何性质标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)图形焦点坐标(p2,0)(-p2,0)(0,p2)(0,-p2)准线方程x=-p2x=p2y=-p2y=p2开口方向范围对称轴顶点坐标离心率【诊断分析】判断正误.(请在括号中打“√”或“×”)(1)抛物线关于原点对称.( )(2)抛物线只有一个焦点、一条对称轴,无对称中心. ( )(3)抛物线的标准方程虽然各不相同,但是其离心率都相同.( )◆知识点二抛物线的焦半径、焦点弦与通径1.焦半径与焦点弦(1)抛物线上一点与焦点F连接的线段叫作焦半径.(2)过抛物线焦点的直线与抛物线相交,直线被抛物线所截得的线段称为抛物线的.设A(x0,y0)为抛物线上任意一点,则四种标准方程形式下的焦半径公式和焦点弦长|MN|(M(x1,y1),N(x2,y2))为标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0)x2=-2py(p>0)焦半径|AF|焦点弦长|MN|x1+x2+p-x1-x2+p y1+y2+p-y1-y2+p2.通径经过抛物线的焦点作垂直于对称轴的直线交抛物线于A,B两点,线段AB称为抛物线的通径,通径的长|AB|为.【诊断分析】判断正误.(请在括号中打“√”或“×”)(1)抛物线x2=4y,y2=4x的焦点到准线的距离是相同的,离心率也相同.( )(2)过抛物线的焦点且垂直于对称轴的弦长是p(p>0).( )(3)P(x1,y1)是抛物线y2=2px(p>0)上一点,F是抛物线的焦点,则|PF|=x1+p.( )◆探究点一抛物线的几何性质例1 (1)已知抛物线y2=8x,求出变量x的范围及该抛物线的顶点、焦点、准线、对称轴.(2)抛物线的顶点在原点,对称轴与椭圆9x2+4y2=36的短轴所在的直线重合,抛物线的焦点到顶点的距离为3,求抛物线的标准方程及抛物线的准线方程.变式已知等边三角形AOB的边长为2,O为坐标原点,AB⊥x轴,且点A在第一象限.(1)求以O为顶点且过点A,B的抛物线的方程;(2)求(1)中所求抛物线的焦点坐标、准线方程及离心率e.[素养小结]运用抛物线的几何性质要把握三个要点:(1)定性:由抛物线的标准方程看抛物线的开口方向,关键是看准二次项是x还是y,一次项的系数是正还是负.(2)定量:确定焦点到准线的距离p(p>0).(3)转化:抛物线上的一点到焦点的距离与到准线的距离相等,解题时适时转化可起到事半功倍的效果.◆探究点二焦点弦的性质问题例2已知直线l经过抛物线y2=6x的焦点F,且与抛物线交于A,B两点.(1)若直线l的倾斜角为60°,求|AB|的值;(2)若|AB|=9,求线段AB的中点M到准线的距离.变式 (多选题)经过抛物线y2=2px(p>0)的焦点F的直线交抛物线于A,B两点,设A(x1,y1),B(x2,y2),则下列说法中正确的是( )A.当AB与x轴垂直时,|AB|最小B.1|AF|+1|BF|=p2C.以弦AB为直径的圆与直线x=-p2相离D.y1y2=-p2[素养小结]抛物线焦点弦长的求法:设过抛物线y2=2px(p>0)的焦点F的弦的端点为A(x1,y1),B(x2,y2),利用弦所在直线的方程(注意方程的设法)与抛物线方程联立、消元,由根与系数的关系求出x1+x2,由公式|AB|=x1+x2+p求出焦点弦长.◆探究点三抛物线几何性质的应用例3 (1)已知等边三角形的一个顶点位于原点,另外两个顶点在抛物线y2=4x上,则这个等边三角形的边长为( )A.8√3B.4√2C.4√3D.3√2(2)已知抛物线C:y2=4√2x的焦点为F,O为坐标原点,P为抛物线C上一点,且满足|PF|=3√2,则△POF的面积为.变式 (1)以抛物线C:y2=4x的焦点F为端点的射线与C及C的准线l分别交于A,B两点,过B且平行于x轴的直线交C于点P,过A且平行于x轴的直线交l于点Q,若|AQ|=43,则△PBF的周长为( )A.16B.12C.10D.6(2)已知A,B是抛物线y2=2px(p>0)上不同的两点,O为坐标原点,若|OA|=|OB|,且△AOB的垂心恰是此抛物线的焦点,求直线AB的方程.[素养小结]利用抛物线的性质可以解决的问题:(1)对称性:解决抛物线的内接三角形问题.(2)焦点、准线:解决与抛物线的定义有关的问题.(3)范围:解决与抛物线有关的最值问题.(4)焦点:解决焦点弦问题.。
抛物线的简单几何性质教案

抛物线的简单几何性质(一)导学案【教学目标】知识与技能:了解抛物线的范围、对称性、顶点、焦点、准线等几何性质.使学生理解并掌握抛物线的几何性质,从定义和标准方程出发,探究有关抛物线的焦半径和焦点弦的常见性质.过程与方法:从抛物线的定义和标准方程出发,结合几何分析和坐标运算,推导抛物线的性质。
培养学生分析、归纳、推理等能力.情感态度与价值观:使学生进一步掌握利用方程研究曲线性质的基本方法,加深对直角坐标系中曲线方程的关系概念的理解,解决抛物线中的弦的问题.【学法指导】结合椭圆和双曲线的几何性质,类比抛物线的性质,通过对抛物线的标准方程的讨论,进一步理解用代数方法研究几何性质的优越性,感受坐标法和数形结合的基本思想.教学重难点:1.重点:有关抛物线焦半径和焦点弦几何性质的推理过程中所应用的方法、技巧和结论.2.难点:对抛物线的几何性质和焦点弦几何性质推理和应用的方法渗透.学情分析:【知识回顾】1.抛物线的定义、标准方程。
(生口述完成)2.焦半径直线过抛物线y2=2px (p>0)的焦点F,与抛物线交于A(x1,y1)、B(x2,y2)两点,由抛物线的定义知,|AF|=x1+p2,|BF|=x2+p2,3.填空(顶点在原点,焦点在坐标轴)方程,焦点,准线,开口.1.26y x=2.()1,0F-3.1y=-4.2270x y+=二、新课讲授【问题探究一】探究点一抛物线的几何性质问题1类比椭圆、双曲线的几何性质,结合图象,说出抛物线y2=2px (p>0)的范围、对称性、顶点、离心率.怎样用方程验证?(生通过预习,完成导学案上的表格,并小组之间互相分享结果,互相讨论)1.抛物线的几何性质(方程的方法进行验证)(生口述完成) 研究抛物线)0(22>=p px y : (1)范围因为0>p ,由方程可知0≥x ,所以抛物线在y 轴的右侧,当x 的值增大时,||y 也增大,这说明抛物线向右上方和右下方无限延伸. (2)对称性以y -代y ,方程不变,所以抛物线关于x 轴对称.我们把抛物线的对称轴叫做抛物线的轴. (3)顶点抛物线与它的轴的交点叫做抛物线的顶点,在方程中,当0=y 时0=x ,因此抛物线的顶点就是坐标原点.(4)离心率抛物线上的点与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,由抛物线的定义可知1=e例题1:【引题】已知斜率为1直线经过抛物线y 2=4x 的焦点F ,且与抛物线相交于A 、B 两点.求线段AB 的长。
《2.3.2抛物线的简单几何性质》导学案(新部编)3

教师学科教案[ 20 – 20 学年度第__学期]任教学科:_____________任教年级:_____________任教老师:_____________xx市实验学校《抛物线的简单几何性质》导学案学习目标:1.掌握抛物线的几何性质;2.根据几何性质确定抛物线的标准方程.学习过程:一、课前准备 复习1:准线方程为x =2的抛物线的标准方程是___________________.复习2:双曲线221169x y -=有哪些几何性质? 二、新课导学 ※ 学习探究探究1:类比椭圆、双曲线的几何性质,抛物线又会有怎样的几何性质? 新知:抛物线的几何性质 图形标准方程焦点(0,)2p -准线 2p y =-顶点 (0,0)(0,0)对称轴 x 轴 离心率试试:画出抛物线8y x =的图形,顶点坐标( )、焦点坐标( )、准线方程( )、对称轴( )、离心率( ). ※ 典型例题例1已知抛物线关于x 轴对称,它的顶点在坐标原点,并且经过点(2,22)M -,求它的标准方程.变式:顶点在坐标原点,对称轴是坐标轴,并且经过点(2,22)M -的抛物线有几条?求出它们的标准方程.小结:一般,过一点的抛物线会有两条,根据其开口方向,用待定系数法求解. 例2斜率为1的直线l 经过抛物线24y x =的焦点F ,且与抛物线相交于A ,B 两点,求线段AB 的长 .变式:过点(2,0)M 作斜率为1的直线l ,交抛物线24y x =于A ,B 两点,求AB . 小结:求过抛物线焦点的弦长:可用弦长公式,也可利用抛物线的定义求解. ※ 动手试试练1. 求适合下列条件的抛物线的标准方程: ⑴顶点在原点,关于x 轴对称,并且经过点 (5M ,4)-;⑵顶点在原点,焦点是(0,5)F ; ⑶焦点是(0,8)F -,准线是8y =. 三、总结提升 ※ 学习小结1.抛物线的几何性质 ; 2.求过一点的抛物线方程; 3.求抛物线的弦长. ※ 知识拓展抛物线的通径:过抛物线的焦点且与对称轴垂直的直线,与抛物线相交所得的弦叫抛物线的通径.其长为2p .※ 当堂检测(时量:5分钟 满分:10分)计分: 1.下列抛物线中,开口最大的是( ). A .212y x =B .2y x =C .22y x =D .24y x =2.顶点在原点,焦点是(0,5)F 的抛物线方程( ) . A .220y x = B .220x y = C .2120y x =D .2120x y = 3.过抛物线24y x =的焦点作直线l ,交抛物线于A ,B 两点,若线段AB 中点的横坐标为3,则AB 等于( ).A .10B .8C .6D .4 4.抛物线2(0)y ax a =≠的准线方程是 .5.过抛物线22y x =的焦点作直线交抛物线于11(,)A x y ,22(,)B x y 两点,如果126x x +=,则AB=______________________.课后作业1.根据下列条件,求抛物线的标准方程,并画出图形:⑴顶点在原点,对称轴是x轴,并且顶点与焦点的距离等到于6;P--.⑵顶点在原点,对称轴是y轴,并且经过点(6,3)2.M是抛物线24=上一点,F是抛物线的焦点,60y x∠=o,求FA.xFM。
高二数学《抛物线的简单几何性质》学案(第课时)

§2。
3。
2抛物线的简单几何性质(第1课时)[自学目标]:1.掌握抛物线的图形和简单几何性质[重点]:抛物线的简单几何性质的应用[难点]:运用抛物线的定义解决问题[教材助读]:抛物线的几何性质:[1.范围:因为p>0,由方程()022>y可知,这条抛物线上的点M=ppx的坐标(x,y)满足不等式x≥0,所以这条抛物线在y轴的右侧;当x的值增大时,|y|也增大,这说明抛物线向和无限延伸.2.对称性:以-y代y,方程()022>y不变,所以这条抛物线关于px=p对称,我们把抛物线的对称轴叫做抛物线的.3.顶点:抛物线和它的轴的交点叫做.在方程()022>ypx=p中,当y=0时,x=0,因此抛物线()022>y的顶点就是.=ppx4.离心率:抛物线上的点M与和它到的比,叫做抛物线的离心率,用e表示,由抛物线的定义可知,e= 。
源:]()022>=p px y x yO F l()022>-=p px y x yO F l()022>=p py x()022>-=p py x[预习自测]1、求适合下列条件的抛物线方程①顶点在原点,关于 轴对称,并且经过点(5,4)M -, 。
②顶点在原点,焦点是(0,5)F , 。
③顶点在原点,准线是4x = 。
④焦点是(0,8)F - ,准线是8y =, 。
2、若抛物线过点(1,2),则抛物线的标准方程为: 。
x yO F l x yOF l3、有一抛物线型拱桥,当水面距拱顶4米时,水面宽40米,当水面下降1米时,水面宽是多少米?待课堂上与老师和同学探究解决.[合作探究展示点评]探究一:抛物线的定义与性质的应用例1、已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M ,(2,求它的标准方程探究二:实际应用例2、探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯的圆的直径60cm,灯深为40cm,求抛物线的标准方程和焦点位置。
高中数学《抛物线的简单几何性质》(导学案)
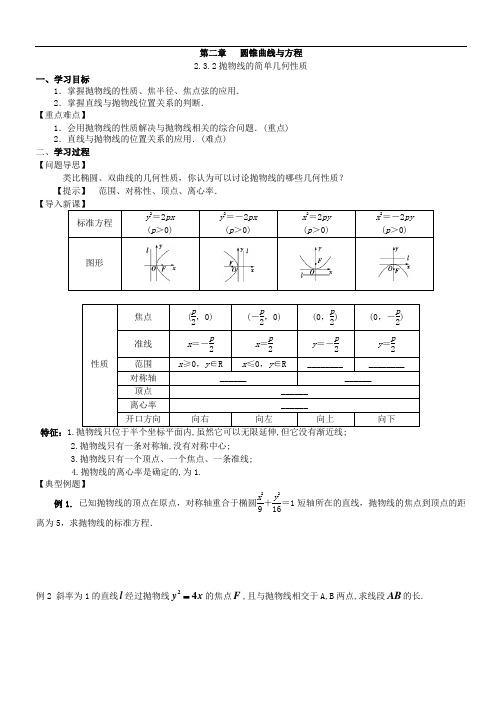
第二章 圆锥曲线与方程 2.3.2抛物线的简单几何性质一、学习目标1.掌握抛物线的性质、焦半径、焦点弦的应用. 2.掌握直线与抛物线位置关系的判断. 【重点难点】1.会用抛物线的性质解决与抛物线相关的综合问题.(重点)2.直线与抛物线的位置关系的应用.(难点) 二、学习过程 【问题导思】类比椭圆、双曲线的几何性质,你认为可以讨论抛物线的哪些几何性质? 【提示】 范围、对称性、顶点、离心率. 【导入新课】标准方程y 2=2px (p >0) y 2=-2px (p >0) x 2=2py(p >0)x 2=-2py(p >0)图形性质焦点 (p2,0) (-p2,0) (0,p2)(0,-p2)准线x =-p 2x =p 2y =-p 2y =p 2范围 x ≥0,y ∈R x ≤0,y ∈R________________对称轴 ____________顶点 ______ 离心率 ______ 开口方向向右 向左向上向下特征:1.2.抛物线只有一条对称轴,没有对称中心;3.抛物线只有一个顶点、一个焦点、一条准线;4.抛物线的离心率是确定的,为1. 【典型例题】例1. 已知抛物线的顶点在原点,对称轴重合于椭圆x 29+y 216=1短轴所在的直线,抛物线的焦点到顶点的距离为5,求抛物线的标准方程.例2 斜率为1的直线l 经过抛物线24y x 的焦点F ,且与抛物线相交于A,B 两点,求线段AB 的长.例3 求过点P(0,1)且与抛物线y2=2x只有一个公共点的直线方程.【变式拓展】1.已知抛物线的顶点在原点,对称轴为y轴,顶点到准线的距离为4,求该抛物线的方程并指出焦点坐标与准线方程.2.直线l:y=kx+1,抛物线C:y2=4x,当k为何值时,l与C有:(1)一个公共点;(2)两个公共点;(3)没有公共点.3.求顶点在原点,焦点在x轴上且截直线2x-y+1=0所得弦长为15的抛物线方程.三、总结反思(1)本节课我们学习了抛物线的几个简单几何性质:范围、对称性、顶点坐标、离心率等概念及其几何意义. (2)了解了研究抛物线的焦半径,焦点弦和通径这对我们解决抛物线中的相关问题有很大的帮助.(3)在对曲线的问题的处理过程中,我们更多的是从方程的角度来挖掘题目中的条件,认识并熟练掌握数与形的联系.在本节课中,我们运用了数形结合,待定系数法来求解抛物线方程,在解题过程中,准确体现了函数与方程以及分类讨论的数学思想.求抛物线弦长问题的方法:(1)一般弦长公式|AB|=|x1-x2|·1+k2=|y1-y2|·1+1k2.(2)焦点弦长设AB是抛物线y2=2px(p>0)的一条过焦点F的弦,A(x1,y1),B(x2,y2),则弦长:|AB|=|AF|+|BF|=x1+x2+p.即求抛物线的焦点弦长,通常是利用焦半径,把点点距转化为点线距(点到准线的距离)解决,这体现了抛物线的特殊性以及求抛物线焦点弦的便捷特点.四、随堂检测1.抛物线x2=-8y的通径为线段AB,O为抛物线的顶点,则AB长是( )A.2B.4C.8D.12.(2015·兰州高二检测)过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=6,那么|AB|= ( )A.6B.8C.9D.103.(2015·阜新高二检测)已知直线l过抛物线C的焦点,且与C的对称轴垂直,l与C交于A,B两点,|AB|=12,点P为C的准线上一点,则△ABP的面积为( )A.18B.24C.36D.484.已知过抛物线y2=6x焦点的弦长为12,则该弦所在直线的倾斜角是( )A.错误!未找到引用源。
抛物线的简单几何性质导学案

2.3.2抛物线的简单几何性质导学案一、学习目标1.能叙述抛物线的简单几何性质,如范围、对称性、顶点和离心率等。
学习过程:在直角坐标系中,顶点在原点,轴与坐标轴重合的共有四种情况,因此抛物线的方程相应也有四种形式,它们都叫抛物线的标准方程。
二、新知探究:以22(0)y px p =>为例来研究(类比椭圆和双曲线用两种方法进行探究) 1、对称性:方法一:观察抛物线:22(0)y px p =>关于____对称,有______条对称轴。
方法二:通过方程证明:2范围:方法一:观察抛物线:22(0)y px p =>的图像在____________, 方法二:通过方程证明:所以抛物线的范围是 。
3、顶点:方法一:观察抛物线:22(0)y px p => 顶点方法二:抛物线22(0)y px p =>令____0==x y 得:所以顶点是___;双曲线有__个顶点,椭圆___个顶点。
4、离心率: ,抛物线22(0)y px p =>的离心率e______。
5、思考:抛物线标准方程中的p 对抛物线开口的影响.在同一坐标系中画出下列抛物线的草图:(1)x y 212= (2)2;y x = (3)22;y x = (4)24.y x = 说明抛物线的开口大小取决于___________________________________。
三、填写下表(用类比的方法):设焦点到准线的距离为P(P>0)1、已知抛物线关于x轴对称,它的顶点在坐标原点,通过点)22,2(-,且以坐标轴为轴,求该抛物线的标准方程.(类比椭圆或双曲线标准方程求法)2、探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处。
已知灯口圆的直径为60cm,灯深40cm,求抛物线的标准方程和焦点位置。
3、P是抛物线24y x=上的点,若P到准线的距离是5,求P点的坐标。
4. P是抛物线24y x=上的点,若P到准线的距离是5,求P点的坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
抛物线的简单几何性质(教师版)
一、学习目标
1.掌握抛物线的范围、对称性、顶点、离心率等几何性质 2.能根据抛物线的几何性质求出抛物线的标准方程
3.在抛物线几何性质的讨论中,注意数与形的结合与转化
二、学习过程 1、复习回顾 (1) 抛物线定义: 叫做抛物线; 叫
做抛物线的焦点; 叫做抛物线的准线。
(2)抛物线的标准方程
2、新课探究(类比椭圆、双曲线的几何性质)
现在我们结合抛物线)0(22>=p px y 的标准方程和图形,共同探究其几何性质: ①范围 : ②对称性: ③顶点: ④离心率:
图形
x
y
O F
l
x
y
O F
l
方程 焦点 准线
x
y O F
l
x
y
O
F l
3、请同学们自主完成下表(思考1)
标准方程
()
022>=p px
y
()
022>=p py
x
图形
x
y
O F
l
范围 0,≥∈y R x
对称性 x 轴
y 轴
顶点
()0,0
焦点
⎪⎭
⎫ ⎝⎛-0,2p
准线方程 2
p x -
=
2
p y -
= 离心率
1=e
4、归纳特点:(师生互动)
(1)__________________________________________________________ (2)___________________________________________________________ (3)___________________________________________________________ (4)___________________________________________________________ 5、例题讲解:
例1、已知抛物线关于x 轴为对称,它的顶点在坐标原点,并且经过点)22,2(-M ,求它的标准方程.
变式:(思考2)
顶点在坐标原点,对称轴是坐标轴,并且经过点M ),(222-的抛物线有几
条?求出它们的标准方程.
例2、斜率为1的直线l 经过抛物线x y 42=的焦点F ,且与抛物线交于B A ,两点, 求线段AB 的长.
知识拓展(思考3)
倾斜角为α的直线经过抛物线)0(22>=p px y 的焦点,与抛物线相交于
B A 、两点.(1)求线段AB 的长. (2)求|AB|的最小值.
发现新结论:(1)________________________(2)_______________________
6、课堂小结:
课后练习与提高
1.过抛物线x y 42=的焦点作直线交抛物线于()11,y x A ,()22,y x B 两点,如果
621=+x x ,那么||AB =( )
(A )10 (B )8 (C )6 (D )4
2.已知M 为抛物线x y 42=上一动点,F 为抛物线的焦点,定点()1,3P ,则
||||MF MP +的最小值为( )
(A )3 (B )4 (C )5 (D )6
3.过抛物线()02>=a ax y 的焦点F 作直线交抛物线于P 、Q 两点,若线段PF 、
QF 的长分别是p 、q ,则
q
p 1
1+=( ) (A )a 2 (B )
a 21 (C )a 4 (D )a
4 4.过抛物线焦点F 的直线与抛物线交于A 、B 两点,若A 、B 在准线上的射影是
A 2,
B 2,则∠A 2FB 2等于
抛物线的简单几何性质
教学目的:
1.掌握抛物线的范围、对称性、顶点、离心率等几何性质;
2.能根据抛物线的几何性质对抛物线方程进行讨论,在此基础上列表、描点、画抛物线图形;
3.在对抛物线几何性质的讨论中,注意数与形的结合与转化
教学重点:抛物线的几何性质及其运用 教学难点:抛物线几何性质的运用
授课类型:新授课 课时安排:1课时
教 具:多媒体、实物投影仪 内容分析:
“抛物线的简单几何性质”是课本第八章最后一节,它在全章占有重要的地位和作用本节知识在生产、生活和科学技术中经常用到,也是大纲规定的必须掌握的内容,还是将来大学学习的基础知识之一 对于训练学生用坐标法解题,本节一如前面各节一样起着相当重要的作用
研究抛物线的几何性质和研究椭圆、双曲线的几何性质一样,按范围、对称性、顶点、离心率顺序来研究,完全可以独立探索得出结论 已知抛物线的标准方程,求它的焦点坐标和准线方程时,首先要判断抛物线的对称轴和开口方向,一次项的变量如果为x (或y ),则x 轴(或y 轴)是抛物线的对称轴,一次项的符号决定开口方向,由已知条件求抛物线的标准方程时,首先要根据已知条件确定抛物线标准方程的类型,再求出方程中的参数p
本节分两课时进行教学 第一课时内容主要讲抛物线的四个几何性质、抛物线的画图、例1、例2、及其它例题;第二课时主要内容焦半径公式、通径、例3 教学过程:
一、复习引入: 1.抛物线定义:
平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹叫做抛物线 定点F 叫做抛
物线的焦点,定直线l 叫做抛物线的准线 2.抛物线的标准方程:
相同点:(1)抛物线都过原点;(2)对称轴为坐标轴;(3)准线都与对称轴垂直,垂足与
图形
x
y
O F
l
x
y
O F
l
方
程 )0(22>=p px y )0(22>-=p px y )0(22>=p py x )0(22>-=p py x
焦点 )0,2
(p )0,2(p -
)2,0(p
)2,0(p -
准线
2
p x -=
2
p x =
2p y -=
2
p y =
x
y O F
l
x
y
O
F l
焦点在对称轴上关于原点对称 它们到原点的距离都等于一次项系数绝对值的
4
1
,即2
42p p = 不同点:(1)图形关于X 轴对称时,X 为一次项,Y 为二次项,方程右端为px 2±、左端为2y ;图形关于Y 轴对称时,X 为二次项,Y 为一次项,方程右端为py 2±,左端为2
x
(2)开口方向在X 轴(或Y 轴)正向时,焦点在X 轴(或Y 轴)的正半轴上,方程右端取正号;开口在X 轴(或Y 轴)负向时,焦点在X 轴(或Y 轴)负半轴时,方程右端取负号
二、讲解新课:
抛物线的几何性质 1.范围
因为p >0,由方程()022
>=p px y 可知,这条抛物线上的点M 的坐标(x ,y)满足不
等式x≥0,所以这条抛物线在y 轴的右侧;当x 的值增大时,|y|也增大,这说明抛物线向右上方和右下方无限延伸. 2.对称性
以-y 代y ,方程()022
>=p px y 不变,所以这条抛物线关于x 轴对称,我们把抛物线
的对称轴叫做抛物线的轴. 3.顶点
抛物线和它的轴的交点叫做抛物线的顶点.在方程()022
>=p px y 中,当y=0时,x=0,
因此抛物线()022
>=p px y 的顶点就是坐标原点.
4.离心率
抛物线上的点M 与焦点的距离和它到准线的距离的比,叫做抛物线的离心率,用e 表示.由抛物线的定义可知,e=1.
对于其它几种形式的方程,列表如下:
标准方程
图形
顶点 对称轴 焦点 准线 离心率
()
022>=p px
y
x
y
O F
l
()0,0
x 轴
⎪⎭
⎫ ⎝⎛0,2p 2
p x -
= 1=e
()
022>-=p px
y
x
y
O F
l
()0,0
x 轴
⎪⎭
⎫ ⎝⎛-0,2p 2
p x =
1=e
()
022>=p py
x
()0,0
y 轴
⎪⎭
⎫ ⎝⎛2,0p 2
p y -
= 1=e
()
022>-=p py
x
()0,0
y 轴
⎪⎭⎫ ⎝
⎛
-2,0p
2
p
y =
1=e
注意强调p 的几何意义:是焦点到准线的距离
抛物线不是双曲线的一支,抛物线不存在渐近线
通过图形的分析找出双曲线与抛物线上的点的性质差异,当抛物线上的点趋向于无穷远时,抛物线在这一点的切线斜率接近于对称轴所在直线的斜率,也就是说接近于和对称轴所在直线平行,而双曲线上的点趋向于无穷远时,它的切线斜率接近于其渐近线的斜率 三、讲解范例:
例1 已知抛物线关于x 轴为对称,它的顶点在坐标原点,并且经过点)22,2(-M ,求它的标准方程,并用描点法画出图形.
分析:首先由已知点坐标代入方程,求参数p .
解:由题意,可设抛物线方程为px y 22
=,因为它过点)22,2(-M , 所以 22)22(2
⋅=-p ,即 2=p 因此,所求的抛物线方程为x y 42
=.。
