四边形复习导学案
四边形中考备考复习导学案

四边形中考备考复习导学案第21课四边形【课标要求】1、多边形的内角和外角和公式、正多边形的概念、四边形的不稳定性2、平行四边形、矩形、菱形、正方形、梯形、等腰梯形的概念和性质3、四边形成为平行四边形、矩形、菱形、正方形、等腰梯形的条件4、线、矩形、平行四边形、三角形的重心及物理意义5、任意一个三角形、四边形或正六边形可以镶嵌平面6、用几种图形进行简单的镶嵌设计【知识要点】四边形有关知识⑴ n边形的内角和为,外角和为。
⑵ 如果一个多边形的边数增加一条,那么它的内角和增加,外角和增加。
⑶ n边形过每一个顶点的对角线有条,n边形的对角线总共有条。
2.平行四边形的性质(1)平行四边形对边__________,对角______;角平分线___________;邻角______。
(2)平行四边形两个邻角的平分线互相______,两个对角的平分线互相______。
(填“平行”或“垂直”)(3)平行四边形的面积公式_________________。
3.平行四边形的判定(1)定义法:________________________________________________。
(2)边:①一组对边_____________________________________________;②两组对边_____________________________________________。
(3 )角:________________________________________________。
(4)对角线:________________________________________________。
特殊的平行四边形的之间的关系5. 特殊的平行四边形的判别条件要使□ABCD成为矩形,需增加的条件是;要使□ABCD成为菱形,需增加的条件是;要使矩形ABCD成为正方形,需增加的条件是;要使菱形ABCD成为正方形,需增加的条件是。
四边形复习导学案

例6.如图,已知E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线BD相交于M、N,若∠EAF=50°,则∠CME+∠CNF=.
类型四、与三角形中位线定理相关的问题
例7.如图,BD=AC,M、N分别为AD、BC的中点,AC、BD交于E,MN与BD、AC分别交于点F、G,求证:EF=EG.
求证:四边形BFDE是平行四边形.
23.如图所示,已知在平行四边形ABCD中,E是边DA的延长线上一点,且AE=AD,连结EC,分别交AB、BD于点F、G。
求证:AF=BF.
导学案
课题
平行四边形复习
科目
数学
类型
上课时间
年级
八年级
班级
学生姓名
编写教师
教研组长
教务处
学校
检查时间
1.平行四边形与特殊的平行四边形的关系:
矩形
有一个角是直角,
平行四边形且有一组邻边相等正方形
菱形
用集合表示为:
2.平行四边形与特殊的平行四边形的性质与判定:
平行四边形
矩形
菱形
正方形
性
质
边
对边平行且相等
13.在平行四边形ABCD中,对角线AC、BD相交于点O,AF⊥BD,CE⊥BD,垂足分别为E、F;连结AE、CF,得四边形AFCE,求证:AFCE是平行四边形.
14.□ABCD中,AE、CF、BF、DE分别为四个内角平分线,求证:EGFH是矩形.
15.如图,∠BAC=90o,BF平分∠ABC交AC于F,EF⊥BC于E,AD⊥BC于D,交BF于G.求证:四边形AGEF为菱形.
11.如图,是用形状、大小完全相同的等腰梯形密铺成的图案,则这个图案中的等腰梯形的底角(指锐角)是___________度.
第十九章四边形复习导学案

第十九章四边形复习导学案学习目标:1.回顾本单元知识,领会四边形以及特殊四边形的概念、性质、判定,以及三角形中位线定理,发展合情推理能力.2.经历四边形基本性质,常见判定方法的复习交流过程,使学生学会“合乎逻辑地思考”,建立知识体系,获得一定的技能基础.学习重点:理解和掌握几种常见特殊四边形的性质、判定.学习难点:发展合情推理和初步的演绎推理能力.一、预习导航:你能试着完成下面四边形及其特殊四边形的关系图吗?四边形2、菱形的周长为40cm,一对角线长是16cm,则另一对角线长____,面积_____,高是______;3、四边形ABCD,E,F,G,H分别是四边的中点,则①四边形EFGH是________;②当四边形ABCD满足条件______时,四边形EFGH是矩形;当四边形ABCD满足条件______时,四边形EFGH是菱形;当四边形ABCD满足条件______时,四边形EFGH是正方形;4、直角梯形中,斜腰与底的夹角为60°,若这腰与上底的长都是8cm,则这梯形的周长是().A.24+43 B.26+43 C.28+43 D.32+435、如图,□ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3 cm,则AB的长为 ( )A.3 cm B.6 cm C.9 cm D.12 cm6、用两个全等的直角三角形拼下列图形:①平行四边形(不包含菱形、矩形、正方形);②矩形;③菱形;④正方形;⑤等腰三角形.一定可以拼成的图形是__________________________(填序号)二、合作交流:1、平行四边形ABCD的周长32,5AB=3BC,则对角线AC的取值范围为( )A. 6<AC<10B. 6<AC<16C. 10<AC<16D. 4<AC<162、菱形ABCD,AB=2,∠DAB=60°,E是AB中点,P是AC上任一点,则PE+PB的最小值是____;3已知:如图,四边形ABCD是平行四边形,DE//AC,交BC的延长线于点E,EF⊥AB于点F,求证:AD=CF。
四边形复习(预习、展示)导学案
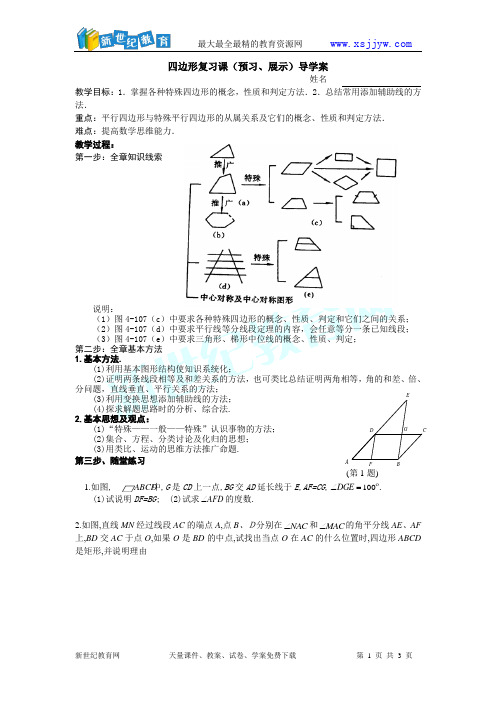
四边形复习课(预习、展示)导学案姓名教学目标:1.掌握各种特殊四边形的概念,性质和判定方法.2.总结常用添加辅助线的方法.重点:平行四边形与特殊平行四边形的从属关系及它们的概念、性质和判定方法. 难点:提高数学思维能力. 教学过程:第一步:全章知识线索说明:(1)图4-107(c )中要求各种特殊四边形的概念、性质、判定和它们之间的关系; (2)图4-107(d )中要求平行线等分线段定理的内容,会任意等分一条已知线段; (3)图4-107(e )中要求三角形、梯形中位线的概念、性质、判定; 第二步:全章基本方法 1.基本方法.(1)利用基本图形结构使知识系统化;(2)证明两条线段相等及和差关系的方法,也可类比总结证明两角相等,角的和差、倍、分问题,直线垂直、平行关系的方法;(3)利用变换思想添加辅助线的方法; (4)探求解题思路时的分析、综合法. 2.基本思想及观点:(1)“特殊——一般——特殊”认识事物的方法; (2)集合、方程、分类讨论及化归的思想; (3)用类比、运动的思维方法推广命题. 第三步、随堂练习 (第1题)1.如图中,G 是CD 上一点,BG 交AD 延长线于E ,AF=CG , 100=∠DGE . (1)试说明DF=BG ; (2)试求AFD ∠的度数.2.如图,直线MN 经过线段AC 的端点A ,点B 、D分别在NAC ∠和MAC ∠的角平分线AE 、AF 上,BD 交AC 于点O ,如果O 是BD 的中点,试找出当点O 在AC 的什么位置时,四边形ABCD 是矩形,并说明理由A B CD FEGMNABEODCF(第2题)形形。
⑥是中心对称图形相平分的四边形。
矩形有一个角是直角的平行四边形叫矩形。
除具有平行四边形的性质外,还有①四个角都是直角 ②对角线相等 ③既是中心对称图形又是轴对称图形。
①有三个角是直角的四边形是矩形; ②对角线相等的平行四边形是矩形; ③定义。
三年级复习《四边形》导学案

三年级数学上册《四边形》复习导学案一、基本概念:认识四边形的特征、认识平行四边形,知道周长的含义。
二、解决问题:会在方格纸上画相应图形,求长方形和正方形的周长及相关题型。
一、典型示例:1、用一条长16厘米长的红丝带围成一个正方形,这个正方形的周长是( )厘米,它的边长是( )厘米。
2.用3个边长是2厘米的小正方形拼成一个大的长方形,这个长方形的周长是( )厘米。
3、给一个边长为4米的正方形菜地围上栅栏,菜地一面靠墙,栅栏至少要()米。
4、画两个周长为16厘米的正方形或长方形。
5、用两个长是6厘米,宽是3厘米的长方形拼成一个长方形和一个正方形。
拼成的长方形和正方形的周长是多少厘米?二、对应练习:1、选择(1)、用两个边长3厘米的正方形拼成一个长方形,这个长方形的周长是()。
A、4厘米B、12厘米C、18厘米(2)、把正方形的边长扩大2倍后,这个正方形的周长()。
A、也扩大2倍B、不变C缩小2倍2、一个长8厘米,宽4厘米的长方形的周长与一个正方形的周长相等,正方形的周长是多少厘米?边长是多少厘米?3、如图,这个长方形的长是12厘米,宽是8厘米,如果在里面剪一个最大的正方形,正方形的边长是多少厘米?正方形的周长是多少厘米?剩下的图形的周长是多少厘米?4、我想把桌子的一周围上一圈装饰布,这张桌子宽4分米,长是宽的2倍,算一算,至少需要买多少分米的装饰布?5、一根铁丝可以围成一个边长是8米的正方形,现在改围成一个长方形,如果这个长方形的宽是7米,那么长是多少米?三、课堂测试:1、判断(1)、周长相等的两个长方形,它的形状、大小都一样。
()(2)、平形四边形不一定是四边形。
()(3)、四条边相等的四边形一定是正方形。
()(4)、知道长方形的两条边的长度可以求出它的周长。
()2、一块靠墙的长方形菜地,菜地的长是7米,宽是3米,给菜地的四周围上栅栏,栅栏长多少米?3、一张方桌的边长是2米,用一条90分米长的彩带能够围一圈吗?4、妈妈买回来一块方形的桌布,边长是10分米,现在要给这块桌布缝上一圈花边,请问要准备多长的花边?5、光明广场长350,宽比长短200米,小明沿着广场的四周骑自行车,小明一圈骑了多少米?。
四边形专题复习导学案
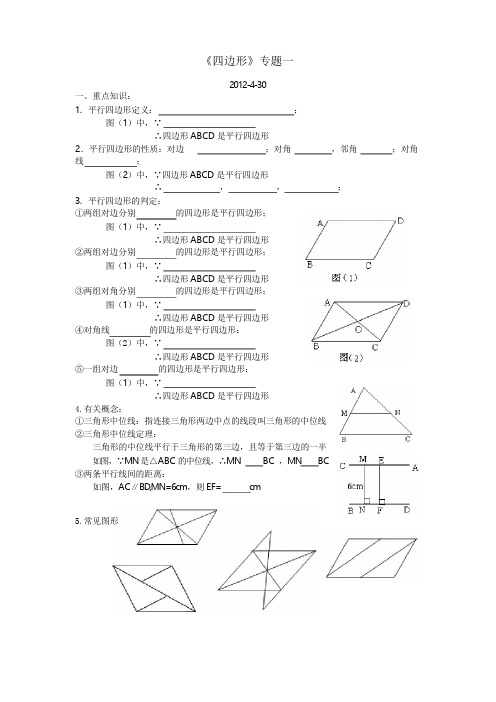
《四边形》专题一2012-4-30一、重点知识:1.平行四边形定义:;图(1)中,∵∴四边形ABCD是平行四边形2.平行四边形的性质:对边;对角,邻角;对角线;图(2)中,∵四边形ABCD是平行四边形∴,,;3.平行四边形的判定:①两组对边分别的四边形是平行四边形;图(1)中,∵∴四边形ABCD是平行四边形②两组对边分别的四边形是平行四边形;图(1)中,∵∴四边形ABCD是平行四边形③两组对角分别的四边形是平行四边形;图(1)中,∵∴四边形ABCD是平行四边形④对角线的四边形是平行四边形;图(2)中,∵∴四边形ABCD是平行四边形⑤一组对边的四边形是平行四边形;图(1)中,∵∴四边形ABCD是平行四边形4.有关概念:①三角形中位线:指连接三角形两边中点的线段叫三角形的中位线②三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半如图,∵MN是△ABC的中位线,∴MN BC,MN BC③两条平行线间的距离:如图,AC∥BD,MN=6cm,则EF=cm5.常见图形二、常见题型(1)利用平行四边形的性质证角相等、线段相等或进行角的计算线段的计算(2)利用平行四边形的性质证线段相等或进行(3)平行四边形判定定理的灵活应用(4)运用三角形中位线定理解题例1.在ABCD中AE⊥BC,AF⊥CD,E、F是垂足,①若∠B=50°,求ABCD的其它三个角和∠EAF的度数;②若ABCD的周长为36cm,A E=43cm,AF=53cm求这个平行四边形的面积;例2.四边形ABCD和四边形AECF都是平行四边形,证明:∠BAE=∠DCF例3.ABCD中,对角线AC、BD交于点O,①ABCD的周长32△cm,AOB比△BOC的周长少4cm,求ABCD各边的长;②过O的直线交AD、BC于E、F,求证:OE=OF③若AB=5cm,BC=8cm,OE=3cm,求四边形ABFE的周长例4.ABCD中,E、F分别是中点,AF、BE交于G,CE、DF交于H,试说明四边形GFHE的形状。
第十九章 四边形复习课导学案
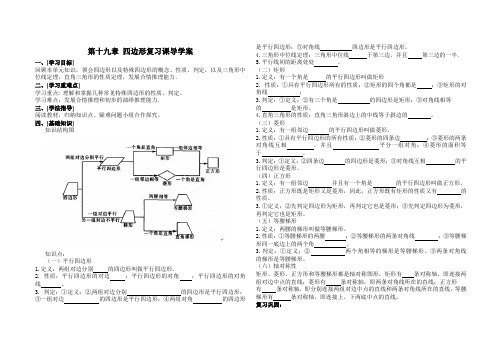
第十九章四边形复习课导学案一、[学习目标]回顾本单元知识,领会四边形以及特殊四边形的概念、性质、判定,以及三角形中位线定理,直角三角形的性质定理,发展合情推理能力.二、[学习重难点]学习重点:理解和掌握几种常见特殊四边形的性质、判定。
学习难点:发展合情推理和初步的演绎推理能力.三、[学法指导]阅读教材,归纳知识点、疑难问题小组合作探究。
四、[基础知识]知识结构图知识点:(一)平行四边形1.定义:两组对边分别的四边形叫做平行四边形。
2. 性质:平行四边形的对边;平行四边形的对角;平行四边形的对角线。
3. 判定:①定义;②两组对边分别的四边形是平行四边形;③一组对边的四边形是平行四边形;④两组对角的四边形是平行四边形;⑤对角线四边形是平行四边形。
4.三角形中位线定理:三角形中位线于第三边,并且第三边的一半.5.平行线间的距离处处。
(二)矩形1.定义:有一个角是的平行四边形叫做矩形2. 性质:①具有平行四边形所有的性质;②矩形的四个角都是;③矩形的对角线;3.判定:①定义;②有三个角是的四边形是矩形;③对角线相等的是矩形。
4.直角三角形的性质:直角三角形斜边上的中线等于斜边的。
(三)菱形1.定义:有一组邻边的平行四边形叫做菱形。
2.性质:①具有平行四边形的所有性质;②菱形的四条边;③菱形的两条对角线互相,并且平分一组对角;④菱形的面积等于。
3.判定:①定义;②四条边的四边形是菱形;③对角线互相的平行四边形是菱形。
(四)正方形1.定义:有一组邻边并且有一个角是的平行四边形叫做正方形。
2.性质:正方形既是矩形又是菱形,因此,正方形既有矩形的性质又有的性质。
3.①定义;②先判定四边形为矩形,再判定它也是菱形;③先判定四边形为菱形,再判定它也是矩形。
(五)等腰梯形1.定义:两腰的梯形叫做等腰梯形。
2.性质:①等腰梯形的两腰;②等腰梯形的两条对角线;③等腰梯形同一底边上的两个角。
3.判定:①定义;②两个角相等的梯形是等腰梯形。
四边形复习 精品导学案
精品“正版”资料系列,由本公司独创。
旨在将“人教版”、”苏教版“、”北师大版“、”华师大版“等涵盖几乎所有版本的教材教案、课件、导学案及同步练习和检测题分享给需要的朋友。
本资源创作于2020年8月,是当前最新版本的教材资源。
包含本课对应内容,是您备课、上课、课后练习以及寒暑假预习的最佳选择。
导学稿姓名:班级:审核:四边形复习教学目标:掌握特殊平行四边形、梯形的相关概念通过添加辅助线灵活几何解决问题课前准备:本章知识结构图:(2)三角形的中位线:___________________________________________三角形中位线定理:_________________________________________________直角三角形斜边上的中线______________________斜边一半 菱形的面积公式:___________________________________梯形的中位线定理:______________________________________________ 梯形的面积公式:____________________________________________自我检测: 一、选择题1. 如图,梯形ABCD 中,AD ∥BC ,设AC ,BD 交于O 点,则图中共有对面积相等的三角形. A. 2B. 3C. 4D. 522 Rt △ABC 的两边长分别是3和4,若一个正方形的边长是△ABC 的第三边,则这个正方形的面积是 A.25 B.7 C.12 D.25或73. 已知菱形的边长等于2cm,菱形的一条对角线也是长2cm,则另一条对角线长是 A.4cm B.32cm C.cm 3 D.3cm4. 两条对角线相等且互相平分的四边形是A.平行四边形B.菱形C.正方形D.矩形5.平行四边形的周长为24cm ,相邻两边长的比为3:1,•那么这个平行四边形较短的边长为( ).(A )6cm (B )3cm (C )9cm (D )12cm 6.下列说法正确的是( ).(A )有两组对边分别平行的图形是平行四边形 (B )平行四边形的对角线相等(C )平行四边形的对角互补,邻角相等 (D )平行四边形的对边平行且相等7.在四边形ABCD 中,AD ∥BC ,若ABCD 是平行四边形,则还应满足( ). (A )∠A+∠C=180° (B )∠B+∠D=180°ODCA(C )∠A+∠B=180° (D )∠A+∠D=180°8.一个多边形的内角和等于外角和的一半,那么这个多边形是( ) (A )三角形 (B )四边形 (C )五边形 (D )六边形二、填空题11. 若菱形ABCD 中,,于E BC AE ⊥菱形ABCD 的面积为248cm ,cm AE 6=,则AB 的长度为 _________12. 如图,平行四边形ABCD 的对角线AC 、BD 交于O,EF 过点O 与AD 、BC 分别交于E 、F,若AB=4,BC=5,OE=1.5,则四边形EFCD 的周长_________13. 梯形中ABCD ,AD ∥BC ,︒=∠90B ,4=AD , 8=AB ,,10=BC 则=CD _________14. 平行四边形ABCD 中,cm AB 6=,cm BC 12=,对边AD 和BC 之间的距离是cm 4,则对边AB 和CD 间的距离是_____________14.已知平行四边形的面积是144cm 2,相邻两边上的高分别为8cm 和9cm ,则这个平行四边形的周长为________.15.平行四边形两邻角的平分线相交所成的角为_________.16.如图1,P 是四边形ABCD 的DC 边上的一个动点.当四边形ABCD 满足条件______时,△PBA 的面积始终保持不变(注:只需填上你认为正确的一种条件即可).(1) (2) (3) 17.如图2,在ABCD 中,∠A 的平分线交BC 于点E .若AB=10cm ,AD=14cm ,则BE=______,EC=________.18.如图3,用9个全等的等边三角形,按图拼成一个几何图案,从该图案中可找出____个平行四边形.三、解答题19.如图,在ABCD中,DB=CD,∠C=70°,AE⊥BD于点E.试求∠DAE 的度数.20.已知:如图,在△ABC中,中线BE,CD交于点O,F,G分别是OB,OC 的中点.求证:四边形DFGE是平行四边形.21.如图,正方形网格中的每个小正方形边长都是1,•每个小格的顶点叫做格点.以格点为顶点分别按下列要求画图:(1)在图甲中,画出一个平行四边形,使其面积为6;(2)在图乙中,画出一个梯形,使其两底和为5.22.如图,BC为固定的木条,AB,AC为可伸缩的橡皮筋.当点A在与BC•平行的轨道上滑动时,你能说明△ABC的面积将如何变化吗?并说明你的理由.23.小明为测量池塘的宽度,在池塘的两侧A,B引两条直线AC,BC相交于点C,在BC上取点E,G,使BE=CG,再分别过点E,G作EF∥AB,GH∥AB,交AC于点F,H.测出EF=10m,GH=4m(如图).小明就得出了结论:池塘的宽AB为14m.你认为小明的结论正确吗?请说明你的理由.24.李大伯家有一口如图所示的四边形的池塘,在它的四个角上均有一棵大柳树.李大伯准备开挖池塘,使池塘面积扩大一倍,又想保持柳树不动.如果要求新池塘成平行四边形的形状.请问李大伯的愿望能否实现?若能,请画出你的设计;若不能,请说明理由.本课教学反思英语教案注重培养学生听、说、读、写四方面技能以及这四种技能综合运用的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
八年级数学学科导学案
主编人:_董魁__校编人:_荣伟伟__学科组长:_董魁__包科领导:__张其舜_
课题第20章四边形的复习课
使用说明与学法指导:本节课主要对20章知识点进行梳理,让学生回顾本单元知识,领会四边形以及特殊四边形的概念、性质、判定,以及三角形中位线定理,发展合情推理能力.通过类比的方法掌握各种四边形的规律、特点、性质、判定,并会将之运用在实际实际问题中。
学习目标: 1、经历四边形基本性质,常见判定方法的复习交流过程,使学生学会“合乎逻辑地思考”,建立知识体系,获得一定的技能基础.
2、让学生理解平面几何观念的基本途径是多种多样的,感知和体验几何图形的现实意义,体验二维空间相互转换关系.
教学重难点:
重点:理解和掌握几种常见特殊四边形的性质、判定.
难点:发展合情推理和初步的演绎推理能力.
【课前预习案】
「自主学习·整体感知」
1.旧知回顾:
①.认知起点:在学完四边形、特殊四边形的内容后进行小结.
②.知识线索:本章知识是在相交线、•平行线和三角形知识的基础上发展起来的,基本上按四边形、特殊四边形及其性质与判定思路展开知识.
③.学习方式:合作、交流、探究、归纳.
2.知识结构:
【学生活动】:首先参与教师的回顾,然后分成四人小组进行交流,最后进行小组汇报,弄清本单元的知识体系.
【设计意图】采用师生互动,发挥学生主动复习的意识,提高知识层面.
【课内探究案】
「合作探究·展示点评」
1.四边形的内角和外角和都是360°,这两个定理点四边形的角度计算和四边形的推理证明的基础. 2.任意多边形问题,常设法应用三角形的知识去解决.
【课堂演练】(投影显示)
演练题:如图,已知四边形ABCD中,AB=3,BC=4,CD=13,AD=12,∠B=90°,求四边形ABCD的面积S.
思路点拨:把不规则的四边形转化成几个规划的三角形或熟悉的图形,如,矩形,平行四边形等,本题由∠B=90°启发,连接AC,这样把问题归结到Rt△中,•应用勾股定理以及逆定理解决.因为AC2=AB2+BC2=9+16=25,∴AC=5,
又∵AD2+AC2=CD2,∴∠DAC=Rt∠,
∴S=S△ABC+S△DAC=
1
2
AB·BC+
1
2
AD·AC=36.
学生活动:先独立完成演练题,然后再踊跃上台演示,并归纳小结知识点,和解题方法.
教师活动:关注学生的思维,请一些学生上台演示,然后与学生一起纠正.
导语:对本章的知识点用问题的形式列举出来。
A类探究点:
1.平行四边形是一类特殊的四边形,它包括了矩形、菱形、正方形.•平行四边形是中心对称图形(以后再学).
2.平行四边形主要性质:对边相等,对角相等,对边平行,•对角线互相平分.
3.平行四边形性质是证明或计算的基础.如,应用边的性质(对边平行、•对边相等),可以求解(证)边长、周长、对角线长以及平行等问题;应用角的性质(对角相等、邻角互补),可以求解(证)角的问题;应用对角线性质(对角线互相平分),可证明两个三角形全等,再通过三角形全等研究角或线段之间的关系.
4.由平行四边形的性质可以得出一些角与线段的相等关系,特别地,•还可以知道平行线间的距离处处相等.
5.平行四边形判定的题目,应根据不同条件,灵活选用,•证明中不论选用什么方法,都离不开线段的平行、相等,直角的相等关系.
B类探究点
演练题:已知:如图,E、F为 ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种证法).
思路点拨:证法1:运用 ABCD的性质证明△ABE≌△CDF的条件,从而证出BE=DF.证法2:连结DE、BF、BD,设BD与AC相交于O,去证明四边形BFDE是平行四边形即可.学生活动:先独立完成演练题,然后以此为素材进行思维归纳、交流.
教师活动:操作投影仪,显示演练题,巡视、引导学生进行演练,关注“学困生”.请部分学生上台演练,然后纠正.
评析:在有关特殊四边形的问题中,通常转化为三角形或直接运用特殊四边形自身性质来解决.思路不唯一,但应选择较好的方法.
【训练案】
A类训练题
1:如图,矩形ABCD的对角线AC、BD相交于点O,CE⊥BO于E,且DE:EB=3:1,OF⊥AB 于F,OF=3.6cm,求矩形对角线长.
2:已知:如图,EG、FH过正方形ABCD的对角线交点O,EG⊥FH,求证:四边形EFGH是正方形.(用两种证法)
第一题思路点拨:CD⊥平分OB,可以得到△OBC是等边三角形,推出∠CBO=60°,•因此可得∠OBF=30°,∴OB=2OF=7.2.求出矩形对角线长为14.4cm,这里用到了Rt△中,30°角所对的边等于斜边的一半.
第二题思路点拨:证法1:•应用正方形的性质来证明三角形全等的条件,•证△DOE•≌△COF.从而解决问题;证法2:通过证法1中,△DOE≌△COF.得ED=FC.同理,ED=•FC=•GB=HA,得Rt△FDE≌Rt △GCF≌Rt△HBG≌Rt△EAH,∴EF=FG=HG=EH.再应用∠BEF+•∠BFE=90°,得出∠FEH=90°.
B类训练题
1:已知:如图,在梯形ABCD中,AD∥BC,E、G、F、H分别是AB、DC•的中点,EF分别交BD、AC于G、H,AD=4cm,BC=6cm,求GH的长.
2:矩形ABCD中,E、F分别在对角线AC、BD上,且AE=DF•,•求证:四边形EBCF是等腰梯形.
第一题思路点拨:本题应分别把EH、EG当作△ABC、△ABD的中位线,利用三角形中位线定理求解GH=1.
第二题思路点拨:思路点拨:利用矩形性质,中位线定理证EF∥BC且EF≠BC,再证BE=FC.【预习指导】
名称定义性质判定面积
平
行
四
边
形
两组对边
分别平行
的四边形
叫做平行
四边形。
①对边平行;②对边相
等;③对角相等;④邻角
互补;⑤对角线互相平
分;⑥是中心对称图形。
①定义;②两组对边
分别相等的四边形;
③一组对边平行且相
等的四边形;④两组
对角分别相等的四边
形;⑤对角线互相平
分的四边形。
S=ah(a为一边长,
h为这条边上的高)
矩
形
有一个角
是直角的
平行四边
形叫做矩
形
除具有平行四边形的性
质外,还有:①四个角都
是直角;②对角线相等;
③既是中心对称图形又
是轴对称图形。
①有三个角是直角的
四边形是矩形;②对
角线相等的平行四边
形是矩形;③定义。
S=ab(a为一边长,b
为另一边长)
菱
形
有一组邻
边相等的
平行四边
形叫做菱
形。
除具有平行四边形的性
质外,还有:①四条边相
等;②对角线互相垂直,
且每一条对角线平分一
组对角;③既是中心对称
图形又是轴对称图形。
①四条边相等的四边
形是菱形;②对角线
垂直的平行四边形是
菱形;③定义。
①S=ah(a为一边长,
h为这条边上的高);
②S=
1
2
bc(b、c为两
条对角线的长)
正方形
有一组邻
边相等且
有一个角
是直角的
平行四边
形叫做正
方形
具有平行四边形、矩形、
菱形的性质:①四个角是
直角,四条边相等;②对
角线相等,互相垂直平
分,每一条对角线平分一
组对角;③既是中心对称
图形又是轴对称图形。
①有一组邻边相等的
矩形是正方形;②有
一个角是直角的菱形
是正方形;③定义。
①S=a2(a为边长);
②S=
1
2
b2(b为对角
线长)。
