抛物线的焦点弦问题重要结论绝对经典.doc
抛物线焦点弦性质总结
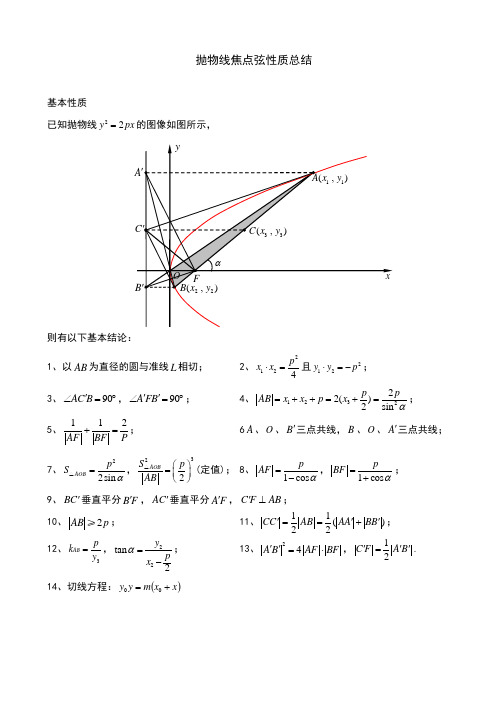
抛物线焦点弦性质总结基本性质已知抛物线22y px =的图像如图所示,则有以下基本结论:1、以AB 为直径的圆与准线L 相切;2、2124p x x ⋅=且212y y p ⋅=-;3、90AC B '∠=︒,90A FB ''∠=︒;4、123222()2sin p p AB x x p x α=++=+=;5、112AF BF P +=;6A 、O 、B '三点共线,B 、O 、A '三点共线;7、22sin AOB p S α=△,322AOB S p AB ⎛⎫= ⎪⎝⎭△(定值); 8、1cos p AF α=-,1cos p BF α=+; 9、BC '垂直平分B F ',AC '垂直平分A F ', C F AB '⊥;10、2AB p ≥;11、11()22CC AB AA BB '''==+; 12、3AB p k y =,22tan 2y p x α=-; 13、24A B AF BF ''=⋅,12C F A B '''=. 14、切线方程:()x x m y y +=00性质深究一、焦点弦与切线结论1、过抛物线焦点弦的两端点作抛物线的切线,两切线交点在准线上.特别地,当弦x AB ⊥轴时,则点P 的坐标为,02p ⎛⎫- ⎪⎝⎭. 结论2、切线交点与弦中点连线平行于对称轴结论3、弦AB 不过焦点即切线交点P 不在准线上时,切线交点与弦中点的连线也平行于对称轴.结论4、过抛物线准线上任一点作抛物线的切线,则过两切点的弦必过焦点. 特别地,过准线与x 轴的交点作抛物线的切线,则过两切点AB 的弦必过焦点.结论5、过准线上任一点作抛物线的切线,过两切点的弦最短时,即为通径.AB 是抛物线px y 22=(p >0)焦点弦,Q 是AB 的中点,l 是抛物线的准线,l AA ⊥1,l BB ⊥1,过A ,B 的切线相交于P ,PQ 与抛物线交于点M .则有结论6、PA ⊥PB .结论7、PF ⊥AB . 结论8、M 平分PQ . 结论9、PA 平分∠A 1AB ,PB 平分∠B 1BA .结论102FB FA =结论11、PAB S ∆2min p =二、非焦点弦与切线 当弦AB 不过焦点,切线交于P 点时,也有与上述结论类似结果:结论12、①p y y x p 221=,221y y y p += 结论13、PA 平分∠A 1AB ,同理PB 平分∠B 1BA .结论14、PFB PFA ∠=∠结论15、点M 平分PQ结论162PF FB FA =。
抛物线过焦点的弦的八个结论

抛物线过焦点的弦的八个结论关于抛物线过焦点的弦,基本上我们可以得出八个结论。
首先,任何抛物线都可以用焦点和直线来描述,而这些直线就是抛物线的弦。
这些弦是由焦点和抛物线的两个端点组成的,它们可以帮助我们确定抛物线的方向和形状。
其次,这些弦经常穿过抛物线上的焦点。
它们是从抛物线的端点到焦点的一条直线,这条直线是抛物线的一部分。
这通常被称为“焦点弦”,它可以帮助我们更好地理解抛物线的形状,特别是当它穿过焦点时。
第三,这些弦有时也会穿过抛物线上的端点。
这可以帮助我们更好地理解抛物线的形状,特别是当抛物线的两个端点在同一条直线上时。
第四,这些弦可以帮助我们确定抛物线的方向和形状。
例如,如果抛物线的弦是从左到右的,那么它的焦点就会位于右侧,这意味着抛物线会向右延伸。
第五,抛物线的弦可以用来求出抛物线的长度。
这是因为弦的长度就是两个端点之间的距离,而抛物线的长度就是两个端点之间的距离。
第六,抛物线的弦可以帮助我们求出抛物线的面积。
这是因为抛物线的面积是由两个端点之间的弦组成的,而弦的面积就是这些端点之间的距离。
第七,抛物线的弦可以用来求出抛物线的切线。
这是因为弦的切线也是由两个端点之间的距离组成的,而抛物线的切线也是由两个端点之间的距离组成的。
最后,抛物线的弦还可以用来计算抛物线的曲率。
这是因为抛物线的曲率是由两个端点之间的弦组成的,而弦的曲率也是由两个端点之间的距离组成的。
总的来说,焦点弦对于理解抛物线的形状和方向至关重要,它们还可以帮助我们求出抛物线的长度、面积、切线和曲率。
因此,了解抛物线的弦可以帮助我们更好地理解抛物线的特性,从而帮助我们更好地求解抛物线的问题。
抛物线的焦点弦的性质
过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交 点为A(x1,y1)、B(x2,y2),
思考:点A、B在抛物线准线上的射影为A1, B1,
∠ A1FB1的大小是多少?
A1
B1
结论6: ∠ A1FB1 =90
过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交 点为A(x1,y1)、B(x2,y2),
1 cos
1 cos
FA FB p
过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交 点为A(x1,y1)、B(x2,y2),
思考:若直线AB与x轴的夹角为,焦点∆AOB的面积如何用表示
结论(4)
SAOB
p2
2sin
过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交 点为A(x1,y1)、B(x2,y2), 思考:以线段AB为直径的圆与准线有怎样的位置关系? 思考:以线段AF为直径的圆与y轴有怎样的位置关系?
例1. 设F为抛物线C:y2=3x的焦点,过点F且倾斜角为30°的 直线交C于A,B两点, 则(1)|AB|=( );(2)S∆AOB=( )。
变式:将本题中条件倾斜角30o改为|AF|=3,求S∆AOB。
1.如图,过抛物线C: y2=2px(p>0)的焦点F的直线交抛物线于点A,B,交其准 线L于点C,若F是AC的中点,且|AF|=4则线段AB的长为( )
2.已知抛物线C: y2=2px(p>0)的焦点为F,过F的直线与该抛物线交于P,Q两个 不同的点,P,Q两点在抛物线的准线上的射影分别为M,N,若|MF|=4, |NF|=4, 则p=( )
证明抛物线焦点弦的18个结论

证明抛物线焦点弦的18个结论
抛物线是一种椭圆形的函数图形,它是由抛物线焦点弦决定的。
抛物线焦点弦是指抛物线的两个焦点和连接它们的弦段。
围绕抛物线焦点弦可以建立18个结论。
1. 两个焦点之间的距离与抛物线弦段长度相同,即它们之间的距离等于抛物线弦段的1倍。
2. 弦段连接抛物线的两个焦点,因此,任何一点的垂直距离都等于其焦点的距离。
3. 对抛物线的焦点取中对称,则其两点之间的距离一定是直线的1倍.
5. 相对于一个焦点而言,另一个焦点总是处于弦段的同一边,而且位于弦段上面。
6. 抛物线是对称的,即抛物线的对称轴是连接两个焦点的直线段。
8. 抛物线准线与切线交于抛物线的焦点。
12. 对任意点A而言,从A点向任意点B连线便构成一条直线,此直线连接A点和B 点的距离有正有负,正值表示线段到抛物线焦点的距离是它的弦段长度所乘以2倍的直线段距离,负值则表示抛物线焦点到线段的距离也是它的弦段长度乘以2倍的直线段距离。
17. 抛物线的对称轴与它的弦段垂直,因此它的弦段将对称轴分为2个相等的距离。
以上就是抛物线焦点弦的十八个结论,也是其对称性规律、准确性和完整性的总结。
抛物线焦点弦的这些结论,既给抛物线函数提供了数学化的更直观的解释,又为描述抛物线的属性提供了一定的参考依据。
(完整版)抛物线的焦点弦_经典性质及其证明过程
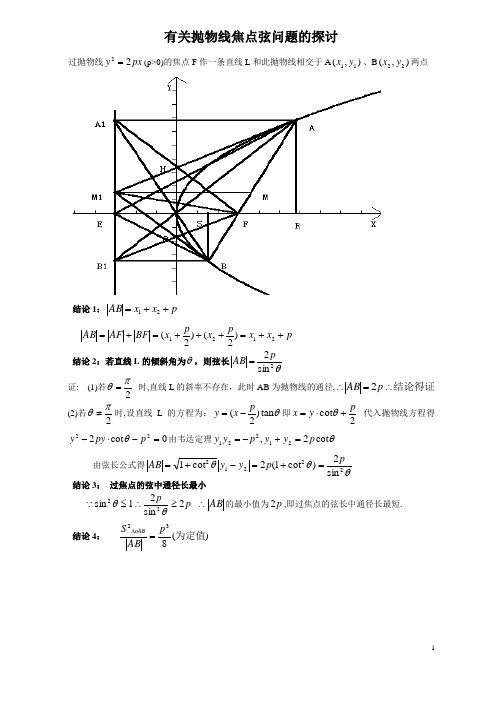
有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1:p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB =证: (1)若2πθ= 时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3: 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4: )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5: (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P Py y x x p y x p y x ==∴== 结论6:以AB 为直径的圆与抛物线的准线相切证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1, 过M 点作准线的垂线MM 1,由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7:连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8:(1)AM 1⊥BM 1 (2)M 1F ⊥AB (3)BF AF FM ⋅=21(4)设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 则M 1,Q ,F ,H 四点共圆 (5)2121214M M B M AM =+证:由结论(6)知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9: (1)、A O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3)设直线AO 与抛物线的准线的交点为B 1,则BB 1平行于X 轴(4)设直线BO 与抛物线的准线的交点为A 1,则AA 1平行于X 轴证:因为p y p y k y p p y y x y k oB oA 2212111122,221-=-====,而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。
[很全]抛物线焦点弦的有关结论
![[很全]抛物线焦点弦的有关结论](https://img.taocdn.com/s3/m/ef2d77a3c1c708a1284a44ba.png)
p2 .
4
综上: x1x2
p2 .
4
(2)Q x1
y12 2p
,
x2
y22 2p
, y12 y2 2
p4
y1 y2
p2,
但 y1 y2 0, y1 y2 p 2
(2)另证:设
AB :
x
my
p 2
与
y2
2 px 联立,得
y2
2 pmy
p2
0,
y1 y2
y 2 2 px
t
y2
2 pay
2 pt
0
y1 y2 2 pt ②
由①②得 t p 2
AB 恒过焦点 p ,0 2
5
抛物线 y 2 2 pxp 0
成立。
,过(2p,0)的直线与之交于 A、B 两点,则 OA⊥OB。反之也
小结: (1)抛物线中的焦点弦问题很多都可以转化为这个直角梯形中的问题,在解决这类问题 时注意对这个梯形的运用; (2)万变不离其宗,解决问题的关键仍然是抛物线定义.
m
n
mn
sin y1 y2 mn
S AOB
1 m nt
2
y1 y2 1 m nt
mn 2 mn
y1 y2
而 S AOB
p2 4
n m
m n
1 2
m n
mn
p2 2
t
y1 y2
p2 2
①
l : x ay 又可设
[很全]抛物线焦点弦的有关结论附答案
![[很全]抛物线焦点弦的有关结论附答案](https://img.taocdn.com/s3/m/4d4653f1ec3a87c24028c4c5.png)
[很全]抛物线焦点弦的有关结论知识点1:若是过抛物线的焦点的弦。
设,AB ()022>=p px y F (),,11y x A ()22,y x B 则(1);(2)4221p x x =221p y y -=证明:如图,(1)若的斜率不存在时,AB 依题意,221px x ==4221p x x =∴若的斜率存在时,设为则AB ,k ⎝⎛=:k y AB ()42222222222=++-⇒=⎪⎭⎫ ⎝⎛-p k px k x k px p x k 综上:.4221p x x =∴.4221p x x =(2),p y x p y x 2,2222211==Q ,22142221p y y p y y ±=⇒=∴但22121,0p y y y y -=∴<(2)另证:设与联立,得2:pmy x AB +=px y 22=22122,02p y y p pmy y -=∴=--知识点2:若是过抛物线的焦点的弦。
设,AB ()022>=p px y F (),,11y x A ()22,y x B 则(1)(2)设直线的倾斜角为;21p x x AB ++=AB α证明:(1)由抛物线的定义知,2,221px BF p x AF +=+=p x x BF AF AB ++=+=∴21(2)若由(1)知,2,90210p x x ===则α2p AB ==若联立,得px y p x k y AB 2,2:,9020=⎪⎭⎫ ⎝⎛-=≠与设α()42222222222=++-⇒=⎪⎭⎫ ⎝⎛-p k px k x k px p x k ,而,(),22221k k p x x +=+∴()222112k k p p x x AB +=++=∴αtan =k ()ααα222sin 2tan tan 12pp AB =+=∴知识点3:若是过抛物线的焦点的弦,则以为直径的圆与AB ()022>=p px y F AB 抛物线的准线相切。
抛物线焦点弦性质总结
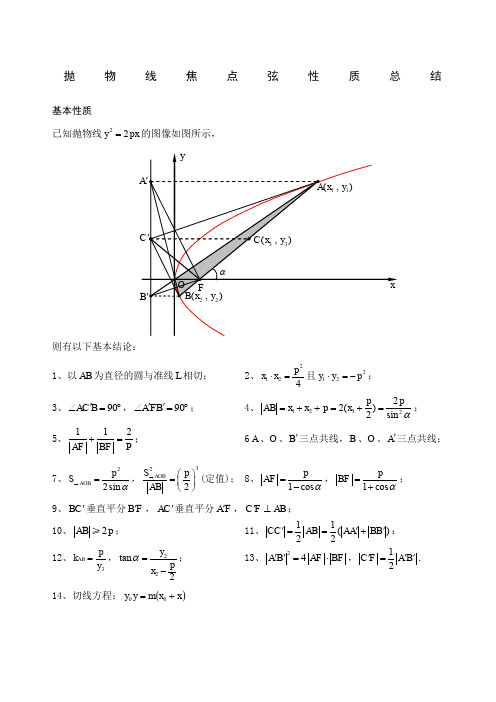
抛物线焦点弦性质总结基本性质 已知抛物线22y px =的图像如图所示,则有以下基本结论:1、以AB 为直径的圆与准线L 相切;2、2124p x x ⋅=且212y y p ⋅=-;3、90AC B '∠=︒,90A FB ''∠=︒;4、123222()2sin p p AB x x p x α=++=+=;5、112AF BF P +=;6A 、O 、B '三点共线,B 、O 、A '三点共线;7、22sin AOB p S α=△,322AOB S p AB ⎛⎫= ⎪⎝⎭△(定值); 8、1cos p AF α=-,1cos p BF α=+; 9、BC '垂直平分B F ',AC '垂直平分A F ', C F AB '⊥;10、2AB p ≥;11、11()22CC AB AA BB '''==+; 12、3AB p k y =,22tan 2y p x α=-; 13、24A B AF BF ''=⋅,12C F A B '''=. 14、切线方程:()x x m y y +=00性质深究一、焦点弦与切线结论1、过抛物线焦点弦的两端点作抛物线的切线,两切线交点在准线上.特别地,当弦x AB ⊥轴时,则点P 的坐标为,02p ⎛⎫- ⎪⎝⎭. 结论2、切线交点与弦中点连线平行于对称轴结论3、弦AB 不过焦点即切线交点P 不在准线上时,切线交点与弦中点的连线也平行于对称轴.结论4、过抛物线准线上任一点作抛物线的切线,则过两切点的弦必过焦点.特别地,过准线与x 轴的交点作抛物线的切线,则过两切点AB 的弦必过焦点.结论5、过准线上任一点作抛物线的切线,过两切点的弦最短时,即为通径.AB 是抛物线px y 22=(p >0)焦点弦,Q 是AB 的中点,l 是抛物线的准线,l AA ⊥1,l BB ⊥1,过A ,B 的切线相交于P ,PQ 与抛物线交于点M .则有结论6、PA ⊥PB .结论7、PF ⊥AB . 结论8、M 平分PQ . 结论9、PA 平分∠A 1AB ,PB 平分∠B 1BA .结论102PF =结论11、PAB S ∆2min p =二、非焦点弦与切线 当弦AB 不过焦点,切线交于P 点时,也有与上述结论类似结果:结论12、①p y y x p 221=,221y y y p += 结论13、PA 平分∠A 1AB ,同理PB 平分∠B 1BA .结论14、PFB PFA ∠=∠结论15、点M 平分PQ结论162=。
