电路课件12-3 4 5
合集下载
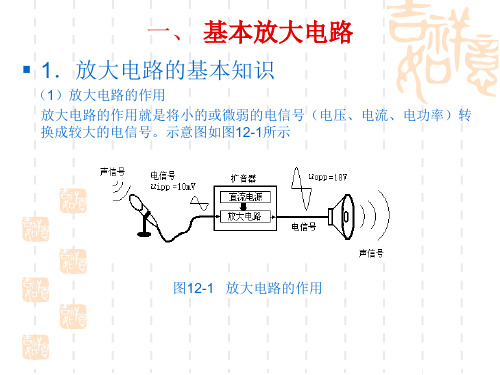
基本放大电路ppt课件
首先,画出直流通路;在输入特性曲线上,作出直线VBE =VCC-IBRb,
两线的交点即是Q点,得到IBQ 。在输出特性曲线上,作出直流负载线
VCE=VCC-ICRC,与IBQ曲线的交点即为Q点,从而得到VCEQ 和ICQ 。
图12-8 静态工作情况图解
②动态工作情况分析 Ⅰ 交流通路及交流负载线 过输出特性曲线上的Q点做一条斜率为-1/(RL∥Rc)直线,该直线即为交流 负载线。交流负载线是有交流输入信号时Q点的运动轨迹。R'L= RL∥Rc,是交流负载电阻。 Ⅱ 输入交流信号时的图解分析 通过图解分析,可得如下结论:
(1)vi vBE iB iC vCE | vo | (2)vo与vi相位相反; (3)可以测量出放大电路的电压放大倍数; (4)可以确定最大不失真输出幅度。
图12-9 动态工作情况图解
3.放大电路三种 基本组态的比较
共发射极放大电路
共集电极放大电路
共基极放大电路
电 路 组 态
电
压 增
(RC // RL )
图12-3 放大电路的幅频特性曲线
▪ 2.共射极放大电路
根据放大器输入输出回路公共端的不同,放大器有共发射极、共集电极和共基 极三种基本组态,下面介绍共发射极放大电路。 (1)电路组成 共射极基本放大电路如图12-4所示。
图12-4 共发射极基本放大电路
▪ 具体分析如下: ▪ ①Vcc:集电极回路的直流电源 ▪ ②VBB:基极回路的直流电源 ▪ ③三极管T:放大电路的核心器件,具有电流放大
便于计算和调试。
(2)因为耦合电容的容量较
(2)电路比较简单,体积 大,故不易集成化。
较小。
(1)元件少,体积小,易 集成化。
(2)既可放大交流信号, 也可放大直流和缓变信号。
两线的交点即是Q点,得到IBQ 。在输出特性曲线上,作出直流负载线
VCE=VCC-ICRC,与IBQ曲线的交点即为Q点,从而得到VCEQ 和ICQ 。
图12-8 静态工作情况图解
②动态工作情况分析 Ⅰ 交流通路及交流负载线 过输出特性曲线上的Q点做一条斜率为-1/(RL∥Rc)直线,该直线即为交流 负载线。交流负载线是有交流输入信号时Q点的运动轨迹。R'L= RL∥Rc,是交流负载电阻。 Ⅱ 输入交流信号时的图解分析 通过图解分析,可得如下结论:
(1)vi vBE iB iC vCE | vo | (2)vo与vi相位相反; (3)可以测量出放大电路的电压放大倍数; (4)可以确定最大不失真输出幅度。
图12-9 动态工作情况图解
3.放大电路三种 基本组态的比较
共发射极放大电路
共集电极放大电路
共基极放大电路
电 路 组 态
电
压 增
(RC // RL )
图12-3 放大电路的幅频特性曲线
▪ 2.共射极放大电路
根据放大器输入输出回路公共端的不同,放大器有共发射极、共集电极和共基 极三种基本组态,下面介绍共发射极放大电路。 (1)电路组成 共射极基本放大电路如图12-4所示。
图12-4 共发射极基本放大电路
▪ 具体分析如下: ▪ ①Vcc:集电极回路的直流电源 ▪ ②VBB:基极回路的直流电源 ▪ ③三极管T:放大电路的核心器件,具有电流放大
便于计算和调试。
(2)因为耦合电容的容量较
(2)电路比较简单,体积 大,故不易集成化。
较小。
(1)元件少,体积小,易 集成化。
(2)既可放大交流信号, 也可放大直流和缓变信号。
12_3实验:电池电动势和内阻的测量 课件-高二上学期物理人教版(2019)必修第三册

<
r
误差来源于电压表的分流作用,适宜测小内阻电源。
误差分析
R
.
V
.
Er s A
电流表看成内电路的一部分,故实际 测出的是电池和电流表这个整体等效 的r和E。
E测=E
r测=r+RA>r
误差来源于电流表的分压作用,适宜 测大内阻电源。
课堂练习
1.(1)请画出能使本实验测量精确程度较高的实验电路图。 ( 2 ) 电 路 中 电 流 表 应 选 用 _ _ _ _ _ _ _A_ _ _ , 电 压 表 应 选 用 _ _ _ _ _C_ _ _ _ _ , 滑 动 变
方法二:图象法
I/A U/V
1
2
U/V
3
E.
4
5 6
O
. I/A
r E
I短
思考:考虑电压表的分流作用,大致画出U-I真实图线
误差分析
A R
.
V
.
Er
s
把图中的R和电流表看成外电路,则
电压表看成内电路的一部分,故实际
测出的是电池和电压表这个整体等效
的r和E。
E测
=
Rvr Rv +r
E
<
E
r测
=
R vr Rv +r
(3)如图丙所示
注意:闭合开关前,要使滑动变阻器接入电路的电阻最大,即滑 到最左端。
答案:(1)如图乙所示 (3)如图丙所示
课堂练习
2.在测电源的电动势和内阻时。某次实验记录数据画出U-I图象,下列 关于这个图象的说法中正确的是( A ) A.纵轴截距表示待测电源的电动势,即E=3V B.横轴截距表示短路电流,即I短=0.6A C.根据r=E/ I短 ,计算出待测电源内阻为5Ω D.该实验中电源的内阻为2Ω
电工电子学完整ppt课件

K
u k ( t ) 0 或
u降 u升 或 uR US
k 1
式中 uk(t) 为该回路中第 k 条支路电压,K 为该回路处的支路数
示例
R2 i2
+ US_1
+ u2 _ +
R1 i1
+ _u1
_u3 _ u4 +
_ US4+ R4 i4
R3 i3
① 标定各元件电压、电流参考方向 ② 选定回路绕行方向,顺时针或逆时针 顺时针
小结 · 分析电路前必须选定电压和电流的参考方向
· 参考方向一经选定,必须在图中相应位置标注 (包括方向和符号), 在计算过程中不得任意改变。
· 参考方向也称为假定正方向,以后讨论均在参考方向下进行,不考虑 实际方向。
· 电路中电位参考点可任意选择,参考点一经选定,电路中各点的电位
值就是唯一的,当选择不同的电位参考点时,电路中各点电位值将
Lumped parameter element
集总条件 实际电路的尺寸远小于使用时其最高工作频率所对应的
波长 d
注意
• 采用集总电路模型意味着不考虑电路中电场与磁场的相互作用, 不考虑电磁波的传播现象,认为电能的传送是瞬时完成的
• 集总假设为本课程的基本假设,以后所述的电路基本定律、定理 等均是以该假设为前提成立的
_
R1
+ US2
_
R2
b=3
n=2
R3
l=3
m=2
精品课件
22
2. 基尔霍夫电流定律 (KCL)
在集总参数电路中,任意时刻,对任意节点流出或流入该节点电流的代数 和等于零。
K
ik (t) 0
教学课件 数字电子技术第六版 阎石

故
(173)10 (10101101 )2
0
二、十-二转换
小数部分: ( S )10 k1 21 k2 22 km 2m 左右同乘以2
2( S )10 k1+(k2 21 k3 22 km 2m1 ) 同理
例:
2(k2 21 k3 22 km 2m1 ) k2+(k3 21 km 2m2 )
(0101 ,1110 .1011 ,0010 )2
(5
E
B
2)16
四、十六-二转换
例:将(8FA.C6)16化为二进制
(8
F
A.
C
6)16
(1000 1111 1010 . 1100 0110 )2
五、八进制数与二进制数的转换
例:将(011110.010111)2化为八进制 (011 110 . 010 111)2
0.8125
2 1.6250
整数部分= 1 =k1
0.6250
2 1.2500
整数部分= 1 =k2
故
(0.8125 )10 (0.1101 )2
0.2500
2 0.5000
整数部分= 0 =k3
0.5000
2 1.000
整数部分= 1 =k4
三、二-十六转换
例:将(01011110.10110010)2化为十六进制
码
两个补码表示的二进制数相加时的符号位讨论
例:用二进制补码运算求出
13+10 、13-10 、-13+10 、-13-10
13 0 01101
13 0 01101
解:
10 0 01010
10 1 10110
23 0 10111
3 0 00011
电气线路 -精品课件

22
磁极旋转
导线切割磁力线产生感应电动势
e B l v (右手定则)
磁感应强度
导线长度
切割速度
闭合导线产生电流 i
通电导线在磁场中受力
f Bli
N
n0 f
n
ei
(左手定则)
S
23
结论: 1. 线圈跟着磁铁转→两者转动方向一致
2. 线圈比磁场转得慢
n n0
n0 f
n
N
ei
异步
S
24
三相感应电动机的转速小于磁场速度
17
电动机的分类:
电动机
交流电动机 直流电动机
异步机 同步机
鼠笼式 绕线式
他励、异励、串励、复励
鼠笼式交流异步电动机授课内容: 基本结构、工作原理、 机械特性、控制方法
18
第一节 三相异步电动机的构造
三相定子绕组:产生旋转 磁场。
转子:在旋转磁场作用下, 产生感应电动势或 电流。
绕线式
定子绕组 (三相)
iA iB iC
Im
t
n0 60
A
Y
Z
N
CS
B
X
t 60
n0
A
Y
Z
C
B
X
t 120
n0
A
Y
Z
C
B
X
t 180 28
三相感应电动机的工作原理(图解) N
n1 f T n f S
29
S N
旋转磁场的定性分析图解
U1 V2 W2
W1 V1 U2
i U VW 123 4 5 6
分析规定: 电流 I 为正时,从首端流入、末端流出; 电流 I 为负时,从首端流出、末端流入。
磁极旋转
导线切割磁力线产生感应电动势
e B l v (右手定则)
磁感应强度
导线长度
切割速度
闭合导线产生电流 i
通电导线在磁场中受力
f Bli
N
n0 f
n
ei
(左手定则)
S
23
结论: 1. 线圈跟着磁铁转→两者转动方向一致
2. 线圈比磁场转得慢
n n0
n0 f
n
N
ei
异步
S
24
三相感应电动机的转速小于磁场速度
17
电动机的分类:
电动机
交流电动机 直流电动机
异步机 同步机
鼠笼式 绕线式
他励、异励、串励、复励
鼠笼式交流异步电动机授课内容: 基本结构、工作原理、 机械特性、控制方法
18
第一节 三相异步电动机的构造
三相定子绕组:产生旋转 磁场。
转子:在旋转磁场作用下, 产生感应电动势或 电流。
绕线式
定子绕组 (三相)
iA iB iC
Im
t
n0 60
A
Y
Z
N
CS
B
X
t 60
n0
A
Y
Z
C
B
X
t 120
n0
A
Y
Z
C
B
X
t 180 28
三相感应电动机的工作原理(图解) N
n1 f T n f S
29
S N
旋转磁场的定性分析图解
U1 V2 W2
W1 V1 U2
i U VW 123 4 5 6
分析规定: 电流 I 为正时,从首端流入、末端流出; 电流 I 为负时,从首端流出、末端流入。
高中物理实验(全)PPT课件

(这时图线与横轴的交点不再是短路电流)
例2. 如图示的电路中,R1 、R2为标
R1
准电阻,测定电源的电动势和内阻时,
如果偶然误差可以忽略不计,则电动
R2
势的测量值
等真于实值,内阻的测
A
量值
偏真大实值,产生误差的原因
Er
是
电流表有内。阻
E=I1(R1+ RA+ r) ①
E真
I1I 2 I1 I2
(R 2
E
由U =E -Ir 可知,U
是I 的一次函数。
0
I短 I/A
(1)图象在纵轴上的截距为电源的电动势E (I=0)
(2)图象在横轴上的截距为短路电流I短 (U=0)
(3)图象斜率的绝对值为电源内阻
r E U I短 r
思考
1、给你一节使用过的干电池、一个滑动变阻 器、一块电流表、一块电压表、一个电键和导线 若干,如何测量这节电池的电动势和内阻。
R1)
E=I2(R2+ RA+ r) ②
r真
I2R 2 I1R1 I1 I2
RA
练习 在测定电源的电动势和内阻的实验中,待测电池、开关和
即为所测电源的电动势和内阻。
②图象法
由U =E -Ir 可知,U 是I 的一次函数。
U/V
E
图象在横轴上的截距
还是短路电流吗?
U0
0
I短 I/A
讨论:将图线延长,与横纵轴的交点各代表什么情况? (1)图象在纵轴上的截距为电源的电动势E (I=0)
(2)图象在横轴上的截距为短路电流I短 (U=0)
(3)图象斜率的绝对值为电源内阻
6.18 mm
0
1
例2. 如图示的电路中,R1 、R2为标
R1
准电阻,测定电源的电动势和内阻时,
如果偶然误差可以忽略不计,则电动
R2
势的测量值
等真于实值,内阻的测
A
量值
偏真大实值,产生误差的原因
Er
是
电流表有内。阻
E=I1(R1+ RA+ r) ①
E真
I1I 2 I1 I2
(R 2
E
由U =E -Ir 可知,U
是I 的一次函数。
0
I短 I/A
(1)图象在纵轴上的截距为电源的电动势E (I=0)
(2)图象在横轴上的截距为短路电流I短 (U=0)
(3)图象斜率的绝对值为电源内阻
r E U I短 r
思考
1、给你一节使用过的干电池、一个滑动变阻 器、一块电流表、一块电压表、一个电键和导线 若干,如何测量这节电池的电动势和内阻。
R1)
E=I2(R2+ RA+ r) ②
r真
I2R 2 I1R1 I1 I2
RA
练习 在测定电源的电动势和内阻的实验中,待测电池、开关和
即为所测电源的电动势和内阻。
②图象法
由U =E -Ir 可知,U 是I 的一次函数。
U/V
E
图象在横轴上的截距
还是短路电流吗?
U0
0
I短 I/A
讨论:将图线延长,与横纵轴的交点各代表什么情况? (1)图象在纵轴上的截距为电源的电动势E (I=0)
(2)图象在横轴上的截距为短路电流I短 (U=0)
(3)图象斜率的绝对值为电源内阻
6.18 mm
0
1
《电子电工技术》课件——第四章 三相电路

2
I 3I 30
L3
3
U 31
I
3
I 3
I
U 12
1
I 2 U
I
2 I 3
I L1
23
负载对称时三角形接法的特点
L1
U 31 L2 L3
I L1
U 12
I 1
I
L2
U I
23
L3
I 3
ZZ Z
I 2
每相负载电压=电源线电压
I 3I
l
p
各线电流滞后于相应各相电流30°
第三节 三相负载的功率 每相负载
定子 W2
•
V1 转子
三相电动势 分别称为U、V、W相或1、2、3相
e E sin t
1
m
e E sint 120
2
m
e E sint 240
3
m
Em sin( t 120)
E E0 1
E E 120 2
E3 E 120
三相电动势的特征: 大小相等,频率相同,相位互差120º
称为对称电动势。
e 2
3
L2
L3
L1
e 1
e
L2
2
L3
(2)三相负载
星形负载
Z
Z
Z
三角形负载
Z
Z
Z
(3)三相电路计算
负载不对称时:各相电压、电流单独计算。 负载对称时:电压对称、电流对称,只需计算一相。
电流其余按对称原则,相线电流的关系一一写出。
三相电路的计算要特别注意相位问题。
负载Y形接法
I I
l
P
负载Y形接法有中线时
高考物理一轮复习课件 第九章 第1讲 电路的基本概念及电路分析

2021·全国乙卷·T23
2018·全国卷Ⅱ·T22 2019·全国卷Ⅰ·T23 2019·全国卷Ⅲ·T23 2019·全国卷Ⅱ·T23
生活实践类
在日常生产生活和科技方面的主要试题情境有家用电器、电表的原理与应用等,涉及这类情境的题目往往考查纯电阻电路和非纯 电阻电路的分析与计算、串并联电路的规律与应用、电路故障的分析与判断等
U (2)表达式:I= R .
(3)适用范围:金属导电和电解质溶液导电,不适用于气态导体或半导体 元件. (4)导体的伏安特性曲线(I-U图线).(如图). ①比较电阻的大小:图线的斜率k=UI =R1 ,图中R1 > R2(选 填“>”“<”或“=”);
②线性元件:伏安特性曲线是过原点的直线的电学元件, 适用于欧姆定律; ③非线性元件:伏安特性曲线是曲线的电学元件,不适 用于欧姆定律.
√C.对应P点,小灯泡的电阻为R=I2U-1I1
D.对应P点,小灯泡的功率为图中矩形PQOM所围的面积
由题图可知,U越大,小灯泡的电阻越大,故A
说法正确. R=UI 中的U、I与小灯泡所处状态下的电压与电流 相对应,故B说法正确,C说法错误.
对应P点,小灯泡的功率P=U1I2,与题图中PQOM所围的面积相等, 故D说法正确.
方法技巧 提升关键能力
电阻的决定式和定义式的区别
公式
R=ρSl 电阻的决定式
R=UI 电阻的定义式
区别
说明了电阻的决定因素
提供了一种测电阻的方法,并 不说明电阻与U和I有关
只适用于粗细均匀的金属导体和 浓度均匀的电解质溶液
适用于任何纯电阻导体
考向1 欧姆定律的理解和应用
例3 小灯泡通电后其电流I随所加电压U变化的图线如图所示,P为图线 上一点,PN为图线在P点的切线,PQ为U轴的垂线,PM为I轴的垂线, 则下列说法中错误的是 A.随着所加电压的增大,小灯泡的电阻增大 B.对应P点,小灯泡的电阻为R=UI21
2018·全国卷Ⅱ·T22 2019·全国卷Ⅰ·T23 2019·全国卷Ⅲ·T23 2019·全国卷Ⅱ·T23
生活实践类
在日常生产生活和科技方面的主要试题情境有家用电器、电表的原理与应用等,涉及这类情境的题目往往考查纯电阻电路和非纯 电阻电路的分析与计算、串并联电路的规律与应用、电路故障的分析与判断等
U (2)表达式:I= R .
(3)适用范围:金属导电和电解质溶液导电,不适用于气态导体或半导体 元件. (4)导体的伏安特性曲线(I-U图线).(如图). ①比较电阻的大小:图线的斜率k=UI =R1 ,图中R1 > R2(选 填“>”“<”或“=”);
②线性元件:伏安特性曲线是过原点的直线的电学元件, 适用于欧姆定律; ③非线性元件:伏安特性曲线是曲线的电学元件,不适 用于欧姆定律.
√C.对应P点,小灯泡的电阻为R=I2U-1I1
D.对应P点,小灯泡的功率为图中矩形PQOM所围的面积
由题图可知,U越大,小灯泡的电阻越大,故A
说法正确. R=UI 中的U、I与小灯泡所处状态下的电压与电流 相对应,故B说法正确,C说法错误.
对应P点,小灯泡的功率P=U1I2,与题图中PQOM所围的面积相等, 故D说法正确.
方法技巧 提升关键能力
电阻的决定式和定义式的区别
公式
R=ρSl 电阻的决定式
R=UI 电阻的定义式
区别
说明了电阻的决定因素
提供了一种测电阻的方法,并 不说明电阻与U和I有关
只适用于粗细均匀的金属导体和 浓度均匀的电解质溶液
适用于任何纯电阻导体
考向1 欧姆定律的理解和应用
例3 小灯泡通电后其电流I随所加电压U变化的图线如图所示,P为图线 上一点,PN为图线在P点的切线,PQ为U轴的垂线,PM为I轴的垂线, 则下列说法中错误的是 A.随着所加电压的增大,小灯泡的电阻增大 B.对应P点,小灯泡的电阻为R=UI21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• • • • •
Ul = 3U p
Il = I p
A
CA
C
AB
° & 2 & & ′ ′ = 3∠30 ⋅U ′ ′ = a U ′ ′ UB C BN AB & ′ ′ = 3∠30° ⋅U ′ ′ = aU ′ ′ & & UC A CN AB 对称△ 对称△形负载
& & U A'B' = 3∠30° ⋅U A' N ' ° & & = 3∠30 ⋅U U B'C B' N ' & = 3∠30° ⋅U & UC ' A' C'N '
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 U 对称三相四线制Y
•
A
A + B + C + ZN
u B = 220 2 cos(ωt − 120°)V
uC = 220 3 cos(ωt + 120°)V
§12-3 12-
对称三相电路的计算
二、对称三相电路的一相计算法 已知: 已知: 12例12-1 Zl = (1 + j 2)Ω,Z = (5 + j6)Ω
u AB = 380 2 cos(ωt + 30 )V 试求负载中各电流相量。 试求负载中各电流相量。
UA –
•
A +
Zl A' Zl B' Zl C' ZN
Z Z Z N'
Y形负载 形负载
N
UB
–
UC
•
•Байду номын сангаас
B + C +
–
中线阻抗
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 对称三相四线制Y 三相四线制Y-Y电路的计算方法: 电路的计算方法: 三相四线制 电路的计算方法 – 选择电源的中性点 中性点N为 选择电源的中性点 为 N UB B Zl 参考结点, 参考结点, 结点电压方程 – 为 Zl UC C 1 1 1 1 & – ( + + + )U N ′N Zl + Z Z l + Z Z l + Z Z N ZN & & & UA UB UC = + + Zl + Z Z l + Z Z l + Z 重要结论: 重要结论: 1 & & & = (U A + U B + UC ) & U N ′N = 0 Zl + Z + +
& & & & U A′N ′ + U B′N ′ + UC′N ′ = (1 + a 2 + a) I A = 0
– N UB –
UC
•
•
B' Z C' Z
& IB
& IB
–
& IN
根据对称三相电路中Y负载线电压与相电压之间的关系, 根据对称三相电路中 负载线电压与相电压之间的关系,得 负载线电压与相电压之间的关系
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 对称三相四线制Y
& & = UA IA Zl + Z & & UB a2U A & = & = = a2 I A IB Zl + Z Z l + Z & & UC aU A & & IC = = = aI A Zl + Z Zl + Z
B' Z
& IB
试求负载中各电流相量。 试求负载中各电流相量。 解 依据线电压的对称性: 依据线电压的对称性:
uBC = 380 2 cos(ωt − 90 )V uCA = 380 2 cos(ωt +150° )V
°
C'
& IB
& IN
Z
–
依据线电压与相电压的关系: 依据线电压与相电压的关系: U = U l = 380 = 219.393V 3 3 三相电源的相电压: 三相电源的相电压: u A = 220 2 cos(ωt )V
UA
•
A + B + C +
Zl Zl Zl
& IA
& IB
A'
Z
–
UB
•
N
B' Z C' Z
–
UC
•
N'
–
& & U A′N ' = ZI A & 2 & 2 & & U B′N ' = ZI B = a ZI A = a U A′N ' & & & & UC′N ' = ZIC = aZI A = aU A′N '
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 对称三相四线制Y
UA
•
A + B + C + ZN
Zl Zl Zl
& IA
A'
Z N'
计算负载的相电压: 计算负载的相电压:
& & U A′N ' = ZI A & 2 & 2 & & U B′N ' = ZI B = a ZI A = a U A′N ' & & & & UC′N ' = ZIC = aZI A = aU A′N '
AB A′N ′
对称Y形负载 对称 形负载 & & U ′ ′ = 3∠30° ⋅U
线
Ul = 3U p
线 电 压 与 相 电 压 的 关 系
电 流 与 相 电 流
Il = I p
& & I A = 3∠ − 30° ⋅ I A'B' & ° & 2& I B = 3∠ − 30 ⋅ I B'C ' = a I A & & & IC = 3∠ − 30° ⋅ IC ' A' = aI A
Il = 3I
Ul = U p
的 关 系
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 对称三相四线制Y 首先以典型的对称三相四线制 三相四线制Y-Y电路为例进行讨论 。 电路为例进行讨论 首先以典型的对称三相四线制 电路 三相四线制Y 三相四线制Y-Y电路
端线阻抗
Y形电源 形电源
强调
相量分析法; 对称三相电路的分析与计算方法——相量分析法; 相量分析法 对称三相电路的分析与计算方法 第八、九和第十章的各种分析与计算的方法均适用于本章; 第八、九和第十章的各种分析与计算的方法均适用于本章; 利用对称三相电路的对称性(特殊性),可简化计算过程。 ),可简化计算过程 利用对称三相电路的对称性(特殊性),可简化计算过程。 本节是本章的重点内容,应熟练掌握。 本节是本章的重点内容,应熟练掌握。
Zl Zl Zl
& IA
& IB
A'
Z N'
结论
& U N ′N = 0
–
& & = U N′N = 0 IN ZN
N UB –
UC
•
•
B' Z C' Z
电源的中性点N与负载的中 ① 电源的中性点 与负载的中 性点 Nˊ等电位。 ˊ等电位。 中线电流为零, 中线电流为零,中线相当于 开路(断开) 开路(断开)。 在工程中, 在工程中,只有三相电路对 称时,才允许不接中线。 称时,才允许不接中线。 N
& IB
& IB
–
& IN
& U A = U∠0o = U & & U = U∠ −120o = a2U
B
A
& & UC = U∠120o = aU A
& & & & I A + I B + I C = (1 + a 2 + a) I A = 0
& & & & I A + I B + I C = I N = 0 (KCL)
§12-3 12-
对称三相电路的计算
二、对称三相电路的一相计算法 例12-1 12已知: 已知:
Zl = (1 + j 2)Ω,Z = (5 + j6)Ω
UA
•
A + B + C + ZN
Zl Zl Zl
& IA
A'
Z N'
– N UB –
UC
•
•
u AB = 380 2 cos(ωt + 30° )V
§12-3 对称三相电路的计算 12-
在对称的三相电路中,有下面的重要关系: 在对称的三相电路中,有下面的重要关系: 对称Y形电源 对称 形电源 UA= U∠0o = U & & U AB = 3∠30° ⋅U A & & & UB = U∠ −120o = a2 UA U BC = 3∠30° ⋅U B = a2U AB & & & U = 3∠30° ⋅U = aU UC = U∠120o = a U
Ul = 3U p
Il = I p
A
CA
C
AB
° & 2 & & ′ ′ = 3∠30 ⋅U ′ ′ = a U ′ ′ UB C BN AB & ′ ′ = 3∠30° ⋅U ′ ′ = aU ′ ′ & & UC A CN AB 对称△ 对称△形负载
& & U A'B' = 3∠30° ⋅U A' N ' ° & & = 3∠30 ⋅U U B'C B' N ' & = 3∠30° ⋅U & UC ' A' C'N '
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 U 对称三相四线制Y
•
A
A + B + C + ZN
u B = 220 2 cos(ωt − 120°)V
uC = 220 3 cos(ωt + 120°)V
§12-3 12-
对称三相电路的计算
二、对称三相电路的一相计算法 已知: 已知: 12例12-1 Zl = (1 + j 2)Ω,Z = (5 + j6)Ω
u AB = 380 2 cos(ωt + 30 )V 试求负载中各电流相量。 试求负载中各电流相量。
UA –
•
A +
Zl A' Zl B' Zl C' ZN
Z Z Z N'
Y形负载 形负载
N
UB
–
UC
•
•Байду номын сангаас
B + C +
–
中线阻抗
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 对称三相四线制Y 三相四线制Y-Y电路的计算方法: 电路的计算方法: 三相四线制 电路的计算方法 – 选择电源的中性点 中性点N为 选择电源的中性点 为 N UB B Zl 参考结点, 参考结点, 结点电压方程 – 为 Zl UC C 1 1 1 1 & – ( + + + )U N ′N Zl + Z Z l + Z Z l + Z Z N ZN & & & UA UB UC = + + Zl + Z Z l + Z Z l + Z 重要结论: 重要结论: 1 & & & = (U A + U B + UC ) & U N ′N = 0 Zl + Z + +
& & & & U A′N ′ + U B′N ′ + UC′N ′ = (1 + a 2 + a) I A = 0
– N UB –
UC
•
•
B' Z C' Z
& IB
& IB
–
& IN
根据对称三相电路中Y负载线电压与相电压之间的关系, 根据对称三相电路中 负载线电压与相电压之间的关系,得 负载线电压与相电压之间的关系
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 对称三相四线制Y
& & = UA IA Zl + Z & & UB a2U A & = & = = a2 I A IB Zl + Z Z l + Z & & UC aU A & & IC = = = aI A Zl + Z Zl + Z
B' Z
& IB
试求负载中各电流相量。 试求负载中各电流相量。 解 依据线电压的对称性: 依据线电压的对称性:
uBC = 380 2 cos(ωt − 90 )V uCA = 380 2 cos(ωt +150° )V
°
C'
& IB
& IN
Z
–
依据线电压与相电压的关系: 依据线电压与相电压的关系: U = U l = 380 = 219.393V 3 3 三相电源的相电压: 三相电源的相电压: u A = 220 2 cos(ωt )V
UA
•
A + B + C +
Zl Zl Zl
& IA
& IB
A'
Z
–
UB
•
N
B' Z C' Z
–
UC
•
N'
–
& & U A′N ' = ZI A & 2 & 2 & & U B′N ' = ZI B = a ZI A = a U A′N ' & & & & UC′N ' = ZIC = aZI A = aU A′N '
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 对称三相四线制Y
UA
•
A + B + C + ZN
Zl Zl Zl
& IA
A'
Z N'
计算负载的相电压: 计算负载的相电压:
& & U A′N ' = ZI A & 2 & 2 & & U B′N ' = ZI B = a ZI A = a U A′N ' & & & & UC′N ' = ZIC = aZI A = aU A′N '
AB A′N ′
对称Y形负载 对称 形负载 & & U ′ ′ = 3∠30° ⋅U
线
Ul = 3U p
线 电 压 与 相 电 压 的 关 系
电 流 与 相 电 流
Il = I p
& & I A = 3∠ − 30° ⋅ I A'B' & ° & 2& I B = 3∠ − 30 ⋅ I B'C ' = a I A & & & IC = 3∠ − 30° ⋅ IC ' A' = aI A
Il = 3I
Ul = U p
的 关 系
§12-3 12-
对称三相电路的计算
一、对称三相四线制Y-Y电路的分析 对称三相四线制Y 首先以典型的对称三相四线制 三相四线制Y-Y电路为例进行讨论 。 电路为例进行讨论 首先以典型的对称三相四线制 电路 三相四线制Y 三相四线制Y-Y电路
端线阻抗
Y形电源 形电源
强调
相量分析法; 对称三相电路的分析与计算方法——相量分析法; 相量分析法 对称三相电路的分析与计算方法 第八、九和第十章的各种分析与计算的方法均适用于本章; 第八、九和第十章的各种分析与计算的方法均适用于本章; 利用对称三相电路的对称性(特殊性),可简化计算过程。 ),可简化计算过程 利用对称三相电路的对称性(特殊性),可简化计算过程。 本节是本章的重点内容,应熟练掌握。 本节是本章的重点内容,应熟练掌握。
Zl Zl Zl
& IA
& IB
A'
Z N'
结论
& U N ′N = 0
–
& & = U N′N = 0 IN ZN
N UB –
UC
•
•
B' Z C' Z
电源的中性点N与负载的中 ① 电源的中性点 与负载的中 性点 Nˊ等电位。 ˊ等电位。 中线电流为零, 中线电流为零,中线相当于 开路(断开) 开路(断开)。 在工程中, 在工程中,只有三相电路对 称时,才允许不接中线。 称时,才允许不接中线。 N
& IB
& IB
–
& IN
& U A = U∠0o = U & & U = U∠ −120o = a2U
B
A
& & UC = U∠120o = aU A
& & & & I A + I B + I C = (1 + a 2 + a) I A = 0
& & & & I A + I B + I C = I N = 0 (KCL)
§12-3 12-
对称三相电路的计算
二、对称三相电路的一相计算法 例12-1 12已知: 已知:
Zl = (1 + j 2)Ω,Z = (5 + j6)Ω
UA
•
A + B + C + ZN
Zl Zl Zl
& IA
A'
Z N'
– N UB –
UC
•
•
u AB = 380 2 cos(ωt + 30° )V
§12-3 对称三相电路的计算 12-
在对称的三相电路中,有下面的重要关系: 在对称的三相电路中,有下面的重要关系: 对称Y形电源 对称 形电源 UA= U∠0o = U & & U AB = 3∠30° ⋅U A & & & UB = U∠ −120o = a2 UA U BC = 3∠30° ⋅U B = a2U AB & & & U = 3∠30° ⋅U = aU UC = U∠120o = a U
