2020版高考数学(理)刷题小卷练: 25 Word版含解析
2020版高考数学(理)刷题小卷练:2Word版含解析

答案: C
解析:根据逆否命题的定义可得命题 p:“若 a≥b,则 a+b>2 012
且 a>- b”的逆否命题是:若 a+b≤2 012 或 a≤-b,则 a<b.故选
C.
7.[2019 ·山东诊断 ]已知命题 p:|x+1|>2;命题 q:x≤a,且綈 p
是綈 q 的充分不必要条件,则 a 的取值范围是 ( )
6.[2019 ·安徽联考 ]命题 p:“若 a≥b,则 a+b>2 012 且 a>-b”
的逆否命题是 ( )
A .若 a+b≤2 012 且 a≤- b,则 a<b
B.若 a+b≤2 012 且 a≤- b,则 a>b
C.若 a+b≤2 012 或 a≤- b,则 a<b
D.若 a+b≤2 012 或 a≤- b,则 a>b
x 2.[2019 ·福建模拟 ]命题“ ? x>0,x-1>0”的否定是 ( )
A.?
x0<0,
x0 x0-
1≤
0
B.?
x0>0,
x0 x0-
1≤
0
C.?
x x>0,x-
1≤
0
D.?
x<0,
x x-
1≤0
答案: B
解析: 易知命题的否定是
?
x0>0,
x0 x0-
1≤
0,故选
B.
3.[2019 ·河南郑州模拟 ]下列说法正确的是 ( ) A .“若 a>1,则 a2>1”的否命题是“若 a>1,则 a2≤1” B.“若 am2<bm2,则 a<b”的逆命题为真命题
2020版高考数学(理)刷题小卷练: 4 Word版含解析

C.-1-e D.e+1答案:A解析:∵y=f(x-1)的图象关于点(1,0)对称,∴f(x)的图象关于原点对称.∵当x≥0时恒有f(x)=f(x+2),∴函数f(x)的周期为2.∴f(2 016)+f(-2 015)=f(0)-f(1)=1-e.故选A.8.定义在R上的奇函数f(x)满足f(x+2)=-f(x),且在[0,2)上单调递减,则下列结论正确的是()A.0<f(1)<f(3) B.f(3)<0<f(1)C.f(1)<0<f(3) D.f(3)<f(1)<0答案:C解析:由函数f(x)是定义在R上的奇函数,得f(0)=0.由f(x+2)=-f(x),得f(x+4)=-f(x+2)=f(x),故函数f(x)是以4为周期的周期函数,所以f(3)=f(-1).又f(x)在[0,2)上单调递减,所以函数f(x)在(-2,2)上单调递减,所以f(-1)>f(0)>f(1),即f(1)<0<f(3).故选C.二、非选择题9.已知f(x)是定义在[m-4,m]上的奇函数,则f(0)+m=________.答案:2解析:∵f(x)是定义在[m-4,m]上的奇函数,∴m-4+m=0,解得m=2,又f(0)=0,∴f(0)+m=2.10.已知定义在R上的函数f(x)满足:∀x∈R,都有f(-x)+f(x)=0,f(x+1)=f(5-x)成立.若f(-2)=-1,则f(2 018)=________.答案:1解析:由题意得f(x)=f(6-x)=-f(x-6),即f(x-6)=-f(x),则f(x-12)=-f(x-6)=f(x),所以函数f(x)的周期为12.故f(2 018)=f(12×168+2)=f(2)=-f(-2)=1.11.已知函数y=f(x)是偶函数,且在[0,+∞)上单调递减.若f(a)<f(2),求实数a的取值范围为________.答案:(-∞,-2)∪(2,+∞)解析:∵y=f(x)是偶函数,∴f(a)=f(|a|).2)=0(a>0且a≠1)在(-2,6)内有的图象与y=log a(x+2)的图象在(-2,6)。
2020版高考数学(理)刷题小卷练: 20 Word版含解析

1.[2019·福建闽侯模拟]若数列的前4项分别是,-,,-,则此数列的一个通项公式为()
A.B.
C.D.
答案:A
解析:由数列的前4项分别是,-,,-,知奇数项为正数,偶数项为负数,从而第n项的绝对值等于,故数列的一个通项公式为an=.故选A.
2.[2019·山东济宁模拟]已知数列{an}满足an=若对任意的n∈N*都有an<an+1成立,则实数a的取值范围为()
4.[2019·全国名校大联考]若数列{an}满足a1=2,a+a=2an+1·an(n∈N*),则数列{an}的前32项和为()
A.64 B.32
C.16 D.128
答案:A
解析:由a+a=2an+1·an(n∈N*),得(an+1-an)2=0,an+1=an.∵a1=2,∴an=2,∴数列{an}的前32项和S32=2×32=64.故选A.
12.[2019·山东枣庄第三中学质检]已知数列{an}的前n项和Sn=5n2+2n+1,则数列的通项公式为an=________.
答案:
解析:当n=1时,a1=8;当n≥2时,Sn-1=5(n-1)2+2(n-1)+1.所以an=Sn-Sn-1=10n-3,此式对n=1不成立,故an=
刷题课时增分练⑳综合提能力 课时练 赢高分
答案:C
解析:∵a1=1,an+1=-,∴a2=-=-,a3=-=-2,a4=-=1.由上述可知该数列为周期数列,其周期为3.又∵2 018=3×672+2,∴a2 018=a2=-.故选C.
7.[2019·石家庄模拟]数列{an}:1,-,,-,…的一个通项公式是()
A.an=(-1)n+1(n∈N*)
解法二==,
令>1,解得n<2;令=1,解得n=2;令<1,解得n>2.又an>0,
2020年全国统一高考数学理科试卷(附答案解析)

依圆的知识可知,四点 四点共圆,且 ,所以 ,而 ,
A. 2B. 3C. 6D. 9
【答案】C
【解析】
【分析】
利用抛物线的定义建立方程即可得到答案.
【详解】设抛物线的焦点为F,由抛物线的定义知 ,即 ,解得 .
故选:C.
【点晴】本题主要考查利用抛物线的定义计算焦半径,考查学生转化与化归思想,是一道容易题.
5.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:°C)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据 得到下面的散点图:
【答案】C
【解析】
【分析】
求得 展开式的通项公式为 ( 且 ),即可求得 与 展开式的乘积为 或 形式,对 分别赋值为3,1即可求得 的系数,问题得解.
【详解】 展开式的通项公式为 ( 且 )
所以 与 展开式的乘积可表示为:
或
在 中,令 ,可得: ,该项中 的系数为 ,
在 中,令 ,可得: ,该项中 的系数为
由此散点图,在10°C至40°C之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是( )
A. B.
C. D.
【答案】D
【解析】
【分析】
根据散点图的分布可选择合适的函数模型.
【详解】由散点图分布可知,散点图分布在一个对数函数的图象附近,
因此,最适合作为发芽率 和温度 的回归方程类型的是 .
【点睛】本题考查利用导数求解函图象的切线方程,考查计算能力,属于基础题
7.设函数 在 的图像大致如下图,则f(x)的最小正周期为( )
A. B.
C. D.
【答案】C
2020版高考数学(理)刷题小卷练: 42 Word版含解析

刷题增分练 小题基础练提分快
一、选择题
1.[2018·全国卷Ⅱ]i(2+3i)=()
A.3-2iB.3+2i
C.-3-2i D.-3+2i
答案:D
解析:i(2+3i)=2i+3i2=-3+2i.故选D.
2.[2019·河南联考]已知i是虚数单位,则复数 -(1-i)2-4i=()
A.0B.2
刷题课时增分练 综合提能力 课时练 赢高分
一、选择题
1.[2018·全国卷Ⅲ](1+i)(2-i)=()
A.-3-iB.-3+i
C.3-iD.3+i
答案:D
解析:(1+i)(2-i)=2+2i-i-i2=3+i.故选D.
2.[2019·广东七校联考]如果复数 是纯虚数,那么实数m等于()
A.-1B.0
二、非选择题
9.[2019·天津实验中学模拟]已知复数z= + i是纯虚数(i为虚数单位),则tan =________.
答案:-7
解析:因为cosθ- =0,sinθ- ≠0⇒cosθ= ,sinθ=- ⇒tanθ=- ,所以tan = =-7.
10.已知复数z=x+yi,|z-2|= ,则 的最大值为________.
由z= 知,1-a2=0,故a=±1.
当a=1时,|z|=0;当a=-1时,|z|=6.
(2)由已知得,复数的实部和虚部皆大于0,即 ,
即 ,
所以a的取值范围为(-1,1).
7.[2019·宁夏银川月考]设i为虚数单位,复数(2-i)z=1+i,则z的共轭复数 在复平面内对应的点在()
A.第一象限B.第二象限
C.第三象限D.第四象限
答案:D
解析:∵(2-i)z=1+i,∴z= = = = + i,∴z的共轭复数为 - i,对应点为 ,在第四象限.
2020版高考数学人教版理科一轮复习课时作业:25 解三角形的应用 Word版含解析
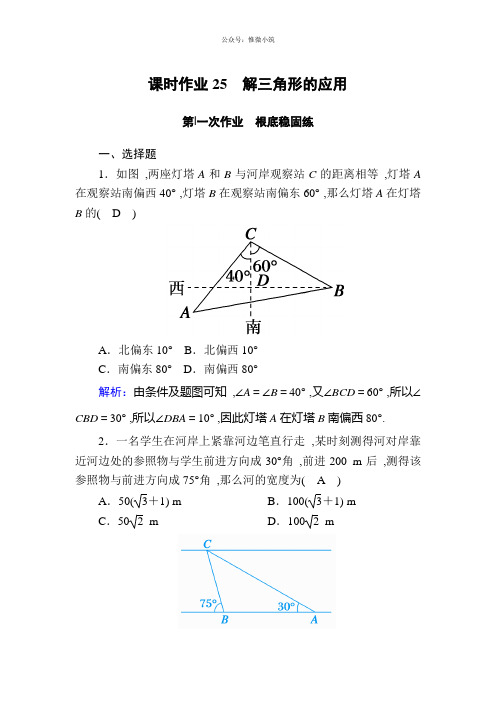
课时作业25解三角形的应用第|一次作业根底稳固练一、选择题1.如图,两座灯塔A和B与河岸观察站C的距离相等,灯塔A 在观察站南偏西40° ,灯塔B在观察站南偏东60° ,那么灯塔A在灯塔B的(D)A.北偏东10°B.北偏西10°C.南偏东80°D.南偏西80°解析:由条件及题图可知,∠A=∠B=40° ,又∠BCD=60° ,所以∠CBD=30° ,所以∠DBA=10° ,因此灯塔A在灯塔B南偏西80°.2.一名学生在河岸上紧靠河边笔直行走,某时刻测得河对岸靠近河边处的参照物与学生前进方向成30°角,前进200 m后,测得该参照物与前进方向成75°角,那么河的宽度为(A)A.50(3+1) m B.100(3+1) mC.50 2 m D.100 2 m解析:如下图 ,在△ABC 中 ,∠BAC =30° ,∠ACB =75°-30°=45° ,AB =200 m ,由正弦定理 ,得BC =200×sin30°sin45°=1002(m) ,所以河的宽度为BC sin75°=1002×2+64=50(3+1)(m). 3.为测出所住小区的面积 ,某人进行了一些测量工作 ,所得数据如下图 ,那么小区的面积是( D )A.3+64 km 2B.3-64 km 2C.6+34 km 2D.6-34 km 2解析:连接AC ,根据余弦定理可得AC = 3 km ,故△ABC 为直角三角形.且∠ACB =90° ,∠BAC =30° ,故△ADC 为等腰三角形 ,设AD=DC =x km ,根据余弦定理得x 2+x 2+3x 2=3 ,即x 2=32+3=3×(2-3) ,所以所求的面积为12×1×3+12×3×(2-3)×12=23+6-334=6-34(km 2). 4.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .假设a =b cos C +c sin B ,且△ABC 的面积为1+ 2 ,那么b 的最|小值为( A )A .2B .3 C. 2 D. 3解析:由a =b cos C +c sin B 及正弦定理 ,得sin A =sin B cos C +sin C sin B ,即sin(B +C )=sin B cos C +sin C sin B ,得sin C cos B =sin C sin B ,又sin C ≠0 ,所以tan B =1.因为B ∈(0 ,π) ,所以B =π4.由S △ABC =12ac sin B=1+ 2 ,得ac =22+4.又b 2=a 2+c 2-2ac cos B ≥2ac -2ac =(2-2)(4+22)=4 ,当且仅当a =c 时等号成立 ,所以b ≥2 ,b 的最|小值为2.应选A.5.(2021·郑州质量预测)在△ABC 中 ,角A ,B ,C 的对边分别为a ,b ,c ,且2c cos B =2a +b ,假设△ABC 的面积S =3c ,那么ab 的最|小值为( C )A .28B .36C .48D .56解析:在△ABC 中 ,2c cos B =2a +b ,由正弦定理 ,得2sin C cos B =2sin A +sin B .又A =π-(B +C ) ,所以sin A =sin[π-(B +C )]=sin(B +C ) ,所以2sin C cos B =2sin(B +C )+sin B =2sin B cos C +2cos B sin C +sin B ,得2sin B cos C +sin B =0 ,因为sin B ≠0 ,所以cos C =-12 ,又0<C <π ,所以C=2π3.由S =3c =12ab sin C =12ab ×32 ,得c =ab 4.由余弦定理得 ,c 2=a 2+b 2-2ab cos C =a 2+b 2+ab ≥2ab +ab =3ab (当且仅当a =b 时取等号) ,所以(ab 4)2≥3ab ,得ab ≥48 ,所以ab 的最|小值为48 ,应选C.6. (2021·山东日照二模)如下图 ,在平面四边形ABCD 中 ,AB =1 ,BC =2 ,△ACD 为正三角形 ,那么△BCD 面积的最|大值为( D )A .23+2 B.3+12 C.32+2D.3+1解析:在△ABC 中 ,设∠ABC =α ,∠ACB =β ,由余弦定理得:AC 2=12+22-2×1×2cos α ,∵△ACD 为正三角形 ,∴CD 2=AC 2=5-4cos α ,S △BCD =12·2·CD ·sin ⎝ ⎛⎭⎪⎫π3+β=CD ·sin ⎝ ⎛⎭⎪⎫π3+β=32CD ·cos β+12CD ·sin β ,在△ABC 中 ,由正弦定理得:1sin β=AC sin α ,∴AC ·sin β=sin α ,∴CD ·sin β=sin α ,∴(CD ·cos β)2=CD 2(1-sin 2β)=CD 2-sin 2α=5-4cos α-sin 2α=(2-cos α)2 ,∵β<∠BAC ,∴β为锐角 ,CD ·cos β=2-cos α ,∴S △BCD =32CD ·cos β+12CD ·sin β=32·(2-cos α)+12sin α=3+sin ⎝ ⎛⎭⎪⎫α-π3 ,当α=5π6时 ,(S △BCD )max =3+1.二、填空题7.如下图 ,测量河对岸的塔高AB 时可以选与塔底B 在同一水平面内的两个测点C 与D ,测得∠BCD =15° ,∠BDC =30° ,CD =30 ,并在点C 测得塔顶A 的仰角为60° ,那么塔高AB 等于15 6.解析:在△BCD 中 ,∠CBD =180°-15°-30°=135°. 由正弦定理得BC sin30°=CD sin135° ,所以BC =15 2.在Rt △ABC 中 ,AB =BC tan ∠ACB =152×3=15 6.8.如下图 ,在△ABC 中 ,C =π3 ,BC =4 ,点D 在边AC 上 ,AD =DB ,DE ⊥AB ,E 为垂足 ,假设DE =2 2 ,那么cos A =64.解析:∵AD =DB ,∴∠A =∠ABD ,∠BDC =2∠A .设AD =BD =x ,∴在△BCD 中 ,BC sin ∠CDB=BD sin C ,可得4sin2A =x sin60°.① 在△AED 中 ,ED sin A =AD sin ∠AED,可得22sin A =x 1.② ∴联立①②可得42sin A cos A =22sin A 32,解得cos A =64.9.在△ABC 中 ,BC =2 ,AB →·AC →=2 ,那么△ABC 面积的最|大值是3.解析:由BC →=AC →-AB → ,得BC →2=(AC →-AB →)2 ,设|AB →|=c ,|AC →|=b ,那么b 2+c 2=8 ,又因为AB →·AC →=bc ·cos A =2 ,所以cos A =2bc ,所以sin 2A =1-4(bc )2 ,设△ABC 的面积为S ,那么S 2=14(bc )2sin 2A =14(b 2c 2-4) ,因为bc ≤b 2+c 22=4 ,所以S 2≤3 ,所以S ≤ 3.所以△ABC 面积的最|大值是 3.10.(2021·武汉市调研测试)在钝角△ABC 中 ,内角A ,B ,C 的对边分别为a ,b ,c ,假设a =4 ,b =3 ,那么c 的取值范围是(1 ,7)∪(5,7).解析:三角形中两边之和大于第三边 ,两边之差小于第三边 ,据此可得1<c <7 ,①假设∠C 为钝角 ,那么cos C =a 2+b 2-c 22ab =25-c 224<0 ,解得c >5 ,②假设∠A 为钝角 ,那么cos A =b 2+c 2-a 22bc =c 2-76c <0 ,解得0<c <7 ,③结合①②③可得c 的取值范围是(1 ,7)∪(5,7).三、解答题11.(2021·全国卷Ⅰ)在平面四边形ABCD 中 ,∠ADC =90° ,∠A =45° ,AB =2 ,BD =5.(1)求cos ∠ADB ;(2)假设DC =2 2 ,求BC .解:(1)在△ABD 中 ,由正弦定理得BD sin A =AB sin ∠ADB. 由题设知 ,5sin45°=2sin ∠ADB, 所以sin ∠ADB =25.由题设知 ,∠ADB <90° ,所以cos ∠ADB =1-225=235.(2)由题设及(1)知 ,cos ∠BDC =sin ∠ADB =25.在△BCD 中 ,由余弦定理得BC 2=BD 2+DC 2-2·BD ·DC ·cos ∠BDC =25+8-2×5×22×25=25.所以BC =5.12.(2021·潮州二模)在锐角△ABC 中 ,角A ,B ,C 所对的边分别为a ,b ,c ,且a cos B +b cos A c =233sin C . (1)求C 的值;(2)假设a sin A =2 ,求△ABC 的面积S 的最|大值.解:(1)∵a cos B +b cos A c =233sin C , 由正弦定理可得sin A cos B +sin B cos A =233sin 2C ,∴sin(A +B )=233sin 2C ,∴sin C =233sin 2C .∵sin C >0 ,∴sin C =32 ,∵C 为锐角 ,∴C =60°.(2)由C =60°及c sin C =a sin A =2 ,可得c = 3.由余弦定理得3=b 2+a 2-ab ≥ab (当且仅当a =b 时取等号) ,∴S =12ab sin C ≤12×3×32=334 ,∴△ABC 的面积S 的最|大值为334.第二次作业 (高|考)·模拟解答题体验1.(2021·北京卷)在△ABC 中 ,a =7 ,b =8 ,cos B =-17.(1)求∠A ;(2)求AC 边上的高.解:(1)在△ABC 中 ,因为cos B =-17 ,所以sin B =1-cos 2B =437.由正弦定理得sin A =a sin B b =32.由题设知π2<∠B <π ,所以0<∠A <π2.所以∠A =π3.(2)在△ABC 中 ,因为sin C =sin(A +B )=sin A cos B +cos A sin B =3314 ,所以AC 边上的高为a sin C =7×3314=332.2.(2021·益阳·湘潭调研考试)锐角△ABC 中 ,内角A ,B ,C 的对边分别为a ,b ,c ,且2a -b c =cos B cos C .(1)求角C 的大小;(2)求函数y =sin A +sin B 的值域.解:(1)由2a -b c =cos B cos C ,利用正弦定理可得2sin A cos C -sin B cos C=sin C cos B ,可化为2sin A cos C =sin(C +B )=sin A ,∵sin A ≠0 ,∴cos C =12 ,∵C ∈(0 ,π2) ,∴C =π3.(2)y =sin A +sin B =sin A +sin(π-π3-A )=sin A +32cos A +12sin A =3sin(A +π6) ,∵A +B =2π3 ,0<A <π2 ,0<B <π2 , ∴π6<A <π2 ,∴π3<A +π6<2π3 ,∴sin(A +π6)∈(32 ,1] ,∴y ∈(32 ,3].3.锐角三角形ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且满足cos 2B -cos 2C -sin 2A =-sin A sin B ,sin(A -B )=cos(A +B ).(1)求角A ,B ,C ;(2)假设a = 2 ,求三角形ABC 的边长b 的值及三角形ABC 的面积.解:(1)∵cos 2B -cos 2C -sin 2A =-sin A sin B ,∴sin 2C +sin A sin B =sin 2A +sin 2B ,∴由正弦定理得c 2+ab =a 2+b 2 ,∴cos C =a 2+b 2-c 22ab =ab 2ab =12 ,∵0<C <π ,∴C =π3.∵sin(A -B )=cos(A +B ) ,∴sin A cos B -cos A sin B =cos A cos B -sin A sin B ,∴sin A (sin B +cos B )=cos A (sin B +cos B ) ,∴sin A =cos A ,∴由A 为锐角 ,可得A =π4 ,B =π-A -C =5π12.(2)∵a = 2 ,A =π4 ,B =5π12 ,∴由正弦定理可得b =a ·sin B sin A =6+22 , ∴三角形ABC 的面积S =12ab sin C =12×2×6+22×32=3+34.4.(2021·武汉市调研测试)在锐角△ABC 中 ,内角A ,B ,C 的对边分别是a ,b ,c ,满足cos2A -cos2B +2cos(π6-B )cos(π6+B )=0.(1)求角A 的值;(2)假设b =3且b ≤a ,求a 的取值范围.解:(1)由cos2A -cos2B +2cos(π6-B )cos(π6+B )=0 ,得2sin 2B -2sin 2A +2(34cos 2B -14sin 2B )=0 ,化简得sin A =32 ,又△ABC 为锐角三角形 ,故A =π3.(2)∵b =3≤a ,∴c ≥a ,∴π3≤C <π2 ,π6<B ≤π3 ,∴12<sin B ≤32.由正弦定理a sin A =b sin B ,得a 32=3sin B ,∴a =32sin B ,由sin B ∈(12 ,32]得a ∈[ 3 ,3).5.如下图 ,在△ABC 中 ,C =π4 ,CA →·CB →=48 ,点D 在BC 边上 ,且AD =5 2 ,cos ∠ADB =35.(1)求AC ,CD 的长;(2)求cos ∠BAD 的值.解:(1)在△ABD 中 ,∵cos ∠ADB =35 ,∴sin ∠ADB =45.∴sin ∠CAD =sin(∠ADB -∠ACD )=sin ∠ADB cos π4-cos ∠ADB sin π4=45×22-35×22=210.在△ADC 中 ,由正弦定理得AC sin ∠ADC =CD sin ∠CAD =AD sin ∠ACD,即AC 45=CD 210=5222,解得AC =8 ,CD = 2.(2)∵CA →·CB →=48 ,∴8·CB ·22=48 ,解得CB =6 2 ,∴BD =CB -CD =5 2.在△ABC 中 ,AB =82+(62)2-2×8×62×22=210.在△ABD 中 ,cos ∠BAD =(210)2+(52)2-(52)22×210×52=55. 6.在△ABC 中 ,内角A ,B ,C 的对边分别为a ,b ,c ,假设b 2+c 2-a 2=bc .(1)求角A 的大小;(2)假设a = 3 ,求BC 边上的中线AM 的最|大值.解:(1)∵b 2+c 2-a 2=bc ,∴cos A =b 2+c 2-a 22bc =12.又0<A <π ,∴A =π3.(2)在△ABC 中 ,A =π3 ,a = 3 ,由余弦定理a 2=b 2+c 2-2bc cos A 得b 2+c 2=bc +3.那么b 2+c 2=bc +3≥2bc ,得bc ≤3(当且仅当b =c 时取等号).在△ABC 中 ,由余弦定理 ,得cos B =a 2+c 2-b 22ac .在△ABM 中 ,由余弦定理 ,得AM 2=AB 2+BM 2-2·AB ·BM ·cos B=c 2+a 24-2·c ·12a ·a 2+c 2-b 22ac=2c 2+2b 2-a 24=2bc +34≤94 , ∴AM ≤32.∴AM 的最|大值是32.。
2020版高考数学(理)刷题小卷练: 20 Word版含解析

A.nB. n-1
C.n2D.2n-1
答案:A
解析:由an=n(an+1-an),得 = ,所以数列 为常数列,所以 = =…= =1,所以an=n,故选A.
7.[2019·咸阳模拟]我国古代数学名著《九章算术》中,有已知长方形面积求一边的算法,其方法的前两步为:
所以a1<a2=a3,a3>a4>a5>…>an,
所以数列{an}中的最大项为a2或a3,且a2=a3=2× 2= .故选A.
解法二 = = ,
令 >1,解得n<2;令 =1,解得n=2;令 <1,解得n>2.又an>0,
故a1<a2=a3,a3>a4>a5>…>an,
所以数列{an}中的最大项为a2或a3,且a2=a3=2× 2= .故选A.
12.[2019·山东枣庄第三中学质检]已知数列{an}的前n项和Sn=5n2+2n+1,则数列的通项公式为an=________.
答案:
解析:当n=1时,a1=8;当n≥2时,Sn-1=5(n-1)2+2(n-1)+1.所以an=Sn-Sn-1=10n-3,此式对n=1不成立,故an=
刷题课时增分练⑳综合提能力 课时练 赢高分
(1)构造数列1, , , ,…, ;①
(2)将数列①的各项乘以 ,得到一个新数列a1,a2,a3,a4,…,an.则a1a2+a2a3+a3a4+…+an-1an=()
A. B.
C. D.
答案:C
解析:依题意可得新数列为 , , ,…, × ,所以a1a2+a2a3+…+an-1an= + +…+ = = × = .故选C.
2020版高考数学(理)刷题小卷练: 23 Word版含解析

A. B. -
C. D. -
答案:B
解析:因为a1+a2+…+an= =n(n+2),所以bn= = ,故Tn= = - ,故选B.
7.[2019·合肥质检]已知数列{an}的前n项和为Sn,若3Sn=2an-3n,则a2 018=()
A.12里B.24里
C.36里D.48里
答案:B
解析:设第一天走a1里,则每天走的里数组成的数列{an}是以a1为首项,以 为公比的等比数列,由题意得S6= =378,解得a1=192(里),∴a4=a1× 3=192× =24(里),故选B.
5.[2019·湖南郴州质量监测]在等差数列{an}中,a4=5,a7=11.设bn=(-1)n·an,则数列{bn}的前100项和S100=()
4.[2019·黑龙江大庆模拟]中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思是“有一个人走路,第一天健步行走,从第二天起脚痛,每天走的路程是前一天的一半,走了6天,共走378里.”请问第四天走了()
4.[2019·甘肃张掖月考]数列 的前2 017项的和为()
A. +1 B. -1
C. +1 D. -1
答案:B
解析:通过已知条件得到 = - ,裂项累加得S2 017= - + - +…+ -1= -1,故选B.
5.[2019·资阳诊断]已知数列{an}中,a1=a2=1,an+2= 则数列{an}的前20项和为()
A.1 121 B.1 122
C.1 123 D.1 124
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中表示的区域(用阴影部分表示)是( )
C
由y ·(x +y -2)≥0,得⎩⎪⎨⎪⎧ y ≥0,x +y -2≥0或⎩⎪⎨⎪⎧y ≤0,
x +y -2≤
作出不等式组表示的平面区域,,由图知,当直线u=x-
12,符合题意,故k=
河州统一检测]
若目标函数z=ax+by(a>0
a b
=4x-2+1
4x-5
的最大值为,所以5-4x>0,则f(x)
作出满足约束条件的可行域如图阴影部分所示.
=-32x +z
2.
x .平移直线l 0,当直线y =-取最大值,z max =3×2+2×.某高科技企业生产产品A 和产品B 需要甲、乙两种新型材
由题意,设产品A 生产x 件,产品,线性约束条件为
⎩⎪⎨⎪
⎧
1.5x +0.5y ≤150,
x +0.3y ≤90,5x +3y ≤600,x ≥0,y ≥0,
作出不等式组表示的平面区域如图中阴
影部分所示,又由x ∈N ,y ∈N ,可知取得最大值时的最优解为(60,100),所以z max =2 100×60+900×100=216 000(元).
得m 的值为负数,在点A 处m 取得最小值,联立⎩
⎪⎨⎪⎧
y =7-3x ,
x +3y =13,解得
x =1,y =4,此时m min =2×1-3×4+4=-6,则|m |max =6,在直线
2x -3y +4=0下方并满足约束条件的区域使得m 的值为正数,在点C
处m 取得最大值,联立⎩
⎪⎨⎪⎧
y =7-3x ,
x =y +1,解得x =2,y =1,即C (2,1),
此时m max =5,|m |max =5,故|m |max =6,故z =⎝ ⎛⎭
⎪⎫12|2x -3y +4|
在点A (1,4)处
取得最小值,最小值为z =⎝ ⎛⎭
⎪⎫126=1
64,故选D.
二、非选择题
9.[2018·全国卷Ⅱ]若x ,y 满足约束条件⎩⎪⎨⎪
⎧
x +2y -5≥0,x -2y +3≥0,
x -5≤0,
则z
=x +y 的最大值为________.
答案:9
解析:由不等式组画出可行域,如图(阴影部分).x +y 取得最大值⇔斜率为-1的直线x +y =z (z 看做常数)的横截距最大,
由图可得直线x +y =z 过点C 时z 取得最大值. 由⎩
⎪⎨⎪⎧
x =5,x -2y +3=0得点C (5,4), ∴ z max =5+4=9.
10.[2019·郑州模拟]已知不等式组⎩⎪⎨⎪
⎧
x -y +1≥0,x +y -1≥0,
3x -y -3≤0
表示的平面
的中点即可.
,0,
解得A (1,0). ,0,解得B (2,3). 的中点坐标为 ⎛⎪⎫32,32,代入直线方程
即f(x)在[0,+∞)上为增函数.所以f(x)min=f(0)=a.。
