安徽省六安市高二数学下学期第一次统考(开学考试)试题理
安徽省六安市高二数学下学期第一次统考(开学考试)试题 文

舒城中学2017—2018学年度第二学期第一次统考高二文数(时间:120分钟 满分:150分)命题: 审题:一. 选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合要求的,请你将符合要求的项的序号填在括号内) 1.已知集合A ={}|2x x <,B ={}|320x x ->,则( ) A .AB =3|2x x ⎧⎫<⎨⎬⎩⎭B .A B =∅C .AB 3|2x x ⎧⎫=<⎨⎬⎩⎭D .A B=R2.下列函数中,定义域是R 且为增函数的是( )A.x y e -=B.3y x = C.ln y x = D.y x =3. 函数)sin()(ϕϖ+=x A x f (其中)0,0,0πϕω<<>>A 的部分 图象如图所示,则下列说法正确的是( )A. A.)(x f 图象可由)8sin(22x y π=图象向左平移4π个单位得到 B. B.)(x f 图象可由)8sin(22x y π=图象向左平移2个单位得到 C. C.)(x f 图象可由)8sin(22x y π=图象向右平移2个单位得到 D. D.)(x f 图象可由)8sin(22x y π=图象向右平移4π个单位得到 4.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( ) A .1 B .25. 已知m ,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )A. 若α,β垂直于同一平面,则α与β平行B. 若αβα⊂⊥m ,,则β⊥mC. 若α,β不平行,则在α内不存在与β平行的直线D. 若m ,n 不平行,则m 与n 不可能垂直于同一平面 不可能垂直于同一平面6.若0a b >>,0c d <<,则一定有( )A .a bd c> B .a bd c< C .a bc d> D . a b c d <7. 过点)0,1(-作抛物线12++=x x y 的切线,则其中一条切线为( ) A. 02y x 2=++B. 03y x 3=+-C. 01y x =++D. 01y x =+-8.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )A .16πB .20πC .24πD .32π9.直线:1l y kx =+与圆22:1O x y +=相交于,A B 两点,则"1"k =是“OAB ∆的面积为12”的( )A.充分不必要条件B.必要不充分条件C.既不充分也不必要条件D.充要条件10. ABC ∆的内角C B A ,,的对边分别为c b a ,,.已知0)cos (sin sin sin =-+C C A B ,,2=a 2=c .则=C( ) A .π12B .π6C .π4D .π311.已知04πθ<<,则双曲线22122:1cos sin x y C θθ-=与222222:1sin sin tan y x C θθθ-=的()A .实轴长相等B .虚轴长相等C .焦距相等D .离心率相等12.在平面直角坐标系中,第一象限有一系列圆n O ,所有圆均与x 轴和直线03=-y x 相 切,且任何相邻两圆外切;圆n O 的半径为n r ,其中01>>+n n r r .若圆1O 的半径11=r , 则数列}{n r 的前n 项和=n S( )A.n)21(2-B.])31(1[23n- C.])41(1[34n-D.])51(1[45n-二.填空题(本大题共4小题,每小题5分,共20分)13. 在平面直角坐标系x y O 中,已知四边形CD AB 是平行四边形,()1,2AB =-,()D 2,1A =,则D C A ⋅A = .14. 已知)2,0(πα∈,2tan =α,,则=-)4cos(πα . 15. 记不等式组0,34,34,x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域为D ,若直线()1y a x =+与D 有公共点,则a 的取值范围是 .16. 抛物线22(0)y px p =>的焦点为F ,准线为l ,A B 、是抛物线上的两个动点,且满足3AFB π∠=.设线段AB 的中点M 在l 上的投影为N ,则MN AB的最大值是 .三. 解答题(本大题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤) 17.(本小题满分10分)已知函数x ax x x f 3)(23--=. (Ⅰ)若()f x 在),1[+∞上是增函数,求a 的范围;(Ⅱ)若31-=x 是()f x 的极值点,求()f x 在[1,]a 上的最大值.18.(本小题满分12分)在ABC △中,内角,,A B C 所对的边分别为,,a b c .已知s i n 4s i na Ab B =,222)ac a b c =--.(I )求cos A 的值; (II )求sin(2)B A -的值.19.(本小题满分12分)设等差数列}{n a 的公差为d ,且1>d ,前n 项和为n S ,等比数列}{n b 的公比为q .已知100,,2,10211====S d q b a b .(Ⅰ)求数列}{n a ,}{n b 的通项公式; (Ⅱ)记nnn b a c =,求数列}{n c 的前n 项和n T .20.(本小题满分12分)如图,在直四棱柱1111ABCD A BC D -中,已知122DC DD AD AB ===,AD DC AB DC ⊥,∥.(Ⅰ)求证:11DC AC ⊥;(Ⅱ)设1=AD ,且E 是DC 上一动点,当//1E D 平面BD A 1时,求三棱锥BD A E 1-的体积.21.(本小题满分12分)如图,点)1,0(-P 是椭圆)0(1:22221>>=+b a by a x C 的一个顶点,1C 的长轴是圆4:222=+y x C 的直径21,l l 是过点P 且互相垂直的两条直线,其中1l 交圆2C 于B A ,两点,2l 交椭圆1C 于另一点D .(Ⅰ)求椭圆1C 的方程;(Ⅱ)求ABD ∆面积取最大值时直线1l 的方程.22.(本题满分12分)已知函数()2(1)ln 2x ax a x f x =+++.(Ⅰ)讨论()f x 的单调性; (Ⅱ)当0a <时,证明3()24f x a≤--.高二文科数学参考答案(高二下第一次统考) 1-5:ABBCD 6-10:BDCAB 11-12:DB 13. 5 . 14.10103 . 15. ]4,21[ . 16. 1 17解答:(1)0≤a (2)6-18题解答(Ⅰ)解:由sin 4sin a A b B =,及sin sin a bA B=,得2a b =由222)ac a b c =--,及余弦定理,得2225cos 25b c a A bcac +-===-(Ⅱ)解:由(Ⅰ),可得sin 5A =, 代入sin 4sin a A b B =,得sin sin 4a A B b ==由(Ⅰ)知,A为钝角,所以cos B == 于是4sin 22sin cos 5B B B ==,23cos 212sin 5B B =-=, 故sin(2)sin 2cos cos 2sin B A B A B A -=-43(55=⨯-= 19解答:(Ⅰ)由题意有,111045100,2,a d a d +=⎧⎨=⎩即112920,2,a d a d +=⎧⎨=⎩解得11,2,a d =⎧⎨=⎩ 故121,2.n n n a n b -=-⎧⎪⎨=⎪⎩ (Ⅱ)1212n n n C --=23413579211...22222n n n T --=++++++ ①234511357921 (2222222)n n n T -=++++++ ② ①-②可得2321111121232 (32222222)n n n n n n T --+=+++++-=- 故12362n n n T -+=-20解答:(1)省略(2)解答:31=v 21题答案:(1)1422=+y x (2)1210-±=x y 22解答:(1)f(x)的定义域为(0,)+∞,1(1)(21)()221x ax f x ax a x x++'=+++=若0a ≥,则当(0,)x ∈+∞时,()0f x '>,故()f x 在(0,)+∞单调递增若0a <,则当1(0,)2x a ∈-时,()0f x '>;当1(,)2x a∈-+∞时,()0f x '< 故()f x 在1(0,)2a -单调递增,在1(,)2a-+∞单调递减.(2)由(1)知,当0a <时,()f x 在12x a=-取得最大值,最大值为 111()ln()1224f a a a -=---所以3()24f x a ≤--等价于113ln()12244a a a ---≤--,即11ln()1022a a-++≤设()ln 1g x x x =-+,则1()1g x x'=-当(0,1)x ∈时,()0g x '>;当(1,)x ∈+∞,()0g x '<. 所以()g x 在(0,1)单调递增,在(1,)+∞单调递减. 故当1x =时,()g x 取得最大值,最大值为(1)0g = 所以当0x >时,()0g x ≤ 从而当0a <时,11ln()1022a a -++≤,即3()24f x a≤--。
安徽省六安市高二数学下学期第一次阶段检测试题理(扫描版)

安徽省六安市2016-2017学年高二数学下学期第一次阶段检测试题理
(扫描版)
尊敬的读者:
本文由我和我的同事在百忙中收集整编出来,本文稿在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
安徽省六安市新安中学2021-2022学年高二下学期开学考试数学试题

C. D.
B
由向量的加法和减法运算法则计算即可.
故选:B
7.椭圆 的焦点在y轴上,长轴长是短轴长的 倍,则m的值为()
A. 2B. C. 4D. 6
B
根据已知条件列方程,化简求得 的值.
依题意,方程 ,表示焦点在 轴上的椭圆,
所以 , ,故 ,只有B选项符合.
,由于长轴长是短轴长的 倍,
即 ,即 ,解得 .故选:B
安徽省六安市新安中学2021-2022学年高二下学期开学考试数学试题
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知直线m经过 , 两点,则直线m的斜率为()
A.-2B. C. D.2
A
根据斜率公式求得正确答案.
直线 斜率为: .故选:A
2.已知数列 满足 , ,则 ()
离心率为 ,易知选项BCD正确.
故选:BCD
12.已知数列 的前 项和为 ,则下列说法正确的是()
A. B. 为 的最小值
C. D.
AC
利用和与项的关系,分 和 分别求得数列的通项公式,检验合并即可判定A;
根据数列的项的正负情况可以否定B;根据前16项都是正值可计算判定C;注意到 可计算后否定D.
,
8.在各项均为正数的等比数列 中,若 ,则
A.6B.7C.8D.9
D
由等比数列的性质可得b5=2,再利用对数的运算性质即可得出.
已知 ,由等比数列的性质可得 ,
又等比数列各项为正数,b5>0,可得b5=2.
则 =log2(b1b2•…•b9)=log2 =9.故选D.
本题考查等比数列的性质 (其中m+n=p+q)、对数的运算性质的应用,考查推理能力与计算能力,属于中档题.
2023-2024学年安徽省六安市高二下学期第一次段考数学质量检测模拟试题(含解析)

2023-2024学年安徽省六安市高二下册第一次段考数学模拟试题一、单选题1.已知数列na为等比数列,若20a,4816aa,则6a()
A.-4B.2C.4D.4
【正确答案】C
【分析】运用等比数列的下标性质进行求解即可.
【详解】264816aaa,∴64a,又20a,∴4620aaq,所以64a,故选:C
2.已知数列na满足214a,且1212nnnaaa,则2023a()
A.14B.1C.32D.23
【正确答案】B
【分析】计算123a,214a,31a,432a,523a,确定na为周期是4的数列,计算得到答案.
【详解】1212nnnaaa,故12121124aaa,123a,2322112aaa,34321322aaa,45
4
212
23aa
a
,L,故na为周期是4的数列,
20233
1aa.
故选:B
3.设033
lim6
x
fxfx
x
,则3f()
A.12B.3C.3D.12【正确答案】B
【分析】根据导数的定义进行转化即可.
【详解】Δ0Δ03Δ3Δ3Δ3Δlim2lim236Δ2Δxxfxfxfxfxfxx,33f.故选:B
4.开学伊始,甲、乙、丙、丁四名防疫专家分别前往A,B,C三所中学开展防疫知识宣传,若每个学校至少安排一名专家,且甲必须安排到A中学,则不同的安排方式有()A.6种B.12种C.15种D.18种【正确答案】B
【分析】由题意被安排到A中学的防疫专家有2种情况,结合分步乘法原理及分类加法原理即可.
【详解】①若甲单独安排到A中学,则剩下的3名防疫专家分成两组到,BC两个中学,共有:2232CA6
种方式,
②若甲和另一名防疫专家被安排到A中学,则有:13C3
种方式,
则剩下的2名防疫专家分到到,BC两个中学,有:22A2
安徽省六安市第一中学高二数学下学期第一次阶段性考试试题理(扫描(2021年整理)

安徽省六安市第一中学2017-2018学年高二数学下学期第一次阶段性考试试题理(扫描版)
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(安徽省六安市第一中学2017-2018学年高二数学下学期第一次阶段性考试试题理(扫描版))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为安徽省六安市第一中学2017-2018学年高二数学下学期第一次阶段性考试试题理(扫描版)的全部内容。
安徽省六安市第一中学2017-2018学年高二数学下学期第一次阶段性考试试题 理(扫描版)
11 /
11。
安徽省2021学年高二数学下学期开学考试试题理

最新 Word高二数学放学期开学考试一试题理试卷分值: 150 分考试时间120分钟第Ⅰ卷(选择题,共60 分)一、选择题:本大题共12 小题,每题 5 分,共 60 分 . 在每题给出的A, B,C, D 的四个选项中,只有一个选项是切合题目要求的,请将正确答案的字母代号填涂到答题卡相应地点. 1.若复数z 知足(1 2i ) z 5 ,则复数z 在复平面上的对应点在第( ) 象限A. 一B. 二C. 三D. 四2.我们从这个商标中抽象出一个图象如图,其对应的函数可能是()A.B.C.D.3.已知函数,若 f (0)<0,则此函数的单一减区间是()A.(﹣∞,﹣1] B.[ ﹣ 1, +∞)C.(﹣ 3,﹣ 1] D .[ ﹣1,1)4.已知正实数a, b, c 知足:,则()A.a<b<c B.c<b<a C.b<c<a D.c<a<b5.已知 f x =sin x x3 1, x 2 ,2 ,若 f x 的最大值为M,f x 的最小值为N,则 M+N等于()A. 0 B.2 C.4 D.8 36.已知函数 f ( x)=,若对于x 的方程[ f(x)] 2+mf(x)+m﹣ 1= 0 恰有 3 个不一样的实数解,则实数m的取值范围是()A.(﹣∞,2)∪(2,+∞) B .(1﹣, +∞) C .( 1,e) D .(1﹣, 1)x1,7.已知y= f ( x+2)是奇函数,若函数g( x)= f ( x)﹣有 k 个不一样的零点,记为x2,,x k,则x1+x2++x k=()A.0 B.k C. 2k D. 4k最新Word 8.已知函数 f ( x)=sin cos ωx﹣(ω> 0)在 [0 ,] 上有且仅有三个零点,则ω 的取值范围是()A.(,)B.[ ,] C.[4 ,] D. [4 ,)9.已知函数,若对随意两个不相等的正数x1,x2,都有恒建立,则 a 的取值范围为()A.[4 , +∞)B.( 4, +∞)C.(﹣∞, 4] D.(﹣∞, 4)10.已知函数f (x)=(2﹣2 )x,若方程f()=a有 3个不一样的实根x1,2,x3(1<x x e x x xx2< x3),则的取值范围是()A.(,0) B .(,0) C .(,) D .(0,)11.函数f x 2x ln x x2 ax 3 恰有一个零点,则实数a的值为()A. 4 B. 3 C. 6 D. 312. 设函数f '( x)是函数 f ( x)( x R) 的导函数,当x 0 时, f ' ( x) 3 f ( x) < 0,则函数1xg ( x) f ( x) x3的零点个数为()A. 3第Ⅱ卷(非选择题,共90 分)二、填空题:本大题共 4 小题,每题 5 分,共 20 分 .13.已知f ( x) x , x 0 ,若 f1 (x) f (x), f n 1 (x) f ( f n ( x)), n N ,则 f2014 ( x) 的表1 x达式为 ________.14. 已知奇函数 y f ( x)( x R) 知足:对全部x R, f 1 x f 1 x ,且 x 0,1 时,f ( x ) e x 1, 则 f [ f ( 2019 )] .15. 已知 x1是函数f x 2x x 2 的零点,x2是函数 g x log 2 x 1 x 3 的零点,则x1 x2的值为__________16.. 已知函数f(x)= 2x﹣a,g(x)= 1+x3,若存在x1,x2∈[0 , 1] ,使得 f ( x1)= g( x2)建立,则实数 a 的取值范围是.三、解答题:本大题共17.(10分)若f ( x)6 小题,共70 分 . 解答应写出说明文字、演算式。
2019-2020学年安徽省六安市第一中学高二下学期第一次在线自测数学(理)试题(解析版)

2019-2020学年安徽省六安市第一中学高二下学期第一次在线自测数学(理)试题一、单选题1.下列命题中正确的是( ) A .一个函数的极大值总是比极小值大 B .函数的导数为0时对应的点不一定是极值点C .一个函数的极大值总比最大值小D .一个函数的最大值可以比最小值小【答案】B【解析】根据极值的定义,以及极值和最值之间的关系,对选项进行逐一分析即可. 【详解】一个函数的极大值有可能比某个极小值小,A 不正确; B 中,函数3()f x x =的导函数2()3f x x '=,当0x =时,()0f x '=,但0x =不是函数3()f x x =的极值点,B 正确;一个函数的极大值可能是最大值,C 不正确; 一个函数的最大值不可能比最小值小,D 不正确. 故选:B. 【点睛】本题考查函数极值和最值之间的关系,属基础题. 2.已知函数()ln f x x x =+,则0(2)(2)limx x f x∆→+∆-=∆( )A .2B .32 C .54D .3【答案】B【解析】根据导数的定义,以及导数的计算,即可求得结果. 【详解】根据题意,对函数()f x ,有0(2)(2)lim (2)x x f f x∆→+∆-'=∆,又由()ln f x x x =+, 则1()1f x x '=+,则有13(2)122f '=+=.故选:B. 【点睛】本题考查导数的定义,以及导数的计算,属综合基础题. 3.设函数f (x )=2x+lnx ,则 ( ) A .x=12为f(x)的极大值点 B .x=12为f(x)的极小值点 C .x=2为 f(x)的极大值点 D .x=2为 f(x)的极小值点【答案】D 【解析】【详解】22212'()x f x x x x-=-+=, 由'()0f x =得2x =, 又函数定义域为(0,)+∞,当02x <<时,'()0f x <,()f x 递减, 当2x >时,'()0f x >,()f x 递增, 因此2x =是函数()f x 的极小值点.故选D . 【考点】函数的极值.4.已知曲线e ln x y a x x =+在点()1,ae 处的切线方程为2y x b =+,则( ) A .,1a e b ==- B .,1a e b ==C .1,1a e b -==D .1,1a e b -==-【答案】D【解析】通过求导数,确定得到切线斜率的表达式,求得a ,将点的坐标代入直线方程,求得b . 【详解】详解:ln 1,xy ae x '=++1|12x k y ae ='==+=,1a e -∴=将(1,1)代入2y x b =+得21,1b b +==-,故选D . 【点睛】本题关键得到含有a ,b 的等式,利用导数几何意义和点在曲线上得到方程关系.5.如图,两曲线23y x =-与221y x x =--所围成的图形面积是( )A .6B .9C .12D .3【答案】B【解析】求出两个函数的交点坐标,根据定积分的计算公式即可求得. 【详解】由223,21,y x y x x ⎧=-⎨=--⎩得1,2,x y =-⎧⎨=⎩或2,1.x y =⎧⎨=-⎩ 故两曲线所围成的阴影部分的面积2212[(3)(21)]x x x S dx ----=-⎰221[(224)x x S dx --=++⎰23212(4)3x x x -=-++162481433⎛⎫⎛⎫=-++-+- ⎪ ⎪⎝⎭⎝⎭9=故选:B. 【点睛】本题考查利用定积分求解曲边梯形的面积,属中档题.6.若一球的半径为r ,则内接于球的圆柱的侧面积最大为( ) A .22r π B .2r π C .24r π D .212r π 【答案】A【解析】如图,设内接圆柱的底面半径为R ,母线长为l ,求出S 侧=2πr cos θ·2r sin θ=4πr 2sin θcos θ,再利用导数求函数的最值. 【详解】如图,设内接圆柱的底面半径为R ,母线长为l ,则R =r cos θ,l =2r sin θ.∴S 侧=2πr cos θ·2r sin θ=4πr 2sin θcos θ. S ′=4πr 2(cos 2θ-sin 2θ)=4πr 2cos 2θ=0, ∴θ=4π.当θ=4π,即R =22r 时,S 侧最大且S 侧max =2πr 2. 【点睛】本题主要考查利用导数求函数的最值,意在考查学生对这些知识的掌握水平和分析推理能力,解题关键是设内接圆柱的底面半径为R ,母线长为l ,求出R =r cos θ,l =2r sin θ. 7.若函数3()3f x x x =-在2(,6)a a -上有最小值,则实数的取值范围是( ) A .(5,1)- B .[5,1)-C .[)2,1-D .(2,1)-【答案】C【解析】由f′(x)=3x 2-3=0,得x =±1,且x =1为函数的极小值点,x =-1为函数的极大值点.函数f(x)在区间(a ,6-a 2)上有最小值,则函数f(x)的极小值点必在区间(a ,6-a 2)内,且左端点的函数值不小于f(1),即实数a 满足a<1<6-a 2且f(a)=a 3-3a≥f(1)=-2,即221{5120a a a a <<≥,,(-)(+),解得1{552a a a <<<≥,-,-,故实数a 的取值范围是[-2,1).8.一辆汽车在高速公路上行驶,由于遇到紧急情况而刹车,以速度()25731v t t t=-++(t 的单位:s ,v 的单位:/m s )行驶至停止.在此期间汽车继续行驶的距离(单位:m )是( ) A .125ln5+ B .11825ln3+ C .425ln5+ D .450ln 2+【答案】C【解析】【详解】试题分析:令得,故44203()725ln(1)425ln 52t s v t dt t t ⎡⎤==-++=+⎢⎥⎣⎦⎰,故选C【考点】定积分的几何意义9.等比数列{}n a 中,12a =,84a =,函数128()()()()f x x x a x a x a L =---,则(0)f '=A .62B .92C .122D .152【答案】C【解析】将函数看做x 与()()()128x a x a x a --⋅⋅⋅-的乘积,利用乘法运算的求导法则,代入0x =可求得()1280f a a a '=⋅⋅⋅;根据等比数列性质可求得结果. 【详解】()()()()128f x x a x x a x a --⋅''=⎡⋅-⎤⎣⎦⋅ ()()()()()()128128x a x a x a x a x a x a x x ''=+--⋅⋅⋅---⋅⋅⋅⎡⎤⎡⎤⎣⎦⎣⎦- ()()()()()()128128x x a x a x a x a x a x a --⋅⋅⋅---⋅⋅'=+⎡⎤-⎡⎤⎣⎦⎣⎦⋅ ()1280f a a a '∴=⋅⋅⋅又18273645a a a a a a a a ===()()441218082f a a '∴===本题正确选项:C 【点睛】本题考查导数运算中的乘法运算法则的应用,涉及到等比数列性质应用的问题,关键是能够将函数拆解为合适的两个部分,从而求解导数值时直接构造出数列各项之间的关系.10.已知函数()y f x =是R 上的可导函数,当0x ≠时,有()()0f x f x x'+>,则函数1()()F x xf x x=+的零点个数是( ) A .0 B .1C .2D .3【答案】B【解析】试题分析:令11()()0,()F x xf x xf x x x =+==-.()()()'()()0xf x xf x f x f x f x x x x⎡⎤+⎣⎦''='+=>,即当0x >时,()'0xf x ⎡⎤>⎣⎦,为增函数,当0x <时,()'0xf x ⎡⎤<⎣⎦,为减函数,函数1y x=-在区间()()0,,,0+∞-∞上为增函数,故在区间(),0-∞上有一个交点.即1()()F x xf x x=+的零点个数是1.【考点】1.函数与导数;2.零点.【思路点晴】零点问题一种解法是变为两个函数图象的交点,如本题中的1()()F x xf x x =+的零点,可以转化为1()xf x x =-,也就是左右两个函数图象的交点个数,函数1y x =-在区间()()0,,,0+∞-∞上为增函数,通过已知条件分析()()()'()()0xf x xf x f x f x f x x x x⎡⎤+⎣⎦''='+=>,即当0x >时,()'0xf x ⎡⎤>⎣⎦,为增函数,当0x <时,()'0xf x ⎡⎤<⎣⎦,为减函数,由此判断这两个函数在区间(),0-∞上有一个交点. 11.已知3211()(1)(1)132f x x a x a b x =++++++,若方程()0f x '=的两个实数根可以分别作为一个椭圆和双曲线的离心率,则 A .3a b -<- B .3a b -≤-C .3a b ->-D .3a b -≥-【答案】A【解析】结合椭圆及双曲线的性质可得:2()(1)(1)0f x x a x a b '=+++++=有一个大于1的根,一个小于1大于0,则10230a b a b ++>⎧⎨++<⎩,作出不等式组所表示的平面区域,利用线性规划的知识可求Z a b =-的范围. 【详解】2()(1)(1)f x x a x a b '=+++++结合椭圆及双曲线的性质可得:2()(1)(1)0f x x a x a b '=+++++=有一个大于1的根,一个小于1大于0作出不等式组则10230a b a b ++>⎧⎨++<⎩所表示的平面区域如图所示,令Z a b =-作直线0:0l a b -=,把直线向可行域平移到(2,1)A -时,max 3Z =-3a b ∴-<-所以A 选项是正确的.【点睛】本题主要考查了函数的零点和根的分布,椭圆与双曲线的几何性质以及,线性规划的基础知识.考查基础知识的综合运用.属于难题. 12.定义在R 上的函数()f x 的导函数为'()f x ,若()0f x <,且()'()2112f x f x +⎛⎫> ⎪⎝⎭,则( )A .()()22213f f e< B .()()21f f e< C .()()2212f f e< D .()()231f e f <⋅【答案】C 【解析】由()'()2112f x f x +⎛⎫> ⎪⎝⎭得()2'()0f x f x +<,构造函数:2()()x g x e f x =⋅,求导判单调性得(2)(1)g g >,进而得22(2)(1)e f f ⋅>则可求【详解】 因为()'()0211122f x f x +⎛⎫⎛⎫>= ⎪⎪⎝⎭⎝⎭,所以()2'()0f x f x +<.构造函数:2()()x g x e f x =⋅,所以2'()()2()'()xxg x e f x e f x f x =⋅+⋅⋅()[()2'()]0xe f x f x f x =⋅⋅+>.所以函数()g x 在R 上单调递增,所以(2)(1)g g >,即222(2)(1)e f e f ⋅>⋅,即()()2212f f e<故选:C 【点睛】本题考查导数与函数的单调性,考查构造函数的思想,考查逻辑推理能力,是中档题二、填空题 13.已知21()2(2019)2019ln 2f x x xf x =++',则(1)f '=_______. 【答案】2020-【解析】先对函数求导,然后求出(2019)f ',进而求出答案。
六安市舒城中学2020_2021学年高二数学下学期开学考试试题理
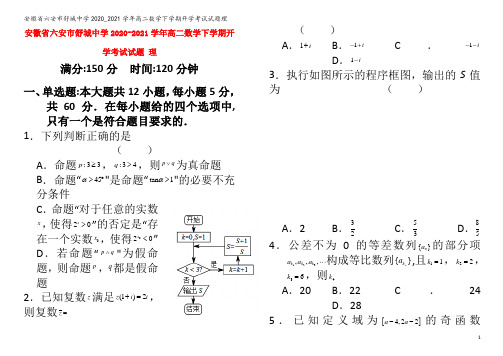
安徽省六安市舒城中学2020-2021学年高二数学下学期开学考试试题理满分:150分时间:120分钟一、单选题:本大题共12小题,每小题5分,共60分.在每小题给的四个选项中,只有一个是符合题目要求的.1.下列判断正确的是()A.命题:33p≥,:34q>,则p q∨为真命题B.命题“45α>︒"是命题“tan1α>"的必要不充分条件C.命题“对于任意的实数x,使得20x>”的否定是“存在一个实数0x,使得020x<”D.若命题“p q∧"为假命题,则命题p,q都是假命题2.已知复数z满足(1)2z i i+=,则复数z=()A.1i+B.1i-+C.1i--D.1i-3.执行如图所示的程序框图,输出的S值为()A.2 B.32C.53D.85 4.公差不为0的等差数列{}n a的部分项123,,,k k ka a a构成等比数列{}n k a,且11k=,22k=,36k=,则4kA.20 B.22 C.24D.285.已知定义域为[]4,22a a--的奇函数()32016sin 2f x x x b =-++,则()()f a f b += ( )A .0B .1C .2D .46.如图所示,点P 是函数()()2sin ,0y x x R ωϕω=+∈>的图象的一个最高点,M ,N 是图象与x轴的交点.若0PM PN ⋅=,则ω的值为 ( )A 。
8B 。
4C .4πD .8π7.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,则ABC 的面积222221()22a b c S ab ⎛⎫+-=- ⎪⎝⎭根据此公式,若cos (2)cos 0a B b c A +-=,且2224b c a ,则ABC 的面积为 ( )A .6B .23C .3D .328.已知正四面体ABCD 中, 4,4AE AB CF CD ==则直线DE 与BF 所成角的余弦值为 ( ) A .313 B .413 C .313- D .413-9.设A B C D ,,,是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为 ( )A .123B .183C .243 D .54310.已知(,)P x y 是直线)0(04>=++k y kx 上一动点,PA PB 、是圆C:0222=-+y y x 的两条切线,A B 、是切点,若四边形PACB 的最小面积是2,则k 的值为 ( ) A .22 B .2 C .3D .212 11.在直三棱柱111A B C ABC-中,2BAC π∠=,11AB AC AA ===.已知G与E分别为11A B 和1CC 的中点,D与F分别为线段AC 和AB 上的动点(不包括端点).若GD EF ⊥,则线段DF 的长度的取值范围为 ( )A .1, 15⎡⎫⎪⎢⎣⎭B.1, 25⎡⎫⎪⎢⎣⎭ C .)1, 2⎡⎣ D .1, 25⎡⎫⎪⎢⎣⎭12.设1F ,2F 分别是椭圆22221(0)x y C a b a b +=>>:的左、右焦点,直线l 过1F 交椭圆C 于A ,B两点,交y 轴于C 点,若满足1132FC AF =且1230CF F ∠=,则椭圆的离心率为( )A .16B .13C .36D .33二、填空题:本大题共4小题,每小题5分,共20分.13.设,x y 满足约束条件2102700x y x y x --≤⎧⎪+-≤⎨⎪≥⎩,则3z x y =+的最大值为___________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
舒城中学2017—2018学年度第二学期第一次统考 高二理数 时间:120分钟 满分:150分 命题: 审题: 一、选择题。本大题共12小题;每小题5分,共60分,在每小题给出的四个选项中,只有一项是最符合题目要求的。 1.数列na为等差数列,321,,aaa成等比数列,15a,则10a ( ) A.5 B.-1 C.0 D.1 2. 已知)(),(xgxf分别是定义在R上的偶函数和奇函数,且1)()(23xxxgxf ,则)1()1(gf ( ) A.-3 B.-1 C.1 D.3 3. 一个多面体的三视图如图所示,则该多面体的表面积为 ( )
A.321 B.318 C.21 D.18
4. 函数)(xfy的图象在点5x处的切线方程是8xy,则)5()5(ff等于 ( )
A.1 B.2 C.0 D.12 5. 下列命题正确的个数为 ( ) “Rx都有02x”的否定是“Rx0使得020x”; “3x”是“3x”成立的充分条件; 命题“若21m,则方程0222xmx有实数根”的否命题 A. 0 B. 1 C. 2 D. 3 6.若0,0,lglglgababab,则ab的最小值为( ) A.8 B.6 C.4 D.2 7.正四面体ABCD中,点E为BC中点,点F为AD中点,则异面直线AE与CF所成角的余弦值( )
A.13 B.12 C.23 D.63 8.双曲线122ayx的一条渐近线与直线032yx垂直,则a= ( ) A. 2 B.4 C.-2 D.-4
9.已知点P在椭圆)0(12222babyax上,点F为椭圆的右焦点,PF的最大值与最小值的比为2,则这个椭圆的离心率为 ( )
A.12 B.13 C.14 D.22 10.已知(,)Pxy是直线)0(04kykx上一动点,PAPB、是圆C:0222yyx的两条切线,AB、是切点,若四边形PACB的最小面积是2,则k的值为 ( )
A.3 B.212 C.22 D.2 11.直线l过抛物线)0(22ppxy的焦点,且交抛物线于BA,两点,交其准线于C点,已知BFCBAF3,4||,则p ( ) A.2 B.34 C.38 D. 4 12.已知边长为23的菱形ABCD中,60BAD,沿对角线BD折成二面角ABDC为120的四面体ABCD,则四面体的外接球的表面积为
( ) A.25 B.26 C.27 D.28 二、填空题:本大题共4小题;每小题5分,共20分,把答案填写在答题纸的相应位置上
13.已知方程)(13122Rkkykx表示焦点在x轴上的椭圆,则k的取值范围是 . 14. 若命题:"01,"2kxkxRx是真命题,则实数k的取值范围是 .
15.如右图,抛物线pxyC2:21和圆:2C 222()24ppxy,其中0p,直线l经过1C的焦点,依次交21,CC于DCBA,,,四点,则CDAB的值为 . 16.定义在R上的函数()fx满足:()1()fxfx,(0)6f, ()fx是()fx的导函
数,则不等式()5xxefxe(其中e为自然对数的底数)的解集为 . 三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤 17.(10分)
已知函数axexfx)((a为常数)的图象与y轴交于点A,曲线)(xfy在点A处的切线斜率为1 (1)求a的值及函数)(xf的极值; (2)证明:当0x时,xex2
18.(12分)已知过抛物线)0(22ppxy的焦点,斜率为22的直线交抛物线于))(,(),,(212211xxyxByxA两点,且9AB. (1)求该抛物线的方程; (2) O为坐标原点,C为抛物线上一点,若OBOAOC,求的值.
19.(12分)如图甲,四边形ABCD中,E是BC的中点, 2,5,1,2ADABBCDCDB.将(图甲)沿直线BD折起,使二面角
CBDA为o60(如图乙).
(1)求证:AE⊥平面BDC (2)求点B到平面ACD的距离.
20.(12分) 如图,在底面为正方形的四棱锥ABCDP中,侧棱PD⊥底面ABCD,DCPD,点E是线段PC的中点.
(1)求异面直线AP与BE所成角的大小;
(2)若点F在线段PB上,使得二面角BDEF的正弦值为33,求PBPF的值. 21. (12分) 在平面直角坐标系xOy中,经过点(02),且斜率为k的直线l与椭圆2212xy
有两个不同的交点P和Q.
(1)求k的取值范围; (2)设椭圆与x轴正半轴、y轴正半轴的交点分别为AB,,是否存在常数k,使得向量OPOQ与AB共线?如果存在,求k值;如果不存在,请说明理由.
22.(12分) 已知函数2lnfxkxxkR. (1)试讨论函数fx的单调性; (2)证明:4444ln2ln3ln4ln1...2,2342nnnNne.
2017-2018学年度第二学期寒假作业检测考试
高二数学(理)答案
一、选择题 DCABB CCBBD CD
二、填空题: 13. 1
三、解答题: 17.(10分) 解 (1)由f(x)=ex-ax,得f′(x)=ex-a. 又f′(0)=1-a=-1,得a=2. 所以f(x)=ex-2x,f′(x)=ex-2. 令f′(x)=0,得x=ln2.
A B C D
F
P E
(第20题) 当xln2时,f′(x)>0,f(x)单调递增. 所以当x=ln2时,f(x)取得极小值,且极小值为f(ln2)=eln2-2ln2=2-ln4,f(x)无极大值. (2)令g(x)=ex-x2,则g′(x)=ex-2x. 由(1)得g′(x)=f(x)≥f(ln2)>0, 故g(x)在R上单调递增,又g(0)=1>0,因此,当x>0时,g(x)>g(0)>0,即x218.(12分)
解 (1)直线AB的方程是y=22x-p2,与y2=2px联立,从而有4x2-5px+p2=0,
所以x1+x2=5p4. 由抛物线定义得|AB|=x1+x2+p=9, 所以p=4,从而抛物线方程是y2=8x. (2)由p=4,知4x2-5px+p2=0可化为x2-5x+4=0, 从而x1=1,x2=4,y1=-22,y2=42,从而A(1,-22),B(4,42). 设OC→=(x3,y3)=(1,-22)+λ(4,42)=(4λ+1,42λ-22), 又y23=8x3, 所以[22(2λ-1)]2=8(4λ+1),即(2λ-1)2=4λ+1, 解得λ=0,或λ=2. 19.(12分) (Ⅰ)证明:如图4,取BD中点M,连接AM,ME.
因为AB=AD=2,所以AM⊥BD, 因为DB=2,DC=1,BC=5,满足:DB 2+DC 2=BC 2, 所以△BCD是以BC为斜边的直角三角形,BD⊥DC,因为E是BC的中点,所以ME为△BCD的中位线,ME ∥12CD,ME⊥BD,ME=12 ∠AME是二面角A-BD-C的平面角,AME=60°. AMBD,MEBD且AM、ME是平面AME内两条相交于点M的直线, BDAEM平面,AE平面AEM,BDAE.
2ABAD,2DB,ABD△为等腰直角三角形,112AMBD,在△AME中,由余弦定理得: 22232cos2AEAMMEAMMEAMEAE,
2221AEMEAMAEME,,
BDMEMBDBDCMEBDC,平面,平面,AEBDC平面. (Ⅱ)解法一:等体积法. 解法二:如图5,以M为原点,MB所在直线为x轴,ME所在直线为y轴, 平行于EA的直线为z轴,建立空间直角坐标系,
图4 图5 则由(Ⅰ)及已知条件可知B(1,0,0),1002E,,,13022A,,,D(100),,,C(110),,.则131(010)22ABCD,,,,,,
13122AD,,,设平面ACD的法向量为n=()xyz,,,
则13·0022·00nADxyznCDy,,,令3x,则z=-2,(302)n,,, 记点B到平面ACD的距离为d,则 ABndn,所以d2230322173)0(2)(. 20.(12分) (1)6π;(2)12. 21. (12分) (1)由已知条件,直线l的方程为2ykx,
代入椭圆方程得22(2)12xkx.整理得22122102kxkx ①
直线l与椭圆有两个不同的交点P和Q等价于2221844202kkk, 解得22k或22k.即k的取值范围为2222,,∞∞. (2)设1122()()PxyQxy,,,,则1212()OPOQxxyy,, 由方程①,1224212kxxk. ② 又1212()22yykxx. ③ 而(20)(01)(21)ABAB,,,,,. 所以OPOQ与AB共线等价于12122()xxyy,将②③代入上式,解得22k. 由(1)知22k或22k,故没有符合题意的常数k. 22.(12分)
