标量衍射理论角谱及其传播

合集下载

11-标量衍射理论3-衍射的角谱理论、菲涅耳衍射

即为普遍的衍射公式。
使用时需要化简。在不同的近似条件下，可以得到菲涅耳衍射公式和夫琅禾费衍射公式
§2-3 标量衍射的角谱理论
3、菲涅耳衍射公式
x0
x
y0
y
近似条件：
z
孔径和观察平面
z
x02maxy02max
之间的距离远远大于孔径的线度
z
xm 2 axym 2 ax
只对轴附近的一个
U 0 ( x 0 ,y 0 )ex j2 k z ( p x 0 2 [ y 0 2 ) ] fx x z ,fy y z
§2-3 标量衍射的角谱理论
3、菲涅耳衍射公式：频域形式
或写成卷积式: U (x ,y) U 0(x ,y) h (x ,y)
其中, 脉冲响应函数为:
h(x,y)j1 zexjp k)e z (x jp 2 kz(x2y2)
§2-3 标量衍射的角谱理论
3、菲涅耳衍射公式：F.T.形式
由菲涅耳衍射的空域表达式：
p U ( x ,y ,z ) ejx j z) k p U z ( x ( ,y , ) ex jz [ p x (x { ) ( y y ) ]d } d x
§2-3 标量衍射的角谱理论
2、基于平面波角谱的衍射理论
从频域的角度即用平面波角谱方法来讨论衍射问题
xyz平面的光场分布与x0y00平面光场分布的关系：
U(x,y,z) U(x0,y0,0)exjp2p(z 12fx22fy2)

exjp 2p{ [fx(xx0)fy(yy0)]d}0xd0ydxfdyf
xyz平面上复振幅分布U(x,y,z)的空间频谱, 其空间频率宗量用传播矢量的方向余弦表示

标量衍射的角谱理论

6
按传播距离划分衍射区
1 9 0 6
7
用角谱衍射理论导菲涅耳公式（1）角谱衍射理论导菲涅耳公式（
1 9 0 6
假定孔径和观察平面之间的距离远远大于孔径的线度，假定孔径和观察平面之间的距离远远大于孔径的线度，并且只对轴附近的一个小区域内进行观察，并且只对轴附近的一个小区域内进行观察，则有
2 2 z >> x0max + y0max
13
夫琅和费衍射举例（夫琅和费衍射举例（续2）
1 9 0 6
函数的分布可知，由 sin c 函数的分布可知，每个 sin c 函数的主瓣的宽度正比于 λz l ，而由上式可见，这三个函数主瓣之间的距离大得多，为 f 0 λz ，若光栅频率 f 0 比 1 l 大得多，即光栅的周期 d = 1 f 0 小得多，那么三个函数（主瓣）比光栅的尺寸 l 小得多，那么三个函数（主瓣）之间不存在交叠，那么平方时不存在交叉项，因而交叠，那么平方时不存在交叉项，
及
2 2 z >> xmax + ymax
因而 λ f x = cos α ≈
x x0 y y0 << 1, λ f y = cos β ≈ << 1 z z
用二项式展开，只保留一次项，略去高次项，用二项式展开，只保留一次项，略去高次项，则
1 1 λ 2 f x2 λ2 f y2 ≈ 1 λ 2 ( f x2 + f y2 ) 2
jλr ∞
在傍轴近似下，并利用二项式近似在傍轴近似下，并利用二项式近似
) K (θ ≈1
r = z +(x x0 ) +(y y0 )

10标量衍射的角谱理论

进而可以表示为
H
fx, fy
exp jkz
1 λfx 2 λf y2 0fFra bibliotek2 x
f
2 y
1 λ2
其他
因而，可以把光波的传播现象看作一个空间滤波器。它具有有限
的带宽（见下图）。在频率平面上的半径为的圆形区域内，传递
函数的模为1，对各频率分量的振幅没有影响
对空域中比波长还要小的精细结构，或者说空间频率大于的信息，在单色光照明下不能沿方向向前传递。光在自由空间传播时，携带信息的能力是有限的
角谱的展宽就是在出射波中除了包含与入射光波相同方向传播的分量之外，还增加了一些与入射光波传播方向不同的平面波分量，即增加了一些高空间频率的波，这就是衍射波。
平面波角谱的衍射理论
本书的重点是从频域的角度即用平面波角谱方法来讨论衍射问题
前面已经讨论过频域的角谱传播问题，在由已知平面上的光场分布 U (x, y,0) 可通过傅里叶变换得到其角谱
U (x, y, z)
可以分别记作
U (x, y,)
A(cos
, cos
,) exp[ j (cos
x
cos
y)]d(cos )d(cos )
U (x, y, z)
A(cos
, cos
, z) exp[ j (cos
x
cos
y)]d(cos )d(cos )
研究角谱的传播就是要找到上面两个角谱，即 z 0 平面上的角谱和 z z 平面上的角谱之间的关系
exp{ j[ f x (x x ) f y ( y y )]}df x df y dxdy
上式的四重积分是类似基尔霍夫公式的一个精确的表达式，尽管它不含三角函数，但是使用起来仍很不方便。下面还是要按照菲涅耳的办法进行化简，首先对不同传播距离衍射的情况做个直观的说明

2.2 角谱传播2010

讨论：讨论：
(1) 当 cos 2 α + cos 2 β < 1 时,
1 − cos 2 α − cos 2 β
是实数. 是实数
对于某一确定的(α β 该式表示沿空间某一确定方向传对于某一确定的 α,β), 该式表示沿空间某一确定方向传播的平面波. 取不同值时, 播的平面波当(α,β)取不同值时该式表示光场中各个角 α β 取不同值时谱分量的传播情况. 谱分量的传播情况
§2.2
衍射的角谱理论
2.2.1 单色平面波与本征函数平面上的复振幅分布为：在 z=0 平面上的复振幅分布为： exp j 2π ( f x i x + f y i y ) = exp [ j 2π ( ux + vy ) ]
cos β cos α x+ y = exp j 2π λ λ
λ
ቤተ መጻሕፍቲ ባይዱ
z0 )
2.2.2 角谱的传播
x0 y0
U 0 ( x0 , y0 ;0)
xy
U z ( x , y; z )
Az ( cos α cos β , ; z)
平面波角谱的传播
A0 ( cos α cos β , ;0)
z
λ
λ
z=0
U 0 ( x0 , y0 ;0) =
z=z
λ
λ
−∞ −∞
∫∫
∞ ∞
(
( 1 − (λ u) − (λ v ) )
2 2
)
Az(u,v)和A0(u,v)分别看成是线性不变系统输出函数和输入函和分别看成是线性不变系统输出函数和输入函数的频谱，传递函数为：数的频谱，传递函数为：

第三章-标量衍射理论2-角谱及其传播

l
l

l
l
cos cos A( , , z)
l
l
称为xyz平面上复振幅分布的角谱, 表示不同传播方向()的单色平面波的振幅(|A|) 和初位相(arg{A})
角谱是xyz平面上复振幅分布U(x,y,z)的空间频谱, 其空间频率宗量用传播矢量的方向余弦表示
复振幅分布的角谱：例
在x-y平面上, 光场复振幅分布为余弦型: 可以分解为:
Angular Spectrum of Complex Amplitude Distribution
对在 z 处的x-y平面上单色光场的复振幅分布U(x,y,z)作傅里叶变换: 称为x-y平面 A( f x , f y , z) U ( x, y, z) exp[ j 2 ( f x x f y y)]dxdy 上复振幅分布的频谱其逆变换为：
2、平面波角谱的传播
角谱是传播距离 z 的函数
在孔径平面(x,y, 0)的光场U0(x, y , 0) :
U 0 ( x, y,0) A(

cos cos cos cos cos cos , ,0) exp[ j 2 ( x y)]d ( )d ( )
l
l
l
普遍的光振动的复振幅表达式： U(P) = a(P) e jj(P)
光强分布: I = UU*
a0 jkr e 球面波的复振幅表示（三维空间）：U ( P ) r
(P(x,y,z)) 球面波的复振幅表示（x-y 平面）： y a0 k 2 (r 2 U ( P) U ( x, y) exp( jkz) exp j ( x x0 ) ( y y0 ) k z 2z

信息光学Chap.2-衍射理论-角谱及其传播

U (x, y, z)

A(cos

,
, z) exp[ jp (cos
x
cos
y)]d(cos )d(cos )

代入亥姆霍兹方程 (2+k2)U(x,y,z)=0, 并交换积分和微分的顺序

(2

复振幅分布的角谱
第一步: 写出屏的透过率函数 t(x,y):
第二步: 写出入射波的复振幅分布U0(x,y ,0) 单位振幅的单色平面波垂直入射照明, U0(x,y,0)=1
第三步: 写出紧靠屏后平面上的透射光场复振幅分布U (x,y , 0)
U (x,y, 0)=U0(x,y, 0) t(x,y)= t(x,y)
第二部分衍射理论
一、衍射二、角谱理论
一、衍射
衍射规律：是光波传播的基本规律；基尔霍夫的衍射理论：是描述光波传播规律的基本理论；光波作为标量的条件:
一、衍射
1、衍射的概念：
1）索末菲的定义：“不能用反射或折射来解释的光线对直线光路的任何偏离”，是对现象的描述；
2）惠更斯-菲涅尔原理：把光波在传播过程中波面产生破缺的现象；是对圆孔、单缝等衍射现象解释而提出；
球面子波源
U (P)

c
U (P0 )K ( )
e jkr r
ds
源点
源点处的面元法线
所考虑的传播方向与面元法线的夹角源点到场点的距离
场点
原波阵面成功: 可计算简单孔径的衍射图样强度分布.
局限:难以确定K( ).无法引入-p /2的相移
2)基尔霍夫衍射公式
在单色点光源照明平面孔径的情况下: 惠-菲原理
A(cos , cos , z)

2 标量衍射理论

第二章标量衍射理论（Scalar diffraction theory）
衍射
l Sommerfeld定义
标量衍射理论（ scalar diffraction theory）的适用范围
电场的偏振性可以忽略，（傍轴近似paraxial aproximation）.
以Kirchhoff衍射公式讨论衍射问题，并利用线性系统理论赋予新的解释。

r = z x- x y - y

x- x y- y 忽略倾斜因子的变化后，就可以 z z z \把光波过一个线性不变系统。
U ( x, y ) = U ( x0 , y0 )h( x - x0 , y - y0 )dx0 dy0
近似条件当
j =
2p x - x0 y - y 0 8z 3
2

2 2

x - x0 2 y - y0 2
即
取最大值时，Δj<<2pz3来自1 8x - x
0

2
y - y0
2 2 max

充分但非必要条件在一般问题中，菲涅尔衍射很容易实现
2 f 2
其
1 λ2 他
等价于低通滤波器，截止频率1/
基尔霍夫理论空域角谱理论频域平面波球面子波系统的脉冲响应：球面子波在观察平面上的复振幅分布
系统的传递函数：脉冲响应的傅立叶变换
三、孔径对角谱的影响
入射到孔径平面的光场
U i ( x0 , y0 )
衍射屏的复振幅透过率 t ( x0 , y0 ) 衍射屏后表面光场

chap2标量衍射的角谱理论

U ( x, y, z) U0 ( x0 , y0 ,0)e
(4)式：
jkz
x d f y dx0 dy0

e U ( x, y, z ) U 0 ( x0 , y0 ,0)e jz
(5)式：
j
[( x x0 ) 2 ( y y0 ) 2 ] z dx
U ( x, y, z ) U 0 ( x0 , y0 ,0)e
当： 1
2
j
2 z 12 f x2 2 f y2 j 2 [ f ( x x ) f ( y y )] x 0 y 0 e df
x d f y dx0 dy0
f x2 2 f y2
df x df y
, A( f x , f y , z) A( cos
2012
cos

, z)
角谱的传播
• z=0平面上
U ( x, y,0) A( f x , f y ,0)e

j 2 ( xf x yf y )
df x df y
• z=z平面上
U ( x, y, z ) A( f x , f y , z )e
j [( x x0 ) 2 ( y y0 ) 2 ] e z ]dx0 dy0
j [( x x0 ) 2 ( y y0 ) 2 ] U 0 ( x0 , y0 ,0)e z dx0 dy0 2012
平面波角谱衍射理论
• 由平面波角谱衍射理论得到的精确表达式：
j 2 z 12 f x2 2 f y2 j 2 [ f ( x x ) f ( y y )] e x 0 y 0 df
a0 jkr e r •平面波的复振幅表示 U (P) ae jk r

10标量衍射理论2角谱及其传播

不改变, 但经受不同的相移.
方向余弦 cos2 cos2 的平面波, /, k 在xy 平面,不
沿 z 轴传播.
cos2 cos2 > : 代表倏逝波
2、平面波角谱的传播
传播现象作为线性空不变系统
A cos , cos , z A cos , cos ,0 exp( jkz 1 cos2 cos2 ) l l l l
§2-2 复振幅分布的角谱及角谱的传播
1、复振幅分布的角谱
Angular Spectrum of Complex Amplitude Distribution
对在 z 处的x-y平面上单色光场的复振幅分布U(x,y,z)作傅里叶变换:
称为x-y平面
A( fx , f y , z) U (x, y, z) exp[ j2 ( fx x f y y)]dxdy 上复振幅分
fx
f0 )]
U(x,y)的空间角谱函数: cos cos
A(
l
,
l
)
A( fx ,
fy)
f
x
c
os l
,
f
y
cos l
A( c os l
,
cos l
)
A 2
cos l
f0
cos l
f0
复振幅分布的角谱练习: P47, 2.2
第一步: 写出屏的透过率函数 t(x,y):
第二步: 写出入射波的复振幅分布U0(x,y ,0) 单位振幅的单色平面波垂直入射照明, U0(x,y,0)=1
§2-2 复振幅分布的角谱及角谱的传播
2、平面波角谱的传播
Propagation of Plane-Wave Angular Spectrum

傅里叶光学第3章标量衍射理论

标量衍射理论
衍射现象光波传播的规律标量理论的条件空间域和频率域两种分析方法最基本的光波形式
本章主要内容
1、光波的数学描述 2、基尔霍夫衍射理论 3、衍射的角谱理论 4、菲涅耳衍射 5、夫朗和费衍射 6、衍射的巴比涅原理 7、衍射光栅 8、菲涅耳衍射和分数傅里叶变换*
1、光波的数学描述
其中，
U x, y, z a exp jk x cos y cos z cos
（1）a 是常量振幅；
（2）cos、cos、cos 为传播方向的方向余弦，而且有
cos2 cos2 cos2 1
1、光波的数学描述
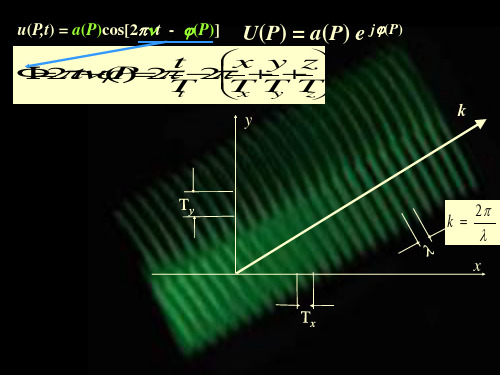
对于如右图所示的沿某一确定方向传播的平面波，在xy平面上的复振幅为：
1.1 单色光波场的复振幅表示单色光波场中某点P(x,y,z)在t时刻的光振动u(x,y,z,t)可表示为
u x, y, z,t a x, y, z cos 2 t x, y, z
其中，v是光波的时间频率；a(x,y,z)和(x,y,z)分别是P点光振动的振幅和初相位。根据欧拉公式，可将该波函数表示为复指数函数取实部的形式：
u x, y, z, t Re a x, y, z e j2tx,y,z
Re a x, y, z e e jx,y,z j2t
式中，Re{ }表示对括号内复函数取实部。为简单，去掉“Re”而直接用
复指数函数表示简谐波的波函数，并定义一个新的物理量：
U x, y, z a exp jkz cos exp jk x cos y cos

a
exp

jkz
1
cos2

标量衍射的角谱理论

U ( x, y, z ) U ( x , y ,) exp( j

z

f x f y )

exp{j [ f x ( x x ) f y ( y y )]}df x df y dx dy
上式的四重积分是类似基尔霍夫公式的一个精确的表达式，尽管它不含三角函数，但是使用起来仍很不方便。下面还是要按照菲涅耳的办法进行化简，首先对不同传播距离衍射的情况做个直观的说明

其后，可以求出它传播到平面 z z 上的角谱
A( cos cos cos cos , , z ) A( , ,) exp jkz cos cos

最后，通过傅里叶反变换可以进而得到用已知的 U ( x, y,) 表示的衍射光场分布，从而得到空域中的衍射公式
jr
在傍轴近似下，并利用二项式近似
K θ
r z x x y y

x x y y z z z
上述近似均代入得到菲涅尔衍射计算公式
1 k x x0 2 y y0 2 U x, y exp jkz U 0 x0 , y0 exp j dx0 dy0 jz 2 z
5
平面波角谱衍射理论的基本公式
1 9 0 6
作傅里叶反变换有
U ( x, y, z) A ( f x , f y ,) exp( j

z f x f y ) exp[ j ( f x x f y y)]df x df y
代入在衍射平面上的角谱的表达式得到

3标量衍射理论

n
r P’ r’ ∑ p
z
说明： k ( ) 1 ⑴若p, p’距离孔径∑足够远，则有 ⑵ 有值内
U( p )
0
0
外
1
⑶积分限∑ （-∞，+∞）透过率函数 t ( x, y )
0
内外
基于以上假设： Huggens——Fresnel原理公式可变为：
1 e U ( x, y) u t ( x 0, y ) ds 0 i r
cos cos A( , )

A0 z
2 对该频率的光波，透过孔径后，波沿垂直Z向传播，而不沿Z传播
2、当(cos cos )＝1时，u cos 0,
2 2

3、当(cos 2 cos 2 ) 1时 E合理存在于是有： H ( fx , f y ) exp(ikz 1 cos 2 cos 2 ) exp(ikz 1 cos cos )
球面波场中等位相线
二、单色平面波光场中任意平面上的振幅分布 1、平面波函数
E A cos(kr t ) A exp(ikr )exp(it )
复振幅： U ( x, y, z) A exp[ik ( x cos y cos z cos )]
二、孔径对角谱的影响
1、当(cos 2 cos 2 ) 1时，u i cos 2 cos 2 1 cos cos cos cos A( , ) A0 ( , ) exp(ikz cos 2 cos 2 1)

故该情况下为一倏逝波
2 2
当f x f y

第二章标量衍射理论

仅由惠更斯—菲涅耳原理无法解释子波源这一特殊性质。
倾斜因子K()的具体函数形式也难以确定。
基尔霍夫利用格林函数，通过求解波动方程，导出了严格的衍射积分公式，解决了上述问题，从而把惠更斯—菲涅耳原理置于更为可靠的波动理论基础上。
2.1.1 惠更斯—菲涅耳原理与基尔霍夫衍射公式
单色光场中任意一点Q的光振动M应满足标量波动方程
2.1.1 惠更斯—菲涅耳原理与基尔霍夫衍射公式
一般地说，不论以什么方式改变光波波面，或是以一定形式限制波面范围或使振幅以一定分布衰减，或是以一定的空间分布使相位延迟，或是兼而有之，都会引起衍射．所以障碍物的概念除去不
透明屏上有开孔这种情况以外，还包含具有一定复振幅的透明片．
论其脉冲响应和传递函数．
2.1 基尔霍夫衍射理论
2.1.1 惠更斯—菲涅耳原理与基尔霍夫衍射公式
惠更斯—菲涅耳原理是在惠更斯子波假设与杨氏干涉原理的基础上提出的，它是描述光传播过程的基本原理．
该原理指出：光场中任一给定曲面上的诸面元可以看做是子波源，如果这些子波源是相干的，则在波继续传播的空间上任一点处的光振动，都可看做是这些子波源各自发出的子波在该点相干叠加的结果．
因为总可以把任意复杂的光波分解成简单的球面波的线性组合．波动方程的线性性质允许对每一单个球面波分别应用上述原理，再把它们在Q点的贡献更加起来．
2.1.1 惠更斯—菲涅耳原理与基尔霍夫衍射公式
根据基尔霍夫对平面屏幕假设的边界条件，孔径外的阴影区内U0(P)=0, 基尔霍夫衍射公式的积分限可以扩展到无穷，从而有
2.1.1 惠更斯—菲涅耳原理与基尔霍夫衍射公式
当然，这里所说的光场中任一给定曲面无须是等位相面，即不是原始惠更斯—菲涅耳原理中所说的波面．

衍射的角谱理论

§2.3 衍射的角谱理论
• 由标量衍射理论知，相干光场在给定二平面间的传播过程就是通过一个二维线性系统（除夫琅和费衍射外）；一定条件下为线性空不变系统。 j2 (f x x+f y y) 是二维线性空不变系统的本 • 函数 exp 征函数 • 函数 exp j 2 ( f x f y ) 表示振幅为1的平面波在xy 平面上形成的复振幅分布 f y cos / 与平面波的传播方向相 • f x cos / 联系 ,表示了单色平面波的传播方向
jkz exp H ( fx , f y ) 0 1 1 ( f x ) 2 ( f y ) 2 f x 2 f y 2 2 其他
• 这表明该系统的传递函数相当于一个低通滤波器， 1/ 截止频率为．在频率平面上，这个滤波器的半径为的圆孔. • 对于孔径比波长还小的精细结构，或者说空间频率高于 1/ 的信息，在单色平面波照明下不能沿 z方向向前传播
cos cos cos cos , ) A0 ( , ) exp jkz 1 cos 2 cos 2
A(

几种情况讨论（2）
•
cos2 cos2 1
A(
公式中的平方根是虚数

2
cos cos cos cos , ) A0 ( , ) exp( z )
x y
傅里叶反变换的物理意义

f ( x, y )

F( f
x
, f y )exp[ j2 ( f x x f y y )]df xdf y
• F( f x , f y ) 被称为 f ( x, y ) 光场分布的角谱。

标量衍射的角谱理论

l2 2 ly I ( x, y ) sin c 2z z 2 m2 m l 2 lx 2 l sin c sin c ( x f 0 z ) sin c 2 ( x f 0 z ) z 4 z 4 z
13
夫琅和费衍射举例（续2）
1 9 0 6
由 sin c 函数的分布可知，每个 sin c 函数的主瓣的宽度正比于 z l ，而由上式可见，这三个函数主瓣之间的距离为 f 0 z ，若光栅频率 f 0 比 1 l 大得多，即光栅的周期 d 1 f 0 比光栅的尺寸 l 小得多，那么三个函数（主瓣）之间不存在交叠，那么平方时不存在交叉项，因而
10
夫琅和费衍射与傅里叶变换
1 9 0 6
夫琅和费衍射: 在菲涅耳衍射公式中，对衍射孔采取更强的限制条件，即取 1 2 2
z 2 k ( x0 y0 )
则平方位相因子在整个孔径上近似为1，于是
U ( x, y , z ) exp( jkz ) k exp[ j ( x 2 y 2 )] j z 2z 2 U ( x , y , 0) exp[ j ( xx yy0 )]dx0 dy0 0 0 z 0 2 x y exp[ j ( xx0 yy0 )] f x , fy exp[ j 2 ( f x x0 f y y0 )] z z z
5
平面波角谱衍射理论的基本公式
1 9 0 6
作傅里叶反变换有
U ( x, y, z) A ( f x , f y ,) exp( j

z f x f y ) exp[ j ( f x x f y y)]df x df y

标量衍射的角谱理论

第2章标量衍射的角谱理论光的传播是光学研究的基本问题之一,也是光能够记录、存储、处理和传送信息的基础。

众所周知，几何光学的基本定律——光沿直线传播，是光的波动理论的近似。

作为电磁波的光的传播要用衍射理论才能准确说明。

衍射，按照索末菲定义是“不能用反射或折射来解释的光线对直线光路的任何偏离”。

衍射是波动传播过程的普遍属性，是光具有波动性的表现。

电磁波是矢量波，精确解决光的衍射问题，必须考虑光波的矢量性。

用矢量波处理衍射过程非常复杂，这是因为电磁场矢量的各个分量通过麦克斯韦方程联系在一起，不能单独处理。

但是在光的干涉、衍射等许多现象中，只要满足：（1）衍射孔径比波长大很多，（2）观察点离衍射孔不太靠近；不考虑电磁场矢量的各个分量之间的联系，把光作为标量处理的结果与实际极其接近。

在本书涉及的情况下这些条件基本上是满足的，因此只讨论光的标量衍射理论。

经典的标量衍射理论最初是1678年惠更斯提出的。

他设想波动所到达的面上每一点是次级子波源，每一个次级波源发出的次级球面波向四面八方扩展，所有这些次级波的包络面形成新的波前。

1818年菲涅耳引入干涉的概念补充了惠更斯原理，考虑到子波源是相干的，认为空间光场是子波干涉的结果。

而后1882年基尔霍夫利用格林定理，采用球面波作为求解波动方程的格林函数，导出了严格的标量衍射公式。

在基尔霍夫衍射理论中，球面波是传播过程的基元函数。

由于任意光波场可以展开为平面波的叠加，因此用平面波作为基元函数也可以来描述衍射现象，这就是研究衍射的角谱方法。

光学课程中已经由基尔霍夫公式出发详细讨论了菲涅耳衍射公式，本章将采用平面波角谱理论导出同样的衍射公式，说明光的传播过程作为线性系统用频谱（角谱）方法在频域中分析，与用脉冲响应（点光源传播）方法在空域中分析是等价的。

进而用角谱方法讨论菲涅耳衍射和夫琅和费衍射。

最后，本章还要介绍分数傅里叶变换以及用分数傅里叶变换来表示菲涅耳衍射的优越性。

3.3 标量衍射的角谱理论

后来，菲涅耳补充了惠更斯原理，提出了惠更斯-菲涅尔耳原理，波前上任何一个未受阻挡的点，都可以看作是一个次级子波源（频率与原波相同），在其后空间任何一点处的光振动是这些子波的相干叠加。
U0(x1,y1) 推广后的惠更斯-菲涅尔耳原理可以写作: x1
x
U
(P ) = U ( x , y ) e 0 1 1
也就是对于(x02+ y02)一切可能值中的最大值有
2 x0 y 0 max
2 2
(
)

2z
2
z
(x 2
1
2 0
y 0 max
2
)
满足式的z值范围的衍射叫做夫琅和费衍射。显然夫琅和费衍射是在菲涅耳衍射的基础上进一步近似所得的结果，其衍射公式为:
2 x0 y 0 max
夫琅和费衍射
U ( x, y , z ) =

exp ( jk z ) j z
k 2 2 exp j ( x y ) 2z
xx0 yy 0 U 0 ( x0 , y 0 ,0 ) exp jk dx0 dy 0 z

jkr
ds
dx dy
1 1
r
p y z
r
y1
上式在解决衍射问题中，在相当大的范围内是正确的，但它是近似的.其中一个原因是没有考虑子波在不同方向上作用的差异。实际上每一小面元ds对观察点的作用还与面元法线和面元到观察点联线的夹角有关。对于普便的情况，菲涅尔提出必须引入体现子波在不同方向上作用的因子倾斜因子 k (q )

夫琅和费衍射公式
菲涅耳衍射
U ( x, y ) =

第2章光的标量衍射理论(二)

对于单位振幅平面波垂直照射衍射屏这种特殊情况
即因而
cos cos cos cos cos cos cos cos Ao , , T , T ,
Chapter 2
第二章
Scalar diffraction theory
标量的衍射理论
2.2 衍射的角谱理论
预备知识；
Plane wave k (波矢量)
x
k x轴, y轴
(wavefront 为一个与前
进方向垂直的等相平面）

2 k （波数）
y
0
U Ae j
2.3.4 . 角谱的衍射 (Diffraction of Angular Spectrum)
引入光瞳函数 p(x,y)
Ui ( x, y)
Ut ( x, y)
At (
Aperture
Ut ( x, y) Ui ( x, y) p( x, y)

(2.3-1)
cos cos cos cos cos cos , ) Ai ( , ) P( , )
x
．
(X,y) 0
k与x轴夹角为 , 与y轴夹角为，
U ( x, y) exp j (kx cos ky cos )
y
3D
k与x轴夹角为 , 与y轴夹角为，与z轴夹角为
x
k
(X,y,z) ．
z
y
U ( x, y, z ) exp j (kx cos ky cos kz cos )
c(
cos cos , )

傅立叶光学第三章总结

傅⽴叶光学第三章总结第三章标量衍射理论标量衍射理论是⼀种近似理论，所谓衍射就是指光波在传播的过程中波⾯受到限制时表现出来的现象。

由于我们⼀般遇到的问题都能满⾜标量衍射理论的两个条件（衍射孔径⽐波长⼤得多；不在太靠近孔径的地⽅观察衍射场），标量衍射理论给出的结果与实际⼗分相符。

第三章从基尔霍夫衍射理论和⾓谱理论出发讨论衍射问题，可以分别把它们看作是衍射的球⾯波理论和平⾯波理论。

这两种理论分别从空间域和频率域讨论衍射现象，在本质上是⼀致的。

根据衍射光波传播距离的长短实际衍射现象可分为两种：菲涅⽿衍射与夫琅⽲费衍射。

为了简化这两类衍射现象的计算，通常要做出不同程度的近似。

课本还给出了⼏种常见典型孔径的夫琅⽲费衍射图样。

对于具有周期性重复排列结构的衍射光栅可以利⽤列阵定理分析其衍射现象。

复振幅：定义P 点复振幅()()()j P U P a P e=，()a P 为P 点振幅，()j P e表⽰初相位。

球⾯波：()()00jkrjkr a U P e ra U P e r-== 发散球⾯波会聚球⾯波，2k πλ=在直⾓坐标系中，根据傍轴条件得到光源在()00,x y ，与其相距z 的xy 平⾯上的光场分布为：()()()()()()()()2200022000,exp exp 2,exp exp 2a kU x y jkz j x x y y z z a k U x y jkz j x x y y z z =-+-=---+-发散会聚平⾯波：()(),exp cos cos U x y a jk x y αβ=+平⾯波的空间频率cos cos x y f f αλβλ==基尔霍夫衍射理论：根据惠更斯⼦波原理发展⽽来,从空间域讨论衍射问题。

把孔径平⾯光场看作点光源的集合，观察平⾯上的场分布是它们所发出的带不同权重因⼦的球⾯⼦波的相⼲叠加。

球⾯⼦波在观察平⾯上的复振幅分布就是系统的脉冲响应。

菲涅⽿-基尔霍夫衍射公式：()()()01d jkre U P U P K S j rθλ∑=??由于这⾥的⼦波都是球⾯波，将光的传播看作⼀个线性系统。

标量衍射理论角谱及其传播

11-标量衍射理论3-衍射的角谱理论、菲涅耳衍射

标量衍射的角谱理论

10标量衍射的角谱理论

2.2 角谱传播2010

第三章-标量衍射理论2-角谱及其传播

信息光学Chap.2-衍射理论-角谱及其传播

2 标量衍射理论

chap2标量衍射的角谱理论

10标量衍射理论2角谱及其传播

傅里叶光学第3章 标量衍射理论

标量衍射的角谱理论

3标量衍射理论

第二章 标量衍射理论

衍射的角谱理论

标量衍射的角谱理论

标量衍射的角谱理论

3.3 标量衍射的角谱理论

第2章 光的标量衍射理论(二)

傅立叶光学第三章总结

傅里叶光学第3章标量衍射理论

第二章标量衍射理论

第2章光的标量衍射理论(二)