excel交通规划“四阶段法”教程
EXCEL规划求解功能操作说明

EXCEL规划求解功能操作说明Excel规划求解功能是Excel内置的解决最优化问题的工具,可用于线性规划、整数规划、非线性规划等诸多领域。
该功能十分便捷灵活,可以帮助用户快速找到问题的最优解。
一、添加求解功能1.打开Excel表格,点击“文件”>“选项”>“加载项”。
2.在弹出的窗口中选择“Excel加载项”>“转到”>“excel加载项”>“管理”。
在“可用的加载项”中勾选“求解器”并关闭窗口。
3.返回Excel表格,在数据选项卡中选择“分析”>“求解”,弹出求解对话框。
二、建立规划模型1.确定目标:需要确定最终要达到的目标或绩效指标,例如最大化利润、最小化成本等。
2.确定决策变量:需要确定影响目标的变量,例如销售量、成本等。
3.建立约束:需要确定影响决策变量的条件,例如材料成本、生产时间等。
注意约束需要用等式、不等式等数学形式表示。
例如,在一个玩具生产厂家的例子中,有以下规划问题:在有限的资源下,最大化玩具的利润。
目标:最大化利润。
决策变量:生产每种玩具的数量。
三、设置求解参数1.目标单元格:选择Excel表格中目标单元格,该单元格包含要优化的方程式。
4.变量单元格必须满足约束:勾选此项,保证变量单元格满足约束条件。
5.求解方法:选择要使用的求解算法,包括线性规划、非线性规划和整数规划等。
1.点击“求解”按钮,系统会自动寻找目标单元格、变量单元格和约束单元格区域。
2.系统执行计算,找到最优解并将其展示在新的单元格区域中。
3.若求解成功,单击“继续”将结果保存在Excel表中。
总之,利用Excel规划求解功能,用户可以通过建立规划模型,设置求解参数和运行求解功能轻轻松松地优化各种最优化问题。
EXCEL规划求解功能操作说明

E X C E L规划求解功能操作说明集团标准化办公室:[VV986T-J682P28-JP266L8-68PNN]Excel规划求解功能操作说明以Microsoft Excel2003为例,说明使用Excel的求解线性规划问题功能的使用方法。
一、加载规划求解功能1.点击【工具】按钮,在下拉菜单中选择【加载宏】功能。
2.在弹出的【可加载宏】选项卡中勾选【规划求解】,点击确定按钮。
此时,【工具】下拉菜单中增加规划求解功能,表示加载成功。
二、构造表格Excel表格并填入各项数据以教材18页【例题2-8】为例,构造表格如下:标题栏约束条件区目标函数区计算结果显示区1.录入约束条件系数约束条件(1)为5x 1+x 2-x 3+x 4=3,则在约束系数的第一行的x 1,x 2,x 3,x 4,x 5,限制条件,常数b 列下分别录入5,1,-1,1,0,=,3如下图所示。
约束系数区的第二行录入约束条件(2)的系数、限制符号及常数b ,即-10,6,2,0,1,=,2;约束系数区的第三行录入约束条件(3)(x1≥0)的系数、限制符号及常数b,即1,0,0,0,0,≥,0;约束系数区的第四行录入约束条件(4)(x2≥0)的系数、限制符号及常数b,即0,1,0,0,0,≥,0;约束系数区的第五行录入约束条件(5)(x3≥0)的系数、限制符号及常数b,即0,0,1,0,0,≥,0;约束系数区的第六行录入约束条件(6)(x4≥0)的系数、限制符号及常数b,即0,0,0,1,0,≥,0;约束系数区的第七行录入约束条件(7)(x5≥0)的系数、限制符号及常数b,即0,0,0,0,1,≥,0。
如下图所示。
2.录入目标函数系数目标函数为maxZ=4x1-2x2-x3,则在目标函数的x1,x2,x3,x4,x5列下分别录入4,-2,-1,0,0,如下图所示。
3. 录入约束条件的计算公式双击约束条件(1)行的“总和”单元格,录入以下内容:“=B3*B12+C3*C12+D3*D12+E3*E12+F3*F12”说明:录入的内容即是约束条件(1)的计算公式,其中“B3*B12”代表5x1; “C3*C12”代表1x2;“D3*D12”代表-1x3;“E3*E12”代表1x4;“F3*F12”代表0x5。
Excel规划求解功能的使用教程

本文整理于网络,仅供阅读参考
Excel规划求解功能的使用教程
excel规划求解功能的使用教程:
规划求解使用步骤1:安装规划求解:规划求解是excel的一个插件,需要安装。
打开新建文档左上角office按钮——excel 选项——自定义——从下列位置选择命令(所有命令)——加载宏——添加——确定。
点击“加载宏”工具,弹出【加载宏】对话框,勾选“分析工具库“和”规划求解加载项“,点击”确定“。
随即弹出microsoft office excel对话框,点击”是“。
开始安装。
规划求解使用步骤2:创建表格,如下。
单击“数据“工具栏,选择”规划求解“,随即弹出【规划求解参数】对话框,在【设置目标单元格】中输入“$b$12”;在【可变单元格】中输入“$c$3:$c$5”,单击“添加”按钮,弹出【添加约束】对话框,在【单元格引用位置】输入“$b$10”,在其右侧的下拉列表中选择【看了excel规划求解功能的使用教程。
Excel规划求解使用教程(图)
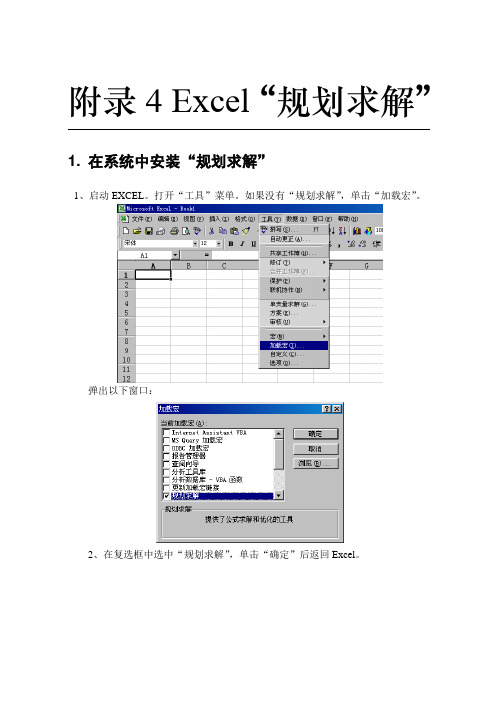
附录4 Excel“规划求解”1. 在系统中安装“规划求解”1、启动EXCEL。
打开“工具”菜单。
如果没有“规划求解”,单击“加载宏”。
弹出以下窗口:2、在复选框中选中“规划求解”,单击“确定”后返回Excel。
这时在“工具”菜单中出现“规划求解”。
关闭“工具”菜单2. 在Excel中创建线性规划模型1、输入线性规划模型的约束条件系数、右边常数和目标函数系数。
定义线性规划的变量单元格、约束条件左边单元格和目标函数单元格。
2、定义“设备能力占用”(即约束条件左边)以及“总利润”的计算公式。
首先定义设备A的“能力占用”单元格(G3)的计算公式,界面如下:其次定义设备B的“能力占用”单元格(G4)的计算公式,界面如下:再次定义设备C的“能力占用”单元格(G5)的计算公式,界面如下:最后定义“总利润”单元格(C8)的计算公式,界面如下:3、将光标停留在“总利润”值的单元格(C8)中,打开“工具/规划求解”,弹出以下窗口:4、设置目标函数单元格:检查“设置目标函数单元格”是否在“$C$8”,如不是,单击文本框右侧的图标,重新选定目标函数单元格,也可以直接单击Excel表中的“C8”。
5、设置变量:单击“规划求解窗口”中“可变单元格”文本框,然后在Excel工作表中选定变量单元格(C7、D7、E7和F7),在文本框中出现“$C$7:$F$7”,如下图所示。
6、设置约束单击“添加”,弹出以下窗口:单击“单元格引用位置”文本框空白处,然后单击工作表G3单元格,“单元格引用位置”文本框中出现“$G$3”;打开“单元格引用位置”和“约束值”之间的下拉文本框,选定“<=”;单击“约束值”文本框空白处,然后单击工作表H3单元格。
结果如下图所示。
单击“添加”,完成第一个约束设置。
继续设置第二、第三个约束,最后设置所有变量非负。
约束设置完成以后,单击“确定”,返回“规划求解参数”窗口,如下图所示。
7、设置叠代参数。
单击“选项”,弹出以下窗口:输入“最长运行时间”、“叠代次数”、“精度”、“允许误差”、“收敛度”等叠代参数。
【必须收藏】只用60秒就能解决的Excel线性规划,你却熬了整个通宵...

【必须收藏】只用60秒就能解决的Excel线性规划,你却熬
了整个通宵...
箭头处“蓝色字”,
每天学一个表格技能!
领导给小王同志12个金额,让他凑数据,凑成26005元和33459元。
左拼右凑这个金额,凑了一个通宵,还没凑对,十分着急,同事3分钟就给解决了
❶在Excel中调出线性规划我们在Excel选项里面,找到加载项然后勾选规划求解加载项,点击确定
❷我们在C1单元格输入公式:=SUMPRODUCT(A2:A13*B2:B13)
❸前面加载了加载项之后,在数据选项卡下,就有了规划求解进行相关设置后,运行得到最终的结果,操作动图如下所示:
其中的设置是,设置目标是C1单元格,目标值是26005,可变的单元格区域是B2:B13,遵守约束是B2:B13是二进制
最终B2:B13单元格中的数据为1的这些值累加起来,正好就能得到我们需要的26005了
剩下的数据正好就是33459元了。
模糊凑数据
如果给定的一个金额是系统也不可能准确的凑出来,Excel一直在计算的过程中的时候,可以随时按ESC退出
或者我们改变公式,使得进行模糊的凑数据接近这个值,我们现在要把这些数据最接近30000
我们可以在C1输入公式:=ABS(SUMPRODUCT(A2:A13,B2:B13)-30000)
然后在线性规划中的设置是:C1是最小值
然后运行,这个时候,会一直在那里转,这个时候,我们需要按ESC,然后
保留求解
得到了一组结果。
这个例子还是找到了正好等于30000的数据。
如果不等于的话,那么会得出一个最接近的结果。
当然,平时不用这个功能的时候,需要把这个功能给关闭了,否则每次打开Excel的速度会变慢一点。
Excel表格法求解路径规划问题

实验四: Excel 表格法求解路径规划问题
根据题意及决策变量与目标函数得出本问题的 线性规划模型。
minY=6×X11+3×X12+2×X13+5×X14+7×X21+5×X2 2+8×X23+4×X24+3×X31+2×X32 +9×X33+7×X34
s.t. X11+ X12+ X13+ X14=5(满足A1矿的产量) X21+ X22+ X23+ X24=2(满足A2矿的产量) X31+ X32+ X33+ X34=3(满足A3矿的产量) X11+ X21+ X31 =2(满足B1厂的需求量) X12+ X22 +X32 =3(满足B2矿的需求量) X13+ X23 +X33 =1(满足B3矿的需求量) X14+ X24 +X34 =4(满足B4矿的需求量) Xij >=0(i=1,2,3,j=1,2,3,4)(决策变量非负约束)
执行【工具】→【加载宏】 菜单命令,这时将出现 “加载宏”的对话框,在 “可用加载宏”窗口的 “规划求解”选项上打 “√”。当需要进行规划求 解操作时,直接进行该命 令,就可进入“规划求解 参数”对话框。
实验四: Excel 表格法求解路径规划问题
根据题意,设置本问题的决策变量和目标 函数。 设:Xij为每天从Ai矿运往Bj厂的矿石数量 (百吨),Y为总运费 Y=6×X11+3×X12+2×X13+5×X14+7 ×X21+5×X22+8×X23+4×X24+3×X3 1+2×X32 +9×X33+7×X34 ,则本问题 表格法求解路径规划问题
Excel规划求解使用说明
规划模型的线性规划标准型式为:
2-21
规划求解使用说明
5.规划求解小结..............................................................................................................................19 6.Excel补注 ....................................................................................................................................19
Max z = C T X
⎧ AX = bΒιβλιοθήκη s .t .⎨ ⎩X
≥0
X 为决策变量向量 其中: C 为价值向量
b 为资源向量 A 为技术矩阵
这些都是经济生产中所具有的现实意义。
1.3.利用规划求解解决现实问题的步骤
z 建立对应的规划模型 z 在 Excel 表中输入已知数据(如线性规划模型的 A、b、C),以及指定规划模型三
4.人员安排模型..............................................................................................................................16 4.1.Excel关于规划求解自带的系统示例文件......................................................................16 4.2.问题描述...........................................................................................................................17 4.3.模型分析、建立...............................................................................................................17 4.4.规划求解...........................................................................................................................18
交通规划四阶段法模型
交通规划四阶段法模型TransCAD核心--交通规划模型TransCAD以交通规划“四阶段法”为基础,提供了完善的交通规划模型算法。
其中包括需求预测模型、公交模型、OD矩阵推算、路径模型、路网分析模型、物流模型等。
1(“四阶段法”交通规划模型? 出行产生/吸引模型交叉分类法:交叉分类法是根据一定的社会经济特点将一个城区的人口划分为若干类型。
然后,经验地估计每种类型的家庭或出行者的平均出行率,由此产生的出行率表,可用于预测该研究区的出行产生量。
回归分析模型:普遍采用两种回归分析模型。
第一种,使用以交通小区为标准的集计数据,将每个家庭的平均出行量作为因变量,小区特征属性的平均值作为说明变量(自变量)。
第二种,使用以单个的家庭或出行者为标准的非集计数据,以每个家庭或出行者的出行量作为因变量,家庭和出行者的特征属性作为说明变量(自变量)。
离散选择法: 离散选择法是使用非集计的家庭或单个出行者的数据估算它们的出行概率。
再将所得的结论集计起来即为预测的出行产生量。
? 产生/吸引平衡模型保持出行产生量不变:保持出行产生量不变,调整出行吸引量,使得吸引总量与产生总量相等。
保持出行吸引量不变:保持出行吸引量不变,调整出行产生量,使出行产生总量与吸引总量相等。
用户指定出行总量系数:同时调整出行产生量和出行吸引量,使产生量和吸引量之和等于出行总量乘以用户给定系数之积。
用户指定的出行总量:同时调整出行产生量和吸引量,使产生量和吸引量之和等于用户给定的值。
? 出行分布模型1增长系数法:是通过对现有的矩阵乘以系数实现的(增长系数由未来的出行产生量除以出行现状的产生量计算得出的)。
在无法获悉路网交通小区间距离、出行时间或综合费用等信息时,常常使用该方法。
——常增长系数法——出行产生受约束的增长系数法——出行吸引受约束的增长系数法——全约束增长系数(Fratar福来特法 )重力模型:主要的原理——两个地区之间的空间交流量与出行产生量/吸引量的乘积成正比,与两地之间的交通阻抗成反比。
浅谈“四阶段法”在交通量预测中的应用
未来客流预测的发展方向与挑战主要体现在以下几个方面:一是如何提高预 测精度,避免出现较大误差;二是如何结合新兴技术,如、大数据等,实现对客 流预测的实时动态监控;三是如何考虑多种影响因素,如天气、节假日等,以提 高预测结果的可靠性。
谢谢观看
六、结论与展望
“四阶段法”在交通量预测中具有广泛的应用价值。它通过系统化的数据处 理和分析,能够较为准确地预测未来的交通状况。然而,这种方法的应用并非一 成不变,需要根据具体的交通环境和数据进行适当的调整。
展望未来,随着大数据等技术的发展,交通量预测的方法和技术将不断进步。 例如,基于深度学习的预测模型可能进一步提高交通量预测的精度;实时感知技 术和大数据分析方法将使得交通量预测能够更加及时、准确地反映实际交通情况。 因此,“四阶段法”在未来的应用中,需要不断适应新的技术环境,以提升其在 交通量预测中的效率和准确性。
此外,随着智能化城市和交通强国等战略的推进,交通量预测将越来越受到。 这不仅要求我们有更高的预测精度,还需要我们能够处理更复杂的交通问题,如 城市群交通、多模式交通等。因此,“四阶段法”的应用和发展需要紧密结合实 际交通需求,以推动交通管理和服务水平的不断提升。
参考内容
一、背景介绍
城市轨道交通是现代城市交通的重要组成部分,客流预测对于其运营管理和 优化具有重要的实际意义。准确的客流预测可以帮助城市轨道交通管理部门提前 做好运营计划,提高运输效率,避免客流拥堵等问题。四阶段法是一种常见的客 流预测方法,它将客流预测分为四个阶段进行,包括建立预测模型、数据预处理、 特征提取和模型评估。这种方法在城市轨道交通客流预测中得到了广泛应用。
在TransCAD中,可以使用统计回归、神经网络等算法构建客流预测模型。以 神经网络为例,可以采用深度学习的方法,利用时间序列数据和其他相关数据训 练模型,以实现对未来客流的预测。
用Excel软件求解规划问题的方法
用Excel 软件求解规划的方法Microsoft Excel 软件是当今十分流行的功能强大操作方便的软件。
在Microsoft Excel 软件中,具有规划求解功能。
如图1,在工具菜单下,一般有“规划求解”项,若未有,则应先运行“加载宏”项目把其安装上。
图1 图21 一般线性规划的求解现在让我们以下面的模型为例,介绍如何利用Microsoft Excel 软件求解线性规划模型的操作方法。
首先,打开Microsoft Excel 的一个工作簿,把模型的约束系数矩阵置于A1至B4范围,约束常数置于D1至D4范围,而利润系数则置于A5至B5范围。
选择A7至B7范围作可变单元(即这两个格相当于变量X1与X2),并输入初值0。
然后,在单元格C1处输入“=A1*A7+B1*B7”,即第一个约束不等式的左边;同理,在单元格C2处输入“=A2*A7+B2*B7”,即第二个约束不等式的左边;对C3与C4也同样处理。
最后,以单元格C5作目标单元格,输入“=A5*A7+B5*B7”。
如图2。
接下来,按下主菜单的工具处,再在下拉菜单处选择“规划求解”,则弹出窗口如图3。
⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥≤+≤≤≤0x 0,x x x x x x 4+x s.t. x +x =f max 21112121222700050122700075.182700025.56270000155.75.2图3 图4在“设置目标单元格”处输入“C5”,然后选“最大值”,再在“可变单元格”处输入“A7:B7”,在“约束”处按一下“添加”按钮,又弹出如图4的窗口。
在此,我们要添加5个约束:“C1 <= D1”、“C2 <= D2”、“C3 <= D3”、“C4 <= D4”、“A7:B7 >= 0”。
对第一个约束,在“单元格引用位置”处输入“C1”,在中间下拉框选择“<=”, 再在“约束值”处输入“D1”。
然后按“添加”按钮,再类似地添加其它约束。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Low
Middle
High Low
Middle
0
0
0
0
0
2000
8000 10000
0 4000
8000
22000 30000
0 16000
Input 4: Trip Production Table: Cars/HH
0
1
2
HH Income
HBW
Low
Middle
High
Low
Middle
High
5
5
Origin
Input 7: Friction Factor Coefficients:
Trip Purpose
a
HBW HBO
NHB
b
28507 139173
c
-0.02 -0.123 -1.285 -0.094
219113
-1.332 -0.1
Friction Factor Model: (Gamma Model)
Low
Middle
High
Source: based on
Martin and
McGuckin (1998),
Table 7, pg. 27.
Martin,W.A. and
N.A.McGuckin
(1998). Travel
Estimation
Techniques for
Urban Planning,
1.7 10 2
Other 1.7 0.5 2.5
Trip Distribution Objective: Estimate the number of trips made between each zone Inputs: Productions, Attractions, Travel time between zones Outputs: # of Person Trips from Zone i to Zone j
Input 6: Travel Time Table: Time in (minutes)
Destination
TAZ 1 TAZ 2 TAZ 3 TAZ 4
TAZ 1
5 6
TAZ 2 TAZ 3 TAZ 4
2.5
10
20
20
10
2.5
20
20
20
20
2.5
10
20
20
10
2.5
5
5
15
15
15
15
NCHRP Report 365,
Transportation
Research Board,
Washington, DC.
# of Productions/HH
HBO
NHB
Total
0.5
2
0.9
3.4
1.1
3
1.2
5.3
1.4
3.9
1.8
7.1
0.8
3.2
1.3
5.3
1.5
3.9
1.6
7
1.8
4.9
Given Household Characteristics Data:
Input 2: Household Demographic IDensfcorimpationn: and income
Income 0 Cars 1 Car 2 Cars
Identifies # of households in each zone with the specified car ownership
Zone 1
Zone 2
Low
Middle
High Low
Middle
4000
8000 8000 2000 4000
12000
32000 36000 8000 26000
4000
20000 16000 10000 30000
Zone 3
Zone 4
Income 0 Cars 1 Car 2 Cars
# of HH
Retail
0
0.9
0.5
ITE Trip
Attraction Rates
Employment Type
Service Other
1.45 1.45 1.45
9
1.7
0.5
4.1
1.2
0.5
HBO = 0.9(# of Households) + 9(Retail Employment) + 1.7(Service Employment) + 0.5(Other Employment) NHB = 0.5(# of Households) + 4.1(Retail Employment) + 1.2(Service Employment) + 0.5(Other Employment)
2.2
8.9
1.4
5.2
2.1
8.7
2.1
5.7
2.3 10.1
2.5
6.8
3.1 12.4
Input 5: Trip Attraction Coefficient Table Trip Attraction Table Trip Type HBW HBO NHB
Reference: HBW = 1.45(Total Equation Employment)
Input 1: Traffic Network
from_node_id
to_node_ length_i number_o
id
n_mile f_lanes
1
2
10
4
1
3
20
4
1
5
5
4
2
1
10
4
2
4
20
4
2
5
5
4
3
1
20
4
3
4
10
4
3
6
5
4
4
2
20
4
4
3
10
4
4
6
5
4
5
1
5
4
5
2
5
4
5
6
10
5
6
3
5
4
6
4
5
4
6
5
10
5
Trip Generation Objective: Estimate the number of trips entering and leaving each zone Inputs: Zone Characteristics (# of HH, HH Income, Auto Ownership, Employment, etc.) Outputs: # of Productions, # of Attractions
SOLUTION PROCESS Trip Productions
i= origin zone
j= destinat ion zone
Method:
Cross Classification
Process:
Trip Production Table:
Cars/HH 0 1 2
HH Income Low Middle High Low Middle High Low Middle High
Alternative Trip
Attraction Table
Trip Type HBW
# of HH
Retail 0
HBO
1
NHB
0.5
Quick Response
Method Tables
Source:
(NCHRP 187, Sosslau et al., 1978)
Employment Type
