偏最小二乘法回归建模案例
偏最小二乘法PLS回归NIPALS算法的Matlab程序及例子

偏最小二乘法PLS回归NIPALS算法的Matlab程序及例子②function [T,P,W,Wstar,U,b,C,B_pls,...Bpls_star,Xori_rec,Yori_rec,...R2_X,R2_Y]=PLS_nipals(X,Y,nfactor)% USAGE: [T,P,W,Wstar,U,b,C,Bpls,Bpls_star,Xhat,Yhat,R2X,R2Y]=PLS_nipals(X,Y,nfact) % PLS regression NIPALS algorithm PLS回归NIPALS算法% Compute the PLS regression coefficients PLS回归系数的计算% X=T*P' Y=T*B*C'=X*Bpls X and Y being Z-scores% B=diag(b)% Y=X*Bpls_star with X being augmented with a col of ones% and Y and X having their original units% T'*T=I (NB normalization <> SAS)% W'*W=I%% Test for PLS regression% Herve Abdi November 2002/rev November 2004%%% Version with T, W, and C being unit normalized% U, P are not% nfact=number of latent variables to keep 保持潜在变量的数量% default = rank(X)X_ori=X;Y_ori=Y;if exist('nfactor')~=1;nfactor=rank(X);endM_X=mean(X);M_Y=mean(Y);S_X=std(X);S_Y=std(Y);X=zscore(X);Y=zscore(Y);[nn,np]=size(X) ;[n,nq]=size(Y) ;if nn~= n;error(['Incompatible # of rows for X and Y']);end% Precision for convergenceepsilon=eps;% # of components kepts% Initialistion% The Y setU=zeros(n,nfactor);C=zeros(nq,nfactor);% The X setT=zeros(n,nfactor);P=zeros(np,nfactor);W=zeros(np,nfactor);b=zeros(1,nfactor);R2_X=zeros(1,nfactor);R2_Y=zeros(1,nfactor);Xres=X;Yres=Y;SS_X=sum(sum(X.^2));SS_Y=sum(sum(Y.^2));for l=1:nfactort=normaliz(Yres(:,1));t0=normaliz(rand(n,1)*10);u=t;nstep=0;maxstep=100;while ( ( (t0-t)'*(t0-t) > epsilon/2) & (nstep < maxstep));nstep=nstep+1;disp(['Latent Variable #',int2str(l),' Iteration #:',int2str(nstep)]) t0=t;w=normaliz(Xres'*u);t=normaliz(Xres*w);% t=Xres*w;c=normaliz(Yres'*t);u=Yres*c;end;disp(['Latent Variable #',int2str(l),', convergence reached at step ',...int2str(nstep)]);%X loadingsp=Xres'*t;% b coefb_l=((t'*t)^(-1))*(u'*t);b_1=u'*t;% Store in matricesb(l)=b_l;P(:,l)=p;W(:,l)=w;T(:,l)=t;U(:,l)=u;C(:,l)=c;% deflation of X and YXres=Xres-t*p';Yres=Yres-(b(l)*(t*c'));R2_X(l)=(t'*t)*(p'*p)./SS_X;R2_Y(l)=(t'*t)*(b(l).^2)*(c'*c)./SS_Y;end%Yhat=X*B_pls;X_rec=T*P';Y_rec=T*diag(b)*C';%Y_residual=Y-Y_rec;%% Bring back X and Y to their original units%Xori_rec=X_rec*diag(S_X)+(ones(n,1)*M_X);Yori_rec=Y_rec*diag(S_Y)+(ones(n,1)*M_Y);%Unscaled_Y_hat=Yhat*diag(S_Y)+(ones(n,1)*M_Y);% The Wstart weights gives T=X*Wstar%Wstar=W*inv(P'*W);B_pls=Wstar*diag(b)*C';%% Bpls_star Y=[1|1|X]*Bpls_star%Bpls_star=[M_Y;[-M_X;eye(np,np)]*diag(S_X.^(-1))*B_pls*diag(S_Y)] Bpls_star=[[-M_X;eye(np,np)]*diag(S_X.^(-1))*B_pls*diag(S_Y)];Bpls_star(1,:)=Bpls_star(1,:)+M_Y;%%%%%%%%%%%%% FunctionsHere %%%%%%%%%%%%%%%%%%%%%%%function [f]=normaliz(F);%USAGE: [f]=normaliz(F);% normalize send back a matrix normalized by column% (i.e., each column vector has a norm of 1)[ni,nj]=size(F);v=ones(1,nj) ./ sqrt(sum(F.^2));f=F*diag(v);function z=zscore(x);% USAGE function z=zscore(x);% gives back the z-normalization for x% if X is a matrix Z is normalized by column% Z-scores are computed with% sample standard deviation (i.e. N-1)% see zscorepop[ni,nj]=size(x);m=mean(x);s=std(x);un=ones(ni,1);z=(x-(un*m))./(un*s);应用例子%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%% example_pls.m: PLS example% RM3 Fall 2004% November 16 2004%% This script shows how to run% a Partial least square regression% (PLS).% Need Programs: PLS_nipals plotxyha% The example is the% Wine example from Abdi H. (2003)% See /~herve %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%clearclc;disp(['Example of a PLS program. See Abdi H. (2003)']); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%************************************************************%% -> This is your title.%% -> Change it to fit your dataze_title=['PLS. Wines. '];%% **********************************************************%% This is the data matrix of the Predictors (IV)%% -> Change it for your exampleX=[...7 7 13 74 3 14 710 5 12 516 7 11 313 3 10 3];%%% get the # of rows andcolumns %%%%%%%%%%%%%%%%%%%%%%%%%%[nI,nJ]=size(X);%************************************************************ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%% -> These are your predictors names.% -> Change them to fit your data% You need as many names as mcX has columnsn=0;%n=n+1;nom_x(n)={' Price'};n=n+1;nom_x(n)={' Sugar'};n=n+1;nom_x(n)={' Alcohol'};n=n+1;nom_x(n)={' Acidity'};%%% Test the # of colums namesif nJ~=n;erreur(['Error -> (Wrong # of column names)!']);end%%*********************************************************** %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%% -> These are your observations names.% -> Change them to fit your datal=0;l=l+1;nom_r{l}={'W_1'};l=l+1;nom_r{l}={'W_2'};l=l+1;nom_r{l}={'W_3'};l=l+1;nom_r{l}={'W_4'};l=l+1;nom_r{l}={'W_5'};if nI~=l;erreur(['Error -> (Wrong # of row names)!']);end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%% **********************************************************%% This is the data matrix of the Dependant Variables (DV)%% -> Change it for your exampleY=[...14 7 810 7 68 5 52 4 76 2 4];%%% get the # of rows andcolumns %%%%%%%%%%%%%%%%%%%%%%%%%%[nI2,nK]=size(Y);%************************************************************ %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%% -> These are your predictors names.% -> Change them to fit your data% You need as many names as mcX has columnsm=0;%m=m+1;nom_y(m)={' Hedonic'};m=m+1;nom_y(m)={' Meat'};m=m+1;nom_y(m)={' Dessert'};%%% Test the # of colums namesif nK~=m;erreur(['Error -> (Wrong # of column names)!']);end%%*********************************************************** %%%%%%%%%%%% Call PLS_nipals %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%nfact2keep=2 ;%%% nfact gives the number of latent variables%%% the default is equal to the rank of X[T,P,W,Wstar,U,b,C,Bpls,Bpls_star,Xhat,Yhat,R2X,R2Y]=...PLS_nipals(X,Y,nfact2keep)%%%%%%%%%%%% Plot the Observations (T vectors) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%percent_of_inertiaX=100*R2X;percent_of_inertiaY=100*R2Y; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%% The axes to keep for the plotsaxe_horizontal=1;axe_vertical=2; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%le_taux=[...' {\tau_X}_',int2str(axe_horizontal),'=',...int2str(percent_of_inertiaX(axe_horizontal)),'%,', ...' {\tau_X}_',int2str(axe_vertical),'=',...int2str(percent_of_inertiaX(axe_vertical)),'%', ...' {\tau_Y}_',int2str(axe_horizontal),'=',...int2str(percent_of_inertiaY(axe_horizontal)),'%,', ...' {\tau_Y}_',int2str(axe_vertical),'=',...int2str(percent_of_inertiaY(axe_vertical)),'%'];%%%% Plothere %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%figure(1);clf %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Now plot the Observations Scores T%%ze_tRC=[ze_title,' Observations (T).'];titre=[ze_tRC, le_taux];plotxyha(T,1,2,titre,nom_r');axis('equal') ; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%% Now plot the X Scores W%%figure(2);clfze_tRC=[ze_title,' Predictors (W).'];titre=[ze_tRC, le_taux];plotxyha(W,1,2,titre,nom_x');axis('equal') ; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%% Now plot the Y Scores U%%figure(3);clfze_tRC=[ze_title,' DV (C -> Non Ortho).'];titre=[ze_tRC, le_taux];plotxyha(C,1,2,titre,nom_y');% axis('equal') ; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%作图函数plotxy定义function plotxy(F,axe1,axe2,titre,noms);% % ***** This is a Test Version *******% July 1998 Herve Abdi% Usage plotxy(F,axe1,axe2,title,names);% plotxy plots a MDS or PCA or CA graph of component #'Axe1' vs #'Axe2' % F is a matrix of coordinates% axe1 is the Horizontal Axis% axe2 is the Vertical Axis% title will be the title of the graph% Axes are labelled 'Principal Component number'% names give the names of the points to plot (def=numbers)nomdim='Dimension';[nrow,ncol]=size(F);if exist('noms')==0;noms{nrow,1}=[];for k=1:nrow;noms{k,1}=int2str(k);endendminx=min(F(:,axe1));maxx=max(F(:,axe1));miny=min(F(:,axe2));maxy=max(F(:,axe2));hold off; clf;hold on;rangex=maxx-minx;epx=rangex/10;rangey=maxy-miny;epy=rangey/10; axis('equal'); axis([minx-epx,maxx+epx,miny-epy,maxy+epy]) ; %axis('equal');%axis;plot ( F(:,axe1),F(:,axe2 ),'.');label=[nomdim,' '];labelx=[label, num2str(axe1) ];labely=[label, num2str(axe2) ];xlabel (labelx);ylabel (labely );plot([minx-epx,maxx+epx],[0,0] ,'b');% holdplot ([0,0],[miny-epy,maxy+epy],'b');for i=1:nrow,text(F(i,axe1),F(i,axe2),noms{i,1});end;title(titre);。
偏最小二乘法

偏最小二乘法 ( PLS)是光谱多元定量校正最常用的一种方法 , 已被广泛应用 于近红外 、 红外 、拉曼 、核磁和质谱等波谱定量模型的建立 , 几乎成为光谱分析中建立线性定量校正模型的通用方法 〔1, 2〕 。
近年来 , 随着 PLS 方法在光谱分析尤其是分子光谱如近红外 、 红外和拉曼中应用 的深入开展 , PLS 方法还被用来解决模式识别 、定量校正模型适用性判断以及异常样本检测等定性分析问题 。
由于 PLS 方法同时从光谱阵和浓度阵中提取载荷和得分 , 克服主成分分析 ( PCA)方法没有利用浓度阵的缺点 , 可有效降维 , 并消除光谱间可能存在的复共线关系 , 因此取得令人非常满意的定性分析结果 〔3 ~ 5〕 。
本文主要介绍PLS 方法在光谱定性分析方面的原理及应用 实例 。
偏最小二乘方法(PLS-Partial Least Squares))是近年来发展起来的一种新的多元统计分析法, 现已成功地应用于分析化学, 如紫外光谱、气相色谱和电分析化学等等。
该种方法,在化合物结构-活性/性质相关性研究中是一种非常有用的手段。
如美国Tripos 公司用于化合物三维构效关系研究的CoMFA (Comparative Molecular Field Analysis)方法, 其中,数据统计处理部分主要是PLS 。
在PLS 方法中用的是替潜变量,其数学基础是主成分分析。
替潜变量的个数一般少于原自变量的个数,所以PLS 特别适用于自变量的个数多于试样个数的情况。
在此种情况下,亦可运用主成分回归方法,但不能够运用一般的多元回归分析,因为一般多元回归分析要求试样的个数必须多于自变量的个数。
§§ 6.3.1 基本原理6.3 偏最小二乘(PLS )为了叙述上的方便,我们首先引进“因子”的概念。
一个因子为原来变量的线性组合,所以矩阵的某一主成分即为一因子,而某矩阵的诸主成分是彼此相互正交的,但因子不一定,因为一因子可由某一成分经坐标旋转而得。
正交偏最小二乘法

正交偏最小二乘法正交偏最小二乘法(Orthogonal Partial Least Squares, OPLS)是一种常用的多元统计分析方法,广泛应用于数据建模、特征选择、变量筛选等领域。
本文将介绍正交偏最小二乘法的原理、应用和优势,以及其在实际问题中的应用案例。
正交偏最小二乘法是基于偏最小二乘法(Partial Least Squares, PLS)的改进方法。
偏最小二乘法是一种回归分析的方法,通过将自变量和因变量进行线性组合,建立回归模型。
但是在应用过程中,偏最小二乘法可能存在多个潜在的自变量对应一个因变量的情况,这就导致了模型的不稳定性和可解释性差。
正交偏最小二乘法通过引入正交化的步骤,解决了偏最小二乘法的不足。
其基本思想是,在建立回归模型的过程中,除了考虑与因变量相关的部分(预测分量),还引入与因变量不相关的部分(正交分量),从而提高模型的解释能力和稳定性。
通过正交化的操作,正交偏最小二乘法能够将数据进行更好的降维,去除噪声和冗余信息,提取出对预测结果有用的信息。
正交偏最小二乘法在实际问题中具有广泛的应用。
例如,在药物研发领域,研究人员可以利用正交偏最小二乘法对大量的分子结构和活性数据进行建模和预测,快速筛选出具有潜在药效的化合物。
在工业过程控制中,正交偏最小二乘法可以用于建立传感器数据与产品质量之间的关系,实现对产品质量的在线监测和控制。
此外,正交偏最小二乘法还可以应用于生物信息学、化学分析、图像处理等领域。
与其他方法相比,正交偏最小二乘法具有以下优势。
首先,正交偏最小二乘法能够解决多重共线性问题,降低模型的复杂度,提高模型的解释能力。
其次,正交偏最小二乘法能够处理高维数据,提取出对预测结果有用的特征,减少冗余信息的干扰。
此外,正交偏最小二乘法还可以进行特征选择,帮助研究人员挖掘出对预测结果具有重要影响的变量。
下面以一个实际应用案例来说明正交偏最小二乘法的应用。
假设我们需要建立一个模型来预测商品的销售量。
偏最小二乘回归分析—案例
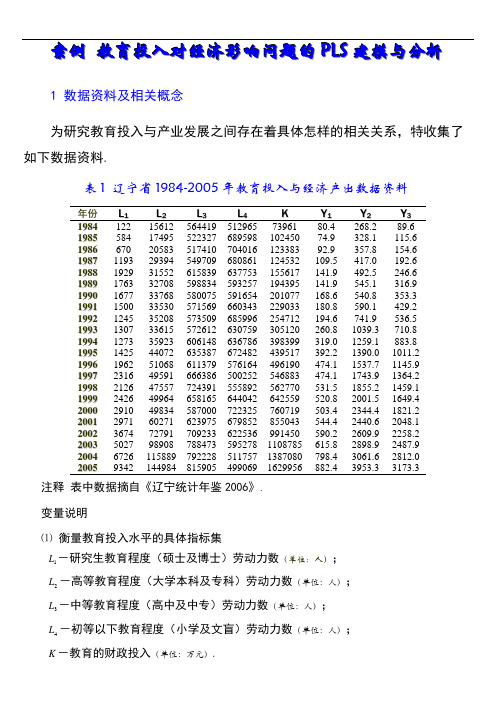
案例教育投入对经济影响问题的P L S建模与分析1 数据资料及相关概念为研究教育投入与产业发展之间存在着具体怎样的相关关系,特收集了如下数据资料.表1 辽宁省1984-2005年教育投入与经济产出数据资料年份L1L2L3L4K Y1Y2Y31984122 15612 564419 512965 73961 80.4 268.2 89.61985584 17495 522327 689598 102450 74.9 328.1 115.61986670 20583 517410 704016 123383 92.9 357.8 154.619871193 29394 549709 680861 124532 109.5 417.0 192.619881929 31552 615839 637753 155617 141.9 492.5 246.619891763 32708 598834 593257 194395 141.9 545.1 316.919901677 33768 580075 591654 201077 168.6 540.8 353.319911500 33530 571569 660343 229033 180.8 590.1 429.219921245 35208 573509 685996 254712 194.6 741.9 536.519931307 33615 572612 630759 305120 260.8 1039.3 710.819941273 35923 606148 636786 398399 319.0 1259.1 883.819951425 44072 635387 672482 439517 392.2 1390.0 1011.219961962 51068 611379 576164 496190 474.1 1537.7 1145.919972316 49591 666386 500252 546883 474.1 1743.9 1364.219982126 47557 724391 555892 562770 531.5 1855.2 1459.119992426 49964 658165 644042 642559 520.8 2001.5 1649.420002910 49834 587000 722325 760719 503.4 2344.4 1821.220012971 60271 623975 679852 855043 544.4 2440.6 2048.120023674 72791 709233 622536 991450 590.2 2609.9 2258.220035027 98908 788473 595278 1108785 615.8 2898.9 2487.920046726 115889 792228 511757 1387080 798.4 3061.6 2812.020059342 144984 815905 499069 1629956 882.4 3953.3 3173.3 注释表中数据摘自《辽宁统计年鉴2006》.变量说明⑴衡量教育投入水平的具体指标集L-研究生教育程度(硕士及博士)劳动力数(单位:人);1L-高等教育程度(大学本科及专科)劳动力数(单位:人);2L-中等教育程度(高中及中专)劳动力数(单位:人);3L-初等以下教育程度(小学及文盲)劳动力数(单位:人);4K-教育的财政投入(单位:万元).⑵经济产出的指标集Y-第一产业(包括林业、牧业、渔业等)产出值(单位:亿元);1Y-第二产业(包括工业和建筑业)产出值(单位:亿元);2Y-第三产业(包括流通类的交通运输业、邮电通讯业、商业饮食业、物资供销和3仓储业及金融、保险业,地质普查业,房地产、公用事业,居民服务业,旅游业,咨询信息服务业和各类技术服务业,等等)产出值(单位:亿元).2 多重相关性诊断⑴计算自变量与因变量之间的相关系数.load jytrjjcc %装载原始数据cr=corrcoef(jytrjjcc);%计算变量之间的相关系数计算结果整理如下:表2 因变量与自变量之间的相关系数r L1L2L3L4K Y1Y2Y3L1 1.0000 0.98470.8737 -0.4847 0.9447 0.8643 0.8906 0.8895L2 1.0000 0.9117 -0.4944 0.9695 0.9088 0.9250 0.9278L3 1.0000 -0.6196 0.8944 0.8940 0.8776 0.8870L4 1.0000 -0.4177 -0.4436 -0.3751 -0.3803K 1.0000 0.9635 0.9833 0.9871Y1 1.0000 0.9827 0.9818Y2 1.0000 0.9961Y3 1.0000 由表中可以看出:自变量之间的相关系数最高达0.9847,表明自变量之间存在严重的自相关性.注意,初等以下教育程度劳动力数与其它自变量之间呈负相关关系因变量与自变量之间的相关系数最高达0.9871,表明自变量系统与因变量系统之间存在较高的相关性.注意,研究生、高等、中等教育程度劳动力数以及财政投入与三大产业产出之间存在着明显的正相关关系,而初等以下教育程度劳动力数与三大产业产出之间存在着的较弱的负相关关系.⑵建立普通最小二乘回归方程原始数据标准化,得到自变量的标准化数据矩阵0E 和因变量的标准化数据矩阵0F ,再建立二者之间的多重(多因变量)多元线性回归方程.E0=stand(jytrjjcc(:,1:5));%标准化自变量数据 F0=stand(jytrjjcc(:,6:8));%标准化因变量数据MMLR=inv((E0'*E0))*(E0'*F0);%估计多重多元线性回归方程系数根据上述计算结果,可得下列多重多元线性回归方程:05040302010132924.10578.01873.01685.04171.0E E E E E F +-+--=,0504030201023867.10071.00209.01647.02410.0E E E E E F +----=, 0504030201033674.10270.01530.03039.02237.0E E E E E F +++--=.从这一组回归方程可以看出,三大产业产出值与研究生教育、高等教育竟然负相关,这与客观事实相违背,也与相关系数矩阵中得到的结论相悖.所以,在自变量之间、以及自变量与因变量之间存在复杂的相关关系时,普通最小二乘回归方法建立的模型不能准确的反映实际情况.3 建立偏最小二乘回归模型⑴ 提取所有可能的主成分clearload jytrjjccX=jytrjjcc(:,1:5); Y=jytrjjcc(:,6:8); E0=stand(X); F0=stand(Y); A=rank(E0);[W,C,T,U,P,R]=plspcr(E0,F0); %提取所有可能的主成分⑵ 主成分解释能力分析复测定系数RA=plsra(T,R,F0,A)RA =Columns 1 through 40.8727 0.9209 0.9739 0.9870 Column 50.9879抽取不同个数的主成分时,对应的回归方程的复测定系数见表3.表3 复测定系数的取值主成分累积 1 2 3 4 5 复测定系数0.87270.92090.97390.98700.9879由表3可知,当抽取一个主成分时,回归方程的复测定系数已达到87.27%.通常,系统信息的可解释变异达到总变异的85%即可认为回归方程的精度已达到满意效果.因此,根据模型从简的原则,我们只需选取一个主成分建模.第一主成分为05040302011015208.02128.04719.04902.04694.0E E E E E w E t -+---==.主成分的信息解释能力[Rdx,RdX,RdXt,Rdy,RdY,RdYt]=plsrd(E0,F0,T,A)Rdx =Columns 1 through 40.9421 0.0092 0.0444 0.0017 0.9744 0.0110 0.0083 0.0006 0.9108 0.0054 0.0306 0.0530 0.3490 0.6425 0.0046 0.0040 0.9335 0.0433 0.0080 0.0150 Column 5 0.0025 0.0057 0.0003 0.0000 0.0001 RdX =Columns 1 through 40.8220 0.1423 0.0192 0.0149 Column 5 0.0017 RdXt =1.0000 Rdy =Columns 1 through 40.8573 0.0252 0.0670 0.0104 0.8650 0.0597 0.0415 0.0153 0.8728 0.0584 0.0493 0.0130 Column 5 0.0001 0.0018 0.0009 RdY =Columns 1 through 40.8650 0.0478 0.0526 0.0129 Column 5 0.0009 RdYt =0.9793表4 主成分t 1和t 2对变量的解释能力Rd L 1L 2L 3L 4KY 1 Y 2 Y 3 X Yt 1 0.9421 0.9744 0.9108 0.3490 0.9335 0.8573 0.8650 0.8728 0.8220 0.8650 t 20.00920.01100.00540.64250.04330.0252 0.0597 0.0584 0.1423 0.0478从表4中可以看出,主成分1t 除综合解释了原自变量系统82.20%的变异信息,对原自变量系统有非常好的代表性.同时,综合解释了因变量系统86.50%的信息,对因变量系统的贡献很大.而第二个主成分2t 对原自(因)变量系统信息变异的解释能力较低.经计算当增加第二个主成分2t 时,模型的精度没有明显的改善.因此,从主成分的信息解释能力的角度以及模型从简的原则,只选一个主成分建模是适宜的.第一主成分间的相关性cr =plsutcor(U,T) %绘制ui/t1图cr =1.0000 0.9342 -6-5-4-3-2-10123-4-3-2-112t1u 1t1/u1图从图中可以看出,两个第一主成分间的相关性很强.⑶ 求PLS 回归方程的系数✧ 求标准化变量回归方程的系数SCOEFF=pls(1,5,W,P,R)SCOEFF =0.2153 0.2163 0.2172 0.2248 0.2258 0.2269 0.2164 0.2174 0.2184 -0.0976 -0.0980 -0.0985 0.2389 0.2399 0.2410✧ 求原始变量回归方程的系数[COEFF,INTERCEP]=plsiscoeff(X,Y,SCOEFF)COEFF =0.0242 0.1072 0.0966 0.0017 0.0074 0.0067 0.0006 0.0027 0.0024 -0.0003 -0.0015 -0.0014 0.0001 0.0006 0.0005 INTERCEP =-17.9677 -233.0059 -388.83280F 关于成分1t 的回归方程为1111014586.0t t r F -≈=,1212024607.0t t r F -≈=, 1313034627.0t t r F -≈=;0F 关于0E 的回归方程为0504030201012389.00976.02164.02248.02153.0E E E E E F +-++≈,0504030201022399.00980.02174.02258.02163.0E E E E E F +-++≈, 0504030201032410.00985.02184.02269.02172.0E E E E E F +-++≈;原始因变量关于自变量的回归方程为K L L L L y0001.00003.00006.00017.00242.09677.17ˆ43211+-+++-=, K L L L L y0006.00015.00027.00074.01072.00059.233ˆ43212+-+++-=, K L L L L y0005.00014.00024.00067.00966.08328.388ˆ43213+-+++-=.可见,所建的回归方程没有出现反符号现象,受中等以上教育的劳动力人数、财政投入与经济的产出都是呈正相关的,只有初等教育劳动力人数(包括文盲)呈负相关,这与相关系数符号完全一致.⑶ 回归方程中自变量对因变量的解释能力(变量投影重要性)VIP=plsvip(W,RdY,RdYt,1)VIP =Columns 1 through 40.9866 1.0303 0.9918 0.4472 Column 5 1.0946变量投影重要性指标是用来测度第j 个自变量对因变量的解释能力的. 因此,从预测的角度,如果某个自变量在解释因变量时起得作用很小,则可以考虑删去这个变量后重新建模.由于VIP 4明显较小,故删除变量L 4重新用偏最小二乘回归方法建模,得到的回归方程为K L L L y 0001.00006.00018.00260.07.2703211++++-=, K L L L y 0006.00029.00080.01158.079.13743212++++-=, K L L L y 0005.00026.00072.01043.01.14163213++++-=,与未删除变量L 4前的回归方程对比,发现方程的回归系数变化很小.深入的精度分析结果见表5.表5 改进后模型应用效果比对分析Rdx Rdy SS PRESS包含L4的模型0.8220 0.8650 8.5034 8.3149删除L4的模型0.9476 0.8893 6.9714 6.4205 表5中,SS值表示的是回归方程对所有样本点的拟合误差平方和,PRESS值表示的是预测误差平方和,计算公式详见《偏最小二乘回归方法及其应用》(王惠文.国防工业出版社,1999).由表5可知,删除变量L4后的模型,无论是建模的主成分t1对自(因)变量的解释能力Rdx(Rdy),还是拟合与预测效果上都有很明显的提高.因此,基于VIP对自变量指标筛选后的偏最小二乘回归模型效果更佳.需要强调的是,删除L4的模型对分析教育投入与经济产出二者之间关系来说意义并不是很大,但若考虑对辽宁经济产出进行短期预测,采用该模型的预测精度会更高.4 由模型得到的信息Ⅰ. 从因变量与自变量之间的相关系数和变量投影重要性指标值可以看出,辽宁省的教育投入对经济发展有着深刻、全面的促进作用.对三大产业经济产出促进作用最大的就是教育的财政投入,然后依次是高等、中等、研究生、初等教育程度的劳动力人数.教育投入对三大产业经济产出的边际作用结构上是相似的,财政投入对第三产业产出值的边际贡献最大.Ⅱ. 由Ⅰ,国家的高校扩招政策对经济产生了积极的影响.据辽宁省教育厅日前的统计,辽宁省高等教育35.3%的毛入学率表明,辽宁省已经率先进入大众化高等教育时代.表1中的数据表明,辽宁省高校招生人数的持续增长,特别是2001年以来的快速增长,与辽宁省的经济增长是适应的,反过来说大众化的高等教育对经济的增长直接促进作用开始显现.Ⅲ. 由Ⅰ,初等教育程度劳动力人数对经济产出影响最小甚至是负面的.由于义务教育的普及和辽宁省较高的中等教育普及率,文盲和新增初等教育程度的劳动力人数逐渐减少,因此该项指标对经济产出的解释能力变小.初等教育程度劳动力人数与其它各项指标的负相关性表明,中等以上教育程度劳动力人数增加的必然结果是初等教育程度劳动力人数的下降,而教育财政投入的增加是抑制初等教育程度劳动力人数的最重要因素,初等教育程度劳动力的就业对全社会经济的增长是一种负担.Ⅳ. 由Ⅰ,我们认为研究生教育的规模应当适当扩大,经费投入应当增加和多样化.研究生教育程度劳动力人数对经济的影响重要性排名靠后,主要原因是研究生招生规模小、人数少,教育经费主要依赖财政投入.另外,研究生教育程度的劳动力人数对经济的影响可能要通过科技投入类指标间接的反映到经济产出上.这也表明教育投入对经济产出的影响是复杂的.Ⅴ. 在Ⅰ至Ⅳ的基础上深入分析,我们认为教育投入的强度和投入渠道的多样化对经济产出是有着重要、广泛和深远的影响.高等和中等教育程度劳动力人数对经济产出影响的重要性排名靠前,而初等和研究生教育程度劳动力人数排名靠后,这与我国目前相应的教育经费筹措渠道的不同有关.目前,我国的高等和中等教育的经费除国家的财政性投入之外,社会与个人的投入力度较大,高、中等教育程度劳动力人数的增加实质上是相应教育经费投入的增加.但初等和研究生教育的经费渠道相对单一,相应教育阶段的经费总投入相对较低是其对经济产出的解释能力较低的重要原因.Ⅵ. 在模型自身方面,从变量投影重要性的角度,剔除解释能力较小的自变量,能够有效的提高模型的预测效果.但这一点对具体问题需要进行谨慎分析.。
R语言实现偏最小二乘回归法partialleastsquares(PLS)回归

R语言实现偏最小二乘回归法partialleastsquares(PLS)回归原文链接:/?p=8652偏最小二乘回归是一种回归形式。
当使用pls时,新的线性组合有助于解释模型中的自变量和因变量。
在本文中,我们将使用pls在“ Mroz”数据集中预测“收入”。
library(pls);library(Ecdat)data("Mroz")str(Mroz)## 'data.frame': 753 obs. of 18 variables:## $ work : Factor w/ 2 levels "yes","no": 2 2 2 22 2 2 2 22 ...## $ hoursw : int 1610 16561980 4561568 20321440 1 0201458 1600 ...## $ child6 : int 1 0 1 01 0 0 000 ...## $ child618 : int 0 2 3 32 0 2 022 ...## $ agew : int 32 30 35 3431 54 37 544839 ...## $ educw : int 12 12 12 1214 12 16 121212 ...## $ hearnw : num 3.35 1.394.55 1.14.59 ...## $ wagew : num 2.65 2.654.04 3.253.6 4.75.95 9.980 4.15 ...## $ hoursh : int 2708 23103072 19202000 10402670 4 1201995 2100 ...## $ ageh : int 34 30 40 5332 57 37 535243 ...## $ educh : int 12 9 12 1012 11 12 8412 ...## $ wageh : num 4.03 8.443.58 3.5410 ...## $ income : int 16310 2180021040 730027300 19495 21152 1890020405 20425 ...## $ educwm : int 12 7 12 712 14 14 377 ...## $ educwf : int 7 7 7 714 7 7 377 ...## $ unemprate : num 5 11 5 59.5 7.55 5 3 5 ...## $ city : Factor w/ 2 levels "no","yes": 1 2 1 12 2 1 11 1 ...## $ experience: int 14 5 15 67 33 11 352421 ...首先,我们必须通过将数据分为训练和测试集来准备数据。
偏最小二乘回归

偏最小二乘回归偏最小二乘回归(Partial Least Squares Regression,简称PLSR)是一种主成分回归方法,旨在解决多元线性回归中自变量数目较多,且存在共线性或多重共线性的问题。
本文将介绍偏最小二乘回归的原理、应用案例以及优缺点。
1. 偏最小二乘回归原理偏最小二乘回归是基于多元线性回归的一种方法,通过压缩自变量的空间,将高维的自变量转化为低维的潜在变量,从而避免了多重共线性的问题。
在偏最小二乘回归中,我们定义两个主成分,其中第一个主成分能最大化自变量与因变量之间的协方差,而第二个主成分垂直于第一个主成分,以此类推。
2. 偏最小二乘回归应用案例偏最小二乘回归在众多领域都有广泛的应用。
以下是一些常见的应用案例:2.1 化学分析在化学领域中,我们常常需要使用红外光谱仪等仪器进行样本的分析。
然而,由于样本中存在大量的杂质,导致光谱数据存在共线性等问题。
通过偏最小二乘回归可以降低样本数据的维度,提取出有用的信息,从而准确地进行化学成分的分析。
2.2 生物医学在生物医学领域中,研究人员常常需要通过大量的生理指标预测某种疾病的发生风险。
然而,由于生理指标之间存在相互关联,使用传统的线性回归模型时,很容易出现共线性的问题。
通过偏最小二乘回归,可以降低指标的维度,减少共线性对预测结果的影响,提高疾病预测的准确性。
2.3 金融领域在金融领域中,偏最小二乘回归也有广泛的应用。
例如,在股票市场的分析中,研究人员常常需要通过一系列宏观经济指标预测股票的涨跌趋势。
然而,这些指标之间往往存在较强的相关性,导致传统的回归模型难以提取出有效的信息。
通过偏最小二乘回归,可以从多个指标中提取出潜在的主成分,预测股票的涨跌趋势。
3. 偏最小二乘回归的优缺点3.1 优点(1)解决了多重共线性问题:偏最小二乘回归通过降低自变量的维度,有效地解决了多重共线性问题,提高了模型的稳定性和准确性。
(2)提取了潜在的主成分:通过偏最小二乘回归,我们可以从高维的自变量中提取出潜在的主成分,这些主成分更具有解释性,有助于理解自变量与因变量之间的关系。
偏最小二乘法回归建模案例

偏最小二乘法回归建模案例1.问题陈述假设我们有一份关于电子产品销售的数据集,包含了多个特征变量和一个连续的目标变量(销售量)。
我们希望通过分析这些特征变量与销售量之间的关系,建立一个准确的预测模型。
2.数据预处理在进行任何分析之前,我们首先需要对数据进行预处理。
这包括处理缺失值、异常值和标准化数据。
我们还可以使用特征选择方法,从所有特征变量中选择出最重要的变量。
这一步骤有助于减少模型复杂度,并提高模型的准确性。
3.拆分数据集为了评估模型的性能,我们将数据集拆分为训练集和测试集。
训练集用于建立模型,而测试集用于评估模型的预测性能。
通常,约80%的数据用于训练,20%的数据用于测试。
4.PLS回归建模在拆分数据集后,我们可以使用PLS回归算法来建立预测模型。
PLS 回归的主要目标是最大化解释方差,并建立特征与目标变量之间的线性关系。
通过计算得到的权重系数可以解释每个特征变量与目标变量之间的重要程度。
5.模型评估建立模型后,我们需要评估模型的性能。
常用的评估指标包括均方根误差(Root Mean Squared Error,RMSE)、均方误差(Mean SquaredError,MSE)和决定系数(Coefficient of Determination,R²)。
这些指标可以帮助我们了解模型的精确性和泛化能力。
6.模型优化如果模型的性能不令人满意,我们可以尝试优化模型。
一种优化方法是调整PLS回归模型的参数,如成分个数。
此外,我们还可以尝试使用其他机器学习算法,如岭回归、支持向量回归等。
这些方法可以帮助我们找到更好的模型。
7.模型应用通过建立准确的预测模型,我们可以对新的数据进行销售量预测。
这有助于制定合理的生产计划和销售策略,以满足市场需求并最大化利润。
总结:本文使用了PLS回归建模方法来预测电子产品的销售量。
通过对数据进行预处理、拆分数据集、PLS回归建模、模型评估和优化等步骤,我们得到了一个准确的预测模型。
偏最小二乘路径建模(pls-pm)结构方程

偏最小二乘路径建模(PLS-PM)结构方程一、变量间关系偏最小二乘路径建模(PLS-PM)是一种探索变量间关系的统计方法。
它通过路径图来描述变量之间的因果关系,并使用偏最小二乘回归(PLS)进行模型估计。
PLS-PM适用于变量间存在复杂关系的情境,可以处理多个因变量和自变量,并考虑测量误差和潜在变量的影响。
二、因果关系在PLS-PM中,因果关系是核心概念。
通过路径图,我们可以直观地展示变量之间的因果关系,并根据专业知识或实证数据来构建路径。
在路径图中,箭头表示因果关系,箭头的方向表示因果关系的方向。
通过因果关系,我们可以分析一个变量对另一个变量的影响,以及这种影响是如何传递的。
三、路径图构建构建路径图是PLS-PM的重要步骤。
路径图需要基于理论或实证数据来构建,并遵循一定的原则,如因果关系应该基于理论或实证证据,箭头指向表示因果关系的方向等。
构建路径图时,我们需要确定因变量和自变量,并考虑潜在变量的影响。
路径图可以帮助我们更好地理解变量之间的关系,并为后续的模型估计提供基础。
四、模型估计在PLS-PM中,模型估计使用偏最小二乘回归(PLS)进行。
PLS 是一种广义的线性模型,通过迭代的方式对模型进行拟合,并考虑到测量误差和潜在变量的影响。
在模型估计过程中,我们需要确定合适的模型拟合指标,如R方、Q方等,并对模型的拟合效果进行评估。
五、模型评估模型评估是PLS-PM的重要环节。
我们需要评估模型的拟合效果、预测能力和解释能力。
通过比较模型拟合指标和竞争模型的性能,我们可以判断模型的优劣。
此外,我们还可以使用交叉验证、敏感度分析等方法来评估模型的稳定性。
如果模型拟合效果不理想,我们需要重新审视路径图和模型估计过程,并进行相应的调整。
六、模型应用与拓展模型应用是PLS-PM的目的之一。
我们可以将建立好的模型应用于实际情境中,预测新数据或对未知数据进行解释。
此外,我们还可以将PLS-PM应用于其他相关领域,以探索变量之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《人工智能》课程论文论文题目:偏最小二乘算法(PLS)回归建模学生姓名:***学号: ********* 专业:机械制造及其自动化所在学院:机械工程学院年月日目录偏最小二乘回归....................................... - 2 -摘要................................................. - 2 -§1偏最小二乘回归原理................................ - 2 -§2一种更简洁的计算方法.............................. - 6 -§3案例分析 ......................................... - 7 -致谢................................................ - 16 -附件:.............................................. - 17 -偏最小二乘回归摘要在实际问题中,经常遇到需要研究两组多重相关变量间的相互依赖关系,并研究用一组变量(常称为自变量或预测变量)去预测另一组变量(常称为因变量或响应变量),除了最小二乘准则下的经典多元线性回归分析(MLR ),提取自变量组主成分的主成分回归分析(PCR )等方法外,还有近年发展起来的偏最小二乘(PLS )回归方法。
偏最小二乘回归提供一种多对多线性回归建模的方法,特别当两组变量的个数很多,且都存在多重相关性,而观测数据的数量(样本量)又较少时,用偏最小二乘回归建立的模型具有传统的经典回归分析等方法所没有的优点。
偏最小二乘回归分析在建模过程中集中了主成分分析,典型相关分析和线性回归分析方法的特点,因此在分析结果中,除了可以提供一个更为合理的回归模型外,还可以同时完成一些类似于主成分分析和典型相关分析的研究内容,提供更丰富、深入的一些信息。
本文介绍偏最小二乘回归分析的建模方法;通过例子从预测角度对所建立的回归模型进行比较。
关键词:主元分析、主元回归、回归建模1 偏最小二乘回归原理考虑p 个变量p y y y ,...,21与m 个自变量m x x x ,...,21 的建模问题。
偏最小二乘回归的基本作法是首先在自变量集中提出第一成分t ₁(t ₁是m x x x ,...,21的线性组合,且尽可能多地提取原自变量集中的变异信息);同时在因变量集中也提取第一成分u ₁,并要求t ₁与u ₁相关程度达到最大。
然后建立因变量p y y y , (21)t ₁的回归,如果回归方程已达到满意的精度,则算法中止。
否则继续第二对成分的提取,直到能达到满意的精度为止。
若最终对自变量集提取r 个成分r t t t ,...,21,偏最小二乘回归将通过建立p y y y ,...,21与r t t t ,...,21的回归式,然后再表示为p y y y ,...,21与原自变量的回归方程式,即偏最小二乘回归方程式。
为了方便起见,不妨假定p 个因变量p y y y ,...,21与m 个自变量m x x x ,...,21均为标准化变量。
因变量组和自变量组的n 次标准化观测数据阵分别记为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=nm n m np n p x x x x y y y y F E ..........:..........,............: (1111011110)偏最小二乘回归分析建模的具体步骤如下:(1)分别提取两变量组的第一对成分,并使之相关性达最大。
(2)假设从两组变量分别提出第一对t ₁和u ₁,t ₁是自变量集()Tm x x X ,...,1=,的线性组合:X w x w x w t T m m 111111...=++=,u ₁是因变量集()Tp y y Y ,..,1=的线性组合:Y v y v y v u T p p 111111...=++=。
为了回归分析的需要,要求:① t1和u1各自尽可能多地提取所在变量组的变异信息; ② t1和u1的相关程度达到最大。
由两组变量集的标准化观测数据阵0E 和0F ,可以计算第一对成分的得分向量,记 为1∧t 和1∧u :⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==∧1111111111101::.........:.........n m nm n m t t w w x x x x w E t ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==∧1111111111101::..........:..........n p np n p u u v v y y y y v F u 第一对成分1t 和1u 的协方差),(11u t Cov 可用第一对成分的得分向量1∧t 和1∧u 的内积来计算。
故而以上两个要求可化为数学上的条件极值问题:⎪⎩⎪⎨⎧====⇒>=>=<<∧∧1,1max,,21112111001101011v v v w w w x F E w v Y w E u t TTT T利用Lagrange 乘数法,问题化为求单位向量1w 和1v ,使⇒=10011V F E w T T θ最大。
问题的求解只须通过计算m m ⨯矩阵0000E F F E M T T =的特征值和特征向量,且M 的最大特征值为21θ,相应的单位特征向量就是所求的解1w ,而1v 可由1w 计算得到100111w E F v T θ=。
(3)建立p y y y ,...,21,对1t 的回归及m x x ,...,1,对1t 的回归。
假定回归模型为:⎪⎩⎪⎨⎧+=+=∧∧11101110F u F E tE TT βα其中()()TpTm 11111111,...,,,...,βββααα==分别是多对一的回归模型中的参数向量,1E 和1F 是残差阵。
回归系数向量11,βα的最小二乘估计为:⎪⎪⎩⎪⎪⎨⎧==∧∧∧∧2110121101//t t F t t E T Tβα称11,βα为模型效应负荷量。
(4)用残差阵1E 和1F 代替0E 和0F 重复以上步骤。
记,,110110T Tt F t E βα∧∧∧∧==则残差阵001101,∧∧-=-=F F F E E E 。
如果残差阵1F 中元素的绝对值近似为0,则认为用第一个成分建立的回归式精度已满足需要了,可以停止抽取成分。
否则用残差阵1E 和1F 代替0E 和0F 重复以上步骤即得:()()Tm T m v v v w w w 22122212,...,;,...,==分别为第二对成分的权数。
而212211,v F u w E t ==∧∧为第二对成分的得分向量。
2221222212/,/∧∧∧∧==t t F t t E T T βα分别为X,Y 的第二对成分的负荷量。
这时有⎪⎩⎪⎨⎧++=++=∧∧∧∧222110222110F t t F E t tE TT T T ββαα (5)设n ×m 数据阵0E 的秩为r<=min(n-1,m),则存在r 个成分r t t t ,...,21,使得:⎪⎩⎪⎨⎧+++=+++=∧∧∧∧r Trr T r T r r T F t t F E t tE ββαα (110110)把),,...,2,1(...11r k x w x w t m km k k =++=代入,...11r r t t Y ββ++=,即得p 个因变量的偏最小二乘回归方程式:),...,2,1(,...11m j x a x a y m jm j j =++=(6) 交叉有效性检验。
一般情况下,偏最小二乘法并不需要选用存在的r 个成分p y y y ,...,21来建立回归式,而像主成分分析一样,只选用前l 个成分(l ≤r ),即可得到预测能力较好的回归模型。
对于建模所需提取的主成分个数l ,可以通过交叉有效性检验来确定。
每次舍去第i 个观测),...2,1(n i=,用余下的n-1个观测值按偏最小二乘回归方法建模,并考虑抽取h 个成分后拟合的回归式,然后把舍去的第i 个观测点代入所拟合的回归方程式,得到在第i 个观测点代入所拟合的预测值)()(h y j i ∧。
对i=1,2,…n 重复以上的验证,即得抽取h 个成分时第j 个因变量),...2,1(p j y j =的预测误差平方和为:),...2,1())((21)(jp j h y y h PRESS ni j i ij =-=∑=∧)(T p y y Y ),...,(1=的预测误差平方和为:)((1h PRESS h PRESS jPi ∑==)。
另外,再采用所有的样本点,拟合含h 个成分的回归方程。
这时,记第i 个样本点的预测值为)(h y ij ∧,则可以定义j y 的误差平方和为:21))(((∑=∧-=n i ij ij j h y y h SS )定义Y 的误差平方和为:)((1h ss h SS pj j ∑==)当)h PRESS (达到最小值时,对应的h 即为所求的成分个数。
通常,总有)h PRESS (大于)h SS (,而)h SS (则小于)1(-h SS 。
因此,在提取成分时,总希望比值)h PRESS (,)1(-h SS 越小越好;一般可设定限制值为0.05,即当2295.0)05.01()1(/(=-<=-h SS h PRESS )时,增加成分h t 有利于模型精度的提高。
或者反过来说,当295.0)1(/(>-h SS h PRESS )时,就认为增加新的成分h t ,对减少方程的预测误差无明显的改善作用。
为此,定义交叉有效性为),1(/)(12--=h SS h PRESS Q h这样,在建模的每一步计算结束前,均进行交叉有效性检验,如果在第h 步有),1(/(12--=h SS h PRESS Q h )则模型达到精度要求,可停止提取成分;若,0985.095.0122=-<hQ 表示第h 步提取的ht成分的边际贡献显著,应继续第h+1步计算。
§2 一种更简洁的计算方法上面介绍的算法原则和推导过程的思路在目前的文献中是最为常见的。
然而,还有一种更为简洁的计算方法,即直接在10,...-r E E 矩阵中提取成分r t t ,...0 (r ≤m)。
要求h t 能尽可能多地携带X 中的信息,同时,h t 对因变量系统0F 有最大的解释能力。
注意,无需在0F 中提取成分得分h u ,这可以使计算过程大为简化,并且对算法结论的解释也更为方便。
