力的投影及力矩
合集下载
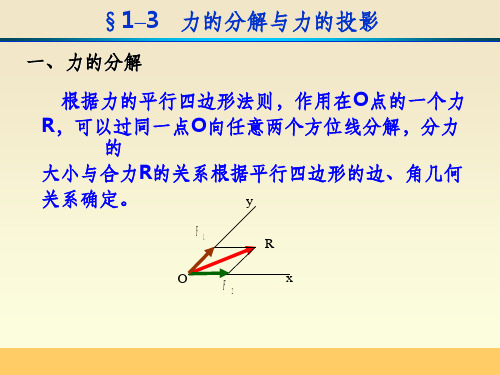
理论力学-力的分解与力的投影以及平面力系中的力矩
F Fx2 Fy2
cos Fx
F
cos Fy
F
式中的α和β分别表示力F与x轴和y轴正向间的夹角。
第一章 静力学的基本公理与受力分析
合力投影定理
合力在任一轴上的投影等于各分力在同一轴上投影的代数和。
F R F 1 F 2 L L F nF
F R F x i F y j,F i F x ii F y ij( i 1 ,2 ,L n )
第一章 静力学的基本公理与受力分析
例题
平面基本力系
合力的大小：
FR Fx2Fy217.31N
合力与轴x，y夹角的方向余弦为：
cos Fx 0 .754
FR
cos F y 0 .656
FR
所以，合力与轴x，y的夹角分别为：
40.99
49.01
第一章 静力学的基本公理与受力分析
F2 y
三、力在空间坐标轴上的投影
力在空间正交坐标轴上的投影可用两种方法来计算
直接投影法
z
Fx F cos
F
y
F
cos
F z F c o s
F
F = Fx+Fy+Fz= Fx i+Fy j+Fz k
O
y
x
第一章 静力学的基本公理与受力分析
二次投影法
z
F = Fx+Fy+Fz= Fx i+Fy j+Fz k
力F使物体绕O点转动效果的量度取决于三个因素： （1）力F的大小与力臂的乘积，即力矩的大小； （2）力F与矩心O所确定的平面的方位，即力矩的作用面； （3）在作用面内，力F绕矩心O的转向。
第一章 静力学的基本公理与受力分析
cos Fx
F
cos Fy
F
式中的α和β分别表示力F与x轴和y轴正向间的夹角。
第一章 静力学的基本公理与受力分析
合力投影定理
合力在任一轴上的投影等于各分力在同一轴上投影的代数和。
F R F 1 F 2 L L F nF
F R F x i F y j,F i F x ii F y ij( i 1 ,2 ,L n )
第一章 静力学的基本公理与受力分析
例题
平面基本力系
合力的大小：
FR Fx2Fy217.31N
合力与轴x，y夹角的方向余弦为：
cos Fx 0 .754
FR
cos F y 0 .656
FR
所以，合力与轴x，y的夹角分别为：
40.99
49.01
第一章 静力学的基本公理与受力分析
F2 y
三、力在空间坐标轴上的投影
力在空间正交坐标轴上的投影可用两种方法来计算
直接投影法
z
Fx F cos
F
y
F
cos
F z F c o s
F
F = Fx+Fy+Fz= Fx i+Fy j+Fz k
O
y
x
第一章 静力学的基本公理与受力分析
二次投影法
z
F = Fx+Fy+Fz= Fx i+Fy j+Fz k
力F使物体绕O点转动效果的量度取决于三个因素： （1）力F的大小与力臂的乘积，即力矩的大小； （2）力F与矩心O所确定的平面的方位，即力矩的作用面； （3）在作用面内，力F绕矩心O的转向。
第一章 静力学的基本公理与受力分析
理论力学课件 第一章力的投影,主矩主矢
•
•
v Fn
=
X niv
•
+ Yn
vj
+
v Znk
z
Fn O x
Fi
F1 y
F2
∑ X1 + X 2 +L+ X n = X
∑ Y1 + Y2 + L + Yn = Y
∑ Z1 + Z2 + L + Zn = Z
v FV
=
(∑
X
)iv
+ (∑Y )vj
+ (∑ Z )kv
1.1 力的投影、力系的主矢、汇交力系的合力
1.1 力的投影、力系的主矢、汇交力系的合力
合力解析表达式Fv形R式= (−153.6iv −170.5 vj )N
合力的大小和方向
∑ ∑ FR = ( X )2 + ( Y )2 = 229.5N
θ
=
arctan
∑Y ∑X
= 47.98°
y
θO x
FR
1.1 力的投影、力系的主矢、汇交力系的合力 2、汇交力系合成的几何法
例1-4：边长为a的正方体受到四个大小都等于F的力， 方向如图，求此力系的主矢。
z A
G
F4
O
F1
E x
B
F2
H
F3
C y
D
1.1 力的投影、力系的主矢、汇交力系的合力
z
解
A
B 四力的矢量解析表达式：
G
F2
H
v F1
=
F
⎜⎜⎝⎛
2
v i
+
2
2 2
v j
第三章 力矩
攻丝时为什么要两个手施力,用一个手会有 什么不好之处
?
几个性质
(1) 当力线平移时，力的大小、方向都不改变，但附加力
偶的矩的大小与正负一般要随指定O点的位置的不同而不同。
(2) 力线平移的过程是可逆的，由此可得重要结论：
作用在同一平面内的一个力和一个力偶，总可以归纳为
一个和原力大小相等的平行力。 (3) 力线平移定理是把刚体上平面任意力系分解为一个平 面共点力系和一个平面力偶系的依据。
F'R
MO
FR′≠0，MO≠0，且FR′与 MO 不垂直
力螺旋
O
一个力和一个力偶组成的力系，且这个力垂直
于力偶的作用面。这样的力系称为力螺旋。
FR′ MO FR′
MO
(4) 力系平衡 FR′=0，MO = 0
力螺旋
MO O
FR′
z
O
x d M1 y
A
FR″
M 2 M O sin d FR FR
F′ F′ M F B d B A
A
F′′
M Fd M B ( F )
可以把作用于刚体上点A的力F平行移到同一刚体上 的任意点B，但必须同时附加一个力偶，这个附加 力偶的矩等于原来的力F对新作用点B的矩。 物理含义: 力可使物体移动和转动 力的平移定理说明一个力和一个力偶可 以进一步合成为一个力。
( Fx , Fy , Fz ) (100 14,150 14,50 14)
力F矢量对三个坐标轴的矩为： M x ( F ) yFz zFy 3 50 14 0 100 14
150 14( N m) 同理有：M y ( F ) zFx xFz 100 14( N m) M z ( F ) xFy yFx 0( N m) 力F矢量对O之矩为：
第二章力系的简化
A
x
i j k
y
F
MA r F l 2l 0 对点A的力矩： F sin 0 F cos 2Fl cosi Fl cosj 2Fl sin k
15
三.力偶 1.力偶定义 两个等值、反向、不共线的平行力。记为 ( F , F ) 力偶不能合成为一个力，故也不能与 一个力平衡，因此力和力偶都是基本力学 F 量。 F M 静止时力偶 M 与F 平衡吗? 力偶只能使物体转动，用力偶矩衡量
22
2.主矢与主矩——原力系的特征量 1)定义
' 主矢：（各力的矢量和）FR Fi Fi' ，与简化中心无关
主矩： （各力对O点取矩的矢量和）
MO MO (Fi ) ，与简化中心有关
2)简化结果 一般力系向某一点简化，可以得到一个力和一 个力偶，该力作用在简化中心，其大小，方向与原 力系主矢相同；该力偶矩等于原力系对简化中心的 主矩。
F
三要素:
大小、力偶作用面方位、转向.
16
F
2.力偶矩矢
A
rB A
F
F
B
h
rA
M
M
rB
O
定 义: 而
MO F ,F rA F rB F
F ' F
rA rB rB A
M0 F , F (rA rB ) F rBA F rAB F M
5
力矩的解析表达式：
由于F Fx i Fy j Fz k
M O (F ) r F x Fx i
r xi y j zk
学习任务4：投影、力矩、力偶
？
l
3 o
θ
2
C
1
G
解: MO(F) = Fd
位置1: MO(F) = Gd = 0 位置2: MO(F) = －G －Glsinθ
Gd=lsinθ 位置3: MO(F) = －Gl
陕西铁路工程职业技术学院结构教研室
LOGO
三、力偶及力偶矩
由大小相等、方向相反、不共线的两个力组d成 F′
的力系称为力偶。(F,F’) 力偶对物体的效应：只产生转动效应，而无F移动效应。
M=±F.d
陕西铁路工程职业技术学院结构教研室
d F′
d F′
F
F
❖ ⑴力偶没有合力。一个力偶不能用一个力代替，也不能与一个 力平衡。力偶在任一轴上的投影为零。
平面汇交力系的合力在某轴上的投影等于力系 中各分力在同一轴上投影的代数和。即：
Rx = X1 + X2 + ···Xn= ∑ X Ry = Y1 + Y2 + ···Yn = ∑ Y
R = √ (∑X )2 + (∑ Y ) 2
∑Y Tanα= ∑ X
陕西铁路工程职业技术学院结构教研室
合力投影定理应用
1.6 力矩和力偶
陕西铁路工程职业技术学院结构教研室
一、力矩
❖ 定义：力与力臂的乘积冠以正、负号定义为力F对O点的力 矩。
表达式：Mo(F) = ±F·d
F1 F2
O — 转动的中心。称为力矩中
O
心，简称矩心
d — 转动中心到力作用线之 间的距离称为力臂(注意单位)
正负号规定：若力使物体绕矩心作逆时针 转向转动力矩取正号,反之取负号。
1.5 力的投影
一、力在平面直角坐标轴上的投影
l
3 o
θ
2
C
1
G
解: MO(F) = Fd
位置1: MO(F) = Gd = 0 位置2: MO(F) = －G －Glsinθ
Gd=lsinθ 位置3: MO(F) = －Gl
陕西铁路工程职业技术学院结构教研室
LOGO
三、力偶及力偶矩
由大小相等、方向相反、不共线的两个力组d成 F′
的力系称为力偶。(F,F’) 力偶对物体的效应：只产生转动效应，而无F移动效应。
M=±F.d
陕西铁路工程职业技术学院结构教研室
d F′
d F′
F
F
❖ ⑴力偶没有合力。一个力偶不能用一个力代替，也不能与一个 力平衡。力偶在任一轴上的投影为零。
平面汇交力系的合力在某轴上的投影等于力系 中各分力在同一轴上投影的代数和。即：
Rx = X1 + X2 + ···Xn= ∑ X Ry = Y1 + Y2 + ···Yn = ∑ Y
R = √ (∑X )2 + (∑ Y ) 2
∑Y Tanα= ∑ X
陕西铁路工程职业技术学院结构教研室
合力投影定理应用
1.6 力矩和力偶
陕西铁路工程职业技术学院结构教研室
一、力矩
❖ 定义：力与力臂的乘积冠以正、负号定义为力F对O点的力 矩。
表达式：Mo(F) = ±F·d
F1 F2
O — 转动的中心。称为力矩中
O
心，简称矩心
d — 转动中心到力作用线之 间的距离称为力臂(注意单位)
正负号规定：若力使物体绕矩心作逆时针 转向转动力矩取正号,反之取负号。
1.5 力的投影
一、力在平面直角坐标轴上的投影
知识点2：平面力系
知识点2：平面力系一、平面汇交力系的合成与平衡的几何法(1)平面汇交力系的合成用力多边形法则，合力的大小和方向由力多边形的封闭边来表示，其作用线通过各力的汇交点，即合力等于力系中各力的矢量和，即∑=+++=F F F F F n R 21(2)平面汇交力系的平衡平面汇交力系平衡的必要和充分的几何条件是力多边形自行封闭。
即0==∑F F R二、平面汇交力系的合成与平衡的解析法1．力在坐标轴上的投影力在坐标轴上的投影等于力的模乘以力与投影轴正向间夹角的余弦，如图2-1所示，它是一标量，即θcos F F x =； θβs i n c o s F F y == （2-1）图2-1 图2-22．力沿坐标轴的分解力沿坐标轴的分力是一矢量，其合力与分力之间应满足力的平行四边形公理。
如图2-2所示。
力沿坐标轴分解的分力的大小为xyxyx)sin(sin βθβ+=F F x ； )s i n (s i nβθθ+=F F y（2-2）由此可见，在一般情况下，力沿坐标轴分解的分力的大小不等于力在坐标轴上投影的大小。
当2πβθ=+时，在同一坐标上分力的大小和投影相等，如图2-3所示。
（a ）（b ）图2-33．合力投影定理合力在某轴上的投影等于各分力在同一轴上投影的代数和，即∑=x Rx F F ； ∑=y Ry F F（2-3）当投影轴x 与y 垂直时，其合力的大小与方向为22RyRx R F F F +=，R RxR F F =),cos(i F ，RRy R F F =),cos(j F （2-4）4．平面汇交力系的合成当两坐标轴间的夹角为2π时有2222)()(∑∑+=+=y x Ry Rx R F F F F F（2-5）RxR F F∑=),cos(i F ，RyR F F∑=),cos(j F5．平面汇交力系的平衡 由几何法知0=R F代入前面的代数表达式有0)()(2222=+=+=∑∑y x Ry Rx R F F F F Fx F y即0=∑xF；0=∑yF（2-6）平面汇交力系平衡的解析条件是力系中各力在两个坐标轴中每一轴上的投影的代数和均等于零。
机械设计基础3-静力学基础(3)
Fy F1 sin30 F2 sin60 F3 sin45 F4 sin45
100 150 3 50 2 125 2 112.35N
FR的大小： FR FX 2 Fy 2 171.3N
FR与x轴正向所夹锐角α为：
静力学基础
力矩和力偶
0.6 1400cos20 389.32Nm
静力学基础
2.力对轴之矩:是指力使物体绕轴转动效应的量度
平面内所讲的力对点之矩，对空间而言就是力对通过 矩心且垂直于力的作用面的轴之矩
M z (F ) M o (Fxy ) Fxyd
力与轴相交或与轴平行（力与轴在同一平面内）时， 力对该轴的矩为零。
0 0
M C (F ) 0
A、B、C不共线
3.解题步骤
• 选取研究对象，画受力图 • 建立直角坐标系 • 列平衡方程并求解
静力学基础
已知F=15kN，M=3kN.m，求A、B处支座反 力
画受力图，建立坐标系
列平衡方程：
Fx 0 FAx 0
Fy 0
FAy FB F 0
力的作用线的垂直距离d 有关，用F·d 来度量
平面内:力对点之矩为标量 mo F F d
表示
空间内:力对点之矩为失量 mo F F r
静力学基础
力矩的性质
1)力矩的大小和转向与矩心位置有关，同一力对不 同矩心的力矩不同。
2)力沿其作用线滑移时力对点之矩不变。 3)当力的作用线通过矩心时，力臂为零力矩也为零。
将各力分别向X、Y轴投影得：
静力学基础
若某汇交力系由n个力组成，则合力FR可以表示为
100 150 3 50 2 125 2 112.35N
FR的大小： FR FX 2 Fy 2 171.3N
FR与x轴正向所夹锐角α为：
静力学基础
力矩和力偶
0.6 1400cos20 389.32Nm
静力学基础
2.力对轴之矩:是指力使物体绕轴转动效应的量度
平面内所讲的力对点之矩，对空间而言就是力对通过 矩心且垂直于力的作用面的轴之矩
M z (F ) M o (Fxy ) Fxyd
力与轴相交或与轴平行（力与轴在同一平面内）时， 力对该轴的矩为零。
0 0
M C (F ) 0
A、B、C不共线
3.解题步骤
• 选取研究对象，画受力图 • 建立直角坐标系 • 列平衡方程并求解
静力学基础
已知F=15kN，M=3kN.m，求A、B处支座反 力
画受力图，建立坐标系
列平衡方程：
Fx 0 FAx 0
Fy 0
FAy FB F 0
力的作用线的垂直距离d 有关，用F·d 来度量
平面内:力对点之矩为标量 mo F F d
表示
空间内:力对点之矩为失量 mo F F r
静力学基础
力矩的性质
1)力矩的大小和转向与矩心位置有关，同一力对不 同矩心的力矩不同。
2)力沿其作用线滑移时力对点之矩不变。 3)当力的作用线通过矩心时，力臂为零力矩也为零。
将各力分别向X、Y轴投影得：
静力学基础
若某汇交力系由n个力组成，则合力FR可以表示为
ch2力矩、力偶、力系的简化
力对点之矩与力对轴之矩的关系
MO (F )
= ( yFz - zFy )i + ( zFx - xFz ) j + ( xFy - yFx )k
= [ M O ( F )]x i + [ M O ( F )] y j + [ M O ( F )] y k
M x ( F ) = -zFy + yFz
F z = F ⋅ cos γ = F ⋅ sin θ
与平面情形类似
F = Fx2 + Fy2 + Fz2
Fy F F x cosα = ,cos β = ,cosγ = z F F F
Fz Fy Fx
Fx = Fx , Fy = Fy , Fz = Fz
Fx = Fx i , Fy = Fy j,Fz = Fz k F = Fx + Fy + Fz = Fx i + Fy j + Fz k
②投影法（解析法） 投影法（解析法） 建立坐标系如图所示， 建立坐标系如图所示， 三个力在坐标轴上的投影分 别为
F1 x = 0
F2 x = 4kN
F1 y = −3kN
F2 y = 0
F3 x = 5cos 30o = 4.33kN
F3 y = 5sin 30o = 2.5kN
合力F 合力 R 在坐标轴上的投影为
= [MO (F )]x i +[MO (F )]y j +[MO (F )]z k
力矩矢的合成
力对点之矩矢服从矢量合成法则。 力对点之矩矢服从矢量合成法则。力系对刚体产 矢量合成法则 生的绕某点的转动效应可用一个矩矢度量。 一个矩矢度量 生的绕某点的转动效应可用一个矩矢度量。
理论力学05空间力系_2力对轴的矩
x、y、z 轴上的投影。
三、力对轴的合力矩定理 合力对任一轴的矩就等于其各分力对同一轴的矩的代数和，即
Mx FR Mx Fi M y FR M y Fi Mz FR Mz Fi
z
四、力对点的矩的矢量定义
力F 对点O 的矩的矢量定义为
MO F r F
式中，r 为矩心 O 至力F 作用点
Mz F xFy yFx 0 l aF sin F l asin
两种计算方法结果相同
[例2] 如图，长方体边长分别为a、b、c，沿其对角线 AB 作用一力 F。试求力F 对 x ，z 及 y1三轴的矩。
解： 将力F 作三维正交分解， 其中各分力大小
Fx
a
F
a2 b2 c2
z
Fy
b F
a2 b2 c2
c
Fz
F a2 b2 c2
c
Fy
a
x
b
Fz
y
Fx
y1
Fx
a F
a2 b2 c2
Fy
b F
a2 b2 c2
Fz
c
F
a2 b2 c2
利用力对轴的矩的合力矩定理，即得
M x F M x Fz
bc F
a2 b2 c2
M z F M z Fx
Mz F Mz Fx Mz Fz Fx AB CD 0 F l asin
解法二： 利用力对轴的矩的解析算式
力的作用点的坐标为
x l y l a z 0
力F 在 x、y、z 轴上的投影为 Fx F sin Fy 0 Fz F cos 代入解析算式，即得
Fx
Fz
Mx F yFz zFy l aF cos 0 F l acos My (F) zFx xFz 0 lF cos Fl cos
三、力对轴的合力矩定理 合力对任一轴的矩就等于其各分力对同一轴的矩的代数和，即
Mx FR Mx Fi M y FR M y Fi Mz FR Mz Fi
z
四、力对点的矩的矢量定义
力F 对点O 的矩的矢量定义为
MO F r F
式中，r 为矩心 O 至力F 作用点
Mz F xFy yFx 0 l aF sin F l asin
两种计算方法结果相同
[例2] 如图，长方体边长分别为a、b、c，沿其对角线 AB 作用一力 F。试求力F 对 x ，z 及 y1三轴的矩。
解： 将力F 作三维正交分解， 其中各分力大小
Fx
a
F
a2 b2 c2
z
Fy
b F
a2 b2 c2
c
Fz
F a2 b2 c2
c
Fy
a
x
b
Fz
y
Fx
y1
Fx
a F
a2 b2 c2
Fy
b F
a2 b2 c2
Fz
c
F
a2 b2 c2
利用力对轴的矩的合力矩定理，即得
M x F M x Fz
bc F
a2 b2 c2
M z F M z Fx
Mz F Mz Fx Mz Fz Fx AB CD 0 F l asin
解法二： 利用力对轴的矩的解析算式
力的作用点的坐标为
x l y l a z 0
力F 在 x、y、z 轴上的投影为 Fx F sin Fy 0 Fz F cos 代入解析算式，即得
Fx
Fz
Mx F yFz zFy l aF cos 0 F l acos My (F) zFx xFz 0 lF cos Fl cos
刚体静力学基础
哈尔滨师范大学-通用技术
工程力学
第一章 刚体静力学基础
刚体静力学以刚体为研究对象。所谓刚体，是受力时不变形的物体。刚体 静力学的任务是研究物体的受力分析、力系的等效替换和各种力系的平衡条件 及其应用。刚体静力学在工程中有广泛的应用，同时其它力学分支的基础。
本章介绍刚体静力学理论的基础知识，包括力和力矩的概念，静力学公理 和任意力系的简化方法。
6
哈尔滨师范大学-通用技术
工程力学
态保持不变。若拉力改成压力，则柔绳不 能平衡，就不能将其刚化。
公理五表明，变形体的平衡条件包括 了刚体的平衡条件。因此，可以把任何已 处于平衡的变形体看成是刚体，而对它应 用刚体静力学的全部理论。这就是公理五 的意义所在。
图1–13 刚化公理
1.3 力偶及其性质
● 力偶
图1–10表示了力的可传性的证明思路，其中 F2 F1 F 。显然，公理二及 其推论也都只适用于刚体而不适用于变形体。对于变形体，力将产生内效应， 当力沿作用线移动时，将改变它的内效应。
● 公理三 力的平行四边形公理
作用在物体上同一点的两个力，可以合成一个力。合力的作用点仍在该点， 合力的大小和方向，由这两个力为邻边的平行四边形的对角线确定。
(1–1)
Fx F k F cos
其中 、 和 是力 F 与各坐标轴的正向夹角，如图1–1所示。显然，力在轴上
的投影是代数量。
如已知力在各轴上的投影，则可将力沿直角坐标轴分解
F Fxi Fy j Fz k
(1–2)
如图1–2所示，计算力在直角坐标轴上的投影，也可以使用二次投影法。 Fx Fxy cos F sin cos
平衡时，此三力的作用线必然交汇于同一点。简称三力汇交定理。
工程力学
第一章 刚体静力学基础
刚体静力学以刚体为研究对象。所谓刚体，是受力时不变形的物体。刚体 静力学的任务是研究物体的受力分析、力系的等效替换和各种力系的平衡条件 及其应用。刚体静力学在工程中有广泛的应用，同时其它力学分支的基础。
本章介绍刚体静力学理论的基础知识，包括力和力矩的概念，静力学公理 和任意力系的简化方法。
6
哈尔滨师范大学-通用技术
工程力学
态保持不变。若拉力改成压力，则柔绳不 能平衡，就不能将其刚化。
公理五表明，变形体的平衡条件包括 了刚体的平衡条件。因此，可以把任何已 处于平衡的变形体看成是刚体，而对它应 用刚体静力学的全部理论。这就是公理五 的意义所在。
图1–13 刚化公理
1.3 力偶及其性质
● 力偶
图1–10表示了力的可传性的证明思路，其中 F2 F1 F 。显然，公理二及 其推论也都只适用于刚体而不适用于变形体。对于变形体，力将产生内效应， 当力沿作用线移动时，将改变它的内效应。
● 公理三 力的平行四边形公理
作用在物体上同一点的两个力，可以合成一个力。合力的作用点仍在该点， 合力的大小和方向，由这两个力为邻边的平行四边形的对角线确定。
(1–1)
Fx F k F cos
其中 、 和 是力 F 与各坐标轴的正向夹角，如图1–1所示。显然，力在轴上
的投影是代数量。
如已知力在各轴上的投影，则可将力沿直角坐标轴分解
F Fxi Fy j Fz k
(1–2)
如图1–2所示，计算力在直角坐标轴上的投影，也可以使用二次投影法。 Fx Fxy cos F sin cos
平衡时，此三力的作用线必然交汇于同一点。简称三力汇交定理。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
12/18
1
再 见 ！
13/18
8/18
1
二
生活中的力矩
力 矩
电钻 自行车 钳子
9/18
2
二
力矩的概念
力 矩
10/18
2
二
力矩的概念
力矩的正负号：
力 矩
-
+
11/18
3
力矩的性质
二 当力的大小等于零（F=0），或者力的作用线通过矩心 （即力臂d=0），力矩等于零。
力 矩
当力沿作用线移动时，不会改变力对某点的矩。 （力矩的大小不变）
力的投影和力矩
Байду номын сангаас
建筑工程学部| 聂亚荔 |2016.6
理解力的投影的概念与性质 掌握力投影大小的计算方法和步骤
力 的 投 影 和 力 矩
理解力矩的概念与性质
掌握力矩大小计算的方法和步骤
2/18
主要内容：
力 的 投 影 和 力 矩
重点：
力的投影的概念和性质 力矩的概念和性质
难点：
力的投影大小的求解 力矩大小的求解 3/18
4/18
1
一
力 的 投 影
生活中的投影
平面投影
立体投影
5/18
2
一
力 的 投 影
力在坐标轴上的投影
6/18
3
力的投影的性质
一 当力与坐标轴垂直时，力在该轴上的投影为零。
当力与坐标轴平行时，其投影的绝对值与该力的大小相等。
力 y 的 当力平行移动后，在坐标轴上的投影不变。 投 影
o
x 7/18