明渠非均匀流
名词水流的判别方法及标准有

名词水流的判别方法及标准有
五种判别明渠水流三种流态的方法如下:
(1)明渠水流的分类:明渠恒定均匀流、明渠恒定非均匀流、明渠非恒定非均匀流、明渠非恒定均匀流在自然界是不可能出现的。
明渠非均匀流根据其流线不平行和弯曲的程度,又可以分为渐变流和急变流。
(2)明渠梯形断面水力要素的计算公式:水面宽度 B = b+2 mh (5—1)过水断面面积 A =(b+ mh)h (5—2)湿周(5—3)水力半径(5—4)式中:b为梯形断面底宽,m为梯形断面边坡系数,h为梯形断面水深。
(3)当渠道的断面形状和尺寸沿流程不变的长直渠道我们称为棱柱体渠道。
(4)掌握明渠底坡的定义,明渠有三种底坡:正坡(i>0)平坡(i=0)和逆坡(i<0。
明渠均匀流特性和计算公式:
明渠均匀流的特征:均匀流过水断面的形状、尺寸沿流程不变,特别是水深h沿程不变,这个水深也称为正常水深。
过水断面上的流速分布和断面平均流速沿流程不变。
总水头线坡度、水面坡度、渠底坡度三者相等,J = Js = I。
即水流的总水头线、水面线和渠底线三条线平行。
从力学意义上来说:均匀流在水流方向上的重力分量必须与渠道边界的摩擦阻力相等才能形成均匀流。
因此只有在正坡渠道上才可能形成均匀流。
第六章明渠恒定非均匀流

第16讲(2课时)第六章 明渠恒定非均匀流明渠非均匀流特点:明渠大的底坡线、水面线、总水头线彼此互不平行。
产生非均匀流的原因:断面几何形状或尺寸沿流程改变,粗糙度或底坡沿流程改变,或有局部干扰。
分为渐变流和急变流。
分析水深的变化规律,)(s f h =;为区别将均匀流的水深称为正常水深,并以0h 表示。
★6-1 明渠水流的三种流态微波波速(相对速度)w V ,断面平均流速V 。
w V V <时,水流为缓流,干扰波能向上游传播; w V V =时,水流为临界流,干扰波不能向上游传播; w V V >时,水流为急流,干扰波不能向上游传播。
由连续方程2)(V h h hV w ∆+=及能量方程gV h h gV h w 2222221αα+∆+=+,可得:gh h h h h gh V w ≈∆+∆+=)2/1()/1(2,若为任意断面时,h g V w =,B A h /=平均水深。
定义佛汝德数(Froude ), hg V Fr =则:当Fr<1时,水流为缓流;当Fr=1时,水流为临界流;当Fr>1时,水流为急流。
佛汝德数的物理意义是,一单位动能与单位势能之比的两倍开方;二惯性力与重力的对比。
★6-2 断面比能与临界水深一、断面比能、比能曲线断面比能:以渠底为基准面,所计算得到的单位总能量,以s E 表示。
2222222cos gAQ h gV h gV h E s αααθ+=+≈+=当流量和过水断面的形状尺寸一定时,断面比能仅是水深的函数。
即)(h f E s =。
比能曲线:断面比能随水深变化的关系曲线。
以h 为纵坐标,以比能为横坐标。
比能曲线特征:当0→h 时,0→A ,则∞→222gAQ α,故∞→s E ;当∞→h 时,∞→A ,则0222→gA Q α,故∞→s E 。
比能曲线是一支二次抛物线,曲线的下端以水平线为渐进线,上端以过原点的45度直线为渐进线。
有一最小值,将曲线分为两支。
水力学第7章明渠非均匀流

水面曲线定性分析的理论基础:明渠恒定渐变流的基本微分方程
对于正底坡渠道i>0
对于平底坡渠道i=0
对于反底坡渠道i<0
dh/ds取不同值时的几何意义
dh/ds>0时,水深沿程增加,产生雍水曲线;
dh/ds<0时,水深沿程减少,产生降水曲线;
dh/ds→0时,水深趋于正常水深,即水面线与均匀流水面线渐近相切;
水跃稳定,消能效率高,跃后水面也较平稳。
由缓流向急流过渡时一定经过临界水深hcr,此时会产生水面降落的局部水力现象,此现象称为水跌或跌水。
水跌
缓坡接陡坡的渠道会产生水跌现象
图a中前段渠道i1<icr,后一段渠道i2>icr;
图b中缓坡渠道末端有一跌坎;可以将跌坎看作为i→∞的陡坡渠道;
因J>0,故在平坡i=0和逆坡i<0时:
;在顺坡i>0时:
则要看J和i的大小来决定了。
断面比能函数的特点
当流量、断面形状及尺寸一定时,断面比能Es只是水深h的函数
当h→0时A→0,于是e→∞,即断面比能函数曲线与水平轴渐近相切;
当h→∞时A→∞,于是e→∞,即断面比能曲线与过坐标原点的45°线渐近相切。
是一个无量纲的数,称为弗劳德数,用Fr表示。
流动是临界流时,弗劳德数等于1。所以液体在明渠中的流动 状态也可用弗劳德数来进行判别。
定义弗劳德(Froude)数
当 时,水流为缓流,
当 时,水流为急流,
当 时,水流为临界流,
vw
vw’
将石子投入等速运动的水流中,则波传播速度是水流流速与波速向量和。当水流流速小于波速(v < vw)时,微波向下游传播的绝对速度为(v + vw),向上游传播的绝对速度为( vw- v)。
水力学第八章明渠恒定非均匀流

本章主要研究的任务:就是分析水面线的变 化及其计算,以便确定明渠边墙高度,以及回水 淹没的范围等。
4 TRANSPORTATION COLLEGE OF SOUTHEAST UNIVERSITY
二、 明渠水流的两种流态
1、缓流和急流 现象 河流溪涧中障碍物对水流的影响。
5 TRANSPORTATION COLLEGE OF SOUTHEAST UNIVERSITY
gh
h
表示过水断面单位重量液体平均动能与平 均势能之比的二倍开平方,Fr愈大,意味 着水流的平均动能所占的比例愈大。
[Fr]
[惯性力] [重力]
表示水流的惯性力与重力两种作用力的对 比关系。急流时,惯性力对水流起主导作
用;缓流时,重力对水流起主导作用。
11 TRANSPORTATION COLLEGE OF SOUTHEAST UNIVERSITY
缓流:水流流速小,水势 平稳,遇到干扰,干扰的 影响既能向下游传播,又 能向上游传播
急流:水流流速大,水势 湍急,遇到干扰,干扰的 影响只能向下游传播,而 不能向上游传播
6 TRANSPORTATION COLLEGE OF SOUTHEAST UNIVERSITY
2、明渠中干扰微波的波速
试验
平底矩形断面水渠,水体静止,水深为h。直立平板 移动后引起一孤立波,以速度C从左向右传播。取 运动坐标系随波峰运动,相对于这个运动坐标系而 言,波是静止的,水流可视为以波速C从右向左流 动的恒定流。
现场观测和实验结论
对非矩形断面,CC gg AA gghhhhAA//BB
为断面平均水深,B为水BB 面宽度,h 相当
于把过水断面A化为宽为B的矩形时的水 深。
9 TRANSPORTATION COLLEGE OF SOUTHEAST UNIVERSITY
水力学第7章 明渠恒定非均匀流
三、当缓坡渠道末端自由跌落时
相当于缓坡变陡坡下游底坡变成铅锤跌坎
36
三、当缓坡渠道末端自由跌落时
37
四、当水流自水库进入陡坡渠道时
水库中水流为缓流,而陡坡渠道中均匀流为急 流,水流由缓流过渡到急流时,必经过临界水深。
38
重量液体所具有的
总能量为:E
z v 2
2g
z0
h cos
v 2
2g
9
如果我们把参考基准面选在渠底这一特殊位置,把对
通过渠底的水平面0′-0′所计算得到的单位能量称为断面比 能,并以 Es 来表示,则
Es
h cos
2
2g
在实用上,因一般明渠底坡较小,可认为 cos 1
故常采用
Es
h
Q 2
q Q 30m3 / s 3.75m3 / s m b 8m
hK
3
aq2 g
3
1 (3.75m2 / s)2 (9.8m / s2 )
1.13m
22
(2)当渠中水深 h = 3 m 时
渠中流速 Q 30m3 / s 1.25m / s
bh 8m 3m
弗劳德数 Fr
2
gh
(1.25m / s)2 (9.8m / s2 ) (3m)
(7-17)
17
Q2 AK3 (6.15)
g BK
(1)试算法
当给定流量 Q 及明渠断面形状、尺寸后,(7-17)式的
左端 aQ2 为一定值,该式的右端 A3 乃仅仅是水深的
g
B
函数。于是可以假定若干个水深 h ,从而可算出若干
个与之对应的 A3 值,当某一 A3 值刚好与 aQ2 相等
水力学课件 第8章 明渠非均匀流w

Q 2
ds ( 2gA2 ) gA3
dA ds
Q 2
gA3
Bdh ds
Fr2
dh ds
3. dhw ds
J
Q2 K2
i dh Fr2 dh J 0
ds
ds
明渠恒定非均匀渐变流的基本方程
dh
iJ
i
Q2 K2
ds 1 Fr2 1 Fr2
(二) 棱柱体明渠渐变流水面曲线形状分析
单位重量流体所具有的机械能
E z p v2 g 2g
断面单位能量
Es
h v2
2g
h
Q2
2 gA2
(1)断面单位能量(cross-sectional unit energy)
1.
E
z0
Es
z0
h
v2
2g
两者区别
2. dE 0 ds
dEs 0; dEs 0; dEs 0 ds ds ds
1)
水跃分类 波 状 水 跃 1 Fr1 1.7 弱 水 跃 1.7 Fr1 2.5 K j 20% 不 稳 定 水 跃 2.5 Fr1 4.5 K j 20% ~ 45% 稳 定 水 跃 4.5 Fr1 9 K j 45% ~ 70% 强 水 跃 9 Fr1 K j 85%
一.明渠水流的两种流态及其判别
1.明渠水流的两种流态
急流(Supercritical flow ) 当底坡陡峻,水流湍急,遇到障 碍物时,水面在障碍物顶上或稍 向上游隆起。但是障碍物对上游 较远处的水流并不发生影响。这 种水流状态称为急流。
一.明渠水流的两种流态及其判别
1.明渠水流的两种流态
缓流Subcritical Flow 底坡平缓,流速较小,遇到 渠底有阻水的障碍物时,在 障碍物处水面形成跌落,而 在其上游则普遍壅高,一直 影响到上游较远处。这种水
明渠恒定非均匀流

思路:
1、 Q2 Ak3 g Bk
A3 h~
B
2、由q查hK’,由hK’m/b查hK /hK’,求得hK 3、比较均匀流水深h与hK
(一)Q12 / g 182 / 9.81 6.53 假设一系列的水深h,计算值列于下表:
h (m) B (m) A (m2) A3/B
0.20 8.40 1.64 0.53
Q2 A3 — —临界水深的方程式 gB
6.6 试分析并定性绘出图中三种底坡变化情况时,上下游渠道 水面线的形式。已知上下游渠道断面形状,尺寸及粗糙系数均 相同并为长直棱柱体明渠。
6.14 如图所示矩形渠道设置一潜坎,试证明缓流通 过潜坎时,水面要下降,而急流通过潜坎时,水 面要上升(不计损失)。
dQ dA 2g
2g (1)
dh dh
(Es h) A 2 Es h
由 dA B dQ B
dh
dh
2g (Es h)
2g A 2 Es h
令 dQ 0 B dh
2g
(Es
h)
2g A 0 2 Es h
A 2B Q2
Q2B
B(Es h) 2 A (h 2gA2 h) 1 gA3 1
6-4 证明:当断面比能Es以及渠道断面形式、尺寸(b、m)一 定时,最大流量相应的水深是临界水深。
思路:
Es
h
Q2 2gA 2
Q
A
2g
(Es
h)
其中:A (b mh)h
由 dQ 0,此时h对应的Q最大。 dh
证明:Es
h
Q2 2gA 2
Q
A
2g (Es h)
当Es、b、m一定时,Q只与h有关。
明渠恒定均匀流和非均匀流概述
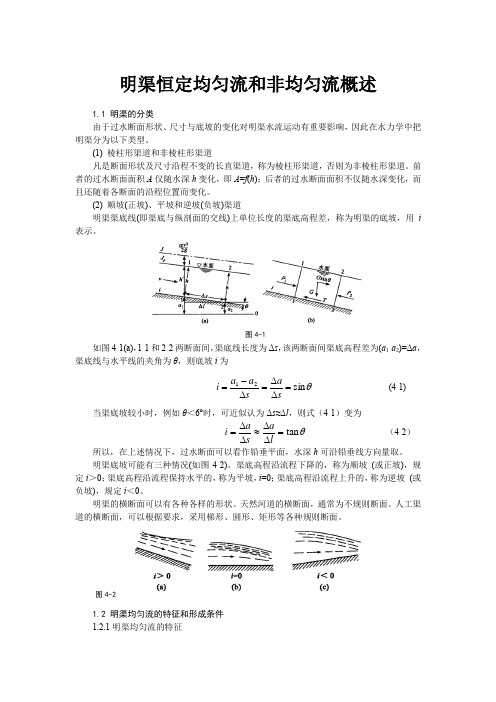
明渠恒定均匀流和非均匀流概述1.1 明渠的分类由于过水断面形状、尺寸与底坡的变化对明渠水流运动有重要影响,因此在水力学中把明渠分为以下类型。
(1) 棱柱形渠道和非棱柱形渠道凡是断面形状及尺寸沿程不变的长直渠道,称为棱柱形渠道,否则为非棱柱形渠道。
前者的过水断面面积A 仅随水深h 变化,即A =f (h );后者的过水断面面积不仅随水深变化,而且还随着各断面的沿程位置而变化。
(2) 顺坡(正坡)、平坡和逆坡(负坡)渠道明渠渠底线(即渠底与纵剖面的交线)上单位长度的渠底高程差,称为明渠的底坡,用i 表示。
图4-1如图4-1(a),1-1和2-2两断面间,渠底线长度为Δs ,该两断面间渠底高程差为(a 1-a 2)=Δa ,渠底线与水平线的夹角为θ,则底坡i 为θsin 21=∆∆=∆-=sa s a a i (4-1) 当渠底坡较小时,例如θ<6°时,可近似认为Δs ≈Δl ,则式(4-1)变为 θtan =∆∆≈∆∆=la s a i (4-2) 所以,在上述情况下,过水断面可以看作铅垂平面,水深h 可沿铅垂线方向量取。
明渠底坡可能有三种情况(如图4-2)。
渠底高程沿流程下降的,称为顺坡 (或正坡),规定i >0;渠底高程沿流程保持水平的,称为平坡,i =0;渠底高程沿流程上升的,称为逆坡 (或负坡),规定i <0。
明渠的横断面可以有各种各样的形状。
天然河道的横断面,通常为不规则断面。
人工渠道的横断面,可以根据要求,采用梯形、圆形、矩形等各种规则断面。
图4-21.2 明渠均匀流的特征和形成条件1.2.1明渠均匀流的特征明渠均匀流有下列特性:(1) 过水断面的形状和尺寸、流速分布、水深,沿流程都不变;(2) 总水头线、测压管水头线(在明渠水流中,就是水面线)和渠底线三者为相互平行的直线(图4-1a),因而它们的坡度相等,即J=J p=i(4-3)1.2.2明渠均匀流的形成条件对明渠恒定均匀流,图4-1(b),取1-1、2-2断面之间的水体作为研究对象,分析这块水体上的受力,并沿流向写动力平衡方程为P1-P2+G sinθ-T=0式中P1和P2为1-1和2-2过水断面的动水压力,G为Δs流段水体重量,T为边壁(包括岸壁和渠底)阻力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弗劳德(Froude)数的物理意义:
V2 V 2g Fr 2 h gh
表示过水断面单位重量液体平均动 能与平均势能之比的二倍开平方, Fr愈大,意味着水流的平均动能 所占的比例愈大。 表示水流的惯性力与重力两种作用的 导作用;缓流时,重力对水流起主导
[惯性力] [ Fr ] 对比关系。急流时,惯性对水流起主 [重力]
dEs 0 dh
V2 V2 h Q h 定义断面比能: Es h cos 2 gA2 2g 影响临界水深的因素: 2 g 2 dEs Q2 dA 流量、过水断面形状及尺 Q2 B 1 V 1 Fr 2 1 1 3 流态分析 当流量和断面的形状 gh gA3 寸 dh gA dh 尺寸一定时,断面比 定义临界水深:相应于断面比能最小值的水深,用hk表示 能仅仅是水深的函数。 3 2 A Q 临界水深方程式 k g Bk
当正常水深恰好与临界水深相等时的底坡,称为临界底坡ik
h0
hk
Q
i1>0
h0 h k
hk
Q
i2>i1
h0
Q
i ik h0 hk
i ik 缓坡 h0 hk
i ik 临界坡 h0 hk
陡坡
均匀流为缓流
均匀流为临界流
均匀流为急流
明渠水流流态的各种判别方法
判别 法 流态
按波速Vk
按佛汝德数 Fr
' Q2
gA2
yc 2 A2
根据平底棱柱体渠道水跃方程(Jump equation)
' Q2
gA 1 yc1 A1
' Q2
gA2
yc 2 A2
显然,等式两边都是水深的函数,称为水 跃函数(Jump function)。
' Q2
gA yc A J (h)
h
' 2 1 3 2 1
E j E1
E j q h 2 gh'2
' 2
8 1 8Fr12 1 2 Fr12
1 8Fr
2 1
3
3
水跃的消能效果与来流的佛汝德数Fr1有关 。 Fr1=9时消能率可达70%, Fr1>9时消能率更大,不过这时下游波浪较 大。 比较理想的范围是Fr1=4.5~9。
临界水深的计算
Q2
Ak3 g Bk
单宽流量
矩形断面明渠时: hk 3
Q2
gb
2
3
q2
g
h
试算法 梯形断面明渠时:
图解——试算法 hk
O
图解法:查附图
Q2
g
A3 B
临界底坡、缓坡与陡坡
影响临界水深的因素:流量、断面形状及尺寸 影响正常水深的因素:流量、断面形状及尺寸、糙率、底坡
水跃的消能功率为Δ
Nj=γ QΔ Ej
水跌简介
水流由缓流过渡到急流称为水跌。 由于急变流的水面变化规律与渐变 流不同,水流流线很弯曲,实际上 跌坎断面的水深hD约为0.7hK,而 水深等于hK的断面约在跌坎断面上 游(3~4)hK处 。
明渠恒定渐变流水面曲线分析
断面比能 <6°
Es h cos
用弗劳德数Fr表示的共轭水深计算公式
hk 3 q 2 v 2 ( ) Fr 2 h gh3 gh
h" h 2 h' h" 2
'
1 8Fr 1 8Fr
2 2
2 1
1
1
h" 1 Fr 2 / 3 2 ( 1 8Fr 1) ( 1 ) 1 h' 2 Fr2
明渠水流的流态
缓流:水流流速小,水势 平稳,遇到干扰,干扰的 影响既能向下游传播,又 能向上游传播
急流:水流流速大,水势 湍急,遇到干扰,干扰的 影响只能向下游传播,而 不能向上游传播
明渠流流态分类 ① 微波波速C V<C 缓流 (Subcritical flow) V=C 临界流 (Critical flow) V>C 急流 (Supercritical flow)
Fr2 8 Fr12 ( 1 8 Fr 1)
2 1 3
Fr1
8 Fr22 ( 1 8 Fr22 1) 3
以上两式可用于非矩形棱柱体渠道。
5、水跃尺寸
h"h' 1)跃高 2)跃长l j 一般说来,跃后断面并不是渐变流断面。旋 滚后2~3倍旋滚长 ly 的一段水流仍有一定的消 能能力,故定义水跃长度: lj=ly+l0=f(h′, h〞, Fr1)
作用。
断面比能与临界水深
h θ z z0 O O z0
h cos
缓流Fr<1,h>hk, 断面比能随水深的增 V<Vw dEs h 加而增加 0
dh
O′
O′ hk
K
45°
Esmin 急流Fr>1,h<hk , V>Vw 断面比能随水深的
o
Es
o
o
增加而减小
V2 V2 E z0 h cos 断面上单位重量液体所具有的总能量: z 2g 2g 2
棱柱体明渠中恒定非均匀渐变流水面曲线分析 明渠恒定非均匀渐变流水面曲线的计算
明渠的三种流态
缓流和急流的动力学分析
干扰微波在明渠静水中传
播的相对波速:
C Vw gh
h 式中: A B
为断面平均水深
设水流流速为V, 则微波传播的绝对速度为
V gh V gh
顺水流方向 逆水流方向
1)微波波速C (Microwave velocity) ① V=0,静水。微波以同心圆向四周传播; ② V<C,缓流。微波以C-V向上游、以C+V向下游 传播 ③ V=C,临界流。微波以C+V向下游传播; ④ V>C,急流。微波以C-V和C+V向下游传播。
dh iJ ds 1 Fr 2
2.影响水深沿程变化的因素
N K a1 b1 c1 i>0,i<ik (N) a3 c3 (N) N K K
底坡i 流态Fr,用hk直观反映 i>0时,比较h与h0
b0 c0 i=0 b′ K
i>0,i=ik a2 c2 i>0,i>ik
c′
b2 i<0
3.分区命名
N K
a1 b1 c1
i>0,i<ik
N
K
h h0 , J i
h hK Fr 1 1 Fr 2 0
水力学与桥涵水文
主讲:王亚玲
题 解
产生明渠均匀流的诸多条件中只要有一个条件不满
足,明渠上将产生非均匀流动。 明渠非均匀流的特点是明渠的底坡线、水面线、总 水头线彼此不平行, J J z i 。 水深沿程变化。
V12 2g
总水头线 水面线
V1
V22 2g
h1
h2
V2
题 解
渐变流 非均匀流 急变流 水跌
A C g B ,对于矩形断面 C gh 微波波速是判别明渠流态的重要参数。
弗劳德(Froude)数
临界流时, V
gh ,所以
V gh
1
V gh
定义弗劳德(Froude)数
Fr
当 Fr 1 当 Fr 1 当 Fr 1
时,水流为缓流, 时,水流为临界流, 时,水流为急流,
Fr 0 1 Fr 1
2ቤተ መጻሕፍቲ ባይዱ
dh i ds
以水平线为渐近线
a1 N N
i<ik
缓坡b区的水面线分析
dh iJ ds 1 Fr 2
该区实际水流的水深 hK h h0
N K
a1 b1 c1
i>0,i<ik
N
K
h h0 , J i
h hk , Fr 1
向上游
dh 0 ds
降水曲线
以N-N线为渐近线
h h0 , dh / ds 0
向下游 h hK Fr 1 1 Fr 2 0
dh 与K-K线有成垂直的趋势 ds
N K i<ik b1
N K
缓坡C区的水面线分析
dh iJ ds 1 Fr 2
该区实际水流的水深 h hK h0
跃长经验公式:(仅作估算用) ① 美国垦务局公式 lj=6.1h〞 Fr1=4.5~10 ② Elevatorski 公式
lj= 6.9 ( h〞- h′) ③ 成科大公式 lj=1.08h′(Fr1-1)0.93 Fr1=1.72~19.55 ④ 陈椿庭公式 lj=9.4h′(Fr1-1) ⑤ 切尔托乌索夫公式 lj=10.3h′(Fr1-1)0.81
缓坡a区的水面线分析
dh iJ ds 1 Fr 2
该区实际水流的水深 h h0 hK
N K
a1 b1 c1
i>0,i<ik
N
K
h h0 , J i
h hk , Fr 1
向上游
dh 0 ds
壅水曲线
以N-N线为渐近线
向下游 h
h h0 , dh / ds 0 J 0
状态过渡到急流状态时,
水面急剧下降的局部水 力现象,称为水跌现象。 当明渠水流从急流状 态过渡到缓流状态时,水 面突然跃起的特殊的局部 水力现象,称为水跃现象。
缓流
