零力杆件零力杆件
工程力学第6章内力和内力图

工程力学教程电子教案
例题 6-1
K
FFE
FFA
FFC
内力和内力图
15
FAy A
FAx
K
E FE FB
a a aa
CD B
FC
取节点K,受力分析如图。由平衡方程
Fx 0, FFE FFA cos 45 0
Fy 0, FFC FFA cos 45 0
解得 FFE 2 kN,FFC 2 kN
B
C
F1
C
D
D
E
F
G
A
B
H
(a)
(b)
工程力学教程电子教案
内力和内力图
26
4. 小 结 (1) 节点法
(a)一般先研究整体,求支座约束力;
(b) 逐个取各节点为研究对象; (c) 求杆件内力; (d) 所选节点的未知力数目不大于2,由此开始计算。
(2) 截面法
(a)一般先研究整体,求支座约束力; (b) 根据待求内力杆件,恰当选择截面;
上,对于平面桁架,各力的作用线都在桁架的平 面内。
根据上述假设,桁架的各个杆件都是二力杆。 我们能比较合理的地选用材料,充分发挥材料的作 用,在同样跨度和荷载情况下,桁架比梁更能节省 材料,减轻自重。
工程力学教程电子教案
内力和内力图
10
3. 平面简单桁架的构成
节点
杆件
在平面问题中,为保证桁架几何形状不变,可 以由基本三角形ABC为基础,这时是3个节点,以后 每增加一个节点,相应增加两根不在一条直线上的 杆件,依次类推,最后将整个结构简支,这样构成 的桁架称为平面简单桁架。
2C
∑MF (F)=0
F
零力杆的四种判断方法

零力杆的四种判断方法零力杆是解决力学问题时常用的一种分析工具,可以帮助我们确定物体的受力情况。
在使用零力杆进行力学分析时,有四种判断方法,即力的平衡条件、力矩平衡条件、力的分解和合成、以及力的转向判断。
本文将分别介绍这四种判断方法,并通过具体例子加以说明。
第一种判断方法是力的平衡条件。
根据牛顿第一定律,当物体受到的合外力为零时,物体将保持静止或匀速直线运动。
因此,当我们在分析一个物体受力情况时,如果物体处于静止状态或匀速直线运动状态,且合外力为零,则可以判断该物体力的平衡。
例如,一个静止的书本放在桌子上,由于合外力为零,我们可以判断书本受到的力是平衡的。
第二种判断方法是力矩平衡条件。
力矩是力对物体产生旋转效果的力矩。
根据力矩平衡条件,当物体处于平衡状态时,物体所受外力的力矩和为零。
换句话说,物体在平衡状态下,物体受到的合外力在任意一点的力矩之和为零。
例如,一个悬挂在天花板上的吊灯,由于吊灯保持静止,我们可以判断吊灯所受外力的力矩和为零。
第三种判断方法是力的分解和合成。
力的分解是将一个力分解为多个分力,力的合成是将多个分力合成为一个力。
在使用零力杆进行力学分析时,我们可以将一个复杂的力分解为若干个简单的力,然后分别分析这些力对物体的作用效果。
例如,一个物体受到两个斜向上的力,我们可以将这两个力分解为水平方向和竖直方向的分力,然后分别分析这两个分力对物体的作用效果。
第四种判断方法是力的转向判断。
力的转向指的是力的作用方向。
在使用零力杆进行力学分析时,我们需要判断力的作用方向,以确定物体受力情况。
例如,一个物体受到多个力的作用,我们可以通过观察力的作用方向,判断这些力是使物体向左还是向右运动,或是使物体产生转动。
根据力的转向判断,我们可以推断物体所受力的方向和大小。
在实际应用中,我们常常需要结合这四种判断方法来分析物体的受力情况。
通过力的平衡条件,我们可以判断物体是否受到平衡力;通过力矩平衡条件,我们可以判断物体是否处于平衡状态;通过力的分解和合成,我们可以分析物体所受力的作用效果;通过力的转向判断,我们可以确定物体所受力的方向和大小。
《结构力学》课程知识 复习 学习材料 试题与参考答案

《结构力学》课程知识复习学习材料试题与参考答案一、单选题1.力矩分配法是基于( A )原理推导出来的。
A.位移法B.力法 C.叠加法D.图乘法2.位移法中的形常数是( B )计算出来的。
A.用力矩分配法 B.力法C.叠加法D.图乘法3. ( A )不是力法的三要素。
A.基础连接方式 B. 力法方程C.基本结构 D. 基本未知量4.( B )可以作为结构A.瞬变体系B.几何不变体系C.有多余约束的可变体系D.自由度小于零的体系5.不属于画梁结构Q图的控制载面是( A )A.力偶作用面B.集中力作用面C.均布荷载的始截面D.均布荷载的末截面6.( A )不称为性线变形体系的互等定理A.功能互等定理B.功的互等定理C.位移互等定理D.反力互等定理7.超静定次数不可以用( D )方法求取A.求多余未知力个数 B.求结构自由度数C. 撤除多余约束D.分析外载形式8.(C )不是位移法的三要素A.基本未知量 B.基本体系 C.基本参数 D.基本方程9.载常数是利用(D )求出来的A.位移法 B.叠加法 C.图乘法 D.力法10.力矩分配法的主要步骤顺序是(C )A.分配与传递叠加求杆端弯矩求分配系数求固端弯矩B. 分配与传递叠加求杆端弯矩求固端弯矩求分配系数C. 求固端弯矩求固端弯矩分配与传递叠加求杆端弯矩D. 求固端弯矩求固端弯矩叠加求杆端弯矩分配与传递11.结构力学中主要研究的对象是( D )。
A.单个杆件B. 板壳C. 实体D. 杆系结构12.以下( D )不可以看成一个刚片。
A单个杆件 B.某一个几何不变的部分 C.地基 D. 某一几何可变的部分13.静定结构因支座移动,( B )A、会产生内力,但无位移B、会产生位移,但无内力C、内力和位移均不会产生D、内力和位移均会产生14. 结构的计算校核不包含有( B )。
A.计算过程的校核 B. 支座反力的校核C.平衡条件的校核 D. 位移条件的校核15. 零力杆是指( B )的杆件。
零力杆名词解释

零力杆名词解释
零力杆是指主内力为零。
架中内力为零的杆件称为零杆。
零杆的判断对桁架内力的计算具有积极的意义。
一节点上有三根杆件,如果节点上无外力的作用,其中两根共线,则另一杆为零杆;一节点上只有两根不共线杆件,如果节点上无外力的作用,则两杆件均为零杆。
零杆一般指在桁架中内力为零的杆,且是伴随着荷载而存在的。
也就是说,一个结构中不存在绝对的零杆。
举个例子,桁架中一个T形节点,当不直接承受荷载时,为保持节点平衡,竖直杆的内力必然为0,故为零杆;但是,当有竖向荷载作用于该节点时,竖直杆必然产生一个轴向力与之平衡,故不为零杆。
由此可看出,一种荷载下的零杆,在另外的荷载作用下就有可能承载。
而且,桁架中的零杆虽然不受力,但却是保持结构完整所必须的。
桁架中常常有些杆件不受力,受力为0的杆件称为“0杆”。
虽然,0杆是桁架在某种载荷情况下内力为零的杆件,但它对保证桁架几何形状来说是不可缺的,在实际工程中不能去掉,但在理论受力分析时可以拿掉。
单辉祖工力-6静力学专题1

yC
yili li
yi li l
xC
zili li
zi li l
z
C Pi
P
zi
zC
O
yi
xi
xC y
x
yC
2. 确定重心的常用方法
• 当物体具有对称轴、对称面或对称中心时,它 的重心一定在对称轴、对称面或对称中心上。
• 对于几何形状较复杂的均质物体,往往采用分 割法和负面积法
S 3 = 9. 81kN
YA +S2 ·sin 60°-P1 = 0 S 2 = 1. 15kN
● 零力杆的判断 零力杆:杆件内力为零的杆件
节点只连接两根不共线的杆件
0 0
节点无外力 则此两根杆为零力杆
节点只连接两根不共线的杆件
0
外力作用线沿某一根杆
则另一根杆为零力杆
节点连接三根杆件
0
若其中两根共线且节点无外力
称重法
• 然后将其一端支承于 A 点,另一端放在磅称 B上, 测得两点的水平距离 l 及 B 处的约束反力 FB , 假定为 G , 由
∑MA( F ) = 0 , P xC - FB l = 0
xc
FBl P
G P
l
O x
zi
yi yC
P
zC
xi
xC y
为了求坐标 zC, 将物体连同直角坐 标系 Oxyz 一起绕 x 轴逆时针旋转90°
重力的方向并无改变 对 x 轴取矩,有
P zC = (P1z1 + P2z2 + …+ Pnzn) = ∑Pi zi
重心的坐标公式
z
y
Mi
△Vi Mi
PCi P
工程力学课后习题答案静力学基本概念及物体的受力分析答案
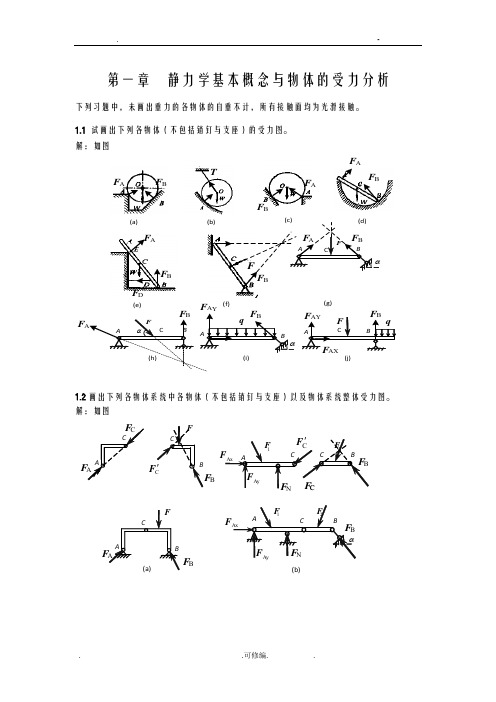
第一章 静力学基本概念与物体的受力分析下列习题中,未画出重力的各物体的自重不计,所有接触面均为光滑接触。
1.1 试画出下列各物体(不包括销钉与支座)的受力图。
解:如图(g)(j)P (a)(e)(f)WWF F A BF DF BF AF ATF BA1.2画出下列各物体系统中各物体(不包括销钉与支座)以及物体系统整体受力图。
解:如图F BB(b)(c)C(d)CF D(e)AFD(f)FD(g)(h)EOBO E F O(i)(j) BYFB XBFXE(k)1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成,如题1.3图所示。
在定滑轮上吊有重为W的物体H。
试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。
解:如图'D1.4题1.4图示齿轮传动系统,O1为主动轮,旋转方向如图所示。
试分别画出两齿轮的受力图。
解:1F2o xF2o yF o yFFF'1.5 结构如题1.5图所示,试画出各个部分的受力图。
解:第二章 汇交力系2.1 在刚体的A 点作用有四个平面汇交力。
其中F 1=2kN ,F 2=3kN ,F 3=lkN , F 4=2.5kN ,方向如题2.1图所示。
用解析法求该力系的合成结果。
解 00001423cos30cos45cos60cos45 1.29Rx F X F F F F KN ==+--=∑00001423sin30cos45sin60cos45 2.54Ry F Y F F F F KN ==-+-=∑2.85R F KN ==0(,)tan63.07Ry R RxF F X arc F ∠==2.2 题2.2图所示固定环受三条绳的作用,已知F 1=1kN ,F 2=2kN ,F 3=l.5kN 。
求该力系的合成结果。
解:2.2图示可简化为如右图所示023cos60 2.75Rx F X F F KN ==+=∑ 013sin600.3Ry F Y F F KN ==-=-∑2.77R F KN ==0(,)tan6.2Ry R RxF F X arc F ∠==-2.3 力系如题2.3图所示。
理论力学零杆判断方法

理论力学零杆判断方法理论力学中,零杆是指在静力学中不会产生任何反力的杆,也就是杆上所有的反力和力矩都为零。
在力学的问题求解中,可以将零杆作为一个条件来简化问题,从而更容易求解。
判断一个杆是否为零杆的方法主要有以下几种:1.杆两端受到固定支撑:当一个杆的两个端点都受到固定支撑时,可以判断该杆为零杆。
固定支撑会给杆施加相等大小、方向相反的反力,从而使杆处于平衡状态。
此时,杆上任意一点的反力和力矩都为零。
2.杆一端受到固定支撑,另一端支撑在滑动的平面上:当一个杆的一端受到固定支撑,另一端支撑在滑动的平面上时,可以判断该杆为零杆。
这种情况下,固定支撑会给杆施加一个反力,而滑动平面的支撑力可以看作沿着杆的方向的一个力矩,从而使杆处于平衡状态。
此时,杆上任意一点的反力和力矩都为零。
3.杆一端受到固定支撑,另一端作为铰链:当一个杆的一端受到固定支撑,另一端作为铰链时,可以判断该杆为零杆。
这种情况下,固定支撑会给杆施加一个反力,而铰链作用力只能沿着杆的方向,从而使杆处于平衡状态。
此时,杆上任意一点的反力和力矩都为零。
需要注意的是,零杆的判断方法是基于杆处于平衡状态的原理。
也就是说,只有在没有外界力矩作用的情况下,才能判断杆是零杆。
如果杆存在外力或外力矩作用,那么即使满足上述条件,杆也不一定是零杆。
对于一个刚体来说,当它平衡时,不受外力的作用,整个刚体的合外力和合外力矩都为零。
因此,对于一个零杆,在整个刚体的平衡条件中,也应满足其合外力和合外力矩都为零。
这是判断零杆是否正确的依据。
在实际问题中,判断零杆的方法是非常有用的。
通过将杆作为零杆来简化问题,可以大大缩减计算量,提高解题效率。
然而,在使用零杆的方法时,也要注意杆是否满足条件,以避免出现错误的结果。
总之,在理论力学中,判断零杆的方法主要有杆两端受到固定支撑、杆一端受到固定支撑另一端支撑在滑动平面上、杆一端受到固定支撑另一端作为铰链等。
需要注意的是,上述判断方法是建立在杆处于平衡状态的基础上的,也就是说,只有在没有外界力矩作用的情况下,才能判断杆是零杆。
杆机构构件的受力分析和强度

横截面的正应力σ计算公式为:
mn
σ= FN MPa F
F
A
mn
FN 表示横截面轴力(N) F A 表示横截面面积(mm2)
FN
46
轴向拉压杆的强度计算:
1.强度条件
为了使构件不发生拉(压)破坏,保证构件安全工作的 条件是:最大工作应力不超过材料的许用应力。
max
FN max A
≤[
]
应用该条件式可以解决以下三类问题:
3.平面汇交力系的平衡方程:
33
课内练习:计算力的大小:
已知: OA=R,AB= l, F , 不计物体自重与摩擦,
系统在图示位置平衡;
求:
力偶矩M 的大小,轴承O处的约 束力,连杆AB受力,冲头给导轨
的侧压力.
解: 取冲头B,画受力图.
Fiy 0 F FBl
FB cos l 2 R2
38
知识点总结 轴向拉伸(压缩)
受力特点:
外力(或外力的合力)沿 F
F
杆件的轴线作用,且作
用线与轴线重合。
变形特点:
F
F
杆沿轴线方向伸长(或 缩短),沿横向缩短 (或伸长)。
39
拉(压)杆的变形
1)绝对变形: 轴向变形和横向变形统称为绝对变形。 规定:L—等直杆的原长 d—横向尺寸 L1—拉(压)后纵向长度 d1—拉(压)后横向尺寸
应力单位是帕斯卡,简称帕,记作Pa,即l平方米 的面积上作用1牛顿的力为1帕,1N/m2=1Pa。
1kPa=103Pa,1MPa=106Pa 1GPa=109Pa
45
2.拉(压)杆横截面上的应力
根据杆件变形的平面假设和材料均匀连续性假设可推断:轴
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
•四根桿件連接在一節點上並形成對稱之K字型時,若無任何 外力作用於該節點,則兩斜桿之內力必大小相等,當其中一桿 為拉力時,則另一桿必為壓力。
•若Nx、 Ny分表軸向力N在x及y方向上之分量;而Lx、 Ly分表桿件長度在x及y方向上的投影長度,則桿件的軸向 力與桿件長度之間具有以下的比例關係: N / L = Nx / Lx = Ny /Ly
ห้องสมุดไป่ตู้
桁架分析的基本假設
作用在桁架上的外力及桿件之應力在
同一平面,且均作用在節點上。
每一根桿件皆為二力桿件。 節點均視為無摩擦力的插銷接點。 桁架中桿件均為剛體,構件的重量可
忽略。
桁架分析的基本假設
真實接點可能為鉚接、焊接或以螺栓栓接
桁架分析的基本假設
真實接點可能為鉚接、焊接或以螺栓栓接
桁架分析的基本假設
桁架構件為二力構件,只在接點上受力。
節點法(method of joint)
一個結構通常由多個零件組合而成。 如果構件整體處於平衡狀態,則個別零組件或 零組件群也處於平衡狀態。 如果桁架整體處於平衡狀態,則個別節點也處 於平衡狀態。
桁架構件受力:張力或壓力
構件受張力,力量遠離節點
T T T
斷面法分析步驟
將桁架自某部分(此部分很可能包含欲求內力之桿件)切開,然後 取出自由體,並應用該自由體之平衡條件來計算桿件之內力。由於平 面力系的平衡方程式有三個,因此對斷面法而言,雖然每次所切斷的 桿件個數不受限制,但在所切斷的桿件中,仍須限制最多僅三根桿件 的內力為未知(但特殊桁架,如K桁架,則例外),且此三根桿件之 內力作用線不得相互平行或交會於一點。另外,在每次的切開過程中, 同一桿件不得切過兩次,否則此桿件無法由平衡方程式解得。 斷面法多用於求解某些特定桿件之內力。在切開的斷面上,除欲求 的桿件外,其餘內力為未知的桿件若相互平行,則可利用剪力法來解 出此欲求桿件的內力 另外,在切開的斷面上,除欲求的桿件外,其餘內力為未知的桿件 若其作用線交會於一點,則可利用彎矩法來解出此欲求桿件的內力。
桁架分析
桁架是承重用的結構,為了減輕重量、節省材料,採
用細長桿件以特定方式組合而成。
高壓電塔、衛星接收天線、建築工地的天車、某類橋
樑與簡易型鐵皮屋的屋頂等,都常使用桁架結構。
一般由頭、尾相接的細長形構件所組成。 構件重遠小於所支承的載重。 桁架構件主要用來承受軸向力,而非垂直於軸線的橫 向力或彎曲力矩,為確保此點,外力必須作用在節點上。
(2) 二根桿件連接於一節點而不共線時,若其中一根桿 件與外力共線,則此桿件之內力大小必等於此外力之 大小,且二者方向相反,而另一根桿件則為零桿件。 (3) 三根桿件連接於一節點時,若其中二根桿件共線, 且無任何外力作用於該節點,則共線的二桿件,其內 力必大小相等方向相反,而第三根桿件必為零桿件。 (4) 四根桿件連接在一節點上,當無任何外力作用於該 節點時,共線桿件之內力必大小相等而方向相反。
T
構件受壓力,力量靠近節點
C C C C
節點法分析步驟
利用整體的平衡來求支撐點的反作用力 。 找出零力桿件。
選擇只有兩個(或一個)未知數的節點分析,以 該節點的平衡求相關構件的作用力。 利用剩餘的節點,核驗答案。
零力桿件
零力桿件
(1) 二根桿件連接於一節點而不共線時,若無任何外力 作用於該節點,則此二根桿件均為零桿件。
+
乘x倍
桁架分析
桁架分析:對稱與反對稱
(1) 對於對稱桁架而言,可僅分析半邊結構,因為所有位 置對稱之桿件,其內力必等值同號。由此特性亦可研判出 更多的零桿件。 (2) 對於反對稱桁架而言,亦可僅分析半邊結構,因為所 有位置對稱之桿件,其內力必等值異號。由此特性可知, 與對稱軸重合或正交的桿件必為零桿件。 (3) 對於幾何對稱的桁架而言,若承受非對稱亦非反對稱 之荷載作用時,可利用疊加原理將此桁架化成對稱桁架與 反對稱桁架來分析。
