21 2008～2019年江苏高考数学分类汇编(解析版)---概率加试

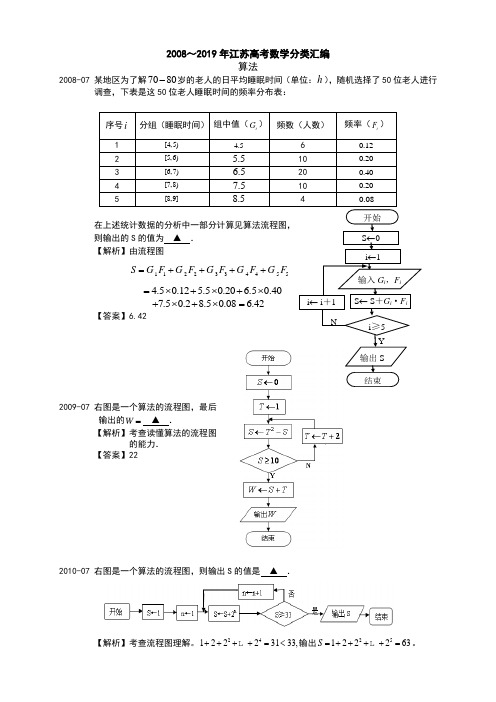
2008～2019年江苏高考数学分类汇编
概率
2009-23 对于正整数n ≥2，用n T 表示关于x 的一元二次方程2
20x ax b ++=有实数根的有序数组
(,)a b 的组数，
其中{},1,2,,a b n ∈L （a 和b 可以相等）；对于随机选取的{},1,2,,a b n ∈L （a 和b 可以相等），记n P 为关于x 的一元二次方程2
20x ax b ++=有实数根的概率。

（1）求2n T 和2n P ；
（2）求证：对任意正整数n ≥2，有1n P n
>. 【解析】本小题主要考查概率的基本知识和记数原理，考查探究能力。

2010-22 某工厂生产甲、乙两种产品，甲产品的一等品率为80%，二等品率为20%；乙产品的一等品
率为90%，二等品率为10%．生产1件甲产品，若是一等品则获得利润4万元，若是二等品则亏损1万元；生产1件乙产品，若是一等品则获得利润6万元，若是二等品则亏损2万元．设生产各种产品相互独立．
(1)记X （单位：万元）为生产1件甲产品和1件乙产品可获得的总利润，求X 的分布列； (2)求生产4件甲产品所获得的利润不少于10万元的概率． 【解析】本题主要考查概率的有关知识，考查运算求解能力．
解：（1）由题设知，X 的可能取值为10，5，2，-3，且
P （X=10）=0.8×0.9=0.72，P （X=5）=0.2×0.9=0.18， P （X=2）=0.8×0.1=0.08， P （X=-3）=0.2×0.1=0.02． 由此得X 的分布列为：
X 10 5 2 -3 P
0.72
0.18
0.08
0.02
（2）设生产的4件甲产品中一等品有件，则二等品有4n -件．
由题设知4(4)10n n --≥，解得14
5
n ≥， 又n N ∈，得3n =，或4n =．
所求概率为3
344
0.80.20.80.8192P C =⨯⨯+= 答：生产4件甲产品所获得的利润不少于10万元的概率为0.8192．
2012-22 设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，0ξ=；当两
条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，1ξ=．
（1）求概率(0)P ξ=； （2）求ξ的分布列，并求其数学期望()E ξ．
【点评】本题主要考查概率统计知识：离散型随机变量的分布列、数学期望的求解、随机
事件的基本运算．本题属于基础题目，难度中等偏上.考查离散型随机变量的分布列和期望的求解，在列分布列时，要注意ξ的取值情况，不要遗漏ξ的取值情况．
2014-22 盒中共有9个球，其中有4个红球，3个黄球和2个绿球，这些球除颜色外完全相同．
（1）从盒中一次随机抽出2个球，求取出的2个球的颜色相同的概率；
（2）从盒中一次随机抽出4个球，其中红球、黄球、绿球的个数分别为123,,x x x ，随
机变量X 表示123,,x x x 的最大数，求X 的概率分布和数学期望()E X ．
2017-23 已知一个口袋中有m 个白球，n 个黑球(,*,2m n n ∈N ≥)，这些球除颜色外全部相同．现将
口袋中的球随机地逐个取出，并放入如图所示的编号为1,2,3,,m n +L 的抽屉内，其中第k
(1,2,3,,)k m n =+L （1）试求编号为2的抽屉内放的是黑球的概率；
（2）随机变量X 表示最后一个取出的黑球所在抽屉编号的倒数，()E X 是X 的数学期望，
证明：()()(1)
n
E X m n n <+-．
【解析】（1）编号为2的抽屉内放的是黑球的概率p 为：11C C n m
n n m n n p m n
-+-+==+． （2）随机变量X 的概率分布为
随机变量X 的期望为1
1
C 111(1)!
()C C (1)!()!
n m n
m n
k n n
k n k n m n
m n k E X k k n k n -++-==++-=⋅=⋅--∑∑． 所以1(2)!1
(2)!
()C (1)!()!(1)C (2)!()!m n
m n n n k n k n
m n
m n
k k E X n k n n n k n ++==++--<
=-----∑∑
222
121(1C C C )(1)C n n n n n m n n
m n
n ----+-+=
++++-L 1222
1121(C C C C )(1)C n n n n n n n m n n
m n
n ------+-+=
++++-L 122
21(C C C )(1)C n n n n n m n n
m n
n ---+-+=
+++-L 12
221(C C )(1)C n n m n m n n
m n
n --+-+-+==
+-L 11
C (1)C ()(1)n m n n m n
n n m n n -+-+==-+-， 即()()(1)
n
E X m n n <
+-．
【考点】古典概型概率、排列组合、随机变量及其分布、数学期望 【名师点睛】求解离散型随机变量的数学期望的一般步骤为：
（1）“判断取值”，即判断随机变量的所有可能取值，以及取每个值所表示
的意义；
（2）“探求概率”，即利用排列组合、枚举法、概率公式(常见的有古典概型
公式、几何概型公式、互斥事件的概率和公式、独立事件的概率积公式，以及对立事件的概率公式等)，求出随机变量取每个值时的概率； （3）“写分布列”，即按规范形式写出分布列，并注意用分布列的性质检验
所求的分布列或某事件的概率是否正确；
（4）“求期望值”，一般利用离散型随机变量的数学期望的定义求期望的值，
对于有些实际问题中的随机变量，如果能够断定它服从某常见的典型分
布(如二项分布(,)X B n p :)，则此随机变量的期望可直接利用这种典型分布的期望公式(()E X np =)求得．因此，应熟记常见的典型分布的期望公式，可加快解题速度．
2019-23 在平面直角坐标系xOy 中，设点集{(0,0),(1,0),(2,0),,(,0)}n A n =⋯，
{(0,1),(,1)},{(0,2),(1,2),(2,2),,(,2)},.n n B n C n n N *==∈L 令n n n n M A B C =U U .从
集合M n 中任取两个不同的点，用随机变量X 表示它们之间的距离. （1）当n =1时，求X 的概率分布； （2）对给定的正整数n （n ≥3），求概率P （X ≤n ）（用n 表示）.
【分析】(1)由题意首先确定X 可能的取值，然后利用古典概型计算公式求得相应的概率值
即可确定分布列；
(2)将原问题转化为对立事件的问题求解()P X n >的值，据此分类讨论①.b d =，②.0,1b d ==，③.0,2b d ==，④.1,2b d ==四种情况确定X 满足X n >的所有可能的取值，然后求解相应的概率值即可确定()P X n ≤的值.
【详解】（1）当1n =时，X
的所有可能取值是12
X
的概率分布为22667744
(1),(C 15C 15
P X P X ==
====，
22662222
(2),(C 15C 15
P X P X ==
====． （2）设()A a b ，
和()B c d ，是从n M 中取出的两个点． 因为()1()P X n P X n ≤=->，所以仅需考虑X n >的情况． ①若b d =，则AB n ≤，不存在X n >的取法；
②若01b d ==，
，则AB =≤X n >
当且仅当
AB 0 a c n ==，
或 0a n c ==，，有2种取法； ③若02b d ==，
，则AB =≤，因为当3n ≥时，
n ≤，所以X n >
当且仅当AB =0 a c n ==，或 0a n c ==，，有2种取法； ④若12b d ==，
，则AB =≤X n >
当且仅当
AB 0 a c n ==，
或 0a n c ==，，有2种取法． 综上，当X n >时，X
，且
22
24
24
42
(,(C C n n P X P X ++==
==
．
因此，224
6()1((1C n P X n P X P X +≤=-=-==-
．
【点睛】本题主要考查计数原理、古典概型、随机变量及其概率分布等基础知识，考查逻
辑思维能力和推理论证能力．。