mathematica软件基本操作
mathematica使用指南

mathematica使用指南Mathematica是一款功能强大的数学软件,具备广泛的应用领域,包括数学、统计学、物理学、工程学等等。
本文将为您提供一份Mathematica的使用指南,帮助您快速入门并提高使用效率。
1. Mathematica简介Mathematica是由Wolfram Research公司开发的一款通用计算软件,它具备数值计算、符号计算、图形绘制等多种功能。
Mathematica基于Wolfram Language语言,用户可以直接在其中编写代码进行计算和分析。
2. 安装与启动首先您需要从Wolfram Research公司官方网站下载Mathematica安装文件,并按照安装向导完成安装过程。
安装完成后,您可以在计算机上找到Mathematica的启动图标,点击即可启动该软件。
3. Mathematica界面介绍Mathematica的主界面由菜单栏、工具栏、输入区域和输出区域组成。
菜单栏提供了各种功能选项,工具栏包含常用工具按钮,输入区域用于输入代码,而输出区域用于显示计算结果。
4. 基本计算在输入区域中,您可以直接输入数学表达式进行计算。
例如,输入"2 + 3",然后按下Enter键即可得到计算结果"5"。
Mathematica支持基本的算术运算、三角函数、指数函数等数学操作。
5. 变量与函数您可以使用Mathematica定义变量并进行计算。
例如,输入"x = 2",然后再输入"y = x^2",按下Enter键后,变量y会被赋值为2的平方,即4。
定义的变量可以在后续计算中使用。
6. 图形绘制Mathematica提供了丰富的图形绘制功能。
您可以使用Plot函数绘制函数曲线,使用ListPlot函数绘制离散数据点,还可以绘制3D图形等等。
通过调整参数和选项,您可以自定义图形的样式和外观。
mathematica用法

Mathematica是一款非常强大的数学软件,它支持符号计算、数值计算和图形可视化等功能。
以下是一些Mathematica的基本用法:
表达式输入:在Mathematica中,可以通过输入表达式来得到结果。
例如,输入 2 + 3,然后按下回车键,就会得到结果5。
定义变量:使用Let 命令可以定义变量,例如Let[x = 5]。
使用函数:Mathematica提供了大量的内置函数,可以直接使用。
例如,Sin[x] 可以计算sin(x)的值。
使用Pattern替换:Mathematica支持模式替换,可以通过/. 操作进行。
例如,设 a 是一个变量,有a/.a->1 就可以将所有出现的a 替换为1。
使用纯函数:纯函数是一个没有副作用的函数,它对参数进行操作并返回结果,不会改变参数的值。
在Mathematica中,可以使用Function 命令定义纯函数。
例如,f = Function[{x}, x^2] 可以定义一个对输入的x进行平方操作的纯函数。
使用Plot和ParametricPlot:Plot 和ParametricPlot 是Mathematica中用于绘图的命令,可以用来绘制函数的图像或者参数方程的图像。
例如,Plot[Sin[x], {x, 0, 2*Pi}] 就会绘制sin(x)的图像。
mathematic使用指南
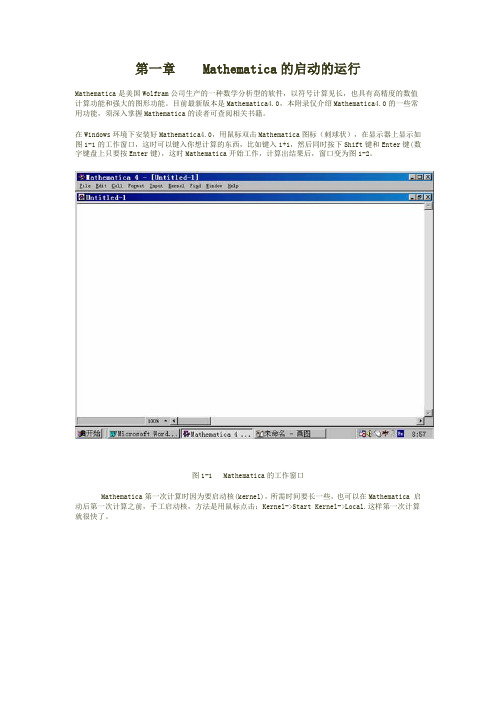
第一章Mathematica的启动的运行Mathematica是美国Wolfram公司生产的一种数学分析型的软件,以符号计算见长,也具有高精度的数值计算功能和强大的图形功能。
目前最新版本是Mathematica4.0,本附录仅介绍Mathematica4.0的一些常用功能,须深入掌握Mathematica的读者可查阅相关书籍。
在Windows环境下安装好Mathematica4.0,用鼠标双击Mathematica图标(刺球状),在显示器上显示如图1-1的工作窗口,这时可以键入你想计算的东西,比如键入1+1,然后同时按下Shift键和Enter键(数字键盘上只要按Enter键),这时Mathematica开始工作,计算出结果后,窗口变为图1-2。
图1-1 Mathematica的工作窗口Mathematica第一次计算时因为要启动核(kernel),所需时间要长一些,也可以在Mathematica 启动后第一次计算之前,手工启动核,方法是用鼠标点击:Kernel->Start Kernel->Local.这样第一次计算就很快了。
图1-2 完成运算后的Mathematica的窗口图1-2中的“In[1]:=”表示第一个输入;“Out[1]=”表示第一个输出结果。
接下来可键入第二个输入,按这样的方式可利用Mathematica进行“会话式”计算。
要注意的是:“In[1]:= ”和“Out[1]=”是系统自动添加的,不需用户键入。
Mathematica还提供“批处理”运行方式,即可以将Mathematica作为一种算法语言,编写程序,让计算机执行,这在第七章将会作简要介绍。
第二章 Mathematica的基本运算功能2.1 算术运算Mathematica最基本的功能是进行算术运算,包括加(+),减(-),乘(*),除(/),乘方(^),阶乘(!)等。
注意:1 在Mathematica中,也可用空格代表乘号;数字和字母相乘,乘号可以省去,例如:3*2可写成3 2,2*x可写成2x,但字母和字母相乘,乘号不能省去。
mathematica简明使用教程

mathematica简明使用教程Mathematica是一种强大的数学软件,广泛应用于科学研究、工程计算和数据分析等领域。
本文将简要介绍Mathematica的使用方法,帮助读者快速上手。
一、安装和启动Mathematica我们需要下载并安装Mathematica软件。
在安装完成后,可以通过桌面图标或开始菜单中的快捷方式来启动Mathematica。
二、界面介绍Mathematica的界面分为菜单栏、工具栏、输入区域和输出区域四部分。
菜单栏提供了各种功能选项,工具栏包含了常用的工具按钮,输入区域用于输入代码或表达式,而输出区域则显示执行结果。
三、基本操作1. 输入和输出在输入区域输入代码或表达式后,按下Shift+Enter键即可执行,并在输出区域显示结果。
Mathematica会自动对输入进行求解或计算,并返回相应的输出结果。
2. 变量定义可以使用等号“=”来定义变量。
例如,输入“a = 3”,然后执行,就会将3赋值给变量a。
定义的变量可以在后续的计算中使用。
3. 函数调用Mathematica内置了许多常用的数学函数,可以直接调用使用。
例如,输入“Sin[π/2]”,然后执行,就会返回正弦函数在π/2处的值。
4. 注释和注解在代码中添加注释可以提高代码的可读性。
在Mathematica中,可以使用“(*注释内容*)”的格式来添加注释。
四、数学运算Mathematica支持各种数学运算,包括基本的加减乘除,以及更复杂的求导、积分、矩阵运算等。
下面简要介绍几个常用的数学运算:1. 求导可以使用D函数来求导。
例如,输入“D[Sin[x], x]”,然后执行,就会返回正弦函数的导数。
2. 积分可以使用Integrate函数来进行积分运算。
例如,输入“Integrate[x^2, x]”,然后执行,就会返回x的平方的不定积分。
3. 矩阵运算Mathematica提供了丰富的矩阵运算函数,可以进行矩阵的加减乘除、转置、求逆等操作。
Mathematica数学软件系统使用入门

Ch1. a Mathematic 概述1.1a Mathematic 的工作环境a Mathematic 的基本系统是用C 语言编写的,因此能够方便的移植到各种计算机系统上。
打开a Mathematic ,可以看到它是一个窗口软件,包括一个执行各种功能的工作条(屏幕顶端)和一个工作区窗口。
激活工作区窗口,输入希望的计算式(如:“3+8-4”),同时按下“Shift ”和“Enter ”键便可执行计算。
使用a Mathematic 的几个注意点:1. 每次使用a Mathematic ,第一次计算时间较长,这是系统在进行初始化工作,从第二次计算开始就很快了。
2. 输入计算公式和普通文本输入一样,系统将把每次输入记录在案,并自动给每个输入记录用“In[n]”编号,计算结果用“Out[n]”编号。
“%”表示上一次计算结果,“%n ”表示“Out[n]”的内容,这样可以减少重复输入。
3. 输完计算式后,同时按下“Shift ”和“Enter ”键,a Mathematic 将完成计算。
4. 必须严格按照系统所规定的格式输入算式,否则将无法完成计算任务,通常给出一段文字,告诉你出错的(可能)原因。
1.2a Mathematic 的基本功能1.基本计算功能,如: In[1]:= 3+8-4 Out[1]= 7In[2]:= 12.5^3 (*即12.53*) Out[2]= 1953.132.强大的符号计算功能a Mathematic 的最大特点是能进行符号计算。
如: (1) 解方程x a x 2=+ In[3]:= Out[3]=I注意,方程的解用“ ”代替了“=”。
(2) 求不定积分dx x e x ⎰sin In[4]:= Out[4]= 注意,不定积分的任意常数C 均省略。
3.绘图功能a Mathematic 有强大的图形功能,可作各种二维、三维图形。
如: (1) 作函数x x y 6.1sin sin +=的二维图形--Graphics (2) 作函数)sin(xy z =的三维图形In[6]:=--phics SurfaceGra1.3从a Mathematic 中获得帮助信息1. 点击工作条中的Help 可获得帮助信息。
mathmatic 基本用法

mathmatic 基本用法Mathematica是一种强大的数学软件,它具有广泛的数学计算和可视化功能。
基本用法包括使用Mathematica进行数学运算、求解方程、绘制图表等。
1.数学运算:Mathematica可以进行基本的数学运算,如加减乘除、幂运算、三角函数、对数函数等。
例如,可以输入"2+3"得到结果"5",输入"Sin[π/2]"得到结果"1"。
2.方程求解:Mathematica可以求解各种类型的方程。
例如,可以输入"Solve[x^2 - 3x + 2 == 0, x]"来求解这个二次方程,得到结果"x == 1 || x == 2"。
3.符号计算:Mathematica可以进行符号计算,包括展开、化简、因式分解等。
例如,可以输入"Simplify[(x^2 + x - 6)/(x + 3)]"来化简这个表达式,得到结果"x - 2"。
4.绘图功能:Mathematica可以生成各种类型的图表,包括二维曲线图、三维曲面图、柱状图、散点图等。
例如,可以输入"Plot[Sin[x], {x, 0, 2π}]"来绘制正弦函数的曲线图。
除了基本用法外,Mathematica还有许多其他功能,如矩阵计算、微积分、概率统计、符号推导、动态演示等。
它还提供了大量的内置函数和算法,可以用于求解复杂的数学问题。
使用Mathematica还可以进行科学计算、工程计算、数据分析等各种应用领域。
总之,Mathematica是一款功能强大的数学软件,可以帮助用户进行各种数学计算和可视化操作。
mathematica简单算例

mathematica简单算例Mathematica是一款强大的数学软件,可以用于解决各种数学问题和进行数值计算。
在本文中,我们将介绍一些简单的算例,展示Mathematica的基本用法和功能。
一、求解方程假设我们需要求解一个简单的一元二次方程,比如x^2-5x+6=0。
我们可以使用Mathematica的Solve函数来解这个方程。
代码如下:```mathematicaSolve[x^2 - 5x + 6 == 0, x]```运行以上代码后,Mathematica会给出方程的解,即x=2和x=3。
通过这个例子,我们可以看到Mathematica可以方便地解决各种复杂的方程。
二、绘制函数图像Mathematica还可以用来绘制函数的图像。
假设我们想要绘制函数y=x^2的图像,我们可以使用Mathematica的Plot函数。
代码如下:```mathematicaPlot[x^2, {x, -10, 10}]```运行以上代码后,Mathematica会生成一个关于y=x^2的图像,x 的取值范围为-10到10。
通过这个例子,我们可以看到Mathematica可以帮助我们直观地理解数学函数。
三、计算数列Mathematica还可以用来计算数列的和。
假设我们需要计算斐波那契数列的前20项的和。
我们可以使用Mathematica的Sum函数来计算。
代码如下:```mathematicaSum[Fibonacci[n], {n, 1, 20}]```运行以上代码后,Mathematica会计算出斐波那契数列的前20项的和。
通过这个例子,我们可以看到Mathematica可以帮助我们快速计算各种数学问题。
四、符号计算Mathematica还可以进行符号计算。
假设我们需要对一个多项式进行展开,比如(x+1)^3。
我们可以使用Mathematica的Expand函数来展开多项式。
代码如下:```mathematicaExpand[(x + 1)^3]```运行以上代码后,Mathematica会展开多项式(x+1)^3,结果为x^3+3x^2+3x+1。
Mathematica用法I

Plot3D[z,{x,a,b},{y,c,d}] 三维曲面绘图
ParametricPlot3D[{x,y,z},{u, a,b},{v,c,d}]
三维曲面参数方程绘图
Print[x,y,...]
在屏幕输出变量的值
初学者易犯的错误 ⑴ 大小写错误:系统的内部操作命令及内部函数的首写字
母都是大写,第二个单词的首字母一般也是大写; ⑵ 括号错误:大、中、小三种括号用法错误;或括号个数
绝对值 幂函数 x y 平方根 以 e 为底的指数函数 以 e 和 b 为底的对数函数 m 除以 n 的余数 m 除以 n 的整数商 三角函数 反三角函数 生成 [a,b] 内的一个随机实数 生成 [a,b] 内的一个随机整数 判断 n 是否为素数 求方程(组)的精确解 用Newton法求方程组的一个近似解
① 所有命令和内置函数都是以大写字母开始 ② 函数的参数是在方括号中给出 ③ 乘法运算符可以用空格代替(不建议这么做) ④ 可以运行单个命令或语句,也可输入全部语句后
再按执行键shift+Enter ⑤ 命令(语句)分隔符:回车或分号 ⑥ 如果不需要显示运行结果:在语句后面加分号 ⑦ 输入和输出标识符:In[n]: 和 Out[n]:
请同学们在Notebook上完成如下输入,观察输出结果。
Abs[2+3 I]
Power[2,1ቤተ መጻሕፍቲ ባይዱ0]
Sqrt[-3]
Exp[0]
Mod[100,9]
Sin[Pi/4]
PrimeQ[97]
N[Pi,1000000]
Random[Integer,{1,14}]
(2)符号计算功能 Mathematica的主要特点就是进行符号运算,如下所示:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
mathematica软件基本操作(一).实验类型:验证型(二).实验类别:基础实验(三).每组人数:1(四).实验要求:选修(五). 实验学时:3个学时(三).实验目的:(1)掌握Mathematica软件的计算器功能;(2)学会使用Mathematica软件求各种类型方程(或方程组)的数值解和符号解;(3)通过本实验深刻理解极限概念;(4)学习并掌握利用Mathematica求极限的基本方法。
(5)通过本实验加深理解积分理论中分割、近似、求和、取极限的思想方法;(6)学习并掌握二重积分及线性积分的计算方法;(7)学习常用积分命令。
(8)掌握求函数的导函数和偏导数方法;(9)学会使用Mathematica软件进行函数的幂级数展开。
(四)【预备知识】(1)方程(或方程组)代数解法的基本理论,函数的零点,方程(或方程组)的解及数值解;(2)本实验所用命令:●用“= =”连接两个代数表达式构成一个方程●求方程(组)的代数解:Solve[方程或方程组,变量或变量组]●求方程(组)的数值解:NSolve[方程或方程组,变量或变量组]●从初始值开始搜索方程或方程组的解:FindRoot[方程或方程组,变量或变量组初值]●在界定范围内搜索方程或方程组的解:FindRoot[方程或方程组,变量或变量组范围]●绘图命令:Plot[表达式,{变量,上限,下限},可选项]●微分方程求解命令:DSolve[微分方程,y[x],x](3)极限、左极限、右极限的概念;(4)本实验所用Mathematica 有关命令:●Limit[expr , x ->x 0] 求表达式在0x x →时的极限 ● Limit[expr ,x ->x 0,Direction -> 1] 求左极限 ●Limit[expr ,x ->x 0,Direction ->-1] 求右极限(5)定积分的概念、几何意义,二重积分的概念、二重积分化为定积分的过程及其计算方法;(6)本实验所用Mathematica 有关命令:● 无限积分:Integrate[f,x]●定积分:Integrate[f,{x ,上限,下限}](7)函数的导函数、偏导数以及函数的幂级数展开式; (8)本实验所用的Mathematica 函数提示:(a )求导数(或偏导数)● D[表达式F,x] 求F 对于变量x 的导数;● D[表达式F,x1,x2,...] 按顺序求F 关于x 1,x 2,…的偏导数; ● D[表达式F,{x,n}] 求F 对x 的n 阶导数。
(b )幂级数展开●Series[表达式F,{x,x0,n}] 求F 关于变量x 在x 0的n 阶泰勒展式。
(五).实验内容(1)计算54564546⨯;4567646545。
(2)对于方程0342234=+--x x x ,试用Solve 和Nsolve 分别对它进行求解,并比较得到的结果,体会代数解即精确解与数值解的差别。
(3)先观察函数x x x f cos sin )(-=的图形,然后选择一个初始点求解,并且根据图形确定在某个区间中搜索它的零点。
(4)求方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的解,然后代入系数和常数项的一组初值,并求解。
(5)求微分方程x x y x y x y e )(2)(3)(=+'+''的通解。
(6)用 Mathematica 软件计算下列极限:(1)1233lim ++-∞→n n n n ; (2)x πx tan lim 2-→; (3)x πx tan lim2+→;(4)xx xxx ---∞→+-3333lim; (5)nn z n z n ⎪⎭⎫⎝⎛-+-∞→22lim ; (6)210)sin(lim x x xx ⎪⎭⎫ ⎝⎛→;(7)⎪⎪⎭⎫⎝⎛-+→x x a x 1)1(lim 0;(8)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛+∞→∞→222lim lim y x y x x y ;(9)()⎪⎭⎫⎝⎛+-→→y xy y xx y 3252223lim lim ;(10)()⎪⎪⎭⎫ ⎝⎛+-→→y xy y x y x 3252232lim lim ;(11)⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛+∞→∞→222lim lim y x y x y x ;(12)⎪⎭⎫⎝⎛→)1sin(lim 0x x 。
(7)求函数32)sin(x x a f =的原函数;(8)求x ax nd ⎰;(9)求⎰10d x ax n ; (10)求⎰⎰+10122d d x x y xy x ; (11)求⎰⎰xy y x x 00d cos d π。
(12)求出被积函数F (x )=5312+++x x x 的原函数和导函数,并画出被积函数、原函数和导函数的图形,试分辨出哪一条曲线属于哪个函数。
(13)对函数sin x 在0点展开10阶和20阶,并以图形方式对比展开的结果和sin x 的差别,并分析阶数高的展式对于原来函数的逼近程度是否优于阶数低的展式。
(六)【实验操作】(1)学会N[]和expr//N 的使用方法,并学会用Precision[]研究误差。
In[1]:=N[Exp[3],12] In[2]:= Precision[%]In[3]:=546*54564 // NIn[4]:=46545^45676 // N(2)学会Solve[]和NSolve[]的使用方法。
In[5]:= p=x^4-2x^3-4x^2+3;Solve[p==0,x]In[6]:=NSolve[p= =0,x](3)学会Clear[]和FindRoot[]的使用方法In[7]:=Clear[x]In[8]:=f=Sin[x]-Cos[x]In[9]:=Plot[f,{x,-4,4}]In[10]:=FindRoot[f,{x,1}]In[11]:=FindRoot[f,{x,{0,1}}](4)学会用Solve[]求解方程组。
In[12]:=Clear[a1,a2,b1,b2,c1,c2]In[13]:=Solve[{a1*x+b1*y= =c1,a2*x+b2*y= =c2},{x,y}](5)学会DSolve[]的使用方法In[14]:=DSolve[y''[x]+3y'[x]+2y[x]= =Exp[x],y[x],x](6)用Mathematica软件计算下列极限:(1)In[1]:= Limit[(n^3)/(-n^3+n^2+1),n ->Infinity];(2)In[2]:= Limit[Tan[x],x->Pi/2,Direction->1](3)In[3]:= Limit[Tan[x],x->Pi/2,Direction->-1](4)In[4]:= Limit 3x3x3x3x,x(5)In[5]:= Limit 2n z2n zn,n(6)In[6]:=Limit Sin xx 1x2,x0(7)In[7]:=Limit[((1+x)^a-1)/x,x->0] (*Mathematica也能处理符号极限*)(8)In[8]:=Limit Limit x2y22xy53y,y3,x2(9)In[9]:=Limit Limit x2y22xy53y,x2,y3(10)In[10]:=Limit Limitx2yx2y2,x,y(11)In[11]:=Limit Limitx2yx2y2,y,x(12)In[12]:=Limit[Sin[1/x], x->0] (*无极限的例子*)(13)In[1]:=Integrate[a*Sin[x^2]x^3,x](14)In[2]:=Integrate[a*x^n, x](15)In[3]:=Integrate[a*x^n, {x, 0, 1}](16)In[4]:=Integrate[Integrate[x*y, {y, 2x, x^2 + 1}], {x, 0, 1}] (17)In[5]:=Integrate[x*Cos[y],{x,0,Pi},{y,0,x}](18)In[1]:=f1=(x+1)/(x^2+3x+5)In[2]:=f2=Integrate[f1,x]In[3]:=f3=D[f1,x]In[4]:=Plot[{f1,f2,f3},{x,-1,1}](19)In[5]:=s1=Series[Sin[x],{x,0,10}]In[6]:=s2=Series[Sin[x],{x,0,20}]In[7]:=g1=Normal[s1]In[8]:=g2=Normal[s2]In[9]:=Plot[{g1,Sin[x]},{x,-5,5}]In[10]:=Plot[{g2,Sin[x]},{x,-5,5}]In[11]:=Plot[g1-g2,{x,-5,5}]。
