4.3角 练习题
4.3角练习题及答案

4.3角同步训练一、选择题1. 下列语句中,正确的是()A.比直角大的角是钝角 B •比平角小的角是锐角C .钝角的平分线把钝角分为两个锐角D .钝角与锐角的差一定是锐角2. 两个锐角的和()A .一定是锐角B .一定是直角C .一定是钝角D .可能是锐角,可能是直角,也可能是钝角3. 在时刻8: 30,时钟的时针和分针之间的夹角是()A . 85°B . 75° C. 70° D. 60°4. 如果/ A和/B互为余角,/ B和/C互为补角,/ A与/ C的和等于120°,那么这三个角分别是()A . 20°,80°, 80°B . 20°, 70°, 90°C . 30°,60°, 90°D . 70°, 20°, 100°5. 如果/a =m,而/a既有余角,也有补角,那么n的取值范围是()A . 0°< m< 90° B. m= 90° C . 90°< m< 180° D . m= 180°二、填空题6 .如图所示,将一副三角板叠放在一起,?使直角的顶点重合于点O,则/AOC+ /DOB的度数为_______ 度.7. 如果/a =47°28',/a 的余角/B = ______________ ,/ a 的补角/丫= _____ , /丫一/a = ___ .8. 已知:如图,△ ABC 中,AB = AC , BD 为/ABC 的平分线,/ BDC = 84° ,则/ A = ____ .A三、解答题9. 如下图所示,已知/ B0D=2/ AOB , OC 是/BOD 的平分线,试表示出图中相等的角.10. 在飞机飞行时,飞行方向是用飞行路线与实际的南或北方向线之间的夹角 大小来表示的.如图,用 AN (南北线)与飞行线之间顺时针方向夹角作为飞 行方向角.从A 到B 的飞行方向角为35°,从A 到C 的飞行方向角为60 °, 从A 到D 的飞行方向角为145°,试求AB 与AC 之间夹角为多少度? AD 与AC 之间夹角为多少度?并画出从 A 飞出且方向角为105°的飞行线.答案:1. C2. D3. B4. B5. A6. 1807. 42° 32' , 132 ° 32' , 85 ° 4'8. 52°9. Z AOB= / BOC= / COD ,/ AOC= / BOD10. AB 与AC 之间夹角为25°,AD 与AC 之间夹角85。
七年级数学上册4.3 角的比较 练习(含答案)

4.3 角的比较一、填空:1.如图1,∠AOB______∠AOC,∠AOB_______∠BOC(填>,=,<); 用量角器度量∠BOC=____°,∠AOC=______°,∠AOC______∠BOC.OC(1)ABOD C(2)ABODC(3)AB2.如图2,∠AOC=______+______=______-______;∠BOC=______-______= _____-________.3.OC是∠AOB内部的一条射线,若∠AOC=12________,则OC平分∠AOB;若OC 是∠AOB的角平分线,则_________=2∠AOC.二、选择:4.下列说法错误的是( )A.角的大小与角的边画出部分的长短没有关系;B.角的大小与它们的度数大小是一致的;C.角的和差倍分的度数等于它们的度数的和差倍分;D.若∠A+∠B>∠C,那么∠A一定大于∠C。
5.用一副三角板不能画出( )A.75°角B.135°角C.160°角D.105°角6.如图3,若∠AOC=∠BO D,那么∠AOD与∠BOC的关系是( )A.∠AOD>∠BOCB.∠AO D<∠BOC;C.∠AOD=∠BOCD.无法确定7.如果∠1-∠2=∠3,且∠4+∠2=∠1,那么∠3和∠4间的关系是( )A.∠3>∠4B.∠3=∠4;C.∠3<∠4D.不确定8.OC是从∠AOB的顶点O引出的一条射线,若∠AOB=90°,∠AOB= 2∠BOC, 求∠AOC的度数.9.如图,把∠AOB绕着O点按逆时针方向旋转一个角度,得∠A′OB′,指出图中所有相等的角,并简要说明理由.OABB 'A '10.如图,BD 平分∠ABC,BE 分∠ABC 分2:5两部分,∠DBE=21°,求∠ABC 的度数.D CAE B11.如图,已知∠α、∠β ,画一个角∠γ,使∠γ=3∠β-12∠α. βα12.如图,A 、B 两地隔着湖水,从C 地测得CA=50m,CB=60m,∠ACB=145°,用1 厘米代表10米(就是1:1000的比例尺)画出如图的图形.量出AB 的长(精确到1毫米), 再换算出A 、B 间的实际距离.CAB13.如图,∠AOB 是平角,O D 、OC 、OE 是三条射线,OD 是∠AOC 的平分线, 请你补充一个条件,使∠DOE=90°,并说明你的理由.OD CAE B答案: 1.略。
北师大版七年级上册数学 4.3 角 同步练习(含解析)
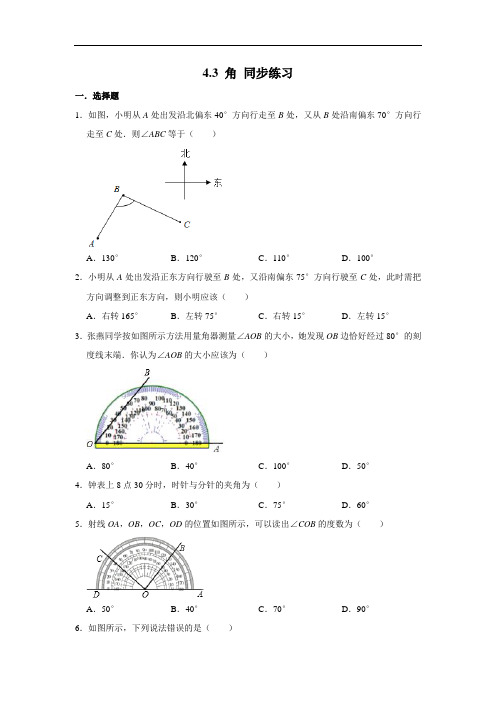
4.3 角同步练习一.选择题1.如图,小明从A处出发沿北偏东40°方向行走至B处,又从B处沿南偏东70°方向行走至C处.则∠ABC等于()A.130°B.120°C.110°D.100°2.小明从A处出发沿正东方向行驶至B处,又沿南偏东75°方向行驶至C处,此时需把方向调整到正东方向,则小明应该()A.右转165°B.左转75°C.右转15°D.左转15°3.张燕同学按如图所示方法用量角器测量∠AOB的大小,她发现OB边恰好经过80°的刻度线末端.你认为∠AOB的大小应该为()A.80°B.40°C.100°D.50°4.钟表上8点30分时,时针与分针的夹角为()A.15°B.30°C.75°D.60°5.射线OA,OB,OC,OD的位置如图所示,可以读出∠COB的度数为()A.50°B.40°C.70°D.90°6.如图所示,下列说法错误的是()A.∠DAO可用∠DAC表示B.∠COB也可用∠O表示C.∠2也可用∠OBC表示D.∠CDB也可用∠1表示7.如图所示,下列表示角的方法错误的是()A.∠1与∠PON表示同一个角B.∠α表示的是∠MOPC.∠MON也可用∠O表示D.图中共有三个角∠MON,∠POM,∠PON8.下列四个图形中的∠1也可用∠AOB,∠O表示的是()A.B.C.D.9.如图,∠AOB=148°,在灯塔O处观测到轮船A位于北偏西51°的方向,则在灯塔O 处观测轮船B的方向为()A.南偏东17°B.南偏东19°C.东偏南17°D.东偏南73°10.嘉淇乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km(最小圆的半径是1km),下列关于小艇A,B的位置描述,正确的是()A.小艇A在游船的北偏东60°方向上,且与游船的距离是3kmB.游船在小艇A的南偏西60°方向上,且与小艇A的距离是3kmC.小艇B在游船的北偏西30°方向上;且与游船的距离是2kmD.游船在小艇B的南偏东60°方向上,且与小艇B的距离是2km二.填空题11.已知如图,点A在点O的东南方向,则∠AOB=°.12.时钟上八点二十的时候,时针与分针所夹锐角的度数是.13.如图,在一笔直的海岸线上有A、B两个观测站,A在B的正西方向,从A测得船C在北偏东52°的方向,从B测得船C在北偏西30°的方向,则∠ACB=°.14.如图,O是直线AB上的一点,∠AOC=26°17,则∠COB=15.小红从O点出发向北偏西32°方向走到A点,小明从O点出发向南偏西54°方向走到B点,则∠AOB的度数是.三.解答题16.如图(1)利用尺规作∠CED,使得∠CED=∠A.(不写作法,保留作图痕迹).(2)判断直线DE与AB的位置关系:.17.如图,货轮O在航行过程中,发现灯塔A在它北偏东60°的方向上,同时,在它南偏西20°、西北(即北偏西45°)方向上又分别发现了客轮B和海岛C,仿照表示灯塔方位的方法,画出表示客轮B和海岛C方向的射线.18.如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,点A表示轮船的初始位置,点B 表示轮船行进中某一时刻的位置.(1)当轮船从A点行驶到B点时,请根据图中所标数据求∠ACB的大小;(2)当轮船从点行驶到距离灯塔最近点时,∠ACB=.参考答案1.解:如图:∵小明从A处沿北偏东40°方向行走至点B处,又从点B处沿南偏东70°方向行走至点C处,∴∠DAB=40°,∠CBE=70°,∵向北方向线是平行的,即AD∥BE,∴∠ABE=∠DAB=40°,∴∠ABC=∠ABE+∠EBC=40°+70°=110°.故选:C.2.解:由题意得:∠BEC=75°,∵AB∥CD,∴∠DCF=75°,∵需把方向调整到正东方向,∴∠FCD=15°,∴左转15°,故选:D.3.解:如图,由图可知,∠ACD=100°,根据同弧所对的圆周角等于它所对圆心角的一半可知,∠AOB=.故选:D.4.解:∵8点30分,时针在8和9正中间,分针指向6,中间相差两个半大格,而钟表12个数字,每相邻两个数字之间的夹角为30°,∴8点30分时,时针与分针的夹角的度数为:30°×2.5=75°.故选:C.5.解:∠COB=∠AOC﹣∠AOB=140°﹣50°=90°,故选:D.6.解:A、∠DAO可用∠DAC表示,本选项说法正确;B、∠COB不能用∠O表示,本选项说法错误;C、∠2也可用∠OBC表示,本选项说法正确;D、∠CDB也可用∠1表示,本选项说法正确;故选:B.7.解:A、∠1与∠PON表示同一个角是正确的,不符合题意;B、∠α表示的是∠MOP是正确的,不符合题意;C、∠MON不能用∠O表示,原来的说法错误,符合题意;D、图中共有三个角∠MON,∠POM,∠PON是正确的,不符合题意.故选:C.8.解:A、图形中的∠1可用∠AOB,但不能用∠O表示,故此选项错误;B、图形中的∠1可用∠AOB,也可用∠O表示,故此选项正确;C、图形中的∠1不可用∠AOB和∠O表示,故此选项错误;D、图形中的∠1可用∠AOB,但不能用∠O表示,故此选项错误;故选:B.9.解:如图,∠1=∠AOB﹣90°﹣(90°﹣51°)=148°﹣90°﹣(90°﹣51°)=19°.故在灯塔O处观测轮船B的方向为南偏东19°,故选:B.10.解:A、小艇A在游船的北偏东30°,且距游船3km,故本选项不符合题意;B、游船在小艇A的南偏西30°方向上,且与小艇A的距离是3km,故本选项不符合题意;C、小艇B在游船的北偏西60°,且距游船2km,故本选项不符合题意;D、游船在小艇B的南偏东60°方向上,且与小艇B的距离是2km,故本选项符合题意.故选:D.11.解:如图所示:∵点A在点O的东南方向,∴∠COA=45°,则∠AOB=90°+45°=135°.故答案为:135.12.解:4×30°+20×0.5°=120°+10°=130°.故答案为:130°.13.解:∵∠CAB=90°﹣52°=38°,∠CBA=90°﹣30°=60°,∴∠ACB=180°﹣38°﹣60°=82°.故答案为:82.14.解:∵∠AOC+∠BOC=180°,∴∠COB=180°﹣∠AOC=180°﹣26°17′=153°43′故答案为:153°43′.15.解:根据题意得:∠AOB=180°﹣32°﹣54°=94°.故答案为:94°.16.解:(1)如图1,如图2;(2)如图1,∵∠CED=∠A,∴DE∥AB,;如图2,DE与AB相交.故答案为平行或相交.17.解:如图所示,18.解:(1)如图所示,过点C作CE⊥AB,交AB延长线于点E,则轮船行驶到点C时距离灯塔最近;当轮船从A点行驶到B点时,∠ACB的度数是72°﹣29°=43°;(2)当轮船行驶到距离灯塔的最近点时,即∠ACB=∠ACE=61°.故答案为:61°.。
《4.3角》练习题

《4.3 角》2一、单项选择题1.如果∠A和∠B互为余角,∠A和∠C互为补角,∠B与∠C的和等于120°,那么这三个角分别是().A.50°,30°,130°; B.75°,15°,105°; C.60°,30°,120°;D.70°,20°,110°2.下列关于角的说法正确的是()A.两条射线组成的图形叫角B.角的大小与这个角的两边长短无关C.延长一个角的两边D.角的两边是射线,所以角不可以度量3.如图所示,∠α+∠β=90°,∠β+∠γ=90°,则().A.∠α=βB.∠β=∠γC.∠α=∠β=∠γD.∠α=∠γ4.两个锐角的和().A.必定是锐角;B.必定是钝角;C.必定是直角;D.可能是锐角,可能是直角,也可能是钝角5.经过2小时钟表的时针旋转的角度为()A. 60° B. 90° C. 180° D. 360°6.如图,小明在操场上从A点出发,先沿南偏东30°方向走到B点,再沿南偏东60°方向走到C点.这时,∠ABC的度数是()A. 120°B. 135°C. 150°D. 160°7.下列语句中,正确的是().A.比直角大的角钝角B.比平角小的角是钝角C.钝角的平分线把钝角分为两个锐角D.钝角与锐角的差是锐角8.已知∠α=35°19′,则∠α的补角是()A. 144°41′B. 54°41′C. 144°81′D. 54°81′9.若∠1=25°12′,∠2=25.12°,∠3=25.2°,则下列结论正确的是()A. ∠1=∠2B. ∠2=∠3C. ∠1=∠3D. ∠1=∠2=∠310.下列说法中正确的是().①两条射线所组成的图形叫做角②角的大小与边的长短无关③角的两边可以一样长,也可以一长一短④角的两边是两条射线A.①②B.②④C.②③D.③④11.如图所示,点A位于点O的()方向上.A. 南偏东25°B. 北偏西65°C. 南偏东65°D. 南偏西65°13.40°15′的一半是().A.20°B.20°7′C.20°8′D.20°7′30″14.将两个三角板按如图所示的位置摆放,已知∠α=32°,则∠β=()A. 69°B. 32°C. 58°D. 148°15.如图,光照到平面镜AB上发生反射,已知OC⊥AB,∠DOC=∠COE,下列判断不正确的是()A. ∠AOD=∠BOEB. ∠AOE=∠BODC. ∠DOC+∠BOE=90°D. ∠DOC+∠COE=90°16.下列说法中正确的个数是().①直线AB是一个平角②两锐角的角的和不一定大于90°③两个锐角的和不一定大于180°④周角只有一条边A.0B.1C.2D.317.下列说法正确的个数有()①直线是平角,②射线是周角,③平角是一条直线,④周角是一条直线.A. 0个B. 1个C. 2个D. 3个18.两个角的和与这两个角的差互补,则这两个角().A.一个是锐角,一个是钝角;B.都是钝角;C.都是直角;D.必有一个是直角19.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠BOC=80°,则∠AOE的度数是()A. 40°B. 50°C. 80°D. 100°20.下列各式中,正确的角度互化是( )A. 63.5°=63°50′B. 23°12′36″=25.48°C. 18°18′18″=3.33°D. 22.25°=22°15′21.下列说法错误的是().A.两个互余的角都是锐角;B.一个角的补角大于这个角本身;C.互为补角的两个角不可能都是锐角;D.互为补角的两个角不可能都是钝角22.如果两个角互为补角,而其中一个角比另一个角的4倍少30°,那么这两个角是().A.42°,138°或40°,130°;B.42°,138°;C.30°,150°;D.以上答案都不对二、解答题1.如图,已知OE是的角平分线,OD是的平分线.(1)若,求的度数;(2)若,求的度数.2.钟表2时15分时,你知道时针与分针的夹角是多少度吗?3.计算:(1)77°52′+32°43′-21°17′;(2)37°15′×3;(3)175°52′÷3.(4)23°45′+24°16′(5)53°25′28″×5(6)15°20′÷64.如图所示,直线AB、CD相交于O,OE为射线,试问,图中小于平角的角共有几个?请一一列出.5.如图所示,直线AB上一点O,任意画射线OC,已知OD、OE分别是∠AOC、∠BOC的角平分线,求∠DOE的度数.6.如图,从一点O出发引射线OA、OB、OC、OD、OE,请你数一数图中有多少个角.7.如图所示,已知∠AOB=165°,∠AOC=∠BOD=90°,求∠COD.三、填空题(共10题,共30分)1.∠1=∠A,∠2=∠A,则∠1和∠2的关系是_______.2.如图,小于平角的角有______个,∠EOC=_____+_______.3.如图,已知OE平分∠AOB,OD平分∠BCO,∠AOB为直角,∠EOD=70°,则∠BOC的度数为_______.4.计算90°-57°34′44″的结果为_______________.5.如图,是直角,,则度.6.用度、分、秒表示52.73°为____度____分____秒.7.在内部过顶点O引3条射线,则共有___________个角,如果引出99条射线,则共有_____________个角.8.4.75°=______°________′___________″.9.如图,射线OA表示北偏东_____,射线OB表示_____30°,射线OD表示南偏西_______,射线OC表示________方向.10.6点50分钟面上时针与分针所成的角为________度.。
人教版七年级数学上册《4.3 角》课后训练及答案

4.3 角课后训练(基础巩固+能力提升)基础巩固1.下图中表示∠ABC的图是( ).2.下列关于平角、周角的说法正确的是( ).A.平角是一条直线B.周角是一条射线C.反向延长射线OA,就形成一个平角D.两个锐角的和不一定小于平角3.已知∠α=18°18′,∠β=18.18°,∠γ=18.3°,下列结论正确的是( ).A.∠α=∠βB.∠α<∠βC.∠α=∠γD.∠β>∠γ4.如图所示,如果∠AOD>∠BOC,那么下列说法正确的是( ).A.∠COD>∠AOB B.∠AOB>∠CODC.∠COD=∠AOB D.∠AOB与∠COD的大小关系不能确定5.下列说法中,正确的是( ).A.一个锐角的余角比这个角大B.一个锐角的余角比这个角小C.一个锐角的补角比这个角大D.一个锐角的补角比这个角小6.(1)把周角平均分成360份,每份就是_______的角,1°=_______,1′=________.(2)25.72°=__________°__________′__________″.(3)15°48′36″=__________°.(4)3 600″=__________′=__________°.7.如图所示,将一个矩形沿图中的虚线折叠,请用量角器测量一下其中的∠α,∠β,得∠α__________∠β(填“>”“<”“=”).8.已知:如图所示,AB是直线,∠BOC=∠AOC=90°,OD,OE是射线,则图中有__________对互余的角,__________对互补的角.9.计算下列各题:(1)153°19′42″+26°40′28″;(2)90°3″-57°21′44″;(3)33°15′16″×5.10.一个角的余角比这个角的补角的13还小10°,求这个角的余角及这个角的补角.能力提升11.淘气有一张地图,有A,B,C三地,但地图被墨迹污染,C地具体位置看不清楚了,但知道C地在A地的北偏东30°,在B地的南偏东45°,你能帮淘气确定C地的位置吗?12.如图所示,将一副三角板叠放在一起,使直角的顶点重合于点O,则∠AOC+∠DOB 的度数为__________.13.(1)1点20分时,时钟的时针与分针的夹角是几度?2点15分时,时钟的时针与分针的夹角又是几度?(2)从1点15分到1点35分,时钟的分针与时针各转过了多大角度?(3)时钟的分针从4点整的位置起,按顺时针方向旋转多少度时才能与时针重合?14.如图所示,OM平分∠AOB,ON平分∠COD,∠MON=90°,∠BOC=26°,求∠AOD 的度数.15.将一张长方形纸ABCD的两个角按如图所示方式折叠,且BE与EC的一部分重合,请问,∠α与∠β是有什么关系的两个角,并说明理由.16.如图甲所示,∠AOB,∠COD都是直角.(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系,你能用推理的方法说明你的猜想是否合理吗?(2)当∠COD绕点O旋转到图乙的位置时,你原来的猜想还成立吗?参考答案1答案:C 点拨:用三个大写字母表示角,表示角顶点的字母在中间.2答案:C 点拨:根据定义可知A,B不正确;锐角大于0°而小于90°,所以两个锐角的和小于180°,D不正确;反向延长射线OA,O成为角的顶点,故选C.3答案:C 点拨:1°=60′,∴18′=1860⎛⎫︒⎪⎝⎭=0.3°,∴18°18′=18°+0.3°=18.3°,即∠α=∠γ.4答案:B 点拨:因为∠AOD与∠BOC中都包含∠BOD,所以都减去它,由∠AOD>∠BOC,得∠AOD-∠BOD>∠BOC-∠BOD,即∠AOB>∠COD.5答案:C6答案:(1)1°60′60″(2)25 43 12 (3)15.81 (4)60 17答案:=8答案:2 3 点拨:∠AOE与∠EOC,∠BOD与∠COD互余;∠AOE与∠BOE, ∠BOD与∠AOD,∠AOC与∠BOC互补.9解:(1)153°19′42″+26°40′28″=179°59′70″=179°60′10″=180°10″;(2)90°3″-57°21′44″=89°59′63″-57°21′44″=32°38′19″;(3)33°15′16″×5=165°75′80″=165°76′20″=166°16′20″.10解:设这个角为x°,则这个角的余角为(90-x)°,这个角的补角为(180-x)°,根据题意,得90-x=1(180)3x--10,90-x=60-13x-10,23x=40,x=60.则90-x=30,180-x=120.答:这个角的余角是30°,补角是120°.11解:如图,C在图中两线的交点上.点拨:根据方位角的概念画出:A地的北偏东30°,B地的南偏东45°两条直线,两直线的交点就是C.12答案:180°点拨:∵∠AOC=90°+∠BOC①,∠DOB=90°-∠BOC②,①+②得∠AOC+∠DOB=180°.1314解:由OM平分∠AOB,ON平分∠COD,设∠AOM=∠MOB=x,∠CON=∠NOD=y,∵∠MON=90°,∠BOC=26°,∴∠NOC+∠BOC+∠BOM=90°,∴x+y+26°=90°,∴x+y=64°.∵∠AOD=2x+2y+26°=2×64°+26°=154°.15解:互余(即∠α+∠β=90°).理由:由折叠可知∠B′EF=∠α,∠GEC′=∠β,而∠BEC=180°.所以∠α+∠FEB′+∠GEC+∠GEC′=180°.即2∠α+2∠β=180°,所以∠α+∠β=90°.16解:(1)互补.理由:∵∠AOB=∠COD=90°,∴∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=90°+90°=180°,∴∠AOD和∠BOC互补.(2)成立.理由:∵∠AOB=∠COD=90°,∴∠AOD+∠BOC=360°-∠AOB-∠COD=360°-90°-90°=180°,∴∠AO D与∠BOC互补.。
人教版七年级数学上册第四章《角》课时练习题(含答案)
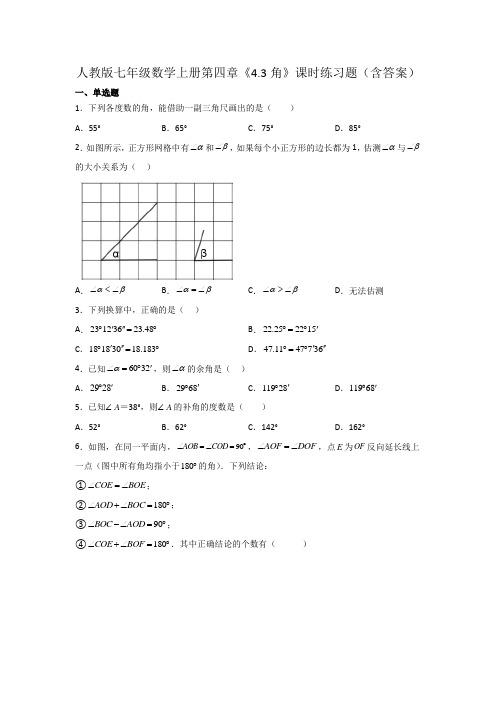
人教版七年级数学上册第四章《4.3角》课时练习题(含答案)一、单选题1.下列各度数的角,能借助一副三角尺画出的是( )A .55°B .65°C .75°D .85°2.如图所示,正方形网格中有α∠和∠β,如果每个小正方形的边长都为1,估测α∠与∠β的大小关系为( )A .αβ∠<∠B .αβ∠=∠C .αβ∠>∠D .无法估测3.下列换算中,正确的是( )A .23123623.48'''︒=︒B .22.252215'︒=︒C .18183018.183'''︒=︒D .47.1147736︒︒'=''4.已知6032α'∠=︒,则α∠的余角是( )A .2928'︒B .2968'︒C .11928'︒D .11968'︒5.已知∠A =38°,则∠A 的补角的度数是( )A .52°B .62°C .142°D .162° 6.如图,在同一平面内,90AOB COD ∠=∠=︒,AOF DOF ∠=∠,点E 为OF 反向延长线上一点(图中所有角均指小于180︒的角).下列结论:①COE BOE ∠=∠;②180AOD BOC ∠+∠=︒;③90BOC AOD ∠-∠=︒;④180COE BOF ∠+∠=︒.其中正确结论的个数有( )A .1个B .2个C .3个D .4个7.如图,68AOB ∠=︒,OC 平分AOD ∠且15COD ∠=︒,则BOD ∠的度数为( ).A .28︒B .38︒C .48︒D .53︒8.一个角的补角为138︒,则这个角的余角为( )A .38︒B .42︒C .48︒D .132︒二、填空题9.如图,过直线AB 上一点O 作射线OC ,∠BOC =29°18′,则∠AOC 的度数为_____.10.如图,直线,AB CD 相交于O ,OE 平分,∠⊥AOC OF OE ,若46BOD ∠=︒,则DOF ∠的度数为______︒.11.已知,如图,A 、O 、B 在同一直线上,OF 平分AOB ∠,12∠=∠,3=4∠∠.(1)射线OD 是_______的角平分线;(2)AOC ∠的补角是_______;(3)AOC ∠的余角是_______;(4)_______是2∠的余角;(5)DOB ∠的补角是_______;(6)_______是COF ∠的补角.12.如图,若OC 、OD 三等分AOB ∠,则AOB ∠=_______AOC ∠=_______AOD ∠,COD ∠=_______AOB ∠,BOC ∠=∠_______.13.如图,已知∠AOB =90°,射线OC 在∠AOB 内部,OD 平分∠AOC ,OE 平分∠BOC ,则∠DOE =_____°.14.如图,将一副三角尺的两个锐角(30°角和45°角)的顶点P 叠放在一起,没有重叠的部分分别记作∠1和∠2,若∠1与∠2的和为61°,则∠APC 的度数是 _____.三、解答题15.如图,点P 是直线l 外一点,过点P 画直线P A ,PB ,PC ,…,分别交直线l 于点A ,B ,C ,….用量角器量出1∠,2∠,3∠的度数,并量出P A ,PB ,PC 的长度,你发现了什么?16.如图,两个直角三角形的直角顶点重合,∠AOC =40°,求∠BOD 的度数.结合图形,完成填空:解:因为∠AOC+∠COB = °,∠COB+∠BOD = ①所以∠AOC = .②因为∠AOC =40°,所以∠BOD = °.在上面①到②的推导过程中,理由依据是: .17.如图①,已知线段AB=18cm,CD=2cm,线段CD在线段AB上运动,E,F分别是AC,BD的中点.(1)若AC=4cm,则EF=cm;(2)当线段CD在线段AB上运动时,试判断EF的长度是否发生变化?如果不变,请求出EF的长度,如果变化,请说明理由.(3)a.我们发现角的很多规律和线段一样,如图②,已知∠COD在∠AOB内部转动,OE,OF分别平分∠AOC和∠BOD,若∠AOB=140°,∠COD=40°,求∠EOF.b.由此,你猜想∠EOF,∠AOB和∠COD会有怎样的数量关系.(直接写出猜想即可)18.如图1,点O为直线AB上一点,过O点作射线OC,使∠BOC=120°.将一块直角三角板的直角顶点放在点O处,边OM与射线OB重合,另一边ON位于直线AB的下方.(1)将图1的三角板绕点O逆时针旋转至图2,使边OM在∠BOC的内部,且恰好平分∠BOC,问:此时ON所在直线是否平分∠AOC?请说明理由;(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,设旋转时间为t秒,在旋转的过程中,ON所在直线或OM所在直线何时会恰好平分∠AOC?请求所有满足条件的t值;(3)将图1中的三角板绕点O顺时针旋转至图3,使边ON在∠AOC的内部,试探索在旋转过程中,∠AOM和∠CON的差是否会发生变化?若不变,请求出这个定值;若变化,请求出变化范围.19.已知:160AOD ∠=︒,OB 、OM 、ON 是AOD ∠内的射线.(1)如图1,若OM 平分AOB ∠,ON 平分BOD ∠.当射线OB 绕点O 在AOD ∠内旋转时,求MON ∠的度数.(2)OC 也是AOD ∠内的射线,如图2,若20BOC ∠=︒,OM 平分AOC ∠,ON 平分BOD ∠,当射线OB 绕点O 在AOD ∠内旋转时,求MON ∠的大小.20.【阅读理解】定义:在一条直线同侧的三条具有公共端点的射线之间若满足以下关系,其中一条射线分别与另外两条射线组成的角恰好满足2倍的数量关系,则称该射线是另外两条射线的“双倍和谐线”.如图1,点P 在直线l 上,射线PR ,PS ,PT 位于直线l 同侧,若PS 平分∠RPT ,则有∠RPT =2∠RPS ,所以我们称射线PR 是射线PS ,PT 的“双倍和谐线”.【迁移运用】(1)如图1,射线PS(选填“是”或“不是”)射线PR,PT的“双倍和谐线”;射线PT(选填“是”或“不是”)射线PS,PR的“双倍和谐线”;(2)如图2,点O在直线MN上,OA MN,∠AOB=40°,射线OC从ON出发,绕点O以每秒4°的速度逆时针旋转,运动时间为t秒,当射线OC与射线OA重合时,运动停止.①当射线OA是射线OB,OC的“双倍和谐线”时,求t的值;②若在射线OC旋转的同时,∠AOB绕点O以每秒2°的速度逆时针旋转,且在旋转过程中,射线OD平分∠AOB.当射线OC位于射线OD左侧且射线OC是射线OM,OD的“双倍和谐线”时,求∠CON的度数。
4.3角(提高)巩固练习(含答案)

角(提高)巩固练习 班级 姓名 一、选择题 1.关于平角、周角的说法正确的是( ).A .平角是一条直线.B .周角是一条射线C .反向延长射线OA ,就成一个平角.D .两个锐角的和不一定小于平角2.在时刻2∶15时,时钟上的时针与分针间的夹角是 ( )A .22.5°B .85°C .75 °D .60°3.如图所示,将一幅三角板叠在一起,使直角的顶点重合于点O ,则∠AOB+∠DOC 的值( )A .小于180°B .等于180°C .大于180°D .不能确定4.如图,是由四个1×1的小正方形组成的大正方形,则∠1+∠2+∠3+∠4=( )A .180°B .150°C .135°D .120°5.如图所示,∠1是锐角,则∠1的余角是( ). A .1212∠-∠ B .132122∠-∠ C .1(21)2∠-∠ D .1(21)3∠+∠ 6.如图,OB 、OC 是∠AOD 的任意两条射线,OM 平分∠AOB ,ON平分∠COD ,若∠MON=α,∠BOC=β,则表示∠AOD 的式子是( )A .2α-βB .α-βC .α+βD .以上都不正确7.书店、学校、食堂在同一个平面上,分别用点A 、B 、C 来表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC 应该是( ).A .65°B .35°C .165°D .135°8.如图将长方形纸片ABCD 的角C 沿着GF 折叠(点F 在BC 上,不与B 、C 重合),使得点C 落在长方形内部点E 处,若FH 平分∠BFE ,则关于∠GFH 的度数α说法正确的是( )A . 90°﹤α﹤180°B . 0°﹤α﹤90°C . α= 90°D .α随折痕GF 位置的变化而变化二、填空题9.把一个平角16等分,则每份(用度、分、秒表示)为_______. 10.如图所示,∠AOC 与∠BOD 都是直角,且∠AOB :∠AOD =2:11,则∠AOB =_______.11. 如图所示,某测绘装置有一枚指针,原来指向南偏西50°,把这枚指针按顺时针方向旋转14周: (1)指针所指的方向为北偏西_____;(2)图中互余的角有________对;与∠BOC 互补的角是_____ __.12. 如图,已知直线AB 和CD 相交于点O ,∠COE 是直角,OF 平分∠AOE .(1)写出∠AOC 与∠BOD 的大小关系: ,判断的依据是 .(2)若∠COF=35°,∠BOD= .A B C D G E F H13.如图,在一个正方体的两个面上画了两条对角线 AB ,AC , 那么这两条对角线的夹角等于 .14.如图,在AOE 的内部从O 引出3条射线,那么图中共有________个角;如果引出5条射线,有 __ 个角;如果引出n 条射线, 有 _ 个角.三、解答题15.若∠AOB =2∠BOC ,则OC 为∠AOB 的平分线,这句话对吗?15.如图所示,已知∠AOC =2∠BOC ,∠AOC的余角比∠BOC 小30°.(1)求∠AOB 的度数.(2)过点O 作射线OD ,使得∠AOC =4∠AOD ,求∠COD 的度数。
北师大版七年级上册4.3 角同步测试

4.3 角(含答案)一.选择题:(四个选项中只有一个是正确的,选出正确选项填在题目的括号内)1.下列关于角的说法正确的个数是( )①角是由两条射线组成的图形;②角的边越长,角越大;③在角一边延长线上取一点D;④角可以看成由一条射线绕着它的端点旋转而形成的图形.A. 1个B. 2个C. 3个D. 4个2.如图,下列说法错误的是()A.∠B也可以表示为∠ABC B.∠BAC也可以表示为∠A C.∠1也可以表示为∠C D.以C为顶点且小于180º的角有3个3.如图,能用一个字母表示的角有()A.3个B.4个C.5个D.0个4.下列说法正确的是()A.平角是一条直线B.一条射线是一个周角C.两条射线组成的图形叫角D.两边成一直线的角是平角5.如图,其中以已标注大写字母的点为顶点的角(小于180 º)共有()A.12个B.16个C.20个D.24个6.如图,下列表示角的方法错误的是( D )A.∠1和∠AOB是表示同一个角B.∠β表示的是∠BOCC .图中共有三个角,即:∠AOB ,∠AOC ,∠BOCD .∠AOC 也可用 ∠O 表示7.21.21º可化为( )A .21º21´B .21º20´1"C .21º12´6"D .21º12´36"8.如图,直线AB 与直线CD 相交于点O ,已知∠AOE=90°,∠BOD=45°,则∠COE 的度数是( )A.125°B.135°C.145°D.155°9.中午12点15分时,钟表上的时针和分针所成的角是( )A .90ºB .75ºC .82.5ºD .60º10.图中共有( )个小于平角的角A .7B .8C .9D .10二.填空题:(将正确答案填在题目的横线上)11.将图中的角用不同的方法表示出来,填在表格内:12.计算: (1)38.15°=_____°_____′______";(2)38°第10题图15′=________°;(3)2°12′36"=_______°;(4)2700"=_________′=_______°;13.如图,点O在直线AB上,∠COE=90°,∠BOD=90°.(1)图中除∠COE、∠BOD外,是直角的还有__________;(2)图中相等的锐角有__________.14. 时钟的分针1分钟转______°角;1小时转______°角;15.如图,∠1,∠2表示的角可分别用大写字母表示为__________,__________;∠A也可表示为__________,还可以表示为__________;三.解答题:(写出必要的说明过程,解答步骤)16.用度(°)表示下列各角:(1)35°25′48";(2)45°12′36";17.把下列各角转化为度分秒表示:(1)32.26°;(2)25.72°;(3)14400";18.计算:(1)20°26′+35°54′;(2)27°28′+53°46′;(3)90°-43°18′;(4)90°-79°18′38";19.如图,以B为顶点的角有几个?把它们表示出来.以D为顶点且小于平角的角有几个?把它们表示出来.20.如图,直线AB交CD于O,∠AOE=90°;(1)若∠EOD=20°,求∠AOC的度数;(2)若∠AOC:∠BOC=1:2,求∠EOD的度数.21. 画出小于平角的∠MON;(1)并过点O在∠MON内部画射线OP,OQ,图中共有多少个小于平角的角?用三个字母的记法表示这些角;(2)若在∠MON内部画射线4条以点O为端点的射线,图中共有多少个小于平角的角?(3)由(1),(2)能得出这类问题的一般方法结论吗?请写出这个一般方法结论;4.3 角参考答案:1~10 ACADB CDBCD11.先填上行,再填下行:ɑ,∠2,∠B,∠BAD;12.(1)38,9,0;(2)38.25;(3)2.21;(4)45,0.75;13.∠AOD;∠COB=∠DOE;14. 6,360;15.∠ADE,∠AED;∠BAC,∠DAE;16.(1)35.43°;(2)45.21°;17.(1)32°15′36";(2)25°43′12";(3)4°;18.(1)20°26′+35°54′=55°80′=56°20′;(2)27°28′+53°46′=80°74′=81°14′;(3)90°-43°18′=89°60′-43°18′=46°42′;(4)90°-79°18′38"=89°59′60"-79°18′38"=10°41′22";19.图中以B为顶点的角有∠ABD,∠ABC,∠DBC,共3个;以D为顶点且小于平角的角有∠ADE,∠ADB,∠BDC,∠EDC,共4个.20.(1)∵直线AB交CD于O,∠AOE=90°∴∠BOE=180°-∠AOE =180°-90°=90°∵∠EOD=20° ∴∠BOD=∠BOE-∠EOD =90°-20°=70°∴∠AOC=∠BOD=70°(2) ∵∠AOC:∠BOC=1:2 即∠BOC=2∠AOC又∠AOC+∠BOC=180°得:∠AOC=60°∴∠EOD=180°-∠AOC-∠AOE=180°-60°-90°=30°∴∠EOD=30°21.(1)如图,图中共有6个小于平角的角;这些角用三个字母的记法表示为:∠MON,∠MOP,∠MOQ,∠NOP,∠NOQ,∠POQ;(2)若在∠MON内部画射线4条以点O为端点的射线,图中共有多15个小于平角的角;n n (3)若在∠MON内部有(n-1)条以点O为端点的射线,则共有(1)2多少个小于平角的角;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
角
班级:___________姓名:___________得分:__________
一、选择题(每小题8分,共40分)
1.下列对角的表示方法理解错误的是()
A.角可用三个大写字母表示,顶点字母写在中间,每边上的点写在两旁
B.任何角都可以用一个字母表示
C.记角时可靠近顶点处加上弧线,注上数字表示
D.记角时可靠近顶点处加上弧线,注上希腊字母来表示
2. 下列说法中正确的是()
A.两条射线组成的图形叫做角
B.两边成一直线的角是平角
C.一条射线是一个周角
D.平角是一条直线
3. 四点这一时刻,分针和时针的夹角是()
A.70°B.75°C.90°D.120°
A、B、C、D、
4.下列说法中正确的有()
①由两条射线组成的图形叫做角②角的大小与边的长短无关,只与两条边张开的角度有关③角的两边是两条射线④把一个角放到一个放大10倍的放大镜下观看,角度数也扩大10倍
A、1个
B、2个
C、 3个
D、4个
5.下图中表示∠ABC的是()
二、填空题(每小题8分,共40分)
6.如下图,用大写字母表示图中用小写希腊字母标注的角,则∠α= __________ ,∠β=___________ ,∠γ=________,∠θ= ____________
7.图中以O为顶点的角有________ 个,它们是___________
8.如图,有一只蚂蚁从点A出发,按顺时针方向沿图所示的方向爬行,最后又爬回到A点,那么蚂蚁在此过程中共转_________°
9.下列说法错误的有________
①有公共点的两条射线形成的图形是角②从一点引出的两条射线形成的图形是角③角的大小与两边所画的长度有关④线段绕着一个端点旋转也可以形成角
10.如图所示,B处在A处的南偏西45°方向上,C处在A处的南偏东30°方向,C处在B处的北偏东60°,求∠ACB是_________度?
三、解答题(共20分)
11. 计算
如图,已知∠1=65°15′,∠2=78°30′,求∠3的度数。
12(1)在∠AOB内部画1条射线OC,则图1中有多少个不同的角;
(2)在∠AOB内部画2条射线OC,OD,则图2中有多少个不同的角;
(3)在∠AOB内部画3条射线OC,OD,OE,则图3中有多少个不同的角;(4)在∠AOB内部画10条射线OC,OD,OE…,则图中有多少个不同的角;(5)在∠AOB内部画n条射线OC,OD,OE…,则图中有多少个不同的角.
参考答案
一、选择题
1.B
【解析】A,C,D都符合角的表示方法的要求,B,当角的顶点处只有一个角时,才能用一个字母表示,B说法错误.
故选B
2.B
【解析】A选项,角由两条射线和这两条射线的公共顶点组成;B选项,是正确的,CD选项都混淆了角的概念,角是由两条射线和公共顶点组成。
故选B
3. D
【解析】钟表上,一周360°,四点是120°
故选
4.B
【解析】①错误,有公共端点的两条射线组成的图形才叫角②正确③正确④错误,放大镜下看角,角的度数没有发生变化,正确的有2个
故选B
5.C
【解析】A选项,是表示∠CAB,B选项不是角,C选项正确,D选项是∠ACD
故选C
二、填空题
6.∠A ,∠B,∠ADE ,∠ACF
【解析】考察角的表示方法。
7.5 ∠AOB ∠AOC ∠AOD ∠BOC ∠BOD ∠COD
【解析】数角的时候,先数一条边,再数另外的边,防止重复和漏掉。
8.1080°
【解析】观察图形,可知蚂蚁从出发到回到起点共旋转三个圆圈,
∴360°×3=1080°.
∴蚂蚁在此过程中共转了1080°的角.
9.①③④
【解析】①是有公共顶点的两条射线,②正确③角的大小与两边的长度无关④错误,角是射线
10.90
【解析】根据题意,得
∠BAE=45°,∠CAE=30°,∠DBC=60°,
∴∠BAC=∠BAE+∠CAE
=45°+30°
=75°.
∵AE∥DB,
∴∠DBA=∠BAE=45°,
∴∠ABC=∠DBC-∠DBA
=60°-45°
=15°,
∴∠ACB=180°-∠ABC-∠BAC
=180°-15°-75°
=90°.
故∠ACB为:90°.
三、解答题
11. 解:由图可知,∠1,∠2,∠3构成平角
即∠1+∠2+∠3=180°
所以∠3=180°-(∠1+∠2)
∠1+∠2=65°15′+78°30′
=143°45′
所以∠3=180°-143°45′=36°15′
12.解:(1)在∠AOB内部画1条射线OC,则图中有3个不同的角,故答案为:3.
(2)在∠AOB内部画2条射线OC,OD,则图中有6个不同的角,故答案为:6.
(3)在∠AOB内部画3条射线OC,OD,OE,则图中有10个不同的角,故答案为:10.(4)在∠AOB内部画10条射线OC,OD,OE,…,则图中有1+2+3+…+10+11=66个不同的角,故答案为:66.
(5)在∠AOB内部画n条射线OC,OD,OE,…,则图中有1+2+3+…+n+(n+1)=
(n+1)(n+2)/2个不同的角.故答案为:(n+1)(n+2)/2。
