等积法
三角形等面积法

三角形等面积法
在三角形的研究中,等面积法是一种十分实用的方法。
它的核心
思想是,对于一个给定的面积值,可以构造出许多不同形状的三角形,它们的面积都相等。
这种方法不仅可以用于解决一些几何问题,还可
以用于设计和制造一些具有特定面积要求的物体。
三角形等面积法的应用非常广泛。
例如,在制造船舶和飞机等大
型物体时,要求它们的底部具有一定的面积,以保证它们的浮力和飞
行稳定性。
这时可以利用等面积法来设计合适的底部形状,从而保证
其满足要求。
此外,在房屋建筑、道路修建和水利工程等领域中,三角形等面
积法也经常得到应用。
例如,在修建水库时,要求水库的底部形状必
须能够容纳一定数量的水,从而保证其正常运营。
通过等面积法,可
以设计出满足要求的水库底部形状。
在日常生活中,三角形等面积法也有着广泛的应用。
例如,在购
买面积相等但形状不同的房屋时,可以利用这种方法计算它们的真实
面积,从而作出更加准确的选择。
总的来说,三角形等面积法是一种非常实用的方法,它不仅可以
解决许多几何问题,还可以在实际工作中得到广泛应用。
因此,学好
这种方法对于我们的学习和职业生涯都非常重要。
椭圆中的等面积法

椭圆中的等面积法在几何学中,椭圆是一个广为研究的形状。
椭圆具有许多独特的性质,其中之一是其面积可以通过等面积法来计算。
等面积法是一种简单而有效的方法,可以用来确定椭圆的面积。
等面积法的原理等面积法的核心概念是将椭圆划分为一系列小区域,然后计算这些小区域的面积之和。
通过逐渐增加小区域的数量,我们可以趋近于椭圆的真正面积。
算法步骤以下是使用等面积法计算椭圆面积的步骤:1. 给定一个椭圆,确定一个适当的精度要求。
也就是说,决定将椭圆划分为多少个小区域。
2. 将椭圆等面积划分为一系列小区域。
可以通过将椭圆等分为多个扇形或椭圆弧来实现。
3. 对每个小区域,计算其面积。
这可以通过应用相应的数学公式来实现。
例如,对于一个椭圆弧,可以使用弧长和半短轴的乘积来计算面积。
4. 将所有小区域的面积相加,得到椭圆的近似面积。
5. 根据所设定的精度要求,如果近似面积已经满足精度要求,那么直接输出该近似面积。
否则,返回第二步,使用更小的小区域数量进行重新计算。
举例说明以下是一个简单的示例来说明等面积法的应用:假设我们有一个椭圆,其长轴长度为6单位,短轴长度为4单位。
我们希望使用等面积法来计算其面积。
1. 我们决定将椭圆划分为12个相等的扇形。
2. 对每个扇形,我们可以使用扇形面积公式来计算其面积。
3. 将所有扇形的面积相加,得到近似面积。
4. 如果近似面积已经满足我们的精度要求,我们结束计算并输出结果。
否则,我们可以继续增加扇形数量进行重新计算。
结论等面积法是一种简单而有效的方法,用于计算椭圆的近似面积。
通过将椭圆等分为小区域,并计算这些小区域的面积之和,我们可以逼近椭圆的真实面积。
这种方法可以根据所设定的精度要求进行调整,以获得所需的精确度。
在实际应用中,等面积法可以用于计算椭圆的面积,以及其他涉及等面积的几何形状的相关问题。
参考文献1. 冯华阳. (2013). 数学分析教程. 清华大学出版社.。
2021年中考数学必考点培优系列 14 等面积法的应用(有答案)

等面积法的应用在解决几何问题时,通常可采用等积法来解决一些问题,即同一个图形采用不同的面积表示方法来建立等式.等积法也常在证明某些定理时被用到.【例题讲解】例题1 已知:如图,在Rt △ABC 中,∠BAC =90°,AB =4,AC =3,AD ⊥BC ,求AD 的长为 .D CB A答案: AD =2.4.例题2、如图,E 是边长为1的正方形ABCD 的对角线上一点,且BE =BC ,P 为CE 上任意一点,PQ ⊥BC 于点Q ,PR ⊥BE 于点R ,则PQ +PR 的值为 .RQPEDCBA. 【解析】连接BP ,易知BEC S △=BEP S △+BCP S △,所以12·BE ·CM =12·BE ·PR +12·BC ·PQ ,由BC =BE ,等号两边同时约掉,剩下CM =PR +PQ ,所以CMBC. 连接BP ,过C 作CM ⊥BD , ∵BEC S △=BEP S △+BCP S △ =BC ×PQ ×12+BE ×PR ×12=BC ×(PQ +PR )×12=BE ×CM ×12, BC =BE , ∴PQ +PR =CM ,∵BE =BC =1,且正方形对角线BD又∵BC =CD ,CM =BD ,∴M 为BD 中点,又△BDC 为直角三角形, ∴CM =12BD,即PQ +PR. MR QPEDCBA【对于填空选择题,可用特殊值法!】例题3 如图,正方形ABCD 的边长为1,点P 为边BC 上任意一点(可与B 点或C 点重合),分别过B 、C 、D 作射线AP 的垂线,垂足分别是B '、C '、D ',则B B '+C C '+D D '的最大值为 ,最小值为 .PB'C 'D 'DCBA答案:2【解析】连接AC 、DP , ABCD S 正方形=1×1×1,由勾股定理得:AC∵AB =1, ∴1≤APDPC S ∆=APC S ∆=12AP ×C C ', 1=ABCD S 正方形=ABP S ∆+ADP S ∆+DPC S ∆=12AP (B B '+C C '+D D '), B B '+C C '+D D '=2AP, ∵1≤APB B '+C C '+D D '≤2,PB'C'D'D CBA【巩固练习】1、如图,点P为等边△ABC内任意一点,AB=2,则点P到△ABC三边的距离之和为 .2、如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE⊥BD,PE⊥AC,E、F分别是垂足,则PE+PF的长为.3、如图,D是Rt△ABC斜边AB上一点,且BD=BC=AC=1,P为CD上任意一点,PF⊥BC于点F,PE ⊥AB于点E,则PE+PF的值是 .4.如图,已知直线y=2x-2上有一动点Q,点P坐标为(-1,0),则PQ的最小值为 .【请用等积法】5.如图,在Rt △ABC 中,∠ABC =90°,点D 是斜边上的中点,点P 在AB 上,PE ⊥BD 于E ,PF ⊥AC 于F ,若AB =6,BC =3.,则PE +PF = .PFE D CBA6.将两个全等的直角三角形按图1所示摆放,其中∠DAB =90°,求证:a ²+b ²=c ².7.如图,在△ABC 中,∠ A =90°,D 是AC 上的一点,BD =DC ,P 是BC 上的任一点,PE ⊥BD ,PF ⊥AC ,E 、F 为垂足.求证:PE +PF =AB .PFE D CBA8.如图,平行四边形ABCD 中,AB : BC =3:2,∠DAB =60°,E 在AB 上,且AE : EB =1:2,F 是BC 的中点,过D 分别作DP ⊥AF 于P ,DQ ⊥CE 于Q ,求证:DP CEDQ AFQP FEDCBA图4 图59.在△ABC 中,AB =13,BC =14.(1)如图1,AD ⊥BC 于点D ,且BD =5,则△ABC 的面积为 ;(2)在(1)的条件下,如图2,点H 是线段AC 上任意一点,分别过点A ,C 作直线BH 的垂线,垂足为E ,F ,设BH =x ,AE =m ,CF =n ,请用含x 的代数式表示m +n ,并求m +n 的最大值和最小值.CBA HFEDCB A10.【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC 中,AB =AC ,点P 为边BC 上的任一点,过点P 作PD ⊥AB ,PE ⊥AC ,垂足分别为D 、E ,过点C 作CF ⊥AB ,垂足为F .求证:PD +PE =CF .FE PD CBA FGE PD CBAEFABC DP小军的证明思路是:如图2,连接AP ,由△ABP 与△ACP 面积之和等于△ABC 的面积可以证得:PD +PE =CF .小俊的证明思路是:如图2,过点P 作PG ⊥CF ,垂足为G ,可以证得:PD =GF ,PE =CG ,则PD +PE =CF .【变式探究】如图3,当点P 在BC 延长线上时,其余条件不变,求证:PD -PE =CF ; 请运用上述解答中所积累的经验和方法完成下列两题:【结论运用】如图4,将矩形ABCD 沿EF 折叠,使点D 落在点B 上,点C 落在点C 处,点P P 为折痕EF 上的任一点,过点P 作PG ⊥BE 、PH ⊥BC ,垂足分别为G 、H ,若AD =8,CF =3,求PG +PH 的值;C'PH GFEDCBA【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD 中,E 为AB 边上的一点,ED ⊥AD ,EC ⊥CB ,垂足分别为D 、C ,且AD ·CE =DE ·BC ,AB =,AD =3dm ,BD .M 、N 分别为AE 、BE 的中点,连接DM 、CN ,求△DEM 与△CEN 的周长之和.NM E DCBA参考答案1..2.答案:60 13.3.答案:2.【解析】如图所示,过C作CH AB⊥于H,D是Rt ABC∆斜边AB上一点,且1BD BC AC===,CH∴=∴111222BDCS BD CH∆==⨯=,又1111112222BCD BPC BPDS S S BD PE BC PF PE PF∆∆∆=+=+=⨯⨯+⨯⨯,PE PF∴+=.HPFDCBA4..【解析】如图,过点P作PQ⊥AB于点Q,过点Q作QC+QB,则∵y=2x-2∴A(0,-2),B(1,0)∵△PQB∽△AOB∴BQOB=PBAB∵AB,PB=2,OB=1∴1BQ∴BQ∴PQ.5.65如图作BM ⊥AC 于M ,连接PD .MPFE D CBA∵∠ABC =90°,AD =DC ,AB =6,BC =3, ∴BD =AD =DC ,AC 22AB BC +35 ∵12·AB ·BC =12·AC ·BM , ∴BM 65∴ABD S ∆=ADP S ∆+BDP S ∆, ∴12·AD ·BM =12·AD ·PF =12·BD ·PE , ∴PE +PF =BM 65MPFE D CBA6.答案:连接DB ,过点D 作BC 边上的高DF ,则DF =EC =b -a . ∵ADCB S 四边形=ACD S ∆+ABC S ∆=12b ²+12ab . 又∵ADCB S 四边形=ADB S ∆+DCB S ∆=12c ²+12a (b -a ) ∴12b ²+12ab =12c ²+12a (b -a ) ∴a ²+b ²=c ².FDBFb EA请参照上述证法,利用图2证明:a ²+b ²=c ².【解析】连结BD ,过点B 作DE 边上的高BF ,可得BF =b -a , ∵ACBED S 五边形=ACB S ∆+ABE S ∆+ADE S ∆=12ab +12b ²+12ab , 又ACBED S 五边形=ACB S ∆+ABD S ∆+BDE S ∆=12ab +12c ²+12a (b -a ), ∴12ab +12b ²+12ab =12ab +12c ²+12a (b -a ), ∴a ²+b ²=c ².Fb A7.【解析】过P 作PG ⊥AB 于G ,交BD 于O , ∵PF ⊥AC ,∠A =90°, ∴∠A =∠AGP =∠PF A =90°, ∴四边形AGPF 是矩形, ∴AG =PF ,PG ∥AC , ∵BD =DC ,∴∠C =∠GPB =∠DBP , ∴OB =OP ,∵PG ⊥AB ,PE ⊥BD , ∴∠BGO =∠PEO =90°, 在△BGO 和△PEO 中 BGO PEO GOB EOP OB OP ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BGO ≌△PEO , ∴PE =BG , ∵AB =BG +AG , ∴PE +PF =AB .G O P FED CBA8.【解析】连接DE 、DF ,∵根据三角形的面积和平行四边形的面积得:12DEC DFA ABCD S S S ∆∆==平行四边形,即12AF ×DF =12CE ×DQ ,∴AF ×DP =CE ×DQ , ∴DP CE DQ AF=. Q PFE DCB A9.【解析】(1)在Rt △ABD 中,AB =13,BD =5, ∴AD12.∵BC =14,∴ABC S △=12BC ·AD =12×14×12=84. 故答案为:84.(2)∵ABC S △=ABH S △+BHC S △, ∴12BH ·AE +12BH ·CF =84. ∴xm +xn =168.∴m +n =168x∵AD =12,DC =14-5=9,∴AC=15,∵m +n 与x 成反比,∴当BH ⊥AC 时,m +n 有最大值.∴(m +n )BH =AC ·BH .∴m +n =AC =15.∵m +n 与x 成反比,∴当BH 值最大时,m +n 有最小值.∴当点H 与点C 重合时m +n 有最小值.∴m +n =16814, ∴m +n 等于12.∴m +n 的最大值为15,最小值为12.10.【解析】【问题情境】证明:(小军的方法)连接AP ,如图②∵PD ⊥AB ,PE ⊥AC ,CF ⊥AB ,且ABC S △=ABP S △+ACP S △, ∴12AB ·CF =12AB ·PD +12AC ·PE . ∵AB =AC ,∴CF =PD +PE .(小俊的方法)过点P 作PG ⊥CF ,垂足为G ,如图②. ∵PD ⊥AB ,CF ⊥AB ,PG ⊥FC ,∴∠CFD =∠FDP =∠FGP =90°∴四边形PDFG 是矩形.∴DP =FG ,∠DPG =90°.∴∠CGP =90°∵PE ⊥AC ,∴∠CEP =90°,∴∠PGC =∠CEP .∵∠BDP =∠DPG =90°,∴PG ∥AB .∴∠GPC =∠B .∵AB =AC ,∴∠B =∠ACB .∴∠GPC =∠ECP .在△PGC 和△CEP 中,PGC CEP GPC ECP PC CP ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△PGC ≌△CEP .∴CG =PE .CF =CG +FG=PE +PDG E P FDC BA【变式探究】证明:连接AP ,如图③.∵PD ⊥AB ,PE ⊥AC ,CF =AB ,且ABC S △=ABP S △-ACP S △, ∴12AB ·CF =12AB ·PD -12AC ·PE . ∵AB =AC ,∴CF =PD -PE .GE FABC DP【结论运用】过点E 作EQ ⊥BC ,垂足为Q ,如图④,∵四边形ABCD 是矩形,∴AD =BC ,∠C =∠ADC =90°.∵AD =8,CF =3,∴BF =BC -CF =AD -CF =5.由折叠可得:DF =BF ,∠BEF =∠DEF .∴DF =5.∵∠C =90°,∴DC=4.∵EQ ⊥BC ,∠C =∠ADC =90°,∴∠EQC =90°=∠C =∠ADC .∴四边形EQCD 是矩形.∴EQ =DC =4.∵AD ∥BC ,∴∠DEF =∠EFB .∵∠BEF =∠DEF ,∴∠BEF =∠EFB .∴BE =BF .由问题情境中的结论可得:PG +PH =EQ .∴PG +PH =4.∴PG +PH 的值为4.Q C 'P H G FEDCB A【迁移拓展】延长AD 、BC 交于点F ,作BH ⊥AF ,垂足为H ,如图⑤. ∵AD ·CE =DE ·BC , ∴AD DE =BC EC . ∵ED ⊥AD ,EC ⊥CB ,∴∠ADE =∠BCE =90°.∴△ADE ∽△BCE .∴∠A =∠CBE .∴F A =FB .由问题情境中的结论可得:ED +EC =BH .设DH =x dm ,则AH =AD +DH =(3+x )dm .∵BH ⊥AF ,∴∠BHA =90°.∴BH ²=BD ²-DH ²=AB ²-AH ².∵AB=AD =3,BDx²=()²-(3+x )².解得:x =1.∴BH ²=BD ²-DH ²=37-1=36.∴BH =6dm.∴ED +EC =6.∵∠ADE =∠BCE =90°,且M 、N 分别为AE 、BE 的中点,∴DM =AM =EM =12AE ,CN =BN =EN =12BE . ∴△DEM 与△CEN 的周长之和=DE +DM +EM +CN +EN +EC=DE +AE +BE +EC=DE +AB +EC=DE +EC +AB=6+∴△DEM 与△CEN 的周长之和为(6+dm . FHNM E DC BA。
综合与实践 面积与代数恒等式(等面积法)

问题分析与解决
问题分析
首先需要明确问题的背景和要求, 分析问题所涉及的数学知识点, 包括面积和代数恒等式的概念、 性质和应用。
解决方案设计
根据问题分析,设计合适的解决方 案,包括选择适当的数学方法和公 式,建立数学模型,并确定解题步 骤。
实施解决方案
按照设计的解决方案进行计算和推 理,得出积表示为基底与高的乘积。对于更复杂的图形,可 以通过分割、重组或近似等方法将其转化为简单的几何图形,再利用基底和高 的关系计算面积。
恒等式的几何意义
恒等式是数学中一个重要的概念,它描述了数或代数式之间 的等价关系。
恒等式的几何意义是将代数关系转化为几何图形。通过将代 数恒等式中的变量视为几何图形中的长度、角度或面积等参 数,可以直观地理解恒等式的几何意义。
课程展望
未来发展方向
研究等面积法在解决复杂 问题中的新方法和技巧。
培养学生对数学知识的综 合运用能力。
01
02
03
04
05
06
探索面积与代数恒等式在其 他数学分支的交叉应用。
学生能力培养
提高学生的数学建模和解 决实际问题的能力。
THANKS
感谢观看
面积与代数恒等式的概念及其 关系。
重点与难点解析
难点:如何运用等面积法解决 实际问题。
后续学习建议
深化知识点
01
探索等面积法在解决复杂问题中的技巧和 策略。
03
02
进一步研究面积与代数恒等式在其他数学领 域的应用。
04
实践与应用
结合实际问题,运用等面积法进行建模和 求解。
05
06
参与数学建模竞赛,提高解决实际问题的 能力。
解决方案的验证与优化
初二数学等面积法练习题

初二数学等面积法练习题一、简答题:1. 什么是等面积法?等面积法是一种通过等面积关系来解决数学问题的方法。
在几何学中,图形的面积是指图形所占有的平面面积的大小。
等面积法通过将一个图形分解成若干个已知面积的简单图形,或将一个已知面积的图形组合起来,从而求解未知的面积或其他相关量。
二、计算题:1. 如图所示,正方形ABCDE的边长为2cm,点M、N、P分别位于AE、BC、CD上,且AM = BN = CP。
求MN和NP的长度。
(图省略)解:首先,我们需要找到一个能分解成已知面积的简单图形。
由于正方形的面积为边长的平方,所以正方形ABCDE的面积为2^2 =4cm^2。
根据题目中所给的条件,AM = BN = CP,可以得知三角形AMP、BNQ和CPR的面积相等,且等于正方形ABCDE的面积的一半,即2cm^2。
将正方形ABCDE分解成三角形AMP、BNQ和CPR,如图所示:(图省略)由于三角形AMP、BNQ和CPR的面积相等,所以它们的高相等。
且可以观察到三角形AMP和三角形BNQ以及三角形AMP和三角形CPR是全等的,所以它们的底边相等。
因此,MN = NP,而且MN + NP = 2cm,所以MN和NP的长度均为1cm。
2. 如图所示,矩形ABCD的长为6cm,宽为4cm,矩形XYUT的长为3cm,宽为x cm。
若矩形XYUT的面积等于矩形ABCD的面积的一半,求矩形XYUT的宽度。
(图省略)解:首先,计算矩形ABCD的面积为6cm × 4cm = 24cm^2。
根据题目中所给的条件,矩形XYUT的面积等于矩形ABCD的面积的一半,即24cm^2的一半,也就是12cm^2。
设矩形XYUT的宽度为y cm,则矩形XYUT的面积为3cm × y cm = 12cm^2。
解上述方程可以得到y = 4cm,所以矩形XYUT的宽度为4cm。
三、实际应用题:1. 某公司拥有一块形状为长方形的土地,长为20m,宽为15m。
等积法的应用

等积法的应用以等积法的应用为标题,我们来探讨一下等积法在实际生活中的应用。
等积法是一种数学解题方法,常常用于解决几何问题。
它基于一个基本原理:如果两个形状的面积相等,那么它们的某些特征也相等。
这个原理在解决各种实际问题中非常有用,下面我们将介绍几个例子来说明等积法的应用。
等积法在建筑设计中有着广泛的应用。
设计师在进行建筑设计时,常常需要考虑到建筑物的比例和平衡性。
通过运用等积法,设计师可以根据建筑物的总体面积和布局,确定各个部分的大小和位置。
例如,在设计一座大厦时,设计师可以通过等积法来确定每层的面积和高度,从而使整个建筑在视觉上更加和谐和平衡。
等积法在农业生产中也有着重要的应用。
农民在进行农田规划时,需要合理安排不同作物的种植面积和间距,以提高土地的利用效率。
通过运用等积法,农民可以根据作物的需求和农田的面积,确定每种作物的种植面积,以达到最佳的产量和质量。
同时,等积法也可以帮助农民确定灌溉系统的设计,以确保每块土地都能得到适当的水源供应。
等积法还可以应用于交通规划和城市规划中。
在规划道路和交叉口时,交通工程师需要考虑到不同道路的通行能力和流量。
通过等积法,他们可以根据道路的宽度和长度,确定合适的车道数量和交叉口的布局,以提高交通系统的效率和安全性。
类似地,在城市规划中,等积法可以帮助规划师确定不同区域的用地面积,从而实现城市的合理布局和功能分区。
等积法还可以应用于商业领域。
在零售业中,商家常常需要决定不同商品的陈列位置和面积。
通过等积法,他们可以根据商品的销售额和利润率,确定每种商品的陈列面积和位置,以最大化销售量和利润。
此外,在广告设计中,等积法也可以用来确定不同元素的尺寸和位置,以实现视觉效果的平衡和吸引力。
等积法在实际生活中有着广泛的应用。
无论是建筑设计、农业生产、交通规划还是商业领域,等积法都可以帮助我们解决各种问题,并找到最优解决方案。
通过合理运用等积法,我们可以提高效率、优化资源利用,并实现更好的结果。
【例题讲解】“等积法”求面积例 完整版课件
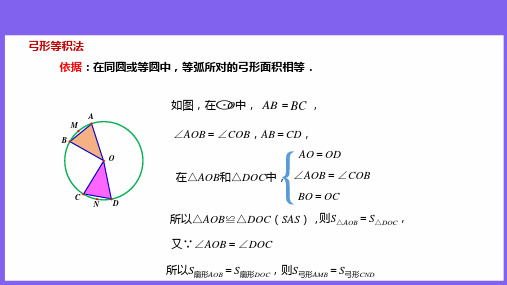
A M B
O
C ND
如图,在 O中, AB =BC ,
∠AOB=ห้องสมุดไป่ตู้COB,AB=CD, AO=OD
在△AOB和△DOC中, ∠AOB=∠COB BO=OC
所以△AOB≌△DOC(SAS),则S△AOB=S△DOC, 又∵∠AOB=∠DOC
所以S扇形AOB=S扇形DOC,则S弓形AMB=S弓形CND
∴∠AOE= ∠COD, ∴AE=CD=4, S弓形AME=S弓形CND,
在Rt△ABE中,根据勾股定理可得:BE2=AE2+AB2,∴BE= 82 42=4 5 .
∴S阴影=S半圆-SRt△ABE
=1 2
π
4
5 2
2
1 2
8
4=10
π-16.
主要利用了等弧所对的弓形面积相等,将阴影面积进行等积变换,起到简化的作用.
再见
例 点A、B、C、D是圆周上四点,AB CD AC BD ,弦AB=8,CD=4,求两个阴影部分的
面积之和.
A
B
分析
连接AE
弦AE等于弦CD
S弓形AME = S弓形CND
M
O
D
E
N
C
解答 作圆O的直径BE,连接AE,OA,OC,OD 则∠BAE=90°
∵ AB CD AC BD ∴∠AOB+∠COD= ∠AOC+∠BOD=180°, ,∵ ∠AOB+∠AOE=180°,
等面积法例题初二数学

等面积法例题初二数学摘要:一、等面积法基本概念1.等面积法的定义2.等面积法在初二数学中的应用二、等面积法例题解析1.例题一1.题目描述2.解题思路3.解题步骤2.例题二1.题目描述2.解题思路3.解题步骤3.例题三1.题目描述2.解题思路3.解题步骤三、等面积法在数学中的意义1.等面积法在几何证明中的应用2.等面积法在实际问题中的应用四、等面积法的学习方法与技巧1.掌握基本概念2.多做例题练习3.培养空间想象力正文:一、等面积法基本概念等面积法,是数学中一种常用的解题方法。
它是指在解决数学问题时,如果已知两个或多个图形的面积相等,那么可以通过面积相等这一条件,推导出其他相关量之间的关系。
在初二数学中,等面积法常常应用于几何证明和实际问题解决。
二、等面积法例题解析为了更好地理解等面积法的应用,我们通过以下三个例题来进行解析:例题一:已知矩形ABCD的面积为12平方厘米,矩形EFGH的面积为6平方厘米,若矩形ABCD与矩形EFGH的长和宽之和相等,求矩形ABCD与矩形EFGH的长和宽。
解题思路:由于已知矩形ABCD与矩形EFGH的面积之和,我们可以利用等面积法,设矩形ABCD的长为x,宽为y,矩形EFGH的长为a,宽为b,则有xy=ab=12和x+y=a+b。
通过解这个方程组,我们可以求得矩形ABCD与矩形EFGH的长和宽。
解题步骤:1.根据已知条件列出方程组:xy=12, x+y=a+b2.将第一个方程变形得到:y=12/x,代入第二个方程得到:x+12/x=a+b3.化简得到:x^2-ab+12=04.求解得到:x=2, y=6, a=3, b=2所以,矩形ABCD的长为2厘米,宽为6厘米,矩形EFGH的长为3厘米,宽为2厘米。
例题二:已知等腰三角形ABC,底边BC=6厘米,高AD=8厘米,求等腰三角形ABC的面积。
解题思路:由于已知等腰三角形ABC的底边和高,我们可以利用等面积法,设等腰三角形ABC的腰长为x,则有x^2=8^2+(6/2)^2=64+9=73。
