浙教版数学七年级上册2.5《有理数的乘方1》教案
浙教版初中数学七年级上册 2.5 有理数的乘方 教案
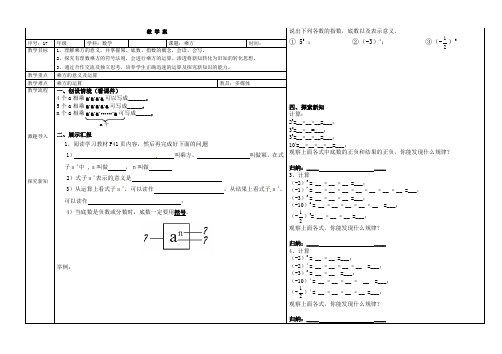
教 学 案说出下列各数的指数,底数以及表示意义。
① 53 ; ②(-3)4; ③(-21)3四、探索新知 计算:23=__×__×__=___; 32=__×__=___;33=__×__×__=___;104=__×__×__×__=___;观察上面各式中底数的正负和结果的正负,你能发现什么规律?归纳:____ ____3、计算(-2)3 = __ × __ × __ =___;(-1)7 = __ × __ × __ × __ × __ × __ × __ =___;(-3)3 = __ × __ × __ =___;(-10)5 = __ × __ × __ × __ × __ =___;(-21)3= __ × __ × __ =___;观察上面各式,你能发现什么规律?归纳:____ ____ 4、计算 (-2)2= __ × __ =___; (-2)4= __ × __ × __ × __ =___; (-3)2 = __ × __ =___; (-10)4 = __ × __ × __ × __ =___; (-21)4 = __ × __ × __ × __ =___; 观察上面各式,你能发现什么规律? 归纳:____ ____序号:17 年级 学科:数学 课题:乘方时间:教学目标 1、理解乘方的意义,并掌握幂、底数、指数的概念,会读、会写。
2、探究有理数乘方的符号法则,会进行乘方的运算。
渗透将新知转化为旧知的转化思想。
3、通过合作交流及独立思考,培养学生正确迅速的运算及探究新知识的能力。
2.5.1 有理数的乘方 浙教版数学七年级上册课件

(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的正整数次幂都是零
4.注意: an与 an 二者的区别及相互关系;
b
n
与
b
n
的区别.
a a
a
a
你会算正方形的面积和正方体的体积吗?
(1)正方形的面积计算公式:S = a×a
a × a 简记作 a,2 读作a的平方(或二次方)
(2)正方体的体积计算公式:V = a×a×a
a × a × a 简.记作 a3, 读作a的立方(或三次方)
★ 类似的,n个相同的因数a相乘,记作an,即
n个a
a× a ×...× a= an
10个a
(3)34 底数、指数、幂分别是多少? 34 的底数是3,指数是4,幂是81
(4)3的底数、指数、幂分别是多少? 3的底数是3,指数是1,幂是3
典例精析
例1.计算: (1)(4)3
(2)(2)4
解:(1)(4)3 (4) (4) (4) 64
(2)(2)4 (2) (2) (2) (2) 16
6. 10n (n为正整数)表示的数是
A.10个n相乘的积 B. n 个10相乘的积 C.1后面有(n-1)个零 D.1后面有(n+1)个零
( B)
课堂小结
1.这种求几个相同因数的积的运算,叫做乘方,
乘方的结果叫做幂. a n中,a叫做底数,n叫做指数. 2.乘方的读法: a n 读作a的n次方,看作a的n次方的
2.5.1 有理数的乘方
教学目标
1.在现实背景中,理解有理数乘方的意义. 2.能进行有理数的乘方运算,掌握幂的符号法则. 3.了解用计算器进行乘方运算.
浙教版七年级上2-5有理数的乘方1教案

的平方等于本身,的立方等于本身。
10、用“>”、“<”或“=”填空
①若a<0,则a30; ②若a<0,则a60;
③若a>0,则a50; ④若a=0,则a100;
⑤若a3<0,则a0; ⑤若a4>0,则a0或a0
课后反馈
教 学 过 程
二、3达标导学
1、含乘方运算的混合运算
作业:课后练习及作业本
教
后
随
笔
对科学记数法的书写时中的表达形式 中的a的表达有些同学超过了a的范围,如写成了 等,还有用科学记数法表示1000000,表示为 ,应该表示成
指导
教师
意见
签字:年月日
学校
抽查
意见
签字:年月日
练习:课本P112练习1、2
5、例4如果平均每人每天需要粮食0.5千克,那么全国每天大约需要粮食多少千克一年呢(全国人口约13亿人,结果用科学记数法表示)
解:见书本50页
三、评价总结:本节课学习了含乘方运算的混合运算,运算顺序是先乘方,后乘除,再加减,有括号先算括号内的。在科学记数法中,把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,n比原数的整数位数少1。
教具准备
乘方运算。
2、(-3)5中,-3是,5是,幂是
3、计算:102=,103=,104=,105=
4、(-2)4=,-24=,25=。
5、 =, =
6、2×32=,(2×3)2=,
7、1101=,(-1)101=,0101=。
8、 =, =, =, =。
教 师 备 课 笔 记
上课日期9月20日星期二
课 题
有理数的乘方(二)
课时安排
有理数的乘方(1)(学案)浙教版数学七年级上册

课题
有理数的乘方
单元Байду номын сангаас
2
学科
数学
年级
七年级
知识目标
⒈在现实背景中,理解有理数乘方的意义,掌握有理数乘方的运算。
⒉培养学生观察、分析、比较、归纳、概括的能力,渗透转化的思想。
重点难点
重点:正确理解乘方的意义,掌握乘方的运算法则,进行有理数乘方运算。
难点:正确理解乘方、底数、指数的概念并合理运算。
结论:积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘.
(3)①(-0.125)2014×(-8)2014
=[(-0.125)×(-8)]2014=12014=1;
② × = × =(-1)2015=-1.
三、教材第49页
例1、(1) (-3)23(3) (4)
想一想:幂的符号与指数有怎样的关系?
四、教材第50页
例2 计算:
(1) (2)3× (3) (4)8÷
总结:
有理数的运算法则:。
自主尝试
1.式子(-2)5表示( )
A.5乘以(-2)的积 B.5个(-2)连乘的积
C.2个-5相乘的积 D.5个(-2)相加的和
8. 定义一种新的运算a﹠b=ab,如2﹠3=23=8,那么请试求(3﹠2)﹠2=.
9. 计算:(1) ;(2) ;(3)
10. 已知|x-2|+(y+3)2=0,求(x+y)2016和( )x的值.
11. (1)看一看下面两组式子:(3×5)2与32×52,[(- )×4]2与(- )2×42,每组两个算式的计算结果是否相等?
A.1个 B.2个 C.3个 D.4个
4.2615个位上的数字是 ( )
浙教版数学七年级上册2.5《有理数的乘方》(第1课时)教学设计

浙教版数学七年级上册2.5《有理数的乘方》(第1课时)教学设计一. 教材分析《有理数的乘方》是浙教版数学七年级上册第2.5节的内容,主要介绍了有理数的乘方概念、性质及运算法则。
这部分内容是学生学习数学的基础,对于培养学生的逻辑思维和抽象思维能力具有重要意义。
本节内容与现实生活紧密相连,有利于激发学生的学习兴趣。
二. 学情分析七年级的学生已具备一定的数学基础,掌握了有理数的加减乘除运算。
但学生对于乘方的概念和性质可能较为抽象,需要通过具体的例子和实际操作来理解和掌握。
此外,学生的学习习惯和思维方式各有不同,需要教师在教学中善于引导和调动学生的积极性。
三. 教学目标1.理解有理数的乘方概念,掌握有理数乘方的性质和运算法则。
2.能够运用乘方知识解决实际问题,提高学生的数学应用能力。
3.培养学生的逻辑思维和抽象思维能力,提高学生的数学素养。
4.激发学生学习数学的兴趣,养成良好的学习习惯。
四. 教学重难点1.有理数的乘方概念和性质的理解。
2.有理数乘方的运算法则的掌握。
3.乘方知识在实际问题中的应用。
五. 教学方法1.情境教学法:通过生活实例引入乘方概念,激发学生学习兴趣。
2.引导发现法:教师引导学生发现乘方的性质和运算法则,培养学生的自主学习能力。
3.实践操作法:让学生通过实际操作,加深对乘方知识的理解和掌握。
4.巩固拓展法:通过课堂练习和课后作业,巩固所学知识,提高学生的应用能力。
六. 教学准备1.教学PPT:制作包含乘方概念、性质和运算法则的PPT,以便于课堂展示和讲解。
2.教学案例:准备一些与生活紧密相关的乘方实例,以便于引导学生学习和应用。
3.练习题:准备一些有针对性的练习题,以便于课堂练习和课后巩固。
七. 教学过程1.导入(5分钟)利用生活实例引入乘方概念,如“2的3次方表示3个2相乘,即2×2×2=8”。
通过实例让学生感受乘方的意义,激发学生的学习兴趣。
2.呈现(10分钟)呈现乘方的性质和运算法则,如“乘方的性质:a m×a n=a(m+n);乘方的运算法则:a m÷a n=a(m-n)”。
2.5 有理数的乘方七年级上册数学浙教版

2.5 有理数的乘方
七上数学 ZJ
1.理解有理数乘方的意义,掌握乘方、幂、指数、底数等概念,发展抽象能力。2.会进行有理数的乘方运算,强化运算能力。3.会用科学记数法表示较大的数,会将用科学记数法表示的数还原。
概念
示例
乘方
求几个相同因数的积的运算,叫作乘方。(乘方是一种运算,幂是乘方的结果)
典例2 计算:
(1);
解: 。
(2) ;
解: 。(底数为分数时,要带括号)
注意与 区别
(3) ;
解: 。(底数为分数时,要带括号)
(5) ;
解: 。
(6) 。
解: 。
(4) ;
解: 。
求带分数的乘方时,要先将带分数转化成假分数再计算
对于乘除和乘方的混合运算,应先算乘方,后算乘除;如果遇到括号,就先进行括号里的运算。
个 相乘的积记作
底数可以是任意有理数,指数 是正整数。
概念
示例
幂
乘方的结果叫作幂。
_
底数
在中, 叫作底数。
指数
在中, 叫作指数。
敲黑板(1)一个数可以看作这个数本身的一次方。例如,5就是 ,指数1通常省略不写。(2)指数是2时读作平方或二次方,指数是3时读作立方或三次方。例如,通常读作“5的平方”,也可以读作“5的二次方”; 通常读作“5的立方”,也可以读作“5的三次方”。
敲黑板(1)用科学记数法表示一个带单位的数时,其表示的结果也应该带单位且前后应该一致。(2)用科学记数法表示负数的方法和表示正数的方法一样,只需前面加一个“-”即可。(3)“万”可转化为,“亿”可转化为 。
3.把用科学记数法表示的数还原:(1)中的指数 加上1就得到原数的整数位数,从而确定原数。(2)把中的小数点向右移动 位即可,若向右移动的位数不够,则用“0”补足。
浙教版数学七年级上册2.5《有理数的乘方》(第2课时)教学设计

浙教版数学七年级上册2.5《有理数的乘方》(第2课时)教学设计一. 教材分析浙教版数学七年级上册2.5《有理数的乘方》(第2课时)的教学内容主要是有理数的乘方运算。
这部分内容是在学生已经掌握了有理数的加减乘除、乘方概念等知识的基础上进行学习的,是对有理数运算的进一步拓展和深化。
通过这部分的学习,学生能够掌握有理数乘方的法则,解决实际问题,并为后续学习指数运算、对数等知识打下基础。
二. 学情分析七年级的学生已经具备了一定的数学基础,能够理解和掌握有理数的加减乘除运算。
但是,对于有理数的乘方,学生可能还存在一定的困难,例如理解乘方的概念、掌握乘方的法则等。
因此,在教学过程中,需要教师耐心引导,通过例题、练习等环节,帮助学生理解和掌握有理数的乘方运算。
三. 教学目标1.知识与技能:使学生理解和掌握有理数的乘方概念和乘方法则,能够熟练地进行有理数的乘方运算。
2.过程与方法:通过自主学习、合作交流等环节,培养学生的数学思维能力和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的耐心和细心,使学生感受到数学的美妙和实用。
四. 教学重难点1.教学重点:有理数的乘方概念和乘方法则。
2.教学难点:理解有理数乘方的实质,熟练地进行有理数的乘方运算。
五. 教学方法1.情境教学法:通过生活实例、问题情境等,引发学生的兴趣和思考,引导学生理解和掌握有理数的乘方运算。
2.自主学习法:鼓励学生自主探索、合作交流,培养学生的数学思维能力和解决问题的能力。
3.练习法:通过大量的练习,使学生熟练掌握有理数的乘方运算。
六. 教学准备1.教材:浙教版数学七年级上册。
2.教具:黑板、粉笔、多媒体设备等。
3.学具:练习本、笔等。
七. 教学过程1.导入(5分钟)教师通过生活实例或者问题情境,引发学生的兴趣和思考,如“计算一辆车行驶100公里需要的时间,如果速度是每小时60公里,那么100公里需要多少小时?”让学生认识到有理数乘方的重要性。
浙教版数学七年级上册2.5《有理数的乘方》教学设计1

浙教版数学七年级上册2.5《有理数的乘方》教学设计1一. 教材分析《有理数的乘方》是浙教版数学七年级上册第二章第五节的内容,主要介绍了有理数的乘方概念、性质及其运算方法。
这部分内容是有理数的重要组成部分,也是进一步学习函数、方程等数学知识的基础。
本节课的内容对于学生来说比较抽象,需要通过实例和练习让学生理解和掌握有理数的乘方。
二. 学情分析七年级的学生已经学习了有理数的基本概念和运算,对于简单的数学运算已经有一定的基础。
但是,对于有理数的乘方,学生可能初次接触,理解起来较为困难。
因此,在教学过程中,需要通过实例和练习让学生逐步理解和掌握有理数的乘方。
三. 教学目标1.理解有理数的乘方概念,掌握有理数的乘方性质。
2.能够熟练进行有理数的乘方运算。
3.培养学生的数学思维能力,提高学生的数学素养。
四. 教学重难点1.有理数的乘方概念及其性质。
2.有理数的乘方运算方法。
五. 教学方法1.情境教学法:通过实例和问题情境,引发学生的思考,激发学生的学习兴趣。
2.启发式教学法:引导学生主动探索,发现有理数的乘方规律。
3.练习法:通过大量的练习,让学生巩固所学知识,提高运算能力。
六. 教学准备1.PPT课件:制作有关有理数乘方的PPT课件,包括概念、性质、运算方法等内容。
2.练习题:准备一些有关有理数乘方的练习题,用于课堂练习和课后作业。
七. 教学过程1.导入(5分钟)利用PPT课件展示有理数的乘方实例,引导学生思考有理数乘方的意义和性质。
2.呈现(10分钟)讲解有理数的乘方概念,阐述有理数乘方的性质,让学生理解和掌握。
3.操练(10分钟)让学生进行有理数乘方运算的练习,教师巡回指导,解答学生的疑问。
4.巩固(10分钟)通过一些典型例题,让学生进一步巩固有理数乘方的运算方法。
5.拓展(10分钟)利用有理数乘方的知识,解决实际问题,培养学生的数学应用能力。
6.小结(5分钟)对本节课的内容进行总结,让学生明确有理数乘方的概念、性质和运算方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《有理数的乘方一》教案
教学目标
1、在现实背景中理解有理数乘方的意义;
2、正确理解底数、指数和幂的概念;
3、会进行有理数的乘方运算.
教学重点
学会进行有理数的乘方运算.
教学过程
一、情境引入
情境1:
将一张报纸对折1次变成2层;对折2次变成2×2层;对折3次变成 层;对折4次变成 层;……对折8次变成 层;
情境2:
1根面条拉扣1次成 根;拉扣2次成 根;拉扣3次成 根; ……拉扣6次成 根;……拉扣n 次成多少根?该怎样表示?
你还能举出类似的例子吗?
二、新知展开
1、乘方的表示:
2×2×2×2×2×2记作 ,读作 ;
5×5×5×5记作 ,读作 ;
类似地:a a a a ⋅⋅⋅⋅ 记作 ,读作 ;
a n 个
2、乘方的定义:
(1)观察上面几个式子有什么特点?
(2)定义:求相同因数的积的运算叫做 ,乘方运算的结果叫 .
3、认识底数、指数、幂.
4、练一练:
(1)把下列相同因数的乘积写成幂的形式,并说出底数和指数.
(-6)×(-6)×(-6)记作 ,底数是 ,指数是 .
3
232323232⨯⨯⨯⨯,记作 ,底数是 ,指数是 .
12个
)2()2()2()2(-⨯⨯-⨯-⨯- 记作 ,底数是 ,指数是 . 注意:当底数是负数和分数时,底数应 .
(2)把5)21(-写成几个相同因数相乘的形式.
5、例题教学
计算343
6)4()4()3()3(7)2(2)1(-- 计算43
5)3
2()3()53()2()21
()1(- 6、负数的幂的符号的确定.
(1)计算:
______2
1_____21_____)1(_____)1(54710==-=-)、(-=)(-、、 (2)思考:负数的幂的符号与什么有关?如何确定负数的幂的符号?
小结:
正数的任何次幂都是 ;
负数的奇次幂是 ,负数的偶次幂是 .
7、计算:3222
3)3(3)3()3(18)2(43)1(----÷-+
三、活学活用,解决难题
现在来解决棋盘摆米的数学问题:
第一格放2粒米,即12粒
第二格放4粒米,即22粒
第三格放8粒米,即32粒
……
第六十四格放________米,即642粒,用计算器验证一下第六十四格要放多少粒米? 以此类推,最后一格——第六十四格里是2连乘63次,大约等于922亿亿粒.如一斤米以两万粒计算,就合461万亿斤!将全中国的耕地都拿来种稻米,要好几百年才能收这么多.如果将前面的63格里的米粒也算在内,总数还要增加近一倍!这就是指数的威力,难怪国王不知所措了.
四、课堂练习
1、4)3(-表示 ,34-表示 ;
2、平方等于16的数是 ,立方等于8的数是 ;。
