水力学第五章 第六节
合集下载
流体力学 水力学 第五章

7 H [H0 ] 9m 0.75
§5.3 有压管道恒定流 5.3.1 短管水力计算(Q、d、H) 有压流:水沿管道满管流动的水力现象。 特点:水流充满管道过水断面,管道内不存在自 由水面,管壁上各点承受的压强一般不等于大 气压强。
短管:局部水头损失和 速度水头在总水头损失 中占有相当的比重,计 算时不能忽略的管道. (一般局部损失和速度 水头大于沿程损失 的5% ~ 10%)。一般L/d 1000
1 vc c 0
v
2 0 0
2 gH 0 2 gH 0
v hw h j 2g p c pa
2 c
1 1 流速系数: c 0 1 0
1 1 流速系数: c 0 1 0
实验得: 0.97 ~ 0.98 1 推求: 0 2 1 1 0.06 2 0.97 1
2
d2
5.126m 2g
例5 3:如图所示圆形有压涵管,管长50m, 上下游水位差3m 沿程阻力系数为0.03,局部阻力系数:进口 1=0.5。 第一个转弯 2=0.71,第二个转弯 3=0.65,出口
4=1.0,要求涵管通过流量大约3m 3 / s, 试设计管径d。
2 1 1
2g
v
v
2 2 2
2 2 2
2g
hw
2g
hw
H0 H
v
2 1 1
2g
v
2 2 2
2g
hw
hw h f h j (
l v
v d 2g 2g
2
2
l
v ) d 2g
水力学第五章 有旋流动和有势流动

定义
数。
M(x,y,z)
( x, y, z ) = + u x d x + u y d y + u z d z
M 0 ( x0 , y0 , z 0 )
u x =
x
u y =
y
u z =
z
无旋流动
ij ×u=
xy
xy
无旋流动
k
=0 z
z
等价
有势流动
u=
有势流动
u(t)
u(t+dt)
L是由确定流体质点组成的封闭线,是 一个系统,在流动中会改变位置和形状。
简要的证明
dΓ
du
dt
+ d t d l
L
d dt
+
L
u
δ
l
d
+ d t (u δ l)
L
+
L
d
t
δ
d
lL++
δu
2
du
dl
du
+ d t δ l + + u δ d t + d t δ l + + u δ u
=
( uz
u y) + ( ux
uz ) +
uy (
xy z yz x zx
ux ) = 0 y
由于涡管侧壁没有涡 通量,所以根据涡量场是 无源场可得如下结论:
结论 在同一时刻,穿 过同一涡管的各断面的涡 通量都是相同的。即同一 时刻,一根涡管对应一个 涡管强度。
回答了前面的问题
第五章_给水管网水力分析

管段的水力特性方程: 管段的水力特性方程:hi=siqin 可将管段流量与水头相互转换, 个方程。 可将管段流量与水头相互转换,即N 个未知量对应 N 个方程。 管段流量 相互转换
(3)必须至少有一个定压节点 )
• 管网中无定压节点(R=0)时,恒定流方程组无 管网中无定压节点( ) 解。 • 因为若 j*为方程组解, Hj* +∆H仍为方程组的 因为若H 为方程组解 为方程组解, 仍为方程组的 解,即方程组无解。 即方程组无解。
(H + ∆H ) − (H + ∆H ) = H − H = h
* Fi * Ti * Fi * Ti
* i
5.3 单定压节点树状管网水力分析
比较简单, 比较简单,管段流量可以由节点流量连续性方程 组直接求出,不要求解非线性的能量方程组。 组直接求出,不要求解非线性的能量方程组。 水力分析计算分两步(P89例题 ): 例题5.1): 水力分析计算分两步( 例题 • 1、用流量连续性条件计算管段流量,并计算出管 、用流量连续性条件计算管段流量, 段压降; 段压降; • 2、根据管段能量方程和管段压降,从定压节点出 、根据管段能量方程和管段压降, 发推求各节点水头。 发推求各节点水头。
可以看出:树状网中,各管段流量 可以看出:树状网中,各管段流量qi可以用节点流 表示出来。 量Qj表示出来。
5.1.2 管段能量方程(根据能量守恒定律) 根据能量守恒定律)
管段两端节点水头之差等于该管段的压降: 管段两端节点水头之差等于该管段的压降: HFi –HTi= hi i-1,2,…,M
HFi——管段 的上端点水头; 管段i的上端点水头 管段 的上端点水头; HTi——管段 的下端点水头; 管段i的下端点水头; 管段 的下端点水头 hi——管段 的压降; 管段i的压降 管段 的压降; M——管段模型中的管段总数。 管段模型中的管段总数。 管段模型中的管段总数
(3)必须至少有一个定压节点 )
• 管网中无定压节点(R=0)时,恒定流方程组无 管网中无定压节点( ) 解。 • 因为若 j*为方程组解, Hj* +∆H仍为方程组的 因为若H 为方程组解 为方程组解, 仍为方程组的 解,即方程组无解。 即方程组无解。
(H + ∆H ) − (H + ∆H ) = H − H = h
* Fi * Ti * Fi * Ti
* i
5.3 单定压节点树状管网水力分析
比较简单, 比较简单,管段流量可以由节点流量连续性方程 组直接求出,不要求解非线性的能量方程组。 组直接求出,不要求解非线性的能量方程组。 水力分析计算分两步(P89例题 ): 例题5.1): 水力分析计算分两步( 例题 • 1、用流量连续性条件计算管段流量,并计算出管 、用流量连续性条件计算管段流量, 段压降; 段压降; • 2、根据管段能量方程和管段压降,从定压节点出 、根据管段能量方程和管段压降, 发推求各节点水头。 发推求各节点水头。
可以看出:树状网中,各管段流量 可以看出:树状网中,各管段流量qi可以用节点流 表示出来。 量Qj表示出来。
5.1.2 管段能量方程(根据能量守恒定律) 根据能量守恒定律)
管段两端节点水头之差等于该管段的压降: 管段两端节点水头之差等于该管段的压降: HFi –HTi= hi i-1,2,…,M
HFi——管段 的上端点水头; 管段i的上端点水头 管段 的上端点水头; HTi——管段 的下端点水头; 管段i的下端点水头; 管段 的下端点水头 hi——管段 的压降; 管段i的压降 管段 的压降; M——管段模型中的管段总数。 管段模型中的管段总数。 管段模型中的管段总数
水力学基础课件——第五章 明渠恒定均匀流

A
(b mh)h
R
x b 2h 1 m2
第五章 明渠恒定均匀流
二、明渠的底坡 底坡:明渠渠底倾斜的程度称为底坡。以符号i表
示,i等于渠底线与水平线夹角口的正弦即i=Sinθ。 明渠有三种底坡:顺坡、平坡和逆坡
第五章 明渠恒定均匀流
➢顺坡: i>0,明槽槽底沿程降低者称为正坡或顺坡。 ➢平坡: i=0,明槽槽底高程沿程不变者称为平坡。 ➢逆坡: i<0,明槽槽底沿程增高者称为反坡或逆坡。
第五章 明渠恒定均匀流
5.1 明渠的类型及其对水流运动的影响
明渠的渠身及其沿流动方向的倾斜程度( 称作底坡 ), 是水流边界的几何条件。一定形式的边界几何条件,给 予水流运动一定的影响。所以为了了解水流运动的特征, 必须先对影响明渠水流运动的边界几何条件进行分析。
第五章 明渠恒定均匀流
一、明渠的横断面 人工明渠的横断面,通常作成对称的几何形状。例如
二、允许流速
允许流速是为了保持渠道安全稳定运行在流速上的限 制,包括不冲流速、不淤流速和其它运行管理要求的流 速限制。在实际明渠均匀流计算中必须结合工程要求进 行校核。
第五章 明渠恒定均匀流
➢在设计中,要求渠道流速v在不冲、不淤的允许
流速范围内,即:
式中:
——不冲允许流速(m/s),根据壁面材料定。
➢ 如果您有任何问题, 请毫不犹豫地提出 !
In case of you have any question, DO NOT hesitate to ask me !
第五章 明渠恒定均匀流
5.2 明渠均匀流特性及其产生条件
一、明渠均匀流的特性: 1、均匀流过水断面的形状、尺寸沿流程不变,特别
是水深h沿程不变,这个水深也称为正常水深。 2、过水断面上的流速分布和断面平均流速沿流程不
水力学第五章
第五章
有压管路的水力计算
O
2 0 v0
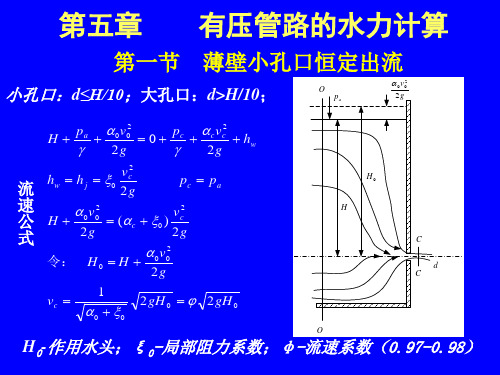
第一节 薄壁小孔口恒定出流
小孔口:d≤H/10;大孔口:d>H/10;
H pa
pa
2g
2 0 v0
2g
0
pc
2 c vc
2g
hw
H0
流 2 2 速 0 v0 vc ( c 0 ) 公 H 2g 2g 式 2
令: H 0 H vc 1 0 0
2 vc hw h j 0 2g
pc pa
H
0 v0
2g
C d
C
2 gH 0 2 gH 0
O
H0-作用水头;ξ 0-局部阻力系数;φ -流速系数(0.97-0.98)
流量公式:
Q v c Ac A
2 gH 0 A 2 gH 0
0.62
0.64
复杂管路都可以分解为:串联管路和并联管路两种。
hf1 hf 2 hf 3
H
q1
q2
l1 d1 Q1
l 2 d 2 Q2
l3 d 3 Q3
串联管路:总水头损失等于各分段水头损失之和;无奇点(流进、 流出)情况下,总流量等于各分流量。
H
h fi
i 1
n
i
n
Ai li Qi2
Q Qi
C
b
hc bw cb pa pc
O
1 2 2 ( 1) 2 n H0 将 1, 0.64, n 0.82 pa pc
pcv
0.756 H 0
有压管路的水力计算
O
2 0 v0
第一节 薄壁小孔口恒定出流
小孔口:d≤H/10;大孔口:d>H/10;
H pa
pa
2g
2 0 v0
2g
0
pc
2 c vc
2g
hw
H0
流 2 2 速 0 v0 vc ( c 0 ) 公 H 2g 2g 式 2
令: H 0 H vc 1 0 0
2 vc hw h j 0 2g
pc pa
H
0 v0
2g
C d
C
2 gH 0 2 gH 0
O
H0-作用水头;ξ 0-局部阻力系数;φ -流速系数(0.97-0.98)
流量公式:
Q v c Ac A
2 gH 0 A 2 gH 0
0.62
0.64
复杂管路都可以分解为:串联管路和并联管路两种。
hf1 hf 2 hf 3
H
q1
q2
l1 d1 Q1
l 2 d 2 Q2
l3 d 3 Q3
串联管路:总水头损失等于各分段水头损失之和;无奇点(流进、 流出)情况下,总流量等于各分流量。
H
h fi
i 1
n
i
n
Ai li Qi2
Q Qi
C
b
hc bw cb pa pc
O
1 2 2 ( 1) 2 n H0 将 1, 0.64, n 0.82 pa pc
pcv
0.756 H 0
水力学第五章 流动阻力和水头损失

沿程阻力(或摩擦力):在边壁沿流程无变化(边 壁形状、尺寸、流动方向均无变化)的均匀流流 段上,产生的流动阻力。
沿程水头损失:由于沿程阻力作功而引起的水头损失, 以hf表示。
局部水头损失:
由局部阻力引起的水头损失,以 h j 表示。
沿程水头损失和局部水头损失,是由于液体 在运动过程中克服阻力作功而引起的,但又具 有不同的特点。
其中 l 称为混合长度
实际工程中总存在扰动,因此上临界雷诺数 Rec 就 没有实际意义。
常以下临界雷诺数 Rec 作为流态的判别标准
管流的雷诺数
Re vd
将 Re 值与临界雷诺数 Rec 2300 比较,便可判别流态
Re Rec 则 v vc 流动是层流
Re Rec 则 v vc 流动是湍流 Re Rec 则 v vc 流动是临界流 2. 非圆通道雷诺数 对于明渠水流和非圆形断面的管流,通过水力半径 代替圆管雷诺数中的直径d后,同样可以用雷诺数判别 流动型态 。
C
d
C
d
C vcd
下临界雷诺数
Rec
vc d
上临界雷诺数
Rec
vc d
实验得出
下临界雷诺数稳定在2000左右,外界扰动几乎与它无关。 上临界雷诺数其数值却是一个不稳定的数值,有的得 12,000,有的得20,000或40,000,这是因为上临界雷 诺数的大小与实验中水流扰动程度有关。
把由层流转化为紊流时的管中平均流速称为上临 界流速,vc
由紊流转化为层流时的管中平均流速称为下临 界流速vc
雷诺试验是在圆管中对水所进行的实验。但对其 他任何边界形状,任何其他实际液体或气体流动, 都可以发现有这两种流动型态。即:任何实际液体 的流动都存在着层流和紊流两种不同的流动型态。
沿程水头损失:由于沿程阻力作功而引起的水头损失, 以hf表示。
局部水头损失:
由局部阻力引起的水头损失,以 h j 表示。
沿程水头损失和局部水头损失,是由于液体 在运动过程中克服阻力作功而引起的,但又具 有不同的特点。
其中 l 称为混合长度
实际工程中总存在扰动,因此上临界雷诺数 Rec 就 没有实际意义。
常以下临界雷诺数 Rec 作为流态的判别标准
管流的雷诺数
Re vd
将 Re 值与临界雷诺数 Rec 2300 比较,便可判别流态
Re Rec 则 v vc 流动是层流
Re Rec 则 v vc 流动是湍流 Re Rec 则 v vc 流动是临界流 2. 非圆通道雷诺数 对于明渠水流和非圆形断面的管流,通过水力半径 代替圆管雷诺数中的直径d后,同样可以用雷诺数判别 流动型态 。
C
d
C
d
C vcd
下临界雷诺数
Rec
vc d
上临界雷诺数
Rec
vc d
实验得出
下临界雷诺数稳定在2000左右,外界扰动几乎与它无关。 上临界雷诺数其数值却是一个不稳定的数值,有的得 12,000,有的得20,000或40,000,这是因为上临界雷 诺数的大小与实验中水流扰动程度有关。
把由层流转化为紊流时的管中平均流速称为上临 界流速,vc
由紊流转化为层流时的管中平均流速称为下临 界流速vc
雷诺试验是在圆管中对水所进行的实验。但对其 他任何边界形状,任何其他实际液体或气体流动, 都可以发现有这两种流动型态。即:任何实际液体 的流动都存在着层流和紊流两种不同的流动型态。
水力学第五章

逐步充满整个断面。
一、圆柱形外管嘴的恒定出流
1
v H 0 00 n 2g 2g 2g 1 v 2gH n 2gH n
n
1
v
2 0 0
v
2
2
l (3 ~ 4)d
H
0 d
c
2
0
பைடு நூலகம்
c
2
n
1
Q v n 2 gH 0
n n 0.82
§5.3 短管的水力计算
1.虹吸管的水力计算
例题2
§5.3 短管的水力计算
2.水泵吸水管的水力计算 hv ,求水泵安装高度 H 。 计算内容:已知 Q、d、l吸、、 进、 弯、
例题3
例题1
在 H 孔口 H n , d 孔口 d n 及流量。 1.流速比较 条件下,试分别比较孔口和管嘴出流的流速
流体力学
主 讲:赵 超
第五章 孔口、管嘴出流和有压管路
§5.1 液体经薄壁孔口的恒定出流 §5.2 液体经管嘴的恒定出流 §5.3 短管的水力计算
第五章 孔口、管嘴出流和有压管路
常用公式 连续性方程: 伯努利方程: 损失公式:
A1v1 A2 v2
2 p1 1v12 p2 2 v2 z1 z2 hw12 g 2g g 2g
2gH0 2gH0
1
c 0
速度系数 收缩系数 流量系数
Q Ac vc A 2 gH 0 A 2 gH 0
c /
三、薄壁小孔口的 淹没出流
2 2 vc vc H1 0 0 H2 0 0 0 se 2g 2g
l 3 ~ 4 d
一、圆柱形外管嘴的恒定出流
1
v H 0 00 n 2g 2g 2g 1 v 2gH n 2gH n
n
1
v
2 0 0
v
2
2
l (3 ~ 4)d
H
0 d
c
2
0
பைடு நூலகம்
c
2
n
1
Q v n 2 gH 0
n n 0.82
§5.3 短管的水力计算
1.虹吸管的水力计算
例题2
§5.3 短管的水力计算
2.水泵吸水管的水力计算 hv ,求水泵安装高度 H 。 计算内容:已知 Q、d、l吸、、 进、 弯、
例题3
例题1
在 H 孔口 H n , d 孔口 d n 及流量。 1.流速比较 条件下,试分别比较孔口和管嘴出流的流速
流体力学
主 讲:赵 超
第五章 孔口、管嘴出流和有压管路
§5.1 液体经薄壁孔口的恒定出流 §5.2 液体经管嘴的恒定出流 §5.3 短管的水力计算
第五章 孔口、管嘴出流和有压管路
常用公式 连续性方程: 伯努利方程: 损失公式:
A1v1 A2 v2
2 p1 1v12 p2 2 v2 z1 z2 hw12 g 2g g 2g
2gH0 2gH0
1
c 0
速度系数 收缩系数 流量系数
Q Ac vc A 2 gH 0 A 2 gH 0
c /
三、薄壁小孔口的 淹没出流
2 2 vc vc H1 0 0 H2 0 0 0 se 2g 2g
l 3 ~ 4 d
水力学课件第五章

紊流
管中为石油时
vd 100 2 333.3 2300 Re 0.6 ν
层流
作业
1、2
均匀流沿程水头损失与切应力的关系
沿程水头损失与切应力的关系 在管道恒定均匀流中,取总流流段1-1到2-2,各 作用力处于平衡状态:F=0。
P1
1
0 0
2
P2 2 z2
z1 z2 sin l
p1 p2 hf g g
m 13600 ( 1)hp ( 1) 0.3 4.23m 900
设流动为层流
4Q v 2.73m / s 2 d
l v 2 64 l v 2 64 l v 2 hf d 2 g Re d 2 g vd d 2 g
Re
d 1.175 0.075 979 < 2300 4 0.9 10
层流
1 2 1 Q 1.175 d 3600 1.175 3.14 0.075 2 3600 18.68m 3 / h 4 4
2、求沿程水头损失
64 64 0.0654 Re 979
T
T
u x u x u x
T
1 1 1 ' ux (ux ux )dt ux dt ux dt ux ux 0 T0 T0 T0
其它运动要素也同样处理:
1 p T 1 p T
T
pdt
0 T 0
p p p
pdt 0
脉动值说明:
—局部损失系数(无量纲)
一般由实验测定
实际液体流动的两种形态
雷诺试验
实验条件:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5 液流形态与水头损失
5.1 水头损失及其分类 5.2 均匀流沿程水头损失与水流阻力关系
5.3 5.4 流动的两种形态与雷诺实验 层流运动
5.5 紊流运动 5.6 紊流的沿程水头损失 5.7 局部水头损失
5.6 沿程阻力系数的变化规律
由本章各节可知,沿程阻力系数的规律,除了层 流已知外,对于紊流到目前为止,尚没有沿程阻力系 数的理论公式。 尼古拉孜为了探求沿程阻力系数的规律,进行了 一系列试验研究,揭示了沿程水头损失的规律。
越 来 越 光 滑
ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ »
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
r0 / Δ
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
l v2 由达西公式 h f 可知,水头损失和断面平均流速 d 2g
的二次方成正比,故该区又称阻力平方区。
下面介绍这一重要的试验研究成果。
5.6.1 实验研究
尼古拉孜试验
试验条件 管道 人工粗糙面:将大小一致的均匀砂粒粘贴在管壁上
注意:这种粗糙面和天然粗糙面完全不同 相对粗糙度:Δ/r0
r0 Δ=d
相对光滑度: r0 /Δ
l
hf
Q
V t
沿程阻力系数的试验装置
方法
对于一系列相对光滑度、量测流速和水头损失hf ,
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
原符号(绝对粗糙度)。
管壁的相对光滑度用Δ/d 表示 ,其他和以上试
验相同。 注意:当量粗糙度不是绝对粗糙度。
各种壁面当量粗糙度值
壁面种类 Δ/mmΔ/mm
清洁铜管、玻璃管 0.00150.45 ~0.01 ~6.0 陶土排水管 橡皮软管 0.01~ 0.03 0.25 ~6.0 涂有珐琅质的排水管 新的无缝钢管 0.04~0.17 0.25~1.25 纯水泥表面 旧钢管、涂柏油的钢管 0.12~0.21 0.45~3.0 非刨平木板制成的木槽、水泥浆粉面 普通新铸铁管 0.25~0.42 0.8~6.0 水泥浆砖砌体 旧的生锈钢管 0.60~0.67 0.8~9.0 混凝土槽 木管 0.25~1.25
蔡克士大的试验
条件:明渠,人工粗糙面。 试验方法:同上
1.7 Ⅰ 1.5
l g (2 50 λ )
R/ Δ Ⅲ
5 7 10 15 20 30 40 50 60 80
1.3 1.1 0.9 0.7 0.5 2.0 2.5 3.0 3.5 lg (Re) 4.0 4.5 5.0 Ⅱ
1.7 Ⅰ 1.5
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
水力光滑管:当Re 较小时,粘性底层厚度就可淹没 粗糙度。图中就是直线Ⅱ,所有的试验点都落在直线上。
1 00 0λ
光滑区
Moody图
Re
1.E+02 100.0
过渡粗糟区 层流区 粗糙区
1.E+03
1.E+04
1.E+05
1.E+06
1.E+07
1.E+08
Δ /d
10.0
1.0
0.000001~0.05 0.05 0.04 0.03 0.02 0.015 0.01 0.008 0.004 0.002 0.001 0.0008 0.0006 0.0004 0.0002 0.0001 0.00005 0.00001 0.000005 0.000001
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
层流区: Re < 2000 (lg Re = 3.30),沿程阻力系数λ与 Re的关系为直线Ⅰ,而与光滑度Δ无关,其方程为: λ = 64 /Re
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
管壁越光滑,沿直线Ⅱ下移的距离越大,保持 在直线Ⅱ上的距离越长,离开直线的雷诺数越大。
壁面种类
凿石护面
Δ/mm
1.25~6.00
土渠 水泥勾缝的普通块石砌体 石砌渠道(干砌中等质量)
卵石河床(粒径70~80mm)
4.00~11.00 6.00~17.00 25.00~45.00
30.00~60.00
Re
1.E+02 100.0
过渡粗糟区 层流区 粗糙区
1.E+03
1.E+04
1.E�.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
过渡区:在直线Ⅱ和直线Ⅲ之间的区域为光滑管到 粗糙管过渡区,壁面越光滑,阻力系数越小。
l g (2 50 λ )
R/ Δ Ⅲ
5 7 10 15 20 30 40 50 60 80
1.3 1.1 0.9 0.7 0.5 2.0 2.5 3.0 3.5 lg (Re) 4.0 4.5 5.0 Ⅱ
明渠中沿程阻力系数的规律和管道中的相同。
Moody 图
以上所得出的沿程阻力系数的规律,除了层流可 以直接用于水力计算外,其他都是在人工粗糙面的条 件下得出的规律,无法应用于实际计算。 原因:实际管道或者明渠边壁的绝对粗糙度在形 状、排列和分布上都不同于人工粗糙面。
越 来 越 光 滑
lg (100Ë ¦ )
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
粗糙区:在直线Ⅲ以右区域:各条不同相对光 滑度的试验曲线近似为直线,表明沿程阻力系数和 Re关系不大,只与r0 /Δ有关。
1944,美国人Moody 对各种工业管道进行了试验
研究。试验用的管道非常广泛,有:玻璃管、混凝土 管、钢管、铜管、木管等,试验条件就是自然管道, 管道的壁面就是天然管壁,而非人工粗糙面。
试验成果的处理:将试验得到的沿程阻力系数和
人工加糙的结果进行对比,把具有相同沿程阻力系数
值的砂粒绝对粗糙度作为管道的当量粗糙度Δ,仍用
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
5.1 水头损失及其分类 5.2 均匀流沿程水头损失与水流阻力关系
5.3 5.4 流动的两种形态与雷诺实验 层流运动
5.5 紊流运动 5.6 紊流的沿程水头损失 5.7 局部水头损失
5.6 沿程阻力系数的变化规律
由本章各节可知,沿程阻力系数的规律,除了层 流已知外,对于紊流到目前为止,尚没有沿程阻力系 数的理论公式。 尼古拉孜为了探求沿程阻力系数的规律,进行了 一系列试验研究,揭示了沿程水头损失的规律。
越 来 越 光 滑
ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ »
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
r0 / Δ
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
l v2 由达西公式 h f 可知,水头损失和断面平均流速 d 2g
的二次方成正比,故该区又称阻力平方区。
下面介绍这一重要的试验研究成果。
5.6.1 实验研究
尼古拉孜试验
试验条件 管道 人工粗糙面:将大小一致的均匀砂粒粘贴在管壁上
注意:这种粗糙面和天然粗糙面完全不同 相对粗糙度:Δ/r0
r0 Δ=d
相对光滑度: r0 /Δ
l
hf
Q
V t
沿程阻力系数的试验装置
方法
对于一系列相对光滑度、量测流速和水头损失hf ,
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
原符号(绝对粗糙度)。
管壁的相对光滑度用Δ/d 表示 ,其他和以上试
验相同。 注意:当量粗糙度不是绝对粗糙度。
各种壁面当量粗糙度值
壁面种类 Δ/mmΔ/mm
清洁铜管、玻璃管 0.00150.45 ~0.01 ~6.0 陶土排水管 橡皮软管 0.01~ 0.03 0.25 ~6.0 涂有珐琅质的排水管 新的无缝钢管 0.04~0.17 0.25~1.25 纯水泥表面 旧钢管、涂柏油的钢管 0.12~0.21 0.45~3.0 非刨平木板制成的木槽、水泥浆粉面 普通新铸铁管 0.25~0.42 0.8~6.0 水泥浆砖砌体 旧的生锈钢管 0.60~0.67 0.8~9.0 混凝土槽 木管 0.25~1.25
蔡克士大的试验
条件:明渠,人工粗糙面。 试验方法:同上
1.7 Ⅰ 1.5
l g (2 50 λ )
R/ Δ Ⅲ
5 7 10 15 20 30 40 50 60 80
1.3 1.1 0.9 0.7 0.5 2.0 2.5 3.0 3.5 lg (Re) 4.0 4.5 5.0 Ⅱ
1.7 Ⅰ 1.5
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
水力光滑管:当Re 较小时,粘性底层厚度就可淹没 粗糙度。图中就是直线Ⅱ,所有的试验点都落在直线上。
1 00 0λ
光滑区
Moody图
Re
1.E+02 100.0
过渡粗糟区 层流区 粗糙区
1.E+03
1.E+04
1.E+05
1.E+06
1.E+07
1.E+08
Δ /d
10.0
1.0
0.000001~0.05 0.05 0.04 0.03 0.02 0.015 0.01 0.008 0.004 0.002 0.001 0.0008 0.0006 0.0004 0.0002 0.0001 0.00005 0.00001 0.000005 0.000001
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
层流区: Re < 2000 (lg Re = 3.30),沿程阻力系数λ与 Re的关系为直线Ⅰ,而与光滑度Δ无关,其方程为: λ = 64 /Re
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
越 来 越 光 滑
lg (100Ë ¦ )
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
管壁越光滑,沿直线Ⅱ下移的距离越大,保持 在直线Ⅱ上的距离越长,离开直线的雷诺数越大。
壁面种类
凿石护面
Δ/mm
1.25~6.00
土渠 水泥勾缝的普通块石砌体 石砌渠道(干砌中等质量)
卵石河床(粒径70~80mm)
4.00~11.00 6.00~17.00 25.00~45.00
30.00~60.00
Re
1.E+02 100.0
过渡粗糟区 层流区 粗糙区
1.E+03
1.E+04
1.E�.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
过渡区:在直线Ⅱ和直线Ⅲ之间的区域为光滑管到 粗糙管过渡区,壁面越光滑,阻力系数越小。
l g (2 50 λ )
R/ Δ Ⅲ
5 7 10 15 20 30 40 50 60 80
1.3 1.1 0.9 0.7 0.5 2.0 2.5 3.0 3.5 lg (Re) 4.0 4.5 5.0 Ⅱ
明渠中沿程阻力系数的规律和管道中的相同。
Moody 图
以上所得出的沿程阻力系数的规律,除了层流可 以直接用于水力计算外,其他都是在人工粗糙面的条 件下得出的规律,无法应用于实际计算。 原因:实际管道或者明渠边壁的绝对粗糙度在形 状、排列和分布上都不同于人工粗糙面。
越 来 越 光 滑
lg (100Ë ¦ )
0.8 0.6 0.4 0.2 0.0
ý ¹ É ¶ ø Ç
2.6 2.8 3.0 3.2 3.4 3.6 3.8 4.0 4.2 4.4 4.6 4.8 5.0 5.2 5.4 5.6 5.8 6.0
lg ( Re )
粗糙区:在直线Ⅲ以右区域:各条不同相对光 滑度的试验曲线近似为直线,表明沿程阻力系数和 Re关系不大,只与r0 /Δ有关。
1944,美国人Moody 对各种工业管道进行了试验
研究。试验用的管道非常广泛,有:玻璃管、混凝土 管、钢管、铜管、木管等,试验条件就是自然管道, 管道的壁面就是天然管壁,而非人工粗糙面。
试验成果的处理:将试验得到的沿程阻力系数和
人工加糙的结果进行对比,把具有相同沿程阻力系数
值的砂粒绝对粗糙度作为管道的当量粗糙度Δ,仍用
r0 / Δ
1.2 1.0 15 30.6 60 126 252 507 ñ ¢ ã ² ô Á ø Ç ã ² ô Á ½ µ É Î ô Á Ä µ ý ¹ É ¶ ø Ç ò ¢ É Î ô Á â ¹ ¬ » ¤ ¦ ó ¢ É Î ô Á Ö ´ Ú ² ø Ç
