整式的加减(公开课)
合集下载
整式的加减(第一课时)课件
基础练习题
总结词：巩固基础
详细描述：基础练习题主要针对整式加减法的基本规则和概念，包括同类项的合并、系数和字母的加 减等。这些题目难度较低，适合初学者熟悉基本操作。
进阶练习题
总结词：提升技能
详细描述：进阶练习题在基础练习题的基础上增加难度，涉 及更复杂的整式加减运算，如多项式的加减、去括号等。这 些题目旨在提高学生的运算能力和对整式加减法的理解。
05
06
解：$3a^2 - 2a + a^2 = (3 + 1)a^2 2a = 4a^2 - 2a$
整式的加减运算技巧
技巧一
合并同类项时，系数直接相加减 ，字母和字母的指数不变
例如
$2x + 3x = 5x$，$3a^2 2a^2 = a^2$。
技巧二
去括号时，注意符号的变化
例如
$3(x + y) = 3x + 3y$，$- (x y) = -x + y$。
整式的加减(第一课时 )ppt课件
• 整式的概念 • 整式的加减运算 • 整式的混合运算 • 整式的加减运算练习
目录
01
整式的概念
什么是整式
整式是由常数、变数、常数乘变数、常数除变数以及括号等符号组成的数学表达式 。
整式中，变数的次数可以是零次、一次或多次。
整式中，变数的指数可以是正整数、负整数或零。
步骤三：合并同类项
整式的加减运算步骤
将带有相同字母的项的系数相加或相减。 步骤四：化简
将整式化简到最简形式。
整式的加减运算实例
例1：
01
02
计算：$2x - 3x + 4x$
解：$2x - 3x + 4x = (2 - 3 + 4)x = 3x$
3整式的加减 公开课课件
2
3 23
=－3x＋y2 .
当x=－2，y= 2 时，
3
原式=
－3
－2＋
2 3
2
=6＋
4 9
=6
4 9
.
知3－讲
先将式子化简， 再代入数值进行 计算比较简便.
（来自教材）
总结
知3－讲
求整式的值时，一般是先化简(去括号、合并同 类项)，再把字母的值代入化简后的式子求值．
知3－练
蔡琰（作者有待考证）的《胡笳十八 拍》 郭璞的《游仙诗》
鲍照的《拟行路难》 庾信的《拟咏怀》
都特别喜欢。不过都是组诗，太长了 ，就不 贴了orz 。
最后还想推一下萧绎的《幽逼诗》四 首：
【南史曰：元帝避建邺则都江陵，外 迫强敌 ，内失 人和。 魏师至 ，方征 兵四方 ，未至 而城见 克。在 幽逼求 酒，饮 之，制 诗四绝 。后为 梁王詧 所害。 】 南风且绝唱，西陵最可悲。今日还蒿 里，终 非封禅 时。 人世逢百六，天道异贞恒。何言异蝼 蚁，一 旦损鲲 鹏。 松风侵晓哀，霜雰当夜来。寂寥千载 后，谁 畏轩辕 台。 夜长无岁月，安知秋与春。原陵五树 杏，空 得动耕 人。
第二章 整式的加减
2.2 整式的加减
第3课时 整式的加减
1 课堂讲解 2 课时流程
整式的加减 整式的加减的应用 求整式的值
逐点 导讲练
课堂 小结
作业 提升
复习回顾：什么是整式、单项式、多项式?
整 单项式（系数和次数） 式 多项式（项和次数）
单项式 多项式
整 式
代 数 式
知识点 1 整式的加减
（来自《典中点》）
知识点 2 整式的加减的应用
知2－讲
整式的加减公开课一等奖优质课大赛微课获奖课件
新课标人教版七年级上
整式的加减第36页
知识要点
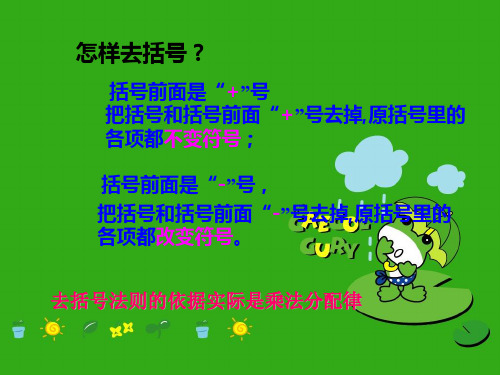
去括号法则 假如括号外因数是正数，去括号后原括 号内各项符号与本来符号相同； 假如括号外因数是负数，去括号后原括 号内各项符号与本来符号相反.
去括号，看符号：
是“＋”号，不变号；
是“－”号，全变
号．
新课标人教版七年级上
整式的加减第37页
下面去括号有无错误?若有错，请更正.
一找
＝（4x2－3x2）+(－8x＋6x) + (5－4） 二移
＝ x2－2x ＋1
三并
合并同类项环节：
1、找出同类项 用不同线标识出各组同类项，注意每一项符号。
2、把同类项移在一起 用括号将同类项结合，括号间用加号连接。
3、合并同类项
系数相加,字母及字母指数不变 。 新课标人教版七年级上
整式的加减第13页
=-a2b-a+1
三并
当a= - 2 ，b =4时，
四代入
原式=- (- 2 )2× 4 -（-2）+1
求值
=-16+2+1
=-13
注意：求代数式值，能化简，要先化简，再
代入求值。
新课标人教版七年级上
整式的加减第23页
例2：(1)求多项式3x2 4x 3 2x2 5x 4x2 2 的值, 其中x=2.
新课标人教版七年级上
整式的加减第16页
1．下列各对不是同类项是（ B）
Ａ．－3x2y与2x2y
B． －2xy2与 3x2y
Ｃ．－5x2y与3yx2
D． 3mn2与2mn2
2．合并同类项正确是（ B）
A．4a＋b＝5ab
B．6xy2－6y2x＝0
整式加减(公开课)
= 1×(a-b+c) × = a-b+c
-(a-b+c) = (-1)×(a-b+c) ×
它前面的“ ”号去掉,括号里各项都 括号里各项都不 它前面的“+”号去掉 括号里各项都不 变号;括号前是 ” 把括号和它前面 括号前是“ 变号 括号前是“-”号,把括号和它前面 括号里各项都改变符号 的“-”号去掉 括号里各项都改变符号 ”号去掉,括号里各项都改变符号;
立志
立德
求真
求实
10
X
朝气蓬勃
校 运 8会 留 念
斗争昂扬 团结一心 勇往直前
8(10 + x) = 80 + 8 x
+(a-b+c)
= -a+b-c 议一议：去括号前后， 发生了什么变化？ 议一议：去括号前后，括号里的各项发生了什么变化？
去括号法则: 括号前是“ ” 把括号和 去括号法则 括号前是“+”号,把括号和
(1)去括号时应将括号前面的符号连同括号 去括号时应将括号前面的符号连同括号 一起去掉. 一起去掉 (2)要注意括号前面是 号时, (2)要注意括号前面是 “-“号时,去掉括号 后, 括号里各项都要改变符号;不能只改变某 括号里各项都要改变符号 不能只改变某 几项而忘记改变其余的符号 (3)若括号前面是数字因数时 应乘以括号里 若括号前面是数字因数时,.应乘以括号里 若括号前面是数字因数时 的每一项,不要漏乘. 不要漏乘 的每一项 不要漏乘
辩一辩：指出下列各式是否正确？如果错误， 辩一辩：指出下列各式是否正确？如果错误， 请指出原因. 请指出原因
(1)a-(b-c+d) = a-b+c+d (2)-(a-b)+(-c+d)= a+b-c-d (3)a-3(b-2c)=a-3b+2c (4) x-2(-y-3z+1)=x-2y+6z
《整式的加减》PPT课件 (公开课获奖)2022年北师大版 (19)
仅要注意符号,还要注意每一项都要乘上系数.
2`如果有同类项，合并同类项。
怎样添括号？
括号前面是“+”号 括到括号里的各项都不变符号；
括号前面是“-”号， 括到括号里的各项都改变符号。
应注意哪些问题呢?
1`符号问题，什么时候变，什么时候不变，哪 些项变，哪些项不变； 2`检查添括号是不是正确，可以用去括号法则检验。
P
AC
D
B
如图,在△ABC
中,DE∥BC,AH分别交DE,BC于 G,H,求证:
DG GE
A
BH HC
D B
E G
H
C
如图：在⊿ABC中， ∠C= 90°,BC=8,AC=6.点P 从点B出发，沿着BC向点C以2cm/秒的速度移动;点 Q从点C出发，沿着CA向点A以1cm/秒的速度移动。 如果P、Q分别从B、C同时出发，问：
添括号与去括号刚好相反，要想检查添括号是不是 正确，可以用去括号法则检验。
情景活动 合作交流
活动一：全班分成多个四人小组，组内每个同学按下列步骤操作。
任意写一个两位数
12 34 87 10a+b
交换它的十位数字与个位数字， 21 43 78 10b+a 又得到一个数
两个数相加
? 33 77 165
经过多少秒时以C、P、Q为顶点的三角形恰 好与⊿ABC相似？ A
A
Q Q
B
P
CB
P
C
如图，已知△PAC∽△QCB ， △PCQ是等边三角形 (1)若AP=1，BQ=4，求PQ的长. (2)求∠ACB的度数. (3)求证:AC2=AP·AB.
C
AP
Q
B
进行整式加减运算时，有括 号先去括号，再合并同类项.
2`如果有同类项，合并同类项。
怎样添括号？
括号前面是“+”号 括到括号里的各项都不变符号；
括号前面是“-”号， 括到括号里的各项都改变符号。
应注意哪些问题呢?
1`符号问题，什么时候变，什么时候不变，哪 些项变，哪些项不变； 2`检查添括号是不是正确，可以用去括号法则检验。
P
AC
D
B
如图,在△ABC
中,DE∥BC,AH分别交DE,BC于 G,H,求证:
DG GE
A
BH HC
D B
E G
H
C
如图：在⊿ABC中， ∠C= 90°,BC=8,AC=6.点P 从点B出发，沿着BC向点C以2cm/秒的速度移动;点 Q从点C出发，沿着CA向点A以1cm/秒的速度移动。 如果P、Q分别从B、C同时出发，问：
添括号与去括号刚好相反，要想检查添括号是不是 正确，可以用去括号法则检验。
情景活动 合作交流
活动一：全班分成多个四人小组，组内每个同学按下列步骤操作。
任意写一个两位数
12 34 87 10a+b
交换它的十位数字与个位数字， 21 43 78 10b+a 又得到一个数
两个数相加
? 33 77 165
经过多少秒时以C、P、Q为顶点的三角形恰 好与⊿ABC相似？ A
A
Q Q
B
P
CB
P
C
如图，已知△PAC∽△QCB ， △PCQ是等边三角形 (1)若AP=1，BQ=4，求PQ的长. (2)求∠ACB的度数. (3)求证:AC2=AP·AB.
C
AP
Q
B
进行整式加减运算时，有括 号先去括号，再合并同类项.
整式的加减(公开课)
整式的加减
复习巩固
1、合并同类项的法则：
合并同类项后，所得项的系数是合并前 各同类项的系数和，且字母连同它的指数 不变。 2、去括号法则：
如果括号外的因数是正数，去括号后原 括号内各项的符号与原来的符号相同。
如果括号外的因数是负数，去括号后原 括号内各项的符号与原来的符号相反。
去括号：
2 6x （1）2（1－3x）=＿＿＿ 6x 3 1)＝＿＿＿＿ 2 2 7a ＿ 14a a 2a）＝＿ （3）+7（
比一比：看谁又快又准！
课本第69页练习的第二题，自 选一个小题。
为本小组争光哟！
例题：求2(a2-ab)-3( a2-ab )的值, 其中 a=2,b=-3.
解:2(a2-ab)-3(
22 a -ab ) 3
=2a2 -2ab -2a2 +3ab
=ab 当a=2,b=-3时 原式=ab =2×(Hale Waihona Puke 3)=-6（2）－3（ 2 x
2
2
2
4x ＿ 12 x （4）－4（x 3x ）＝＿
2
练一练
计算：
(1)（2x-3y)+(5x+4y) (2) (8a-7b)-(4a-5b)
自主学习
1、自学课本第68页的例7和例8. 2、思考： 通过上面的学习，你自己可 以归纳出整式加减的运算方法吗 ？
本节课的重点
练习： 课本第69页练习的第三题。
拓展探索
小组完成：
课本第71页的第11题。
说说本节课你的收获。
整式加减的运算法则： 一般的，几个整式相加减， 如果有括号就先去括号，然 后再合并同类项。
例题：
(1)(x+y-z)+(x-y+z)-(x-y-z)
复习巩固
1、合并同类项的法则：
合并同类项后，所得项的系数是合并前 各同类项的系数和，且字母连同它的指数 不变。 2、去括号法则：
如果括号外的因数是正数，去括号后原 括号内各项的符号与原来的符号相同。
如果括号外的因数是负数，去括号后原 括号内各项的符号与原来的符号相反。
去括号：
2 6x （1）2（1－3x）=＿＿＿ 6x 3 1)＝＿＿＿＿ 2 2 7a ＿ 14a a 2a）＝＿ （3）+7（
比一比：看谁又快又准！
课本第69页练习的第二题，自 选一个小题。
为本小组争光哟！
例题：求2(a2-ab)-3( a2-ab )的值, 其中 a=2,b=-3.
解:2(a2-ab)-3(
22 a -ab ) 3
=2a2 -2ab -2a2 +3ab
=ab 当a=2,b=-3时 原式=ab =2×(Hale Waihona Puke 3)=-6（2）－3（ 2 x
2
2
2
4x ＿ 12 x （4）－4（x 3x ）＝＿
2
练一练
计算：
(1)（2x-3y)+(5x+4y) (2) (8a-7b)-(4a-5b)
自主学习
1、自学课本第68页的例7和例8. 2、思考： 通过上面的学习，你自己可 以归纳出整式加减的运算方法吗 ？
本节课的重点
练习： 课本第69页练习的第三题。
拓展探索
小组完成：
课本第71页的第11题。
说说本节课你的收获。
整式加减的运算法则： 一般的，几个整式相加减， 如果有括号就先去括号，然 后再合并同类项。
例题：
(1)(x+y-z)+(x-y+z)-(x-y-z)
2.2.3《整式的加减》第三课时课件(公开课)
第9页，共14页。
想一想
礼堂第一排有(a-1)个座位,后面每排都比前一排多1个座位.
(1).第二排有_______a___个座位.
(2).第三排有____(_a__+_1__)个座位.
(3).第n排有多少个座位?
解: 第1排 (a-1) 个 第2排 (a-1)+1=a 个 第3排 (a-1)+2=a+1个 第4排 (a-1)+3 =a+2 个 第n排的座位 (a-1)+ (n-1) =a-1+n-1 =a+n-2 (个)
（元），小红买这种笔记本3本，买圆珠笔2枝；小明买 这种笔记本4个，买圆珠笔3枝．小红比小明少花多少？ 〔小红共用 （ 3x+2y）元 小明共用 （4x+3y）元〕
２．你还能根据划线部分的条件，提出不同的问题吗？
总结一下：整式的加减运算在实际问题中是如何应用的?
1.根据题意把题目中的量用式子表示出来。
2
解：做这两个纸盒共用料
（2ab+2bc+2ca）+（6ab+8bc+6ca）
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca(cm )2
第8页，共14页。
（2）做大纸盒比小纸盒多用料多少平方厘米？
分析：小纸盒的表面积是（2ab+2bc+2ca）cm
2
大纸盒的表面积是（6ab+8bc+6ca）cm 2
= 5x+4y -2x+3y 去括号
=5x-2x+4y+3y 找出同类项
=3x+7y
整式的加减(公开课)
解：原式= 2(3x2 5xy) 5(3xy 3x2 ) 3(8x2 5xy)
= 6x2 10 xy 15 xy 15 x2 24 x2 15 xy
= (6x2 15 x2 24 x2 ) (10 xy 15 xy 15 xy) = 45 x2 10 xy
7.如果关于x的多项式 (8x2 6ax 14) (8x2 6x 5) 的值与x
思维分析：把多项式看作一个整体，并用括号
括起来。 见多必括
解 (2x2 -3x + 1）+（ -3x2 + 5x-7） = 2x2 －3x + 1 －3x2 + 5x－7
= (2x2 -3x2 )+(-3x + 5x)+(1-7)
=－ x2 ＋2x － 6
整式的加减混合运算步骤(有括号先去括号)
二：计算
2
3
＝ x－4y2
2
1
当x＝－1,y＝ 时
3ห้องสมุดไป่ตู้
2
12
原式＝ 2 ×（－1）－4× （ 2 ）
见负必括 见分必括
3
5
＝－ 2 －1＝－ 2
练一练： 1，化简下列各式：
(1)(3x 2 2x 1) ( x 2 x 3) (2)(2a 2b 2ab2 ) 3(a 2b 2ab2 )
解：(1)原式＝4x2 3x 2 (2)原式＝ a2b 4ab2
整式的加减
如何进行整式的加减呢？ 八字诀
去括号、合并同类项
括号前面出现系数怎么办？
• -7（a+b）
• 原式= -(7a+7b)=-7a-7b
• 2(x+y)
原式=(2x+2y)=2x+2y
= 6x2 10 xy 15 xy 15 x2 24 x2 15 xy
= (6x2 15 x2 24 x2 ) (10 xy 15 xy 15 xy) = 45 x2 10 xy
7.如果关于x的多项式 (8x2 6ax 14) (8x2 6x 5) 的值与x
思维分析：把多项式看作一个整体，并用括号
括起来。 见多必括
解 (2x2 -3x + 1）+（ -3x2 + 5x-7） = 2x2 －3x + 1 －3x2 + 5x－7
= (2x2 -3x2 )+(-3x + 5x)+(1-7)
=－ x2 ＋2x － 6
整式的加减混合运算步骤(有括号先去括号)
二：计算
2
3
＝ x－4y2
2
1
当x＝－1,y＝ 时
3ห้องสมุดไป่ตู้
2
12
原式＝ 2 ×（－1）－4× （ 2 ）
见负必括 见分必括
3
5
＝－ 2 －1＝－ 2
练一练： 1，化简下列各式：
(1)(3x 2 2x 1) ( x 2 x 3) (2)(2a 2b 2ab2 ) 3(a 2b 2ab2 )
解：(1)原式＝4x2 3x 2 (2)原式＝ a2b 4ab2
整式的加减
如何进行整式的加减呢？ 八字诀
去括号、合并同类项
括号前面出现系数怎么办？
• -7（a+b）
• 原式= -(7a+7b)=-7a-7b
• 2(x+y)
原式=(2x+2y)=2x+2y
整式的加减(公开课)
判断下列哪些式子是单项式：
x 1, , 0, 1 , 2 a2b, x 1, x y, 3(a b)
a
3
2
02 单项式的系数
单项式中的数字因数叫做这个单项式的系数.
单项式 -2ab a2 -a3 3.14 4a -πa2bc3
系数
-2
1
-1
3.14
43
3
-π
在研究单项式的系数问题时，要注意以下几点：
长方体： abh
正方体： a3
运算定律
1.a b c a c b (a c) b
2.a b c a (b c)
3.ab ba
4.abc b(ac)
5.a(b c d ) ab ac ad
6.a b a 1 b
7.1 2 3 n (1 n)n 2
5 7 x3yz2
2
06
34xyz 3
在研究单项式的次数问题时，要注意以下几点：
1、在一个单项式中，所有字母的指数的和才 叫做单项式的次数，与数字的指数无关。
2、单独一个数的次数记为0。
课后思考题
04 同类项
字母相同且相同字母的指数也相同的单项 式叫做同类项。
判断下列式子是否的同项：
-1 xy x2y x yx xy2
1.当单项式的系数是1或-1时，“1”通常省略不写。
2.圆周率π长的字母样，但它是常数。 3.当单项式的系数是带分数时，通常写成假分数。
4.单项式的系数应包括它前面的性质符号。
03 单项式的次数 在一个单项式中，所有字母的指数的和
叫做这个单项式的次数。
单项式 abc -23x πx2y3
次数
31
5
×√ ×
-5xyz 3yzx
x 1, , 0, 1 , 2 a2b, x 1, x y, 3(a b)
a
3
2
02 单项式的系数
单项式中的数字因数叫做这个单项式的系数.
单项式 -2ab a2 -a3 3.14 4a -πa2bc3
系数
-2
1
-1
3.14
43
3
-π
在研究单项式的系数问题时，要注意以下几点：
长方体： abh
正方体： a3
运算定律
1.a b c a c b (a c) b
2.a b c a (b c)
3.ab ba
4.abc b(ac)
5.a(b c d ) ab ac ad
6.a b a 1 b
7.1 2 3 n (1 n)n 2
5 7 x3yz2
2
06
34xyz 3
在研究单项式的次数问题时，要注意以下几点：
1、在一个单项式中，所有字母的指数的和才 叫做单项式的次数，与数字的指数无关。
2、单独一个数的次数记为0。
课后思考题
04 同类项
字母相同且相同字母的指数也相同的单项 式叫做同类项。
判断下列式子是否的同项：
-1 xy x2y x yx xy2
1.当单项式的系数是1或-1时，“1”通常省略不写。
2.圆周率π长的字母样，但它是常数。 3.当单项式的系数是带分数时，通常写成假分数。
4.单项式的系数应包括它前面的性质符号。
03 单项式的次数 在一个单项式中，所有字母的指数的和
叫做这个单项式的次数。
单项式 abc -23x πx2y3
次数
31
5
×√ ×
-5xyz 3yzx
新人教版初中数学七年级上册《第二章整式的加减：2.2整式的加减：合并同类项》公开课教案_1
课题：2.2 整式的加减(1)合并同类项第一课时一、三维目标1、知识与技能（1）了解同类项、合并同类项的概念，掌握合并同类项法则，•能正确合并同类项．（2）能先合并同类项化简后求值．经历类比有理数的运算律，探究合并同类项法则，培养学生观察、探索、分类、归纳等能力．3、情感态度与价值观掌握规范的解题步骤，养成良好的学习习惯，通过比较两种求代数式值的方法，体会合并同类项的作用．二、 教学重、难点与关键（1）重点：掌握合并同类项法则，熟练地合并同类项．（2）难点：多字母同类项的合并．（3）关键：正确理解同类项概念和合并同类项法则．．三、 教学过程，1、引入新课实际生活中，我们身边的同一类事物有很多，为了需要，往往我们要将它们进行分类。
又哪位同学愿意给大家举个例子呢？你会做吗？（1） 卓玛从家里带了3朵花到教室，尼玛从家里带了2朵花到教室。
请问现在教室里到底有几朵花？（2） （2）扎西家里有12头奶牛，有3只绵羊。
请问扎西家共有几头奶牛？2、讲授新课1.试一试 ?312532752222=+=+=+y x ab ab ab aa a2．导学提纲：（议一议)观察下列各单项式，把你认为相同类型的式子归类，并说出分类依据。
0.3ab 2 、 -4a 2b 、9xy 、 -xy -ab 2观察0.3ab 2，-ab 2中都含有相同字母a 和b ，并且相同字母a 的指数都是1, 相同字母b 的指数是2；而9xy 和 –xy 都含有相同字母x 和y,且相同字母x 指数都是1,相同字母y 指数都是1.3、归纳： 像这样，所含字母相同，并且相同字母的指数也分别相等的项叫做同类项，•几个常数项也是同类项．4. 练习。
判断下列各组中的两项是否是同类项，不是同类项的请说明原因：(1) -5ab 3与3a 3b( ) (2)3xy 与3x( )(3)0.5ab 与2ba （ ）(4)53与35 （ ）(5)x 3与53 ( ) (6) -5m 2n 3与2n 3m 2( )理解同类项应注意：两个相同：所含字母相同,相同字母的指数相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、复习
什么是整式、单项式、多项式
整式
单项式（系数和次数） 多项式（项和次数）
单项式 多项式
整 式
代 数 式
定义：由__数__字__或_字__母__的__乘__积__组成的式子。 单独的_一__个__数_或_一__个__字__母_也是单项式。
单项式： 系数： 单项式中的__数_字__因__数__。 次数： 单项式中的___所_有__字__母__的__指_数__和___.
合并同类项法则： 合并同类项时，只把系数相加，字母 和字母的指数不变
同类项
同类项的定义：
1____ 相同，
（两相同）
2._相__同__的__字_母__的__指__数__也_相同。
1.与_系__数_无关
（两无关）
2.与字__母__的__位__置__无关。
注意：几个常数项也是_同__类__项_。
合并同类项概念： _把__多__项_式__中__的__同__类_项__合__并__成__一_项_.
2
1 ＝ x－3x＋4x－6y2＋2y2
2
3
＝ x－4y2
2
1
当x＝－1,y＝ 时
3
2
12
原式＝ 2 ×（－1）－4× （ 2 ）
见负必括 见分必括
3
5
＝－ 2 －1＝－ 2
化简求值
• 1.运用整式的加减进行化简求值，一般先去 括号，合并同类项，再代入字母的值进行 计算，简记为“一化，二代，三计算”
注意的问题：
1.在确定多项式的项时，要连同它前面的符号， 2.一个多项式的次数最高项的次数是几，就说这个多项式是几次 多项式。
3.在多项式中，每个单项式都是这个多项式的项，每一项都有系 数，但对整个多项式来说，没有系数的概念，只有次数的概念。
什么叫同类项
特征（1）含有相同的字母 （2）相同字母的指数也相同 具有这两个特征的项叫同类项
括号前面出现系数怎么办？
• -7（a+b）
• 原式= -(7a+7b)=-7a-7b
• 2(x+y)
原式=(2x+2y)=2x+2y
方法：1、括号前面的系数乘遍括号内的每一 项
•
2、根据括号前面的符号去括号。
• -3(xy+yz+7) 试试
• = -3xy-3yz-21 -3(xy-yz-7)
=-3xy+3yz+21 3（2x2 -3x + 1）
2.若 2x3 yn与 xm y2 是同类项，则m+n=__5_.
3.若 xa6 ya4 与 3x4 yb 的和是一个单项式，则 a b=__4_.
4.若 2a b 3m 5 pa4bn1 7b5a4，则m+n-p=__-_4___
整式的加减 去括号
知识结构：
整式的概念 整式的加减
整式的计算
1.如果括号外的因数是正数，去 括号 后原括号内各项的符号与原来的符号 相同。 2.如果括号外的因数是负数，去括号 后原括号内各项的符号与原来的符号 相反。 去括号的依据是分配律，一要注意符 号，二要注意各项系数的改变。
“去括号，看符号。是‘+’号，不变号，是‘-’号，全变号”
整式的加减混合运算步骤(有括号先去括号)
= (2x2 -3x2 )+(-3x + 5x)+(1-7)
=－ x2 ＋2x － 6
整式的加减运算
• 整式的加减运算可以概括为：第一步：去 括号，第二步：合并同类项两步。
• 一般的，几个整式相加减，如果有括号就 先去括号，然后在进行合并同类项。
整式的加减混合运算步骤(有括号先去括号)
一：去括号 (按照先小括号，再中括号，最后大括号的顺序)
二：计算
1.找同类项，做好标记。
找
2.利用加法的交换律和结合律把同类项
放在一起。
搬
3.利用乘法分配律计算结果。 并
4.按要求按“升”或“降”幂排列。 排
注意：交换项的位置时，要将这一项的符 号一同带走。
先化简，后求值
1 2
x－
3(x＋
2y2)－
2(－2x－y2),其
中
x＝
1 －1，y＝2
1 解：原式＝ x－3x－6y2＋4x＋2y2
注意的问题：
1.当单项式的系数是1或-1时，“1”通常省略不写。 2.当式子分母中出现字母时不是单项式。 3.圆周率π是常数，不能看成字母。 4.当单项式的系数是带分数时，通常写成假分数。 5.单项式的系数应包括它前面的性质符号。
6.单项式次数是指所有字母的次数的和，与数字的次数没 有关系。
7.单独的数字不含字母, 规定它的次数是零次.
• 2.在具体的运算中，也可以先合并同类项， 再去括号，但要按运算顺序去做。
化简+（+2）=2 －(+2)=－2
＋ (5a－3b)=5a-3b
－ (a－2b)=－a+2b
去括号，看符号： 是“＋”号，不变号；
是“－”号，全变号．
计算
a ＋ (5a－3b) － (a－2b) 解：原式= a + 5a－3b － a + 2b
= (a +5a － a) + (－3b + 2b) = 5a － b
=6x2 -9x+3 -3（2x2 -3x + 1） =6x2 + 9x-3
例：计算：
（1）2x2 -3x + 1与 -3x2 + 5x-7 的和
思维分析：把多项式看作一个整体，并用括号
括起来。 见多必括
解 (2x2 -3x + 1）+（ -3x2 + 5x-7） = 2x2 －3x + 1 －3x2 + 5x－7
合并同类项法则： 1.__系_数___相加减;
2._字__母__和__字_母__的__指__数___不变。
1.下列各式中，是同类项的是：__③__⑤_⑥______
① 2x2 y3 与 x3 y2 ② x2 yz 与 x2 y
③10mn与 2 mn
3
④ (a)5与 (3)5 ⑤ 3x2 y 与 0.5yx2 ⑥-125与
多项式
定义：几个_单__项__式__的_和__.
项： 组成多项式中的__每__一_个__单__项__式__. 有几项，就叫做__几__项__式___.
常数项：多项式中__不__含_字__母__的__项____. 多项式的次数：多__项_式__中__次__数__最_高__的__项__的__次_数__。__.
单项式 多项式
系数
次数 项，项数，常数项， 最高次项 次数
同类项与合并同类项 去括号 化简求值
用字母来表示生活中的量
如何进行整式的加减呢？ 八字诀
去括号、合并同类
例如：+ ( 3x－3 ) = 3x－3 例如: －( x － 1) =－x + 1
什么是整式、单项式、多项式
整式
单项式（系数和次数） 多项式（项和次数）
单项式 多项式
整 式
代 数 式
定义：由__数__字__或_字__母__的__乘__积__组成的式子。 单独的_一__个__数_或_一__个__字__母_也是单项式。
单项式： 系数： 单项式中的__数_字__因__数__。 次数： 单项式中的___所_有__字__母__的__指_数__和___.
合并同类项法则： 合并同类项时，只把系数相加，字母 和字母的指数不变
同类项
同类项的定义：
1____ 相同，
（两相同）
2._相__同__的__字_母__的__指__数__也_相同。
1.与_系__数_无关
（两无关）
2.与字__母__的__位__置__无关。
注意：几个常数项也是_同__类__项_。
合并同类项概念： _把__多__项_式__中__的__同__类_项__合__并__成__一_项_.
2
1 ＝ x－3x＋4x－6y2＋2y2
2
3
＝ x－4y2
2
1
当x＝－1,y＝ 时
3
2
12
原式＝ 2 ×（－1）－4× （ 2 ）
见负必括 见分必括
3
5
＝－ 2 －1＝－ 2
化简求值
• 1.运用整式的加减进行化简求值，一般先去 括号，合并同类项，再代入字母的值进行 计算，简记为“一化，二代，三计算”
注意的问题：
1.在确定多项式的项时，要连同它前面的符号， 2.一个多项式的次数最高项的次数是几，就说这个多项式是几次 多项式。
3.在多项式中，每个单项式都是这个多项式的项，每一项都有系 数，但对整个多项式来说，没有系数的概念，只有次数的概念。
什么叫同类项
特征（1）含有相同的字母 （2）相同字母的指数也相同 具有这两个特征的项叫同类项
括号前面出现系数怎么办？
• -7（a+b）
• 原式= -(7a+7b)=-7a-7b
• 2(x+y)
原式=(2x+2y)=2x+2y
方法：1、括号前面的系数乘遍括号内的每一 项
•
2、根据括号前面的符号去括号。
• -3(xy+yz+7) 试试
• = -3xy-3yz-21 -3(xy-yz-7)
=-3xy+3yz+21 3（2x2 -3x + 1）
2.若 2x3 yn与 xm y2 是同类项，则m+n=__5_.
3.若 xa6 ya4 与 3x4 yb 的和是一个单项式，则 a b=__4_.
4.若 2a b 3m 5 pa4bn1 7b5a4，则m+n-p=__-_4___
整式的加减 去括号
知识结构：
整式的概念 整式的加减
整式的计算
1.如果括号外的因数是正数，去 括号 后原括号内各项的符号与原来的符号 相同。 2.如果括号外的因数是负数，去括号 后原括号内各项的符号与原来的符号 相反。 去括号的依据是分配律，一要注意符 号，二要注意各项系数的改变。
“去括号，看符号。是‘+’号，不变号，是‘-’号，全变号”
整式的加减混合运算步骤(有括号先去括号)
= (2x2 -3x2 )+(-3x + 5x)+(1-7)
=－ x2 ＋2x － 6
整式的加减运算
• 整式的加减运算可以概括为：第一步：去 括号，第二步：合并同类项两步。
• 一般的，几个整式相加减，如果有括号就 先去括号，然后在进行合并同类项。
整式的加减混合运算步骤(有括号先去括号)
一：去括号 (按照先小括号，再中括号，最后大括号的顺序)
二：计算
1.找同类项，做好标记。
找
2.利用加法的交换律和结合律把同类项
放在一起。
搬
3.利用乘法分配律计算结果。 并
4.按要求按“升”或“降”幂排列。 排
注意：交换项的位置时，要将这一项的符 号一同带走。
先化简，后求值
1 2
x－
3(x＋
2y2)－
2(－2x－y2),其
中
x＝
1 －1，y＝2
1 解：原式＝ x－3x－6y2＋4x＋2y2
注意的问题：
1.当单项式的系数是1或-1时，“1”通常省略不写。 2.当式子分母中出现字母时不是单项式。 3.圆周率π是常数，不能看成字母。 4.当单项式的系数是带分数时，通常写成假分数。 5.单项式的系数应包括它前面的性质符号。
6.单项式次数是指所有字母的次数的和，与数字的次数没 有关系。
7.单独的数字不含字母, 规定它的次数是零次.
• 2.在具体的运算中，也可以先合并同类项， 再去括号，但要按运算顺序去做。
化简+（+2）=2 －(+2)=－2
＋ (5a－3b)=5a-3b
－ (a－2b)=－a+2b
去括号，看符号： 是“＋”号，不变号；
是“－”号，全变号．
计算
a ＋ (5a－3b) － (a－2b) 解：原式= a + 5a－3b － a + 2b
= (a +5a － a) + (－3b + 2b) = 5a － b
=6x2 -9x+3 -3（2x2 -3x + 1） =6x2 + 9x-3
例：计算：
（1）2x2 -3x + 1与 -3x2 + 5x-7 的和
思维分析：把多项式看作一个整体，并用括号
括起来。 见多必括
解 (2x2 -3x + 1）+（ -3x2 + 5x-7） = 2x2 －3x + 1 －3x2 + 5x－7
合并同类项法则： 1.__系_数___相加减;
2._字__母__和__字_母__的__指__数___不变。
1.下列各式中，是同类项的是：__③__⑤_⑥______
① 2x2 y3 与 x3 y2 ② x2 yz 与 x2 y
③10mn与 2 mn
3
④ (a)5与 (3)5 ⑤ 3x2 y 与 0.5yx2 ⑥-125与
多项式
定义：几个_单__项__式__的_和__.
项： 组成多项式中的__每__一_个__单__项__式__. 有几项，就叫做__几__项__式___.
常数项：多项式中__不__含_字__母__的__项____. 多项式的次数：多__项_式__中__次__数__最_高__的__项__的__次_数__。__.
单项式 多项式
系数
次数 项，项数，常数项， 最高次项 次数
同类项与合并同类项 去括号 化简求值
用字母来表示生活中的量
如何进行整式的加减呢？ 八字诀
去括号、合并同类
例如：+ ( 3x－3 ) = 3x－3 例如: －( x － 1) =－x + 1