ANSYS结构非线性分析指南连载四
ANSYS教程,非线性结构分析过程

ANSYS教程,非线性结构分析过程尽管非线性分析比线性分析变得更加复杂,但处理基本相同。
只是在非线形分析的适当过程中,添加了需要的非线形特性。
非线性结构分析的基本分析过程也主要由建模、加载并求解和观察结果组成。
下面来讲解其主要步骤和各个选项的处理方法。
建模这一步对线性和非线性分析都是必需的,尽管非线性分析在这一步中可能包括特殊的单元或非线性材料性质,如果模型中包含大应变效应,应力─应变数据必须依据真实应力和真实(或对数)应变表示。
加载求解在建立好有限元模型之后,将进入ANSYS求解器(GUI:Main Menu | Solution),并根据分析的问题指定新的分析类型(ANTYPE)。
求解问题的非线性特性在ANSYS中是通过指定不同的分析选项和控制选项来定义的。
非线性分析不同于线性分析之处在于,它通常要求执行多荷载步增量和平衡迭代。
下面就详细讲解一下进行非线性结构分析需要定义的各个求解选项、分析选项和控制选项是如何设置的,以及他们的意义是什么。
求解控制对于一些基本的非线性问题的分析选项,可以通过ANSYS提供的求解控制对话框中的选项设置来完成。
选择菜单路径:Main Menu | Solution | Analysis Type | Sol’n Controls,将弹出求解控制(Solution Controls)对话框,如下图所示。
从图中可以看出该对话框主要包括5个选项卡:基本选项(Basic)、瞬态选项(Transient)、求解选项(Sol’n Options)、非线性选项(Nonlinear)和高级非线性选项(Advanced NL)。
如果开始一项新的分析,在设置分析类型和非线性选项时,选择“Large Displacement Static”选项(不是所有的非线性分析都支持大变形)。
如果想要重新启动一个失败的非线性分析,则选择“Restart Current Analysis”选项。
选中下面的“Calculate prestress effects”单选按钮用于有预应力的模态分析时的预应力计算,具体内容见模态分析部分。
ANSYS结构非线性分析指南

ANSYS结构非线性分析指南ANSYS是一个强大的工程仿真软件,能够对各种复杂的结构进行分析。
其中,结构非线性分析是其中一种重要的分析方法,它能够模拟结构在非线性载荷和变形条件下的行为。
本文将为您提供一个ANSYS结构非线性分析的指南,帮助您更好地理解和应用这个方法。
首先,我们需要明确结构非线性分析的目标。
一般来说,结构非线性分析主要用于研究结构在大变形、材料非线性、接触或摩擦等复杂条件下的响应。
例如,当结构受到极大的外力作用时,其产生的变形可能会导致材料的非线性行为,这时我们就需要进行非线性分析。
在进行非线性分析之前,我们需要进行准备工作。
首先,我们需要准备一个几何模型,可以通过CAD软件导入或者直接在ANSYS中绘制。
然后,我们需要选择合适的材料模型,这将直接影响分析结果的准确性。
ANSYS提供了多种材料模型,例如线弹性模型、塑性模型和粘弹性模型等。
接下来,我们需要定义边界条件和载荷。
边界条件指明了结构的固定边界和自由边界,这决定了结构的位移约束。
载荷是作用在结构上的外力或者外界约束,例如压力、点载荷或者摩擦力等。
在非线性分析中,载荷的大小和施加方式可能会导致结构的非线性响应,因此需要仔细选择。
接下来,我们需要选择适当的非线性分析方法。
ANSYS提供了多种非线性分析方法,例如几何非线性分析、材料非线性分析和接触非线性分析等。
几何非线性分析适用于大变形情况下的分析,材料非线性分析适用于材料的弹塑性行为分析,而接触非线性分析适用于多个结构之间的接触行为分析。
在进行非线性分析之前,我们需要对模型进行预处理,包括网格划分和解算控制参数的设置。
网格划分的精度会直接影响分析结果的准确性,因此需要进行适当的剖分。
解算控制参数的设置涉及到收敛性和稳定性的问题,需要进行合理的调整。
然后,我们可以进行非线性分析了。
ANSYS提供了多种求解器,例如Newton-Raphson方法和弧长法等。
这些求解器可以通过迭代算法来求解非线性方程组,得到结构的响应结果。
04 ANSYS13.0 Workbench 结构非线性培训 一般过程解析

... 建立非线性模型
• 对任何结构单元, DOF(自由度)求解Du 是对节点求解 • 应力和应变是在积分点计算. 由DOF推导而来.
– 例如, 可由位移确定应变 ,经:
Training Manual
Dε BDu
s, e u
– 这里 B 称为 应变-位移矩阵
• 右图所示的一 4节点四边形单元有 2x2个积分点, 红点为积分点. • 在后处理结果中, 积分点的应力/应变值经外插值或复制到节点位置。
Training Manual
– 仅适用于高阶单元. – 当一部件厚度方向只有一个单元时,强制使用完全积分有助于提高精确度.
2-6
Workbench Mechanical - General Nonlinear Procedures
... 建立非线性模型
• WB Mechanical 默认采用高阶单元(有中节点)来划分网格.
第二章
一般过程
Workbench – Mechanical 结构非线性
2-1
Workbench Mechanical - General Nonlinear Procedures
章节概述
•
Training Manual
这章介绍一般工具和程序,不是对特殊来源非线性的详细介绍, 但介绍了 达到收敛的有用措施和后处理结果:
A. B. C. D.
建立非线性模型 分析设置 非线性结果后处理 作业
2-2
Workbench Mechanical - General Nonlinear Procedures
A. 建立非线性模型
什么是建立非线性模型与线性模型的不同?
Training Manual
• 某些情况,它们没有不同!
ANSYS 高级技术分析:非线性_结构分析
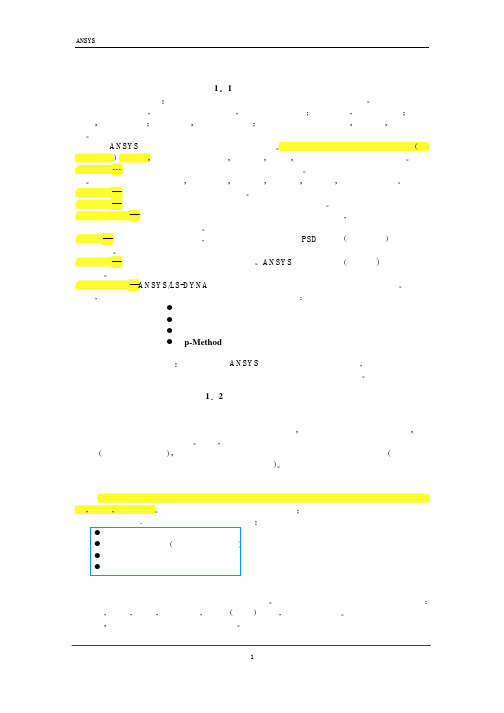
第一章结构静力分析1 1 结构分析概述结构分析的定义结构分析是有限元分析方法最常用的一个应用领域结构这个术语是一个广义的概念它包括土木工程结构如桥梁和建筑物汽车结构如车身骨架海洋结构如船舶结构航空结构如飞机机身等同时还包括机械零部件如活塞传动轴等等在ANSYS产品家族中有七种结构分析的类型结构分析中计算得出的基本未知量节点自由度是位移其他的一些未知量如应变应力和反力可通过节点位移导出静力分析---用于求解静力载荷作用下结构的位移和应力等静力分析包括线性和非线性分析而非线性分析涉及塑性应力刚化大变形大应变超弹性接触面和蠕变模态分析---用于计算结构的固有频率和模态谐波分析---用于确定结构在随时间正弦变化的载荷作用下的响应瞬态动力分析---用于计算结构在随时间任意变化的载荷作用下的响应并且可计及上述提到的静力分析中所有的非线性性质谱分析---是模态分析的应用拓广用于计算由于响应谱或PSD输入随机振动引起的应力和应变曲屈分析---用于计算曲屈载荷和确定曲屈模态ANSYS可进行线性特征值和非线性曲屈分析显式动力分析---ANSYS/LS-DYNA可用于计算高度非线性动力学和复杂的接触问题此外前面提到的七种分析类型还有如下特殊的分析应用断裂力学复合材料疲劳分析p-Method结构分析所用的单元绝大多数的ANSYS单元类型可用于结构分析单元型从简单的杆单元和梁单元一直到较为复杂的层合壳单元和大应变实体单元1 2 结构线性静力分析静力分析的定义静力分析计算在固定不变的载荷作用下结构的效应它不考虑惯性和阻尼的影响如结构受随时间变化载荷的情况可是静力分析可以计算那些固定不变的惯性载荷对结构的影响如重力和离心力以及那些可以近似为等价静力作用的随时间变化载荷如通常在许多建筑规范中所定义的等价静力风载和地震载荷静力分析中的载荷静力分析用于计算由那些不包括惯性和阻尼效应的载荷作用于结构或部件上引起的位移应力应变和力固定不变的载荷和响应是一种假定即假定载荷和结构的响应随时间的变化非常缓慢静力分析所施加的载荷包括外部施加的作用力和压力稳态的惯性力如中力和离心力位移载荷温度载荷线性静力分析和非线性静力分析静力分析既可以是线性的也可以是非线性的非线性静力分析包括所有的非线性类型大变形塑性蠕变应力刚化接触间隙单元超弹性单元等本节主要讨论线性静力分析非线性静力分析在下一节中介绍第1页线性静力分析的求解步骤1建模2施加载荷和边界条件求解3结果评价和分析目录非线性结构分析的定义 1非线性行为的原因 1非线性分析的重要信息 3非线性分析中使用的命令8非线性分析步骤综述8 第一步建模 9第二步加载且得到解 9第三步考察结果16非线性分析例题GUI方法 20第一步设置分析标题 21第二步定义单元类型21第三步定义材料性质22第四步定义双线性各向同性强化数据表22第五步产生矩形22第六步设置单元尺寸23第七步划分网格23第八步定义分析类型和选项23第九步定义初始速度24第十步施加约束24第十一步设置载荷步选项24第十二步求解25第十三步确定柱体的应变25第十四步画等值线26第十五步用Post26定义变量26第十六步计算随时间变化的速度26非线性分析例题命令流方法 271 3 非线性结构静力分析非线性结构的定义在日常生活中,会经常遇到结构非线性例如无论何时用钉书针钉书金属钉书钉将永久地弯曲成一个不同的形状看图1─1a如果你在一个木架上放置重物随着时间的迁移它将越来越下垂看图1─1b当在汽车或卡车上装货时它的轮胎和下面路面间接触将随货物重量的啬而变化看图1─1c如果将上面例子所载荷变形曲线画出来,你将发现它们都显示了非线性结构的基本特征--变化的结构刚性.图1─1 非线性结构行为的普通例子非线性行为的原因引起结构非线性的原因很多它可以被分成三种主要类型状态变化包括接触许多普通结构的表现出一种与状态相关的非线性行为,例如一根只能拉伸的电缆可能是松散的,也可能是绷紧的轴承套可能是接触的,也可能是不接触的, 冻土可能是冻结的,也可能是融化的这些系统的刚度由于系统状态的改变在不同的值之间突然变化状态改变也许和载荷直接有关如在电缆情况中也可能由某种外部原因引起如在冻土中的紊乱热力学条件ANSYS程序中单元的激活与杀死选项用来给这种状态的变化建模接触是一种很普遍的非线性行为接触是状态变化非线性类型形中一个特殊而重要的子集几何非线性它变化的几何形状可能会引起结构的非线性地响应一个例的垂向刚性随着垂向载荷的增加杆不断弯曲以致于动力臂明显地减少导致杆端显示出在较高载荷下不断增长的刚性图1─2 钓鱼杆示范几何非线性材料非线性许多因素可以影响材料的应力第4页──应变性质包括加载历史如在弹─塑性响应状况下环境状况如温度加载的时间总量如在蠕变响应状况下牛顿一拉森方法ANSYS程序的方程求解器计算一系列的联立线性方程来预测工程系统的响应然而非线性结构的行为不能直接用这样一系列的线性方程表示需要一系列的带校正的线性近似来求解非线性问题逐步递增载荷和平衡迭代一种近似的非线性救求解是将载荷分成一系列的载荷增量可以在几个载荷步内或者在一个载步的几个子步内施加载荷增量在每一个增量的求解完成后继续进行下一个载荷增量之前程序调整刚度矩阵以反映结构刚度的非线性变化遗憾的是纯粹的增量近似不可避免地随着每一个载荷增量积累误差导种结果最终失去平衡如图1─3a所示所示.a 纯粹增量式解b)全牛顿拉普森迭代求解2个载荷增量图8─3 纯粹增量近似与牛顿拉普森近似的关系ANSYS程序通过使用牛顿拉普森平衡迭代克服了这种困难它迫使在每一个载荷增量的末端解达到平衡收敛在某个容限范围内图1─3b)描述了在单自由度非线性分析中牛顿拉普森平衡迭代的使用在每次求解前NR方法估算出残差矢量这个矢量是回复力对应于单元应力的载荷和所加载荷的差值程序然后使用非平衡载荷进行线性求解且核查收敛性如果不满足收敛准则重新估算非平衡载荷修改刚度矩阵获得新解持续这种迭代过程直到问题收敛ANSYS程序提供了一系列命令来增强问题的收敛性如自适应下降线性搜索自动载荷步及二分等可被激活来加强问题的收敛性如果不能得到收敛那么程序或者继续计算下一个载荷前或者终止依据你的指示对某些物理意义上不稳定系统的非线性静态分析如果你仅仅使用NR方法正切刚度矩阵可能变为降秩短阵导致严重的收敛问题这样的情况包括独立实体从固定表面分离的静态接触分析结构或者完全崩溃或者突然变成另一个稳定形状的非线性弯曲问题对这样的情况你可以激活另外一种迭代方法弧长方法来帮助稳定求解弧长方法导致NR平衡迭代沿一段弧收敛从而即使当正切刚度矩阵的倾斜为零或负值时也往往阻止发散这种迭代方法以图形表示在图1─4中图1─4传统的NR方法与弧长方法的比较非线性求解的组织级别非线性求解被分成三个操作级别载荷步子步平衡迭代顶层级别由在一定时间范围内你明确定义的载荷步组成假定载荷在载荷步内是线性地变化的在每一个载荷是步内为了逐步加载可以控制程序来执行多次求解子步或时间步在每一个子步内程序将进行一系列的平衡迭代以获得收敛的解图1─5说明了一段用于非线性分析的典型的载荷历史图1─5载荷步子步及时间收敛容限当你对平衡迭代确定收敛容限时你必须答这些问题你想基于载荷变形还是联立二者来确定收敛容限既然径向偏移以弧度度量比对应的平移小你是不是想对这些不同的条目建立不同的收敛准则当你确定收敛准则时ANSYS程序会给你一系列的选择你可以将收敛检查建立在力力矩位移转动或这些项目的任意组合上另外每一个项目可以有不同的收敛容限值对多自由度问题你同样也有收敛准则的选择问题当你确定你的收敛准则时记住以力为基础的收敛提供了收敛的绝对量度而以位移为基础的收敛仅提供了表观收敛的相对量度因此你应当如果需要总是使用以力为基础或以力矩为基础的收敛容限如果需要可以增加以位移为基础或以转动为基础的收敛检查但是通常不单独使用它们图1─6说明了一种单独使用位移收敛检查导致出错情况在第二次迭代后计算出的位移很小可能被认为是收敛的解尽管问题仍旧远离真正的解要防止这样的错误应当使。
ANSYS结构非线性分析指南(一至三章)

ANSYS结构非线性分析指南(一到三章)屈服准则概念:1.理想弹性材料物体发生弹性变形时,应力与应变完全成线性关系,并可假定它从弹性变形过渡到塑性变形是突然的。
2.理想塑性材料(又称全塑性材料)材料发生塑性变形时不产生硬化的材料,这种材料在进入塑性状态之后,应力不再增加,也即在中性载荷时即可连续产生塑性变形。
3.弹塑性材料在研究材料塑性变形时,需要考虑塑性变形之前的弹性变形的材料这里可分两种情况:Ⅰ.理想弹塑性材料在塑性变形时,需要考虑塑性变形之前的弹性变形,而不考虑硬化的材料,也即材料进入塑性状态后,应力不再增加可连续产生塑性变形。
Ⅱ.弹塑性硬化材料在塑性变形时,既要考虑塑性变形之前的弹性变形,又要考虑加工硬化的材料,这种材料在进入塑性状态后,如应力保持不变,则不能进一步变形。
只有在应力不断增加,也即在加载条件下才能连续产生塑性变形。
4.刚塑性材料在研究塑性变形时不考虑塑性变形之前的弹性变形。
这又可分两种情况:Ⅰ.理想刚塑性材料在研究塑性变形时,既不考虑弹性变形,又不考虑变形过程中的加工硬化的材料。
Ⅱ.刚塑性硬化材料在研究塑性变形时,不考虑塑性变形之前的弹性变形,但需要考虑变形过程中的加工硬化材料。
屈服准则的条件:1.受力物体内质点处于单向应力状态时,只要单向应力大到材料的屈服点时,则该质点开始由弹性状态进入塑性状态,即处于屈服。
2.受力物体内质点处于多向应力状态时,必须同时考虑所有的应力分量。
在一定的变形条件(变形温度、变形速度等)下,只有当各应力分量之间符合一定关系时,质点才开始进入塑性状态,这种关系称为屈服准则,也称塑性条件。
它是描述受力物体中不同应力状态下的质点进入塑性状态并使塑性变形继续进行所必须遵守的力学条件,这种力学条件一般可表示为)=Cf(σij又称为屈服函数,式中C是与材料性质有关而与应力状态无关的常数,可通过试验求得。
屈服准则是求解塑性成形问题必要的补充方程。
1.1 什么是结构非线性在日常生活中,经常会遇到结构非线性。
ANSYS结构非线性分析指南_第四章

第四章材料非线性分析4.1 材料非线性概述许多与材料有关的参数可以使结构刚度在分析期间改变。
塑性、非线性弹性、超弹性材料、混凝土材料的非线性应力—应变关系,可以使结构刚度在不同载荷水平下(以及在不同温度下)改变。
蠕变、粘塑性和粘弹性可以引起与时间、率、温度和应力相关的非线性。
膨胀可以引起作为温度、时间、中子流水平(或其他类似量)函数的应变。
ANSYS程序应可以考虑多种材料非线性特性:1.率不相关塑性指材料中产生的不可恢复的即时应变。
2.率相关塑性也可称之为粘塑性,材料的塑性应变大小将是加载速度与时间的函数。
3.材料的蠕变行为也是率相关的,产生随时间变化的不可恢复应变,但蠕变的时间尺度要比率相关塑性大的多。
4.非线性弹性允许材料的非线性应力应变关系,但应变是可以恢复的。
5.超弹性材料应力应变关系由一个应变能密度势函数定义,用于模拟橡胶、泡沫类材料,变形是可以恢复的。
6.粘弹性是一种率相关的材料特性,这种材料应变中包含了弹性应变和粘性应变。
7.混凝土材料具有模拟断裂和压碎的能力。
8.膨胀是指材料在中子流作用下的体积扩大效应。
4.2 塑性分析4.2.1 塑性理论简介许多常用的工程材料,在应力水平低于比例极限时,应力—应变关系为线性的。
超过这一极限后,应力—应变关系变成非线性,但却不一定是非弹性的。
以不可恢复的应变为特征的塑性,则在应力超过屈服点后开始出现。
由于屈服极限与比例极限相差很小,ANSYS程序在塑性分析中,假设这二个点相同,见图4-1。
图4-1 弹塑性应力-应变曲线塑性是一种非保守的(不可逆的),与路径相关的现象。
换句话说,荷载施加的顺序,以及什么时候发生塑性响应,影响最终求解结果。
如果用户预计在分析中会出现塑性响应,则应把荷载处理成一系列的小增量荷载步或时间步,以使模型尽可能附合荷载—响应路径。
最大塑性应变是在输出(Jobname.OUT)文件的子步信息中打印的。
在一个子步中,如果执行了大量的平衡迭代,或得到大于15%的塑性应变增量,则塑性将激活自动时间步选项[AUTOTS ](GUI :Main Menu>Solution> Sol'n Control:Basic Tab 或 MainMenu>Solution>Unabridged Menu> Time /Frequenc>Time and Substps)。
ANSYS高级结构非线性教程

•
的所有分量是精确的。
September 30, 2001 Inventory #001491 TOC-10
单元技术
... 传统位移公式
• • 完全积分、高阶传统位移单元也易于发生体积锁定。
Training Manual
Advanced Structural Nonlinearities 6.0
完全积分、低阶传统位移单元易于发生剪切 和体积锁定,因此很少使用。
• 这个模型呈现剪切锁定了吗?
Training Manual
Advanced Structural Nonlinearities 6.0
单元 182 (B-Bar), 几乎不可压缩的MooneyRivlin 超弹材料的平面应变
答案: 很意外, 没有。 该模型具有超弹材料属性, 以 B-Bar 和增强应变运行, 结果f非常相似.
单元技术
... 本章概述
• 这章的要点是:
– 完全积分的、传统的基于位移的连续单元在一定情形下低估位移
Training Manual
Advanced Structural Nonlinearities 6.0
• 这称为网格锁定
– 因此,有不同的单元公式来处理这些问题, 基于: • 体积或弯曲占优的问题(结构行为) • 弹性,塑性或超弹性(材料行为)
• 回顾积分点的一些重要细节:
– 对任何单元, 自由度解 {Du} 是在结点求出
Training Manual
Advanced Structural Nonlinearities 6.0
– 在积分点计算应力和应变。它们由自由度导出。例如可以由位移通过下式确定 应变:
D e B D u
完全积分的低阶单元变形中,上下两 边保持直线,不再保持直角,gxy 不 为零。
ANSYS结构非线性分析指南

ANSYS结构非线性分析指南ANSYS是一款非常强大的有限元分析软件,广泛应用于各种工程领域的结构分析。
在常规的结构分析中,通常会涉及到线性分析,但一些情况下,结构出现了非线性行为,这时就需要进行非线性分析。
非线性分析可以更准确地模拟结构的真实行为,包括材料的非线性、几何的非线性和接触非线性等。
在进行ANSYS结构非线性分析时,需要考虑以下几个方面:1.材料的非线性:在材料的应力-应变关系中,材料的性质可能会发生变化,如塑性变形、损伤、软化等。
因此在非线性分析中,需要考虑材料的非线性特性,并正确选取材料模型。
2.几何的非线性:在一些情况下,结构本身的几何形态可能会发生较大变化,如大变形、屈曲等。
这需要考虑结构的几何非线性,并在分析中充分考虑结构的形变情况。
3.接触非线性:当结构中存在接触面时,接触面之间的接触力可能是非线性的,如摩擦力、法向压力等。
在进行非线性分析时,需要考虑接触面上的非线性行为,确保接触的可靠性。
在进行ANSYS结构非线性分析时,可以按照以下步骤进行:1.建立模型:首先需要根据实际情况建立结构的有限元模型,包括几何形状、边界条件和加载条件等。
在建立模型时,需要考虑到结构的材料、几何和接触情况,并进行合理的网格划分。
2.设置分析类型:在ANSYS中,可以选择静力分析、动力分析等不同的分析类型。
在进行非线性分析时,需要选择适合的非线性分析模块,并设置相应的参数。
3.设置材料模型:根据结构的材料特性,选择合适的材料模型,如弹塑性模型、本构模型等。
根据实际情况,设置材料的材料参数,确保材料的非线性行为能够得到准确的描述。
4.设置几何非线性:考虑结构的几何非线性时,需要选择合适的几何非线性选项,并设置合适的几何参数。
在进行大变形分析时,需要选择几何非线性选项,确保结构的形变情况能够得到准确的描述。
5.设置接触非线性:当结构存在接触面时,需要考虑接触面上的非线性行为。
在ANSYS中,可以设置接触类型、摩擦系数等参数,确保接触的可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ANSYS结构非线性分析指南连载四--第四章材料非线性分析 (二) (2014-04-27 10:47:15)转载▼标签:it4.3 超弹性分析4.3.1 超弹理论4.3.1.1 超弹的定义一般工程材料(例如金属)的应力状态由一条弹塑性响应曲线来描述,而超弹性材料存在一个弹性势能函数,该函数是一个应变或变形张量的标量函数,而该标量函数对应变分量的导数就是相应的应力分量。
上式中:[S]=第二皮奥拉-克希霍夫应力张量W=单位体积的应变能函数[E]=拉格朗日应变张量拉格朗日应变可以由下式表达:[E]=1/2([C]-I)其中:[I]是单位矩阵,[C]是有柯西-格林应变张量其中[F]是变形梯度张量,其表达式为:x:变形后的节点位置矢量X:初始的节点位置矢量如果使用主拉伸方向作为变形梯度张量和柯西-格林变形张量的方向,则有:其中: J=初始位置与最后位置的体积比材料在第i个方向的拉伸率在ANSYS程序中,我们假定超弹材料是各向同性的,在每个方向都有完全相同的材料特性,在这种情况下,我们既可以根据应变不变量写出应变能密度函数,也可以根据主拉伸率写出应变能密度函数。
应变不变量是一种与坐标系无关的应变表示法。
使用它们就意味着材料被假定是各向同性的。
Mooney -Rivlin和Blatz-Ko应变能密度函数都可以用应变不变量表示,应变不变量可以柯西-格林应变张量和主拉伸率表示出来:一个根据应量不变量写出来的应变能密度函数如下:为材料常数,上式是两个常数的Mooney-Rivlin应变能密度函数。
超弹材料可以承受十分大的弹性变形,百分之几百的应变是很普遍的,既然是纯弹性应变,因此超弹性材料的变形是保守行为,与加载路径无关。
4.3.1.2 不可压缩缩性大多数超弹材料,特别是橡胶和橡胶类材料,都是几乎不可压缩的,泊松比接近于0.5,不可压缩材料在静水压力下不产生变形,几乎不可压缩材料的泊松比一般在0.48至0.5之间(不包含0.5),对这些材料,在单元公式中必须考虑不可压缩条件。
在ANSYS程序中,不可压缩超弹单元修改了应变能密度函数,在单元中明确地包含了压力自由度。
压力自由度使不可压缩条件得到满足,而不降低求解速度。
压力自由度是一种内部自由度,被凝聚在单元内部。
4.3.1.3 超弹单元有三种单元适合于模拟超弹性材料:不可压缩单元有HYPE56,58,74和158,这些单元适用于模拟橡胶材料。
可压缩单元有HYPER84和86,HYPER84既可以是4节点矩形也可以是8节点矩形单元,这种单元主要用来模拟泡沫材料。
18X族单元(除LIMK和BEAM单元外,包括SHELL181,PLANE182,PLANE183,SOLID185,SOLID186,和SOLID187)。
18X族单元消除了体积锁定,既适用于不可压材料,又适用于可压材料。
参见《ANSYS Elements Reference》的“Mixed U-P Formulations”。
4.3.2 超弹材料选项超弹性可用于分析橡胶类材料(elastomers),这种材料可承受大应变和大位移,但体积改变极微(不可压缩)。
这种分析需用到大应变理论[ NLGEOM ,ON]。
图4-13是一个例子。
图4-13 超弹性结构在ANSYS超弹性模型中,材料响应总是假设各向同性和等温性。
由于这一假设,应变能势函数按应变不变量来表示。
除非明确指出,超弹性材料还假设为几乎或完全不可压缩材料。
材料热膨胀也假定为各向同性的。
ANSYS在模拟不可压缩或几乎不可压缩超弹性材料时,应变能势函数有几种选项。
这些选项均适用于SHELL181,PLANE182, PLANE183, SOLID185, SOLID186, SOLID187 单元。
可以通过TB ,HYPER 命令的 TBOPT参数进入这些选项。
其中一个选项,Mooney-Rivhlin 选项,也适用于HYPER56, HYPER58, HYPER74, HYPER158 单元,以及显式动力分析单元PLANE162,SHELL163, SOLID164。
这一选项可通过TB ,MOONEY 命令进入。
4.3.2.1 Mooney-Rivlin超弹性选项(TB,HYPER)请注意本小节论述应用Mooney-Rivlin 选项与单元SHELL181, PLANE182, PLANE183, SOLID185, SOLID186, SOLID187。
如果你想应用Mooney-Rivlin选项于单元HYPER56, HYPER58, HYPER74, HYPER158, PLANE162, SHELL163,SOLID164,则参见§4.3.2.7。
Mooney-Rivlin选项( TB ,HYPER,,,,MOOMEY)是缺省项,允许用户通过 TB命令的 NPTS参数定义2,3,5或9个参数。
例如,为了定义5参数模型,用户采用 TB ,HYPER,1,,5,MOONEY。
2参数Mooney-Rivlin选项,适用于应变大约为100%(拉)和30%(压)的情况。
与其他选项相比,较高阶的Mooney-Rivlin选项,对于较大应变的求解,可得到较好的近似。
下例是3参数Mooney-Rivlin选项的输入实例:TB,HYPER,1,,3,MOONEY !Activate 3 parameter Mooney-Rivlin data tableTBDATA,1,0.163498 !Define c10TBDATA,2,0.125076 !Define c01TBDATA,3,0.014719 !Define c11TBDATA,4,6.93063E-5 !Define incompressibility parameter!(as 2/K, K is the bulk modulus)对于本选项所需要的材料常数的描述,见《ANSYS Elements Reference》。
4.3.2.2 Ogden选项Ogden选项( TB ,HYPER,,,,OGDEN)允许用户通过TB 命令的 NPTS参数定义无限参数,例如,应用TB,HYPER,1,,3,OGDEN 定义3参数模型。
与其他选项相比,Ogden选项通常对大应变水平的求解提供最好的近似。
可应用的应变水平可达到700%。
较高阶的参数可提供更精确的解。
但是这样也可能在拟合材料常数时引起数值困难,而且它要求在用户感兴趣的变形范围内要有足够的数据。
下面是2参数Ogden选项的输入列表:TB,HYPER,1,,2,OGDEN !Activate 2 parameter Ogden data tableTBDATA,1,0.326996 !Define μ1TBDATA,2,2 !Define α1TBDATA,3,-0.250152 !Define μ2TBDATA,4,-2 !Define α2TBDATA,5,6.93063E-5 !Define incompressibility parameter!(as 2/K, K is the bulk modulus)!(Second incompressibility parameter d2 is zero)对于这个选项所需要的材料常数的论述,请参见《ANSYS Elements Reference》。
4.3.2.3 Neo-Hookean超弹性选项Neo-Hookean选项( TB ,HYPER,,,,NEO)代表应变能势能的最简单形式,可用于应变范围20-30%。
下面是Neo-Hookean选项的一个输入列表示例:TB,HYPER,1,,,NEO !Activate Neo-Hookean data tableTBDATA,1,0.577148 !Define incompressibility parameter!(as 2/K, K is the bulk modulus)对于这个选项所需要的材料常数的论述,请参见《ANSYS Elements Reference》。
4.3.2.4 多项式超弹性选项多项式选项( TB ,HYPER,,,,POLY)允许用户通过TB 命令的 NPTS参数定义无限多个参数。
例如应用TB,HYPER,1,,3,POLY 定义3参数模型。
与高阶Mooney-Rivlin选项相似,本选项对高应变水平可提供较好的近似。
在 NPTS =1,常数=0,这一选项等价于Neo-Hookean选项(用户可参见§4.3.2.3)。
在 NPTS =1时,本选项等价于2参数Mooney-Rivlin选项。
在 NPTS =2时,来选项等价于5参数Mooney-Rivlin选项。
在 NPTS =3时,本选项等价于9参数Mooney-Rivlin选项(参见§4.3.2.1)。
对于本选项所要求的材料常数,参见《ANSYS Elements Reference》。
4.3.2.5 Arruda-Boyce超弹性选项Arruda-Boyce选项( TB ,HYPER,,,,BOYCE)可用于直到300%的应变水平。
下面是本选项的一个例子: TB,HYPER,1,,,BOYCE !Activate Arruda-Boyce data tableTBDATA,1,200.0 !Define initial shear modulusTBDATA,2,5.0 !Define limiting network stretchTBDATA,3,0.001 !Define incompressibility parameter!(as 2/K, K is the bulk modulus)对于本选项所要求的材料常数,参见《ANSYS Elements Reference》。
4.3.2.6 用户定义超弹性选项用户定义选项( TB ,HYPER,,,,USER)允许用户应用子程序USERHYPER来定义应变能势对应变不变量的导数,参见《ANSYS Guide to User Programmable Features》。
4.3.2.7 Mooney-Rivlin超弹性选项(TB,MOONEY)请注意这一选项适用于HYPER56,HYPER58,HYPER74,HYPER158,PLANE162,SHELL163,SOLID164 等单元。
如果要应用Mooney-Rivlin选项于SHELL181, PLANE182, PLANE183, SOLID185, SOLID186, SOLID187等单元,请参见§4.3.2.1 。
ANSYS的单元类型HYPER56,HYPER58,HYPER74,HYPER158,应用直到9个Mooney-Rivlin弹性势能函数。
