华中科技大学2016年博士《流体力学(二)》考试大纲
博士研究生入学考试《计算流体力学》考试大纲

博士研究生入学考试《计算流体力学》考试大纲本《计算流体力学》考试大纲适用于动力工程及工程热物理一级学科流体机械及工程专业博士研究生入学考试。
“计算流体力学”是流体力学领域的重要技术之一,使用数值方法在计算机中对流体力学的控制方程进行求解,从而可预测流场的流动。
要求考生掌握计算流体力学的基本原理和方法论,掌握流体力学的控制方程组,掌握基本的数值方法,能够对物理问题进行数学建模,选用合适的CFD方法进行编程求解,具备综合运用所学知识分析和解决问题的能力。
一、考试基本要求1.熟练掌握纳维-斯托克斯(Navier-Stokes)控制方程组的基本概念及推导;2.掌握偏微分方程的分类及不同类型的一般性质;3.掌握方程离散化的基本方法,包括显式法和隐式法,及误差与稳定性分析;4.掌握偏微分方程的数值解法。
5.能够对不可压缩低速流物理问题进行分析建模和数值求解。
二、考试方式与时间博士研究生入学《计算流体力学》考试为笔试,闭卷考试,考试时间为180分钟。
三、考试主要内容和要求(一)流体力学方程及模型方程1、考试内容(1)流体力学的控制方程:连续性方程、动量方程、能量方程;(2)物质导数;(3)速度散度;(4)物理边界条件。
2、考试要求灵活运用空间位置固定的无穷小微团模型或随流体运动的无穷小微团模型进行控制方程的推导,了解式中各项的意义,掌握微分形式中的守恒形式和非守恒形式之间的转换。
(二)偏微分方程的数学性质对CFD的影响1、考试内容(1)偏微分方程的分类:双曲型、抛物型、椭圆型;(2)确定偏微分方程的类型;(3)不同类型偏微分方程的一般性质2、考试要求能够确定偏微分方程的类型并分析不同类型偏微分方程的一般性质(三)偏微分方程的数值解法1、考试内容(1)偏微分方程的离散化方法:有限差分法、有限元方法;(2)误差与稳定性分析2、考试要求掌握有限差分法、有限元方法,能够推导各阶精度的有限差分表达式,并对差分表达式进行稳定性分析。
华中科技大学流体力学课后习题答案完整版

解: v |(1,2) =
v
2 x
+
v
2 y
|(1,2) = 30.41m / s ;
a=
a
2 x
+
a
2 y
|(1,2) =
(∂vx / ∂x ⋅ vx )2 + (∂vy / ∂x ⋅ vx + ∂vy / ∂y ⋅ vy )2 = 167.71m / s2 。
2.4 (1) ax = 35, a y = 15 ;(2)260。
直立部分: P2
=
ρg⎜⎛ h ⎝
+
h ⎟⎞ ⋅ hB 2⎠
=
3 2
ρgh 2 B
方向向左;作用点距离水平面为
yD
=
3 2
h+
Bh3 12 3h 2 ⋅ Bh
=
14 h 9
⇒ L2 = 2h −14h 9 = 4h 9 M 2 = P2 ⋅ L2 = 2ρgh3 B 3
于是关闭闸门所需的力 P 由力矩平衡方程
H2
− h2
设此合力的作用点距底部 x 处,则
( ) R ⋅ x = P1 ⋅ H 3 − P2 ⋅ h 3 = ρgB H 3 − h3 6
将 H = 7.5m
⇒
x
=
H
2 + Hh + h2
3(H + h)
h = 3m B = 5m 代入得 R = 1160KN
x = 2.79m
1.29 解:闸门自动开启,此时压力中心 D 应与 O 点重合;水位超过 H,则压力中心 D 高
解:(1) ax |(2,1) = (∂vx / ∂x ⋅ vx + ∂vx / ∂y ⋅ v y ) |(2,1) = 35 ,
华中科技大学流体力学习题参考答案(1)

严新华主编《水力学(修订本)》教材(科技文献出版社2001年版)部分习题参考答案第一章 习题答案1-1 水的运动粘性系数s m /10006.126-⨯=ν;空气的动力粘性系数s Pa ⋅⨯=-51081.1μ。
1-2 活塞移动速度s m V /49.0=。
1-3 动力粘性系数s Pa ⋅=151.0μ。
1-4 2/5.11m N =τ。
1-5 阻力矩m N M ⋅=6.39。
第二章 习题答案2-1(a )图中2/6.68m KN p A =;绝对压强2/93.169m KN p A='。
(b )图中22/4.29,0,/6.19m KN p p m KN p A B C -===;绝对压强222/93.71,/33.101,/93.120m KN p m KN p m KN p AB C ='='='。
2-2 20/4900m N p -=;液面真空值20/4900m N p V =。
2-3(1)2/54.115m KN p A =';2/47.17m KN p A =。
(2)压力表读数m h m KN p M 213.1,/63.92==。
2-4 A 点表压强2/8.9m KN p A -=;液面空气真空度2/6.19m KN p V =。
2-5 m H 40.0=。
2-6 cm h 1284=。
2-7 O H 84.172mmh V =。
2-8 ①2/22.185m KN p p B A =-;②2/42.175m KN p p B A =-。
2-9 ⑴21/86.1m KN p p B A -=-为油时:ρ;⑵21/784.0m KN p p B A -=-为空气时:ρ。
2-10 ⎪⎭⎫⎝⎛-='b a 1ρρ;gH b a p p BA ρ=-。
2-11 241/1084.118m N p ⨯=。
2-12 )/3.101(/84.37822m KN p m KN p a =='取:。
华中科技大学流体力学复习详解

u y
(2) 斯托克斯定理和开尔文定理
v
L
ds
Ludx vdy wdz
v 2
斯托克斯定理
v
L
ds
A
ndA
A v
ndA
2
A
ndA
I
开尔文定理
理想、正压流体在有势质量力的作用下,
d 0
dt
(3) 不可压缩流体势流的求解途径
v u 0 (无旋) x y
u ,
1
1
Ma = 1 时 = 0
用以上 m 个循环参数与其它 n-m 个物理参数中的每 一个进行组合,组成无量纲参数。
(2) 相似原理
无量纲参数(相似性参数)
Sr L V0t0
斯特罗哈尔数(局部惯性力/对流惯性力)
Eu
p0
V02
欧拉数(压力(差)/惯性力)
Re V0 L V0 L 雷诺数(惯性力/粘性力)
Fr V0 gL
x
v
y
u v 0 (平面不可压) x y
2
2
x2
2
y2
0
u v 0 (平面不可压) x y
u
y
,
v
x
v u 0 (无旋) x y
2
2
x2
2
y 2
0
x y
,
φ ψ y x
柯西—黎曼条件
W(z) φ(x, y) iψ(x, y) 解析
z x iy
W -- 复位势
工程流体力学(II)
总结
1.量纲分析与相似原理
(1) 量纲分析法
定理(布金汉定理)
设一物理现象与 n 个物理参数 ( q1,q2,……,qn ) 相关,即
2016年华中科技大学全日制攻读教育硕士专业学位入学考试大纲(下)

2016年华中科技大学全日制攻读教育硕士专业学位入学考试大纲(下)考试科目:333教育综合【重要说明:我校教育硕士专业学位招收教育管理、学科教学(英语教育)和现代教育技术(科普教育)三个方向的硕士研究生,三个方向的入学考试科目都必考“教育综合”,但三个方向的考试内容和考题不一样,报考教育管理和学科教学(英语教育)两个方向的考生根据本考试大纲第一部分进行复习和备考,报考现代教育技术(科普教育)方向的考生根据本考试大纲第二部分进行复习和备考。
三个方向的试卷将使用同一份试卷,但试卷会给报考不同方向的考生提供不同的试题,考生可根据自己报考的方向选择答题】“五育并举”的教育方针;改革北京大学的教育实践;教育独立思想。
3、新文化运动影响下的教育思潮和教育运动新文化运动抨击传统教育促进教育观念变革;平民教育运动;工读主义教育运动;职业教育思潮;勤工俭学运动;科学教育思潮;国家主义教育思潮。
4、学校教学方法的改革与实验现代西方教学理论在中国的传播;设计教学法;“道尔顿制”;“文纳特卡制”。
5、1922年“新学制”“新学制”的产生过程;“新学制”的标准和体系;“新学制”的特点;“新学制”的课程标准;“新学制”评价。
6.收回教育权运动教会教育的扩张与变革;收回教育权运动。
十、南京国民政府的教育建设1、教育宗旨与教育方针的变迁党化教育;“三民主义”教育宗旨;“战时须作平时看”的教育方针。
2、教育制度改革大学院和大学区制的试行;“戊辰学制”的颁行。
3、学校教育的管理措施训育制度;中小学校的童子军训练;高中以上学生的军训;颁布课程标准,实行教科书审查制度;实行毕业会考。
4、学校教育的发展幼儿教育;初等教育;中等教育;高等教育;抗日战争时期的学校西迁。
十一、中国共产党领导下的教育1、新民主主义教育的发端工农教育;湖南自修大学;上海大学;农民运动讲习所;李大钊的教育思想;恽代英的教育思想。
2、新民主主义教育方针的形成苏维埃文化教育总方针;抗日战争时期中国共产党的教育方针政策;“民族的、科学的、大众的”文化教育方针。
华科 流体力学-参考试题及解答4
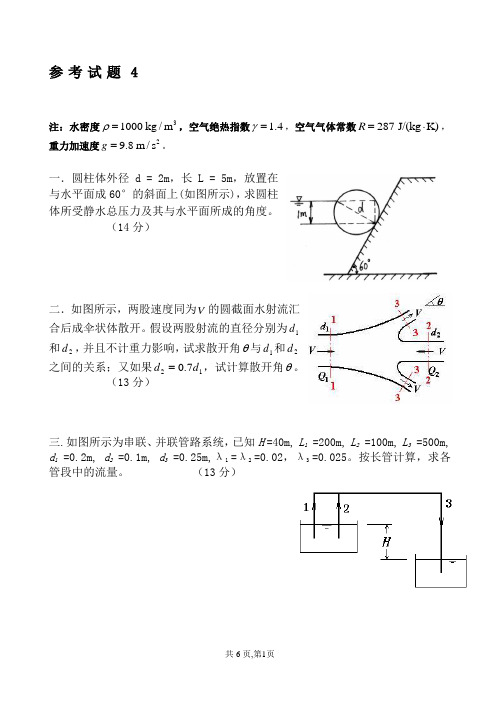
参考试题4注:水密度31000kg /m ρ=,空气绝热指数 1.4γ=,空气气体常数287 J/(kg K)R =⋅,重力加速度29.8m/s g =。
一.圆柱体外径d = 2m ,长L = 5m ,放置在与水平面成60°的斜面上(如图所示),求圆柱体所受静水总压力及其与水平面所成的角度。
(14分)二.如图所示,两股速度同为V 的圆截面水射流汇合后成伞状体散开。
假设两股射流的直径分别为1d 和2d ,并且不计重力影响,试求散开角θ与1d 和2d 之间的关系;又如果127.0d d =,试计算散开角θ。
(13分)三.如图所示为串联、并联管路系统,已知H =40m, L 1 =200m, L 2 =100m, L 3 =500m, d 1 =0.2m, d 2 =0.1m, d 3 =0.25m,λ 1 =λ 2 =0.02,λ 3 =0.025。
按长管计算,求各管段中的流量。
(13分)四.将一个沿x 轴正方向,速度15 m/s V =的直线均匀流与一个位于坐标原点的点涡叠加,已知在叠加后的势流中点(0, 1)是驻点,试求点涡的强度Γ。
(13分)五.长 1.22 m l =,宽1.22 m b =的平板沿长度方向顺流放置在空气气流中,气流速度 3.05m/s U =,空气运动粘度20.149cm /s ν=,密度31.2kg/m ρ=。
假设边界层临界雷诺数5510xc Re =⨯,试计算平板双面的总摩擦阻力D F 。
(10分)提示:层流边界层和湍流边界层的摩擦阻力系数分别为1/21.328L f l C Re -=,1/50.074T f lC Re -=六.如图所示,密度为ρ,动力粘度为μ的流体在相距h 的大平板之间做定常运动,板与水平面的夹角为θ 。
假设上板运动速度为1U ,下板运动速度为2U ,流体中压强沿x 方向不变,试在图示坐标系下导出流体速度分布的表达式。
(13分) 提示:平面定常流动的N-S 方程为22221x u u p u u u v f x y x x y μρρ⎛⎫∂∂∂∂∂+=-++ ⎪∂∂∂∂∂⎝⎭22221y v v p v v u v f x y y x y μρρ⎛⎫∂∂∂∂∂+=-++ ⎪∂∂∂∂∂⎝⎭七.滞止温度0296 K T =,滞止压强50410 Pa p =⨯的超声速空气流进入拉伐尔(缩放)喷管,喷管最小截面积220 cm A *=,假设管内无激波,流动等熵,出口截面马赫数Ma = 0.52。
博士生入学流体力学资料-整理后
x
H
V
五、若无穷远处均匀来流速度为 w ,流过一平板的附面层为零压力梯度层流附面层,若平板层流附面层速度剖面为:
w y y a b( ) 3 (其中a,b为待定常数),试求:(20分) w
(1)平板层流附面层的速度分布; (3)平板壁面上的局部摩擦系数和总摩擦系数。
(2)附面层的厚度 及动量损失厚度
Qs 流线;(3)驻点坐标。(20分) 2 y
V
0 源 Qs
x
五、若无穷远处均匀来流速度为 w ,流过一平板的附面层为零压力梯度层流附面层,若平板层流附面层速度剖面为:
w y y y a b( ) 3 c( ) 4 (其中a,b,c为待定常数),试求:(20分) w
(1)平板层流附面层的速度分布; (2)附面层的厚度 及动量损失厚度
(3)平板壁面上的局部摩擦系数和总摩擦系数。
五、在 (a,0) 与 (a,0) 分别放置一个汇和一个源,其强度均为 Q s ,且有一自左向右的均匀来流,速度为 V ,平行于
x 轴,求叠加后的势函数、流函数与驻点坐标。(20分) y
V
(a,0) 源 Qs
(a,0)
汇 Qs
x
博士学位研究生入学考试试题 (B)
四、若无穷远处均匀来流速度为 w ,流过一平板的附面层为零压力梯度层流附面层,若平板层流附面层速度剖面为:
w y y a b( ) c( ) 2 ,(其中a,b,c为待定常数),试求:(20分) (1)平板层流附面层的速度分布; w
(2)附面层的厚度
及动量损失厚度 2 ;
3 3 单位时间内机械能损失为 AV 。(20 分) 16
三、如图所示,不可压缩粘性流体在与水平面成 角的两
华中科技大学流体力学第七章-2全解
j
p z
k
dxi
dyj
dzk
PF x
dx
PF y
dy
PF z
dz
1
p x
dx
p y
dy
p z
dz
dPF
dp
定义 如果流体密度只是当地压强的单值函数,即
p
该流体为正压流体。
此时,可以定义一空间函数
PF
dp
p
1
或者
PF
p ρ
PF -- 压强函数
PF
dp
p
PF
1 p ρ
解
L udx vdy L 6ydx 8xdy
在圆 x2 + y2 = 1上,
x cos
y sin
其速度环量为
2
2
0 6sind(cos ) 0 8cosd(sin ) 14
2.旋涡强度
涡量 -- 速度场的旋度
v 2
1 v
2
面积A上的涡通量 -- 涡量在 A 上法向分量的积分 也称为旋涡强度(或涡强)
例 密度是常数的均质不可压缩流体 是 正压流体,
ρC
PF
p
例 等熵流动的均质气体 是 正压流体,
p
1 ρ
p
p
C
PF
1
p
1
p
1 ρ
p
1
1
PF
dp
c
p
dp
1
c p 1
1
1
p
c
p
p 1
例 大气层中的空气 不是 正压流体,因为在大气层中 空气的密度不仅随压强变化,还与温度、湿度有关。
华中科技大学博士研究生入学考试大纲-3321+物理化学(二)
华中科技大学博士研究生入学考试《物理化学(二)》考试大纲
第一章热力学第一定律及其应用
1.1 热力学概论
1.2热力学第一定律
1.3 准静态过程与可逆过程
1.4焓
1.5热容
1.6热力学第一定律对理想气体的应用
1.7 Carnot循环
1.8 Joule-Thomson效应
1.9 热化学
1.10 Hess定律
1.11 几种热效应
1.12反应热与温度的关系
1.13 绝热反应
1.14 热力学第一定律的微观说明
第二章热力学第二定律
2.1 自发变化的共同特征
2.2 热力学第二定律
2.3 Carnot定律
2.4 熵的概念.
2.5 克劳修斯不等式与熵增加原理
2.6 熵的计算
2.7 热力学第二定律的本质和熵的统计意义
2.8 亥姆霍兹自由能和吉布斯自由能
2.9 变化的方向和平衡条件
2.10 ΔG的计算
2.11 几个热力学函数间的关系
2.12 热力学第零定律和第三定律
第三章多组分体系热力学在溶液中的应用
3.1 多组分系统的组成表示法
3.2 偏摩尔量
3.3 化学势
3.4 稀溶液的两个经验定律
3.5 理想液态混合物的定义、通性及各组分的化学势
3.6 稀溶液中各组份的化学势
3.7 稀溶液的依数性
3.8 活度与活度因子
3.9分配定律。
华中科技大学 流体力学第二章_1
平衡微分方程
fz
矢量形式:
fy
1 p , y
1 p fz z
由于压强是连续函数,所以
p p p dp dx dy dz f x dx+ f y dy + f z dz x y z
把常数 g 和 R 的值代入后得到 对流层中的压强分布:
g 0.0065R
z p p a 1 44300
5.256
z 11000 m
在对流层的上边界上 ( z = 11000 m) , 压强为
11000 p1 p a 1 44300
5.256
pa
h
倾斜式测压计 可以放大液柱读数。 p1 – p2 = g h = g l sin
p2 h
p1
l
由于 l > h,所以将测压管倾斜能起到放大读数的 作用。一般用于测量微小的压差。
多管压差计 p1– p2 = g ( h1– h2) p2 – p3 = g ( h2 – h3) o 多管压差计一般用于测量管道流动中沿流动方向 的压强变化(各截面之间的压差)。
在求压强分布公式的积 分中,已设密度为常数, 所以公式只能用于密度不变 的单连通区域中的任意两点。 现在用于 D 点和 B 点。
h1
D B C
h2
'
pB pa gh2
再用于 B点和 A点
p p B gh1
综合两式得到
A
D B C
pa h2
h1
p p a ρ gh2 gh1
dp = (f x dx+ f y dy + f z dz )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华中科技大学2016年博士《流体力学(二)》考试大纲第一章流体力学的基本概念
连续介质假说;流体的性质
描述流体运动的两种方法;速度分解定理
变形速度张量的意义;有旋运动与无旋运动
流体运动的分类;作用在流体上的力,应力张量
第二章流体力学基本方程组
连续性方程;运动方程(应力形式)
本构方程;能量方程
状态方程;流体力学基本方程组,初始条件和边界条件
第三章流体静力学
流体静力学基本方程;静止流体中的压强分布
静止流体作用于物体上的力
第四章理想流体动力学基础
理想流体运动问题的数学提法;开尔文定理和拉格朗日定理
涡面,涡线,涡管及涡管强度的保持性定理
伯努利积分;柯西—拉格朗日积分和一维不定常流动
动量定理,动量距定理
第五章理想不可压缩流体的无旋流动
理想不可压缩流体的无旋流动问题的提法
速度势函数和无旋流动的某些性质,动能表达式
平面流动的流函数
不可压缩流体平面无旋流动的复位势与复速度
不可压缩流体平面无旋流动的基本解及其叠加
圆柱的绕流;虚象法
保角变换方法;机翼外部绕流,库塔—儒柯夫斯基条件
定常绕流问题的力与力矩公式;某些最简单的保角变换
区域保角变换时域内奇点的随同变换
在原静止的理想不可压缩均质流体中运动的物体的受力
第六章粘性不可压缩流体运动
粘性不可压缩流体的基本方程组粘性流体运动的一般性质
相似律,层流和紊流粘性不可压缩流体动力学问题的讨论
准确解;绕圆球的小雷诺数流动
普朗特边界层方程;半无穷长平板的层流边界层
动量积分关系式方法;雷诺方程
普朗特混合长理论;圆管内的湍流运动
平板湍流边界层;物体的阻力
第七章气体动力学基础
气体动力学基本方程组;音速
定常一维等熵理论;亚音速,超音速气流的差别
激波理论;定常平面超音速流绕角的等熵膨胀
拉伐尔变工况流动特性
文章来源:文彦考研旗下华中科技大学考研网。
