最新初中九年级数学数题库 学九年级上人教新课标第23章图形的旋转全章测试题
人教版九年级数学上册第23章:旋转 单元测试卷(含答案)

第二十三章试卷[时间:90分钟分值:120分]一、选择题(每小题3分,共30分)1.将数字“6”旋转180°,得到数字“9”,将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( ) A.96 B.69C.66 D.992.下面四个手机应用图标,属于中心对称图形的是( )3.如图1,△A′B′C′是由△ABC经过平移得到的,△A′B′C′还可以看作是由△ABC经过怎样的图形变化得到的?有下列结论:①1次旋转;②1次旋转和1次轴对称;③2次旋转;④2次轴对称.其中正确的结论是( )图1A.①④B.②③C.②④D.③④4.如图2,将一个含30°角的直角三角尺ABC绕点A旋转,使点B,A,C′在同一条直线上,则三角尺ABC旋转的角度是( )图2A.60° B.90°C.120° D.150°5.如图3,将△ABC按顺时针方向转动一个角后成为△AB′C′,下列等式正确的有( )图3①BC=B′C′;②∠BAB′=∠CAC′;③∠ABC=∠AB′C′;④AB=B′C′.A.1个B.2个C.3个D.4个6.如图4,将一朵小花放置在平面直角坐标系中第三象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向下平移2个单位长度到丙位置,则小花顶点A在丙位置中的对应点A′的坐标为( )图4A.(3,1) B.(1,3)C.(3,-1) D.(1,1)7.如图5,将线段AB先向右平移5个单位长度,再将所得线段绕原点按顺时针方向旋转90°,得到线段A′B′,则点B的对应点B′的坐标是( )图5A.(-4,1) B.(-1,2)C.(4,-1) D.(1,-2)8.如图6,Rt△OCB的斜边在y轴上,OC=3,含30°角的顶点与原点重合,直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则点B的对应点B′的坐标是( )图6A.(3,-1) B.(1,-3)C.(2,0) D.(3,0)9.如图7,在△ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到△A′B′C,若点B′恰好落在线段AB上,AC,A′B′交于点O,则∠COA′的度数是( )图7A.50° B.60°C.70° D.80°10.如图8,等边三角形ABC的边长为4,点O是△ABC的中心,∠FOG=120°.绕点O旋转∠FOG,分别交线段AB,BC于D,E两点,连接DE,给出下列四个结论:①OD=OE;②S△ODE=S△BDE;③四边形ODBE的面积始终等于433;④△BDE周长的最小值为6.上述结论正确的个数是( )图8A.1 B.2C.3 D.4二、填空题(每小题4分,共24分)11.若点A(2,1)与点B关于原点对称,则点B的坐标是________.12.如图9,将等边三角形AOB放在平面直角坐标系中,点A的坐标为(0,4),点B在第一象限,将等边三角形AOB绕点O顺时针旋转180°得到△A′OB′,则点B′的坐标是____________.图913.将一副三角尺如图10的方式放置,将三角尺ADE绕点A逆时针旋转α(0°<α<90°),使得三角尺ADE的一边所在的直线与BC垂直,则α的度数为________.图1014.若点M(-1+8n,4-2n)关于原点对称的点在第三象限,则整数n的值为________.15.如图11,四边形ABCD是菱形,O是两条对角线的交点,过点O的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,阴影部分的面积为________.图1116.如图12,在△AOB中,∠AOB=90°,AO=3 cm,BO=4 cm,将△AOB 绕顶点O按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB 的中点,则线段B1D=________cm.图12三、解答题(共66分)17.(8分)如图13,在△ABC中,∠B=10°,∠ACB=20°,AB=4 cm,将△ABC逆时针旋转一定角度后与△ADE重合,且C恰好是AD的中点.(1)指出旋转中心,并求出旋转的度数;(2)求出∠BAE的度数和AE的长.图1318.(10分)如图14,在△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,使点F在AC上.(1)求△CDB旋转的度数;(2)连接DE,判断DE与BC的位置关系,并说明理由.图1419.(10分)△ABC在平面直角坐标系内的位置如图15.(1)分别写出A,B,C三点的坐标;(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出点B1的坐标;(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出点A2的坐标;(4)求出△ABC的面积.图1520.(10分)如图16①,在正方形ABCD和正方形AEFG中,点B在边AG上,点D在线段EA的延长线上,连接BE和DG.(1)如图①,求证:DG⊥BE.(2)如图②,将正方形ABCD绕点A按逆时针方向旋转,使点B恰好落在线段DG上.①求证:DG⊥BE.②若AB=2,AG=3,求线段BE的长.①②图1621.(14分)如图17,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.(1)求证:△COD是等边三角形.(2)当α=150°时,试判断△AOD的形状,并说明理由.(3)探究:当α为多少度时,△AOD是等腰三角形?图1722.(14分)如图18①,△ABC是边长为4 cm的等边三角形,边AB在射线OM上,且OA=6 cm,点D从点O出发,沿OM的方向以1 cm/s的速度运动,设运动时间为t s,当点D不与点A重合时,将△ACD绕点C按逆时针方向旋转60°得到△BCE,连接DE.(1)求证:△CDE是等边三角形.(2)如图18②,当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长;若不存在,请说明理由.(3)如图18③,当点D在射线OM上运动时,是否存在以D,E,B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.参考答案1.B 2.B 3.D 4.D 5.C 6.C 7.D8.A 9.B 10.C11.(-2,-1) 12.(-23,-2) 13.15°或60°14.1 15.12 16.1.517.(1)旋转中心是点A,旋转角度是150°.(2)∠BAE=60°,AE=2 cm.18.(1)旋转角为90°.(2)DE∥BC,理由略.19.(1)A(0,3),B(-4,4),C(-2,1).(2)图略,点B1的坐标为(4,4).(3)图略,点A2的坐标为(0,-3).(4)S△ABC=5.20.(1)略(2)①略②BE=2+721.(1)略(2)△AOD是直角三角形,理由略.(3)当α的度数为125°或110°或140°时,△AOD是等腰三角形.22.(1)略(2)存在,△BDE的最小周长是(23+4) cm.(3)存在,当t的值为2 s或14 s时,以D,E,B为顶点的三角形是直角三角形.。
人教版九年级数学上册第二十三章《旋转》测试带答案解析

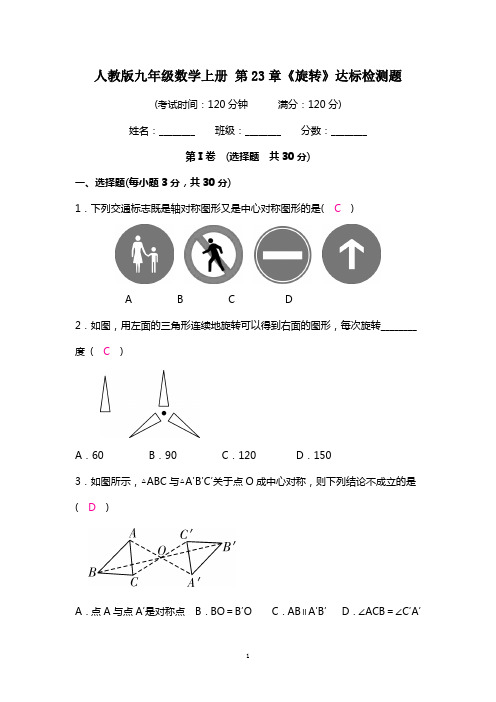
人教版九年级数学上册第二十三章《旋转》测试带答案解析学校:___________姓名:___________班级:___________考号:___________一、单选题(本大题12个小题,每小题4分,共48分)1.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.2.下列垃圾分类的标志中,既是轴对称图形又是中心对称图形的是()A.可回收物B.厨余垃圾C.有害垃圾D.其它垃圾物3.下列垃圾分类图标分别表示:“可回收垃圾”、“有害垃圾”、“厨余垃圾”、“其它垃圾”,其中既是轴对称图形,又是中心对称图形的是()A.B.C.D.4.观察下列图形,其中既是轴对称图形又是中心对称图形的是()A.B.C.D.5.下列图形中,既是中心对称图形又是轴对称图形的是()A.B.C.D.6.为推动世界冰雪运动的发展,我国将于2022年举办北京冬奥会.在此之前进行了冬奥会会标的征集活动,以下是部分参选作品,其文字上方的图案既是轴对称图形又是中心对称图形的是()A.B.C.D.7.2022年油价多次上涨,新能源车企迎来了更多的关注,如图是理想、蔚来、小鹏、哪吒四款新能源汽车的标志,其中既是轴对称图形,又是中心对称图形的是()A.B.C.D.8.如图,在平面直角坐标系中,△ABC的边AB⊥x轴,A(﹣2,0),C(﹣4,1),二次函数y=x2﹣2x﹣3的图象经过点B.将△ABC沿x轴向右平移m(m>0)个单位,使点A平移到点A′,然后绕点A'顺时针旋转90°,若此时点C的对应点C′恰好落在抛物线上,则m的值为()A B C D .9.如图,将ABC 绕点A 逆时针旋转40︒得到ADE ,AD 与BC 相交于点F ,若80E ∠=︒且AFC 是以线段FC 为底边的等腰三角形,则BAC ∠的度数为( )A .55︒B .60︒C .65︒D .70︒10.如图,在平面内将五角星绕其中心旋转180︒后所得到的图案是( )A .B .C .D .11.如图,矩形ABCD 中,AD =2,ABAC 上有一点G (异于A ,C ),连接 DG ,将△AGD 绕点A 逆时针旋转60°得到△AEF ,则BF 的长为( )A B .C D .=60°,在x 轴正半轴上有一点C ,点C 坐标为()1,0,将线段AC 绕点A 逆时针旋转120°,得线段AD ,连接BD .则BD 的长度为( )A .B .4CD .152二、填空题(本大题4个小题,每小题4分,共16分)13.点(6,1)-关于原点的对称点是__________.14.如图,在ABC 中,80ACB ∠=︒,将ABC 在平面内绕点A 逆时针旋转到AB C ''△的位置,使CC '平分B C A ''∠,则旋转角的度数为__________.15.如图,在ABC 中,70CAB ∠=︒,在同一平面内,将ABC 绕点A 逆时针旋转到AB C ''△的位置,使CC AB '∥,作B D AC '∥交BC 于点D ,则AB D '∠=______.16.如图,在ABC 中,90B ,4AB BC ==,将ABC 绕点A 逆时针旋转60︒,得到ADE ,则点D 到BC 的距离是______.三、解答题(共9个小题,17、18每小题8分,19-25每小题10分,共86分)17.如图所示的正方形网格中,画出将△ABC 绕点C 逆时针旋转90°得到的△MNC ,A 、B 的对应点分别为M 、N .18.如图,ABC 的顶点坐标分别为(4,5)A -,(5,2)B -,(3,4)C -.(1)画出与ABC 关于原点O 对称的111A B C △,并写出点1A 的坐标为___________.(2)D 是x 轴上一点,使DB DC 的值最小,画出点D (保图痕迹),D 点坐标为___________.(3)(,0)P t 是x 轴上的动点,将点C 绕点P 顺时针旋转90︒至点E ,直线25y x =-+经过点E ,则t 的值为___________.19.阅读理解,并解答问题:观察发现:如图1是一块正方形瓷砖,分析发现这块瓷砖上的图案是按图2所示的过程设计的,其中虚线所在的直线是正方形的对称轴.问题解决:用四块如图1所示的正方形瓷砖按下列要求拼成一个新的大正方形,并在图3和图4中各画一种拼法.(1)图3中所画拼图拼成的图案是轴对称图形,但不是中心对称图形;(2)图4中所画拼图拼成的图案既是轴对称图形,又是中心对称图形.20.如图,在平面直角坐标系内,ABC 的顶点坐标分别为(4,4)A -,(2,5)B -,(2,1)C -.(1)平移ABC ,使点C 移到点1(2,2)C ,画出平移后的111A B C △;(2)将ABC 绕点(0,0)旋转180︒,得到222A B C △,画出旋转后的222A B C △;(3)连接12A C ,21A C ,求四边形1221A C A C 的面积.21.如图,在平面直角坐标系中,点A 的坐标为()1,1,点B 的坐标为()4,1,点C 的坐标为()3,3.(1)画出将ABC 向下平移5个单位长度得到的111A B C △;(2)画出将ABC 绕点原点O 逆时针旋转90°后得到的222A B C △,写出2C 的坐标.22.如图,在△ABC 中,AB =AC ,∠BAC =α,点D 在边BC 上(不与点B ,C 重合),连接AD ,以点A 为中心,将线段AD 逆时针旋转180°﹣α得到线段AE ,连接BE .(1)∠BAC +∠DAE = °;(2)取CD 中点F ,连接AF ,用等式表示线段AF 与BE 的数量关系,并证明.23.对于平面直角坐标系xOy 中的图形M 和点P ,给出如下定义:将图形M 绕点P 顺时针旋转90 得到图形N ,图形N 称为图形M 关于点P 的“垂直图形”.例如,图1中点D 为点C 关于点P 的“垂直图形”.(1)点A 关于原点O 的“垂直图形”为点B .①若点A 的坐标为()0,3,则点B 的坐标为___________;②若点B 的坐标为()3,1,则点A 的坐标为___________;(2)(3,3)E -,(2,3)F -,(,0)G a ,线段EF 关于点G 的“垂直图形”记为E F '',点E 的对应点为E ',点F 的对应点为F '.①求点E '的坐标(用含a 的式子表示);②若O 的半径为2E F '',上任意一点都在O 内部或圆上,直接写出满足条件的EE '的长度的最大值.24.已知AOB 和MON △都是等腰直角三角形OM OA ⎫<<⎪⎪⎝⎭,90AOB MON ∠=∠=︒.(1)如图1,连接AM ,BN ,求证:AM BN =;(2)将MON △绕点O 顺时针旋转.①如图2,当点M 恰好在AB 边上时,求证:2222AM BM OM +=;②当点A ,M ,N 在同一条直线上时,若4OA =,3OM =,请直接写出线段AM 的长.25.如图,在Rt ABC △中,90BAC ∠=︒,将Rt ABC △绕点A 旋转一定的角度得到Rt ADE △,且点E 恰好落在边BC 上.(1)求证:AE 平分CED ∠;(2)连接BD ,求证:90DBC ∠=︒.参考答案:1.C【分析】根据中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形就叫做中心对称图形;轴对称图形的定义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形.【详解】解:A.是轴对称图形,不是中心对称图形,故本选项不符合题意;B.既不是轴对称图形,也不是中心对称图形,故本选项不符合题意;C.既是轴对称图形,又是中心对称图形,故本选项符合题意;D.既不是轴对称图形,也不是中心对称图形,故本选项不符合题意.故选:C【点睛】本题考查了中心对称图形与轴对称图形的概念,正确掌握相关定义是解题关键.2.C【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.【详解】解:A.既不是中心对称图形,也不是轴对称图形,故本选项不合题意;B.不是中心对称图形,是轴对称图形,故本选项不合题意;C.既是中心对称图形又是轴对称图形,故本选项符合题意;D.既不是中心对称图形,也不是轴对称图形,故本选项不合题意.故选:C.【点睛】本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与原图重合.3.B【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A.既不是轴对称图形,也不是中心对称图形.故本选项不合题意;B.既是轴对称图形,又是中心对称图形.故本选项符合题意;C.是轴对称图形,不是中心对称图形.故本选项不合题意;D.既不是轴对称图形,也不是中心对称图形.故本选项不合题意.故选:B.【点睛】本题考查了中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.4.D【分析】根据轴对称图形和中心对称图形的定义进行判断即可.【详解】A是轴对称图形不是中心对称图形,不符合题意;B是轴对称图形不是中心对称图形,不符合题意;C既不是轴对称图形也不是中心对称图形,不符合题意;D既是轴对称图形又是中心对称图形,符合题意;故选:D.【点睛】本题考查了轴对称图形和中心对称图形的定义,即轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.5.A【分析】根据轴对称图形和中心对称图形的概念,对各选项分析判断即可得解.【详解】解:A.既是轴对称图形,又是中心对称图形,故本选项符合题意;B.是轴对称图形,不是中心对称图形,故本选项不合题意;C.不是轴对称图形,是中心对称图形,故本选项不合题意;D.是轴对称图形,不是中心对称图形,故本选项不合题意.故选:A.【点睛】本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.6.B【分析】根据轴对称图形及中心对称图形的概念可直接进行排除选项.【详解】解:A、文字上方的图案既不是轴对称图形也不是中心对称图形,故不符合题意;B、文字上方的图案既是轴对称图形也是中心对称图形,故符合题意;C、文字上方的图案是轴对称图形但不是中心对称图形,故不符合题意;D、文字上方的图案既不是轴对称图形,也不是中心对称图形,故不符合题意;故选B.【点睛】本题主要考查轴对称图形及中心对称图形的识别,熟练掌握轴对称图形及中心对称图形的概念是解题的关键.7.C【分析】根据轴对称图形与中心对称图形的概念求解.【详解】解:A.既不是轴对称图形,也不是中心对称图形.故本选项不合题意;B.是轴对称图形,不是中心对称图形.故本选项不符合题意;C.既是轴对称图形又是中心对称图形.故本选项符合题意;D.是轴对称图形,不是中心对称图形.故本选项不合题意.故选:C.【点睛】此题考查中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180°后与原图重合.8.C【分析】作CD⊥AB于D,C'D'⊥A'B'于D',先根据已知条件求出点B坐标,由A、B、C三点坐标可得CD=2,AD=1.设点A(﹣2,0)向右平移m个单位后得点A'(m>0),则点A'坐标为(m﹣2,0).进而表示出点C'的坐标为(m﹣1,2),最后将C'坐标代入二次函数解析式中计算即可得到点C坐标.【详解】解:作CD⊥AB于D,C'D'⊥A'B'于D',∵AB⊥x轴,二次函数y=x2﹣2x﹣3的图象经过点B,∴点B(﹣2,5)∵A(﹣2,0),C(﹣4,1),∴CD=2,AD=1.设点A(﹣2,0)向右平移m个单位后得点A'(m>0),则点A'坐标为(m﹣2,0).∵A'D'=AD=1,C'D'=CD=2,∴点C'坐标为(m﹣1,2),又点C'在抛物线上,∴把C'(m﹣1,2)代入y=x2﹣2x﹣3中,得:(m ﹣1)2﹣2(m ﹣1)﹣3=2,整理得:m 2﹣4m ﹣2=0.解得:m 1=m 2=2(舍去).故选:C .【点睛】此题考查了二次函数图象上点的坐标特点,平移的性质,解一元二次方程,正确理解平移的性质是解题的关键.9.B【分析】由旋转的性质得出80E C ∠=∠=︒,40BAD ∠=︒,由等腰三角形的性质得出80C AFC ∠=∠=︒,求出20CAF ∠=︒,根据BAC BAD CAF ∠=∠+∠即可得出答案. 【详解】解:将ABC 绕点A 逆时针旋转40︒得到ADE ,且80E ∠=︒,80E C ∴∠=∠=︒,40BAD ∠=︒,又AFC 是以线段FC 为底边的等腰三角形,AC AF ∴=,80C AFC ∴∠=∠=︒,180180808020CAF C AFC ∴∠=︒-∠-∠=︒-︒-︒=︒,402060BAC BAD CAF ∴∠=∠+∠=︒+︒=︒,故选:B .【点睛】本题考查了旋转的性质、等腰三角形的性质、三角形内角和定理,熟练掌握旋转的性质是解题的关键.10.C【分析】根据旋转的性质找出阴影部分三角形的位置即可得答案.【详解】∵将五角星绕其中心旋转180︒,∴图中阴影部分的三角形应竖直向下,故选:C .【点睛】本题考查旋转的性质,图形旋转前后,对应边相等,对应角相等,前后两个图形全等;熟练掌握旋转的性质是解题关键.11.A【分析】过点F 作FH ⊥BA 交BA 的延长线于点H ,则∠FHA =90°,△AGD 绕点A 逆时针旋转60°得到△AEF ,得∠F AD =60°,AF =AD =2,又由四边形ABCD 是矩形,∠BAD =90°,得AF=1,由勾股定理得AH=,得到到∠F AH=30°,在Rt△AFH中,FH=12BH=AH+AB,再由勾股定理得BF=【详解】解:如图,过点F作FH⊥BA交BA的延长线于点H,则∠FHA=90°,∵△AGD绕点A 逆时针旋转60°得到△AEF∴∠F AD=60°,AF=AD=2,∵四边形ABCD是矩形∴∠BAD=90°∴∠BAF=∠F AD+ ∠BAD=150°∴∠F AH=180°-∠BAF=30°AF=1在Rt△AFH中,FH=12由勾股定理得AH=在Rt△BFH中,FH=1,BH=AH+AB由勾股定理得BF=故BF故选:A【点睛】本题考查了图形的旋转,矩形的性质,含30度角的直角三角形的性质,勾股定理等知识,解决此题的关键在于作出正确的辅助线.12.C【分析】连接CD,过点A作AE⊥CD于点E,过点E作FG⊥x轴于点F,过点A作AG⊥FG于点G,设E(m,n),根据旋转证∠ACG=30°,CE,根据两角对应相等证△AEG∽△ECF,求出74E ⎛ ⎝⎭,52D ⎛ ⎝⎭,结合B (-2,0)求出BD =. 【详解】连接CD ,过点A 作AE ⊥CD 于点E ,过点E 作FG ⊥x 轴于点F ,过点A 作AG ⊥FG 于点G ,则∠AEC =∠OFG =∠G =90°,∵∠AOF =90°,∴∠OAG =90°,∴四边形AOFG 是矩形,∵(0,A ,∴FG =OA设E (m ,n ),∴AG =OF =m ,EF =n ,∴CF =m -1,EGn ,由旋转知,∠CAD =120°,AC =AD ,∴CE =DE ,∠ACG =30°,∴CE,∵∠CEF +∠ECF =∠AEG +∠CEF =90°,∴∠AEG =∠ECF ,∴△AEG ∽△ECF ,∴EF CE AG AE ==,∴=n m∵CF CE EG AE==∴74m =,n∴74E ⎛ ⎝⎭, ∵73144-=,735442+=,∴52D ⎛ ⎝⎭,∵∠ABO=60°,=OA∴OB =2,B (-2,0),∴BD =. 故选C .【点睛】本题主要考查了旋转,等腰三角形,含30°的直角三角形,两点间的距离公式,熟练掌握旋转图形全等性质,三线合一含30°角的直角三角形边的性质,两点间的距离公式是解决此题的关键.13.(6,1)-【分析】根据两个点关于原点对称时,它们的坐标符号相反,即点P (x ,y )关于原点O 的对称点是点P '(﹣x ,﹣y ),进而得出答案.【详解】解:点(6,﹣1)关于原点的对称点的坐标为(﹣6,1).故答案为:(﹣6,1).【点睛】此题主要考查了原点对称点的性质,正确掌握横纵坐标的符号关系是解题关键. 14.100︒##100度【分析】根据旋转的性质得出80B C A ''∠=︒,C A AC '=,再根据角平分线的性质得出40CC A '∠=︒,利用等腰三角形的性质可求旋转角.【详解】解:∵ABC 在平面内绕点A 逆时针旋转到AB C ''△的位置,∴80C B C A A B ∠︒==''∠,C A AC '=,∵CC '平分B C A ''∠,∴1402CC A B C A '''∠=∠=︒,∴40CC A C CA ''∠=∠=︒,∴100C AC '∠=︒,故答案为:100°.【点睛】本题考查了旋转的性质和等腰三角形的性质,解题关键是熟练运用旋转的性质得出角的度数.15.30°##30度【分析】利用旋转的性质可求得AC =AC ′,∠CAB =∠C ′AB ′,由平行线性质和三角形内角和定理可求得∠C ′AC ;进而求得∠CAB ′即可解答;【详解】解:∵CC AB '∥,∴∠C ′CA =∠CAB =70°,由旋转的性质可得:AC =AC ′,∠CAB =∠C ′AB ′=70°,∴∠ACC ′=∠AC ′C =70°,∴∠C ′AC =180°-70°-70°=40°,∴∠CAB ′=∠C ′AB ′-∠C ′AC =70°-40°=30°,∵B D AC '∥,∴∠AB ′D =∠CAB ′=30°,故答案为:30°.【点睛】本题考查了旋转的性质,等腰三角形的性质,三角形内角和定理,平行线的性质;掌握旋转的性质是解题关键.16.2【分析】由旋转的性质可得4AB AD ==,60BAD ∠=︒,可证ABD △是等边三角形,由直角三角形的性质可求解.【详解】解:如图,连接BD ,过点D 作DH BC ⊥于H ,将ABC 绕点A 逆时针旋转60︒,4AB AD ∴==,60BAD ∠=︒,ABD ∴是等边三角形,4BD AB ∴==,60ABD ∠=︒,30DBC ∴∠=︒,DH BC ⊥,122DH BD ∴==, ∴点D 到BC 的距离是2,故答案为:2.【点睛】本题考查了旋转的性质,等边三角形的判定和性质,直角三角形的性质,掌握旋转的性质是解题的关键.17.见解析【分析】根据题意画出旋转后的图形即可;【详解】:如图,【点睛】本题主要考查了图形的旋转,掌握旋转图形的画法是解题的关键.18.(1)作图见详解,(4,5)-(2)作图见详解,13,03⎛⎫- ⎪⎝⎭(3)2-【分析】(1)已知ABC 三点坐标,ABC 关于原点O 对称的111A B C △各对应点的坐标与原坐标的横纵坐标均为相反数,由此即可作图;(2)作点B 关于x 轴的对称点B',连接'CB 交x 轴于点D ,此时BD CD +的值最小; (3)构造全等三角形求出等E 坐标,利用待定系数法即可解问题.【详解】(1)解:已知ABC 三点坐标(4,5)A -,(5,2)B -,(3,4)C -,关于原点对称,则对应点的坐标分别是1(4,5)A -,1(5,2)B -,1(3,4)C -,连接1A ,1B ,1C 所组成的图形为所求图形111A B C △,如图所示,(2)解:作点B 关于x 轴的对称点B',连接'CB 交x 轴于点D ,此时BD CD +的值最小,如图所示,已知(4,5)A -,(5,2)B -,(3,4)C -,点B'是点B 关于x 轴的对称点,∴'(5,2)B --、(34)C -,, ∴直线'BC 解析式为313y x =+,当0y =时,133x , ∴1303D ⎛⎫- ⎪⎝⎭,. (3)解:如图所示,作CH x ⊥轴于H EK x ⊥,轴于K ,根据题意得,(34)C -,,90CHP CPE PKE ∠=∠=∠=︒, ∴9090CPH HCP CPH EPK ∠+∠=︒∠+∠=︒,,∴PCH EPK ∠=∠,∵PC PE =,∴(AAS)PCH EPK △≌△,∴43PK CH EK PH t ====+,,∴4OK t =+,∴(43)E t t ++,,∵点E 在直线25y x =-+上,∴3245t t +=-++(),∴2t =-.【点睛】本题考查平面直角坐标系中图形的旋转变换,一次函数图像上的点的特征,轴对称最短问题等知识,解题的关键是熟练掌握旋转变换的性质,根据题意添加常用辅助线,构造全等三角形解决问题.19.(1)见解析(2)见解析【分析】(1)按照轴对称的意义得出答案即可;(2)按照轴对称的定义和中心对称的定义设计,所设计的图案既是中心对称图形,又是轴对称图形.(1)解:(1)参考图案,如图所示:(2)(2)参考图案,如图所示:【点睛】本题考查利用轴对称或中心对称设计图案,关键是理解轴对称和中心对称的定义.20.(1)见解析(2)见解析(3)6【分析】(1)首先确定C 点的平移规律,依此规律平移A 、B 两点,从而得到111A B C △; (2)利用中心对称的性质作出A 、B 、C 的对应点2A 、2B 、2C 即可;(3)先求112AC C 的面积,四边形1221A C A C 的面积为112AC C 面积的2倍.(1)解:如图所示,111A B C △为所求作;(2)解:如图所示,222A B C △为所求作; (3)解:如图,123C C =,1A 到12C C 距离为2; 则112AC C 的面积为:13232⨯⨯=. ∴由图可得四边形1221A C A C 的面积为236S =⨯=.【点睛】本题考查了坐标的平移,中心对称图形的画法,网格中图形面积的求法,解题的关键是根据题意画出图象. 21.(1)见解析 (2)见解析,()3,3-【分析】(1)利用平移的坐标特征写出1A 、1B 、1C 的坐标,然后描点依次连接即可; (2)利用网格特点和旋转的性质找出 A 、B 、C 的对应点 2A 、2B 、2C ,然后描点依次连接即可得 (1)解:经过平移可得:()11,4A -,()14,4B -,()13,2C -,顺次连接,如图所示:111A B C △即为所求作;(2)解:旋转后的点的坐标分别为:()21,1A -,()21,4B -,()23,3C -,然后顺次连接, 如图所示:222A B C △即为所求作,2C 的坐标()3,3-【点睛】本题考查了作图:平移及旋转变换,找到对应点的坐标,然后顺次连接各点是解题关键. 22.(1)180 (2)12AF BE =,证明见解析;【分析】(1)由旋转可知∠DAE =180°-a ,所以得到:∠BAC +∠DAE =a +180°-a =180°; (2)连接并延长AF ,使FG =AF ,连接DG ,CG ;因为DF =CF ,AF =GF ;可以得到四变形ADGC 为平行四边形;从而有∠DAC +∠ACG =180°,再证∠ACG =∠BAE 继而证明△ABE ≌△CAG 得到BE =AG ,即可得线段AF 与BE 的数量关系; 【详解】(1)解:由旋转可知∠DAE =180°-a , ∠BAC +∠DAE =a +180°-a =180° 故答案为:180(2)解:如图所示:连接并延长AF ,使FG =AF ,连接DG ,CG ; ∵DF =CF ,AF =GF ;∴四变形ADGC 为平行四边形; ∴∠DAC +∠ACG =180°,即∠ACG =180°-∠DAC ,∠BAE =∠BAC +∠DAE-∠DAC =180°-∠DAC , 所以∠ACG =∠BAE ,∵四变形ADGC 为平行四边形; ∴AD =CG , 又∵AD =AE , AE =CG ,在△ABE 和△CAG 中,{AB CA BAE ACG AE CG=∠=∠=∴△ABE ≌△CAG , ∴BE =AG , ∴AF =12AG =12BE ,故线段AF 与BE 的数量关系:AF =12BE ;【点睛】本题考查了旋转的性质,旋转角的定义,以及全等三角形的性质的判定,解题的关键是熟悉并灵活应用以上性质. 23.(1)①()3,0,②()1,3- (2)①(3,3)a a ++,【分析】(1)①②根据“垂直图形”的定义可得答案;(2)①过点E 作EP x ⊥轴于点P ,过点E '作E H x '⊥轴于点H ,利用AAS证明PEG HGE '△≌△得3E H PG a '==+,3GH EP ==,从而得出答案;②由点E '的坐标可知,满足条件的点E '在第一象限的O 上,求出点E '的坐标,从而解决问题. (1)解:①点A 的坐标为()0,3, ∴点B 的坐标为()3,0,故答案为:()3,0;②当()3,1B 时,如图,()1,3A -,故答案为:()1,3-; (2)解:①过点E 作EP x ⊥轴于点P ,过点E '作E H x '⊥轴于点H ,90EGE ∠'=︒,EG E G =',90EGP E GH ∴∠+∠'=︒,90EGP E ∠+∠=︒, E E GH ∴∠=∠',EPG GHE ∠=∠',∴AAS HG PEG E '△≌△(), 3E H PG a ∴'==+,3GH EP ==,3OH a ∴=+,3,3E a a ∴'++();②如图,观察图象知,满足条件的点E '在第一象限的O 上,()3,3E a a '++,2OE '=,()()222332a a ∴+++=,3a +=负值舍去),3a ∴=,E ∴',EE ∴'EE ∴'【点睛】本题是几何变换综合题,主要考查了全等三角形的判定与性质,“垂直图形”的定义,坐标与图形,求出点E '的坐标是解题的关键.24.(1)见解析;(2)①见解析; 【分析】(1)证明△AMO ≌△BNO 即可;(2)①连接BN ,证明△AMO ≌△BNO ,得到∠A =∠OBN =45°,进而得到∠MBN =90°,且△OMN 为等腰直角三角形,再在△BNM 中使用勾股定理即可证明; ②分两种情况分别画出图形即可求解.【详解】解:(1)∵AOB 和MON △都是等腰直角三角形, ∴90OA OB ON OM AOBNOM ,,,又=+=90+AOM NOM AON AON ,=+=90+BON AOB AON AON ,∴=BON AOM , ∴()AMO BNO SAS ≌, ∴AM BN =;(2)①连接BN ,如下图所示:∴==90AOM AOBBOM BOM , ==90BON MONBOM BOM ,且OA OB OM ON ,==, ∴()AMO BNO SAS ≌, ∴45A OBN,AM BN =,∴454590ABNABOOBN,且OMN ∆为等腰直角三角形,∴MN ,在Rt BMN ∆中,由勾股定理可知:22222(2)2BM BN MN OM OM ,且AM BN =∴2222AM BM OM +=; ②分类讨论:情况一:如下图2所示,设AO 与NB 交于点C ,过O 点作OH ⊥AM 于H 点,45HNO ,NHO 为等腰直角三角形,∴332222NO HOHM ,在Rt AHO ∆中,22223223464()222AH AO OH , ∴46322AMAH HM; 情况二:如下图3所示,过O 点作OH ⊥AM 于H 点,45HNO ,NHO 为等腰直角三角形,∴332222NO HOHM ,在Rt AHO ∆中,22223223464()222AH AO OH , ∴46322AM AH HM;故46322AM或.【点睛】本题属于几何变换综合题,考查了全等三角形的判定和性质,等腰直角三角形的性质,勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型. 25.(1)见解析 (2)见解析【分析】(1)根据旋转性质得到对应边相等,对应角相等,进而根据等边对等角性质可将角度进行等量转化,最后可证得结论;(2)根据旋转性质、等腰三角形的性质以及三角形内角和定理对角度进行等量转化可证得结论.【详解】(1)证明:由旋转性质可知:AE AC =,AED C ∠=∠,AEC C ∴∠=∠AED AEC ∴∠=∠AE ∴平分CED ∠.(2)证明:如图所示:由旋转性质可知:AD AB =,90DAE BAC ∠=∠=︒,ADB ABD ∴∠=∠,DAE BAE BAC BAE ∠-∠=∠-∠,即DAB EAC ∠=∠,=1802DAB ABD ∠︒-∠,1802EAC C ∠=︒-∠, ABD C ∴∠=∠,∵在Rt ABC △中,90BAC ∠=︒, 90ABC C ∴∠+∠=︒, 90ABC ABD ∴∠+∠=︒,即90DBC ∠=︒.【点睛】本题考查了三角形的旋转变化,熟练掌握旋转前后图形的对应边相等,对应角相等以及合理利用三角形内角和定理是解决本题的关键.。
人教版九年级数学上册第二十三章《旋转》综合测试卷(含答案)

人教版九年级数学上册第二十三章《旋转》综合测试卷(含答案)班级 座号 姓名 成绩一、选择题(每小题4分,共40分)1. 在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转.下列图形中不能由一个图形通过旋转而构成的是( )A. B . C. D.2.将左图按顺时针方向旋转90°后得到的是( )3.在平面直角坐标系中,点.(4,3)A -关于原点对称点的坐标为( ) A. .(4,3)A --B. .(4,3)A -C. .(4,3)A -D. .(4,3)A4.将△AOB 绕点O 旋转180°得到△DOE ,则下列作图正确的是( )A. B. C. D.5.如图,将三角尺ABC (其中∠ABC=60°,∠C=90°)绕B 点按顺时针方向转动一个角度到A 1BC 1的位置,使得点A ,B ,C 1在同一条直线上,那么这个角度等于( ) A 、120° B 、90° C 、60° D 、30°6.将如图所示的正五角星绕其中心旋转,要使旋转后与它自身重合,则至少应旋转( ).A .36°B .60°C .72°D .180°7.若点A 的坐标为(6,3),O 为坐标原点,将OA 绕点O 按顺时针方向旋转90°得到OA′,则点A′的坐标是( )A 、(3,﹣6)B 、(﹣3,6)C 、(﹣3,﹣6)D 、(3,6) 8. 如图,将△ABC 绕点C 顺时针旋转90°得到△EDC .若点A ,D ,E 在同一条直线上,∠ACB=20°,则∠ADC 的度数是( ) A .55° B .60° C .65° D .70°9.如图,在正方形ABCD 中有一点P ,把⊿ABP 绕点B 旋转到⊿CQB ,连接PQ ,则⊿PBQ 的形状是( )A. 等边三角形B. 等腰三角形C.直角三角形D.等腰直角三角形10. 如图,设P 到等边三角形ABC 两顶点A 、B 的距离分别 为2、3,则PC 所能达到的最大值为( )A .5B .13C .5D .6 二、填空题(每题4分,共24分)11.如图,将ABC △绕点A 顺时针旋转60︒得到AED △, 若线段3AB =,则BE = .12.如图,将Rt △ABC 绕直角顶点C 顺时针旋转90°,得到△A ′B ′C , 连接BB',若∠A′B′B =20°,则∠A 的度数是 .13将点A (-3,2)绕原点O 逆时针旋转90°到点B ,则点B 的坐标为 . 14.若点(2,2)M a -与(2,)N a -关于原点对称,则______.15.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号是_________16.如图,在平面直角坐标系中,已知点A (-3,0),B (0,4),对△AOB 连续作旋转变换,依次得到三角形①,②,③,…,那么第⑤个三角形离原点O 最远距离的坐标是(21,0),第2020个三角形离原点O 最远距离的坐标是 .•第5题图第6题图第8题图第9题图第16题图第15题图第12题图第10题图第11题图三、解答题(共86)17.在平面直角坐标系中,已知点A(4,1),B(2,0),C(3,1).请在如图的坐标系上上画出△ABC,并画出与△ABC关于原点O对称的图形.18.如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1),B(-4,-3),C(-4,-1).C1;(1)作出△ABC关于原点O的中心对称图形△A1B1(2)将△ABC绕原点O按顺时针方向旋转90°后得到△A2B2C2,画出△A2B2C2;19.如图,在等边△ABC中,点D是AB边上一点,连接CD,将线段CD绕点C按顺时针方向旋转60°后得到CE,连接AE.求证:AE∥BC.20.如图,△ABC中,AD是中线.(1)画出将△ACD关于点D成中心对称的△EBD(2)如果AB=7,AC=5,若中线AD长为整数,求AD的最大值21.如图甲,在Rt△ACB中,四边形DECF是正方形.(1)将△AED绕点按逆时针方向旋转°,可变换成图乙,此时∠A1DB的度数是°.(2)若AD=3,BD=4,求△ADE与△BDF的面积之和.22.如图,点O是等腰直角三角形ABC内一点,∠ACB=90°,∠AOB=140°,∠AOC=α.将△AOC绕直角顶点C按顺时针方向旋转90°得△BDC,连接OD.(1)试说明△COD是等腰直角三角形;(2)当α=95°时,试判断△BOD的形状,并说明理由.23.已知△ABC中,△ACB=135°,将△ABC绕点A顺时针旋转90°,得到△AED,连接CD,CE.(1)求证:△ACD为等腰直角三角形;(2)若BC=1,AC=2,求四边形ACED的面积.24.建立模型:(1)如图 1,已知△ABC,AC=BC,△C=90△,顶点C 在直线 l 上。
新人教版九年级上数学第23章《旋转》检测题含答案

人教版九年级数学(上)第23章《旋转》检测题一、选择题(每小题3分,共30分)1、下列图形中,既是轴对称图形又是中心对称图形的是 ( )2、 如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合 的是 ( )A.72° ;B.108° ;C.144° ;D.216°;第2题图 第3题图 第4题图3、如图,△ABC 和△AB′C′成中心对称,A 为对称中心,若∠C =90°, ∠B =30°,BC =1,则BB′的长为 ( )A. 4 ;B. 3 ;C. 3;D. 3; 4、如图,点A 、B 、C 、D 都在方格纸的格点上,若△AOB 绕点O 按逆时 针方向旋转到△COD 的位置,则旋转的角度为 ( )A.30° ;B.45° ;C.90° ;D.135°;5、有一种平面图形,绕着它的中心旋转,不论旋转多少度,所得到的图形都与原图形完全重合,你觉得它可能是 ( D )A.三角形;B.等边三角形;C. 正方形;D. 圆;6、已知点P(-1,m 2+1)与点Q 关于原点对称,则Q 一定在 ( )A .第一象限;B .第二象限;C .第三象限;D .第四象限;7、如图是某药业有限公司商品标志图案,有下列说法:①图案是按照轴对称设计的;②图案是按照旋转设计的;③图案的外层“S”是按照旋转设计的;④图案的内层“V”是按照轴对称设计的.其中正确的有 ( )A .1个;B .2个;C .3个;D .4个; 第7题图8、如图,在平面直角坐标系xOy 中,△A′B′C′由△ABC 绕点P 旋转得到,则点P 的坐标为 ( )A.(0,1) ;B.(1,-1) ;C.(0,-1) ;D.(1,0);9、如图,在平面直角坐标系中,点 A(-1,m)在直线y =2x +3上,连接OA,将线段OA 绕点O 顺时针旋转90°,点A 的对应点B 恰好落在直线y =-x +b 上,则b的值为( )A.-2;B.1;C.32;D.2;第8题图第9题图第10题图10、如图,已知菱形OABC 的顶点O(0,0),B(2,2),若菱形绕点O 逆时针旋转,每秒旋转45°,则第60秒时,菱形的对角线交点D 的坐标为( )A.(1,-1) ;B.(-1,-1) ;C.(2,0) ;D.(0,-2);二、填空题(每空3分,共30分)11、点P(a2+1,|b|+,3)关于原点对称的点P1一定在第象限.12、如图,可以通过平移变换但不能通过旋转变换得到的图案有;可以通过旋转变换但不能通过平移变换得到的图案有;既可通过平移变换,又可通过旋转变换得到的图案有.(均填图案编号)第12题图13、如图,两个全等的三角尺重叠摆放在△ACB的位置,将其中一个三角尺绕着点C 按逆时针方向旋转到△DCE的位置,使点A 恰好落在边DE 上,AB 与CE 相交于点F.已知∠ACB=∠DCE =90°,∠B=30°,AB=8cm,则CF =cm.第13题图第14题图14、如图,在△ABC 中,∠A=70°,AC=BC,以点 B 为旋转中心把△ABC 按顺时针旋转α 度,得到△A′BC′,点A′恰好落在AC 上,连接CC′,则∠ACC′=.15、如图所示的平面直角坐标系中,OA=OB,点A 关于原点O 的对称点的坐标是(3,4),则△AOB 的面积是.第15题图第16题图第17题图16、如图,四边形ABCD 中,∠BAD=∠C=90°,AB=AD,AE⊥BC于E,若线段AE=5,则S四边形ABCD =.17、如图,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC 绕点C逆时针旋转60°,得到△MNC,连接BM,则BM=.18、如图,在直角坐标系中,已知点A(-3,0),B(0,4),对△OAB 连续作旋转变换,依次得到三角形①、②、③、④、…,则三角形⑩的直角顶点的坐标为.第18题图三、解答题(共66分)19、(8分)在平面直角坐标系中,△ABC 的三个顶点坐标分别为A(-2,1),B(-4,5),C(-5,2).(1)画出△ABC 关于y 轴对称的△A1B1C1;(2)画出△ABC 关于原点O 成中心对称的△A2B2C2.第19题图2020(8分)如图,在正方形ABCD 中,AD=1,将△ABD 绕点B 顺时针旋转,45°得到△A′BD′,此时A′D′与CD 交于点E,求DE 的长度.第202021、(8分)如图,将一个钝角△ABC(其中∠ABC=12020绕点B顺时针旋转得△A1BC1,使得C 点落在AB的延长线上的点C1处,连接AA1.(1)写出旋转角的度数;(2)求证:∠A1AC=∠C1.第21题图22、(8分)如图,在Rt△OAB 中,∠OAB=90°,OA=AB=6,将△OAB 绕点O 沿逆时针方向旋转90°得到△OA1B1.(1)线段OA1的长是,∠AOB1的度数是;(2)连接AA1,求证:四边形OAA1B1是平行四边形;(3)求四边形OAA1B1的面积.第22题图23、(8分)如图,△ABC 中,∠BAC=12020以BC为边向外作等边△BCD,把△ABD 绕着点D 按顺时针方向旋转60°到△ECD 的位置,若AB=3,AC=2,求∠BAD 的度数和AD 的长.24、(10分)如图,△ABC中,AB=AC=1,∠BAC=45°, 第23题图△AEF 是由△ABC 绕点A 按顺时针方向旋转得到的,连接BE,CF 并相交于点D.(1)求证:BE=CF;(2)当四边形ACDE 为菱形时,求BD 的长.第24题图25、(10分)通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例,请补充完整.原题:如图①,点E、F分别在正方形ABCD的边BC、CD 上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.第25题图(1)【思路梳理】∵AB=AD,∴把△ABE 绕点 A 逆时针旋转90°至△ADG,可使AB 与AD 重合,∵∠ADG=∠B=90°,∴∠FDG=180°,点F、D、G 共线,根据,易证△AFG≌,得EF=BE+DF;(2)【类比引申】如图②,四边形ABCD 中,AB=AD,∠BAD=90°点E,F 分别在边BC,CD 上,∠EAF=45°,若∠B,∠D 都不是直角,则当∠B 与∠D 满足等量关系时,仍有EF=BE+DF;(3)【联想拓展】如图③,在△ABC 中,∠BAC=90°,AB=AC,点D,E 均在边BC 上,且∠DAE=45°,猜想BD、DE、EC 应满足的等量关系,并写出推理过程.参考答案:1、B;2、B;3、D;4、C;5、D;6、D;7、B;8、B;9、D;10、B;11、三;12、①④,③,②;13、;14、100°;15、10;16、25;17、;18、(36,0);19、解:如图所示(略)2020题意可得∠BDC=45°,∠DA′E=90°,∴∠DEA′=45°,∴A′D=A′E,∵在正方形ABCD 中,AD=1,∴AB=A′B=1,BD,∴A′D-1,∴在Rt△DA′E 中,DE=221、(1)60°.(2)证明:由旋转的性质知△ABC ≌△A1BC1,∴∠ABC=∠A1BC1=12020AB=A1B,∠C=∠C1,∵∠A1BA+∠A1BC1=180°,∴∠ABA1=60°,∴△A1BA 为等边三角形,∴∠A1AB=60°,∵∠A1AB+∠ABC=180°,∴AA1∥BC,∴∠C=∠A1AC,∴∠A1AC=∠C1.22、(1)6;135°;(2)证明:∵∠AOA1=∠OA1B1=90°,∴OA∥A1B1.又∵OA=AB=A1B1,∴四边形OAA1B1是平行四边形.(3)36.23、解:由∠BAC=12020∠ABC+∠ACB=60°.又∵∠ABD=∠ABC+∠CBD=∠DCE,∠CBD=∠BCD=60°,∴∠ACB+∠BCD+∠DCE=∠ACB+∠BCD+∠ABC+∠CBD=180°,即点A、C、E 在一条直线上.又∵AD=ED,∠ADE=60°,∴△ADE 为等边三角形.∴∠BAD=∠E=60°,AD=AE=AC+CE=AC+AB=5.24、(1)证明:由旋转可知∠EAB=∠FAC,AF=AC,AE=AB.又∵AB=AC,∴AE=AF.∴△ABE≌△ACF.∴BE=CF.(2)∵四边形ACDE 是菱形,AB=AC=1,∴AC∥DE,DE=AE=AB=,1.又∵∠BAC=45°,∴∠AEB=∠ABE=∠BAC=45°.∵∠AEB+∠BAE+∠ABE=180°,∴∠BAE=90°.∴BE===BD=BE-DE-1.25、(1)SAS,△AFE;(2)∠B+∠D=180°(3)猜想:DE2=BD2+EC2.证明:将△ABD 绕点A 逆时针旋转90°,则AB 与AC 重合,如图,连接ED′,则△ADE≌△AD′E,∴DE=D′E,又∵Rt△ABC 中,∠B+∠ACB=90°,∠B=∠ACD′,∴∠ACD′+∠ACB=90°,即∠D′CE=90°,∴ED′2=EC2+CD′2,∴DE2=EC2+BD2.。
人教版九年级数学上册第23章《图形的旋转》全章测试题

旋转水平测试题附答案一、精心选一选 (每小题3分,共30分)1.(2008年广东湛江市)下面的图形中,是中心对称图形的是()A.B.C.D.2.平面直角坐标系内一点P(-2,3)关于原点对称的点的坐标是()A.(3,-2)B.(2,3)C.(-2,-3)D.(2,-3)3.3张扑克牌如图1放在桌子上,小敏把其中一张旋转180º后得到如图(2)所示,则她所旋转的牌从左数起是A.第一张B.第二张C.第三张D.第四张4.在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是()5.如图3的方格纸中,左边图形到右边图形的变换是()A.向右平移7格;B.以AB的垂直平分线为对称轴作轴对称,再以AB为对称轴作轴对称;C.绕AB的中点旋转1800,再以AB为对称轴作轴对称;D.以AB为对称轴作轴对称,再向右平移7格6.从数学上对称的角度看,下面几组大写英文字母中,不同于另外三组的一组是()A.A N E G B.K B X NC.X I H O D.Z D W H7.如图4,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( ).A.1对B.2对C.3对D.4对8.下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度是()A ︒30 B ︒45 C ︒60 D ︒909.如图5所示,图中的一个矩形是另一个矩形顺时针方向旋转90°后形成的个数是()ABCA B C DA .l 个B .2个C .3个D .4个10.如图6,ΔABC 和ΔADE 都是等腰直角三角形,∠C 和∠ADE 都是直角,点C 在AE 上,ΔABC 绕着A 点经过逆时针旋转后能够与ΔADE 重合得到图6,再将图6作为“基本图形”绕着A 点经过逆时针连续旋转得到图7.两次旋转的角度分别为( )A .45°,90°B .90°,45°C .60°,30°D .30°,60二、耐心填一填(每小题3分,共24分)11.关于中心对称的两个图形,对称点所连线段都经过 ,而且被_____________平分. 12.在平行四边形、矩形、菱形、正方形、等腰梯形这五种图形中,既是轴对称图形,又是中心对称图形的是_____________.13.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是_____________. 14.如图8,△ABC 以点A 为旋转中心,按逆时针方向旋转60°,得△AB ′C ′,则△ABB ′是 三角形.15.已知a<0,则点P(a2,-a+3)关于原点的对称点P1在第___象限16.如图9,△COD 是△AOB 绕点O 顺时针方向旋转40°后所得的图形,点C 恰好在AB 上,∠AOD =90°,则∠D 的度数是 .17.如图10,在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆的半径为2,则图中阴影部分的面积是___. 18.如图,四边形ABCD 中,∠BAD=∠C=90º,AB=AD ,AE ⊥BC 于E ,若线段AE=5,则S 四边形ABCD= 。
人教版九年级数学上册 第23章《旋转》达标检测题(带答案)
人教版九年级数学上册第23章《旋转》达标检测题(考试时间:120分钟满分:120分)姓名:________ 班级:________ 分数:________第Ⅰ卷(选择题共30分)一、选择题(每小题3分,共30分)1.下列交通标志既是轴对称图形又是中心对称图形的是( C)A B C D2.如图,用左面的三角形连续地旋转可以得到右面的图形,每次旋转________度( C)A.60 B.90 C.120 D.1503.如图所示,△ABC与△A′B′C′关于点O成中心对称,则下列结论不成立的是( D)A.点A与点A′是对称点B.BO=B′O C.AB∥A′B′D.∠ACB=∠C′A′B′4.如图,在矩形ABCD中,AD=5,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为( A)A.5 2 B.5 3 C.8 D.105.如图,在平面直角坐标系中,△ABC的顶点都在方格线的格点上,将△ABC 绕点P逆时针方向旋转90°,得到△A′B′C′,则点P的坐标为( A)A.(2,1) B.(1,1) C.(1,2) D.(0,4)6.将一张平行四边形纸片折一次,使折痕平分这个图形的面积,这样的折法共有( D)A.5种B.1种C.3种D.无数种7.已知点A(1,y)与点B(x,-2)关于原点对称,则点(x,y)到原点的距离是( A) A. 5 B.2 C. 3 D.18.★如图,在等边△ABC中,AC=10,点O在AC上,且AO=3,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D 恰好落在BC上,则AP的长是( C)A.5 B.6 C.7 D.99.欧几里得的《几何原本》中记载了用图解法求解一元二次方程的方法,志豪读了后,想到一个可以求解方程x2-bx+a2=0的图解方法:如图,在矩形ABCD(AB>BC)中,AB=b2,BC=a,以A为旋转中心,逆时针旋转线段AB,得到线段AE=AB,交DC于点E,则该方程的其中一个正根是( B)(第9题图)(第10题图)A.BE的长B.CE的长C.DE的长D.AD的长10.★如图,P是正三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.给出下列四个结论:①PP′=6;②AP2+BP2=CP2;③∠APB=150°;④S△ABC=36+25 3.正确结论的个数为( D)A.1 B.2 C.3 D.4第Ⅱ卷(非选择题共90分)二、填空题(每小题3分,共24分)11.在平面直角坐标系xOy中,点(3,-4)关于原点对称的点的坐标为__(-3,4)__.12.如图,点O,A,B都在正方形网格的格点上,将△OAB绕点O顺时针旋转后得到△OA′B′,点A,B的对应点A′,B′也在格点上,则旋转角α(0°<α<180°)的度数为__90°__.(第12题图)(第13题图)13.如图,将△ABC绕点A逆时针旋转90°得到△ADE,点C和点E是对应点,若AB=1,则BD=__2__.14.如图,直线a,b垂直相交于点O,曲线C关于点O成中心对称,点A的对称点是A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,AB=2,则阴影部分的面积之和为__6__.(第14题图)(第15题图)15.如图,已知△AOB与△DOC成中心对称,△AOB的面积是6,AB=3,则△DOC中CD边上的高是__4__.16.如图,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′,边B′C′交CD于点E.若正方形ABCD的边长为3,则DE的长为__3__.(第16题图)(第17题图)17.★如图,等边△ABC的边长为4,将等边△ABC绕点B顺时针旋转120°得到△A′BC′,若点D为直线A′B上的一动点,则AD+CD的最小值是__8__.18.★如图,正方形ABCD和正方形CEFG的边长分别为a和b,正方形CEFG 绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2.其中正确结论是__①②__(填序号).(第18题图)选择、填空题答题卡一、选择题(每小题3分,共30分)题号 1 2 3 4 5 6 7 8 9 10 得分答案 C C D A A D A C B D二、填空题(每小题3分,共24分)得分:________11.__(-3,4)__12.__90°__13.__2__14.__6__15.__4__16.__3__17.__8__18.__①②__三、解答题(共66分)19.(8分)在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).(1)将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2,C2的坐标.解:(1)如图,△A1B1C1即为所求.(2)如图,△AB2C2即为所求.点B2的坐标为(4,-2),点C2的坐标为(1,-3).20.(8分)如图,△ABC中,AB=AC,∠BAC=90°,点D,E在BC上,∠DAE =45°.(1)画出将△ABD绕点A逆时针旋转90°得到的三角形;(2)若BD=3,CE=4,求DE的长.解:(1)如图,△ACF即为所求.(2)∵AB =AC ,∠BAC =90°, ∴∠B =∠ACB =45°.连接EF.由旋转可知∠ACF =∠ABD =45°,CF =BD =3, ∴∠FCE =90°.易证△ADE ≌△AFE ,∴DE =EF ,∴DE 2=EF 2=CE 2+CF 2=42+32=25,∴DE =5.21.(8分)如图,正方形ABCD 的边长为4,点E 是CD 的中点,AF 平分∠BAE 交BC 于点F ,将△ADE 绕点A 顺时针旋转90°得△ABG ,求CF 的长. 解:过点F 作FM ⊥AD 于M ,FN ⊥AG 于N ,如图,易得四边形CFMD 为矩形,则FM =4,∵正方形ABCD 的边长为4,点E 是CD 的中点,∴DE =2,∴AE =42+22=25.∵△ADE 绕点A 顺时针旋转90°得△ABG , ∴AG =AE =25,BG =DE =2,∠3=∠4,∠GAE =90°,∠ABG =∠D =90°.而∠ABC =90°,∴点G 在CB 的延长线上.∵AF 平分∠BAE 交BC 于点F , ∴∠1=∠2,∴∠2+∠4=∠1+∠3,即FA 平分∠GAD , ∴FN =FM =4.∵12AB ·GF =12FN ·AG ,∴GF =4×254=25,∴CF =CG -GF =4+2-25=6-2 5.22.(10分)如图,在Rt △ABC 中,∠C =90°,∠CAB =35°,BC =7.线段AD 由线段AC 绕点A 按逆时针方向旋转125°得到,△EFG 由△ABC 沿CB 方向平移得到,且直线EF 过点 D.(1)求∠DAE的大小;(2)求DE的长.解:(1)∵△EFG是由△ABC沿CB方向平移得到,∴AE∥CF,∴∠EAC+∠C=180°. 又∵∠C=90°,∴∠EAC=90°,又线段AD是由线段AC绕点A按逆时针方向旋转125°得到,即∠DAC=125°,∴∠DAE=35°.(2)∵△EFG是由△ABC沿CB方向平移得到,∴AE∥CF,EF∥AB,∴∠AED=∠F=∠ABC,又∵∠DAE=∠BAC=35°,AD=AC,∴△AED≌△ABC(AAS),∴DE=BC=7.23.(10分)如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.(1)求证:AE=CE;(2)若BC=2,求AB的长.(1)证明:∵将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,∴△ABC≌△DBE,∴∠BAC=∠CDF.∵∠BAC+∠ACB=90°,∴∠CDF+∠ACB=90°,∴DF⊥AC,且点F是AC中点,∴DF垂直平分AC,∴AE=CE.(2)解:∵△ABC≌△DBE,∴BE=BC=2,∴CE=AE=2,∴AB=AE+BE=2+ 2.24.(10分)如图,△ABC中,AB=BC,将△ABC绕顶点B逆时针旋转α到△A′BC′的位置,AB与A′C′相交于点D,AC与A′C′,BC′分别交于点E,F.(1)求证:△BCF≌△BA′D;(2)当∠C=α时,判断四边形A′BCE的形状,并说明理由.(1)证明:∵△ABC是等腰三角形,∴AB=BC,∠A=∠C.∵将等腰△ABC 绕顶点B 逆时针方向旋转α度到△A ′BC ′的位置, ∴A ′B =AB =BC ,∠A =∠A ′=∠C ,∠A ′BD =∠CBC ′, 在△BCF 与△BA ′D 中,⎩⎪⎨⎪⎧∠A ′=∠C ,A ′B =BC ,∠A ′BD =∠CBF ,∴△BCF ≌△BA ′D(ASA).(2)解:四边形A ′BCE 是菱形,理由:∵将等腰△ABC 绕顶点B 逆时针方向旋转α度到△A ′BC ′的位置, ∴∠A ′=∠A ,∵∠ADE =∠A ′DB ,∴∠AED =∠A ′BD =α,∴∠DEC =180°-α. ∵∠C =α,∴∠A ′=α,∴∠A ′BC =360°-∠A ′-∠C -∠A ′EC =180°-α, ∴∠A ′=∠C ,∠A ′BC =∠A ′EC , ∴四边形A ′BCE 是平行四边形. ∵A ′B =BC ,∴四边形A ′BCE 是菱形.25.(12分)如图,已知∠AOB =60°,在∠AOB 的平分线OM 上有一点C ,将一个120°角的顶点与点C 重合,它的两条边分别与直线OA ,OB 相交于点D ,E. (1)当∠DCE 绕点C 旋转到CD 与OA 垂直时(如图①),请猜想OE +OD 与OC 的数量关系,并说明理由;(2)当∠DCE 绕点C 旋转到CD 与OA 不垂直时,到达图②的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图③中画出图形,若成立,请给予证明;若不成立,线段OD,OE与OC 之间又有怎样的数量关系?请写出你的猜想,不需证明.解:(1)OE+OD=3OC.理由:∵OM是∠AOB的角平分线,∴∠AOC=∠BOC=12∠AOB=30°.∵CD⊥OA,∴∠ODC=90°,∴∠OCD=60°,∴∠OCE=∠DCE-∠OCD=60°,在Rt△OCD中,由勾股定理求得OD=32OC,同理:OE=32OC,∴OD+OE=3OC.(2)(1)中结论仍然成立,理由:过点C作CF⊥OA于F,CG⊥OB于G,∴∠OFC =∠OGC=90°,∵∠AOB=60°,∴∠FCG=120°.同(1)的方法得,OF=32OC,OG=32OC,∴OF+OG=3OC,∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG.∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,∴OF=OD+DF=OD+EG,OG=OE-EG,∴OF+OG=OD+EG+OE-EG=OD+OE,∴OD+OE=3OC.(3)(1)中结论不成立,结论为:OE-OD=3OC,理由:图略.过点C作CF ⊥OA于F,CG⊥OB于G,∴∠OFC=∠OGC=90°.∵∠AOB=60°,∴∠FCG=120°,同(1)的方法得,OF=32OC,OG=32OC,∴OF+OG=3OC.∵CF⊥OA,CG⊥OB,且点C是∠AOB的平分线OM上一点,∴CF=CG.∵∠DCE=120°,∠FCG=120°,∴∠DCF=∠ECG,∴△CFD≌△CGE,∴DF=EG,∴OF=DF-OD=EG-OD,OG=OE-EG,∴OF+OG=EG-OD+OE-EG=OE-OD,∴OE-OD=3OC.。
人教版九年级数学上册第23章《图形的旋转》整章测试题(含答案)
第二十三章《旋转》整章测试题附答案一、填空题:(每题 3 分)1.( 2009 年新疆)下列各组图中,图形甲变成图形乙,既能用平移,又能用旋转的是()甲乙甲乙甲乙甲乙A .B.C.D.2(. 2008 江苏省盐城市)已知如图 1 所示的四张牌,若将其中一张牌旋转180 °后得到图 2.则旋转的牌是()图 1图 2A B C D3.( 2008 湖北省宜昌市)如图,将三角尺ABC(其中∠ ABC=60°,∠ C= 90°)绕 B 点按顺时针方向转动一个角A 1度到 A1BC1的位置,使得点A,B,C1在同一条直线上,C那么这个角度等于().B C1AA .120 °B. 90°C.60°D. 30°(第9题)4.( 2009 年崇左)已知点A的坐标为(a,b),O为坐标原点,连结OA,将线段OA绕点O 按逆时针方向旋转90°得OA1,则点A1的坐标为().A ( a,b)B.(a,b)C.( b,a) D .(b,a)5.( 2009 年山东省日照市)在下图4× 4 的正方形网格中,△MNP 绕D N1 M1某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是A B P1CA.点 A B.点 B C.点 CD.点 D P6. ( 2009 年牡丹江市)△ABC在如图所示的平面直角坐标系中,将MN △ ABC 向右平移3个单位长度后得△ A1B1C1,再将△ A1B1C1绕点y O 旋转 180°后得到△A2B2C2,则下列说法正确的是()4AA .A1的坐标为31,B.S四边形ABB1A133BC21C.B2C 2 2D.AC2O 45°32 11 0 123 x237.( 2008 内蒙古自治区包头市)如图,已知两个全等直角三角形的直角顶点及一条直角边重合,将△ ACB 绕点 C 按顺时针方向旋转到AA △ A CB 的位置,其中 AC 交直线 AD 于点F AE , A B 分别交直线 AD,AC 于点GE BF,G ,则旋转后的图中,全等三角形共有BC D C D()A.2 对B.3 对C.4 对D.5 对8. (2008 河北省)有一个四等分转盘,在它的上、右、下、左的位置分别挂着“众”、“志”、“成”、“城”四个字牌,如图 -1.若将位于上下位置的两个字牌对调,同时将位于左右位置的两个字牌对调,再将转盘顺时针旋转90 ,则完成一次变换.图-2,图 -3 分别表示第 1 次变换和第 2 次变换.按上述规则完成第9 次变换后,“众” 字位于转盘的位置是()第1次变换第2次变换众成志城成城志志城众成成众志城成众城志众图 -1图-2图 -3A .上B.下C.左D.右二、填空题:(每题 3 分)9. ( 2008 甘肃省白银九市)已知等腰三角形的一条腰长是5,底边长是 6,则它底边上的高为.10( 2008 吉林省长春市)如图,在平面内将Rt△ ABC 绕着直角顶点AC 逆时针旋转90 得到Rt△EFC.若 AB5, BC1,则线F段 BE 的长为.E BC11. (2008 辽宁省大连市, 3 分)如图, P 是正△ ABC 内的一点,若将△PAC 绕点 A 逆时针旋转到△ P′AB,则∠ PAP′的度数为.BA P AP′PPB C C CB BA C(第 12(第 13 题)(第 11 题)题)12.( 2008 江苏省扬州市)如图△ ABC 是等腰直角三角形,BC 是斜边, P 为△ ABC 内一点,将△ ABP 绕点 A 逆时针旋转后与△ACP′重合,如果 AP=3 ,那么线段PP的长等于 ____.13.( 2008 四川省宜宾市)将直角边长为5cm 的等腰直角△ABC绕点A逆时针旋转15后得到△ AB C ,则图中阴影部分的面积是cm 2.14.. ( 2008 福建省厦门市)如图,点G 是△ ABC 的重心, CG 的延C长线交 AB于D,GA5cm , GC4cm , GB3cm ,将△ADG绕点 D旋转180得到△ BDE ,则 DE cm,G B D△ ABC 的面积cm2.AE15.( 2007 湖南株洲课改)如图,将边长为 3 的正方形ABCD绕点A逆时针方向旋转30o后得到正方形AB C D ,则图中阴影部分的面积为____________平方单位.16. ( 2007 江苏泰州课改)如图,直角梯形ABCD 中, AD ∥ BC ,EAB BC,AD2,BC 3,BCD45 ,将腰CD以点D为A D中心逆时针旋转90至 ED ,连结 AE,CE ,则△ ADE 的面积B C是.答案:三、解答题:(共 52 分)A17.( 6 分)( 2008 云南省双柏市)如图是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:( 1)作出关于直线AB 的轴对称图形;O( 2)将你画出的部分连同原图形绕点O 逆时针旋转;90°( 3)发挥你的想象,给得到的图案适当涂上阴影,让它变得更加美丽.B18.(9 分)( 2008 山西省)如图,在 4× 3 的网格上,由个数相同的白色方块与黑色方块组成一幅图案,请仿照此图案,在下列网格中分别设计出符合要求的图案(注:①不得与原图案相同;②黑、白方块的个数要相同).( 1)(2)(3)19.( 12 分)(2008 江苏省徐州市)如图,方格纸中的每个小方格都是边长为 1 个单位的正方形,在建立平面直角坐标系后,△ABC 的顶点均在格点上,点 B 的坐标为 (1,0) .(1)画出△ ABC 关于 x 轴对称的△ A1B1C1;(2)画出将△ ABC 绕原点 O 按逆时针方向旋转 90 所得的△ A2B2C2;(3)△ A1B1C1与△ A2B2C2成轴对称吗?若成轴对称,画出所有的对称轴;(4)△ A1B1C1与△ A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.解:yACO B x20.( 12 分)( 2008 山东省枣庄市)把一副三角板如图甲放置,其中∠ ACB ∠ DEC 90 ,∠ A 45 , ∠ D 30 ,斜边 AB6cm , DC 7cm .把三角板 DCE 绕点 C 顺时针旋转 15°得到△ D 1CE 1(如图乙).这时 AB 与 CD 1 相交于点 O ,与 D 1 E 1 相交于点 F .( 1)求 ∠ OFE 1 的度数; ( 2)求线段 AD 1 的长;( 3)若把三角形 D 1CE 1 绕着点 C 顺时针再旋转 30°得△ D 2CE 2,这时点 B 在△ D 2CE 2 的内部、外部、还是边上?说明理由.DD 1AAOFCEBCB(甲)(乙)E 121.( 13 分)(2009 年牡丹江)已知 Rt △ ABC 中, AC B C ,∠ C90 ,D 为 AB 边的中点,EDF 90°, EDF 绕 D 点旋转,它的两边分别交 AC 、 CB (或它们的延长线)于E 、F .当EDF 绕 D 点旋转到 DE AC 于 E 时(如图△△ 1 .1),易证S CEFS ABCS DEF2当 EDF 绕 D 点旋转到 DE 和 AC 不垂直时, 在图 2 和图 3 这两种情况下, 上述结论是否成立?若成立,请给予证明;若不成立, S △DEF 、 S △CEF 、 S △ ABC 又有怎样的数量关系?请写出你的猜想,不需证明.AAADE DDCECBFFBBCFE图 3图 1图 2参考答案一、选择题:1.C2.A3.A4.C5.B6.D7.C8.C二、填空题:9. 90 10. 311. 6012.3225313.14. 2, 1815. 33 16.16三、解答题:17. 答案:如图.三步各计 2 分,共 6 分.AOB 18.解:( 1)(2)(3)19解:(1)如图;(2)如图;(3)成轴对称,对称轴如图;1 1 (4)成中心对称,对称中心坐标( , ) .2 220.解:( 1)如图所示, 3 15,E190 ,AD1∴1275 .5又B45,O4F C3 21∴OFE 1B14575120 .B ( 2)OFE1120 ,∴∠D1FO=60°.E1 CD1 E130,∴490 .又 AC BC, AB 6,∴ OA OB 3.ACB90,∴ CO 1AB163.22又 CD17 ,∴ OD1CD1OC73 4 .在 Rt △ AD1O 中,AD1OA2OD123242 5 .( 3)点B在△D2CE2内部.理由如下:设BC (或延长线)交D2E2于点 P,则PCE2 15 30 45 .在 Rt △ PCE2中, CP2CE272,2CB 3272CP ,∴点 B 在△D2CE2内部.,即 CB221.解:图 2 成立;图 3 不成立.证明图 2:过点 D 作 DM AC,DN BC则DME DNF MDN90°再证MDE NDF ,DM DN有△ DME ≌△ DNFS△DME S△DNFS SDECF S△D EF△SC E F四边形DMCN四边形由信息可知 S四边形DMCN 1S△ABC12S△D EF△△SCEF2S ABC1S△ABC图 3 不成立,S△DEF 、S△CEF、S△ABC的关系是:S△DEF S△CEF2。
人教版九年级数学上册 第23章旋转 单元测试(含解析)
第23章旋转单元测试(时间120分钟,总分值120分)一、选择题(每题3分,共30分)1.以下现象中属于旋转的是()A.摩托车在急刹车时向前滑动B.拧开水龙头C.雪橇在雪地里滑动D.电梯的上升与下降2.如图,△ABC和△DEF关于点O中心对称,要得到△DEF,需要将△ABC绕点O旋转()A.30°B.90°C.180°D.360°3.以下图标中,属于中心对称图形的是()4.以下图案可以通过一个“根本图形〞平移得到的是()5.以下说法中,正确的有()①线段两端点关于它的中点对称;②菱形一组对边关于对角线交点对称;③成中心对称的两个图形一定全等;④假如两个图形全等,那么这两个图形一定关于某点成中心对称;⑤假如两个三角形的对应点连线都经过一点,那么这两个三角形成中心对称.A.2个B.3个C.4个D.5个6.以下图案中,既是中心对称图形又是轴对称图形的有()A.1个B.2个C.3个D.4个7.如图,▱ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA'E',连接DA'.假设∠ADC=60°,∠ADA'=50°,那么∠DA'E'的大小为()A.130°B.150°C.160°D.170°8.如图,△ABD和△BCD都是等边三角形,△ABD旋转后与△BCD重合,那么可以作为旋转中心的点有()A.1个B.2个C.3个D.4个9.如图,在平面直角坐标系中,点B,C,E在y轴上,Rt△ABC经过变换得到Rt△ODE.假设点C的坐标为(0,1),AC=2,那么这种变换可以是()A.△ABC绕点C顺时针旋转90°,再向下平移3个单位B.△ABC绕点C顺时针旋转90°,再向下平移1个单位C.△ABC绕点C逆时针旋转90°,再向下平移1个单位D.△ABC绕点C逆时针旋转90°,再向下平移3个单位10.点(a,a),给出以下变换:①关于x轴的轴对称变换;②关于直线y=-x的轴对称变换;③关于原点的中心对称变换;④绕原点旋转180°.其中通过变换能得到对应点的坐标为(-a,-a)的变换是()A.①②④B.②③④C.③④D.②③二、填空题(每题4分,共24分)11.点P(a,-3)关于原点的对称点P'(-2,b),那么a+b的值是.12.如图,将△ABC绕点A顺时针旋转60°得到△AED,假设线段AB=3,那么BE= .13.如图,在平面直角坐标系中,将点P(-4,2)绕原点顺时针旋转90°,那么其对应点Q的坐标为.14.如图,Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.假设点F是DE的中点,连接AF,那么AF= .15.直角坐标系中,A(3,2),作点A关于y轴对称的点A1,点A1关于原点对称的点A,点A2关于x轴对称的点A3,A3关于y轴对称的点A4,…按此规律,那么点A2 0152的坐标为.16.如图,平面直角坐标系中,▱OABC的顶点A坐标为(6,0),C点坐标为(2,2),假设直线y=mx+2平分▱OABC的周长,那么m的值为.三、解答题(共66分)17.(6分)如图,试说明△A'B'C'是由△ABC通过怎样的图形变换或变换组合(平移、旋转、轴对称)得到的?18.(6分)点A(2a+2,3-3b)与点B(2b-4,3a+6)关于坐标原点对称,求a与b的值.19.(8分)如图,请你画出四边形ABCD关于O对称的图形.20.(8分)如图,在平面直角坐标系中,一个方格的边长为1个单位长度,△MNQ是△ABC经过某种变换后得到的图形.(1)请分别写出点A与点M,点B与点N,点C与点Q的坐标,并观察它们之间的关系;(2)点P是△ABC内一点,其坐标为(-3,2),探究其在△MNQ中的对应点R的坐标,并猜测线段AC和线段MQ的关系.21.(8分)如图,△OBD中,OD=BD,△OBD绕点O逆时针旋转一定角度后得到△OAC,此时B,D,C三点正好在一条直线上,且点D是BC的中点.(1)求∠COD的度数;(2)求证:四边形ODAC是菱形.22.(8分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC和△DEF的顶点都在格点上,结合所给的平面直角坐标系解答以下问题:(1)画出△ABC向上平移4个单位长度后所得到的△A1B1C1;(2)画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1;(3)△A1B1C1和△D1E1F1组成的图形是轴对称图形吗?假如是,请直接写出对称轴所在直线的解析式.23.(10分)设E,F分别在正方形ABCD的边BC,CD上滑动且保持∠EAF=45°.假设AB=5,求△ECF的周长.24.(12分)把两个全等的等腰直角三角形三角板ABC和EFG(其直角边长均为4)叠放在一起(如图①),且使三角板EFG的直角顶点G与三角板ABC的斜边中点O 重合.现将三角板EFG绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠局部(如图②).(1)在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论;(2)连接HK,在上述旋转过程中,设BH=x,△GKH的面积为y,求y与x之间的函数关系式,并写出自变量x的取值范围;(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的5?16假设存在,求出此时x的值;假设不存在,说明理由.参考答案1.B解析:A,摩托车在急刹车时向前滑动不是旋转,故此选项错误;B,拧开水龙头属于旋转,故此选项正确;C,雪橇在雪地里滑动不是旋转,故此选项错误;D,电梯的上升与下降不是旋转,故此选项错误.2.C解析:△ABC和△DEF关于点O中心对称,要得到△DEF,需要将△ABC旋转180°.3.C解析:根据中心对称图形的概念,知A,B,D中图形都不是中心对称图形,不符合题意;C中图形是中心对称图形,符合题意.4.B解析:A,可以由一个“根本图案〞旋转得到,故本选项错误;B,可以由一个“根本图案〞平移得到,故本选项正确;C,是轴对称图形,不是根本图案的组合图形,故本选项错误;D,不是根本图案的组合图形,故本选项错误.5.B解析:①正确;②正确;③正确;④假如两个图形全等,那么这两个图形不一定关于某点成中心对称,关于某点中心对称的两个图形全等,故命题错误;⑤假如两个三角形的对应点连线都经过一点,那么这两个三角形位似,但不一定全等,那么不一定成中心对称,故命题错误.6.B解析:第一个图形既是轴对称图形,又是中心对称图形,第二个图形是轴对称图形,不是中心对称图形,第三个图形是中心对称图形,不是轴对称图形,第四个图形既是轴对称图形,又是中心对称图形,综上所述,既是轴对称图形又是中心对称图形的是第一、四个图形,共2个.7.C 解析:∵四边形ABCD 是平行四边形,∠ADC=60°,∴∠ABC=60°,∠DCB=120°,∵∠ADA'=50°,∴∠A'DC=10°,∴∠DA'B=130°,∵AE ⊥BC 于点E ,∴∠BAE=30°,∵△BAE 顺时针旋转,得到△BA'E',∴∠BA'E'=∠BAE=30°,∴∠DA'E'=∠DA'B+∠BA'E'=160°.8.C 解析:∵△ABD 和△BCD 都是等边三角形,∴AD=AB=BD=BC=CD ,∠ABD=∠ADB=∠CBD=∠CDB=60°,∴将△ABD 绕点B 顺时针旋转60°可得到△DBC 或将△ABD 绕点D 逆时针旋转60°可得到△BCD 或将△ABD 绕BD 的中点旋转180°可得到△CDB.9.A 解析:根据图形可以看出,△ABC 绕点C 顺时针旋转90°,再向下平移3个单位可以得到△ODE.10.B 解析:点(a ,a ),给出以下变换:①关于x 轴的轴对称变换,得出(a ,-a ),故此选项错误;②关于直线y=-x 的轴对称变换,得出(-a ,-a ),故此选项正确;③关于原点的中心对称变换,得出(-a ,-a ),故此选项正确;④绕原点旋转180°,得出(-a ,-a ),故此选项正确.11.5 解析:∵点P (a ,-3)关于原点的对称点P'(-2,b ),∴a=2,b=3,∴a+b=5. 12.3 解析:∵将△ABC 绕点A 顺时针旋转60°得到△AED ,∴∠BAE=60°,AB=AE ,∴△BAE 是等边三角形,∴BE=3.13.(2,4) 解析:作图如下图,分别作PM ,QN 垂直于x 轴,垂足分别为M ,N.∵∠MPO+∠POM=90°,∠QON+∠POM=90°,∴∠MPO=∠QON ,在△PMO 和△ONQ 中,∵{∠PMO =∠ONQ ,∠MPO =∠NOQ ,PO =OQ ,∴△PMO ≌△ONQ , ∴PM=ON ,OM=QN ,∵P 点坐标为(-4,2), ∴Q 点坐标为(2,4).14.5 解析:如下图,作FG ⊥AC ,垂足为G.根据旋转的性质,得EC=BC=4,DC=AC=6,∠ACD=∠ACB=90°,∴FG ∥CD.∵点F 是DE 的中点,∴GF=12CD=12AC=3,EG=12EC=12BC=2,∵AC=6,EC=BC=4,∴AE=2.∴AG=4.根据勾股定理,得AF=5.15.(3,-2) 解析:作点A 关于y 轴的对称点为A 1,是(-3,2);作点A 1关于原点的对称点为A 2,是(3,-2);作点A 2关于x 轴的对称点为A 3,是(3,2).显然此为一循环,按此规律,2 015÷3=671……2,那么点A 2 015的坐标是(3,-2).16.-14 解析:连接CA ,OB 交于点G ,那么点G 的坐标为(4,1),∵直线y=mx+2平分▱OABC 的周长,∴直线y=mx+2经过点G ,那么1=4m+2,解得m=-14.17.分析:观察此图可知此图形状、大小没变,只是位置发生了变化.由旋转、平移的性质可知此图是通过旋转、平移得到.解:通过旋转、平移得到.以B 为中心,逆时针旋转90°,向下平移1个单位,再向右平移5个单位.18.分析:利用关于原点对称的点的性质得出关于a ,b 的等式进而求出即可. 解:∵点A (2a+2,3-3b )与点B (2b-4,3a+6)关于坐标原点对称,∴{2a +2+2b -4=0,3-3b +3a +6=0,解得{a =-1,b =2.19.分析:连接四边形的各顶点与O 并延长一样长度,找到A ,B ,C ,D 的对称点并顺次连接得到图形.解:根据题意画出图形,如下图,∴四边形A'B'C'D'为所求作的四边形.20.分析:(1)根据直角坐标系写出各点的坐标,然后根据关于原点对称的点的特征解答;(2)根据(1)的结论写出点R 的坐标,根据网格构造判断线段AC 与线段MQ 的关系.解:(1)点A (-4,1),点M (4,-1),点B (-1,2),点N (1,-2), 点C (-3,4),点Q (3,-4), 它们分别关于坐标原点对称.(2)点P (-3,2)的对应点R 的坐标为(3,-2),AC ∥MQ 且AC=MQ.BC,求出∠B即可解决21.分析:(1)根据题意证明△OBC为直角三角形,结合OC=12问题.(2)首先证明AC∥OD,结合AC=OD,判断四边形ADOC为平行四边形,根据菱形的定义即可解决问题.解:(1)由题意得OC=OD=BD,∵点D是BC的中点,BC,∴CD=BD,OD=12BC,∴△OBC为直角三角形,而OC=12∴∠B=30°,∠OCD=90°-30°=60°.∵OD=CD,∴∠COD=∠OCD=60°.(2)∵OD=BD,∴∠DOB=∠B=30°,由旋转变换的性质知∠COA=∠CAO=∠B=30°,∴∠AOD=90°-2×30°=30°,∴∠CAO=∠AOD=30°,∴AC∥OD,而AC=OD,∴四边形ADOC为平行四边形,而OC=OD,∴四边形ODAC是菱形.22.分析:(1)根据网格构造找出点A,B,C平移后的对应点A1,B1,C1的位置,然后顺次连接即可;(2)根据网格构造找出点D,E,F绕点O按顺时针方向旋转90°后的对应点D,E1,F1的位置,然后顺次连接即可;1(3)根据轴对称的性质确定出对称轴的位置,然后写出直线解析式即可.解:(1)△A1B1C1如下图.(2)△D1E1F1如下图.(3)△A1B1C1和△D1E1F1组成的图形是轴对称图形,对称轴为直线y=x或y=-x-2.23.分析:将△ABE绕点A逆时针旋转90°至△ADG.首先证明△AFE≌△AFG,进而得到EF=BE+FD,从而将三角形的周长转化为BC+CD的长.解:如下图,将△ABE绕点A逆时针旋转90°至△ADG.∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合, ∴∠BAE=∠DAG,∵∠BAD=90°,∠EAF=45°,∴∠BAE+∠DAF=45°,∴∠EAF=∠FAG,∵∠ADG=∠B=90°,∴∠FDG=180°,点F,D,G共线,在△AFE和△AFG中,{AE=AG,∠EAF=∠FAG, AF=AF,∴△AFE≌△AFG(SAS),∴EF=FG,即EF=BE+DF.∴△EFC的周长=EC+CF+EF=EC+CF+BE+FD=BC+CD=5×2=10.24.分析:(1)可将四边形CHGK分成两局部,然后通过证三角形全等,将四边形的面积进展转换来求解.连接CG,可通过证明三角形CGK与三角形BGH全等来得出它们的面积相等,进而将四边形CHGK的面积转换成三角形CGB的面积也就是三角形ABC面积的一半,由此可得出四边形CHGK的面积是4,所以不会改变;(2)连接HK后,根据(1)中得出的四边形CHGK的面积为4,可根据三角形GHK 的面积=四边形CHGK的面积-三角形CHK的面积来求,假如BH=x,那么根据(1)的结果CK=x,有BC的长为4,那么CH=4-x,由此可得出关于x,y的函数关系式.x的取值范围应该大于零小于4;(3)只需将y=516×8代入(2)的函数式中,可得出x的值,然后判断x是否符合要求即可.解:(1)在上述旋转过程中,BH=CK,四边形CHGK的面积不变.证明:如下图,连接CG,KH,∵△ABC为等腰直角三角形,O(G)为其斜边中点,∴CG=BG,CG⊥AB,∴∠ACG=∠B=45°.∵∠BGH与∠CGK均为旋转角,∠BGH=∠CGK,在△BGH 与△CGK 中,{∠B =∠KCG ,BG =CG ,∠BGH =∠CGK ,∴△BGH ≌△CGK (ASA), ∴BH=CK ,S △BGH =S △CGK .∴S 四边形CHGK =S △CHG +S △CGK =S △CHG +S △BGH =12S △ABC =12×12×4×4=4,即S 四边形CHGK 的面积为4,是一个定值,在旋转过程中没有变化. (2)∵AC=BC=4,BH=x ,∴CH=4-x ,CK=x. 由S △GHK =S 四边形CHGK -S △CHK , 得y=4-12x (4-x ),∴y=12x 2-2x+4. 由0°<α<90°,得0<BH<4,∴0<x<4. (3)存在.根据题意,得12x 2-2x+4=516×8, 解这个方程,得x 1=1,x 2=3,即当x=1或x=3时,△GHK 的面积均等于△ABC 的面积的516.。
人教版九年级数学(上)第二十三章《旋转》检测卷含答案
人教版九年级数学(上)第二十三章《旋转》检测卷(120分钟150分)一、选择题(本大题共10小题,每小题4分,满分40分)1.下列图形,既是轴对称图形,又是中心对称图形的是2.将大写字母E绕点P按顺时针方向旋转90°得到的图形是3.下列说法中,正确的有①平行四边形是中心对称图形;②两个全等三角形一定成中心对称;③中心对称图形的对称中心是连接两对称点的线段的中点;④一个图形若是轴对称图形,则一定不是中心对称图形;⑤一个图形若是中心对称图形,则一定不是轴对称图形.A.1个B.2个C.3个D.4个4.如图,已知点O是六边形ABCDEF的中心,图中所有的三角形都是等边三角形,则下列说法正确的是A.△ODE绕点O顺时针旋转60°得到△OBCB.△ODE绕点O逆时针旋转120°得到△OABC.△ODE绕点F顺时针旋转60°得到△OABD.△ODE绕点C逆时针旋转90°得△OAB5.在直角坐标系中,将点(-2,3)关于原点的对称点向左平移2个单位长度,得到的点的坐标是A.(4,-3)B.(-4,3)C.(0,-3)D.(0,3)6.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,△ABC绕着点B逆时针旋转90°到△A'BC'的位置,则AA'的长为A.10√2B.10C.20D.5√27.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为A.30,2B.60,2D.60,√3C.60,√328.如图,在平面直角坐标系中,将△ABC绕点C(0,1)旋转180°得到△A'B'C,设点A的坐标为(a,b),则点A'的坐标为A.(-a,-b)B.(-a,-b-1)C.(-a,-b+1)D.(-a,-b+2)9.有两个完全重合的直尺,将其中一个始终保持不动,另一个直尺绕其对称中心O按逆时针方向进行旋转,每次均旋转45°,第1次旋转后得到图①,第2次旋转后得到图②,…,则第10次旋转后得到的图形与图①~④中相同的是A.图①B.图②C.图③D.图④10.Rt△ABC中,AB=AC,点D为BC中点.∠MDN=90°,∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点.下列结论:①(BE+CF )=√22BC ;②S △AEF ≤14S △ABC ;③S 四边形AEDF =AD ·EF ;④AD ≥EF ;⑤AD 与EF 可能互相平分,其中正确结论的个数是A.1个B.2个C.3个D.4个二、填空题(本大题共4小题,每小题5分,满分20分)11.已知a<0,则点P (-a 2,-a+1)关于原点的对称点P'在第 四 象限.12.如图所示,把一个直角三角尺ACB 绕着30°角的顶点B 顺时针旋转,使得点A 落在CB 延长线上的点E 处,则∠BDC= 15° .13.如图,在Rt △ABC 中,∠ACB=90°,∠BAC=60°,AB=6,Rt △AB'C'可以看作是由Rt △ABC 绕点A 逆时针方向旋转60°得到的,则线段B'C 的长为 3√7 .14.如图,在Rt △ABC 中,∠ACB=90°,∠A=30°,AC=6√3,BC 的中点为D ,将△ABC 绕点C 顺时针旋转任意一个角度得到△FEC ,EF 的中点为G ,连接DG 在旋转过程中,DG 的最大值是 9 .三、(本大题共2小题,每小题8分,满分16分)15.如图,四边形ABCD绕点O旋转后,顶点A的对应点为点E.试确定旋转后的四边形.解:如图所示,四边形EB'C'D'即为四边形ABCD绕点O旋转后的四边形.AB,请你用旋转的16.如图,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,且AF=12方法说明线段BE和DF之间的关系.AB,∴AE=AF,解:∵四边形ABCD为正方形,∴AD=AB,∠BAD=90°,∵E是AD的中点,AF=12∴△DFA≌△BEA,∴把△ABE绕点A逆时针旋转90°可得到△ADF,∴BE=DF,BE⊥DF.四、(本大题共2小题,每小题8分,满分16分)17.△ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上.(1)作出△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标;(2)作出△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.答案图解:(1)如图,C 1(-3,2). (2)如图,C 2(-3,-2).18.已知点P (x+1,2x-1)关于原点的对称点在第一象限,试化简:|x-3|-|1-x|. 解:∵点P (x+1,2x-1)关于原点的对称点P'的坐标为(-x-1,-2x+1),点P'在第一象限,∴{-x -1>0,-2x +1>0,∴x<-1,∴|x-3|-|1-x|=-x+3-1+x=2.五、(本大题共2小题,每小题10分,满分20分)19.如图,在等边△ABC 中,AC=9,点O 在AC 上,且AO=3,点P 是AB 上的一动点,连接OP ,将线段OP 绕点O 逆时针旋转60°得到线段OD ,要使点D 恰好落在BC 上,求AP 的长. 解:如图,∵AC=9,AO=3,∴OC=6,∵△ABC为等边三角形,∴∠A=∠C=60°,∵线段OP绕点D逆时针旋转60°得到线段OD,要使点D恰好落在BC上,∴OD=OP,∠POD=60°,∵∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,∴∠1+∠2=120°,∠1+∠3=120°,∴∠2=∠3,在△AOP和△CDO中,{∠A=∠C,∠2=∠3, OP=OD,∴△AOP≌△CDO,∴AP=CO=6.20.在平面直角坐标系中,O为原点,B(0,6),A(8,0),以点B为旋转中心把△ABO逆时针旋转,得△A'BO',点O,A旋转后的对应点为O',A',记旋转角为β.(1)如图1,若β=90°,求AA'的长;(2)如图2,若β=120°,求点O'的坐标.解:(1)∵β=90°,∴∠A'BA=90°,∵A(8,0),B(0,6),∴OA=8,OB=6,根据勾股定理得,AB=√OA 2+OB 2=√82+62=10, 由旋转的性质得,A'B=AB=10,在Rt △A'BA 中,根据勾股定理得,AA'=√AB 2+A 'B 2=√102+102=10√2. (2)如图,过点O'作O'C ⊥y 轴于点C , 由旋转的性质得,O'B=OB=6,∵β=120°,∴∠OBO'=120°,∴∠O'BC=180°-120°=60°, ∴BC=12O'B=12×6=3,CO'=√O 'B 2-BC 2=√62-32=3√3,∴OC=OB+BC=6+3=9,∴点O'的坐标为(3√3,9).六、(本题满分12分)21.如图,在等腰△ABC 中,∠CAB=90°,P 是△ABC 内一点,PA=1,PB=3,PC=√7,将△APB 绕点A 逆时针旋转后与△AQC 重合.求: (1)线段PQ 的长; (2)∠APC 的度数.解:(1)∵△APB 绕点A 旋转与△AQC 重合,∴AQ=AP=1,∠QAP=∠CAB=90°, ∴在Rt △APQ 中,PQ=√AQ 2+AP 2=√2.(2)∵∠QAP=90°,AQ=AP,∴∠APQ=45°.∵△APB绕点A旋转与△AQC重合,∴CQ=BP=3.在△CPQ中,PQ=√2,CQ=3,CP=√7,∴CP2+PQ2=CQ2,∴∠CPQ=90°,∴∠APC=∠CPQ+∠APQ=135°.七、(本题满分12分)22.如图,▱ABCD中,AB⊥AC,AB=1,BC=√5,对角线BD,AC交于点O.将直线AC绕点O顺时针旋转分别交BC,AD于点E,F.(1)试说明在旋转过程中,AF与CE总保持相等;(2)证明:当旋转角为90°时,四边形ABEF是平行四边形;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能请说明理由;如果能,求出此时AC绕点O顺时针旋转的角度.解:(1)在▱ABCD中,AD∥BC,OA=OC,∴∠1=∠2,在△AOF和△COE中,{∠1=∠2,OA=OC,∠3=∠4,∴△AOF≌△COE(ASA),∴AF=CE.(2)由题意,∠AOF=90°(如图1),又∵AB ⊥AC ,∴∠BAO=90°,∴∠BAO=∠AOF ,∴AB ∥EF ,∵四边形ABCD 是平行四边形,∴AD ∥BC ,即AF ∥BE , ∵AB ∥EF ,AF ∥BE ,∴四边形ABEF 是平行四边形.(3)当EF ⊥BD 时,四边形BEDF 是菱形(如图2).由(1)知,AF=CE ,∵▱ABCD ,∴AD=BC ,AD ∥BC ,∴DF ∥BE ,DF=BE ,∴四边形BEDF 是平行四边形,又∵EF ⊥BD ,∴▱BEDF 是菱形,∵AB ⊥AC ,∴在△ABC 中,∠BAC=90°,∴BC 2=AB 2+AC 2, ∵AB=1,BC=√5,∴AC=√BC 2-AB 2=√(√5)2-12=2, ∵四边形ABCD 是平行四边形,∴OA=12AC=12×2=1, ∵在△AOB 中,AB=AO=1,∠BAO=90°, ∴∠1=45°,∵EF ⊥BD ,∴∠BOF=90°,∴∠2=∠BOF-∠1=90°-45°=45°,即旋转角为45°. 八、(本题满分14分)23.如图1,在正方形ABCD 中,点M ,N 分别在AD ,CD 上,若∠MBN=45°,易证MN=AM+CN. (1)如图2,在梯形ABCD 中,BC ∥AD ,AB=BC=CD ,点M ,N 分别在AD ,CD 上,若∠MBN=12∠ABC ,试探究线段MN ,AM ,CN 有怎样的数量关系?请写出猜想,并给予证明.(2)如图3,在四边形ABCD 中,AB=BC ,∠ABC+∠ADC=180°,点M ,N 分别在DA ,CD 的延长线上,若∠MBN=12∠ABC ,试探究线段MN ,AM ,CN 又有怎样的数量关系?请直接写出猜想,不需证明.解:(1)MN=AM+CN.理由如下:如图2,∵BC ∥AD ,AB=BC=CD ,∴梯形ABCD 是等腰梯形,∴∠A+∠BCD=180°,把△ABM 绕点B 顺时针旋转使AB 边与BC 边重合,则△ABM ≌△CBM',∴AM=CM',BM=BM',∠A=∠BCM',∠ABM=∠M'BC ,∴∠BCM'+∠BCD=180°,∴点M',C ,N 三点共线,∵∠MBN=12∠ABC ,∴∠M'BN=∠M'BC+∠CBN=∠ABM+∠CBN=∠ABC-∠MBN=12∠ABC ,∴∠MBN=∠M'BN ,在△BMN 和△BM'N 中,{BM =BM ',∠MBN =∠M 'BN ,BN =BN , ∴△BMN ≌△BM'N (SAS),∴MN=M'N ,又∵M'N=CM'+CN=AM+CN ,∴MN=AM+CN.(2)MN=CN-AM.。
新人教版九年级数学上册《第23章旋转》测试(含答案)
新人教版九年级数学上册《第23章旋转》一、选择题1.下面所列图形中是中心对称图形的为()A.B.C.D.2.以如图的右边缘所在直线为轴将该图案向右翻折后,再绕中心旋转180°,所得到的图形是()A.B.C.D.3.用数学的方式理解“当窗理云鬓,对镜贴花黄”和“坐地日行八万里”(只考虑地球的自转),其中蕴含的图形运动是()A.平移和旋转B.对称和旋转C.对称和平移D.旋转和平移4.已知点A(a,2013)与点A′(﹣2014,b)是关于原点O的对称点,则a+b 的值为()A.1 B.5 C.6 D.45.在平面直角坐标系中,若点P(m,m﹣n)与点Q(﹣2,3)关于原点对称,则点M(m,n)在()A.第一象限B.第二象限C.第三象限D.第四象限6.如图是一个标准的五角星,若将它绕旋转中心旋转一定角度后能与自身重合,则至少应将它旋转的度数是()A.60°B.72°C.90°D.144°7.如图,将△OAB绕点O逆时针旋转80°,得到△OCD,若∠A=2∠D=100°,则∠α的度数是()A.50°B.60°C.40°D.30°8.在平面直角坐标系xOy中,A点坐标为(3,4),将OA绕原点O顺时针旋转180°得到OA′,则点A′的坐标是()A.(﹣4,3)B.(﹣3,﹣4)C.(﹣4,﹣3)D.(﹣3,4)9.如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点B、A、B1在同一条直线上,那么旋转角等于()A.30°B.60°C.90°D.180°10.如图,在△ABC中,∠ACB=90°,将△ABC绕点A顺时针旋转90°,得到△ADE,连接BD,若AC=3,DE=1,则线段BD的长为()A.2 B.2 C.4 D.2二、填空题11.把汉字“目”绕其中心旋转90°后,所得图形与汉字相似.12.如图,把Rt△ABC绕点A逆时针旋转44°,得到Rt△AB′C′,点C′恰好落在边AB上,连接BB′,则∠BB′C′=.13.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x 轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(,0),B(0,2),则点B2016的坐标为.14.如图,直线y=﹣x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A 顺时针旋转60°后得到△AO′B′,则点B′的坐标是.15.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是.16.在等腰三角形ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B′处,则BB′的长度为.三、解答题17.如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来图形重合?18.将如图所示的图形面积分成相等的两部分.19.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.20.如图,已知AD=AE,AB=AC.(1)求证:∠B=∠C;(2)若∠A=50°,问△ADC经过怎样的变换能与△AEB重合?21.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴,垂足为A.(1)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;(2)△O′A′B′与△OAB关于原点对称,写出点B′、A′的坐标.22.当m为何值时(1)点A(2,3m)关于原点的对称点在第三象限;(2)点B(3m﹣1,0.5m+2)到x轴的距离等于它到y轴距离的一半?23.直角坐标系中,已知点P(﹣2,﹣1),点T(t,0)是x轴上的一个动点.(1)求点P关于原点的对称点P′的坐标;(2)当t取何值时,△P′TO是等腰三角形?24.等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.(1)求出点B的坐标;(2)当A1与B1的纵坐标相同时,求出a的值;(3)在(2)的条件下直接写出点B1的坐标.新人教版九年级数学上册《第23章旋转》一、选择题1.C;2.A;3.B;4.A;5.A;6.B;7.A;8.B;9.D;10.A;二、填空题11.四;12.22°;13.(6048,2);14.(2,4);15.90°;16.2cm;三、解答题17.如图,说出这个图形的旋转中心,它绕旋转中心至少旋转多大角度才能与原来图形重合?解:这个图形的旋转中心为圆心;∵360°÷6=60°,∴该图形绕中心至少旋转60度后能和原来的图案互相重合.18.将如图所示的图形面积分成相等的两部分.解:由平行四边形的对称性可知当直线过对角线的交点时,可把平行四边形分成面积相等的两部分,当直线过圆心时,把圆的面积分成相等的两部分,∴当直线过平行四边形的对角线的交点和圆的圆心时即可把图形分成面积相等的两部分,如图所示.19.在艺术字中,有些汉字或字母是中心对称图形.下面的汉字或字母,是中心对称图形吗?如果是,请标出它们的对称中心.解:这些艺术字均为中心对称图形,其对称中心为图形中的点O.20.如图,已知AD=AE,AB=AC.(1)求证:∠B=∠C;(2)若∠A=50°,问△ADC经过怎样的变换能与△AEB重合?(1)证明:在△AEB与△ADC中,AB=AC,∠A=∠A,AE=AD;∴△AEB≌△ADC,∴∠B=∠C.(2)解:先将△ADC绕点A逆时针旋转50°,再将△ADC沿直线AE对折,即可得△ADC与△AEB重合.或先将△ADC绕点A顺时针旋转50°,再将△ADC沿直线AB对折,即可得△ADC与△AEB重合.21.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴,垂足为A.(1)将点B绕原点逆时针方向旋转90°后记作点C,求点C的坐标;(2)△O′A′B′与△OAB关于原点对称,写出点B′、A′的坐标.解:(1)如图,点C的坐标为(﹣2,4);(2)点B′、A′的坐标分别为(﹣4,﹣2)、(﹣4,0).22.当m为何值时(1)点A(2,3m)关于原点的对称点在第三象限;(2)点B(3m﹣1,0.5m+2)到x轴的距离等于它到y轴距离的一半?解:(1)∵点A(2,3m),∴关于原点的对称点坐标为(﹣2,﹣3m),∵在第三象限,∴﹣3m<0,∴m>0;(2)由题意得:①0.5m+2=(3m﹣1),解得:m=;②0.5m+2=﹣(3m﹣1),解得:m=﹣.23.直角坐标系中,已知点P(﹣2,﹣1),点T(t,0)是x轴上的一个动点.(1)求点P关于原点的对称点P′的坐标;(2)当t取何值时,△P′TO是等腰三角形?解:(1)点P关于原点的对称点P'的坐标为(2,1);(2),(a)动点T在原点左侧,当时,△P'TO是等腰三角形,∴点,(b)动点T在原点右侧,①当T2O=T2P'时,△P'TO是等腰三角形,得:,②当T3O=P'O时,△P'TO是等腰三角形,得:点,③当T4P'=P'O时,△P'TO是等腰三角形,得:点T4(4,0).综上所述,符合条件的t的值为.24.等边△OAB在平面直角坐标系中,已知点A(2,0),将△OAB绕点O顺时针方向旋转a°(0<a<360)得△OA1B1.(1)求出点B的坐标;(2)当A1与B1的纵坐标相同时,求出a的值;(3)在(2)的条件下直接写出点B1的坐标.解:(1)如图1所示过点B作BC⊥OA,垂足为C.∵△OAB为等边三角形,∴∠BOC=60°,OB=BA.∵OB=AB,BC⊥OA,∴OC=CA=1.在Rt△OBC中,,∴BC=.∴点B的坐标为(1,).(2)如图2所示:∵点B1与点A1的纵坐标相同,∴A1B1∥OA.①如图2所示:当a=300°时,点A1与点B1纵坐标相同.如图3所示:当a=120°时,点A1与点B1纵坐标相同.∴当a=120°或a=300°时,点A1与点B1纵坐标相同.(3)如图2所示:由旋转的性质可知A1B1=AB=2,点B的坐标为(1,2),∴点B1的坐标为(﹣1,).如图3所示:由旋转的性质可知:点B1的坐标为(1,﹣).∴点B1的坐标为(﹣1,)或(1,﹣).第11页(共11页)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九年级(上) 第23章 旋转 水平测试题
一、精心选一选 (每小题3分,共30分)
1.(2008年广东湛江市) 下面的图形中,是中心对称图形的是 ( )
A .
B .
C .
D .
2.平面直角坐标系内一点P (-2,3)关于原点对称的点的坐标是 ( )
A .(3,-2)
B . (2,3)
C .(-2,-3)
D . (2,-3)
3.3张扑克牌如图1所示放在桌子上,小敏把其中一张旋转180º后得到如图(2)所示,则她所旋转的牌从左数起是 ( )
A .第一张
B .第二张
C .第三张
D .第四张
4.在下图右侧的四个三角形中,不能由△ABC 经过旋转或平移得到的是( )
5.如图3的方格纸中,左边图形到右边图形的变换是( )
A .向右平移7格
B .以AB 的垂直平分线为对称轴作轴对称,再以AB 为对称轴作轴对称
A B C
A B C D
C.绕AB的中点旋转1800,再以AB为对称轴作轴对称
D.以AB为对称轴作轴对称,再向右平移7格
6.从数学上对称的角度看,下面几组大写英文字母中,不同于另外三组的一组是()A.A N E G B.K B X N
C.X I H O D.Z D W H
7.如图4,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形
对数有( ).
A.1对B.2对C.3对D.4对
8.下列这些复杂的图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们中每一个图案都可以由一个“基本图案”通过连续旋转得来,旋转的角度是()
A ︒
30 B ︒
45 C ︒
60 D ︒
90
9.如图5所示,图中的一个矩形是另一个矩形顺时针方向旋转90°后形成的个数是()A.l个B.2个
C.3个 D.4个
10.如图6,ΔABC和ΔADE都是等腰直角三角形,∠C和∠ADE
都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能
够与ΔADE重合得到图7,再将图23—A—4作为“基本图形”绕
着A点经过逆时针连续旋转得到图7.两次旋转的角度分别为()
图
6
图
7
A .45°,90°
B .90°,45°
C .60°,30°
D .30°,60
二、耐心填一填(每小题3分,共24分)
11.关于中心对称的两个图形,对称点所连线段都经过 ,而且被_____________平分.
12.在平行四边形、矩形、菱形、正方形、等腰梯形这五种图形中,既是轴对称图形,又是中心对称图形的是_____________.
13.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的旋转角是_____________.
14.如图8,△ABC 以点A 为旋转中心,按逆时针方向旋转60°,得△AB ′C ′,则△ABB ′是 三角形.
15.已知a<0,则点P(a2,-a+3)关于原点的对称点P1在第___象限
16.如图9,△COD 是△AOB 绕点O 顺时针方向旋转40°后所得的图形,点C 恰好在AB 上,∠AOD =90°,则∠D 的度数是 .
17.如图10,在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆的半径为2,则图中阴影部分的面积是___.
18.如图,四边形ABCD 中,∠BAD=∠C=90º,AB=AD ,AE ⊥BC 于E ,若线段AE=5,则S 四边形ABCD = 。
三、细心解一解(共46分)
19.(6分)如图12,四边形ABCD 的∠BAD=∠C=90º,AB=AD,AE ⊥BC 于E,BEA ∆旋转后能与DFA ∆重合。
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)如果点A 是旋转中心,那么点B 经过旋转后,点B 旋转到什么位置?
20.(4分)如图13,请画出ABC ∆关于点O 点为对称中心的对称图形
21.(6分)如图14,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,ABC △的顶点均在格点上,点C 的坐标为(41)-,
.
O D C
B
A
E D B
A
①把ABC △向上平移5个单位后得到对应的111A B C △,画出111A B C △,并写出1C 的坐标; ②以原点O 为对称中心,再画出与111A B C △关于原点O 对称的222A B C △,并写出点2C 的坐标.
22.(4分)如图15,方格中有一条美丽可爱的小金鱼.
(1)若方格的边长为1,则小鱼的面积为 .
(2)画出小鱼向左平移3格后的图形(不要求写作图步骤和过程).
23.(6分)如图16,E 、F 分别是正方形ABCD 的边CD 、DA 上一点,且CE +AF =EF ,请你用旋转的方法求∠EBF 的大小.
24.(6分)如图17所示是一种花瓣图案,它可以看作是一个什么“基本图案”形成的,试用两种方法分析其形成过程.
25.(6分) 已知正方形ABCD 和正方形AEFG 有一个公共点A,点G 、E 分别在线段AD 、AB 上.
(1) 如图18, 连接DF 、BF,若将正方形AEFG 绕点A 按顺时针方向旋转,判断命题:“在旋转的过程中线段DF 与BF 的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明
;
(2) 若将正方形AEFG 绕点A 按顺时针方向旋转, 连接DG,在旋转的过程中,你能否找到一条线段的长与线段DG 的长始终相等.并以图19为例说明理由.
26.(8分)(2008年山西省太原市)将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片ABC △和DEF △.将这两张三角形胶片的顶点B 与顶点E 重合,把DEF △绕点B 顺时针方向旋转,这时AC 与DF 相交于点O .
(1)当D E F △旋转至如图②位置,点()B E ,C D ,在同一直线上时,AFD ∠与DCA ∠的数量关系是 . 2分
(2)当DEF △继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接BO AD ,,探索BO 与AD 之间有怎样的位置关系,并证明.
C A E F B C
D O A F B (
E ) A D O
F C B (E ) 图① 图② 图③
答案
一、精心选一选:
1.D
2.D
3.A
4.B
5.D
6.c
7.C
8.C
9.B
10.A.
二、耐心填一填
11.对称中心,对称中心
12.矩形、菱形、正方形
13.90º
14.等边
15.三
16.60°
17.2π
18.25
三、细心解一解
19.(1)点A, (2)90º,(3)点D
20.略
21.解:①1(44)C ,
; ②
2(44)C --,
如图:
22.解:(1)16
(2)
23.解:将△BCE 以B 为旋转中心,逆时针旋转90º,使BC 落在BA 边上,得△BAM ,则∠MBE=90º,AM=CE,BM=BE,因为CE +AF =EF ,所以MF =EF ,又BF=BF,所以△FBM ≌△FBE,所以∠MBF=∠EBF, 所以∠EBF=0045902
1=⨯ 24.解:方法一:可看作整个花瓣的六分之一部分,图案为
绕中心O 依次旋转
60°、120°、180°、240°、300°而得到整个图案. 方法二:可看作是绕中心O 依次旋转60°、120°得到整个图案的.
方法三:可看作整个花瓣的一半绕中心O 旋转180°得到的,也可看作是花瓣的一半.经过轴对称得到的
25.解:(1)不相等,用图19即可说明;
(2)BE=DG 。
理由:连接BE ,在△ADG 和△ABE 中,∵AD=AB ,∠DAG=
∠BAE ,AG=AE ,∴ADG ≌ABE (SAS ),∴BE=DG 。
26.【解】(1)AFD DCA ∠=∠(或相等)
(2)AFD DCA ∠=∠(或成立),理由如下:
由ABC DEF △≌△,得
AB DE BC EF ==,(或BF EC =),A B C D E F B A C E D F ∠=∠∠=∠
,.
ABC FBC DEF CBF ∴∠-∠=∠-∠,ABF DEC ∴∠=∠.
在ABF △和DEC △中,AB DE ABF DEC BF EC =⎧⎪∠=∠⎨⎪=⎩,,,
ABF DEC BAF EDC ∴∠=∠△≌△,.
BAC BAF EDF EDC FAC CDF ∴∠-∠=∠-∠∠=∠,.
AOD FAC AFD CDF DCA ∠=∠+∠=∠+∠,
AFD DCA ∴∠=∠.
(3)如图,BO AD ⊥.
由ABC DEF △≌△,点B 与点E 重合,
得BAC BDF BA BD ∠=∠=,.
∴点B 在AD 的垂直平分线上,
且BAD BDA ∠=∠.
OAD BAD BAC ∠=∠-∠,
ODA BDA BDF ∠=∠-∠,
OAD ODA ∴∠=∠.
OA OD ∴=,点O 在AD 的垂直平分线上.
∴直线BO 是AD 的垂直平分线,BO AD ⊥.
A D O F C
B (E ) G。
