自然坐标相对运动讲解
合集下载
自然坐标系

t)
-
et
(t)
当: t 0 , 0
et
t
t
O Δ P2
s
et t
有 det et d d
P1
方向
det
et
d et d
d t dt
即en方向
en
et
t
t
et
et
t
4
d ds
at
dv dt
c
an
v2 R
(b ct)2 R
(2) at an
解得 t b R cc
12
§1-3 相对运动
一 时间与空间
在两个作相对运动的参考系中,时间 的测量是绝对的,空间的测量也是绝对的, 与参考系无关.
时间和长度的的绝对性是经典力学或 牛顿力学的基础.
13
二 相对运动
o
at
0.4
M at
a
x
11
例5 一质点沿半径为R的圆周运动,其路程s随时
间t 的变化规律为 s bt 1 ct 2,式中b,c为大于
零的常数,且 b2 Rc 。求(2 1)质点的切向加速
度和法向加速度。(2)经过多长时间,切向加速
度等于法向加速度。
解: (1)
v ds b ct dt
解: 按题意作矢量图
y
v v0 v
v v0 tan 60 10 tan 60m s1
17.3 m s1
y´ x´
v0
v
速度:
v
运动学自然坐标系

υ0
,
2 0
kx2
x 0 (舍去)
k
k
a
dv dt
kR
法向加速度
v2 an R
(kRt )2 k 2Rt 2 R
加速度 a
a 2
a
2 n
kR 2 k 2Rt 2 2
三.圆周运动(circular motion )的角量描述
线量: r r v a
B
A
1. 角量
θ
0
x
半径R 不变,质点位置可
1αt 2
2
ω2 ω022α(θθ0)
对比匀变速率直线运动:
x x0 v t
x
x0
v0t
1 2
at 2
v v0 at
2
2 0
2a( x
x0 )
1.4 两类运动学问题
运动方程是运动学问题的核心
第一类: 已知质点的运动方程,求质点在任 (求导问题) 一时刻的位矢、速度和加速度;
这类问题要应用积分的方法来求,在计算上较为 复杂一些。
dv adt ,
vv0 dv
t adt
t0
dr vdt ,
rr0dr
t vdt
t0
r(t) 求导 vv(t) 求导 a(t)
积分
积分
质点在三维空间运动时,位矢、位移、速度、 加速度是三维矢量;在平面上运动时,是二维矢量; 沿直线运动时,是一维矢量,此时可以取轨道直线 为坐标轴,规定原点和坐标轴的正方向后,可用正 负号表示这些物理量的方向。
相对运动

问题:
牛顿定律的几点说明 1. 牛顿定律只适用于惯性系 2.牛顿第二定律只适用于质点或可看作质点的物体 2.牛顿第二定律只适用于质点或可看作质点的物体
v v 中 v 是物体所受合外力 3. F = ma F 是物体所受合外力
v v 体的质量保持不变时才和 F = ma 等价 r r r d(mv ) r dv r r =m F= = ma d p = F dt dt dt
2.电磁力 2.电磁力
N m /kg
2
2
电磁力: 电磁力 : 存在于静止电荷之间的电性力以及存在 于运动电荷之间的磁性力,总称为电磁力。 于运动电荷之间的磁性力,总称为电磁力。 例如: 弹力、 摩擦力, 气体的压力、 浮力、 例如 : 弹力 、 摩擦力 , 气体的压力 、 浮力 、 粘滞 阻力。 阻力。 3.强力 3.强力 4.弱力 4.弱力
三、牛顿第三定律
对于每一个作用力,总有一个对应的反作用力; 对于每一个作用力,总有一个对应的反作用力; 两者大小相等、方向相反、在同一直线上。 两者大小相等、方向相反、在同一直线上。 数学表达式: 数学表达式:
r r F12 = F21
注意:1.作用力与反作用力同生同灭。 注意:1.作用力与反作用力同生同灭。 :1.作用力与反作用力同生同灭 2.作用力与反作用力分别作用于两个不同的 2.作用力与反作用力分别作用于两个不同的 物体上 3.作用力与反作用力性质相同。 3.作用力与反作用力性质相同。 作用力与反作用力性质相同
v
x
二、常见力
1.重力 1.重力(gravity) 重力 重力:在地球表面的物体, 重力 : 在地球表面的物体 , 受到地球的吸引而使物 体受到的力。 体受到的力。
r r G = mg
牛顿定律的几点说明 1. 牛顿定律只适用于惯性系 2.牛顿第二定律只适用于质点或可看作质点的物体 2.牛顿第二定律只适用于质点或可看作质点的物体
v v 中 v 是物体所受合外力 3. F = ma F 是物体所受合外力
v v 体的质量保持不变时才和 F = ma 等价 r r r d(mv ) r dv r r =m F= = ma d p = F dt dt dt
2.电磁力 2.电磁力
N m /kg
2
2
电磁力: 电磁力 : 存在于静止电荷之间的电性力以及存在 于运动电荷之间的磁性力,总称为电磁力。 于运动电荷之间的磁性力,总称为电磁力。 例如: 弹力、 摩擦力, 气体的压力、 浮力、 例如 : 弹力 、 摩擦力 , 气体的压力 、 浮力 、 粘滞 阻力。 阻力。 3.强力 3.强力 4.弱力 4.弱力
三、牛顿第三定律
对于每一个作用力,总有一个对应的反作用力; 对于每一个作用力,总有一个对应的反作用力; 两者大小相等、方向相反、在同一直线上。 两者大小相等、方向相反、在同一直线上。 数学表达式: 数学表达式:
r r F12 = F21
注意:1.作用力与反作用力同生同灭。 注意:1.作用力与反作用力同生同灭。 :1.作用力与反作用力同生同灭 2.作用力与反作用力分别作用于两个不同的 2.作用力与反作用力分别作用于两个不同的 物体上 3.作用力与反作用力性质相同。 3.作用力与反作用力性质相同。 作用力与反作用力性质相同
v
x
二、常见力
1.重力 1.重力(gravity) 重力 重力:在地球表面的物体, 重力 : 在地球表面的物体 , 受到地球的吸引而使物 体受到的力。 体受到的力。
r r G = mg
§1-4 相对运动

3. 加速度变换
将伽利略速度变换对时间求一次导数
考虑到 t t 伽利略加速度变换
aPK aPK aKK
ax ay
ax ay
az
az
若 aKK 0
则 aPK aPK
例:某人骑摩托车向东前进,其速率为10ms-1时 觉得有南风,当其速率为15ms-1时,又觉得 有东南风,试求风速度。
O 风速的方向:
X (东)
v 102 52
11.2(m / s)
arctg 5 2634
10 为东偏北2634'
例 一升降机以加速度 1.22 m/s2 上升,当一上升
速度为2.44m/s时,有一螺母自升降机的天花 板松落,天花板与升降机的底板相距 2.74m。 计算螺母自天花板落到底板所需的时间及螺 母相对于升降机外固定柱的下降距离。
r xi y j zk
P(x, y, z)
r r
r xi y j zk
o R o' x' x
z z'
r r R 成立的条件:
且 t t
绝对时空观!
绝对时空观
r r R r vt
t t
P(或P)在 K在 系
和 K系的空间坐 标、时间坐标的 对应关系为:
t 2h 0.71 s ga
s
v0t
1 2
a螺地t 2
0.74(m)
§1-4 相对运动
太阳、地球、月球系统
相对运动
运动是绝对的,运动的描述具有相对性。在不 同参考系中研究同一物体的运动状态会完全不同。
7自然坐标系

University ຫໍສະໝຸດ hysics三. 角加速度(描述质点转动角速度变化快
慢的物理量)
o
t : t t :
r
P
lim
(t t ) (t )
dt
角加速度的方向与 dω 的方向相同
t 0
d d 2 k k 2 k dt dt
aτ
aτ
思考 求抛体运动过程中的曲率半径? 对B 点
a
y
2 2 2
aτ 0, an g , v B v 0cos
vo
B
vB (v 0cos ) xm ρ B an g 8 ym
o
C x
Xu Zhongfeng, Xi’an Jiaotong University, 2010
法向加速度
Xu Zhongfeng, Xi’an Jiaotong University, 2010
University Physics
2 2 v d v d s ds 2 1 a an n aτ τ n τ 2 τ ( ) n dt dt dt 2 v 对匀速率圆周运动 a 0 an an n n r 加速度的正交分解 a an n aτ τ Pv • a an a aτ 2 an 2 , tg n
两类问题(圆周运动的角量描述) 1. 第一类问题 已知运动学方程, (t ) 求 ,
P
aτ v
d ω k dt
d d d 2 k 2 k dt dt dt
Xu Zhongfeng, Xi’an Jiaotong University, 2010
自然坐标系-相对运动
1.3
自然坐标系
第一章 运动的描述
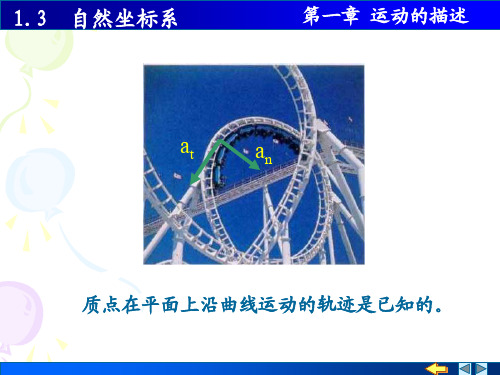
at
an
质点在平面上沿曲线运动的轨迹是已知的。
1.3
自然坐标系
第一章 运动的描述
一、自然坐标系
在已知质点轨迹的情况下,可以选取轨道上任一点O为原 点,并规定正方向,这样可用轨道长度S(t)来描述质点的位 置,这种顺着已知轨道建立起来的坐标系,为自然坐标系。 •切向单位矢量 沿运动轨迹 的切线方向, 正方向与运动方 向一致。
切向加速度 a r
图1-1-11
1.3
自然坐标系
第一章 运动的描述
4.角量与线量的关系
既然作圆周运动的质点的运动既可用线量描述,也可用 角量描述,那么它们间必存在一定的关系。
线量 ds Rd 角量
ds v dt
v2 an R
B
R
s A
X
d R R dt
为运动轨迹的曲率半径。 a 由于速度大小变化产生的加速度; an 由于速度方向变化产生的加速度。 大小
dt
a a a
2
2 n
加速度和速度的夹角
v dv dt an arctg a
2
2
2
1.3
自然坐标系
第一章 运动的描述
1.3
自然坐标系
第一章 运动的描述
例 4 :一物体由静止出发,作半径为 R 的圆周 运动,切向加速度的大小为一常数 a 。 试问:( 1 )经多少 时间 t ,它的总加速 度恰与半径 R 的夹角 为 ; ( 2 )在上述时间内 物体所经过的路程 的s是多少?
图1-1-13
解答见大学物理学习指导与习题解答P17
自然坐标系
第一章 运动的描述
at
an
质点在平面上沿曲线运动的轨迹是已知的。
1.3
自然坐标系
第一章 运动的描述
一、自然坐标系
在已知质点轨迹的情况下,可以选取轨道上任一点O为原 点,并规定正方向,这样可用轨道长度S(t)来描述质点的位 置,这种顺着已知轨道建立起来的坐标系,为自然坐标系。 •切向单位矢量 沿运动轨迹 的切线方向, 正方向与运动方 向一致。
切向加速度 a r
图1-1-11
1.3
自然坐标系
第一章 运动的描述
4.角量与线量的关系
既然作圆周运动的质点的运动既可用线量描述,也可用 角量描述,那么它们间必存在一定的关系。
线量 ds Rd 角量
ds v dt
v2 an R
B
R
s A
X
d R R dt
为运动轨迹的曲率半径。 a 由于速度大小变化产生的加速度; an 由于速度方向变化产生的加速度。 大小
dt
a a a
2
2 n
加速度和速度的夹角
v dv dt an arctg a
2
2
2
1.3
自然坐标系
第一章 运动的描述
1.3
自然坐标系
第一章 运动的描述
例 4 :一物体由静止出发,作半径为 R 的圆周 运动,切向加速度的大小为一常数 a 。 试问:( 1 )经多少 时间 t ,它的总加速 度恰与半径 R 的夹角 为 ; ( 2 )在上述时间内 物体所经过的路程 的s是多少?
图1-1-13
解答见大学物理学习指导与习题解答P17
自然坐标圆周运动相对运动

《关于两门新科学的对话和数学证明对话集》 一书,总结了他的科学思想以及在物理学和天文学 方面的研究成果。
伽利略所取得的巨大成就,开创了近代物理学 的新纪元。
自然坐标、圆周运动、角量描述、相对运动
3、绝对运动、牵连运动、相对运动
(1)位矢的关系
r
r'
质点P在相对作匀速直线运动
的两个坐标系中的移动 y y' u
自然坐标、圆周运动、角量描述、相对运动
2、相对运动
物体运动的轨迹依赖于观察者所处的参考系
自然坐标、圆周运动、角量描述、相对运动
伽利略(Galileo Galilei,1564—1642)
伽利略杰出的意大利物理学家和 天文学家,实验物理学的先驱者。
他提出著名的相对性原理、惯性 原理、抛体的运动定律、摆振动的等 时性等。
2
1 x2g
y 2
v02
y
an
a
g
自然坐标、圆周运动、角量描述、相对运动
(2)
o v0
x
vx v0, vy gt
an
a
y
v
vx2 vy2
v02 g 2t 2
tan 1
gt v0
a
dv dt
g2t v02 g2t2
an g2 a 2
g
v0 g v02 g2t 2
与速度同向
与切向加速度垂直
总结:自然坐标
v v
a a an a ann
a
a
an
切向加速度
法向加速度
反映速度大小变 化的快慢
反映速度方向变 化的快慢程度
dv a dt
an
v2
aa
a 2 an 2
伽利略所取得的巨大成就,开创了近代物理学 的新纪元。
自然坐标、圆周运动、角量描述、相对运动
3、绝对运动、牵连运动、相对运动
(1)位矢的关系
r
r'
质点P在相对作匀速直线运动
的两个坐标系中的移动 y y' u
自然坐标、圆周运动、角量描述、相对运动
2、相对运动
物体运动的轨迹依赖于观察者所处的参考系
自然坐标、圆周运动、角量描述、相对运动
伽利略(Galileo Galilei,1564—1642)
伽利略杰出的意大利物理学家和 天文学家,实验物理学的先驱者。
他提出著名的相对性原理、惯性 原理、抛体的运动定律、摆振动的等 时性等。
2
1 x2g
y 2
v02
y
an
a
g
自然坐标、圆周运动、角量描述、相对运动
(2)
o v0
x
vx v0, vy gt
an
a
y
v
vx2 vy2
v02 g 2t 2
tan 1
gt v0
a
dv dt
g2t v02 g2t2
an g2 a 2
g
v0 g v02 g2t 2
与速度同向
与切向加速度垂直
总结:自然坐标
v v
a a an a ann
a
a
an
切向加速度
法向加速度
反映速度大小变 化的快慢
反映速度方向变 化的快慢程度
dv a dt
an
v2
aa
a 2 an 2
01-2自然坐标系中的描述及相对运动

a
r an
B
vB v A 2 a 23.3m s t 第二讲 自然坐标系:切向加速度和法向加速度、相对运动
o
a
at
dv a dt
vB
分离变量有
vB
vA
dv a dt
0
t
在点 B 的法向加速度
A
an
2 vB
vA
B
r
2
106m s
dr ds v dt dt
p v s p
s o
n
ds v v dt
第二讲 自然坐标系:切向加速度和法向加速度、相对运动
4. 加速度
v 1 A n B
v1 A:
C
v2
F v1 O v n v v2 D v E
(1) a 0 匀速率运动; a 0 变速率运动
(2) an 0 直线运动; an
0
曲线运动
第二讲 自然坐标系:切向加速度和法向加速度、相对运动
例1.由楼窗口以水平初速度v0射出一发子弹,取枪 口为原点,沿v0为x轴,竖直向下为y轴,并取发射 时t=0.试求: (1)子弹在任一时刻t的位置坐标及轨道方程; (2)子弹在t时刻的速度,切向加速度和法向加速度。
解:(1) x v0 t
2
1 2 y gt 2
o
v0
x
1 x g y 2 2 v0
an
y g
a
第二讲 自然坐标系:切向加速度和法向加速度、相对运动
(2) v x v0 , v y gt
o
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
船在江中 向北的航速
绝 船对岸
相 船对水
牵 水对岸
28
例
北
地看雨
南 21.6º
车看雨垂直
88.2 m/s
雨对地
雨对车 车对地
车对地
雨对地 雨对车
雨对地
88. 2 21.6 º
239. 6 m ·s –1
车对地
29
人骑车以速率
向正西行驶
遇到从北向南刮的风 , 速率也是
人感到风 从 什么方向吹来
人对地 风对人 风对人 人对地
2 2
2 v 2 2 a ax ay 2R R
r (R cost )i (R sin t ) j
a ( R cost )i ( R sin t ) j r
2
11
自然坐标系描述:
圆周运动中 s R ,则
y v2 R
o
v1
2 2
解:
y
vo
o
o
x
x
v v0 cos 0 g g
2
2
13
汽车在半径为 R = 200m 的圆弧形公路上 行驶,运动方程为S = 20t - 0.2t2[SI], 试求 汽车在t=5s时的速度和加速度。
解:
ds v 20 0.4t dt
dv a 0.4 dt
在相对作匀速直线运动的参考系中,同一质 点的加速度相同。 22
讨论 空间的绝对性:长度的测量不依赖于参考系” 时间的绝对性:时间的测量不依赖于参考系 绝对时空观: 对于不同的参考系,长度和 时间的测量结果是相同的。 在低速(远低于真空光速)运动情况下,绝 对时空观符合实验结果。
23
伽利略变换是线性的-时空的性质 伽利略变换只适用于低速情况。高速情况 (u ~ c)必须用洛仑兹(Lorentz)变换: 时间的测量依赖于参考系 长度的测量也依赖于参考系 不同参考系中的矢量不能再按平行四边形 法则叠加!
d 曲率半径愈大则曲线的弯曲程度愈小。
轨迹上任一点的弯曲程度不同, ds 引入曲率半径的概念:
A
ds
.
d
4
加速度的表达式:
d 2s ds 2 1 a ( ) n 2 dt dt d 2 n dt
故切向加速度和法向加速度分别为: d 2 a , an dt
头 速度关系: PS 尾
PS uSS
u
称为绝对速度(adsolute velocity)
称为相对速度(relative velocity)
称为牵连速度(convected velocity)
20
PS PS uSS
称为伽利略速度变换 人只在
例 可用速度关系解释:雨天骑车 胸前铺一块塑料布即可遮雨
3
由右图可知: d d 1d
d 方向与 n
1
A
B d d
1
一致,故有:
d d d 1d n n dt dt
代入加速度公式,有:
d n n
2
d 2 s ds d d 2 s ds ds d a 2 n 2 n dt dt dt dt dt dt ds
两组单位矢量 n i jk 与
a
o
an
o
?
的区别是什么?
6
r xi yj ( m ) r xi yj zk (m)
v an R
2
注意:容易出错的地方
a an at
a a a
2 n 2 t
a an at
16
运动的描述是相对的 本节将给出:
同一物体在不同参考系中各自测量的状态量
之间的定量关系
平动速度为u
设参考系S'相对参考系S平动
17
坐标系如图
y S系
S'系 u
y
r
o
r
o
P
x
x
研究的问题是:t 时刻质点运动到P点
S系描述的物理量是: r a S'系描述的物理量是: r a
x
ds d d v ( R ) R R dt dt dt
式中 有:
d dt
是 随时间的变化率,称为角速度
2 2
dv d v ( R ) 2 an R a R R dt dt
12
求抛体轨道顶点的曲率半径.
v v0 cos 0 an g
ds 就是切向单位矢量 的方向,故 . dt dν 对加速度: a dt 将速度的表达式代入,得:
ds dt
2 d d ds d s ds d a ( ) 2 dt dt dt dt dt dt
此处的 d 是什么呢? dt
自然坐标系:
• 如果质点是被约束在已知的轨道上,则可采 用“自然坐标系”。 • 所谓“自然”,意即“顺其自然”,把轨道 当作坐标的“轴”。
质点的坐标是代表路程, 质点的运动方向规定为轨道切线的正方向。
1
自然坐标系
2
在此坐标系中速度和加速度怎么表示?
速度:因为瞬时速度的大小等于瞬时速率(注意平均
速度的大小不等于平均速率),故速度大小为 ,方向
(d) an 0, a 0
变速直线运动
匀速率曲线运动 变速(率)曲线运动
9
10
直角坐标系描述(匀速圆周运动)
y v2
x R cost , y R sin t
x y R
2 2
2
o
P2 v1 R an P 1 t x
dr v (R sin t )i (R cos t ) j dt
所以在自然坐标系中,作曲线运动的质点的加速度可以 分解为两个分量:一个是反映速度大小变化的切向加速 度,一个是反映速度方向变化的法向加速度.
5
自然坐标系中总加速度为:
改变
a a an
a a
1
改变
速度大小
速度方向
加速度 的大小 和方向
a
2
2 n
a
an t an a
24
运动的合成 描述运动三参量变换的约定
绝对量
静系(不动参考系S)的量。
相对量 动系(运动参考系S )的量。 牵连量 动系对静系的量。
25
相对运动
对岸
岸
26
运动目标
(船)
绝
相
牵 动系 (水)
对
对
对
静系 (岸)
对
对
对
对
对
对
27
例
北岸
江 船 南岸 东
船对岸 水对岸 船对水 绝 牵 相
人
水向东流速
a
2 a2 an
(20 0.4t ) an R v
2
2
2 ( 20 0 . 4 t ) (0.4) 2 ( )2 R
在t=5s时
2 ( 18 ) 2 a a2 an (0.4) 2 ( ) 2 1.67m / s 2 200 14
15
雨对地=雨对人+人对地(骑车)
( ) (′) (u )
人对地(骑车)
雨对地 雨对人
21
加速度的变换
dv dv du a a0 a d t dt dt
a a a0
a a
绝对加速度=相对加速度+牵连加速度 如果参考系相对作匀速直线运动,则
18
牛顿的相对运动关系
引入矢量 rSS
位矢之间的关系:
y
S系
S'系 u
r r o rSS
P
x
y
r r rSS
o
x
通常为了记忆,将上式写为:
S rSS rPS rP
19
S rSS 位矢关系: rPS rP
!
dv 2 v 2 2 a ( ) ( ) dt
20 a 的方向永远指向 曲线凹的一方。
dv v 2 a n dt
8
(2) 讨论:切向加速度和法向加速度为零时 的运动情况:
(a ) an 0, a 0
匀速直线运动
(b) an 0, a 0
(c) an 0, a 0
实质: 已知 北偏西45° 北 由45° 得 西
人对地
风对人
和
风对地
求
风对地
风对地 风对地
人对地 人对地
人对地
45°
风对地 风对人
人感到风 从 北偏西45° 方向吹来
30
7
在自然坐标系中:
a
a
注意:
dv v v a dt d (v ) dv d v dt dt dt
可以证明:
an a a an n
n
a
an v
dv dt
2
1
0
dv a dt
dv a dt
