第二章 控制系统的数学模型习题及答案
《控制工程基础》课程作业习题(含解答)
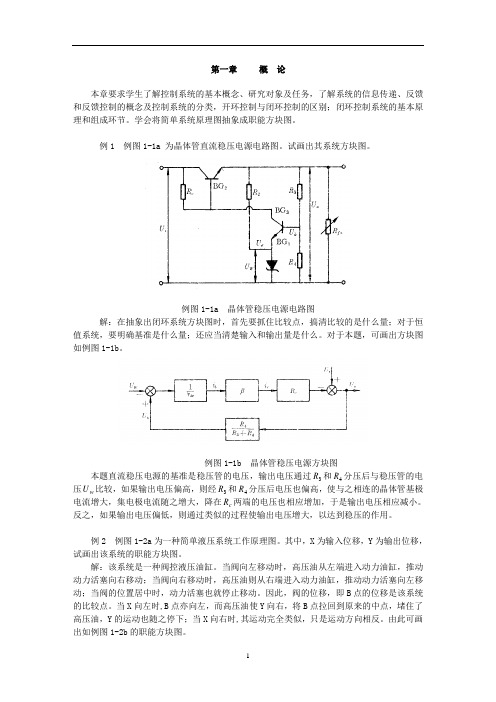
第一章概论本章要求学生了解控制系统的基本概念、研究对象及任务，了解系统的信息传递、反馈和反馈控制的概念及控制系统的分类，开环控制与闭环控制的区别；闭环控制系统的基本原理和组成环节。
学会将简单系统原理图抽象成职能方块图。
例1 例图1-1a 为晶体管直流稳压电源电路图。
试画出其系统方块图。
例图1-1a 晶体管稳压电源电路图解：在抽象出闭环系统方块图时，首先要抓住比较点，搞清比较的是什么量；对于恒值系统，要明确基准是什么量；还应当清楚输入和输出量是什么。
对于本题，可画出方块图如例图1-1b。
例图1-1b 晶体管稳压电源方块图本题直流稳压电源的基准是稳压管的电压，输出电压通过R和4R分压后与稳压管的电3压U比较，如果输出电压偏高，则经3R和4R分压后电压也偏高，使与之相连的晶体管基极w电流增大，集电极电流随之增大，降在R两端的电压也相应增加，于是输出电压相应减小。
c反之，如果输出电压偏低，则通过类似的过程使输出电压增大，以达到稳压的作用。
例2 例图1-2a为一种简单液压系统工作原理图。
其中，X为输入位移，Y为输出位移，试画出该系统的职能方块图。
解：该系统是一种阀控液压油缸。
当阀向左移动时，高压油从左端进入动力油缸，推动动力活塞向右移动；当阀向右移动时，高压油则从右端进入动力油缸，推动动力活塞向左移动；当阀的位置居中时，动力活塞也就停止移动。
因此，阀的位移，即B点的位移是该系统的比较点。
当X向左时,B点亦向左，而高压油使Y向右，将B点拉回到原来的中点，堵住了高压油，Y的运动也随之停下；当X向右时,其运动完全类似，只是运动方向相反。
由此可画出如例图1-2b的职能方块图。
例图1-2a 简单液压系统例图1-2b 职能方块图1．在给出的几种答案里，选择出正确的答案。
（1）以同等精度元件组成的开环系统和闭环系统，其精度比较为_______ （A ）开环高； （B ）闭环高； （C ）相差不多； （D ）一样高。
（2）系统的输出信号对控制作用的影响 （A ）开环有； （B ）闭环有； (C ）都没有； （D ）都有。
第二章控制系统的数学模型例题全
L ddt
Ac ost
L
Asint
A 2 S2
2
另一种解法：
设xt Acost, xs A s
s2 2
x0 Acost A t0
Lddt xt sx(s) x0
Lddt Acost
s s2
s
2
A
A 2
S2 2
7已知f t cost- cos2t,求Fs。 8已知f t 2e-tsin2t,求Fs。 9已知f t te-2t ,求Fs。 10已知f t t n ,求Fs。
dt
2已知Fs
ss
4
2
, 求f
t
。
3已知Fs 1 ,求f 0、f 。
sa
3已知Fs 1 ,求f 0、f 。
sa
f 0
lims Fs s
lims s
s
1 a
1
f
lims s0
s
1 a
0
• Using the laplace transform methodes solve the differential equations
第二章控制系统的数学模型 例题
1已知f t d Acost,求Fs。
dt
2已知f t 3t 4e2t ,求Fs。
3已知f t e3tsin4t,求Fs。
t
4已知f t Acostdt,求Fs。
0
5已知f t sint ,求Fs。
6已知f t 8e-100t - 5e-200t ,求Fs。
G1
-1
- G2
N1
C
G2
C 1 G 2 G 3
N1 1 G 2 G1G 2G3
自动控制原理C作业(第二章)答案
4 3
0.1
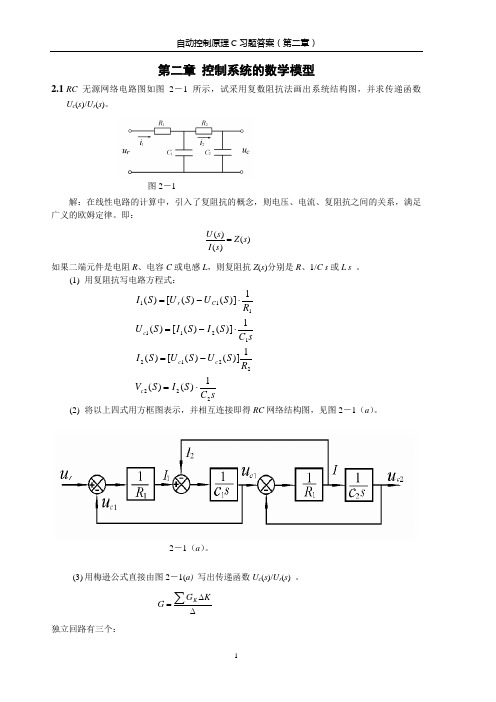
图 3-1 二阶控制系统的单位阶跃响应
解 在单位阶跃作用下响应的稳态值为 3，故此系统的增益不是 1，而是 3。系统模型为
(s)
s2
3
2 n
2n s
2 n
然后由响应的 p % 、 t p 及相应公式，即可换算出 、 n 。
p%
c(t p ) c() c()
4
3
3
33%
t p 0.1（s）
P1 G1G2
1 1
P2 G2G4
2 1
因此，传递函数为
C(s) P11 P2 2
R(s)
G2G1 G4G2 1 G1G2G3
3
自动控制原理 C 习题答案（第二章）
2.4 用梅森公式求系统传递函数。
R(S)
－
_
＋ G1(s)
－ _
G2(s)
+ C(S)
+
图 2－4 解： 单独回路 5 个，即
L1
1 R
1 C1S
1 R1C1S
11
1
L2
R2
C2S
R2C2 S
L3
1 C1S
1 R2
1 R2C1S
回路相互不接触的情况只有 L1 和 L2 两个回路。则
L12
L1L2
1 R1C1R2C2S 2
由上式可写出特征式为：
1
( L1
L2
L3 )
L1 L2
1
1 R1C1S
1 R2C2 S
1 R2C1S
1 R1C1R2C2S 2
益 K1 和速度反馈系数 Kt 。同时，确定在此 K1 和 Kt 数值下系统的延迟时间、上升时间和调节时间。
第二章 控制系统的数学模型习题讲解
X o(s) G3 G3 = = G2 H2 Xi 2 (s) 1+ G G (G H + H2 ) 1+ G3 (G1H1 + ) 3 4 1 1 G2 1+ G2H3 G2
X o(s) G3 (1+ G2H3 ) = Xi 2 (s) 1+ G2H3 + G3H2 + G1G2G3H1
证明题图2 13中(a)与(b)表示的系统是 2－13 证明题图2－13中(a)与(b)表示的系统是 相似系统（ 相似系统（即证明两个系统的传递函数具有相似 的形式）。 的形式）。
H2 Xi (s) G1
G2
A
Xo (s) G3
H1 G4
-
06-7-20
控制工程基础
11
G5 (s) H2 Xi (s) G1
G7 (s) G6 (s)
G2
A
Xo (s) G3
H1 H1 G4
1 G3
-
G2 G5G3 G2G3 G5 = G6 = = 1 + G2 H1 1 + G5G3 H 2 1 + G2 H1 + G2G3 H 2
a2 = [F (s)(s +1) ] s=−1 = −1 d 2 a1 = [F (s)(s +1) ] s=−1 = 2 ds a3 = [F (s)(s + 2)] s=−2 = −2
2
f (t ) = ( − t • e + 2 • e − 2 • e
06-7-20 控制工程基础
−t
−t
−2 t
6
π
s
06-7-20
2 5 9•e = + +2+ 2 2 s + 20 ( s + 20 ) s +9
第二章 控制系统的数学模型习题及答案
第二章 控制系统的数学模型习题及答案2-1 试建立下图所示各系统的微分方程。
其中电压)(t u r 和位移)(t x 为输入量；电压)(t u c 和位移)(t y 为输出量；R （电阻），C （电容），k （弹性系数），和f （阻尼系数），均为常数。
解：（a ）应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= （1） 2)()(R s Uc s I =（2） 联立式（1）、（2），可解得：CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为:r r c c u CR dt du u R CR R R dt du 121211+=++ （b ）如图解2-1(b)所示，取A,B 两点分别进行受力分析。
对A 点有 )()(111dtdydt dx f x x k -=- （1） 对B 点有 y k dtdydt dx f 21)(=- （2） 联立式（1）、（2）可得：dtdx k k k y k k f k k dt dy2112121)(+=++ 2-2 试证明下图所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。
解：(a) 取A 、B 两点分别进行受力分析，如图解所示。
对A 点有)()()(1122y y f y xf y x k -=-+- (1) 对B 点有1111)(y k y yf =- (2) 对式（1）、（2）分别取拉氏变换，消去中间变量1y ，整理后得)()(s X s Y = 21212121221212212121()1()1f f f fs s k k k k f f f f f s s k k k k k +++++++21221221221211221221k k s )k f k f k f (s f f k k s )k f k f (s f f +++++++= (b) 由图可写出sC R s U c 221)(+= sC R s C R sC R s U r 111112111)(+⋅++整理得)()(s U s U r c = 1)(1)(21221122121221122121+++++++s C R C R C R s C C R R s C R C R s C C R R 比较两系统的传递函数，如果设112211221,1,,,R k R k C f C f ====则两系统的传递函数相同，所以两系统是相似的。
第二章控制系统数学模型
有极限存在。
终值定理在分析研究系统的稳态性能时(例如分析系统的稳态误差，求取系统
输出量的稳态值等)有着很多的应用。因此终值定理也是一个经常用到的运算
定理。
7.初值定理： lim f (t) lim sF (s)
18
2
例2-1：写出RLC串联电路的微分方程。
ui
L
R
i
C
uo
ui 输入
uo 输出
[解]：据基尔霍夫电路定理：
L di dt
Ri
1 C
idt
ui
①
uo
1 C
idt
②
由②： i C d，uo代入①得： dt
LC
d 2uo dt 2
RC
duo dt
uo
ui
这是一个线性定常二阶微分方程。
3
例2-2 设一弹簧、质量块、阻尼器组成的系统如图所示，当外力 F(t)作用于系统时，系统将产生运动。试写出外力F(t)与质量块的 位移y(t)之间的微分方程。
uR uc Us
把 uR i R
和
ic
C
duc dt
代入电路，可得到电路的
微分方程：
RC
duc dt
uc
Us
23
现在对于上面的微分方程，我们用Laplace变换求解。
首先，利用Laplace变换中的微分定理，将微分方程变换成如下形式：
RC
duc dt
uc
Us
RCsU c (s) Uc (s) Us R(s)
利用待定系数法可求得：
A 1 ARC B 0
F (s) L[ f (t)] f (t)e st dt 0
第二章 控制系统的数学模型
= Ur (s)
传递函数为: di + u ur= R · + L i c dt Uc (s) 1 = duc G (s) = i = C dt Ur (s) LCs2 + RCs + 1
电气系统三要素：电阻、电容、电感
+ ί(t) R –
u(t)= ί(t)· R
u (t )
ί(t) C
–
u(t) ί(t)= R
图2-9 速度控制系统
+
R1 R2 R2 R1 k2
ui
R1
k1 u 1
c
u2
功 ua 放
m
SM
ω
负 载
ut
TG
运算放大器
uu+ ii+
_ +
+
Add
uo
差模输入电压等于零
u+= u-
运放同相输入端与反向输入端两点的电压相等，如同该 两点短路一样，称为虚短。
i+=i-=0
运放同相输入端与反向输入端的电流都等于零，如同该 两点被断开一样，称为虚断。
Tm s m ( s ) m (t ) K1U a ( s )
Tm s 1 m ( s) K1U a ( s)
m ( s) K1 G ( s) U a ( s) Tm s 1
m ( s) K2 G ( s) M c ( s) Tm s 1
传递函数的性质（续）
（5）传递函数与微分方程有相通性;
b1s b2 C (s) G ( s) R( s ) a0 s 2 a1s a2
对角线相乘
a0 s 2 a1s a2 C ( s ) b1s b2 R ( s )
第2章 控制系统的数学模型 参考答案
1.已知无源网络如题图2.1所示，其中i ()u t 为输入电压，o ()u t 为输出电压，试列写动态微分方程。
（a ） （b ） （c ）题图2.1 无源网络1.（a ）因为 12i i i =-，1i o u u u =-故 i o 1111o2i o 12d()d d d u u u i R R u i R u u ui C Ct t -⎧==⎪⎪⎪=⎨⎪⎪-==⎪⎩i o o i o 12d()d u u u u u CR R t--∴=- 整理得到o i 1212o 122i d d ()d d u uR R C R R u R R C R u t t++=+（b ）因为i o 1121d i uu i R u R i R i i t C -⎧=⎪⎪⎨⎪=++⎪⎩⎰整理得到o i 12o 2i d d ()d d u uR R C u R C u t t++=+（c ）因为i 1121o 1122o 1o 2()d d d d u u i i i i R u u i i C R t u L u u R t ⎧-=+=⎪⎪⎪⎪==⎨⎪⎪-=⎪⎪⎩得到oi 1112o 1o2()d d d d u u u u C R R t u L u u R t -⎧=+⎪⎪⎨⎪=+⎪⎩2o o oo o i 2111222d d d d d d u u u u u u L CL C R R R R t R t R t --=++ 整理得到2o o 11212o 2i 2d d ()()d d u uR LC R R C L R R u R u t t++++=2.试求题图2.2中各无源网络的传递函数。
)（a ） （b ）)C（c ） （d ）题图2.2 习题2的无源网络2. （a ）因为111111R Z R Cs R Cs ==+ 所以o 2122i 121212()()()U s R R R Cs R G s U s Z R R R Cs R R +===+++ （b ）因为11111111R Z R C s R C s ==+，22222211R C s Z R C s C s +=+= 所以o 211222i 121212112212()(1)(1)()()()1U s Z R C s R C s G s U s Z Z R R C C s R C R C R C s ++===+++++ （c ）因为()()()22122221111R Ls R Ls Cs Z R Ls Cs LCs R Cs R Ls Cs++=+==++++ 所以o 122i 1111212()()()()U s Z Ls R G s U s R Z R LCs R R C L s R R +===+++++ （d ）因为1212112111211()1R R C s R Z R R C s R C s R C s +=+=++，32232211R C s Z R C s C s+=+=所以2o 3121211213222i 121223131211212232()()()1()()()()1U s R R R C C s R C R C R C s Z G s U s Z Z R R R R R R C C s R C R C R C R C s +++++===++++++++ 3. 试求题图2.3中各有源网络的传递函数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 控制系统的数学模型习题及答案2-1 试建立下图所示各系统的微分方程。
其中电压)(t u r 和位移)(t x 为输入量；电压)(t u c 和位移)(t y 为输出量；R （电阻），C （电容），k （弹性系数），和f （阻尼系数），均为常数。
解：（a ）应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= （1） 2)()(R s Uc s I =（2） 联立式（1）、（2），可解得：CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为:r r c c u CR dt du u R CR R R dt du 121211+=++ （b ）如图解2-1(b)所示，取A,B 两点分别进行受力分析。
对A 点有 )()(111dtdydt dx f x x k -=- （1） 对B 点有 y k dtdydt dx f 21)(=- （2） 联立式（1）、（2）可得：dtdx k k k y k k f k k dt dy2112121)(+=++ 2-2 试证明下图所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。
解：(a) 取A 、B 两点分别进行受力分析，如图解所示。
对A 点有)()()(1122y y f y xf y x k -=-+- (1) 对B 点有1111)(y k y yf =- (2) 对式（1）、（2）分别取拉氏变换，消去中间变量1y ，整理后得)()(s X s Y = 21212121221212212121()1()1f f f fs s k k k k f f f f f s s k k k k k +++++++21221221221211221221k k s )k f k f k f (s f f k k s )k f k f (s f f +++++++= (b) 由图可写出sC R s U c 221)(+= sC R s C R sC R s U r 111112111)(+⋅++整理得)()(s U s U r c = 1)(1)(21221122121221122121+++++++s C R C R C R s C C R R s C R C R s C C R R 比较两系统的传递函数，如果设112211221,1,,,R k R k C f C f ====则两系统的传递函数相同，所以两系统是相似的。
2-3 求下图所示各有源网络的传递函数)()(s U s U r c 。
解： (a) 根据运算放大器 “虚地”概念，可写出12)()(R Rs U s U r c -=(b) s C R )s C R 1)(s C R 1(sC 1R s C 1R s C 1R )s (U )s (U 212211111122r c ++-=+⋅+-=(c) )1(11)()(212122Cs R R R R Cs R Cs R s U s U r c +-=+⋅-=2-4 已知在零初始条件下，系统的单位阶跃响应为 t t e e t c --+-=221)(，试求系统的单位脉冲响应和传递函数。
解t 2t e 4e dt)t (dc )t (k ---==)2s )(1s (23s 1s 12s 4)]t (k [L )s (+++=+-+==Φ2-5 系统传递函数2s 3s 2)s (R )s (C 2++=，试求初始条件为1)0(c -=、0)0(c= 时系统在输入)t (1)t (r =作用下的输出)t (c 。
解： 得时，由)t (2r )t (2c )t (c 3)t (c 0)0(c,1)0(c =++=-= )s (2R )s (2C )0(3c )s (3sC )0(c)0(sc )s (C s 2=+-+-- 代入初始条件得：2s 21s 4s 1)2s )(1s (s 3s s 2)s (C 2+++-=++--= 2t t2e 4e1)t (c --+-=2-6 飞机俯仰角控制系统结构图如图所示，试求闭环传递函数)s (Q )s (Q r c 。
解： 经结构图等效变换可得闭环系统的传递函数68.0s )K 42.018.1(s )K 7.09.0(s )6.0s (7.0)s (Q )s (Q 23r c ++++++= 2-7 已知系统方程组如下，试绘制系统结构图，并求闭环传递函数)s (R )s (C 。
解： 系统结构图如下：利用结构图等效化简或梅逊增益公式可求出系统的闭环传递函数为84321743215436324321G G G G G G G G G G G G G G G G 1G G G G )s (R )s (C -+++=2-8 试用结构图等效变换法化简下图所示系统，并求各系统的传递函数)s (R )s (C 。
解： （a ）⎪⎪⎩⎪⎪⎨⎧=-=-=--=)()()()()]()()([)()]()()()[()()()]()()[()()()(3435233612287111s X s G s C s G s G s C s X s X s X s G s X s G s X s C s G s G s G s R s G s X所以： 43213243214321G G G G G G G G G G 1G G G G )s (R )s (C ++++=（b ）所以：HG 1G G )s (R )s (C 221--=（c ）所以：3213221321G G G G G G G 1G G G )s (R )s (C +++=2-9 试用梅逊增益公式求下图中各系统的闭环传递函数。
解： （a ）图中有1条前向通路，4个回路1G G G G P 143211=∆=，)L L L L (1H G G L H G G G G L H G G G L H G G L 43212434443213332121321+++-=∆-==-==，，，，243443213321132432111H G G H G G G G H G G G H G G 1G G G G P )s (R )s (C +-+-=∆∆= （b ）图中有4条前向通路，5个回路，，，，1242321211G G P G P G G P G P ===-= ，，，，，2151242321211G G L G G L G L G G L G L -=-=-=-== ，，)L L L L (1143214321+++-=∆=∆=∆=∆=∆∆∆+∆+∆+∆=44332211P P P P )s (R )s (C 2121212121122211122211G G 3G G 1G G G G 2G G G G G G G G 1G G G G G G ++-+-=++++-+++-=（c ）图中有2条前向通路，3个回路，有1对互不接触回路，，，，1234213211L 1G G P 1G G G P -=∆-==∆= ，，，3232321211H G L H G L H G G L -=-=-= ，21321L L )L L L (1+++-=∆213213223121121343212211H H G G G H G H G H G G 1)H G G 1(G G G G G P P )s (R )s (C +++++-=∆∆+∆= 2-10 已知系统的结构图如下，图中)(s R 为输入信号，)(s N 为干扰信号，试求总输出C(s)。
解：（a ）令0)s (N =，求)s (R )s (C 。
图中有2条前向通路,3个回路，有1对互不接触回路。
，，，，H G 1L 1G G P 1G G P 2123121211+=-=∆==∆=，，，31321221G G L G G L H G L -=-=-= ，31321L L )L L L (1+++-=∆ 则有HG G G G G G G H G 1)H G 1(G G G G P P )s (R )s (C 32131212231212211++++++=∆∆+∆= 令0)s (R =，求)s (N )s (C 。
有3条前向通路，回路不变。
，，，，1G G G P L 11P 22142111=∆=-=∆-= ，，133143L 1G G G P -=∆=，31321L L )L L L (1+++-=∆HG G G G G G G H G 1)H G 1(G G G G G G H G 1P P P )s (N )s (C 3213121223142142332211+++++++--=∆∆+∆+∆=HG G G G G G G H G 1)]H G (1G G G G G G H G 1)[s (N )]H G 1(G G G R(s)[G )s (C 321312122314214223121+++++++--+++=（b ）令0)s (N 0)s (N 21==，，求)s (R )s (C 。
图中有1条前向通路，1个回路。
，，，，1111L 12s )1s (K 2L 12s Ks P -=∆++-==∆+=则有)1K (2s )1K 2(KsP )s (R )s (C 11+++=∆∆= 令0)s (N 0)s (R 2==，，求)s (N )s (C 1。
图中有1条前向通路，回路不变。
，，1s P 11=∆=则有)1K (2s )1K 2()2s (s P )s (N )s (C 111++++=∆∆= 令0)s (N 0)s (R 1==，，求)s (N )s (C 2。
图中有1条前向通路，回路不变。
12s K2P 11=∆+-=，则有)1K (2s )1K 2(K2P )s (N )s (C 112+++-=∆∆= 1)2(k 1)s (2k )s (2kN )s (N )2s (s ksR(s))s (C 21+++-++=（c ）令0)s (N =，求)s (R )s (C 。
图中有3条前向通路，2个回路。
，，，，，，1G G G P 1G G P 1G G P 3421324321421=∆==∆==∆= ，，，)L L (1G G L G G L 21432421+-=∆-=-= 则有43424214342332211G G G G 1G G G G G G G P P P )s (R )s (C ++++=∆∆+∆+∆= 令0)s (R =，求)s (N )s (C 。
有1条前向通路，回路不变。
，，1G P 141=∆= 则有4342411G G G G 1G P )s (N )s (C ++=∆∆= 434244214342G G G G 1G )s (N ]G G G G G G G )[s (R )s (C +++++=2-11)s (R H G H G H H H G G G H G H G 1G H H H G G )H G 1(G )s (Y 33113213213311112334331-+-+--=。