新2021年高考数学专题讲义第57讲 二项式定理(解析版)
高中数学《二项式定理》课件
03
二项式定理的证明
数学归纳法的应用
数学归纳法是一种证明数学命题的重 要方法，尤其在证明二项式定理时， 它能够通过有限步骤来证明无限递推 关系。
然后，通过假设当$n=k$时二项式定 理成立，推导出当$n=k+1$时二项 式定理也成立。
在二项式定理的证明中，数学归纳法 首先证明基础步骤，即当$n=0$或 $n=1$时，二项式定理成立。
二项式定理的推导
二项式定理推导思路
通过组合数的性质，将二项式定理展开式中的每一项表示为组合数的形式，从而推导出二项式定理的 展开式。
二项式定理的推导过程
根据组合数的性质，将二项式定理展开式中的每一项表示为C(n, k)的形式，其中k表示二项式中某一 项的次数。通过计算，可以得到二项式定理的展开式为C(n, 0) + C(n, 1)x + C(n, 2)x^2 + ... + C(n, n)x^n。
C(n, m) = C(n, n-m)，即从n个不同元素中取出m个元素和取出n-m个元素的 组合数相等。
组合数的性质2
C(n+1, m) = C(n, m-1) + C(n, m)，即从n+1个不同元素中取出m个元素的组 合数等于从n个不同元素中取出m-1个元素的组合数加上从n个不同元素中取出 m个元素的组合数。
详细描述
二项式定理的应用场景非常广泛。在多项式的展开中，二项式定理可以用来求解形如$(x+y)^n$的多项式的展开 结果。在组合数学中，二项式定理可以用来计算组合数和排列数等。在概率论中，二项式定理可以用来计算事件 的概率和期望值等。此外，二项式定理在统计学、物理、工程等领域也有广泛的应用。
02
二项式定理的推导过程
2021年高考数学总复习课时作业(五十七)第57讲二项式定理理
2021年高考数学总复习课时作业（五十七）第57讲二项式定理理基础热身1.[2021·丽水模拟]二项式(x+2)7的展开式中含x5项的系数是 ()A.21B.35C.84D.2802.若(1+2x)n的展开式中,x2的系数是x系数的7倍,则n的值为()A.5B.6C.7D.83.[2021·吉林调研]+n的展开式中,各项系数之和为A,各项的二项式系数之和为B,若=32,则n=()A.5B.6C.7D.84.[2021·长沙长郡中学月考]2-(1-2x)4的展开式中x2的系数为.5.[2021·东北育才学校月考] (3-x)n的展开式中各项系数之和为64,则展开式中x5的系数为.能力提升6.[2021·石家庄三模]x+2x-5的展开式的常数项为()A.120B.40C.-40D.807.[2021·嘉兴五校联考]x2-x+6的展开式中,x6的系数为 ()A.240B.241C.-239D.-2408.[2021·牡丹江第一中学期中]若(x+1)n=a0+a1(x-1)+a2(x-1)2+…+a n(x-1)n,a0+a1+…+a n=243,则(n-x)n展开式的二项式系数之和为()A.16B.32C.64D.10249.[2021·福州一中质检]“杨辉三角形”是古代重要的数学成就,它比西方的“帕斯卡三角形”早了300多年,图K57-1是三角形数阵,记a n为图中第n行各数之和,则a5+a11的值为()图K57-1A.528B.1020C.1038D.104010.已知(2+ax)(1-2x)5的展开式中,含x2项的系数为70,则实数a的值为()A.1B.-1C.2D.-211.若(1-2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,则= .12.[2021·黄陵中学模拟]若(x-1)5=a5(x+1)5+a4(x+1)4+a3(x+1)3+a2(x+1)2+a1(x+1)+a0,则a1+a2+a3+a4+a5= .13.[2021·盘锦二模]在1-x+9的展开式中,含x3项的系数为.难点突破14.(5分)已知n为满足S=a++++…+(a≥3)能被9整除的正数a的最小值,则x-n的展开式中,二项式系数最大的项为()A.第6项B.第7项C.第11项D.第6项和第7项15.(5分)[2021·西安模拟]若(2x+)4=a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为.课时作业(五十七)1.C[解析] 二项式(x+2)7的展开式中含x5项的系数为×22=84.故选C.2.D[解析] (1+2x)n的展开式的通项为T r+1=(2x)r=2r x r,∵x2的系数是x系数的7倍,即22=7×2,即22·=7×2·n,∴n=8.3.A[解析] 令x=1,得各项系数之和A=4n,又二项式系数之和B=2n,故==32,解得n=5,故选A.4.80[解析] 展开式中x2的系数为2(-2)2-(-2)3=48+32=80.5.-18[解析] (3-x)n的展开式中各项系数之和为64,令x=1,则2n=64,解得n=6,则展开式中x5的系数为×3×(-1)5=-18.6.B[解析] 展开式的常数项为22×(-1)3+23×(-1)2=-40+80=40,选B.7.C[解析] x2-x+6=x6x+-16,因此展开式中x6的系数为(-1)6+22×(-1)1=-239.故选C.8.B[解析] 在(x+1)n=a0+a1(x-1)+a2(x-1)2+…+a n(x-1)n中,令x=2,可得a0+a1+a2+…+a n=3n=243,解得n=5,因此(n-x)n=(5-x)5,其展开式的二项式系数之和为25=32,故选B.9.D[解析] a5=++++=24=16,a11=+++…+=210=1024,∴a5+a11=1040,故选D.10.A[解析] (2+ax)(1-2x)5=2(1-2x)5+ax(1-2x)5,(1-2x)5展开式的通项为T r+1=15-r×(-2x)r=(-2)r x r.取r=2,含有x2的项为2×(-2)2x2=80x2,取r=1,含有x2的项为ax(-2)1x=-10ax2,结合题意由80-10a=70,解得a=1.11.-2[解析] a3=·(-2)3=-80,a2=·(-2)2=40,因此=-2.12.31[解析] 令x=-1,可得a0=-32;令x=0,可得a0+a1+a2+a3+a4+a5=-1.因此a1+a2+a3+a4+a5=-1-a0=-1+32=31.13.-84[解析] 因为(1-x)+9=(1-x)9+(1-x)8+…+,因此x3项只能在(1-x)9=(1-x)9中显现,其展开式的通项为T r+1=(-x)r,可知x3的系数为(-1)3=-84.14.B[解析] 由于S=a++++…+=a+227-1=89+a-1=(9-1)9+a-1=×99-×98+…+×9-+a-1=9×(×98-×97+…+)+a-2,a≥3,因此n=11,从而x-11的展开式中的系数与二项式系数只有符号差异,又中间两项的二项式系数最大,中间两项为第6项和第7项,且第6项系数为负,因此第7项系数最大.15.1[解析] 由题意,令x=1,则a0+a1+a2+a3+a4=(2+)4,令x=-1,则a0-a1+a2-a3+a4=(-2+)4,因此(a0+a2+a4)2-(a1+a3)2=(a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4)=(2+)4×(-2+)4=[(2+)×(-2+ )]4=1.。
2021高考北京版数学教师用书(课件)10.2 二项式定理(讲解部分)
中x3y3的系数为-40+80=40.
答案 (1)C (2)C
方法技巧
方法1 求展开式中的特定项
求二项展开式的特定项问题,实质是考查通项Tk+1= Cknan-k·bk的特点,一般需要 建立方程求k,再将k的值代回通项求解,注意k的取值范围(k=0,1,2,…,n). (1)第m项:此时k+1=m,直接代入通项; (2)常数项:即该项中不含“变元”,令通项中“变元”的幂指数为0建立方 程; (3)有理项:令通项中“变元”的幂指数为整数建立方程. 特定项的系数问题及相关参数值的求解等都可依据上述方法求解.
答案 -160
方法2 二项式系数与项的系数
1.二项式系数与项的系数是不同的两个概念,二项式系数是指 C0n, C1n,…, Cnn,
它只与各项的项数有关,而与a,b的值无关;而项的系数是指该项中除变量
外的常数部分,它不仅与各项的项数有关,也与a,b的值有关,如(a+bx)n的展 开式中,第k+1项的二项式系数是 Ckn ,而项的系数是 Ckn an-kbk.
1.二项式的项数与项 (1)二项式的展开式共有n+1项, Crnan-rbr是第r+1项.即r+1是项数, Crn an-rbr是项. (2)通项是Tr+1= Crn an-rbr(r=0,1,2,…,n).其中含有Tr+1,a,b,n,r五个元素,只要知道 其中四个即可求第五个元素.
2.二项式系数与展开式项的系数的异同
2x2
-
1 x
7
的展开式的通项为Tr+1= C7r
(2x2)7-r·
-
1 x
r
=(-1)r·27-rC 7r
考点35二项式定理（讲解）（解析版）
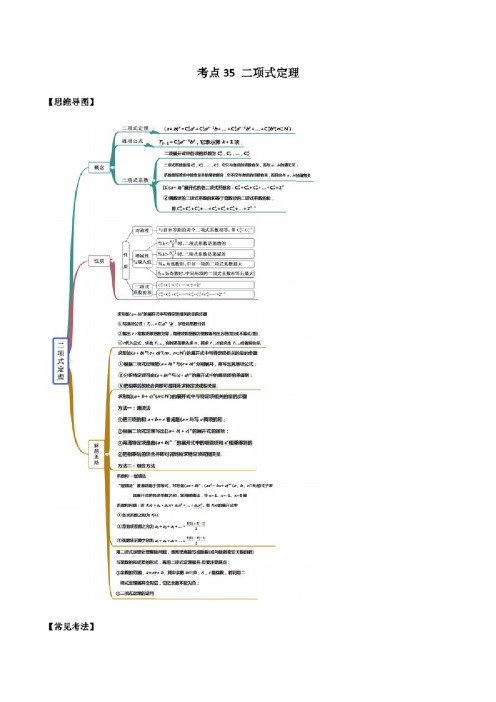
考点35二项式定理【思维导图】一项式定虔（・♦姻咯♦…'"，_・C5kn）云术1敷的组杞Y6・7v丸，smr政用-iJE^irWWft^C,皿M砖为负；⑴WWKir: 7^・CV*①■58210为0二项式景致升一州.心眼u.ci・5.y・r ■NM1卜3・末等蹈第牌个一#果■［棚等・・。
i:'g”号'N.Ji犬的，■人＜1.怎u*m，・忡而的一沔式，■■人力分ent金*可由：衣啄。
♦"eg n）»ww式中与特回we美的■的壬■方A:砌（法①emMWD■♦b.C■虞■《-•6）与cWHKK；②幅疆二映直建m出【（八«.Cf的（耕式J5SM!:①弄3W卸*®与"'的期式中的■畋》0―相"利的④把由后的项合并即可呷wi*wp瑛ms美・.sa=：»a方溢•FKT MaWTtOBit舞艳・3•”.（特•<TS b.«etjRlt7»g哄gg—•■•-次罕»t Hnmweeewit cwma:【常见考法】考点一指定项系数1.展开式中」r项的系数为（）X）XA.10B.5C.-10D.一5【答案】C（解析】（1-i）5 '.匚匚眉项公式为A=0（—1）—t・=_3，时个r=3，x故展开式中号项的系数为-C；=-10,故选：C.2.若（尸+色）的展开式中/的系数为150,则,2=（）A.20B.15C.10D.25【答案】C【解析】由己知得A=C：（r）ig、|故'l ir=2时，12-3/«=6.于是有7；=C^V=150x6,则〃2=]o.故选：c103.在I1+X+的展开式中，『的系数为（A.10B.30C.45D.120【答案】C【解析】［1+戏餐『10 =(,+x)^-2ima=隽（1+对。
+。
（山），土+席（心）8土+...+徭（1+打土人人通10的展开式中，X2的系数即为(1+4°的F(X(l+x)10展开式的通项为7；引=0'1，令10-r=2,故r=8,所以J的系数为篇=45.故选：C.4.若曲线)，=3ln(x+l)在x=l处的切线斜率为。
二项式定理及应用ppt课件
4．已知二项式(x－1x)n的展开式中含x3的项 是第4项，则n的值为________．
【解析】 ∵通项公式Tr＋1＝Crn(－1)rxn－2r， 又∵第4项为含x3的项， ∴当r＝3时，n－2r＝3，∴n＝9.
• 【答案】 9
5．若(x2＋
1 ax
)6的二项展开式中x3的系数为
联立①②得
a1＋a3＋…＋a99＝(2－
3)100－(2＋ 2
3)100 .
(3)原式＝[(a0＋a2＋…＋a100)＋(a1＋a3＋… ＋a99)]·[(a0＋a2＋…＋a100)－(a1＋a3＋…＋
a99)] ＝(a0＋a1＋a2＋…＋a100)(a0－a1＋a2－a3 ＋…＋a98－a99＋a100) ＝(2－ 3)100(2＋ 3)100＝1.
52，则a＝________(用数字作答)．
【解析】 Tr＋1＝Cr6a－rx12－3r， 当12－3r＝3时，r＝3，∴C63a－3＝52，∴a＝2.
• 【答案】 2
求特定的项或特定项的系数
已知在(3 x－ 1 )n的展开式中，第6 3
2x 项为常数项． (1)求n； (2)求含x2的项的系数； (3)求展开式中所有的有理项．
(4)方法一：∵展开式中，a0，a2， a4，…，a100大于零，而a1，a3，…，a99小 于零，
∴原式＝a0－a1＋a2－a3＋…＋a98－a99＋
a100 ＝(2＋ 3)100.
方法二：|a0|＋|a1|＋|a2|＋…＋|a100|， 即(2＋ 3x)100展开式中各项的系数和， ∴|a0|＋|a1|＋|a2|＋…＋|a100|＝(2＋ 3)100.
• 【思路点拨】 本题给出二项式及其二项展开式求各系
第57讲 二项式定理(教师版) 备战2021年新高考数学微专题讲义
第57讲 二项式定理一、课程标准1、能用多项式运算法则和计数原理证明二项式定理．2、会用二项式定理解决与二项展开式有关的简单问题.基础知识回顾二、基础知识回顾1. 二项式定理公式：(a ＋b)n ＝C 0n a n ＋C 1n a n －1b ＋…＋C k n a n －k b k ＋…＋C n nb n (n ∈N *) 这个公式表示的定理叫做二项式定理．在上式中右边的多项式叫做(a ＋b )n 的二项展开式，其中的系数C k n (k ＝0，1，…，n )叫做二项式系数，式中的C k n a n －k b k 叫做二项展开式的通项，用T k ＋1表示，即T k ＋1＝C k n an－kb k ．2. 二项展开式形式上的特点 (1)项数为__n ＋1__．(2)各项的次数都等于二项式的幂指数n ，即a 与b 的指数的和为n.(3)字母a 按__降幂__排列，从第一项开始，次数由n 逐项减1直到零；字母b 按__升幂__排列，从第一项起，次数由零逐项增1直到n.(4)二项式系数从__C 0n __，C 1n ，一直到C n －1n ，__C nn __．3. “杨辉三角”与二项式系数的性质(1)“杨辉三角”有如下规律：左右两边斜行都是1，其余各数都等于它“肩上”两个数字之和．(2)对称性：在二项展开式中与首末两端“等距离”的两个二项式系数相等，即C m n ＝__C n －mn__．(3)增减性与最大值：二项式系数C k n ，当k ＜n ＋12时，二项式系数逐渐__增大__；当k ＞n ＋12时，二项式系数逐渐__减小__．当n 是偶数时，中间一项的二项式系数最大；当n 是奇数时，中间两项的二项式系数最大．(4)各二项式系数的和：(a ＋b)n 的展开式的各项二项式系数之和为__2n __，即C 0n ＋C 1n ＋…＋C n n ＝__2n __. (5)奇数项的二项式系数之和等于偶数项的二项式系数之和，即C 0n ＋C 2n ＋…＝__C 1n ＋C 3n ＋…__＝__2n －1__． 三、自主热身、归纳总结1、(1＋2x)5的展开式中，x 2的系数为( )A . 10B . 20C . 25D . 40 【答案】 D【解析】 T r ＋1＝C r 5(2x)r ＝C r 52r x r ，当r ＝2时，x 2的系数为C 25·22＝40.故选D . 2、若⎝⎛⎭⎫x ＋1x n展开式的二项式系数之和为64，则展开式的常数项为( )A . 6B . 12C . 20D . 32 【答案】 C【解析】二项式系数之和2n＝64，∴n ＝6，T r ＋1＝C r 6·x6－r·⎝⎛⎭⎫1x r＝C r 6x 6－2r，当6－2r ＝0，即当r ＝3时为常数项，T 4＝C 36＝20.故选C .3、(x －y)n 的二项展开式中，第m 项的系数是( )A . C m nB .C m ＋1n C . C m －1n D . (－1)m －1C m －1n【答案】 D【解析】 (x －y)n 二项展开式第m 项的通项公式为T m ＝C m －1n(－y)m －1x n－m ＋1，∴系数为C m －1n(－1)m －1.故选D .4、(多选)已知(3x －1)n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n ，设(3x －1)n 的展开式的二项式系数之和为S n ，T n ＝a 1＋a 2＋…＋a n ，则( )A ．a 0＝1B ．T n ＝2n －(－1)nC ．n 为奇数时，S n ＜T n ；n 为偶数时，S n ＞T nD ．S n ＝T n 【答案】 BC【解析】由题意知S n ＝2n ，令x ＝0，得a 0＝(－1)n ，令x ＝1，得a 0＋a 1＋a 2＋…＋a n ＝2n ，所以T n ＝2n －(－1)n ，故选B 、C.5、(一题两空)若⎝⎛⎭⎪⎫3x －13x 2m 的展开式中二项式系数之和为128，则m ＝________，展开式中1x 3的系数是________． 【答案】 7 21【解析】由题意可知2m ＝128，∴m ＝7，∴展开式的通项T r ＋1＝C r 7(3x )7－r·⎝⎛⎭⎪⎫－13x 2r ＝C r 737－r (－1)r x 7－5r 3，令7－53r ＝－3，解得r ＝6，∴1x3的系数为C 6737－6(－1)6＝21. 6、(2020·合肥模拟)(x －2)3(2x ＋1)2的展开式中x 的奇次项的系数之和为________． 【答案】 9【解析】依题意得，(x －2)3(2x ＋1)2＝(x 3－6x 2＋12x －8)·(4x 2＋4x ＋1)＝4x 5－20x 4＋25x 3＋10x 2－20x －8，所以展开式中x 的奇次项的系数之和为4＋25－20＝9.11．若⎝⎛⎭⎫x ＋12x n (n ≥4，n ∈N *)的二项展开式中前三项的系数依次成等差数列，则n ＝________.【答案】 8【解析】⎝⎛⎭⎫x ＋12x n 的展开式的通项T r ＋1＝C r n x n －r ⎝⎛⎭⎫12x r ＝C r n 2－r x n －2r ，则前三项的系数分别为1，n 2，n (n －1)8，由其依次成等差数列，得n ＝1＋n (n －1)8，解得n ＝8或n ＝1(舍去)，故n ＝8.四、例题选讲考点一 二项展开式中特定项及系数问题 例1、（1）二项式⎝⎛⎭⎫x 2－2x 10的展开式中，x 项的系数是( )A.152 B ．－152C ．15D ．－15（2）(2019·天津高考)⎝⎛⎭⎫2x －18x 38的展开式中的常数项为________． （3）(2019·浙江高考)在二项式(2＋x )9的展开式中，常数项是________，系数为有理数的项的个数是________．【答案】（1）B （2）28（3）162 5【解析】：（1）选 ⎝⎛⎭⎫x 2－2x 10的二项展开式的通项为T r ＋1＝C r 10⎝⎛⎭⎫x 210－r ⎝⎛⎭⎫－2x r ＝(－1)r 22r －10C r 10x 23- 5r，令5－3r 2＝12，得r ＝3，所以x 项的系数是(－1)3·2－4·C 310＝－152.故选B. （2）：⎝⎛⎭⎫2x －18x 38的通项为T r ＋1＝C r 8()2x 8－r ·⎝⎛⎭⎫－18x 3r ＝C r 828－r ⎝⎛⎭⎫－18r ·x 8－4r .令8－4r ＝0，得r ＝2，∴ 常数项为T 3＝C 2826⎝⎛⎭⎫－182＝28. （3）由二项展开式的通项公式可知T r ＋1＝C r 9·(2)9－r ·x r ，r ∈N,0≤r ≤9， 当项为常数项时，r ＝0，T 1＝C 09·(2)9·x 0＝(2)9＝16 2. 当项的系数为有理数时，9－r 为偶数，可得r ＝1,3,5,7,9，即系数为有理数的项的个数是5.变式1、已知在⎝ ⎛⎭⎪⎪⎫3x －33x n的展开式中，第6项为常数项． (1)求n ；(2)求含x 2项的系数； (3)求展开式中所有的有理项．【解析】 利用通项确定n 的值，进而根据指定项的特征求解．通项公式为T r ＋1＝C r n ·x n －r 3(－3)r ·x －r 3＝(－3)r C r n x n －2r 3. (1)∵第6项为常数项，∴r ＝5时，有n －2r3＝0，解得n ＝10.(2)令10－2r 3＝2，得r ＝12×(10－6)＝2，∴x 2项的系数为C 210(－3)2＝405. (3)由题意知，⎩⎪⎨⎪⎧10－2r3∈Z ，0≤r ≤10，r ∈Z .令10－2r 3＝k (k ∈Z)，则10－2r ＝3k ，即r ＝5－32k ，∵r ∈Z ，且0≤r ≤10，∴k 应为偶数，∴k ＝2，0，－2，即r ＝2，5，8，∴第3项，第6项与第9项为有理项，它们分别为405x 2，－61 236，295 245x －2.变式2、求二项展开式中的特定项或指定项的系数 (1)在(x －1)4的展开式中，x 的系数为________． (2)(x 2＋x ＋y )5的展开式中，x 5y 2的系数为________． 【答案】(1)6 (2)30【解析】(1)由题意可知T r ＋1＝C r 4(x )4－r (－1)r 424C (1)rr rx -＝－，令4－r 2＝1解得r ＝2，所以展开式中 x 的系数为C 24(－1)2＝6．(2)方法一 利用二项展开式的通项公式求解．(x 2＋x ＋y )5＝[(x 2＋x )＋y ]5，含y 2的项为T 3＝C 25(x 2＋x )3·y 2．其中(x 2＋x )3中含x 5的项为C 13x 4·x ＝C 13x 5．所以x 5y 2的系数为C 25C 13＝30．方法二 利用组合知识求解．(x 2＋x ＋y )5为5个x 2＋x ＋y 之积，其中有两个取y ，两个取x 2，一个取x 即可，所以x 5y 2的系数为 C 25C 23＝30．方法总结：求二项展开式中的特定项，一般是利用通项公式进行，化简通项公式后，令字母的指数符合要求(求常数项时，指数为零；求有理项时，指数为整数等)，解出项数r ＋1，代回通项公式即可． 考点二、 二项式系数的和或各项系数的和的问题例2、在(2x －3y )10的展开式中，求： (1) 二项式系数的和； (2) 各项系数的和；(3) 奇数项的二项式系数和与偶数项的二项式系数和； (4) 奇数项系数和与偶数项系数和； (5) x 的奇次项系数和与x 的偶次项系数和．【解析】设(2x －3y )10＝a 0x 10＋a 1x 9y ＋a 2x 8y 2＋…＋a 10y 10，(*)各项系数的和为a 0＋a 1＋…＋a 10，奇数项系数和为a 0＋a 2＋…＋a 10，偶数项系数和为a 1＋a 3＋a 5＋…＋a 9，x 的奇次项系数和为a 1＋a 3＋a 5＋…＋a 9，x 的偶次项系数和为a 0＋a 2＋a 4＋…＋a 10． 由于(*)是恒等式，故可用“赋值法”求出相关的系数和．(1)二项式系数的和为C 010＋C 110＋…＋C 1010＝210．(2)令x ＝y ＝1，各项系数和为(2－3)10＝(－1)10＝1．(3)奇数项的二项式系数和为C 010＋C 210＋…＋C 1010＝29， 偶数项的二项式系数和为C 110＋C 310＋…＋C 910＝29． (4)令x ＝y ＝1，得到a 0＋a 1＋a 2＋…＋a 10＝1，①令x ＝1，y ＝－1(或x ＝－1，y ＝1)，得a 0－a 1＋a 2－a 3＋…＋a 10＝510，② ①＋②得2(a 0＋a 2＋…＋a 10)＝1＋510，∴奇数项系数和为1＋5102； ①－②得2(a 1＋a 3＋…＋a 9)＝1－510，∴偶数项系数和为1－5102． (5)x 的奇次项系数和为a 1＋a 3＋a 5＋…＋a 9＝1－5102；x 的偶次项系数和为a 0＋a 2＋a 4＋…＋a 10＝1＋5102．变式1、(1)(2020·合肥模拟)已知(ax ＋b )6的展开式中x 4项的系数与x 5项的系数分别为135与－18，则(ax ＋b )6的展开式中所有项系数之和为( )A ．－1B ．1C ．32D ．64(2)若(1－x )5＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4＋a 5x 5，则|a 0|－|a 1|＋|a 2|－|a 3|＋|a 4|－|a 5|＝( ) A ．0 B ．1 C ．32D ．－1(3)在(1＋x )n (x ∈N *)的二项展开式中，若只有x 5的系数最大，则n ＝________. 【答案】(1)D (2)A (3)10【解析】 (1)由二项展开式的通项公式可知x 4项的系数为C 26a 4b 2，x 5项的系数为C 16a 5b ，则由题意可得⎩⎪⎨⎪⎧C 26a 4b 2＝135，C 16a 5b ＝－18，解得a ＋b ＝±2，故(ax ＋b )6的展开式中所有项的系数之和为(a ＋b )6＝64. (2)由(1－x )5的展开式的通项T r ＋1＝C r 5(－x )r ＝C r 5(－1)r x r，可知a 1，a 3，a 5都小于0.则|a 0|－|a 1|＋|a 2|－|a 3|＋|a 4|－|a 5|＝a 0＋a 1＋a 2＋a 3＋a 4＋a 5.在原二项展开式中令x ＝1，可得a 0＋a 1＋a 2＋a 3＋a 4＋a 5＝0.(3)二项式中仅x 5的系数最大，其最大值必为C n 2n ，即得n2＝5，解得n ＝10.变式2、对任意实数x ，有()923901239(23)1(1)(1)(1)x a a x a x a x a x -+-+-+-++-═.则下列结论成立的是（ ）A ．2144a =-B ．01a =C ．01291a a a a +++⋯+=D ．9012393a a a a a -+-+-=-【答案】ACD【解析】对任意实数x ，有()923901239(23)1(1)(1)(1)x a a x a x a x a x -+-+-+-++-=═[﹣1+2（x ﹣1）]9，∴a 229C =-⨯22＝﹣144，故A 正确；故令x ＝1，可得a 0＝﹣1，故B 不正确； 令x ＝2，可得a 0+a 1+a 2+…+a 9＝1，故C 正确；令x ＝0，可得a 0﹣a 1+a 2+…﹣a 9＝﹣39，故D 正确；故选：ACD .变式3、（2020·深喀第二高级中学高二期末）已知()512x -250125a a x a x a x =+++⋅⋅⋅+，则123452345a a a a a ++++=_______.【答案】10-【解析】因为()2345501234512a a x a x a x a x a x x =+++-++ 两边同时取导数得()42341234523101524a a x a x a x a x x =+-+-++ 再令1x =得()4123452345101210a a a a a ++++=--=- 故答案为：10-方法总结：“赋值法”普遍适用于恒等式，是一种重要的方法，对形如(ax ＋b )n 、(ax 2＋bx ＋c )m (a 、b ∈R )的式子求其展开式的各项系数之和，常用赋值法，只需令x ＝1即可；对形如(ax ＋by )n (a ，b ∈R )的式子求其展开式各项系数之和，只需令x ＝y ＝1即可．考点三 二项式定理的综合应用例3 (1)1－90C 110＋902C 210－903C 310＋…＋(－1)k 90k C k 10＋…＋9010C 1010除以88的余数是____．(2)设复数x ＝2i 1－i (i 是虚数单位)，则C 12019x ＋C 22019x 2＋C 32019x 3＋…＋C 20192019x 2019＝____． 【答案】（1）1 （2）－i －1【解析】 (1)1－90C 110＋902C 210－903C ＋…＋(－1)k 90k C k 10＋…＋9010C 1010＝(1－90)10＝8910＝(88＋1)10＝8810＋C 110889＋…＋C 91088＋1，∵前10项均能被88整除，∴余数是1. (2)x ＝2i1－i ＝2i （1＋i ）（1－i ）（1＋i ）＝－1＋i ，C 12019x ＋C 22019x 2＋C 32019x 3＋…C 20192019x2019＝(1＋x)2019－1＝i 2019－1＝－i －1变式1、（2020·江苏省南京师大附中高二）已知()21221012211n n n x a a x a x a x ++++=++++，n *∈N ．记()021?nn n k k T k a -==+∑．（1）求2T 的值；（2）化简n T 的表达式，并证明：对任意n *∈N 的，n T 都能被42n +整除． 【答案】（1）30；（2）()21221nn n T n C -=+，证明见解析.【解析】由二项式定理，得()210,1,2,,21ii n a C i n +==+；（1）210221055535+3530T a a a C C C =++=+=；（2）因为()()()()()()()()()12121!212!1!!!!11n kn n n n n k n k k n k n k n n C k ++++++=++⋅=+-+⋅+-⋅+()221n kn n C +=+，所以()()()1212100212121nnnn k n k n n kn n k k k T k ak Ck C -++-++====+=+=+∑∑∑ ()()()()111212121021212121nnnn kn k n kn n n k k k n k n Cn k Cn C +++++++++===⎡⎤=++-+=++-+⎣⎦∑∑∑()()()()()1221221201122121221221222nnn kn kn n n nn n k k n Cn C n C n +++++===+-+=+⋅+-+⋅⋅∑∑()221nn n C =+， ()()()()122121212121221n n n nn n n n n T n C n C C n C ----∴=+=++=+，因为21n n C N *-∈，所以n T 能被42n +整除.变式2、【陕西省黄陵中学高新部2017-2018学年高二下学期开学考试】(1)设.①求； ②求； ③求；(2)求除以9的余数．【答案】（1）16，256，15；（2）7【解析】试题分析：（1）利用赋值法，令，求；（2）令x=-1，与（2）相加求；，；③令，结合二项式系数和即可求出结果；（2）利用二项式系数和，把 分解为9的倍数形式，再求对应的余数． 试题解析：(1)①令x ＝1，得a 0＋a 1＋a 2＋a 3＋a 4＝(3－1)4＝16. ②令x ＝－1得，a 0－a 1＋a 2－a 3＋a 4＝(－3－1)4＝256，而由(1)知a 0＋a 1＋a 2＋a 3＋a 4＝(3－1)4＝16，两式相加，得a 0＋a 2＋a 4＝136. ③令x ＝0得a 0＝(0－1)4＝1，得a 1＋a 2＋a 3＋a 4＝a 0＋a 1＋a 2＋a 3＋a 4－a 0＝16－1＝15. （2）解 S ＝C ＋C ＋…＋C ＝227－1＝89－1＝(9－1)9－1＝C ×99－C ×98＋…＋C ×9－C －1 ＝9(C ×98－C ×97＋…＋C )－2 ＝9(C ×98－C ×97＋…＋C －1)＋7， 显然上式括号内的数是正整数． 故S 被9除的余数为7.方法总结：整除问题，解决整除问题要点为：(1)观察除式与被除式间的关系；(2)将被除式拆成二项式；(3)结合二项式定理得出结论．此外二项式定理还可应用于不等式的证明．五、优化提升与真题演练1、【2019年高考全国Ⅲ卷理数】（1+2x 2 ）（1+x ）4的展开式中x 3的系数为（ ） A ．12B ．16C ．20D ．24()42340123431x a a x a x a x a x -=++++01234a a a a a ++++024a a a ++1234a a a a +++1227272727S C C C =+++1x ＝01234a a a a a ++++024a a a ++0x =S【解析】由题意得x 3的系数为3144C 2C 4812+=+=，故选A ．2、【2020年高考北京】在52)的展开式中，2x 的系数为（ ） A ．5- B ．5C ．10-D ．10【答案】C【解析】)52展开式的通项公式为：()()552155C22C r rrrr r r T x--+=-=-，令522r -=可得：1r =，则2x 的系数为：()()1152C 2510-=-⨯=-. 故选：C.3、【2020年高考全国Ⅰ卷理数】25()()x x y xy ++的展开式中x 3y 3的系数为（ ）A ．5B ．10C ．15D ．20【答案】C【解析】5()x y +展开式的通项公式为515C r r rr T x y -+=（r ∈N 且5r ≤）所以2y x x ⎛⎫+ ⎪⎝⎭的各项与5()x y +展开式的通项的乘积可表示为：56155C C r rrr rrr xT x xy xy --+==和54252152C C r r r r r r r T x y y y y xx x --++==在615C r r r r xT x y -+=中，令3r =，可得：33345C xT x y =，该项中33x y 的系数为10，在42152C r r r r T x xy y -++=中，令1r =，可得：521332C y x T x y =，该项中33x y 的系数为5 所以33x y 的系数为10515+= 故选：C.4、【2018年高考全国Ⅲ卷理数】522x x ⎛⎫+ ⎪⎝⎭的展开式中4x 的系数为（ ）A ．10B ．20C ．40D ．80【解析】由题可得522x x ⎛⎫+ ⎪⎝⎭的展开式的通式为()521031552C C 2rr r rr r r T x x x --+⎛⎫⋅⋅== ⎪⎝⎭，令1034r -=，得2r =，所以展开式中4x 的系数为225C 240⨯=．故选C ．5、【2020年高考全国II 卷理数】4名同学到3个小区参加垃圾分类宣传活动，每名同学只去1个小区，每个小区至少安排1名同则不同的安排方法共有__________种． 【答案】36 【解析】4名同学到3个小区参加垃圾分类宣传活动，每名同学只去1个小区，每个小区至少安排1名同∴先取2名同学看作一组，选法有：24C 6=.现在可看成是3组同学分配到3个小区，分法有：33A 6=，根据分步乘法原理，可得不同的安排方法6636⨯=种， 故答案为：36.6、【2020年高考全国III 卷理数】262()x x+的展开式中常数项是__________（用数字作答）．【答案】240 【解析】622x x ⎛⎫+ ⎪⎝⎭ 其二项式展开通项：()62612C rrrr xx T -+⎛⎫⋅⋅ ⎪⎝⎭= 1226C (2)r r r r x x --⋅⋅=1236C (2)r r r x -=⋅当1230r -=，解得4r =∴622x x ⎛⎫+ ⎪⎝⎭的展开式中常数项是：66442C 2C 161516240⋅=⋅=⨯=. 故答案为：240.【点睛】本题考查二项式定理，利用通项公式求二项展开式中的指定项，解题关键是掌握()na b +的展第 1 页 / 共 3 页 开通项公式1C r n r r r n T a b -+=，考查了分析能力和计算能力，属于基础题.7、【2020年高考天津】在522()x x+的展开式中，2x 的系数是_________． 【答案】10 【解析】因为522x x ⎛⎫+ ⎪⎝⎭的展开式的通项公式为()55315522C C 20,1,2,3,4,5r r r r r r r T x x r x --+⎛⎫==⋅⋅= ⎪⎝⎭，令532r -=，解得1r =．所以2x 的系数为15C 210⨯=．故答案为：10．【点睛】本题主要考查二项展开式的通项公式的应用，属于基础题． 8、【2020年高考浙江】二项展开式23450123545(2)1x a a x a x a x a x a x ++++++=，则4a =_______，135a a a ++=________．【答案】80；122【解析】5(12)x +的通项为155C (2)2C r r r r r r T x x +==，令4r =，则4444552C 80T x x ==，故580a =；1133551355552C 2C 2C 122a a a ++=++=.故答案为：80；122.。
高考专题 二项式定理(全解析)
1 / 4二项式定理一、选择题1．（求项的系数）5(2x +的展开式中，4x 的系数是( )A ．40B ．60C ．80D ．100【答案】C【解析】5(2x二项展开式的通项为5552155(2)2k k kkk kk T C x C x---+=⋅⋅=⋅⋅．令542k-=，得2k =． 因此，二项展开式中4x 的系数为235280C ⋅=，故选C ．2．（知常数项求某一项的系数）若在(a +3x )(1−√x 3)8关于x 的展开式中，常数项为4，则x 2的系数是（ ） A ．56 B ．-56 C ．112 D ．-112【答案】B【解析】由题意得(1−√x 3)8展开式的通项为T r+1=C 8r (−√x 3)r=(−1)r C 8r x r3，r =0,1,2,⋯,8， ∴(a +3x )(1−√x 3)8展开式的常数项为(−1)0C 8⋅a =a =4， ∴(4+3x )(1−√x 3)8展开式中x 2项为4⋅(−1)6C 86x 63+3x ⋅(−1)3C 83x 33=−56x 2∴展开式中x 2的系数是−56. 故选B3．（直常数项求参数）若6ax ⎛- ⎝展开式的常数项为60，则a 值为( )A ．4B ．4±C ．2D ．2±【答案】D【解析】因为6ax ⎛ ⎝展开式的通项为()()3666622166T 11k k k k k k k k k k C a x x C a x -----+=-=-，令3602k -=，则4k =，所以常数项为()44646160C a --=，即21560a =，所以2a =±. 故选D2 / 44．（奇数项系数的和）记6260126(1)(1)(1)...(1)x a a x a x a x -=+++++++，则0246a a a a +++=（ ）A ．81B ．365C ．481D ．728【答案】B【解析】令x=0得1=0126...a a a a ++++，令x=-2得601234563=a a a a a a a -+-+-+，所以0246a a a a +++=1+729=3652. 故选B5．（由系数二项式系数的和求参数）已知n的展开式中，各项系数的和与其各项二项式系数的和之比为64，则n 等于 A ．4 B ．5 C ．6 D ．7【答案】C【解析】二项式n的各项系数的和为()1+34n n=，二项式n的各项二项式系数的和为()1+12n n=， 因为各项系数的和与其各项二项式系数的和之比为64，所以4=2642n nn =，6n =，故选C ．二、填空题6．（集合关系判断）若)22nx -展开式中只有第六项的二项式系数最大，则展开式中的常数项是____．【答案】180【解析】因为)22nx -展开式中只有第六项的二项式系数最大，所以10n =，展开式的通项公式为5510221101022r rrr rrr r TC xC x---+=⋅⋅⋅=⋅⋅，令5502r-=，解得3 / 42r，所以展开式的常数项为22101280C ⋅=.7．（求系数最大项）61x x ⎛⎫- ⎪⎝⎭的展开式中，系数最大的项为第__________项．【答案】3或5【解析】61x x ⎛⎫- ⎪⎝⎭的展开式中系数与二项式系数只有符号差异，又中间项的二项式系数最大，中间项为第4项其系数为负，则第3，5项系数最大. 8．（二项展开式系数的性质应用）在()()25132x x +-的展开式中，所有的奇次幂的系数和为__________．【答案】478- 【解析】设()()25223456701234567132x x a a x a x a x a x a x a x a x +-=+++++++令1x =，得：0123456716a a a a a a a a =+++++++……① 令1x =-，得：01234567972a a a a a a a a =-+-+-+-……② ①-②得：()13579562a a a a -=+++ 解得：1357478a a a a +++=- 本题正确结果：478-9．（二项式与数列）已知数列{}n a 满足11a k=，k *∈N ，[]n a 表示不超过n a 的最大整数（如[]1,61=，记[]n n b a =，数列{}n b 的前n 项和为n T ）.①若数列{}n a 是公差为1的等差数列，则4T =__________； ②若数列{}n a 是公比为1k +的等比数列，则n T =__________．【答案】6 ()211nk kn k+--【解析】①若数列{}n a 是公差为1的等差数列，且11a k =，*2k k N ≥∈，，则11(1,)n a n n n k=+-∈-，所以[]1n n b a n ==-，则401236T =+++=；故填6.4 / 4②若数列{}n a 是公比为1k +的等比数列，且11a k=，*2k k N ≥∈，，则 1112131211(1)(1)n n n n n n n a k k C k C kk k------=⋅+=⋅+++⋅⋅⋅+，则213111n n k n n n b k C k C -----=++⋅⋅⋅+， 221311101(2)(33)()n n k n n n T k k k k C k C -----=+++++++⋅⋅⋅+++⋅⋅⋅+22223332341451[123(1)](1?)(1)n n n n C C C k C C C k---=+++⋅⋅⋅+-++++⋅⋅+++++⋅⋅⋅++⋅⋅⋅+3422(1))2n n n n n n n C k C k C k --=+++⋅⋅⋅+ 223321()n n n n n C k C k C k k =++⋅⋅⋅+ 21[(1)1]n k nk k =+--；故填21[(1)1]n k nk k+--. 10．（二项式与函数）已知二进制和十进制可以相互转化，例如65432108912021212020212=⨯+⨯+⨯+⨯+⨯+⨯+⨯，则十进制数89转化为二进制数为2(1011001).将n 对应的二进制数中0的个数，记为n a （例如：24(100)=，251(110011)=，289(1011001)=，则42a =，512a =，893a =），记()2n a f n =，则2018201820182019(2)(21)(22)...(21)f f f f ++++++-=__________． 【答案】20183【解析】由题意得20182018201820192212221++-，，，，共201920182018222-=个数中所有的数转换为二进制后，总位数都为2019，且最高位都为1而除最高位之外的剩余2018位中，每一位都是0或者1 设其中的数x ，转换为二进制后有k 个0（0k 2018≤≤） ∴()2kf x =在这20182个数中，转换为二进制后有k 个0的数共有2018kC 个 ∴()()()()201820182018201820192018022122 (2)12k kk f f f f C =++++++-=∑由二项式定理，()201820182018201802123k kk C ==+=∑。
高三数学一轮复习课件：第57讲 二项式定理
教学参考
6.[2016·天津卷] x2-1 8 的展开式中 x7
������
的系数为
.(用数字作答)
[答案] -56
[解析] 展开式的通项 Tr+1=C8������ (x2)8-r -���1��� r=(-1)rC8������ x16-3r,由 16-3r=7,得 r=3,所以所求系 数为(-1)3C83=-56.
第57讲 PART 9
二项式定理
教学参考│课前双基巩固│课堂考点探究│教师备用例题
考试说明
会用二项式定理解决与二项展开式有关的简单问题.
教学参考
考情分析
考点
考查方向
二项式定理 通项公式
二项式的 系数与性质
考例
2016全国卷Ⅰ14 2015全国卷Ⅰ10, 2014全国卷Ⅰ13, 2014全国卷Ⅱ13, 2013全国卷Ⅱ5 2017全国卷Ⅲ4, 2017全国卷Ⅰ6, 2015全国卷Ⅱ15, 2013全国卷Ⅰ9
- 1+32 4=-a1+a2-a3+a4-a5,∴
2(a1+a3+a5)=
1 2
4
+
5 2
4
,解得
a1+a3+a5=31163.
课前双基巩固
题组二 常错题 ◆索引:二项展开式的通项记错致误;混淆二项式系数之和与各项系数之和致误.
5.(1-2x)7 的展开式中第 4 项的系数是
.
[答案] -280
教学参考
8.[2014·全国卷Ⅰ] (x-y)(x+y)8 的展开
式中 x2y7 的系数为
.(用数字
填写答案)
[答案] -20
[解析] (x+y)8 的展开式中 xy7 的系数为 C87=8,x2y6 的系数为C86=28,故(x-y)(x+y)8 的展 开式中 x2y7 的系数为 8-28=-20.
2021版江苏高考数学复习讲义：二项式定理含答案
2021版江苏⾼考数学复习讲义：⼆项式定理含答案当n为偶数时、第n 2＋1项的⼆项式系数最⼤、最⼤值为；当n为奇数时、第n＋12项和n＋32项的⼆项式系数最⼤、最⼤值为.3．各⼆项式系数和(1)(a＋b)n展开式的各⼆项式系数和：C0n＋C1n＋C2n＋…＋C n＝2n.(2)偶数项的⼆项式系数的和等于奇数项的⼆项式系数的和、即C0n＋C2n ＋C4n＋…＝C1n＋C3n＋C5n＋…＝2n－1.⼀、思考辨析(正确的打“√”、错误的打“×”)(1)C r n a n－r b r是(a＋b)n的展开式中的第r项．( )(2)⼆项展开式中、系数最⼤的项为中间⼀项或中间两项．( )(3)(a＋b)n的展开式中某⼀项的⼆项式系数与a、b⽆关．( )(4)通项T r＋1＝C r n a n－r b r中的a和b不能互换．( )[答案](1)×(2)×(3)√(4)√⼆、教材改编1．(1－2x)4展开式中第3项的⼆项式系数为( )A．6 B．－6 C．24 D．－24A[(1－2x)4展开式中第3项的⼆项式系数为C24＝6.故选A.]2．⼆项式? ????12x－2y 5的展开式中x 3y 2的系数是( )A ．5B ．－20C ．20D ．－5A [⼆项式? ????12x－2y 5的通项为T r ＋1＝C r 5? ???12x 5－r(－2y )r .根据题意、得5－r＝3，r＝2，解得r ＝2.所以x 3y 2的系数是C 25? ??123×(－2)2＝5.故选A.]3.C02 019＋C12 019＋C22 019＋…＋C2 0192 019C02 020＋C22 020＋C42 020＋…＋C2 0202 020的值为( ) A ．1 B ．2C ．2 019D ．2 019×2 020A [原式＝22 01922 020－1＝22 01922 019＝1.故选A.]4．若(x －1)4＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4、则a 0＋a 2＋a 4的值为． 8 [令x ＝1、则a 0＋a 1＋a 2＋a 3＋a 4＝0、令x ＝－1、则a 0－a 1＋a 2－a 3＋a 4＝16、两式相加得a 0＋a 2＋a 4＝8.]考点1 ⼆项式展开式的通项公式的应⽤160x 6 [因为(x 2－4)5的展开式的第k ＋1项为T k ＋1＝C k 5(x 2)5－k (－4)k ＝(－4)k C k 5x 10－2k 、令10－2k ＝6、得k ＝2、所以含x 6的项为T 3＝(－4)2·C 25x 6＝160x 6.] 2．若? ?x2＋1ax 6的展开式中常数项为1516、则实数a 的值为( )A ．±2 B.12 C ．－2D ．±12形如(a ＋b )n (c ＋d )m 的展开式问题(x 2＋x ＋y )5为5个x 2＋x ＋y 之积、其中有两个取y 、两个取x 2、⼀个取x 即可、所以x 5y 2的系数为C 25C 23C 1＝30.故选C.]2.? ???x －13x －y 6的展开式中含xy 的项的系数为( ) A ．30 B ．60 C ．90D ．120B [展开式中含xy 的项来⾃C 16(－y )1?x －13x 5、? ????x －13x 5展开式通项为T r ＋1＝(－1)r C r 5x 5－43r 、令5－43r ＝1?r ＝3、x －13x 5展开式中x 的系数为(－1)3C 35、所以? ??x －13x －y 6的展开式中含xy 的项的系数为C 16(－1)C 35(－1)3＝60、故选B.]考点2 ⼆项式系数的和与各项的系数和问题赋值法在求各项系数和中的应⽤C．1120 D．1680C[因为偶数项的⼆项式系数之和为2n－1＝128、所以n－1＝7、n＝8、则＝C r8(－展开式共有9项、中间项为第5项、因为(1－2x)8的展开式的通项T r＋12x)r＝C r8(－2)r x r、所以T5＝C48(－2)4x4、其系数为C48(－2)4＝1120.] 2．在(1－x)(1＋x)4的展开式中、含x2项的系数是b.若(2－bx)7＝a0＋a1x＋…＋a7x7、则a1＋a2＋…＋a7＝ .－128[在(1－x)(1＋x)4的展开式中、含x2项的系数是b、则b＝C24－C14＝2.在(2－2x)7＝a0＋a1x＋…＋a7x7中、令x＝0得a0＝27、令x＝1、得a0＋a1＋a2＋…＋a7＝0.∴a1＋a2＋…＋a7＝0－27＝－128.]3．(a＋x)(1＋x)4的展开式中x的奇数次幂项的系数之和为32、则a＝ .3[设(a＋x)(1＋x)4＝a0＋a1x＋a2x2＋a3x3＋a4x4＋a5x5、令x＝1、得16(a＋1)＝a0＋a1＋a2＋a3＋a4＋a5、①令x＝－1、得0＝a0－a1＋a2－a3＋a4－a5.②①－②、得16(a＋1)＝2(a1＋a3＋a5)、即展开式中x的奇数次幂项的系数之和为a1＋a3＋a5＝8(a＋1)、所以8(a＋1)＝32、解得a＝3.]考点3⼆项式系数的性质⼆项式系数的最值问题。
二项式定理归类(解析版)
专题28二项式定理归类目录【题型一】二项式通项公式.............................................................................................................1【题型二】积型求某项.....................................................................................................................3【题型三】展开式二项式系数和...................................................................................................4【题型四】展开式各项系数和.........................................................................................................5【题型五】赋值法求部分项系数和.................................................................................................7【题型六】换元型赋值求系数与系数和.........................................................................................8【题型七】求系数最大项...............................................................................................................10【题型八】杨辉三角形应用...........................................................................................................11【题型九】三项展开式...................................................................................................................13培优第一阶——基础过关练...........................................................................................................15培优第二阶——能力提升练...........................................................................................................17培优第三阶——培优拔尖练.. (19)【题型一】二项式通项公式【典例分析】二项式5的展开式中常数项为（）A ．80B ．80-C ．40-D ．40【答案】B【分析】求出展开式的通项，再令x 的指数等于0，即可得出答案.【详解】解：二项式5的展开式的通项为()15556155C 2C kkkk kkk T x --+⎛=⋅-=- ⎝，令15506k-=，则3k =，所以常数项为()3352C 80-=-.故选：B.1.将二项式8的展开式中所有项重新排成一列，有理式不相邻的排法种数为（）A ．37A B ．6366A A C ．6367A A D ．7377A A 【答案】C【分析】先利用二项式定理判断其展开式中有理式的项数，再利用插空法进行排列即可.【详解】根据题意，得816324418811C C C 22k k kk k kkk k k T x x x ----+⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭，因为08k ≤≤且*N k ∈，当0k =时，16344k-=，即1T 为有理式；当4k =时，16314k-=，即5T 为有理式；当8k =时，16324k-=-，即9T 为有理式；当{}1,2,3,5,6,7k ∈时，163Z 4k-∉，即k T 为无理式；所以8展开式一共有9个项，有3个有理式，6个无理式，先对6个无理式进行排列，共有66A 种方法；再将3个有理式利用“插空法”插入这6个无理式中，共有37A 种方法；利用分步乘法计数原理可得，一共有6367A A 种方法.故选：C.2.在72x x ⎛⎫- ⎪⎝⎭的展开式中，1x 的系数是（）A ．35B ．35-C ．560D ．560-【答案】C【分析】利用二项式展开式的通项公式，求得展开式中1x的系数.【详解】二项式72x x ⎛⎫- ⎪⎝⎭的展开式的通项公式为()7727722rr rr r r C x C x x --⎛⎫⋅⋅-=-⋅⋅ ⎪⎝⎭，令7214r r -=-⇒=，所以72x x ⎛⎫- ⎪⎝⎭的展开式中1x 的系数为()44721635560C -⋅=⨯=.故选：C3.．在622x x ⎛⎫- ⎪⎝⎭的展开式中，第四项为（）A ．160B ．160-C ．3160x D ．3160x -【答案】D【分析】直接根据二项展开式的通项求第四项即可.【详解】在622x x ⎛⎫- ⎪⎝⎭的展开式中，第四项为()()333323334662C 2C 160T x x x x ⎛⎫=-=-=- ⎪⎝⎭.故选：D.【题型二】积型求某项【典例分析】已知()511a x x ⎛⎫++ ⎪⎝⎭的展开式中31x 的系数为10，则实数a 的值为（）A ．12-B ．12C ．2-D ．2【答案】B【分析】因为()555111111a x a x x x x ⎛⎫⎛⎫⎛⎫++=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，结合二项展开的通项公式运算求解.【详解】511x ⎛⎫+ ⎪⎝⎭的展开式的通项公式为515511C 1C rrr r r r T x x -+⎛⎫⎛⎫=⨯⨯= ⎪ ⎪⎝⎭⎝⎭，0,1,2,3,4,5r =，∵()555111111a x a x x x x ⎛⎫⎛⎫⎛⎫++=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，∴3455C C 10510a a +=+=，解得12a =，故选：B.【变式训练】1.．()()8x y x y -+的展开式中36x y 的系数为（）A ．28B ．28-C ．56D ．56-【答案】B【分析】由二项式定理将8()x y +展开，然后得出8()()x y x y -+，即可求出36x y 的系数.【详解】由二项式定理：8()()x y x y -+080171808888()(C C C )x y x y x y x y =-+++080171808080171808888888(C C C )(C C C )x x y x y x y y x y x y x y =+++-+++090181818081172809888888(C C C )(C C C )x y x y x y x y x y x y =+++-+++观察可知36x y 的系数为6523888887876C C C C 2821321⨯⨯⨯-=-==-⨯⨯⨯.故选：B.2.在()()2311x x +-展开式中，含4x 项的系数是（）A ．5-B ．5C ．1-D ．1【答案】D【分析】由题意可得()()()()233211121x x x x x +-=++-，再对()31x -借助于二项展开式分析运算.【详解】∵()()()()233211121x x x x x +-=++-，且()31x -的展开式的通项为()()3133C 11C ,0,1,2,3rrr r r rr T x x r -+=⨯⨯-=-=，则含4x 项的系数是()()32323321C 11C 1⨯-+⨯-=.故选：D.3.()412x x x ⎛⎫++ ⎪⎝⎭的展开式中，常数项为（）A ．2B ．6C ．8D ．12【答案】D【分析】先将()412x x x ⎛⎫++ ⎪⎝⎭展开，再求，41x x ⎛⎫+ ⎪⎝⎭展开式的通项，即可求出答案.【详解】()4442=11+12x x x x x x x x ⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，41x x ⎛⎫+ ⎪⎝⎭展开式的通项为：4421441C C rr r r r r T x x x --+⎛⎫== ⎪⎝⎭，当420r -=即2r =时，242C =12⋅，所以()412x x x ⎛⎫++ ⎪⎝⎭的展开式中，常数项为12.故选：D.【题型三】展开式二项式系数和【典例分析】．()101x -的展开式中所有奇数项的二项式系数和为（）．A ．128B ．256C ．512D ．1024【答案】C【分析】根据奇数项的二项式系数和为22n计算可得；【详解】解：()101x -的展开式中所有奇数项的二项式系数和为1025122=，故选：C ．【变式训练】1.已知2(n x的展开式中，各二项式系数和为64，则x 7的系数为（）A ．15B ．20C ．60D ．80【答案】C【分析】由二项式系数和求得n ，再利用通项可得x 7的系数.【详解】由二项式系数和为264n =，解得6n =，通项为()512622166C C 2rr rr r r r T x x --+==，令51272-=r ，得2r =，则x 7的系数为226260C =.故选：C.2.已知()2*2nx n x ⎛⎫-∈ ⎪⎝⎭N 的展开式中各项的二项式系数之和为64，则其展开式中3x 的系数为（）A ．240-B ．240C ．160-D ．160【答案】C【分析】由二项式系数的性质求出n ，写出二项展开式的通项公式，令x 的指数为3，即可得出答案.【详解】由展开式中各项的二项式系数之和为64，得264n =，得6n =．∵622x x ⎛⎫- ⎪⎝⎭的展开式的通项公式为()()()621231662C 1C ·2·1rrrr r r rr r T x x x --+⎛⎫=-=- ⎪⎝⎭，令1233r -=，则3r =，所以其展开式中3x 的系数为()3336C 21160⨯⨯-=-．故选：C.3.已知二项式212mx x ⎛⎫+ ⎝⎭的展开式的二项式系数之和为64，则展开式中含x 3项的系数是（）A ．1B ．32C ．52D ．3【答案】D【分析】由二项式系数的和的公式解得m 的值，运用二项展开式的通项公式解出r 的值，进而可得3x 项的系数.【详解】由题意知，264m =，解得：6m =，所以621()2x x +的二项展开式的通项公式为663166211C C 22rr r r rr r T x x x --+⎛⎫=⋅= ⎪⎝⎭，令6－3r ＝3，得r ＝1，故含3x 项的系数为161132C =.故选：D.【题型四】展开式各项系数和【典例分析】在3nx⎛⎝的展开式中，各项系数与二项式系数和之比为64，则该展开式中的常数项为（）A ．15B ．45C ．135D ．405【答案】C【分析】令1x =可得展开式各项系数和，再由二项式系数和为2n ，即可得到方程，求出n ，再写出二项式展开式的通项，令x 的指数为0，即可求出r ，再代入计算可得；【详解】解：对于3nx ⎛ ⎝，令1x =，可得各项系数和为4n ，又二项式系数和为2n，所以6426422nn n ===，解得6n =，所以63x ⎛+ ⎝展开式的通项为()36662166C 3C 3rr r r r r r T x x ---+=⋅=⋅，令3602r -=，解得4r =，所以42056C 3135T x =⋅=；故选：C1.．0x ∀≠，101x x ⎛⎫+ ⎪⎝⎭可以写成关于221x x ⎛⎫+ ⎪⎝⎭的多项式，则该多项式各项系数之和为（）.A ．240B ．241C ．242D ．243【答案】D【分析】利用换元法，将101x x ⎛⎫+ ⎪⎝⎭转化为()52t +，从而利用赋值法即可求得该多项式各项系数之和.【详解】因为222112x x x x ⎛⎫+=++ ⎪⎝⎭，令221t x x =+，则()5105221122x x t x x ⎡⎤⎛⎫⎛⎫+=++=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，令1t =，则()5523243t +==，所以该多项式各项系数之和为243.故选：D.2.已知二项式1nx ⎛⎫ ⎪⎝⎭的展开式中，所有项的系数之和为32，则该展开式中x 的系数为（）A ．405-B ．405C ．81-D ．81【答案】A【分析】根据二项式定理，写出通项公式，求出指定项的系数.【详解】令1x =，可得所有项的系数之和为2325n n =⇔=，则11(5)(52)5522155(1)3C (1)3C r r r r rr rr rr r Tx xx------+=-=-，由题意5312r-=，即1r =，所以展开式中含x 项的系数为4153C 405-=-．故选：A ．3.已知5312a x x x x ⎛⎫⎛⎫+- ⎪⎪⎝⎭⎝⎭的展开式中各项系数的和为4，则该展开式中的常数项为（）A ．200B ．280C ．200-D ．280-【答案】D【分析】根据题意将1x =代入，由各项系数的和为4可求得a 的值，再根据二次项展开式求出512x x ⎛⎫- ⎪⎝⎭的通项()5521512C rr r rr T x --+=-，分别与x 和33x相乘得到常数项，可求出r 的值，再合并即可得到结果.【详解】由题意，令1x =，得到展开式的各项系数和为1a +，所以14a +=，解得3a =.所以55553331311312222a x x x x x x x x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-=+-=-+- ⎪⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，512x x ⎛⎫- ⎪⎝⎭展开式的通项为()5521512C r r r rr T x --+=-，令521r -=-，解得3r =；令523-=r ，解得1r =，所以展开式中的常数项为()()35335115512C 312C 280---⨯+⨯-⨯=-.选项D 正确，故选D.【题型五】赋值法求部分项系数和【典例分析】若()6652460126x y a y a xy a x y a x +=+++⋅⋅⋅+，则()()220246135a a a a a a a +++-++的值为（）A ．0B ．32C ．64D ．128【答案】A【分析】先利用赋值法求得0123456a a a a a a a -+-+-+和0123456a a a a a a a ++++++的值，进而求得()()220246135a a a a a a a +++-++的值.【详解】1x =，1y =-时，01234560a a a a a a a =-+-+-+1x =，1y =时，012345664a a a a a a a =++++++()()220246135a a a a a a a +++-++()()012345601234560640a a a a a a a a a a a a a a =-+-+-+++++++=⨯=，故选：A.【变式训练】1.已知()727012752x a a x a x a x -=++++，则0127a a a a ++++=（）A ．128B ．2187C ．78125D ．823543【答案】D【分析】由展开式通项公式可得系数0246a a a a 、、、小于0，系数1357a a a a 、、、大于0，由赋值法令=1x -，所求值即为()7-5-1-2⨯⎡⎤⎣⎦.【详解】()752x -的展开式中第1k +项为()()()77771777C 52C 52=kkkk k kk k k k T x x a x ----+-=-=-，故系数()777C 52kk kk a --=-，即当k 为奇数时，系数0246a a a a 、、、小于0，当k 为偶数时，系数1357a a a a 、、、大于0.()7012701234567-823543----5-1-2a a a a a a a a a a a a ++++=++++=⨯=⎡⎤⎣⎦.故选：D2.()4234012341x a a x a x a x a x +=++++，则01234a a a a a -+-+=（）A ．1B ．3C ．0D ．3-【答案】C【分析】根据展开式，利用赋值法取=1x -即得.【详解】因为()4234012341x a a x a x a x a x +=++++，令=1x -，可得()401234110a a a a a -+-+=-=.故选：C.3.已知()()4529012912x x a a x a x a x -+=++++，则2468a a a a +++=（）A ．40B ．8C ．16-D ．24-【答案】D【分析】设45()(1)(2)f x x x =-+，根据二项式展开式可得0(0)a f =、02468(1)(1)2f f a a a a a -+++++=，即可求解.【详解】设45()(1)(2)f x x x =-+，则50(0)232a f ===，0129(1)0a a a a f ++++==4012349(1)216a a a a a a f -+-+--=-==，所以02468(1)(1)82f f a a a a a -+++++==，所以246883224a a a a +++=-=-.故选：D.【题型六】换元型赋值求系数与系数和【典例分析】已知()()()()20232202301220232111x a a x a x a x -=+++++++，则0122023a a a a ++++=（）A ．40462B ．1C ．20232D ．0【答案】A【分析】首先利用换元，转化为()20232202301220233t a a t a t a t -=++++，再去绝对值后，赋值求和.【详解】令1t x =+，可得1x t =-，则()()20232023220230122023213t t a a t a t a t --=-=++++⎡⎤⎣⎦，二项式()20233t -的展开式通项为()202312023C 3rr rr T t -+=⋅⋅-，则()20232023C 31(02023rr rr a r -=⋅⋅-≤≤且N)r ∈．当r 为奇数时，0r a <，当r 为偶数时，0r a >，因此，()2023404601220210122023312a a a a a a a a ++++=-+--=+=．故选：A ．1.已知10111012C C n n =，设()()()()201223111n nn x a a x a x a x -=+-+-++-，下列说法：①2023n =，②20233n a =-，③0121n a a a a ++++=，④展开式中所有项的二项式系数和为1.其中正确的个数有（）A ．0B ．1C ．2D ．3【答案】C【分析】根据组合数的性质求得n ，根据二项式展开式的通项公式、赋值法、二项式系数和的知识求得正确答案.【详解】101110122023n =+=，①对.()20232202301220232023(23)(1)(1)(1211)x a a x a x a x x -=+-+-+=--⎡⎤⎦+-⎣，所以02023202320232023C 22n a a =⋅==，②错.令2x =得0121n a a a a ++++=，③对.展开式中所有项的二项式系数和为20232，④错.所以正确的说法有2个.故选：C2.已知36C C n n =，设()()()()201223111n n n x a a x a x a x -=+-+-+⋅⋅⋅+-，则12n a a a ++⋅⋅⋅+=（）A ．1-B ．0C ．1D ．2【答案】D【分析】利用组合数的性质可求得n 的值，再利用赋值法可求得0a 和012n a a a a +++⋅⋅⋅+的值，作差可得出所求代数式的值.【详解】因为36C C n n =，所以由组合数的性质得369n =+=，所以()()()()929012923111x a a x a x a x -=+-+-+⋅⋅⋅+-，令2x =，得()90129223a a a a ⨯-=+++⋅⋅⋅+，即01291a a a a +++⋅⋅⋅+=.令1x =，得()902131a ⨯-==-，所以()()12901290112a a a a a a a a +++=+⋅⋅⋅⋅++⋅=⋅+---=，故选：D.3.．已知(1)n x -的二项展开式的奇数项二项式系数和为64，若()2012(1)1(1)(1)n n n x a a x a x a x -=+++++⋯++，则1a 等于（）A ．192B ．448C ．192-D ．448-【答案】B【分析】根据奇数项二项式系数和公式求出n ，再利用展开式求1a .【详解】(1)n x -的二项展开式的奇数项二项式系数和为64，1264n -∴=，即7n =；则77(1)[(1)2]x x -=+-的通项公式为717C (1)(2)k k kk T x -+=+-，令71k -=，则6k =，所以6617C (2)448a =⨯-=.故选：B【题型七】求系数最大项【典例分析】已知22nx ⎫+⎪⎭的展开式中，第3项的系数与倒数第3项的系数之比为116，则展开式中二项式系数最大的项为第（）项.A ．3B ．4C ．5D ．6【答案】C【分析】先求出二项式展开的通项公式，分别求出第3项的系数与倒数第3项的系数，由题意得到关于n 的方程，即可确定其展开式二项式系数最大项.【详解】22nx ⎫⎪⎭的展开式通项公式为52122C C 2rn r n r r r rr n n T x x --+⎛⎫==⋅⋅ ⎪⎝⎭，则第3项的系数为22C 2n ⋅，倒数第3项的系数为22C 2n n n --⋅，因为第3项的系数与倒数第3项的系数之比为116，所以22422C 212C 216n n n n ---⋅==⋅，所以2226C 2C 2n n n n --⋅=⋅，解得8n =，所以展开式中二项式系数最大的项为第5项，故选：C 【变式训练】1.已知2nx ⎫⎪⎭的展开式中只有第5项是二项式系数最大，则该展开式中各项系数的最小值为（）A ．448-B ．1024-C ．1792-D ．5376-【答案】C【分析】先根据二项式系数的性质可得=8n ，再结合二项展开式的通项求各项系数()82C r rr a =-，分析列式求系数最小项时r 的值，代入求系数的最小值.【详解】∵展开式中只有第5项是二项式系数最大，则=8n∴展开式的通项为()83821882C 2C ,0,1,...,8rr rr rr r T x r x --+⎛⎫=-=-= ⎪⎝⎭则该展开式中各项系数()82C ,0,1,...,8r rr a r =-=若求系数的最小值，则r 为奇数且+2200r r r r a a a a --≤-≤⎧⎨⎩，即()()()()+2+28822882C 2C 02C 2C 0r r r r r r r r -----≤---≤⎧⎪⎨⎪⎩，解得=5r ∴系数的最小值为()55582C 1792a =-=-故选：C.2.已知m 为正整数，()2m x y +展开式的二项式系数的最大值为a ，()21m x y ++展开式的二项式系数的最大值为b ，且137a b =，则m 的值为（）A ．4B ．5C ．6D ．7【答案】C【分析】根据二项式系数的性质确定,a b ，由关系137a b =列方程求m 的值.【详解】由题意可知221C ,C m mm m a b +==,137a b =,22113C 7C m mm m +∴=,即()()()2!21!137!!!1!m m m m m m +=⋅⋅+,211371m m +∴=⨯+，解得6m =．故选：C ．3.已知()*(1),n mx n m +∈∈N R 的展开式只有第5项的二项式系数最大，设2012(1)n n n mx a a x a x a x +=++++，若18a =，则23n a a a +++=（）A ．63B ．64C ．247D ．255【答案】C【分析】根据二项式系数的性质求出n ，根据18a =求出m ，再由赋值法求解即可.【详解】因为展开式只有第5项的二项式系数最大，所以展开式共9项，所以8n =，718C 8a m =⋅=，∴1m =，∴8280128(1)x a a x a x a x +=++++，令1x =，得8012382256a a a a a +++++==，令0x =，得01a =，∴2325681247n a a a +++=--=．故选：C ．【题型八】杨辉三角形应用【典例分析】“杨辉三角”是中国古代数学文化的瑰宝之一，它揭示了二项式展开式中的组合数在三角形数表中的一种几何排列规律，如图所示，则下列关于“杨辉三角”的结论正确的是（）A ．222234510C C C C 165+++⋅⋅⋅+=B ．在第2022行中第1011个数最大C ．第6行的第7个数、第7行的第7个数及第8行的第7个数之和等于9行的第8个数D ．第34行中第15个数与第16个数之比为2：3【答案】C【分析】A 选项由11C C C m m m n n n -++=及22222322234510334510C C C C C C C C C 1++++=+++++-即可判断；B 选项由二项式系数的增减性即可判断；C 选项由11C C C m m m n n n -++=及6767C C =即可判断；D 选项直接计算比值即可判断.【详解】由11C C C m m m n n n -++=可得22222322234510334510C C C C C C C C C 1++++=+++++-32223445101111109C C C C 1C 11164321⨯⨯=++++-=-=-=⨯⨯，故A 错误；第2022行中第1011个数为1010101120222022C C <，故B 错误；666766767678778889C C C C C C C C C ++=++=+=，故C 正确；第34行中第15个数与第16个数之比为14153434343321343320C :C :15:203:4141311514131⨯⨯⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯⨯，故D 错误.故选：C.【变式训练】1.将三项式展开，得到下列等式：20(1)1a a ++=212(1)1a a a a ++=++22432(1)2321a a a a a a ++=++++2365432(1)367631a a a a a a a a ++=++++++⋯观察多项式系数之间的关系，可以仿照杨辉三角构造如图所示的广义杨辉三角形，其构造方法为：第0行为1，以下各行每个数是它正上方与左右两肩上的3个数(不足3个数时，缺少的数以0计)之和，第k 行共有21k +个数．则关于x 的多项式()2253(1)a ax x x +-++的展开式中，8x 项的系数（）A ．()2151a a +-B ．()2151a a ++C ．()21523a a ++D ．()21523a a +-【答案】D【分析】直接利用广义杨辉三角和数据的组合的应用求出结果．【详解】根据广义杨辉三角的定义：()5210987654321151530455145301551a a a a a a a a a a a a ++=++++++++++；故()5210987654321151530455145301551x x x x x x x x x x x x ++=++++++++++；关于x 的多项式()()52231a ax x x +-++的展开式中8x 项的系数为()()22315301523aa a a -⨯+⨯=+-.故选：D ．2.当N n ∈时，将三项式()21nx x ++展开，可得到如图所示的三项展开式和“广义杨辉三角形”：若在()()5211ax x x +++的展开式中，8x 的系数为75，则实数a 的值为（）A ．1B ．1-C ．2D ．2-【答案】C【分析】根据广义杨辉三角形可得出()521x x ++的展开式，可得出()()5211ax x x +++的展开式中8x 的系数，即可求得a 的值.【详解】由广义杨辉三角形可得()521098765432151530455145301551xx x x x x x x x x x x ++=++++++++++，故()()5211ax x x +++的展开式中，8x 的系数为153075a +=，解得2a =.故选：C.3.如图，在由二项式系数所构成的杨辉三角形中，若第n 行中从左至右第14与第15个数的比为2:3，则n 的值为___________.【答案】34【分析】根据杨辉三角形中数据的规律可以写出第n 行中从左至右第14与第15个数的表达式，根据比例结果可计算得n 的值.【详解】由题意可知，根据数字规律可以看出第n 行中从左至右第m 个数为1C m n -所以，第n 行中从左至右第14与第15个数分别是13C n 和14C n ；即1314C 2C 3nn =，由组合数计算公式!C !()!m nn m n m =-可得142133n =-，计算的34n =；故答案为：34.【题型九】三项展开式【典例分析】下列各式中，不是()422a a b +-的展开式中的项是（）A ．78aB ．426a bC ．332a b -D ．3224a b -【答案】D【分析】根据题意多项式展开式中，有一个因式选2a ，有2个因式选b -，其余的2个因式选2a ，有1个因式选b -，剩下的3个因式选2a ，分别计算所得项，即可得到结果.【详解】()422a a b +-表示4个因式22a a b +-的乘积，在这4个因式中，有一个因式选2a ，其余的3个因式选2a ，所得的项为()3132743C 2C 8a aa ⨯⨯=，所以78a 是()422a a b +-的展开式中的项，在这4个因式中，有2个因式选b -，其余的2个因式选2a ，所得的项为()()222224242C C 6b a a b ⨯-⨯⨯=，所以426a b 是()422a a b +-的展开式中的项，在这4个因式中，有1个因式选b -，剩下的3个因式选2a ，所得的项为()()313343C C 232b a a b ⨯-⨯=-，所以332a b -是()422a a b +-的展开式中的项，在这4个因式中，有2个因式选b -，其余的2个因式中有一个选2a ，剩下的一个因式选2a ，所得的项为()()2212132421C C C 224b a a a b ⨯-⨯⨯⨯⨯=，所以3224a b -不是()422a a b +-的展开式中的项.故选:D.三项展开式的通项公式：1.411()x y x y+--的展开式的常数项为A ．36B ．36-C ．48D ．48-【答案】A【分析】先对多项式进行变行转化成441()1x y xy ⎛⎫+- ⎪⎝⎭，其展开式要出现常数项，只能第1个括号出22x y 项，第2个括号出221x y 项.【详解】∵4444111()1x y x y x y x y x y xy xy ⎛⎫⎛⎫⎛⎫++--=+-=+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，∴411x y x y ⎛⎫+-- ⎪⎝⎭的展开式中的常数项为22244222(C (C 361))x y x y ⨯=.故选：A.2.在()621x x +-的展开式中，含3x 项的系数为（）A ．30-B ．10-C ．30D ．50【答案】B【分析】把()621x x +-看成6个()21x x +-相乘，利用分类加法计数原理和分步乘法计数原理，即可得到结果.【详解】()621x x +-是6个()21x x +-相乘，需要依次从每个()21x x +-的三项（1，x ，2x -）中选出一项后相乘，就可得到展开式中的一项.得到3x 项的方法有两类：第一类是，6个()21x x +-的1个()21x x +-里选出x ，1个()21x x +-里选出2x -，其余()21x x +-里选出1，相乘得3x -，这类方法，共可得到114654CC C 30⨯⨯=个3x -，合并同类项后即得到330x -；第二类是，6个()21x x +-的3个()21x x +-里选出x ，其余()21x x +-里选出1，相乘得3x ，这类方法，共可得到3363C C 20⨯=个3x ，合并同类项后即得到320x .再将上述两项合并，得333302010x x x -+=-，因此3x 项的系数为10-.故选：B.3.()823x y z ++的展开式中，共有多少项？（）A ．45B ．36C ．28D ．21【答案】A【分析】按照展开式项含有字母个数分类，即可求出项数.【详解】解：当()823x y z ++展开式的项只含有1个字母时，有3项，当()823x y z ++展开式的项只含有2个字母时，有2137C C 21=项,当()823x y z ++展开式的项含有3个字母时，有27C 21=项,所以()823x y z ++的展开式共有45项；故选：A.培优第一阶——基础过关练1．()()412x x --的展开式中，3x 项的系数为（）A ．2B ．14C ．48D ．2-【答案】B 【分析】3x 项由()41x -的2x 项与x 的积和()41x -的3x 项和2-的积组成，再结合二项式定理得出系数.【详解】()41x -展开式的通项为()441C rr rx--，在()()412x x --中，3x 项由()41x -的2x 项与x 的积和()41x -的3x 项和2-的积组成，故可得3x 的系数为()()()2121441C 11C 214-⨯+-⨯-=．故选：B ．2．6⎛⎫ ⎪⎝⎭的展开式中3x 的系数为（）A ．160-B ．64-C ．64D ．160【答案】C【分析】在二项展开式的通项公式中令x 的幂指数为3，求出r 的值，即可求得3x 的系数.【详解】6的展开式的通项公式为663166C (C 2(1)r r r r rr r r T x ---+==⋅-⋅，令33r -=，则0r =，故展开式中3x 的系数为0606C 2(1)64⋅-=.故选：C.3．已知1021001210(1)-=++++x a a x a x a x ,则()01210+++=a a a a （）A ．10-B ．10C ．1D ．1-【答案】D【分析】赋值法分别求0a 和1210a a a +++即可.【详解】令0x =可得01a =,令1x =可得012100a a a a ++++=即121001a a a a +++=-=-,所以()012101a a a a +++=-.故选:D.4．在4(1)(12)()a x y a ++∈N 的展开式中，记m n x y 项的系数为(),f m n ，若()()0,11,06f f +=，则a 的值为（）A ．0B ．1C ．2D ．3【答案】B【分析】利用二项式定理展开公式求解.【详解】()01140,1C C 2,a f =⋅()1041,0C C ,a f =⋅所以()()0,11,0246f f a +=+=解得1a =，故选：B.5．()61x a y x ⎛⎫-+ ⎪⎝⎭的展开式中，含14x y -项的系数为15-，则=a （）A ．1B ．1-C ．1±D ．2±【答案】C【分析】先求出()6a y +的通项公式，然后整理出14x y -项的系数，根据系数相等可得答案.【详解】()6a y +的展开式的通项公式为66C rrr ay -，令4r =，可得6246C 15r r ra y a y -=；所以含14x y -项的系数为215a -，即21515a -=-，解得1a =±.故选：C.6．511(12)x x ⎛⎫+- ⎪⎝⎭的展开式中，常数项是（）A ．9-B ．10-C ．9D ．10【答案】A【分析】由二项式定理的通项公式计算可得结果.【详解】∵555111(12)(12)(12)x x x x x ⎛⎫+--=+- ⎪⎝⎭，5(12)x -第1r +项为：155C (2)C (2)r r r r r r T x x +=-=-，(0,1,,5)r =，51(12)x x -的第1k +项为：11551C (2)C (2)k k kk k k T x x x-+=-=-，(0,1,,5)k =∴展开式中的常数项()()001155C 2C 21109T =-+-=-=-.故选：A.7．已知()na b +的展开式中只有第7项的二项式系数最大，则n =（）A ．11B ．10C ．12D ．13【答案】C【分析】当n 为偶数时，展开式中第12n+项二项式系数最大，当n 为奇数时，展开式中第12n +和32n +项二项式系数最大.【详解】∵只有第7项的二项式系数最大，∴172n+=，∴12n =．故选：C8．若()()()()()42201223222nn x x x a a x a x a x -+=+-+-++-，则564a a a +=（）A ．15B ．25C ．35D ．45【答案】D【分析】将23x x +中含有x 的项都写成2x -的形式，即可得解.【详解】()()()()()442223222107x x x x x x ⎡⎤+⎣⎦-+=---+()()()654272102x x x =-+-+-，所以6541,7,10a a a ===，所以56445a a a +=.故选：D.培优第二阶——能力提升练1．8x ⎛⎝的展开式中，以下为有理项的是（）A ．第3项B ．第4项C ．第5项D ．第6项【答案】AC【分析】根据给定二项式求出其展开式的通项，再求出通项中x 的幂指数为整数的所对项数即可.【详解】8x ⎛⎝的展开式的二项式通项为138822188C C ,0,1,2,3,4,5,6,7,8r r r rr r T xx x r ---+⎛⎫=== ⎪⎝⎭，令823r -为整数，求得0r =，2，4，6，8，所以对应第1,3,5,7,9项为有理项，故选：AC2．在62x x ⎛⎫+ ⎪⎝⎭的展开式中，下列说法正确的是（）A ．常数项为160B ．第3项二项式系数最大C ．所有项的二项式系数和为62D ．所有项的系数和为63【答案】ACD【分析】先求62x x ⎛⎫+ ⎪⎝⎭的通项公式可得选项A 的正误，利用n 的值可得选项B 、C 的正误，所有项的系数和可以利用赋值法求解【详解】62x x ⎛⎫+ ⎪⎝⎭展开式的通项为66261662C 2C rr r r r r r T x xx ---+⎛⎫=⋅= ⎪⎝⎭，由260r -=，得3r =，所以常数项为3362C 160=，A 正确；二项式展开式中共有7项，所以第4项二项式系数最大，B 错误；由6n =及二项式系数和的性质知，所有项的二项式系数和为62，C 正确；令1x =，得()660126213a a a a +++⋯+=+=，所有项的系数和为63，D 正确；故选：ACD.3．若2022220220122022(1)x a a x a x a x -=++++，则（）A ．01a =B ．12022a =C ．1220221a a a +++=-D ．012320221a a a a a -+-++=【答案】AC【分析】对ACD ，由赋值法可判断；对B ，由二项式展开项通项公式可求.【详解】对A ，令0x =得01a =，A 对；对B ，由二项式展开项通项公式可得第2项为()1120212202211C 120222022T x x a x a =-=-=⇒=-，B 错对C ，令1x =得0122022122022001a a a a a a a a +++=++=-+⇒=-+，C 对；对D ，令=1x -得0123220222022a a a a a -+-++=，D 错.故选：AC.4．下列说法中正确的有（）A ．2799C C =B ．233445C C C +=C ．123C C C C 2n n n n n n ++++=D ．()41x +展开式中二项式系数最大的项为第三项【答案】ABD【分析】根据组合数的性质即可判断AB ；根据二项式之和即可判断C ；对于D ，先求出展开式的通项，不妨设第1k +项的系数最大，则有144144C C C C kk k k -+⎧≥⎨≥⎩，从而可得出答案.【详解】对于A ，由组合数的性质可得2799C C =，故A 正确；对于B ，由组合数的性质可得233445C C C +=，故B 正确；对于C ，因为0123C C C C C 2n n n n n n n +++++=，所以1231C C C C 2n n n n n n ++++=-，故C 错误；对于D ，()41x +展开式的通项为14C kkk T x +=，不妨设第1k +项的二项式系数最大，则144144C C C C kk k k -+⎧≥⎨≥⎩，解得2k =，所以()41x +展开式中二项式系数最大的项为第三项，故D 正确.故选：ABD.5．()521x y ++展开式中24x y 的系数为________（用数字作答）.【答案】30【分析】求出()521⎡⎤++⎣⎦x y 的通项令2r =时得()3245C 1+x y ，再求出()31x +展开式中2x 的系数可得答案.【详解】()521⎡⎤++⎣⎦x y 展开式通项为()55211C -+=+rr r r T x y ，{}0,1,2,3,4,5r Î，当2r =时()32425C 1=+T x y ，由()301223333331C +C +C +C +=x x x x 得2x 的系数为3，故24x y 的系数为25C 330⨯=.故答案为：30.6．已知()01311(1)22nn n x a a x a x ⎛⎫+=+++++ ⎪⎝⎭，写出满足条件①②的一个n 的值__________.①*3,n n ≥∈N ；②3,0,1,2,,i a a i n ≥=.【答案】8,9,10或11.（答案不唯一）【分析】令1x t +=，得到1C ,0,1,2,,2ii i na i n ⎛⎫== ⎪⎝⎭，再由3,0,1,2,,i a a i n ≥=求解.【详解】解：令1x t +=，得01112nn n t a a t a t ⎛⎫+=+++ ⎪⎝⎭，1C ,0,1,2,,2ii i n a i n ⎛⎫∴== ⎪⎝⎭，由条件②知32323234343411C C ,,22811,11C C ,22n n n n a a n a a ⎧⎧⎛⎫⎛⎫≥⎪⎪ ⎪ ⎪≥⎪⎪⎝⎭⎝⎭⇒⇒≤≤⎨⎨≥⎛⎫⎛⎫⎪⎪≥ ⎪ ⎪⎪⎪⎝⎭⎝⎭⎩⎩.又*,n n ∈∴N 的值可以为8,9,10或11.（答案不唯一）故答案为：8,9,10或11.（答案不唯一）7．若()()542345321x a bx cx dx ex fx x -=+++++++，其中a ，b ，c ，d ，e ，f 为常数，那么b c d f +++=______.【答案】109【分析】利用赋值法求a b c d e f +++++和a ，利用二项式展开式通项公式求e ，由此可得结果.【详解】因为()()542345321x a bx cx dx ex fx x -=+++++++，令1x =，得316a b c d e f -=++++++，整理得：19a b c d e f +++++=-，令0x =，得961a -=+，97a =-，因为()52x -的展开式的通项公式为()515C 2rr rr T x -+=⋅-，所以()532x -的展开式中含4x 项的系数为()153C 2⋅-，又()41x +的展开式中含4x 项的系数为44C ，所以()153C 21e ⋅-=+，31e =-，将a 、e 代入即可求得109b c d f +++=.故答案为：109.8．0x ∀≠，101x x ⎛⎫+ ⎪⎝⎭可以写成关于221x x ⎛⎫+ ⎪⎝⎭的多项式，则该多项式各项系数之和为_________.【答案】243【分析】利用换元法，将101x x ⎛⎫+ ⎪⎝⎭转化为()52t +，从而利用赋值法即可求得该多项式各项系数之和.【详解】因为222112x x x x ⎛⎫+=++ ⎪⎝⎭，令221t x x =+，则()5105221122x x t x x ⎡⎤⎛⎫⎛⎫+=++=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，令1t =，则()5523243t +==，所以该多项式各项系数之和为243.故答案为：243培优第三阶——培优拔尖练1．已知集合{}2019,12,6,10,5,1,0,1,8,15H =---，记集合H 的非空子集为1M 、2M 、L 、1023M ，且记每个子集中各元素的乘积依次为1m 、2m 、L 、1023m ，则121023m m m +++的值为___________.【答案】1-【分析】构造函数()()()()()()()()()()201912610511815f x x x x x x x x x x x =+++---+++，设该函数展开式中所有项系数之和为T ，则1210231m m m T +++=-，利用赋值法可求得结果.【详解】设集合H 的十个元素分别为1a 、2a 、L 、10a .1210121391012389101210121023m a a a a a a a a a a a a a a a a m m a a =+++++++++++++++.设函数()()()()()()()()()()201912610511815f x x x x x x x x x x x =+++---+++展开式中所有项系数之和为T ，则1210231m m m T +++=-，因为()10T f ==，所以11T -=-．故答案为：1-.【点睛】关键点点睛：本题主要考查的集合子集的判定，构造函数求解，属于难题．本题的关键是根据二项定理的推导过程构造出函数()()()()()()()()()()201912610511815f x x x x x x x x x x x =+++---+++，这种转化思想是本题的难点．2．设0i a i =（，1，2，…，2022）是常数，对于∀x ∈R ，都有()()()()()20220122022112122022x a a x a x x a x x x =+-+--++---（），则012345202120222!3!4!2020!2021!a a a a a a a a -+-+-+-+-=________.【答案】2021【分析】先令1x =，求得0a 的值，再将给定的恒等式两边求关于x 的导数，然后令1x =，从而可得所求的值.【详解】因为()()()()()()20220122022112122022xa a x a x x a x x x =+-+--++---，则令1x =可得01a =.又对()()()()()()20220122022112122022xa a x a x x a x x x =+-+--++---两边求导可得：()()()()()2021122022202212122022x a a x x a x x x ''=+--++---⎡⎤⎡⎤⎣⎦⎣⎦，令()()()()12n f x x x x n =--⨯⨯-，则()()()()()()12+2n f x x x x n x x n ''=--⨯⨯--⨯⨯-⎡⎤⎣⎦，所以()()()()()1112111!n n f n n -'=-⨯⨯-=--，所以()()()12202120211232022202211112!12021!a a a a ⨯=+⨯-⨯+⨯-⨯++⨯-故123202220222!2021!a a a a =-+--，所以012345202120222!3!4!2020!2021!202212021a a a a a a a a -+-+-+-+-=-=.故答案为：2021.【点睛】本题考查函数的导数以及恒等式的系数和的求法，注意根据恒等式的特征选择合适的赋值，本题属于较难题.3．()623a b c +-的展开式中23ab c 的系数为______.【答案】-6480【分析】()()662323a b c a b c +-=+-⎡⎤⎣⎦，利用二项式定理得到()3345402T c a b =-⋅+，再展开()32a b +，计算得到答案.【详解】()()662323a b c a b c +-=+-⎡⎤⎣⎦，展开式的通项为：()()61623rrr r T C a b c -+=+-，取3r =，则()()()63333346235402T C a b c c a b -=+-=-⋅+，()32a b +的展开式的通项为：()3132mm m m T C a b -+=，取2m =，得到()22233212T C a b ab ==，故23ab c 的系数为540126480-⨯=-.故答案为：6480-.【点睛】本题考查了二项式定理的应用，意在考查学生的计算能力和应用能力.4．对任意正整数i ，设函数()414034log 2i f x i =-⋅的零点为i a ，数列{}n a 的前n 项和为()*n S n N ∈，则使得n S 能被2n +整除的正整数n 的个数是________．【答案】0【分析】要求零点，应先把函数()i f x 解析式中的对数化为相同底数，再求函数的零点可得2017i x a i ==，进而写出数列{}n a 的前n 项和201720172017123n S n =++++，用二项式定理和整除思想说明2017n 不能被2n +整除即可。
2020届高考数学(理)一轮必刷题 专题57 二项式定理(解析版)
考点57 二项式定理1．(2-x)(1+2x)5展开式中,含x2项的系数为()A.30B.70C.90D.-150【答案】B【解析】∵展开式的通项公式为T r+1=·,∴展开式中,含x2项的系数为2××22-×2=70,故选B.2．(1－3x)7的展开式的第4项的系数为()A．－27C37B．－81C47C．27C37D．81C47【答案】A【解析】(1－3x)7的展开式的第4项为T3＋1＝C37×17－3×(－3x)3＝－27C37x3，其系数为－27C37，选A.3．设n为正整数,展开式中存在常数项,则n的一个可能取值为()A.16B.10C.4D.2【答案】B【解析】∵展开式的通项公式为=·=(-1)k,令=0,得k=,∴n可取10.4．(x－y)(x＋2y＋z)6的展开式中，x2y3z2的系数为()A．－30 B．120C．240 D．420【答案】B【解析】[(x＋2y)＋z]6的展开式中含z2的项为C26(x＋2y)4z2，(x＋2y)4的展开式中xy3项的系数为C34×23，x2y2项的系数为C24×22，∴(x－y)(x＋2y＋z)6的展开式中x2y3z2的系数为C26C34×23－C26C24×22＝480－360＝120，故选B.5．设a=sin xdx,则的展开式中常数项是()A.160B.-160C.-20D.20【答案】B【解析】由题意得a=sin xdx=(-cos x)=2.∴二项式为,其展开式的通项为T r+1=·=(-1)r·26-r·x3-r,令r=3,则得常数项为T4=-23·=-160.故选B.6．(x＋y＋z)4的展开式的项数为()A．10 B．15C ．20D ．21【答案】B【解析】(x ＋y ＋z )4＝[(x ＋y )＋z ]4＝C 04(x ＋y )4＋C 14(x ＋y )3z ＋C 24(x ＋y )2z 2＋C 34(x ＋y )z 3＋C 44z 4，运用二项式定理展开共有5＋4＋3＋2＋1＝15项，选B. 7．(x 2+3y-y 2)7展开式中x 12y 2的系数为( ) A.7B.-7C.42D.-42【答案】B【解析】将(x 2+3y-y 2)7看作7个因式相乘,要得到x 12y 2项,需要7个因式中有6个因式取x 2,1个因式取-y 2,故x 12y 2的系数为×(-1)=-7.8．1-90+902-903+…+(-1)k 90k +…+9010除以88的余数是( ) A.-1 B.1 C.-87 D.87 【答案】B【解析】1-90+902-903+…+(-1)k 90k +…+9010=(1-90)10=8910=(88+1)10=8810+889+…+88+1.∵前10项均能被88整除, ∴余数是1.9．⎝⎛⎭⎫x 2－3x ＋4x ⎝⎛⎭⎫1－1x 5的展开式中常数项为( ) A ．－30 B ．30 C ．－25 D ．25【答案】C【解析】⎝⎛⎭⎫x 2－3x ＋4x ⎝⎛⎭⎫1－1x 5＝x 2⎝⎛⎭⎫1－1x 5－3x ⎝⎛⎭⎫1－1x 5＋4x ⎝⎛⎭⎫1－1x 5，⎝⎛⎭⎫1－1x 5的展开式的通项T r ＋1＝C r 5(－1)r ⎝⎛⎭⎫1x r ，易知当r ＝4或r ＝2时原式有常数项，令r ＝4，T 5＝C 45(－1)4⎝⎛⎭⎫1x 4，令r ＝2，T 3＝C 25(－1)2⎝⎛⎭⎫1x 2，故所求常数项为C 45－3×C 25＝5－30＝－25，故选C.10．在二项式⎝⎛⎭⎫x ＋3x n 的展开式中，各项系数之和为A ，各项二项式系数之和为B ，且A ＋B ＝72，则展开式中的常数项为( ) A ．6 B ．9 C ．12 D ．18【答案】B【解析】在二项式⎝⎛⎭⎫x ＋3x n 的展开式中，令x ＝1得各项系数之和为4n ，∴A ＝4n ，该二项展开式的二项式系数之和为2n ，∴B ＝2n ，∴4n ＋2n ＝72，解得n ＝3，∴⎝⎛⎭⎫x ＋3x n ＝⎝⎛⎭⎫x ＋3x 3的展开式的通项T r ＋1＝C r 3(x )3－r⎝⎛⎭⎫3x r ＝3r C r3x 3－3r 2，令3－3r 2＝0得r ＝1，故展开式的常数项为T 2＝3C 13＝9，故选B. 11．(x-y)(x+2y+z)6的展开式中,含x 2y 3z 2的项的系数为( ) A.-30 B.120 C.240 D.420【答案】B【解析】由(x-y)(x+2y+z)6=(x-y)[(x+2y)+z]6,得含z 2的项为(x-y)(x+2y)4z 2=z 2[x(x+2y)4-y(x+2y)4], ∵x(x+2y)4-y(x+2y)4中含x 2y 3的项为xx(2y)3-yx 2(2y)2=8x 2y 3, ∴含x 2y 3z 2的项的系数为×8=15×8=120,故选B. 12．若a 0x 2 016+a 1x 2 015(1-x)+a 2x 2 014(1-x)2+…+a 2 016(1-x)2 016=1,则a 0+a 1+a 2+…+a 2 016的值为( ) A.1 B.0 C.22 016 D.22 015 【答案】C【解析】1=[x+(1-x)]2 016=x 2 016+x 2 015(1-x)+…+(1-x)2 016, ∴a 0+a 1+…+a 2 016=++…+=22 016,故选C.13．在二项式⎝⎛⎭⎫ax 2＋1x 5的展开式中，若常数项为－10，则a ＝________. 【答案】－2 【解析】⎝⎛⎭⎫ax 2＋1x 5的展开式的通项T r ＋1＝C r 5(ax 2)5－r ×⎝⎛⎭⎫1x r ＝C r 5a 5－r x 10－5r 2，令10－5r 2＝0，得r ＝4，所以C 45a 5－4＝－10，解得a ＝－2. 14．(1+2x)3(1-x)4展开式中x 2的系数为 . 【答案】-6【解析】∵展开式中x 2项为13(2x)0·12(-x)2+12(2x)1·13(-x)1+11(2x)2·14(-x)0, ∴所求系数为·+·2··(-1)+·22·=6-24+12=-6. 15．若(x －1)5＝a 5(x ＋1)5＋a 4(x ＋1)4＋a 3(x ＋1)3＋a 2(x ＋1)2＋a 1(x ＋1)＋a 0，则a 1＋a 2＋a 3＋a 4＋a 5＝________. 【答案】31【解析】令x ＝－1可得a 0＝－32.令x ＝0可得a 0＋a 1＋a 2＋a 3＋a 4＋a 5＝－1，所以a 1＋a 2＋a 3＋a 4＋a 5＝－1－a 0＝－1＋32＝31.16．⎝⎛⎭⎫x ＋1x ＋25的展开式中x 2的系数是________． 【答案】120【解析】在⎣⎡⎦⎤⎝⎛⎭⎫x ＋1x ＋25的展开式中，含x 2的项为2C 15⎝⎛⎭⎫x ＋1x 4,23C 35⎝⎛⎭⎫x ＋1x 2，所以在这几项的展开式中x 2的系数和为2C 15C 14＋23C 35C 02＝40＋80＝120.17．在(1+x)6(1+y)4的展开式中,记x m y n 项的系数为f(m,n),则f(3,0)+f(2,1)+f(1,2)+f(0,3)= . 【答案】120【解析】∵(1+x)6展开式的通项公式为=x r ,(1+y)4展开式的通项公式为=y h , ∴(1+x)6(1+y)4展开式的通项可以为x r y h . ∴f(m,n)=.∴f(3,0)+f(2,1)+f(1,2)+f(0,3)=+++=20+60+36+4=120.18．若⎝⎛⎭⎫x ＋12x n (n ≥4，n ∈N *)的二项展开式中前三项的系数依次成等差数列，则n ＝________. 【答案】8【解析】⎝⎛⎭⎫x ＋12x n 的展开式的通项T r ＋1＝C r n x n －r ⎝⎛⎭⎫12x r ＝C r n 2－r x n －2r ，则前三项的系数分别为1，n 2，n n －18，由其依次成等差数列，得n ＝1＋nn －18，解得n ＝8或n ＝1(舍去)，故n ＝8. 19．二项式⎝⎛⎭⎫x －2x 6的展开式中，含x 2项的系数是________． 【答案】60【解析】由二项展开式的通项公式得T r ＋1＝C r 6x 6－r ·⎝⎛⎭⎫－2x r＝C r 6x 6－2r (－2)r ，令6－2r ＝2，得r ＝2，所以x 2的系数为C 26(－2)2＝60.20．⎝⎛⎭⎫x ＋ax 210展开式中的常数项为180，则a ＝________. 【答案】±2【解析】⎝⎛⎭⎫x ＋a x 210展开式的通项为C r 10(x )10－r ·⎝⎛⎭⎫a x 2r ＝a r C r 10x 5－52r ，令5－52r ＝0，得r ＝2，又a 2C 210＝180，故a ＝±2.21．设⎝⎛⎭⎫1x ＋x 24的展开式中x 2的系数为m ，则直线y ＝m3x 与曲线y ＝x 2所围成的图形的面积为________． 【答案】43【解析】⎝⎛⎭⎫1x ＋x 24的展开式的通项为T r ＋1＝C r 4x r －4·x 2r ＝C r 4x 3r －4，令3r －4＝2，得r ＝2，则m ＝C 24＝6.又直线y ＝2x 与曲线y ＝x 2的交点坐标为(0,0)和(2,4)，则它们所围成的图形的面积S ＝⎠⎛20(2x －x 2)d x ＝⎝⎛⎭⎫x 2－13x 320＝43.,22．已知二项式⎝⎛⎭⎪⎫3x ＋1x n 的展开式中各项的系数和为256.(1)求n 的值；(2)求展开式中的常数项． 【答案】(1) 8 (2) 8【解析】(1)由题意得C 0n ＋C 1n ＋C 2n ＋…＋C nn ＝256，∴2n ＝256，解得n ＝8.(2)该二项展开式中的第r ＋1项为 T r ＋1＝C r 8(3x)8－r ·⎝⎛⎭⎫1x r ＝C r 8·x 8－4r 3， 令8－4r3＝0，得r ＝2，此时，常数项为T 3＝C 28＝28. 23．已知⎝⎛⎭⎫12＋2x n.(1)若展开式中第5项，第6项与第7项的二项式系数成等差数列，求展开式中二项式系数最大的项的系数； (2)若展开式前三项的二项式系数和等于79，求展开式中系数最大的项． 【答案】(1) 3 432 (2) 16 896x 10【解析】(1)∵C 4n ＋C 6n ＝2C 5n ，∴n 2－21n ＋98＝0.∴n ＝7或n ＝14，当n ＝7时，展开式中二项式系数最大的项是T 4和T 5.∴T 4的系数为C 37⎝⎛⎭⎫124·23＝352， T 5的系数为C 47⎝⎛⎭⎫123·24＝70，当n ＝14时，展开式中二项式系数最大的项是T 8.∴T 8的系数为C 714⎝⎛⎭⎫127·27＝3 432. (2)∵C 0n ＋C 1n ＋C 2n ＝79，∴n 2＋n －156＝0.∴n ＝12或n ＝－13(舍去)．设第r ＋1项的系数最大， ∵⎝⎛⎭⎫12＋2x 12＝⎝⎛⎭⎫1212(1＋4x)12， ∴⎩⎪⎨⎪⎧C r 124r ≥C r －1124r －1，C r 124r ≥C r ＋1124r ＋1. ∴9.4≤r≤10.4，又r ∈N *，∴r ＝10.∴展开式中系数最大的项为第11项，T 11＝C 1012·⎝⎛⎭⎫122·210·x 10＝16 896x 10.。
2021版高考数学(理)第一轮全国经典版课件：二项式定理
触类旁通 二项式定理中赋值法的应用
(1)形如(ax＋b)n，(ax2＋bx＋c)m(a，b，c∈R)的式子求 其展开式的各项系数之和，常用赋值法，只需令 x＝1 即可．
(2)对形如(ax＋by)n(a，b∈R)的式子求其展开式各项系 数之和，只需令 x＝y＝1 即可．
(3)若 f(x)＝a0＋a1x＋a2x2＋…＋anxn，则 f(x)展开式中各 项系数之和为 f(1)，
n
是
奇
数
，
那
么
中
间
两
项
(
第
n＋1 2
项
与
第
n＋2 1＋1项)的二项式系数相等并最大．
2．求展开式系数最大项 如求(a＋bx)n(a，b∈R)的展开式系数最大的项，一般是 采用待定系数法，设展开式各项系数分别为 A1，A2，…， An＋1，且第 k 项系数最大，应用AAkk≥ ≥AAkk－ ＋11 从而解出 k 来， 即得．
板块二 典例探究·考向突破
考向 二项展开式中特定项或系数问题
例 1 (1)(x y－y x)4 的展开式中，x3y3 项的系数为
____6____．
解析 由二项展开式的通项可得 Tr＋1＝Cr4(x· y)4－r·(－ y x)r＝(－1)rCr4x4－r2 ·y2＋2r .
令4－2r＝3 2＋2r＝3
C．1
D．20
解析 令 x＝1，得 a0＋a1＋a2＋…＋a9＋a10＝1，再令 x＝0，得 a0＝1，所以 a1＋a2＋…＋a9＋a10＝0，又易知 a1 ＝C910×21×(－1)9＝－20，所以 a2＋a3＋…＋a9＋a10＝20.
(2)在二项式
x＋3xn 的展开式中，各项系数之和为 A，
2021年上海高中数学 专项讲义 二项式定理(修订版)
2021年上海高中数学专项讲义：二项式定理[基础篇]一、二项式定理：（1）二项式定理：0111*(),n n n r n r r n n n n n n a b C a C a b C a b C b n N --+=+++++∈ （2）通项：1,0,1,2,,.r n r r r n T C a b r n -+== （3）二项式系数的性质：①二项式系数的对称性：与首末两端“对距离”的两个二项式系数相等，即0n n n C C =， (1)k k n n C C -=②二项式系数和：令1a b ==,则二项式系数的和为0122r n n n n n n n C C C C C ++++++= ，变形式1221r n n n n n n C C C C +++++=- ．③奇数项的二项式系数和=偶数项的二项式系数和：在二项式定理中，令1,1a b ==-，则0123(1)(11)0n n n n n n n n C C C C C -+-++-=-= ，从而得到：0242132111222r r n n n n n n n n n C C C C C C C +-++⋅⋅⋅++⋅⋅⋅=++++⋅⋅⋅=⨯= 【注意】①项数：展开式中总共有(1)n +项.②顺序：注意正确选择a ,b ,其顺序不能更改。
()n a b +与()nb a +是不同的.③指数：a 的指数从n 逐项减到0，是降幂排列。
b 的指数从0逐项减到n ，是升幂排列。
各项的次数和等于n .④系数：注意正确区分二项式系数与项的系数，二项式系数依次是012,,,,,,.r n n n n n n C C C C C ⋅⋅⋅⋅⋅⋅项的系数是a 与b 的系数（包括二项式系数）.④奇数项的系数和与偶数项的系数和：0011222012012001122202121001230123()()1, (1)1,(1)n n n n n n nn n n n n n n n n n n n n n n n n n n n n a x C a x C a x C a x C a x a a x a x a x x a C a x C ax C a x C a x a x a x a x a x a a a a a a x a a a a a a ----+=++++=+++++=++++=++++=++++=+---------=--+-++=----- 令则①令则024135(1)(1),()2(1)(1),()2n nn n nn a a a a a a a a a a a a ----++-++++=+---+++= ②①②得奇数项的系数和①②得偶数项的系数和⑤二项式系数的最大项：如果二项式的幂指数n 是偶数时，则中间一项的二项式系数2n n C 取得最大值。
新高考数学二项式定理精品课件
课前基础巩固
4
[解析] 的展开式的通项为Tr+1=·(-1)r·36-r·,若6-r为整数,则r=0,2,4,6,故有理项共有4项.
6. 已知的展开式中,各项系数的和与二项式系数的和之比为64,则n等于 .
课前基础巩固
6
[解析] 二项式的展开式中各项系数的和为(1+3)n=4n,二项式系数的和为2n.因为各项系数的和与二项式系数的和之比为64,所以=2n=64,解得n=6.
课堂考点探究
ACD
将x=-1代入(1-2x)5=a0+a1x+a2x2+a3x3+a4x4+a5x5,得35=a0-a1+a2-a3+a4-a5,故C正确;二项式(1-2x)5的展开式的通项为Tr+1=(-2)rxr,所以当r为奇数时,(-2)r为负数,即ai<0(其中i为奇数),当r为偶数时,(-2)r为正数,即ai>0(其中i为偶数),所以a0-|a1|+a2-|a3|+a4-|a5|=a0+a1+a2+a3+a4+a5=-1,故D正确.故选ACD.
(2)在的展开式中,x2的系数为 .(用数字作答)
课堂考点探究
240
[解析]的展开式的通项为Tr+1=(2x)6-r=(-1)r×26-r,令6-2r=2,解得r=2,∴的展开式中x2的系数为24=240.
考向1 二项式系数例2 (1)[2021·衡水模拟] 已知二项式的展开式中第2项与第3项的二项式系数之比是2∶5,则x3的系数为 .
课前基础巩固
◈ 知识聚焦 ◈
an+an-1b1+…+an-kbk+…+bn
2021高考数学课件11.3二项式定理
的展开式中常数项为
14，
则实数 a 的值为( )
A．± 2
B．±1
C．±12
D．±
2 2
答案：D
解析：展开式通项
Tr＋1＝Cr86
x8－r·－
axr＝Cr8(－1)rarx4－32r，令
4－32r＝0，得 r＝2，故常数项为 T2＋1＝C28a2＝28a2＝14，则 a2＝12，解
得 a＝± 22，故选 D.
答案：A 解析：依题意得 2n＝8，解得 n＝3.取 x＝1 得，该二项展开式每一 项的系数之和为(1－2)3＝－1.
(2)在x＋
3 x
n
的展开式中，各项系数和与二项式系数和之比为
64∶1，则 x3 的系数为( )
A．15 B．45
C．135 D．405
答案：C
解析：由题意知42nn＝64，解得
n＝6，展开式的通项
答案：－15 解析：(x＋1)5(x－2)＝x(x＋1)5－2(x＋1)5，展开式中含有 x2 的项为 C51x2－2C25x2＝－20x2＋5x2＝－15x2，故 x2 的系数为－15.
三、走进高考 5．[2019·全国Ⅲ卷](1＋2x2)(1＋x)4 的展开式中 x3 的系数为( ) A．12 B．16 C．20 D．24
答案：A 解析： 解法一 1×C43＋2C14＝12. 解法二 ∵(1＋2x2)(1＋x)4＝(1＋2x2)·(1＋4x＋6x2＋4x3＋x4)，∴x3 的系数为 1×4＋2×4＝12.
6 ． [2019·浙 江 卷 ] 在 二 项 式 ( 2 ＋ x)9 的 展 开 式 中 ， 常 数 项 是 _1_6__2____，系数为有理数的项的个数是___5_____．
高考数学新增分大一轮复习第十章计数原理10.3二项式定理讲义含解析04111107.docx
§10.3 二项式定理1.二项式定理2.二项式系数的性质 (1)C 0n ＝1，C nn ＝1. C mn ＋1＝C m －1n ＋C mn . (2)C mn ＝C n －mn .(3)当n 是偶数时，12n T +项的二项式系数最大；当n 是奇数时，12n T +与112n T ++项的二项式系数相等且最大.(4)(a ＋b )n展开式的二项式系数和：C 0n ＋C 1n ＋C 2n ＋…＋C n n ＝2n. 概念方法微思考1.(a ＋b )n与(b ＋a )n的展开式有何区别与联系？提示 (a ＋b )n的展开式与(b ＋a )n的展开式的项完全相同，但对应的项不相同而且两个展开式的通项不同.2.二项展开式形式上有什么特点？ 提示 二项展开式形式上的特点 (1)项数为n ＋1.(2)各项的次数都等于二项式的幂指数n ，即a 与b 的指数的和为n .(3)字母a 按降幂排列，从第一项开始，次数由n 逐项减1直到零；字母b 按升幂排列，从第一项起，次数由零逐项增1直到n .(4)二项式的系数从C 0n ，C 1n ，一直到C n －1n ，C nn .3.二项展开式中二项式系数最大时该项的系数就最大吗？提示 不一定最大，当二项式中a ，b 的系数为1时，此时二项式系数等于项的系数，否则不一定.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)C k n an －k b k是二项展开式的第k 项.( × )(2)二项展开式中，系数最大的项为中间一项或中间两项.( × ) (3)(a ＋b )n的展开式中某一项的二项式系数与a ，b 无关.( √ ) (4)(a －b )n的展开式第k ＋1项的系数为C k n an －k b k.( × )(5)(x －1)n的展开式二项式系数和为－2n.( × ) 题组二 教材改编2.[P31例2(2)](1＋2x )5的展开式中，x 2的系数等于( ) A.80B.40C.20D.10 答案 B解析 T k ＋1＝C k5(2x )k＝C k 52k x k，当k ＝2时，x 2的系数为C 25·22＝40.3.[P31例2(2)]若⎝⎛⎭⎪⎫x ＋1x n展开式的二项式系数之和为64，则展开式的常数项为( )A.10B.20C.30D.120 答案 B解析 二项式系数之和2n ＝64，所以n ＝6，T k ＋1＝C k 6·x 6－k·⎝ ⎛⎭⎪⎫1x k ＝C k 6x 6－2k，当6－2k ＝0，即当k ＝3时为常数项，T 4＝C 36＝20.4.[P41B 组T5]若(x －1)4＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4，则a 0＋a 2＋a 4的值为( ) A.9B.8C.7D.6 答案 B解析 令x ＝1，则a 0＋a 1＋a 2＋a 3＋a 4＝0，令x ＝－1，则a 0－a 1＋a 2－a 3＋a 4＝16，两式相加得a 0＋a 2＋a 4＝8. 题组三 易错自纠5.(x －y )n的二项展开式中，第m 项的系数是( ) A.C mn B.C m ＋1n C.C m －1nD.(－1)m －1C m －1n解析 (x －y )n二项展开式第m 项的通项公式为T m ＝C m －1n (－y )m －1x n －m ＋1， 所以系数为C m －1n (－1)m －1.6.已知(x ＋1)10＝a 1＋a 2x ＋a 3x 2＋…＋a 11x 10.若数列a 1，a 2，a 3，…，a k (1≤k ≤11，k ∈N *)是一个单调递增数列，则k 的最大值是( ) A.5B.6C.7D.8 答案 B解析 由二项式定理知，a n ＝C n －110(n ＝1，2，3，…，11). 又(x ＋1)10展开式中二项式系数最大项是第6项， 所以a 6＝C 510，则k 的最大值为6.7.(x y －y x )4的展开式中，x 3y 3项的系数为________. 答案 6解析 二项展开式的通项是T k ＋1＝C k4(x y )4－k·(－y x )k ＝42222(1)C k k kkxy-+－，令4－k2＝2＋k2＝3，解得k ＝2，故展开式中x 3y 3的系数为(－1)2C 24＝6.题型一 二项展开式命题点1 求指定项(或系数)例1 (1)⎝⎛⎭⎪⎫1＋1x2(1＋x )6的展开式中x 2的系数为( )A.15B.20C.30D.35 答案 C解析 因为(1＋x )6的通项为C k 6x k ，所以⎝ ⎛⎭⎪⎫1＋1x 2(1＋x )6的展开式中含x 2的项为1·C 26x 2和1x2·C 46x 4.因为C 26＋C 46＝2C 26＝2×6×52×1＝30，所以⎝⎛⎭⎪⎫1＋1x2(1＋x )6的展开式中x 2的系数为30.(2)(2018·温州市高考适应性测试)在⎝ ⎛⎭⎪⎫1x －2x 9的展开式中，常数项是( )A.C 39 B.－C 39 C.8C 39 D.－8C 39答案 D解析 二项式⎝ ⎛⎭⎪⎫1x －2x 9的展开式的通项公式为C k 9⎝ ⎛⎭⎪⎫1x 9－k (－2x )k＝3929(2)C k k k x －－，令3k －92＝0，得k ＝3，则二项式⎝ ⎛⎭⎪⎫1x －2x 9的展开式中的常数项为(－2)3C 39＝－8C 39，故选D.(3)(x 2＋x ＋y )4的展开式中，x 3y 2的系数是________. 答案 12解析 方法一 (x 2＋x ＋y )4＝[(x 2＋x )＋y ]4， 其展开式的第k ＋1项的通项公式为T k ＋1＝C k 4(x 2＋x )4－k y k，因为要求x 3y 2的系数，所以k ＝2， 所以T 3＝C 24(x 2＋x )4－2y 2＝6(x 2＋x )2y 2.因为(x 2＋x )2的展开式中x 3的系数为2， 所以x 3y 2的系数是6×2＝12.方法二 (x 2＋x ＋y )4表示4个因式x 2＋x ＋y 的乘积，在这4个因式中，有2个因式选y ，其余的2个因式中有一个选x ，剩下的一个选x 2，即可得到含x 3y 2的项，故x 3y 2的系数是C 24·C 12·C 11＝12. 命题点2 求参数例2 (1)若(x 2－a )⎝⎛⎭⎪⎫x ＋1x 10的展开式中x 6的系数为30，则a 等于( )A.13B.12C.1D.2 答案 D解析 由题意得⎝⎛⎭⎪⎫x ＋1x 10的展开式的通项公式是T k ＋1＝C k 10·x 10－k·⎝ ⎛⎭⎪⎫1x k ＝C k 10x 10－2k ，⎝ ⎛⎭⎪⎫x ＋1x 10的展开式中含x 4(当k ＝3时)，x 6(当k ＝2时)项的系数分别为C 310，C 210，因此由题意得C 310－a C 210＝120－45a ＝30，由此解得a ＝2，故选D.(2)若⎝ ⎛⎭⎪⎫x 2＋1ax 6的展开式中常数项为1516，则实数a 的值为( )A.±2B.12C.－2D.±12解析 ⎝⎛⎭⎪⎫x 2＋1ax 6的展开式的通项为T k ＋1＝C k 6(x 2)6－k·⎝ ⎛⎭⎪⎫1ax k ＝C k 6⎝ ⎛⎭⎪⎫1ak x12－3k ，令12－3k ＝0， 得k ＝4.故C 46·⎝ ⎛⎭⎪⎫1a 4＝1516，即⎝ ⎛⎭⎪⎫1a 4＝116，解得a ＝±2，故选A.思维升华求二项展开式中的特定项，一般是化简通项公式后，令字母的指数符合要求(求常数项时，指数为零；求有理项时，指数为整数等)，解出项数k ＋1，代回通项公式即可.跟踪训练 1 (1)(2018·浙江七彩阳光联盟联考)⎝⎛⎭⎪⎫1－1x2(1＋x )6的展开式中x 3的系数为__________. 答案 14解析 在(1＋x )6的展开式中x 3的系数为C 36＝20，1x2·(1＋x )6的展开式中x 3的系数为C 56＝6，所以⎝⎛⎭⎪⎫1－1x 2(1＋x )6的展开式中x 3的系数为20－6＝14.(2)(2018·丽水、衢州、湖州三地教学质量检测)若⎝⎛⎭⎪⎫x －a x26的展开式中x 3的系数为－12，则a ＝______；常数项是________.答案 2 60解析 由于二项展开式的通项T k ＋1＝C k 6x6－k⎝ ⎛⎭⎪⎫－a x 2k ＝(－a )k C k 6x 6－3k ，令6－3k ＝3，则k ＝1，所以(－a )C 16＝－6a ＝－12，a ＝2；令6－3k ＝0，则k ＝2，所以常数项是(－2)2C 26＝4×15＝60. 题型二 二项式系数的和与各项的系数和问题例3 (1)(a ＋x )(1＋x )4的展开式中x 的奇数次幂项的系数之和为32，则a ＝____________. 答案 3解析 设(a ＋x )(1＋x )4＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋a 4x 4＋a 5x 5， 令x ＝1，得16(a ＋1)＝a 0＋a 1＋a 2＋a 3＋a 4＋a 5，① 令x ＝－1，得0＝a 0－a 1＋a 2－a 3＋a 4－a 5.② ①－②，得16(a ＋1)＝2(a 1＋a 3＋a 5)，即展开式中x 的奇数次幂的系数之和为a 1＋a 3＋a 5＝8(a ＋1)，所以8(a ＋1)＝32，解得a ＝3.(2)若(x ＋2＋m )9＝a 0＋a 1(x ＋1)＋a 2(x ＋1)2＋…＋a 9(x ＋1)9，且(a 0＋a 2＋…＋a 8)2－(a 1＋a 3＋…＋a 9)2＝39，则实数m 的值为________. 答案 1或－3解析 令x ＝0，则(2＋m )9＝a 0＋a 1＋a 2＋…＋a 9，令x ＝－2，则m 9＝a 0－a 1＋a 2－a 3＋…－a 9， 又(a 0＋a 2＋…＋a 8)2－(a 1＋a 3＋…＋a 9)2＝(a 0＋a 1＋a 2＋…＋a 9)(a 0－a 1＋a 2－a 3＋…＋a 8－a 9)＝39， ∴(2＋m )9·m 9＝39，∴m (2＋m )＝3， ∴m ＝－3或m ＝1.(3)若⎝⎛⎭⎪⎫x 2－1x n 的展开式中含x 的项为第6项，设(1－3x )n ＝a 0＋a 1x ＋a 2x 2＋…＋a n x n，则a 1＋a 2＋…＋a n 的值为________.答案 255解析 ⎝⎛⎭⎪⎫x 2－1x n展开式的第k ＋1项为T k ＋1＝C k n (x 2)n －k ·⎝ ⎛⎭⎪⎫－1x k ＝C k n (－1)k x 2n －3k， 当k ＝5时，2n －3k ＝1，∴n ＝8. 对(1－3x )8＝a 0＋a 1x ＋a 2x 2＋…＋a 8x 8， 令x ＝1，得a 0＋a 1＋…＋a 8＝28＝256. 又当x ＝0时，a 0＝1， ∴a 1＋a 2＋…＋a 8＝255.思维升华 (1)“赋值法”普遍适用于恒等式，对形如(ax ＋b )n ，(ax 2＋bx ＋c )m(a ，b ，c ∈R )的式子求其展开式的各项系数之和，常用赋值法.(2)若f (x )＝a 0＋a 1x ＋a 2x 2＋…＋a n x n，则f (x )展开式中各项系数之和为f (1)，奇数项系数之和为a 0＋a 2＋a 4＋…＝f (1)＋f (－1)2，偶数项系数之和为a 1＋a 3＋a 5＋…＝f (1)－f (－1)2.跟踪训练2 已知(1－2x )7＝a 0＋a 1x ＋a 2x 2＋…＋a 7x 7. 求：(1)a 1＋a 2＋…＋a 7； (2)a 1＋a 3＋a 5＋a 7； (3)a 0＋a 2＋a 4＋a 6；(4)|a 0|＋|a 1|＋|a 2|＋…＋|a 7|.解 令x ＝1，则a 0＋a 1＋a 2＋a 3＋a 4＋a 5＋a 6＋a 7 ＝－1.①令x ＝－1，则a 0－a 1＋a 2－a 3＋a 4－a 5＋a 6－a 7＝37.② (1)∵a 0＝C 07＝1，∴a 1＋a 2＋a 3＋…＋a 7＝－2. (2)(①－②)÷2，得a 1＋a 3＋a 5＋a 7＝－1－372＝－1094.(3)(①＋②)÷2，得a 0＋a 2＋a 4＋a 6＝－1＋372＝1093.(4)方法一 ∵(1－2x )7展开式中，a 0，a 2，a 4，a 6大于零，而a 1，a 3，a 5，a 7小于零， ∴|a 0|＋|a 1|＋|a 2|＋…＋|a 7|＝(a 0＋a 2＋a 4＋a 6)－(a 1＋a 3＋a 5＋a 7)＝1093－(－1094)＝2187.方法二 |a 0|＋|a 1|＋|a 2|＋…＋|a 7|即为(1＋2x )7展开式中各项的系数和，令x ＝1， ∴|a 0|＋|a 1|＋|a 2|＋…＋|a 7|＝37＝2187.题型三 二项式定理的应用例4 (1)设a ∈Z 且0≤a <13，若512012＋a 能被13整除，则a 等于( )A.0B.1C.11D.12 答案 D 解析 512012＋a ＝(52－1)2012＋a ＝C 02012·522012－C 12012·522011＋…＋C 20112012·52·(－1)2011＋C 20122012·(－1)2012＋a ，∵C 02012·522012－C 12012·522011＋…＋C 20112012·52·(－1)2011能被13整除且512012＋a 能被13整除，∴C 20122012·(－1)2012＋a ＝1＋a 也能被13整除，因此a 的值为12.(2)设复数x ＝2i 1－i(i 是虚数单位)，则C 12017x ＋C 22017x 2＋C 32017x 3＋…＋C 20172017x 2017等于( ) A.i B.－i C.－1＋i D.－1－i答案 C 解析 x ＝2i 1－i ＝2i (1＋i )(1－i )(1＋i )＝－1＋i ， C 12017x ＋C 22017x 2＋C 32017x 3＋…＋C 20172017x 2017＝(1＋x )2017－1＝i2017－1＝i －1.思维升华 (1)逆用二项式定理的关键根据所给式子的特点结合二项展开式的要求，使之具备二项式定理右边的结构，然后逆用二项式定理求解.(2)利用二项式定理解决整除问题的思路 ①观察除式与被除式间的关系； ②将被除式拆成二项式； ③结合二项式定理得出结论.跟踪训练 3 (1)1－90C 110＋902C 210－903C 310＋…＋(－1)k 90k C k 10＋…＋9010C 1010除以88的余数是( )A.－1B.1C.－87D.87 答案 B解析 1－90C 110＋902C 210－903C 310＋…＋(－1)k 90k C k 10＋…＋9010C 1010＝(1－90)10＝8910＝(88＋1)10＝8810＋C 110889＋…＋C 91088＋1， ∵前10项均能被88整除，∴余数是1. (2)若(1－2x )2018＝a 0＋a 1x ＋a 2x 2＋…＋a 2018x2018，则a 12＋a 222＋…＋a 201822018＝________.答案 －1解析 当x ＝0时，左边＝1，右边＝a 0，∴a 0＝1. 当x ＝12时，左边＝0，右边＝a 0＋a 12＋a 222＋…＋a 201822018，∴0＝1＋a 12＋a 222＋…＋a 201822018， 即a 12＋a 222＋…＋a 201822018＝－1.1.在⎝⎛⎭⎪⎫x 2－2x 6的展开式中，常数项为( )A.－240B.－60C.60D.240 答案 D解析 ⎝ ⎛⎭⎪⎫x 2－2x 6的展开式中，通项公式为T k ＋1＝C k 6(x 2)6－k ⎝ ⎛⎭⎪⎫－2x k ＝(－2)k C k 6x 12－3k，令12－3k ＝0，得k ＝4，故常数项为T 5＝(－2)4C 46＝240，故选D.2.(2018·杭州质检)二项式⎝ ⎛⎭⎪⎫2x －1x 5的展开式中含x 3项的系数是( )A.80B.48C.－40D.－80 答案 D解析 ∵⎝ ⎛⎭⎪⎫2x －1x 5展开式的通项为T k ＋1＝C k 5(2x )5－k ·⎝ ⎛⎭⎪⎫－1x k ＝(－1)k 25－k C k 5x 5－2k，5－2k ＝3，则k ＝1，∴含x 3的项为T 2＝(－1)124C 15x 3＝－80x 3，其中系数为－80，故选D.3.(x ＋y )(2x －y )6的展开式中x 4y 3的系数为( ) A.－80B.－40C.40D.80 答案 D解析 (2x －y )6的展开式的通项公式为T k ＋1＝C k 6(2x )6－k(－y )k ，当k ＝2时，T 3＝240x 4y 2，当k＝3时，T 4＝－160x 3y 3，故x 4y 3的系数为240－160＝80，故选D. 4.(1＋3x )n 的展开式中x 5与x 6的系数相等，则x 4的二项式系数为( ) A.21B.35C.45D.28 答案 B解析 ∵T k ＋1＝C k n (3x )k ＝3k C k n x k ，由已知得35C 5n ＝36C 6n ，即C 5n ＝3C 6n ，∴n ＝7，因此，x 4的二项式系数为C 47＝35，故选B.5.(2018·浙江省考前热身联考)⎝ ⎛⎭⎪⎫1x 2＋4x 2＋43展开式的常数项为( )A.120B.160C.200D.240 答案 B解析 ⎝ ⎛⎭⎪⎫1x 2＋4x 2＋43＝⎝ ⎛⎭⎪⎫1x ＋2x 6，展开式的通项为T k ＋1＝C k 6·⎝ ⎛⎭⎪⎫1x 6－k ·(2x )k ＝C k 62k x 2k －6，令2k －6＝0，可得k ＝3，故展开式的常数项为160.6.若在(x ＋1)4(ax －1)的展开式中，x 4项的系数为15，则a 的值为( ) A.－4B.52C.4D.72答案 C解析 ∵(x ＋1)4(ax －1)＝(x 4＋4x 3＋6x 2＋4x ＋1)(ax －1)，∴x 4项的系数为4a －1＝15，∴a ＝4.7.(2018·浙江省重点中学高三调研)⎝ ⎛⎭⎪⎫1x －2x 29的展开式中，除常数项外，各项系数的和为( )A.－671B.671C.672D.673 答案 B解析 令x ＝1，可得该二项展开式各项系数之和为－1.因为该二项展开式的通项公式为T k ＋1＝C k 9⎝ ⎛⎭⎪⎫1x9－k ·(－2x 2)k ＝C k 9(－2)k ·x 3k －9，令3k －9＝0，得k ＝3，所以该二项展开式中的常数项为C 39(－2)3＝－672，所以除常数项外，各项系数的和为－1－(－672)＝671，故选B. 8.若(1－3x )2018＝a 0＋a 1x ＋…＋a 2018x 2018，x ∈R ，则a 1·3＋a 2·32＋…＋a 2018·32018的值为( )A.22018－1B.82018－1C.22018D.82018答案 B解析 由已知，令x ＝0，得a 0＝1，令x ＝3，得a 0＋a 1·3＋a 2·32＋…＋a 2018·32018＝(1－9)2018＝82018，所以a 1·3＋a 2·32＋…＋a 2018·32018＝82018－a 0＝82018－1，故选B.9.(2018·绍兴诸暨期末)已知(2x ＋1)6＝a 6(x ＋1)6＋a 5(x ＋1)5＋a 4(x ＋1)4＋…＋a 1(x ＋1)＋a 0，则a 0＋a 1＋a 2＋…＋a 6＝________，a 2＝________.答案 1 60解析 令x ＝0，即得16＝a 6＋a 5＋…＋a 1＋a 0，又(2x ＋1)6＝[2(x ＋1)－1]6的展开式的通项为T k ＋1＝C k 6[2(x ＋1)]6－k(－1)k，则a 2＝C 4622·(－1)4＝60.10.(2018·杭州四校联考)已知⎝⎛⎭⎪⎪⎫ax ＋13x n 的展开式中只有第7项的二项式系数最大，则n ＝________；若含x 8项的系数为55128，则常数项为________.答案 12552解析 因为展开式中只有第7项的二项式系数最大，所以展开式共有13项，n ＝12，则二项展开式的通项T k ＋1＝1412121212331212C C k kk k kk k a xxax-－－－－＝，令12－43k ＝8，得k ＝3，所以C 312a9＝55128，得12×11×106×a 9＝55128，得a 9＝1512，即a ＝12. 令12－43k ＝0，得k ＝9，故常数项为T 10＝C 912a 3＝12×11×106×⎝ ⎛⎭⎪⎫123＝552.11.9192除以100的余数是________. 答案 81解析 9192＝(90＋1)92＝C 0929092＋C 1929091＋…＋C 9092902＋(C 919290＋C 9292)＝k ×100＋92×90＋1＝k ×100＋82×100＋81(k 为正整数)，所以9192除以100的余数是81.12.若(1＋x ＋x 2)6＝a 0＋a 1x ＋a 2x 2＋…＋a 12x 12，则a 2＋a 4＋…＋a 12＝__________.(用数字作答) 答案 364解析 令x ＝1，得a 0＋a 1＋a 2＋…＋a 12＝36， 令x ＝－1，得a 0－a 1＋a 2－…＋a 12＝1， ∴a 0＋a 2＋a 4＋…＋a 12＝36＋12.令x ＝0，得a 0＝1，∴a 2＋a 4＋…＋a 12＝36＋12－1＝364.13.(2014·浙江)在(1＋x )6(1＋y )4的展开式中，记x m y n项的系数为f (m ，n )，则f (3，0)＋f (2，1)＋f (1，2)＋f (0，3)等于( )A.45B.60C.120D.210答案 C解析 因为f (m ，n )＝C m 6C n 4，所以f (3，0)＋f (2，1)＋f (1，2)＋f (0，3)＝C 36C 04＋C 26C 14＋C 16C 24＋C 06C 34＝120.14.已知⎝ ⎛⎭⎪⎫x －12x n (n ∈N *)的展开式中所有项的二项式系数之和、系数之和分别为p ，q ，则p ＋64q 的最小值为______.答案 16解析 显然p ＝2n .令x ＝1，得q ＝12n . 所以p ＋64q ＝2n ＋642n ≥22n ·642n ＝16， 当且仅当2n ＝642n ， 即n ＝3时取等号，此时p ＋64q 的最小值为16.15.(2018·金华模拟)若(3－2x )10＝a 0＋a 1x ＋a 2x 2＋a 3x 3＋…＋a 10x 10，则a 1＋2a 2＋3a 3＋4a 4＋…＋10a 10＝________.答案 －20解析 对原等式两边求导，得－20(3－2x )9＝a 1＋2a 2x ＋3a 3x 2＋…＋10a 10x 9，令x ＝1，得a 1＋2a 2＋3a 3＋4a 4＋…＋10a 10＝－20. 16.若⎝ ⎛⎭⎪⎪⎫x ＋24x n 展开式中前三项的系数和为163，求： (1)展开式中所有x 的有理项；(2)展开式中系数最大的项.解 易求得展开式前三项的系数为1，2C 1n ，4C 2n .由题意得1＋2C 1n ＋4C 2n ＝163，可得n ＝9.(1)设展开式中的有理项为T k ＋1，由T k ＋1＝C k 9(x )9－k ⎝ ⎛⎭⎪⎪⎫24x k ＝183492C k k k x -， 又∵0≤k ≤9，∴k ＝2，6.故有理项为T 3＝183222492C x -⨯⋅＝144x 3，1836664792C 5 376.T x -⨯⋅⋅＝＝(2)设展开式中T k ＋1项的系数最大，则⎩⎪⎨⎪⎧ 2k C k 9≥2k ＋1C k ＋19，2k C k 9≥2k －1C k －19，∴173≤k ≤203， 又∵k ∈N ，∴k ＝6，故展开式中系数最大的项为T 7＝5376.精美句子1、善思则能“从无字句处读书”。