高等数学(下 ) 第十一章D11_3幂级数
高数下册第11章解析

则 1时级数收敛; 1 时级数发散; 1时失效.
(5) 根值审敛法 (柯西判别法)
设 un 是正项级数,
n1
如果lim n n
un
(为数或 ),
则 1时级数收敛; 1时级数发散; 1时失效.
3、交错级数及其审敛法
定义 正 、负项相间的级数称为交错级数.
(1)n1un或 (1)nun (其中un 0)
如果级数 an x n 在x x0处发散,则它在满足
n0
不等式 x x0 的一切x 处发散.
推论
如果幂级数 an x n 不是仅在x 0 一点收敛,也
n0
不是在整个数轴上都收敛,则必有一个完全确定
的正数 R 存在,它具有下列性质:
当 x R时,幂级数绝对收敛;
当 x R时,幂级数发散;
函数
1、常数项级数
定义
un u1 u2 u3 un
n1
n
级数的部分和 sn u1 u2 un ui
i 1
级数的收敛与发散
常数项级数收敛(发散)
lim
n
sn
存在(不存在).
收敛级数的基本性质
性质1: 级数的每一项同乘一个不为零的常数, 敛散性不变.
性质2:收敛级数可以逐项相加与逐项相减.
(2)
讨论
lim
n
Rn
0
或
f
(n) ( x)
M,
则级数在收敛区间内收敛于 f ( x).
b.间接法 根据唯一性, 利用常见展开式, 通过 变量代换, 四则运算, 恒等变形, 逐项求导, 逐项积 分等方法,求展开式.
(4) 常见函数展开式
e x 1 x 1 x2 1 xn x (,)
《高等数学下册》(资料全集)D113-PPT课件

n
x M x0
n0
n
x M 当 x x 0 时, x0 n 0
故原幂级数绝对收敛 .
n
收敛, a n x n 也收敛,
反之, 若当 x x0 时该幂级数发散 , 下面用反证法证之.
假设有一点 x 1 满足 x 1 x 0 且使级数收敛 , 则由前
面的证明可知, 级数在点 x0 也应收敛, 与所设矛盾, 故假设不真. 所以若当 x x0 时幂级数发散 , 则对一切
0 R , 幂级数在 (-R , R ) 收敛 ; 在[-R , R ]
可能收敛也可能发散 . R 外发散; 在 x
R 称为收敛半径 ,(-R , R ) 称为收敛区间.
(-R , R ) 加上收敛的端点称为收敛域.
收敛 发散
发
散
收
o 敛
发
散
x
YANGZHOU UNIVERSITY
第三节
幂级数
一、函数项级数的概念 二、幂级数及其收敛性 三、幂级数的运算
第十一章
YANGZHOU UNIVERSITY
机动 目录 上页 下页 返回 结束
一、 函数项级数的概念
为定义在区间 I 上的函数, 称 ( x ) ( n 1 , 2 , ) 设u n
n 1
u ( x ) u ( x ) u ( x ) u ( x ) n 1 2 n
为定义在区间 I 上的函数项级数 . 对x I, 若常数项级数 u n ( x 0 ) 收敛, 称 x0 为其收 0
n 1
敛点, 所有收敛点的全体称为其收敛域 ; 若常数项级数 u n ( x 0 ) 发散 , 称 x0 为其发散点, 所有
高考数学知识点精讲幂级数的展开与收敛半径

高考数学知识点精讲幂级数的展开与收敛半径高考数学知识点精讲:幂级数的展开与收敛半径在高考数学中,幂级数是一个重要的知识点,其中幂级数的展开与收敛半径更是理解和解决相关问题的关键。
让我们一起来深入探讨这个知识点,帮助同学们在高考中轻松应对相关题型。
首先,我们来了解一下什么是幂级数。
简单来说,幂级数就是形如∑(n=0 到∞) aₙ xⁿ = a₀+ a₁ x + a₂ x²+ a₃ x³+的无穷级数。
其中,aₙ 被称为幂级数的系数,x 是变量。
那么,为什么要研究幂级数的展开呢?这是因为通过将一些复杂的函数展开成幂级数的形式,我们能够更方便地对其进行分析、计算和研究。
接下来,我们看看幂级数的展开方法。
常见的有直接展开法和间接展开法。
直接展开法是根据幂级数的定义,利用泰勒公式将函数在某一点展开成幂级数。
泰勒公式为:f(x) = f(x₀) + f'(x₀)(x x₀) + f''(x₀)(x x₀)²/ 2! + f'''(x₀)(x x₀)³/ 3! +。
例如,对于函数 f(x) =eˣ,我们想在 x = 0 处将其展开成幂级数。
首先求导可得 f'(x) =eˣ,f''(x) =eˣ,f'''(x) =eˣ,,所以f(0) = 1,f'(0) = 1,f''(0) = 1,,则eˣ = 1 + x + x²/ 2! + x³/ 3! +。
间接展开法则是利用已知的幂级数展开式,通过一些运算(如四则运算、变量代换等)得到新的幂级数展开式。
比如,已知 1 /(1 x) = 1 + x + x²+ x³+(|x| < 1),那么通过将 x 替换为 x²,可以得到 1 /(1 + x²) = 1 x²+ x⁴ x⁶+(|x| < 1)。
讲完了幂级数的展开,我们再来重点探讨一下收敛半径。
大学高数下册试题及答案,第11章

该函数延拓为偶函数,再延拓为周期的周期函数展开得余弦级数,;切入点很棒!的构思挺奇异!高等数学〔Ⅱ〕期末参考答案一、填空题〔每题3分,共30分〕1.已知a(1,1,2),b(0,1,2),则a b 1i j1 1k2(0,2,1) .22.点(1,1,1)到平面3x6y2z140的距离为 3.3.过点(3,0,1)且与平面3x7y5z120平行的平面方程为3x7y5z40 . 4.已知z f(xy,2x e2y),则 t4z xyf12f2 .5.曲线x14413,yt3312,zt22在相应于t1处的法平面方程为(x)(y)(z)0 .10y06.交换积分dx f(x,y)dy的积分次序为 x dyf(x,y)dy.2237.设:z x y22(0z1),则zdS x y 12x y2222dxdy.8.设向量A(x2yz)i(y2zx)j(z2xy)k,则divAP xQ yR z2(x y z).9.设函数f(x)以2为周期,且f(x)x(x),其Fourier 级数为a02n 1(ancosnx bnsinnx),则b221xsin2xdx 1 .10.函数f(x)12x的麦克劳林级数为2(1)2nnx .nn0二、〔8分〕求函数f(x,y)x xy y x y1的极值,并指出是极大值还是微小值.解:fx(x,y)2x y1,fy(x,y)2y x 1,22fx(x,y)02x y10令,得驻点(1,1).由于 , 即f(x,y)02y x10yA fxx(x,y)2,B fxy(x,y)1,C fyy(x,y)2,且(B AC)x112230,A20, y 1则(1,1)为微小值点,微小值为f(1,1) 2.三、〔8分〕求级数(n1)xn的收敛域及它的和函数. n0解:由于 lim|nan1an|lim|nnn 1|1,则R1,当x1时,级数(n1)(1)n均 n0发散,所以收敛域为(1,1).设s(x)(n1)xn0n,则于是x0s(t)dt[(n1)tdt]n0xnn0xn 1x1x,d x1x s(t).s(t)dt20dx(1x)1x四、〔8分〕计算(5x43xyLy)dx(3xy3xy 322其中L是抛物线y x y)dy,22上自点(0,0)到点(1,1)的一段弧.解:P(x,y)5x3xyy,Q(x,y)3xy3xy322y在xoy面偏导数连续,且P yQ x6xy3y,则曲线积分与路径无关,取折线段(0,0)(1,0)(1,1),则 L(5x3xy42y)dx(3xy3xy322y)dy10(5x3x00)dx32113)11610222(31y31y y)dy1(.(z x)dzdx(x y)dxdy,其中是由五、〔8分〕计算曲面积分Ix(y z)dydz柱面x2y21,平面z0,z3所围立体外表的外侧.解:P(x,y,z)x(y z),Q(x,y,z)z x,R(x,y,z)x y在柱面x2y21,平面z0,z3所围立体上偏导数连续,则由高斯公式有Ix(y z)dydz(z x)dzdx(x y)dxdyR z(P xQ y)dv(y z)dvydv30zdv〔第一个积分为0,想想为什么?〕0zdz dxdy z1dz Dz92.六、〔8分〕求以下方程的通解: 1.xy yln yxyxyyxlnyx解:xy yln,方程为齐次微分方程;设u du dxxyx,则y u xu,代入得u(lnu1),两端积分lnu 1d(lnu1)xdx即ln(lnu1)lnx lnC 或lnu Cx 1 将uyx代回得y xe2xCx12.y4y3y e.解:方程为二阶非齐次线性微分方程,对应齐次线性微分方程的特征方程r4r30的特征根为r11,r23;f(x) e2x中2不是特征方程的根,则特解形式为y*Ae2x,代入得Ay C1ex115,在由解的结构得方程的通解为3xC2e115e2x七、〔10分〕设vnun un,wnun un,证明:1.若级数un确定收敛,则级数vn收敛;n 1n 1证:由于un确定收敛,即|un|收敛,则un也收敛,又vn n 1n 1n 112|un|12un,由性质知vn收敛. n12.若级数un条件收敛,则级数wn发散.n 1n 1证:〔反证〕假设wn收敛,已知un收敛,由wnn 1n 1un un,即|un|2wn un及性质知|un|收敛,即un确定收敛,与已知条件矛盾.所以wn发散.n 1n 1n 1八、〔10分〕一均匀物体是由抛物面z x2y2及平面z1所围成.1.求的体积;解:在xoy面投影域D:x y1,则所围体积为V[1(xDy)]dxdy20d(1r)rdr2(2.求的质心.12 14).解:由于是均匀物体及几何体关于yoz面、xoz面对称,则质心坐标应为(0,0,);而z dvdv2d rdr11rzdzV23,所以质心坐标为(0,0,23).九、〔10分〕设D(x,y)|x2y222 2,x0,y0,[1x y]表示不超过221x y的最大整数,计算二重积分xy[1x y]dxdy.22D解:设D1{(x,y)|x2y21,x0,y0},D2{(x,y)|1x y2,x0,y0},则D D1D2,且当(x,y)D1时,[1x2y2]1,当(x,y) D2时,[1x y]2,所以Dxy[1x y]dxdyxy[1x y]dxdy22D1D1D2xy[1x y]dxdy 22xydxdy2xydxdyD2 drsin cos dr2d 20rsin cos dr1821838。
数学分析 第十一讲 幂级数

347第十一讲 幂级数§11.1 幂级数幂级数的一般概念.型如∑∞=-00)(n nn x x a 和 ∑∞=0n n n x a 的幂级数.幂级数由系数数列}{n a 唯一确定.幂级数至少有一个收敛点.以下只讨论型如∑∞=0n n n x a 的幂级数.幂级数是最简单的函数项级数之一. 一、知识结构 1、幂级数的收敛域定理1(Abel 定理)若幂级数∑nn x a 在点0≠=x x 收敛, 则对满足不等式|| ||x x <的任何x ,幂级数∑nn xa 收敛而且绝对收敛;若在点x x =发散,则对满足不等式|| ||x x >的任何x ,幂级数∑nn x a 发散.证明∑n n x a 收敛, {n n x a }有界.设|nn x a |≤M , 有|nn nn nn Mrxx x a x a ≤⋅=|||||,其中 1 ||<=xx r .∑+∞<nMr⇒∑∞+< ||nnx a.定理1的第二部分系第一部分的逆否命题.幂级数∑n n x a 和∑-nn x x a )(0的收敛域的结构:幂级数∑nn x a 收敛域的结构是关于点0=x 的对称区间,∑-nn x x a )(0的收敛域的结构是关于点0x x =的对称区间.348定义幂级数的收敛域长度的一半为收敛半径R ,收敛半径 R 的求法. 定理2 对于幂级数∑nn x a , 若∞→n lim ρ=nn a ||, 则(ⅰ)+∞<<ρ0时, R ρ1=; (ⅱ)ρ=0时+∞=R ;(ⅲ) ρ=∞+时0=R .证明 ∞→n lim=nnn x a ||∞→n lim||||||x x a nn ρ=, (强调开方次数与x 的次数是一致的).⇒ ……由于∞→n lim⇒=+ ||||1ρn n a a ∞→n limρ=nn a ||, 因此亦可用比值法求收敛半径.幂级数∑nn x a 的收敛区间:) , (R R - .幂级数∑n n x a 的收敛域: 一般来说, 收敛区间⊂收敛域. 幂级数∑nn x a 的收敛域是区间) , (R R -、] , (R R -、) , [R R -或] , [R R -之一.2、幂级数的一致收敛性定理3 若幂级数∑nn x a 的收敛半径为R ,则该幂级数在区间) , (R R -内闭一致收敛.证明 ∀] , [b a ⊂) , (R R -, 设} || , || max{b a x =, 则对∈∀x ] , [b a , 有|| ||nn nn x a x a ≤, 级数∑nn xa 绝对收敛, 由优级数判别法⇒ 幂级数∑nn xa 在] , [b a 上一致收敛.因此,幂级数∑nn x a 在区间) , (R R -内闭一致收敛.定理4 设幂级数∑nn x a 的收敛半径为R ) 0 (>,且在点R x =( 或R x -= )收敛,则幂级数∑nn x a 在区间] , 0 [R ( 或] 0 , [R - )上一致收敛 .证明 nn n nn R x R a x a ⎪⎭⎫⎝⎛=.∑nn R a 收敛, 函数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎫ ⎝⎛nR x 在区间] , 0 [R 上递减且一致有界,由Abel 判别法,幂级数∑nn x a 在区间] , 0 [R 上一致收敛.349易见,当幂级数∑nnxa的收敛域为] , [R R -(R ) 0>时,该幂级数即在区间] , [R R -上一致收敛 .3、幂级数的性质(1)逐项求导和积分后的级数设∑∞=='1)(n nn x a ∑∞=-11n n n xna ①,⎰∞==1n xnn dt t a ∑∞=++111n n nxn a ②,①和②仍为幂级数. 我们有定理5 幂级数∑∞=-11n n n xna 和∑∞=++111n n n xn a 与∑nn x a 有相同的收敛半径注: ①和②与∑nn x a 虽有相同的收敛半径(因而有相同的收敛区间),但未必有相同的收敛域, 例如级数∑∞=1n nnx.(2)幂级数的运算性质:定义1 两个幂级数∑∞=0n nn x a 和∑∞=0n n n x b 在点0=x 的某邻域内相等是指:它们在该邻域内收敛且有相同的和函数.定理6 ∑∞=0n n n x a =错误!未找到引用源。
高等数学第十一章知识要点
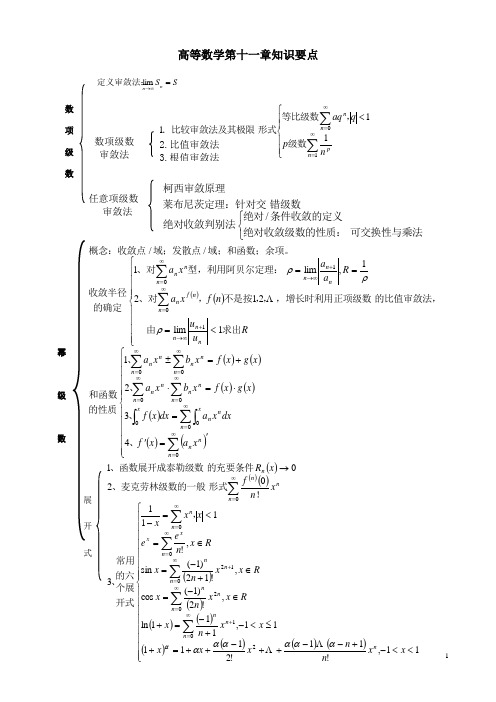
幂
级
数
概念:收敛点/ 域;发散点/ 域;和函数;余项。 a 1 n lim n 1 , R 1、对 a n x 型,利用阿贝尔定理: n a n n 0 收敛半径 2、对 a x f n ,f n 不是按1, 2, ,增长时利用正项级数 的比值审敛法, n 的确定 n 0 u 由 lim n 1 1求出R n u n n n 1、 a n x bn x f x g x n 0 n 0 n 2 、 a x bn x n f x g x n 和函数 n 0 n 0 x 的性质 x 3、 f x dx a n x n dx 0 0 n 0 4、f x an x n n 0
数的正交性: 1, cos x, sin x, cos 2 x, sin 2 x, , cos nx, sin nx, 1.收敛定理:函数展开为 傅立叶级数的充分条件 a 0 a n cos nx bn sin nx, x C 2. f x 2 n 1 1 a f x cos nx, n 0,1,2, 周期为2的函数 n 的傅立叶级数 b 1 sin nx, n 0,1,2, n 1 c x f x 2 f x f x 傅立叶级数 3.正弦级数和余弦级数 a0 f x a n cos nx bn sin nx, x C 2 n 0 a 1 l f x cos nxdx, n 0,1,2, 周期为2l的函数 n l l 的傅立叶级数 1 l bn f x sin nxdx, n 0,1,2, l l 1 c x f x 2 f x f x nx nx i i 1 l 复数形式: f x C n e l , C n f x e l dx l 2l n
高等数学下册第十一章习题答案详解

高等数学下册第十一章习题答案详解1.设L 为xOy 面内直线x a =上的一段,证明:(,)d 0LP x y x =⎰,其中(),P x y 在L 上连续.证:设L 是直线x =a 上由(a ,b 1)到(a ,b 2)这一段,则 L :12x ab t b y t =⎧≤≤⎨=⎩,始点参数为t =b 1,终点参数为t =b 2故 ()()()221d ,d d 0d 0d b b L b b a P x y x P a,t t P a,t t t ⎛⎫=⋅=⋅= ⎪⎝⎭⎰⎰⎰2.设L 为xOy 面内x 轴上从点(,0)a 到点(,0)b 的一段直线,证明:(,)d (,0)d bLaP x y x P x x =⎰⎰,其中(),P x y 在L 上连续.证:L :0x xa xb y =⎧≤≤⎨=⎩,起点参数为x =a ,终点参数为x =b . 故()(),d ,0d bLaP x y x P x x =⎰⎰3.计算下列对坐标的曲线积分: (1)22()d Lxy x -⎰,其中L 是抛物线2y x =上从点(0,0)到点(2,4)的一段弧;(2)d Lxy x ⎰,其中L 为圆周()222x a y a -+=(0)a >及x 轴所围成的在第一象限内的区域的整个边界(按逆时针方向绕行);(3)d d Ly x x y +⎰,其中L 为圆周cos ,sin x R t y R t ==上对应t 从0到π2的一段弧; (4)22()d ()d Lx y x x y y x y+--+⎰,其中L 为圆周222x y a +=(按逆时针方向绕行); (5)2d d d x x z y y z +-⎰Γ,其中Γ为曲线,,x k y acos z asin θθθ===上对应θ从0到π的一段弧;(6) 322d 3d ()d x x zy y xy z ++-⎰Γ,其中Γ是从点3,2,1()到点0,0,0()的一段直线;(7)d d d x y y z -+⎰Γ,其中Γ为有向闭折线ABCA ,这里AB C 、、依次为点1,0,0()、010(,,)、(001),,;(8)22(2)d (2)d Lx xy x y xy y -+-⎰,其中L 是抛物线2y x =上从点(1,1)-到点(1,1)的一段弧.解:(1)L :y =x 2,x 从0变到2,()()22222435001156d d 3515L x y x x x x x x ⎡⎤-=-=-=-⎢⎥⎣⎦⎰⎰ (2)如图11-1所示,L =L 1+L 2.其中L 1的参数方程为图11-1cos 0πsin x a a tt y a t =+⎧≤≤⎨=⎩L 2的方程为y =0(0≤x ≤2a ) 故()()()()()12π20π320ππ32203d d d 1+cost sin cos d 0d sin 1cos d sin d sin dsin π2LL L axy x xy x xy xa a t a a t t x a t t ta t t t ta =+'=⋅++=-+=-+=-⎰⎰⎰⎰⎰⎰⎰⎰(3)()π20π220π220d d sin sin cos cos d cos 2d 1sin 220Ly x x y R t R t R tR t t Rt tR t +=-+⎡⎤⎣⎦=⎡⎤=⎢⎥⎣⎦=⎰⎰⎰(4)圆周的参数方程为:x =a cos t ,y =a sin t ,t :0→2π. 故()()()()()()222π202π220d d 1cos sin sin cos sin cos d 1d 2πLx y x x y yx y a t a t a t a t a t a t t a a t a +--+=+---⎡⎤⎣⎦=-=-⎰⎰⎰(5)()()()2π220π3220π3320332d d d sin sin cos cos d d 131ππ3x xz y y zk k a a a a k a k a k a Γθθθθθθθθθθ+-=⋅+⋅--=-⎡⎤=-⎢⎥⎣⎦=-⎰⎰⎰(6)直线Γ的参数方程是32=⎧⎪=⎨⎪=⎩x t y t z t t 从1→0.故()()322322103141d 3d d 27334292d 87d 1874874x x zy y x y z t t t t t tt tt Γ++-⎡⎤=⋅+⋅⋅+-⋅⎣⎦==⋅=-⎰⎰⎰(7)AB BC CA Γ=++(如图11-2所示)图11-21:0y x AB z =-⎧⎨=⎩,x 从0→1()01d d d 112AB x y y z dx -+=--=-⎡⎤⎣⎦⎰⎰. 0:1x BC y z =⎧⎨=-⎩,z 从0→1()()()1010120d d d 112d 12232BC x y y z z dz z zz z -+=--+-⎡⎤⎣⎦=-⎡⎤=-⎢⎥⎣⎦=⎰⎰⎰0:1y CA z x =⎧⎨=-⎩,x 从0→1[]1d d d 1001CAx y y z dx -+=-+=⎰⎰.故()()d d d d d d 312122LABBCCAx y y zx y y z-+=++-+=-++=⎰⎰⎰⎰(8)()()()()()221224211235412d 2d 222d 224d 1415L x xy x y xy yx x x x x x x xxx x x x---+-⎡⎤=-⋅+-⋅⋅⎣⎦=-+-=-⎰⎰⎰4. 计算()d ()d Lx y x y x y ++-⎰,其中L 分别是:(1)抛物线2y x =上从点(1,1)到点(4,2)的一段弧; (2)从点(1,1)到点(4,2)的直线段;(3)先沿直线从点(1,1)到点(1,2),然后再沿直线到点(4,2)的折线; (4)曲线2221,1x t t y t =++=+上从点(1,1)到点(4,2)的一段弧. 解:(1)L :2x y y y ⎧=⎨=⎩,y :1→2,故()()()()()2221232124321d d 21d 2d 111232343L x y x y x yy y y y y yy y y yy y y ++-⎡⎤=+⋅+-⋅⎣⎦=++⎡⎤=++⎢⎥⎣⎦=⎰⎰⎰ (2)从(1,1)到(4,2)的直线段方程为x =3y -2,y :1→2 故()()()()()2121221d d 32332d 104d 5411L x y x y x yy y y y y y yy y ++-=-+⋅+-+⎡⎤⎣⎦=-⎡⎤=-⎣⎦=⎰⎰⎰ (3)设从点(1,1) 到点(1,2)的线段为L 1,从点(1,2)到(4,2)的线段为L 2,则L =L 1+L 2.且 L 1:1x y y=⎧⎨=⎩,y :1→2;L 2:2x x y =⎧⎨=⎩,x :1→4;故()()()()()12122211d d 101d 1d 212L x y x y x yy y y y y y y ++-=+⋅+-⎡⎤⎣⎦⎡⎤=-=-⎢⎥⎣⎦=⎰⎰⎰()()()()()()24144211d d 220d 12d 22272L x y x y x yx x x x x x ++-=++-⋅⎡⎤⎣⎦⎡⎤=+=+⎢⎥⎣⎦=⎰⎰⎰从而()()()()()12d d d d 1271422LL L x y x y x yx y x y x y++-=+++-=+=⎰⎰⎰(4)易得起点(1,1)对应的参数t 1=0,终点(4,2)对应的参数t 2=1,故()()()()()()122132014320d d 32412d 10592d 10592432323L x y x y x y t t t tt t tt t t tt t t t ++-⎡⎤=++++--⋅⎣⎦=+++⎡⎤=+++⎢⎥⎣⎦=⎰⎰⎰5. 设质点受力作用,力的反方向指向原点,大小与质点离原点的距离成正比.若质点由(,0)a 沿椭圆移动到0,Bb (),求力所做的功. 解:依题意知 F =kxi +kyj ,且L :cos sin x a t y a t=⎧⎨=⎩,t :0→π2()()()()π2022π20π222022d d cos sin sin cos d sin 2d 2cos 2222LW kx x ky yka t t kb t b t t k b a t tk b a t k b a =+=-+⋅⎡⎤⎣⎦-=--⎡⎤=⎢⎥⎣⎦-=⎰⎰⎰(其中k 为比例系数)6. 计算对坐标的曲线积分:(1)d xyz z ⎰Γ,Γ为2221x y z ++=与z y =相交的圆,方向按曲线依次经过第Ⅰ、Ⅱ、Ⅶ、Ⅷ卦限;(2)222222(-)d ()d ()d y z x z x y x y z +-+-⎰Γ,Γ为2221x y z ++=在第Ⅰ卦限部分的边界曲线,方向按曲线依次经过xOy 平面部分,yOz 平面部分和zOx 平面部分. 方向按曲线依次经过xOy 平面部分,yOz 平面部分和zOx 平面部分. 解:(1)Γ:2221x y z y z ⎧++=⎨=⎩ 即2221x z y z ⎧+=⎨=⎩其参数方程为:cos x ty tz t =⎧⎪⎪⎪=⎨⎪⎪=⎪⎩ t :0→2π 故:2π2π2202π202π0222d cos sin sin cos d 2sin cos d 2sin 2d 21cos 4d 22πxyz z t t t t t t t t t t ttΓ=⋅⋅⋅==-==⎰⎰⎰⎰⎰(2)如图11-3所示.图11-3Γ=Γ1+Γ2+Γ3.Γ1:cos sin 0x ty t z =⎧⎪=⎨⎪=⎩t :0→π2,故()()()()()1222222π2220π3320π320d d d sin sin cos cos d sincos d 2sin d 24233yz x z x y x y zt t t t tt t tt t Γ-+-+-⎡⎤=--⋅⎣⎦=-+=-=-⋅=-⎰⎰⎰⎰又根据轮换对称性知()()()()()()1222222222222d d d 3d d d 4334y z x z x y x y z y z x z x y x y zΓΓ-+-+-=-+-+-⎛⎫=⨯- ⎪⎝⎭=-⎰⎰ 习题11-31. 应用格林公式计算下列积分:(1)(24)d (356)d Lx y x x y y -+++-⎰,其中L 为三顶点分别为()()0,0,3,0和(32),的三角形正向边界;(2)222(cos 2sin e )d (sin 2e )d x x Lx y x xy x y x x x y y +-+-⎰,其中L 为正向星形线222333x y a +=0a >();(3)3222(2cos )d (12sin 3)d Lxy y x x y x x y y -+-+⎰,其中L 为抛物线22πx y =上由点0,0()到点π,12⎛⎫⎪⎝⎭的一段弧; (4)22()d (sin )d Lxy x x y y --+⎰,其中L 是圆周22y x x =-上由点0,0()到()1,1的一段弧;(5)(e sin )d (e cos )d x x Ly my x y m y -+-⎰,其中m 为常数,L 为由点(),0a 到0,0()经过圆22x y ax +=上半部分的路线(a 为正数).图11-4解:(1)L 所围区域D 如图11-4所示,P =2x -y +4,Q =3x +5y -6,3Qx∂=∂,1P y ∂=-∂,由格林公式得 ()()d d 24356d d 4d d 4d d 1432212LD DDx yx y x y Q P x y x y x yx y+-++-∂∂⎛⎫-= ⎪∂∂⎝⎭===⨯⨯⨯=⎰⎰⎰⎰⎰⎰⎰(2)P =x 2y cos x +2xy sin x -y 2e x ,Q =x 2sin x -2y e x , 则2cos 2sin 2e x P x x x x y y∂=+-∂,2cos 2sin 2e x Qx x x x y x∂=+-∂.从而P Qy x∂∂=∂∂,由格林公式得.()()222d dcos2sin e sin2ed d++--∂∂⎛⎫-= ⎪∂∂⎝⎭=⎰⎰⎰x xLDx yx y x xy x y x x yQ Px yx y(3)如图11-5所示,记OA,AB,BO围成的区域为D.(其中BO=-L)图11-5P=2xy3-y2cos x,Q=1-2y sin x+3x2y2262cosPxy y xy∂=-∂,262cosQxy y xx∂=-∂由格林公式有:d d d d0L OA AB DQ PP x Q y x yx y-++∂∂⎛⎫-+==⎪∂∂⎝⎭⎰⎰⎰故π2122001222d d d dd d d dππd d12sin3243d12π4π4++=+=+++⎛⎫=+-+⋅⋅⎪⎝⎭⎛⎫=-+⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰L OA ABOA ABP x Q y P x Q yP x Q y P x Q yO x yy yyy y(4)L、AB、BO及D如图11-6所示.图11-6由格林公式有d d d d++∂∂⎛⎫-+=- ⎪∂∂⎝⎭⎰⎰⎰L AB BO DQ PP x Q y x yx y而P=x2-y,Q=-(x+sin2y).1∂=-∂Py ,1∂=-∂Q x,即,0∂∂-=∂∂Q P x y 于是()d d d d 0+++++=+=⎰⎰⎰⎰LABBOL AB BOP x Q y P x Q y从而()()()()()()()22222211220011300d d d d sin d d d d sin sin d d 1sin 131sin 232471sin 264LLBA OB P x Q y x yx y x y x y x yx y x y x y x y y x x y x y y +=--+=-+--+-+=-++⎡⎤⎡⎤=+-+⎢⎥⎢⎥⎣⎦⎣⎦=-+⎰⎰⎰⎰⎰⎰(5)L ,OA 如图11-7所示.图11-7P =e x sin y -my , Q =e x cos y -m , e cos x P y m y ∂=-∂,e cos x Q y x ∂=∂ 由格林公式得:22d d d d d d d d 1π22π8L OA D DDQ P P x Q y x y x y m x ym x ya m m a +∂∂⎛⎫-+= ⎪∂∂⎝⎭==⎛⎫=⋅⋅ ⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰ 于是:()()[]220202πd d d d 8πd 0e sin 00e cos08π0d 8π8+=-+=-+⋅⋅-⋅⋅-=-=⎰⎰⎰⎰L OA a x x a m a P x Q y P x Q y m a xm m m a xm a2. 设a 为正常数,利用曲线积分,求下列曲线所围成的图形的面积:(1) 星形线 33cos ,sin ;x a t y a t == (2) 双纽线 22cos2;r a θ= (3) 圆 22x y ax ++=解:(1) ()()()()()2π3202π2π242222002π202π202π202d sin 3cos d sin 33sin cos d sin 2sin d 43d 1cos 41cos 2163d 1cos 2cos 4cos 2cos 416312π+d cos 2cos 61623π8LA y x a t a t tt a t t t a t t t a t t t a tt t t t a t t t a =-=-⋅-==⋅=--=--+⎡⎤=+⎢⎥⎣⎦=⎰⎰⎰⎰⎰⎰⎰(2)利用极坐标与直角坐标的关系x =r cos θ,y =r sin θ得 cos cos 2x a θ=sin cos 2y a θ=从而x d y -y d x =a 2cos2θd θ. 于是面积为:[]π24π4π24π4212d d 2cos 2d sin 22LA x y y x a a a θθθ--=⋅-===⎰⎰(3)圆x 2+y 2=2ax 的参数方程为 cos 02πsin x a a y a θθθ=+⎧≤≤⎨=⎩故()()[]()2π022π021d d 21d a+acos sin 2d 1cos 2πcos sin L A x y y xa a a a a θθθθθθθ=-=-=+=⋅-⎰⎰⎰ 3. 证明下列曲线积分与路径无关,并计算积分值: (1)(1,1)(0,0)()(d d )x y x y --⎰;(2)(3,4)2322(1,2)(6)d (63)d xy y x x y xy y -+-⎰;(3)(1,2)2(1,1)d d y x x yx +⎰沿在右半平面的路径; (4)(6,8)(1,0)⎰.证:(1)P =x -y ,Q =y -x .显然P ,Q 在xOy 面内有连续偏导数,且1P Q y x∂∂==-∂∂,故积分与路径无关.取L 为从(0,0)到(1,1)的直线段,则L 的方程为:y =x ,x :0→1.于是()()()()11,100,00d 0d d x x y x y ==--⎰⎰(2) P =6xy 2-y 3,Q =6x 2y -3xy 2.显然P ,Q 在xOy 面内有连续偏导数,且2123Pxy y y∂=-∂,2123Qxy y x∂=-∂,有P Q y x ∂∂=∂∂,所以积分与路径无关. 取L 为从(1,2)→(1,4)→(3,4)的折线,则()()()()()()[]3,423221,2432214323212d d 663d d 63966434864236x y xyy x y xy y x y y x y y x x +--=+--=+⎡⎤--⎣⎦=⎰⎰⎰(3)2y P x =,1Q x =-,P ,Q 在右半平面内有连续偏导数,且21P y x ∂=∂,21Q x x ∂=∂,在右半平面内恒有P Qy x∂∂=∂∂,故在右半平面内积分与路径无关. 取L 为从(1,1)到(1,2)的直线段,则()()()21,2211,1d d d 11x y x x y y -==--⎰⎰(4) P =,Q ,且P Qy x∂∂==∂∂分在不含原点的区域内与路径无关, 取L 为从(1,0)→(6,0)→(6,8)的折线,则()()686,811,0801529x y =+⎡=+⎣=⎰⎰⎰4.验证下列()(),d ,d P x y x Q x y y +在整个xOy 平面内是某一函数(),u x y 的全微分,并求这样的一个函数(),u x y :(1)()()2d 2d x y x x y y +++;(2)22d d xy x x y +;(3)223238d 812e d yx y xy x x x y y y ++++()(); (4)222cos cos d 2sin sin d x y y x x y x x y y ++-()(). 解:证:(1)P =x +2y ,Q =2x +y .2P Q y x ∂∂==∂∂,所以(x +2y )d x +(2x +y )d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分. ()()()()()(),0,0022022d d ,22d d 2222222x y xy yu x y x y x y x y x x yx y x y xy x y xy =+++=++⎡⎤=++⎢⎥⎣⎦=++⎰⎰⎰(2)P =2xy ,Q =x 2, 2P Qx y x∂∂==∂∂,故2xy d x +x 2d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分. ()()(),20,02022d d ,0d d x y xy u xy x x y x y x x yx y=+=+=⎰⎰⎰(3)P =3x 2y +8xy 2,Q =x 3+8x 2y +12y e y ,2316∂∂=+=∂∂P Qx xy y x,故(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y )d y 是某个定义在整个xOy 面内函数u (x ,y )的全微分, ()()()()()(),22320,03200322d ,38812e 0d d 812e 412e 12e 12x y y xyyy y u x x y x y x y x x y y x y x x y y x y x y y =++++=+++=++-+⎰⎰⎰(4)P =2x cos y +y 2cos x ,Q =2y sin x -x 2sin y ,2sin 2cos P x y y x y ∂=-+∂,2cos 2sin Qy x x y x∂=-∂, 有P Qy x∂∂=∂∂,故(2x cos y +y 2cos x )d x +(2y sin x -x 2sin y )d y 是某一个定义在整个xOy 面内的函数u (x ,y )的全微分,()()()()()(),220,020022d d ,2cos cos 2sin sin 2d d 2sin sin sin cos x y xyu x y x y x y y x y x x y x x yy x x y y x x y=++-=+-=+⎰⎰⎰5.证明:22xdx ydyx y ++在整个xOy 平面内除y 轴的负半轴及原点外的开区域G 内是某个二元函数的全微分,并求出这样的一个二元函数。
微积分:11.3 幂级数

证 (1)
an x0n收 敛
lim
n
an
x0n
0
n0
从而数列 {an x0n } 有界,即有常数M > 0,
使得 | an x0n | M (n 0,1,2,)
15
| an x0n | M (n 0,1,2,) | x || x0 |
an xn
an x0n
直接用比值判别法!
un ( x)
x 2n1 2n
lim un1( x) n un ( x)
x2n1 2n
lim n
2n1
x 2n1
1 x2, 2
当 1 x2 1, 即 x 2时, 级数绝对收敛,
2
当 1 x2 1, 即 x 2时, 级数发散, 2
28
即 x 2时, 级数绝对收敛,
x 2n1
n1 2n
即 x 2时, 级数发散,
R 2, ( 2, 2 )为 收 敛 区 间,
当x 2时, 当x 2时,
级 数 为
1
,
n1 2
级
数
为
1
,
n1 2
发散 发散
级数的收敛域为 ( 2, 2).
29
讨论幂级数
(1)n1
n0
x4n 3n 1
的收敛域
解 级数为缺项级数,直接用比值法.
lim un1( x) n un ( x)
收敛域(1,1); 发散域(,1][1,);
3
3.和函数 设{sn ( x)} 为函数项级数 un( x)
n1
的前n项和序列, (a, b)为级数收敛域, 则
lim
n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2) 在收敛区间内幂级数的和函数连续;
3) 幂级数在收敛区间内可逐项求导和求积分.
思考与练习
1. 已知
半径是多少 ? 答: 根据Abel 定理可知, 级数在 时发散 . 故收敛半径为 收敛 , 处条件收敛 , 问该级数收敛
机动
目录
上页
下页
返回
结束
2. 在幂级数
中,
b0 1, b1 1, b 0 , n 2 , 3, n
它们的收敛半径均为 R , 但是
1 x x2 xn
其收敛半径只是 R 1 .
机动 目录 上页 下页 返回 结束
定理4 若幂级数
的收敛半径
则其和函
在收敛域上连续, 且在收敛区间内可逐项求导与
收敛,
n
n
当 x x0 时,
故原幂级数绝对收敛 .
也收敛,
反之, 若当 x x0 时该幂级数发散 ,下面用反证法证之.
假设有一点 x1 满足 x1 x0 且使级数收敛 , 则由前
面的证明可知, 级数在点 x 0 也应收敛, 与所设矛盾, 故假设不真. 所以若当 x x0 时幂级数发散 , 则对一切
的系数满足
则
1) 当 ≠0 时, R 1 ;
2) 当 =0 时, R ; 3) 当 =∞时, R 0 .
证:
an 1 x n 1 an 1 lim lim x n n n an an x
1 当 x 1 , 即 x 时, 原级数收敛; 当 x 1 , 即 x 1 时, 原级数发散.
逐项求积分, 运算前后收敛半径相同:
S ( x) an x n nan x n 1 , x ( R , R )
n 0 n 1
0 S ( x) d x
x n 0
x n an x 0
an n 1 x , dx n 0 n 1 x ( R , R )
当4 x2 1 当4 x2 1
( 2 n 1)(2 n 2) 2 lim x 4 x2 n ( n 1 )2 时级数收敛 1 故收敛半径为 R . 2 时级数发散
机动 目录 上页 下页 返回 结束
例4. 解: 令 级数变为
的收敛域.
1 an R lim lim 2 n n n an 1 n
n 0
则对满足不等式
的一切 x 幂级数都绝对收敛.
反之, 若当 时该幂级数发散 , 则对满足不等式 的一切 x , 该幂级数也发散 . 证: 设 收敛, 则必有 于是存在
常数 M > 0, 使
收敛 发散
发
散
收
o
敛
发
阿贝尔 目录 上页
散
下页 返回
x
结束
an x
n
n an x0
x x n a n x0 n x0 x0
三、幂级数的运算
定理3. 设幂级数
及
的收敛半径分别为
R1 , R2 , 令 R min R1 , R2 , 则有 :
n 0
an x n (为常数 )
n n
x R1 x R x R
n 0
an x
n 0
n
bn x (an bn ) x ,
机动 目录 上页 下页
1 n! lim 1 n (n 1) !
0
返回
结束
例3.
的收敛半径 .
解: 级数缺少奇次幂项,不能直接应用定理2, 故直接由 比值审敛法求收敛半径.
[ 2 (n 1) ] ! 2 ( n 1) x 2 [ (n 1) ! ] u n 1 ( x) lim lim [ 2n] ! 2n n u n ( x ) n 2 x [n! ]
0 R , 幂级数在 (-R , R ) 收敛 ; 在[-R , R ]
外发散; 在 x R 可能收敛也可能发散 .
R 称为收敛半径 ,(-R , R ) 称为收敛区间.
(-R , R ) 加上收敛的端点称为收敛域.
收敛 发散
发
散
收
o
敛
机动
发
目录 上页
散
下页
x
返回 结束
定理2. 若
根值判别法成立
机动 目录 上页 下页 返回 结束
备用题 求极限
解: 令
作幂级数
其中
易知其收敛半径为 1, 设其和为
则
机动
目录
上页
下页
返回
结束
S ( x) C e x
x
由S (0) 1 得 S ( x) e , 故得
机动 目录 上页 下页 返回 结束
例6.
的和函数
解: 易求出幂级数的收敛半径为 1 , x=±1 时级数发 散,
x x n x (x )
n
x x 1 x
第三节
幂级数
一、函数项级数的概念 二、幂级数及其收敛性 三、幂级数的运算
第十一章
机动
目录
上页
下页
返回
结束
一、 函数项级数的概念
设 un ( x) (n 1, 2 ,) 为定义在区间 I 上的函数, 称
为定义在区间 I 上的函数项级数 . 对 若常数项级数 收敛, 称 x0 为其收
敛点, 所有收敛点的全体称为其收敛域 ; 若常数项级数 发散 , 称 x0 为其发散点, 所有
机动 目录 上页 下页 返回 结束
1) 若 ≠0, 则根据比值审敛法可知:
因此级数的收敛半径 R
1
2) 若 0, 则根据比值审敛法可知, 对任意 x 原级数 绝对收敛 , 因此 R ; 3) 若 , 则对除 x = 0 以外的一切 x 原级发散 ,
.
因此 R 0 .
满足不等式 x x0 的 x , 原幂级数也发散 .
机动 目录 上页 下页
证毕
返回 结束
由Abel 定理可以看出, 中心的区间.
n 0
an x
n
的收敛域是以原点为
用±R 表示幂级数收敛与发散的分界点, 则 R = 0 时, 幂级数仅在 x = 0 收敛 ; R = 时, 幂级数在 (-∞, +∞) 收敛 ;
说明:据此定理
an 的收敛半径为 R lim n an 1
机动
目录
上页
下页
返回
结束
例1.求幂级数 的收敛半径及收敛域.
1 lim n 1 n n 1
an 解: R lim n an 1
对端点 x = 1, 级数为交错级数
对端点 x =-1, 级数为 故收敛域为 (1, 1] .
机动 目录 上页
收敛;
发散 .
下页
返回
结束
例2. 求下列幂级数的收敛域 :
规定: 0 ! = 1
解: (1)
an R lim n an 1
所以收敛域为 ( , ) . an lim n ! (2) R lim n an 1 n (n 1) ! 所以级数仅在 x = 0 处收敛 .
1 2 n 1 (n 1)
2 n 1 (n 1) 2 lim n 2n n
当 t = 2 时, 级数为
当 t = – 2 时, 级数为
此级数发散;
此级数条件收敛;
因此级数的收敛域为 2 t 2 , 故原级数的收敛域为
即 1 x 3 .
机动 目录 上页 下页 返回 结束
所以级数的收敛域仅为
机动 目录 上页 下页 返回 结束
二、幂级数及其收敛性
形如
的函数项级数称为幂级数, 其中数列 为幂级数的系数 . 下面着重讨论 的情形, 即
称
1 , x 1 即是此种情形. 例如, 幂级数 x 1 x n 0
n
机动 目录 上页 下页 返回 结束
an x n 定理 1. ( Abel定理 ) 若幂级数
n 0 n 0
an x n bn x n cn x n ,
n 0 n 0
其中
以上结论可用部分和 的极限证明 .
机动 目录 上页 下页 返回 结束
说明: 两个幂级数相除所得幂级数的收敛半径可能比
原来两个幂级数的收敛半径小得多. 例如, 设
( a0 1, an 0 , n 1, 2 , )
n 1
n 1
机动
目录
上页
下页
返回
结束
例7. 求级数
的和函数
解: 易求出幂级数的收敛半径为 1 ,
收敛 ,
xn 1 x n 1 S ( x) x n 0 n 1 n 0 n 1
1 1 1 n x dx dx x 0 n 0 x 01 x
x0
机动
目录
上页
下页
返回
结束
例8. 解: 设 S ( x)
n2
n2 1 ,
x
n
则
1 1 1 n S ( x) x n 2 2 n 1 n 1
x x n 1 1 x n 1 2 n 2 n 1 2x n 2 n 1 x xn 1 xn 2 n 1 n 2x n 3 n
(证明见第六节)
注: 逐项积分时, 运算前后端点处的敛散性不变.
机动 目录 上页 下页 返回 结束
