05第五章 气体的流动压缩5-1一元稳定流动的基本方程
合集下载
可压缩气体的流动.
宗燕兵
p RT p C k
p T kk1 ( ) p0 T0
T k1 ( ) 1 0 T0
20
v2 i T 1 2i0 i0 T0
结论：在等熵或绝热情况下： v减小 p、T、都增大； v增大 p、T、都减小。
说明：气流速度增加时，气体在膨胀;
体现了热焓的减小转化为动能的过程
极限状态下的能量方程
2 vm v2 i 0 ax 2 2
vmax
滞止状态下 的能量方程
宗燕兵
k p v2 k p0 0 k 1 2 k 1 0
5.2.1连续性方程
vA C
5.2.2运动方程 欧拉方程
dv dA (或 0） v A
d
1 p dv y Y y dt 1 p dvz Z 宗燕兵 z dt
1 p dvx X x dt 气体密度很小，略去质量力
一维 稳定流动
1 dp dv v dx dx 即 dp vdv 0
第五章 可压缩气体的流动
前几章涉及的不可压缩流体的理论对液体和低速运动的气体 是适用的。 当气体的出流速度很高时（接近或超过音速），必须按不可 压缩气体来处理。 工程上的蒸汽、氧气、压缩空气、天然气的出流过程， 出流速度高达数百米，其出流过程必须按不可压缩流体处理。 5.1 基本概念 5.2 可压缩气体一元稳定等熵流动的基本方程
k 2 k 1
T* 2 , T0 k 1
p* 2 kk ( ) 1 p0 k 1
1 k 1 (1 Ma 2 ) k 1 0 2
上式中令Ma=1，得
宗燕兵
* 2 kk ( ) 1 0 k 1
工程流体力学 第5章 可压缩流体的一元流动
解： 由音速方程：
c1 kRT1 1.4 287 （273＋20）＝343m s
c2 kRT2 1.4 287 （273 55）＝296 m s
uu
Ma2 Ma1 Ma1
c2
u
c1
c1 c2 c2
343 296 296
16%
c1
2020年1月10日
FESTO气动中心
5.3 一元等熵流动基本关系
• 利用伯努利方程来讨论一元等熵流动特 定的状态参数。
2020年1月10日
FESTO气动中心
5.3.1 滞止状态和滞止参数
•
图6.3.1 气体的滞止状态
2020年1月10日
FESTO气动中心
对滞止状态截面和任一截面列能量方程有： 滞止状态时的焓升到最大值，即总焓
2020年1月10日
FESTO气动中心
1.理想气体状态方程：
p RT
R是气体常数，空气R=287 J/(kg·K)；T是热力学温度，单位为K
2.连续性方程：
2020年1月10日
可压缩性气体在流管内的定常流动
FESTO气动中心
1u1 A1 2u2 A2
uA c
ln(uA) ln ln u ln A C
2020年1月10日
FESTO气动中心
马赫角
sin c 1
u Ma
2020年1月10日
FESTO气动中心
例题
• 例 飞机在温度 t 20℃的海平面飞行， 与在同温层 t 55℃时飞行，若速度相等，
试求后一情况的马赫数比前一情况的马 赫数大多少？
2020年1月10日
FESTO气动中心
c1 kRT1 1.4 287 （273＋20）＝343m s
c2 kRT2 1.4 287 （273 55）＝296 m s
uu
Ma2 Ma1 Ma1
c2
u
c1
c1 c2 c2
343 296 296
16%
c1
2020年1月10日
FESTO气动中心
5.3 一元等熵流动基本关系
• 利用伯努利方程来讨论一元等熵流动特 定的状态参数。
2020年1月10日
FESTO气动中心
5.3.1 滞止状态和滞止参数
•
图6.3.1 气体的滞止状态
2020年1月10日
FESTO气动中心
对滞止状态截面和任一截面列能量方程有： 滞止状态时的焓升到最大值，即总焓
2020年1月10日
FESTO气动中心
1.理想气体状态方程：
p RT
R是气体常数，空气R=287 J/(kg·K)；T是热力学温度，单位为K
2.连续性方程：
2020年1月10日
可压缩性气体在流管内的定常流动
FESTO气动中心
1u1 A1 2u2 A2
uA c
ln(uA) ln ln u ln A C
2020年1月10日
FESTO气动中心
马赫角
sin c 1
u Ma
2020年1月10日
FESTO气动中心
例题
• 例 飞机在温度 t 20℃的海平面飞行， 与在同温层 t 55℃时飞行，若速度相等，
试求后一情况的马赫数比前一情况的马 赫数大多少？
2020年1月10日
FESTO气动中心
【精品课件】可压缩气体的流动
P+dP a-dv a
ρ+dρ
A T、P、ρ
n
n
将坐标系固定在扰动面mn上，即观察者随波面mn一起以速度 a向右运动，气体相对于观察者从右向左流动，经过mn。取虚 线范围为控制体。
动量方程为： p A (p d p )A A a d v
有dv dp (a)
a
m
m
dv P+dP
a v=0
A ρ+dρ T、P、ρ
第五章 可压缩气体的流动
前几章涉及的不可压缩流体的理论对液体和低速运动的气体 是适用的。 当气体的出流速度很高时（接近或超过音速），必须按不可 压缩气体来处理。
工程上的蒸汽、氧气、压缩空气、天然气的出流过程， 出流速度高达数百米，其出流过程必须按不可压缩流体处理。
5.1 基本概念 5.2 可压缩气体一元稳定等熵流动的基本方程 5.3 一元稳定等熵流动的基本特性 5.4 理想气体在变截面管中的流动
即 dp vdv 0
复习: 对于欧拉方程，考虑以下特殊条件： 1.理想流体； 2.稳定流动； 3.不可压缩流体； 4.质量力只有重力；5.质点沿一条特定流线运动。
X 1 p dvx
x dt
运动方程:欧拉方程
z p v2 C
2g
能量方程: 伯努利方程
5.2可压缩气体一元稳定等熵流动的基本方程 5.2.3能量方程 dp vdv 0 将上式积分，得
P+dP a-dv a
ρ+dρ
ቤተ መጻሕፍቲ ባይዱ
T、P、ρ
n
n
dv dp (a)
a
连 续 性 方 程 为 : a A ( a d v ) ( d ) A
得：dv ad d
华中科技大学 流体力学第五章_1
能量方程
c p / cV
u2 R T C 2 1
p RT
能量方程
u2 p C 2 1
能量方程
u2 hC 2
u2 c pT C 2 u2 R T C 2 1
u2 p C 2 1
例 27C的空气由大容器经一细 长管流入17C的大气，流动 过程绝热。求气体出流速度。
连续性方程
动量方程
cA d c u A
2 2
d u c d
pA p dp A d c u A c A
比较两式得到
d dp c d c
c c u A
dp u c
d dp c 1 d
e cV T p RT
d 1/ dT s cV R T 1/ cV ln T R ln C
δq de pd 1/ ds T T
cV ln T cV ln cV ln cV ln R cV ln R C cV ln cV ln R T
1.4 1.4 1
5.2 微弱扰动波的传播
1．声波
声速
声波 -- 微弱的压力(密度)扰动波。
2．声速 声速 -- 声波在流体中的传播速度。
声速是微弱压力(密度)扰动波的传播速度，
不是流体质点本身的运动速度。
p p
c y
p+dp x
u
c
T
p +dp c- u + d T + dT
能量方程
u2 c2 C 2 1
能量方程
u2 hC 2
c p / cV
u2 R T C 2 1
p RT
能量方程
u2 p C 2 1
能量方程
u2 hC 2
u2 c pT C 2 u2 R T C 2 1
u2 p C 2 1
例 27C的空气由大容器经一细 长管流入17C的大气，流动 过程绝热。求气体出流速度。
连续性方程
动量方程
cA d c u A
2 2
d u c d
pA p dp A d c u A c A
比较两式得到
d dp c d c
c c u A
dp u c
d dp c 1 d
e cV T p RT
d 1/ dT s cV R T 1/ cV ln T R ln C
δq de pd 1/ ds T T
cV ln T cV ln cV ln cV ln R cV ln R C cV ln cV ln R T
1.4 1.4 1
5.2 微弱扰动波的传播
1．声波
声速
声波 -- 微弱的压力(密度)扰动波。
2．声速 声速 -- 声波在流体中的传播速度。
声速是微弱压力(密度)扰动波的传播速度，
不是流体质点本身的运动速度。
p p
c y
p+dp x
u
c
T
p +dp c- u + d T + dT
能量方程
u2 c2 C 2 1
能量方程
u2 hC 2
5.1管道内燃气流动的基本方程
2024/4/5
21
7.低压管道的基本计算公式4-18ቤተ መጻሕፍቲ ባይዱ
P L
6.26107
Q02 d5
0
T T0
2024/4/5
22
符号意义
ΔP—管道起点燃气的绝对压力，Pa；
λ—燃气管道的水利摩阻系数；
Q0—燃气管道的计算流量，Nm3/h； d—燃气管道的内径，m；
ρ0—标准状况下燃气管道的密度， kg/Nm3；
5.低压燃气管道基本计算公式：
P
P1
P2
1.62
2
Q02 d5
0
P0 Pm
T T0
Z Z0
L
0.81
Q02 d5
0
T T0
Z Z0
L
2024/4/5
19
6.高、中压管道的基本计算公式
考虑城市燃气管道的压力一般都在 1.6MPa以下，Z≈Z0=1,则
中高压管道的计算公式变为：
P12
P22 L
W
0.226
2024/4/5
40
3.紊流区—⑵专用公式
对于新铸铁管，当 W 2.7 106 时
采用式4-30
K1
0.75 d 0.284
0.55 106
W
0.284
2024/4/5
41
3.紊流区—⑵专用公式
③尼古拉兹公式
当
9
Re 597 d 8 时，采用4-31
1
2
2
lg
第一节 管道内燃气流动的基本方程式
一、不稳定流动方程式 二、稳定流动方程式 三、燃气管道的摩擦阻力系数
2024/4/5
1
方程组
第五章 流体力学
称为伯努利方程。
伯努利方程对定常流动的流体中的任一流线也成立。
例题5-3
例题5-3：文丘里流量计。U形管中水银密度为ρ’，流量计中通 过的液体密度为ρ，其他数据如图所示。求流量。
取水平管道中心的流线。
1 2 1 2 由伯努利方程： p1 v1 p2 v 2 2 2
p 1 、 S1
得： p p e 0
gy p0
积分：
p p0
0 y dp g dy p p0 0
p0、ρ0
o
如： 0 1.293kg / m 3 , p0 1.013 10 5 Pa , y 8848 m ( 珠峰 )
得： p 0.33 p0 0.33 atm
例题5-1
1 1 2 2 动能增量：Ek V v 2 V v1 2 2
p1
v1 S1
势能增量： E p g( h2 h1 )V 外力作功：
A A'
h1
S2
v2
B
h2
B'
p2
W p1 S1l1 p2 S2 l 2 p1V p2 V
由功能原理：
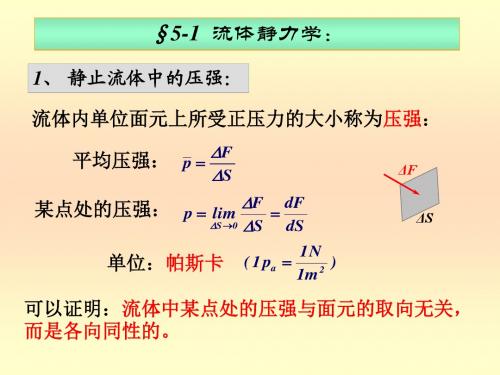
θ z Δx py
Δz
x
当ΔV=0时： p y pl 无论流体时静止还是流动，以上结论都成立。
2、 静止流体中压强的分布：
(1) 静止流体中同一水平面上压强相等。 pA pA pB
A
ΔS B
pB
(2) 静止流体中高度相差h的两点间压强差为ρgh。
pB pA gh
(3) 帕斯卡原理： 密闭容器中的静止液体，当外
单位时间内，容器内水的减少等于从小孔流出的流量： 积分得：t
工程热力学第5章-气体流动和压缩
1.67 c 0.487 1.40 c 0.528 1.30 c 0.546 1.30 c 0.487 1.135 c 0.577
临界流速（喉部流速）
1 2 * * pc cc p v 1 * p 1
0
过程方程 无摩擦时即定熵过程 音速方程
s
pv 常数
p v
2
对理想气体
p cs
p v v s
pv 0 RgT
课堂练习
P137： 习题5-2
喷管
喷管是利用压力降低使流体增速的管道。
喷管流动特点 • 流速高 • 距离短 • 做绝热处理
学习要求 • 气流截面变化原因 • 喷管设计和校核计 算 • 滞止参数的概念
例5-2
解:对空气0=1.4,
*
c 0.528
pc p c 0.8 0.528 0.4224MPa
Why?
p2 0.1 pc
c2 2 0 RgT
*
缩放形喷管
0 1 0
p2 [1 * p 0 1
0
] 511.0m / s
dA 0 dA 0 A dA 0 A
思考题
教材P136: 2.为什么渐放形管道也能使气流加速?渐放 形管道也能使液体加速吗?
不能使液体加速.液体dv=0,不能导出此公 式.
如果将Ma<1的 亚音速气流增速到 Ma>1的超音速 气流该怎么办???
缩放喷管 拉伐尔喷管
dA dc 2 ( Ma 1) A c
气体流动的基本方程和基本概念_图文
例题
画出有正预旋时离心叶轮叶片进口速度三角形，标出u1 、C1 、C1r 、 C1u 、W1 、α1 、β1和β1A（设冲角为零）。再用另一种颜色的笔在同 一张图上针对同一叶轮画出流量增加时的叶片进口速度三角形，请标 出发生变化的量，并说明此时冲角的正负。
C1* C1r* W1* C1 C1r W1
连续方程： 欧拉方程： 能量方程： 伯努力方程： 状态方程： 压缩过程方程：
级效率
离心式压缩机或级的效率是用来表达叶轮传 递给气体的机械能的利用程度。常用的效率 表示有多变效率ηpol、等熵效率ηs和流动效率 ηhyd。
多变效率ηpol 多变效率ηpol是指气体由压力p1增加到压力 p2所需的多变压缩功与实际所耗总功之比
② 对有粘无粘的气体都适用，因为对有粘气体所引 起的能量损失也以热量形式传递给气体，从而式气 体温度(焓)升高；
③ 可认为气体在机器内做绝热运动，q＝0；
④ 该方程适用于一级，也适用于多级整机或其中任 一通流部件，这由所取的进出口截面决定。
伯努利方程
应用伯努力方程将流体所获得的能量区分为有用 能量和能量损失，并引用压缩机中所最关注的压力参 数，以显示出压力的增加。叶轮所做的机械功还可与 级内表征流体压力升高的静压能联系起来，表达成通 用的伯努力方程，对级内流体而言有
解：
例题
测得空气离心压缩机级的下列参数：级进口温度Tin = 293 K ，级进口压力Pin = 101300 Pa，级进口滞止温度T＊out = 350.58 K，级出口压力Pout = 167145 Pa，级进出口速度Cin = Cout = 20 m/s， 空气物性参数为R = 287 J/(Kg·K)，k = 1.4 ; 求： （1）级的多变压缩功Wpol和总耗功Wtot（J/Kg）； （2）级的平均多变效率ηpol ； （3）级中的总损失hloss 。
第五章 不可压缩理想流体一元流动
如图所示的等截面直角形管道 ABC ，垂直段管长 AB ，水平段管长 BC ， AB = BC = L ，管中盛满 水，C 处有阀门，管口接大气，大气压力为 pa ，质 量力为重力。试问：当阀门突然打开，管中压力分 布如何？ 把坐标原点放在水平管的中心线与垂直管的中心线 的交点 B 上，流线从 A 点开始计算。
二．水下球面膨胀 淹没在不可压缩静止流体的球面，以 Rb = Rb (t ) 的 规律膨胀（或收缩），设无穷远处流体 p∞ = const 压力质量力不计，求球面上的压力 pb及流场压力。
Vb = Vbe R = Rbe R Rb 表示物面膨胀速度，流线与eR 重合，通流截面
为一球面。 由连续方程 4π R 2V = 4π Rb2 Rb
V = V (t ) = VA (t ) = VB (t ) 且 zB = − z A ∂V dV 又可知 = dt ∂t B 因而，在两自由液面 A、 之间应用运动方程，有 dV pB pA +UB − −U A = 0 L+ dt ρ ρ
考虑到重力势 U = gz 以及pB = p A ，z B = − z A ，则 运动方程可变为 dVB
pb 为球面压力，是待定函数。
利用 R → ∞, p = p∞ 条件，可确定球面压力 pb
1 2 pb Rb Rb + 2 R + − Rb − =0 ρ 2 ρ
2 b
p∞
即
p p∞
pb
3 2 = + Rb Rb + Rb 2 ρ ρ
p∞
1 Rb2 Rb 2 2 Rb2 Rb + Rb2 Rb = − ( 2 ) + R ρ ρ 2 R
对于一元流动并不需要研究运动是否有旋的问题。 但是对于球对称或平面轴对称问题（对称轴与平面 垂直），从整个流场来看运动是无旋的，可以直接 采用柯西－拉格朗日积分 ∂ϕ V 2 p + + + U = f (t ) ∂t 2 ρ
《空气动力学基础》第5章图文模板
收缩喷管的工作状态
亚临界流态
Mae 1 pe pb
pb p0 cr 完全膨胀
出口外扰动可向管内传播。
14:25
22
第五章 一维定常可压缩管内流动 §5-2 收缩喷管 收缩喷管的工作状态
——气流在喷管内的膨胀加速程度取决于总压和背压。
亚临界流态
特点
判别
Mae 1 pe pb
pb p0 cr
T0
K p0 A q
T0
14:25
17
第五章 一维定常可压缩管内流动 §5-1 理想气体在变截面管道中的流动
流量函数q(λ)
1
q
1 2
1
( )
q(λ) 1.0
0.8
空气γ =1.4
q(λ)不是一个单调函数 ；
y(λ) 临 界 状 态 (λ=1) 下 ， q(λ) 最
5.0
4.0 大值；
§5-4 内压式超声速进气道及其他变截面管流
14:25
11
第五章 一维定常可压缩管内流动 §5-2 收缩喷管 喷管的分类
——使气流不断加速的管道。
气流参数
dp d dTMa<1 Ma<1 pT
Ma 1
M a< 1 M a< 1
Ma 1
M a>1 M a>1
扩 压 M a>1 M a>1
器
dv dMMa<1a v Ma
超临界流态
Mae 1 pe pb
pb p0 cr 不完全膨胀
出口外扰动无法影响喷管内部流动；
且存在膨胀波。
14:25
26
第五章 一维定常可压缩管内流动 §5-2 收缩喷管
收缩喷管的工作状态
亚临界流态
Mae 1 pe pb
pb p0 cr 完全膨胀
出口外扰动可向管内传播。
14:25
22
第五章 一维定常可压缩管内流动 §5-2 收缩喷管 收缩喷管的工作状态
——气流在喷管内的膨胀加速程度取决于总压和背压。
亚临界流态
特点
判别
Mae 1 pe pb
pb p0 cr
T0
K p0 A q
T0
14:25
17
第五章 一维定常可压缩管内流动 §5-1 理想气体在变截面管道中的流动
流量函数q(λ)
1
q
1 2
1
( )
q(λ) 1.0
0.8
空气γ =1.4
q(λ)不是一个单调函数 ；
y(λ) 临 界 状 态 (λ=1) 下 ， q(λ) 最
5.0
4.0 大值；
§5-4 内压式超声速进气道及其他变截面管流
14:25
11
第五章 一维定常可压缩管内流动 §5-2 收缩喷管 喷管的分类
——使气流不断加速的管道。
气流参数
dp d dTMa<1 Ma<1 pT
Ma 1
M a< 1 M a< 1
Ma 1
M a>1 M a>1
扩 压 M a>1 M a>1
器
dv dMMa<1a v Ma
超临界流态
Mae 1 pe pb
pb p0 cr 不完全膨胀
出口外扰动无法影响喷管内部流动；
且存在膨胀波。
14:25
26
第五章 一维定常可压缩管内流动 §5-2 收缩喷管
收缩喷管的工作状态
第5章 可压缩流体的一元流动.ppt
此外，如果流动等熵，则有
ρ0 T =( ) ρ T
1 0 γ −1
= (1+
γ −1
2
M )
1 2 γ −1
p0 T γ −1 2 γ −1 = ( 0 )γ −1 = (1+ M ) p T 2
γ
γ
对空气：
T0 T0 2.5 p0 T0 3.5 2 ρ0 =1+ 0.2Ma ， = ( ) ， = ( ) T ρ T p T
利用连续性方程，得
ρ1v1 A = ρ2v2 A2 1 A2 ρ1v1 ρ1 Ma1 c1 = = A ρ2v2 ρ2 Ma2 c2 1
= Ma1 T ( ) Ma2 T2
1 1 γ −1
T Ma1 .( 1 ) = ( ) T2 Ma2 T2
1 2
γ +1 T1 2(γ −1)
A2 Ma1 [ γ 21 = A Ma2 1+ − Ma2 1 1 2
ρ T γ −1 Qm = ρuA = ρ0 uA = ρA( ) 2Cp (T0 −T ) T0 ρ0
1
2012-3-10 工程流体力学第5章 33
当容器内的气体参数To , p o, ρ0,固定时， Q m是T的函 数。现求最大值Qmax 。
dQm 2 = 0 得T = T0 （ ） T* = Qm = Qmax时, dT γ +1
p
ρ
γ
=c
dp dρ −γ =0 p ρ
dp dρ dv γMa2 dA =γ = −γMa2 = ρ p v Ma2 −1 A
亚音速流,面积增大(d A>0),则速度变小,压强 增大 超音速流,面积增大(d A>0),则速度变大,压强 减小
气体动力学基础笔记手写
气体动力学基础笔记手写一、气体动力学基本概念1. 气体：由大量分子组成的混合物，其分子在不断地运动和碰撞。
2. 温度：气体分子平均动能的量度，与分子平均动能成正比。
3. 压力：气体对容器壁的压强，由大量气体分子对容器壁的碰撞产生。
4. 密度：单位体积内的气体质量，与分子数和分子质量有关。
5. 流场：描述气体流动的空间和时间的函数，由速度、压力、密度等物理量描述。
二、理想气体状态方程1. 理想气体状态方程：pV = nRT，其中p为压力，V为体积，n为摩尔数，R为气体常数，T为温度。
2. 实际气体与理想气体的关系：实际气体在一定条件下可以近似为理想气体，但在某些情况下需要考虑分子间相互作用和分子内能等效应。
三、气体流动的基本方程1. 连续性方程：质量守恒方程，表示单位时间内流入流出控制体的质量流量相等。
2. 动量守恒方程：牛顿第二定律，表示单位时间内流入流出控制体的动量流量等于作用在控制体上的外力之和。
3. 能量守恒方程：热力学第一定律，表示单位时间内流入流出控制体的热量流量等于控制体内能的变化率加上作用在控制体上的外力所做的功。
四、一维定常流1. 一维流：流场中所有点的流速方向都在同一直线上。
2. 定常流：流场中各物理量不随时间变化而变化的流动。
3. 声速：气体中声速与温度和气体种类有关，是气体的特征速度。
4. 马赫数：流场中任意一点上流速与当地声速之比，是描述流动状态的重要参数。
五、膨胀波与压缩波1. 膨胀波：由于流体受压缩而产生的波，传播方向与流体运动方向相反，波前压力低于波后压力。
2. 压缩波：由于流体受扩张而产生的波，传播方向与流体运动方向相同，波前压力高于波后压力。
工程热力学与传热学_气体的流动
ccr a kpcr vcr
归纳： 1）压差是使气流加速的基本条件，几何形状是使 流动可逆必不可少的条件； 2）气流的焓差为气流加速提供了能量； 3）收缩喷管的出口截面上流速小于等于当地音速； 4）拉法尔喷管喉部截面为临界截面，截面上流速 达当地音速，
ccr a kpcr vcr
5-3 气体流经喷管的流速和流量
能量方程
1 2 h1 h2 c2 c12 2
过程方程
Pvk 常数
dp dv 0 p v
§5.2 促使流速改变的条件
工程上常有将气流加速或加压的要求。例如： 利用喷管将蒸汽流加速，冲动汽轮机的叶轮作功； 喷气式发动机则利用喷管将气流加速后喷出，产生巨大的反作 用力来推动装置运动 通过扩压管利用气流的宏观运动动能令气流升压
相应对扩压管的要求：
• 对超音速气流做成渐缩扩压管 • 对亚音速气流做成渐扩扩压管 • 对气流连续降至亚音速时，要做成缩放扩 压管。但这种渐缩渐扩扩压管中气流流动 情况复杂，不能按定熵流动规律实现超音 速到亚音速的连续转变
临界参数
缩放喷管和扩压管的最小截面处，称为喉部。 此处的流速恰好等于当地音速。此处为气流从亚音 速变为超音速，或从超音速变为亚音速的转折点， 通常称为临界状态。对应的状态参数，称为临界参 数。并加以下标cr表示。 M=1，即c=a。
相应对喷管的要求：
• 对亚音速气流做成渐缩喷管 • 对超音速气流做成渐扩喷管 • 对气流由亚音速连续增至超音速时，要做 成缩放喷管，或叫拉法尔喷管（Laval）， 只要这样才能保证气流在喷管中充分膨胀， 达到理想加速后果。
对于扩压管（dc＜ 0) ： M＞1,超声速流动,dA<0,截面收缩； M=1, 声速流动,dA=0,截面缩至最小； M＜1, 亚声速流动,dA>0,截面扩张；
气体流动知识点总结
气体流动知识点总结一、气体流动的基本特性1.1 气体的基本特性气体是一种物态，具有一些特殊的基本性质，如可压缩性、弹性、可扩散性等。
这些特性决定了气体在流动过程中表现出的独特行为。
在理想气体状态下，气体具有简单的状态方程，即PV=RT，其中P为压力，V为体积，T为温度，R为气体常数。
这个方程描述了理想气体的状态，但在实际工程中，气体流动往往还受到多种因素的影响，因此需要更复杂的流动方程来描述。
1.2 气体的流动特性气体流动具有一些与其特性相关的基本规律。
首先是密度的不连续性。
在压缩气体流动的过程中，气体密度会发生突变，导致流场中密度的不连续性。
此外，由于气体分子的热运动，气体流动具有一定的湍流性质，因此在实际的气体流动过程中，需要考虑湍流的影响。
1.3 气体流动的基本方程描述气体流动的基本方程为流体力学方程，即连续性方程、动量方程和能量方程。
这些方程描述了气体流动的守恒性质，分别描述了质量、动量和能量在流动过程中的传递和转化关系。
了解这些方程对于分析和控制气体流动具有重要意义。
二、气体流动的流动方程2.1 连续性方程连续性方程描述了流场中流体的质量守恒关系，它可以用来描述气体流动中流体的流动速度和密度的变化关系。
连续性方程的数学表达形式为：∂ρ/∂t + ∇·(ρu) = 0其中，ρ为流体密度，t为时间，u为流速矢量。
这个方程表明了流体密度的变化与流速的关系，对于描述气体流动的密度分布和流速分布具有重要意义。
2.2 动量方程动量方程描述了流场中流体的动量守恒关系，它可以用来描述气体流动中流体的受力和流动的加速度关系。
动量方程的数学表达形式为：∂(ρu)/∂t + ∇·(ρuu) = -∇p + ∇·τ + ρg其中，p为压力，τ为应力张量，g为重力加速度。
这个方程描述了流体在流动过程中受到的压力、应力和重力等力的作用，对于描述气体流动的力学特性具有重要意义。
2.3 能量方程能量方程描述了流场中流体的能量守恒关系，它可以用来描述气体流动中能量的传递和转化关系。
流体力学第五章
可压缩流动涉及温度变化，变量有 V, p, , T
可以应用 连续性方程 状态方程 动量方程 能量方程
uAC
p RT
可压缩流动能量方程 ?
5.1 可压缩气体一元定常流的基本公式 四、热力学常数
e 单位质量气体内能 h 单位质量气体的焓 S 单位质量气体的熵 q 是单位质量气体的热能
完全气体的比热
5.4 一元等熵气流在变截面管道中的流动 四、缩放喷管（拉伐尔喷管）
1
2
喉部 收缩段
3
扩张段
如何实现超声速流动 ？
例. 收缩喷管空气的滞止参数 p0=10.35105Pa，T0=350K ，出口直径d=15mm。求出口背压分别为pe=7105Pa、 pe=5105Pa时喷管的质量流量。
解 (1) 出口背压 pe=7105Pa （亚音速）
题5-15. 空气从T1=278K， p1=105Pa绝热地压缩为 T2=388K, p2=2105Pa ; 求p01/p02 。
例 解. 绝热流动 T01=T02，但 p01p02。
p01 p1
(T01
)
1
T1
&
p02 p2
(T02
) 1
T2
题
p01
p1 ( T2
γ
)γ1
第五章 可压缩流体的一元流动
§5-1 可压缩气体一元定常流动的基本公式 §5-2 微弱扰动波的传播 声速 §5-3 一元等熵流动的基本关系 §5-4 一元等熵气流在变截面管道中的流动 §5-5 有摩擦和热交换的一元流动
第五章 可压缩流体的一元流动 §5-1 可压缩气体一元定常流动的基本公式 一、状态方程 二、连续性方程 三、运完动全方气程体的状态方程 四、热力学常数
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
对于稳定流动， 根据质量守恒原理可知， 流过流道任何一个截面的流量必定相等
qm1 qm2 qm 常数
A1c1 A2c2 Ac qm 常数 v1 v2 v
一元稳定流动 连续性方程
方程表明：稳定流动中，任何时刻流过流道 任何截面的流量都是不变的常数 连续性方程是流量计算的基本公式，适用于 任何一元稳定流动，不管是什么流体 , 也不 管是可逆过程或是不可逆过程。 需要注意的是，稳定流动中质量流量是不变 的常数，但是，其容积流量不是不变的常数
音速方程
声音在气体中的传播速度（音速cs） 与气体的状态有关
p 2 p cs v v s s
cs pv
理想气体
cs 0 RgT
pv const
p p v v s
声音在理想气体中 的传播速度与绝对 温度的平方根成正 比，温度愈高，音 速愈大
1. 连续方程
截面1
qm1 A1 v1 c1
qm A v c
截面3 qm3 A3 v3 c3
稳定流动质量守恒方程（连续性方程）
qV qmv Ac
Ac qm v Ac qm 常数 v
对稳定流动而言，流量不随时间变化
Ai ci A1c1 常数 qm1 常数 qmi vi v1
第五章 气体的流动与压缩
本章内容
一元稳定流动基本方程 喷管中气流参数变化和喷管截面
积变化的关系
气体流经喷管的流速和流量 压气机的压气过程
气体和蒸汽在管路设备中的流动问题
火箭腾空升 起的力量来 自从其尾喷 管高速喷出 的气体动能 的反作用力
在蒸汽轮机和燃气轮机等动力设备中，使高 温高压的气体通过喷管，产生高速流动，然 后利用高速气流和喷射式抽气器—— 扩压管原理
气体和蒸汽流经阀门、孔板等狭窄 通道时产生的节流现象
5-1 一元稳定流动的基本方程
所谓一元流动，是指流动的一切参数 仅沿一个方向（这个方向可以是弯曲 流道的轴线）有显著变化，而在其它 两个方向上的变化是极小的 所谓稳定流动，是指流道中任意指定 空间的一切参数都不随时间而变
pv const （κ为定值）
k称为定熵指数（亦称绝热指数） 对定比热容理想气体而言，定熵指数等 0 于热容比：
（3）音速方程
根据物理学知道，音速是微小扰动在连续 介质中产生的压力波的传播速度
由于一般扰动很小，内摩擦很小，可以认为 是可逆的，而且扰动传播很快，来不及向外 散热，可以认为是绝热的，所以声音这种扰 动传播是一种定熵过程
4. 流动中常用的其他一些和 流体性质有关的方程 （1）状态方程：流体状态方程的一般形式是：
F p, v, T 0
理想气体的状态方程具有最简单的形式：
pv RgT
（2）过程方程
本章只讨论绝热流动，如果不考虑摩擦，就是定 熵流动，过程方程为定熵过程方程
假定气体（理想气体和实际气体）的定熵过 程遵守如下方程
1 2 2 c2 c1 h1 h2 2
公式可以表述为：绝能（绝热、绝功）过 程中，工质的焓加动能是不变的常数 该式适用于任何工质的绝热稳定流动过程， 不管过程是可逆的或是不可逆的，它是流 速计算的基本公式
3. 动量方程 动量方程 在流体中沿流动方向取一微元柱体。
柱体的截面积为dA，长度为dx。假定作用在 柱体侧面的摩擦力(粘性阻力)为dFf。
动量方程 如果不考虑粘性力（无摩擦），则可得
1 2 dFf dc vdp v vdp wL 2 dA
1 2 dc vdp 2
1 2 dc vdp 2
cdc = - vdp
2 1 2 2 c2 c1 vdp 1 2
本式建立了流速与技术功之间的关系： 对于无摩擦流动，气体膨胀所获得的动 能正好等于气体膨胀作出的技术功，在 后面推导无摩擦流速公式时就利用了这 个公式 庞大数十吨重的飞机所以能够飞起来 就是利用了这个原理
2. 能量方程
稳定流动的能量方程（能量方程）
1 2 2 q h2 h1 c2 c1 g z2 z1 wsh 2
喷管和扩压管的流动，其特点为：
无轴功 气体和外界基本上绝热 重力位能基本上无变化
wsh 0
q0
g z2 z1 0
能量方程变为如下的简单形式
根据牛顿第二定律可知， 在dt时间内，作用在微元 柱体上的冲量必定等于该 柱 体 的 动 量 变 化 ：
dAdx pdA p dp dA dFf d dmdc v dc
dFf dx vdp v dc cdc dA d
1 2 dFf dc vdp v vdp wL 2 dA