力学第二章习题答案
材料力学课后习题答案详细
变形厚的壁厚：
(R r) | (R r) | 30 0.009 29.991(mm)
[习题 2-11] 受轴向拉力 F 作用的箱形薄壁杆如图所示。已知该材料的弹性
常数为 E, ，试求 C 与 D 两点间的距离改
22
N 22 A
10 103 N 400mm 2
25MPa
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-3] 试求图示阶梯状直杆横截面 1-1、2-2 和平 3-3 上的轴力，并作
轴力图。若横截面面积 A1 200mm2 ， A2 300mm2 ， A3 400mm2 ，并求各横截 面上的应力。
A1 11.503cm2 1150.3mm2
AE
N EA A
366.86 103 N 2 1150.3mm2
159.5MPa
EG
N EG A
357.62 103 N 2 1150.3mm2
155.5MPa
[习题 2-5] 石砌桥墩的墩身高 l 10m ，其横截面面尺寸如图所示。荷载
22
N 22 A2
10 103 N 300mm 2
33.3MPa
3
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-4] 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制
成。下面的拉杆和中间竖向撑杆用角钢构成，其截面均
为两个 75mm 8mm 的等边角钢。已知屋面承受集度为
南航理论力学习题答案2(1)
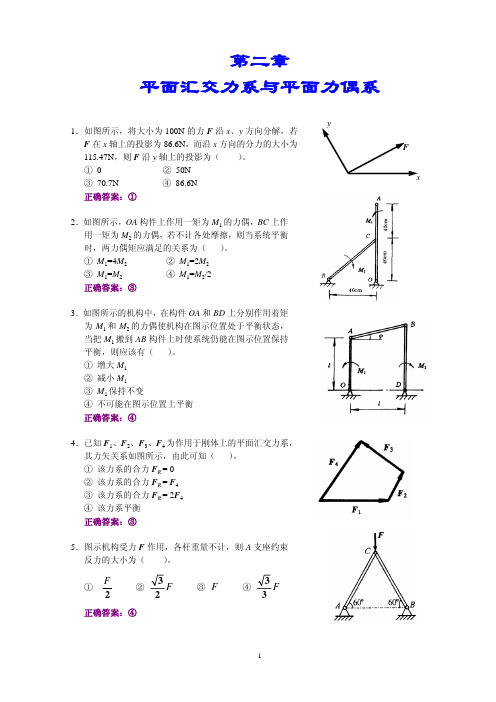
第二章平面汇交力系与平面力偶系1．如图所示，将大小为100N 的力F 沿x 、y 方向分解，若F 在x 轴上的投影为86.6N ，而沿x 方向的分力的大小为115.47N ，则F 沿y 轴上的投影为（ ）。
① 0 ② 50N③ 70.7N ④ 86.6N正确答案：①2．如图所示，OA 构件上作用一矩为M 1的力偶，BC 上作用一矩为M 2的力偶，若不计各处摩擦，则当系统平衡时，两力偶矩应满足的关系为（ ）。
① M 1=4M 2 ② M 1=2M 2③ M 1=M 2 ④ M 1=M 2/2正确答案：③3．如图所示的机构中，在构件OA 和BD 上分别作用着矩为M 1和M 2的力偶使机构在图示位置处于平衡状态，当把M 1搬到AB 构件上时使系统仍能在图示位置保持平衡，则应该有（ ）。
① 增大M 1② 减小M 1③ M 1保持不变④ 不可能在图示位置上平衡正确答案：④4．已知F 1、F 2、F 3、F 4为作用于刚体上的平面汇交力系，其力矢关系如图所示，由此可知（ ）。
① 该力系的合力F R = 0② 该力系的合力F R = F 4③ 该力系的合力F R = 2F 4④ 该力系平衡正确答案：③5．图示机构受力F 作用，各杆重量不计，则A 支座约束反力的大小为（ ）。
① 2F② F 23③ F ④ F 33正确答案：④6．图示杆系结构由相同的细直杆铰接而成，各杆重量不计。
若F A =F C =F ，且垂直BD ，则杆BD 的内力为（ ）。
① F − ② F 3− ③ F 33− ④ F 23− 正确答案：③7．分析图中画出的5个共面力偶，与图（a ）所示的力偶等效的力偶是（ ）。
① 图（b ） ② 图（c ） ③ 图（d ） ④ 图（e ）正确答案：②8．平面汇交力系平衡的几何条件是（ ）；平衡的解析条件是（ ）。
正确答案：力多边形自形封闭 各力在两个坐标轴上投影的代数和分别等于零9．平面内两个力偶等效的条件是（ ）；平面力偶系平衡的充分必要条件是（ ）。
工程力学习题 及最终答案
—————————————— 工程力学习题 ——————————————第一章 绪论思 考 题1） 现代力学有哪些重要的特征？2) 力是物体间的相互作用。
按其是否直接接触如何分类？试举例说明。
3） 工程静力学的基本研究内容和主线是什么？ 4） 试述工程力学研究问题的一般方法.第二章 刚体静力学基本概念与理论习 题2-1 求图中作用在托架上的合力F R 。
2-2， 求图中作用在耳环上的合力F R 。
2-3 F R 。
2-4 α。
使x 轴。
b ）合力为零。
习题2-2图(b)F 1F 1F 2(a )。
为提起木桩，欲使垂直向上的合力为F R =750N,且F 2α角。
o 点之矩。
2(d) (g) 习题2-6图 习题2-7图CDBA2—9 求图中力系的合力F R 及其作用位置。
F R 及其作用位置。
q 1=400N/m ，q 2=900N/m, 若欲使作用在.第三章 静力平衡问题习 题3-1 图示液压夹紧装置中，油缸活塞直径习题2-8图(d) (c)q ( c ) 图B习题2-11图 习题2-9图D=120mm ，压力p =6N/mm 2,若α=30︒， 求工件D 所受到的夹紧力F D 。
3—2 图中为利用绳索拔桩的简易方法。
若施加力F =300N ，α=0.1弧度，求拔桩力F AD 。
(提示 ：α较小时，有tg α≈α）。
•m ，l =0。
8m ，求梁A 、B 处的约束力。
3-4 若F 2=2F 1，求图示梁A 、B 处的约束力。
3q=15kN/m 和集中力偶3—DE 和压杆AC 处于水r=40mm ，a =120mm,b=60mm ，求在力F 作用下，工件受到的夹紧力.习题3-1图习题3-5图习题3-3图的反力。
3—8 汽车吊如图.车重W 1=26kN, 起吊装置重W 2=31kN,作用线通过B 点，起重臂重G =4。
5kN ，求最大起重量P max . （提示:起重量大到临界状态时,A 处将脱离接触,约束力为零.）3-9 求图示夹紧装置中工件受到的夹紧力F E 。
弹性与塑性力学第2,3章习题答案
第二章2.1（曾海斌）物体上某点的应力张量σij 为σij =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡1003100031001000000（应力单位） 求出：（a ）面积单位上应力矢量的大小，该面元上的法线矢量为n =（1/2，1/2，1/2）； （b ）应力主轴的方位；（c ）主应力的大小； （d ）八面体应力的大小； （e ）最大剪应力的大小。
解答：(a)利用式（2.26）计算应力矢量的分量nT i ，得n T 1=σ1j n j =σ11n 1+σ12n 2 +σ13n 3 = 0 ;同样 n T 2= j n j =272.47 nT 3=σ3j n j =157.31所以，应力矢量nT 的大小为=nT [(nT 1 )2+(nT 2 )2+(nT 3)2]1/2=314.62(b)(c)特征方程：σ3—I 1σ2 + I 2σ—I 3=0其中I 1 =σij 的对角项之和、I 2 =σij 的对角项余子式之和、I 3 =σij 的行列式。
从一个三次方程的根的特征性可证明： I 1 =σ1+σ2+σ3 I 2=σ1σ2+σ2σ3+σ3σ1 I 3=σ1σ2σ3其中得，σ1=400、σ2=σ3=0 是特征方程的根。
将σ1、σ2和σ3分别代入（2.43），并使用恒等式n 12+ n 22 + n 32=1 可决定对应于主应力每个值的单位法线n i 的分量（n 1 、n 2 、n 3）： n i （1）=（0， ±0.866，±0.5） n i （2）=（0， μ0.5，±0.866） n i （3）=（±1， 0，0）注意主方向2和3不是唯一的，可以选用与轴1正交的任何两个相互垂直的轴。
(d ）由式（2.96），可算σotc =1/3（0+100+300）=133.3τotc =1/3(90000+40000+10000+6*30000) 1/2=188.56(e) 已经求得σ1=400、σ2=σ3=0，则有（2.91）给出的最大剪应力为τmax =2002.2（曾海斌）对于给定的应力张量σij ，求出主应力以及它们相应的主方向。
结构力学第2章习题及参考答案
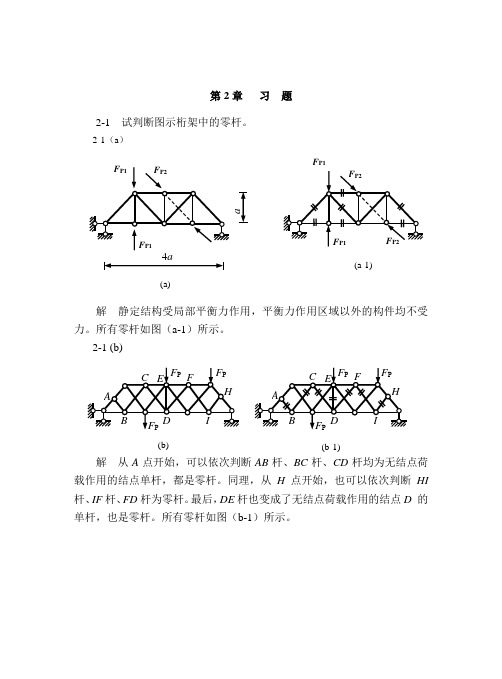
解悬臂刚架，梁部分先求杆端控制弯矩，再区段叠加。柱剪力为零，弯矩图为常数。
2-21(b)
解两刚片三支杆组成单体刚架，先求支座反力，再作弯矩图。注意二杆结点有外力偶作用时，杆端弯矩将产生突变，突变值等于力偶值。
2-21(c)
解（1）铰附近截面作用有集中力偶时，弯矩值等于力偶值，据此，可知顶铰左右两侧截面的弯矩为M，上侧受拉。又因为横梁上没有竖向集中力作用，弯矩图应是一条直线。考虑本题结构对称，荷载也对称，则横梁上的弯矩图为一条水平线。
2-14试作图示多跨静定梁内力图。
解：（1）确定求解顺序：EF→CDE→ABC
（2）求支座反力及各部分之间的相互作用力。结果如图（b）所示。
（3）分别画出每一部分的内力图，组合在一起就是原结构的内力图，如图（c）和（d）所示。
2-15试作图示多跨静定梁弯矩图。
解：（1）确定求解顺序。DEF→DCB→AB。
（2）二杆刚结点上，若无集中力偶作用时，则两个杆的杆端弯矩应该相等，且同时外侧受拉。这样就可以画出两个柱子的弯矩图了。
2-21(d)
解本题为基——附型结构，先算上部、后算下部。两个部分均三铰刚架，分别求解即可。
2-21(e)
2-22试作图示组合结构的弯矩图和轴力图。
FN12= -75kN，FN34=75kN
100kn100kn50kn2520251875knm202550kn截面内力5mcos3025sincos187525295kncossin5050188knsincos5050683kn5m305m5m213求图示三铰拱结构的支座反力链杆轴力并求指定截面k1求支座反力10kn10kn取ceb部分为隔离体截面的弯矩取kad部分为隔离体40knayed20kn4m4m4m4m214试作图示多跨静定梁内力图
结构力学第2章习题及参考答案
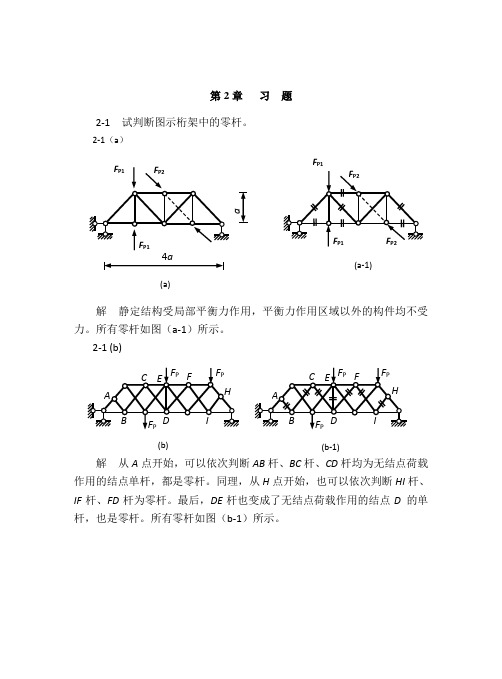
8 kN 20 kN
HI
J ⅠK
L
2 1
AC
D
E ⅠF
G
B
2.5m6 15m
2.5 m
（a）
K
LD
FNJK D
FN2
FNEF FD
G
B
FBy （b
）
解：（1）判断零杆。如图（a）所示。
（2）求支座反力
F x 0 ， FAx 0
M A 0 ， FB y 12.67 kN
F y 0 ， FA y 15.33 kN
5 29
MK
M
0 K
FH yK
510 130 3 120
kN
m
FQK FQ0K cosK FH sinK 52
5 130 29
2 0 29
FNK FN0K sinK FH cosK 52
2 130 29
5 140 kN 29
2-12 图示圆弧三饺拱，求支座反力及截面 D 的 M 、FQ 、FN 值。 20kN/m
D
C
5m
5m
FH
30
A 5m
B 5m
FH
FAy
FBy
习题 2-12 图
解 （1）求支座反力。
FB y 100 kN ， FA y 100 kN ， FH 50 kN
（2）求等代梁 D 截面内力
M
0 D
FAy
2.5
1 2
20 2.52
187.5kNm
FQ0D FAy 20 2.5 50 kN
30 kN A 4 B 30 kN
3×2m
N 1
N
D
N
CN 2 E
N3
清华理论力学课后答案2
kh da
（b）
w.
co
m
4
三角块 V4
V4 = 2 × 3 × 3 ÷ 2 = 9
(1, 7, 1)
2-5 均质折杆及尺寸如图示，求此折杆形心坐标。 解： 将图示折杆简化为折线计算。 折杆有 5 段直线组成， 每一段的长度及形心坐标如表所示。 按形心计算公式，有
xc =
∑iLi xi 200 × (−100) + 100 × (−50) + 100 × 0 + 200 × 100 + 100 × 200 = 200 + 100 + 100 + 200 + 100 ∑iLi = 21.43(mm)
kh da
，
w.
FRx ' = F1 cos 45� − F2 cos 45� = 0 ，
�
co
在坐标轴上的投影为
m
解： 各力均在与坐标平面平行的面内， 且与所在平面的棱边成 45°角。 将力系向 A 点简化， 主矢 FR '
a b c + + = 0。 F1 F2 F3
当主矢与主矩平行时，力系能简化为力螺旋，即从 FR '× M O = 0 得，
yc =
答
案
网
（200，100，-50）
ww w.
3
kh da
题 2-5 图
w.
co
m
题 2-6 图
解: 由对称性知，该图形的形心一定在 x 轴上，即 yc = 0 。用负面积法计算其横坐标。此平面图
按形心计算公式，有
xc =
2-7 工字钢截面尺寸如图示，求此截面的形心坐标。
题 2-7 图
材料力学第2版 课后习题答案 第2章 轴向拉压与伸缩
习题2-1一木柱受力如图示，柱的横截面为边长20cm 的正方形，材料服从虎克定律，其弹性模量MPa ．如不计柱自重，试求：51010.0×=E （1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形．解：（1）轴力图（2）AC 段应力a a ΜΡΡσ5.2105.22.010100623−=×−=×−=CB 段应力aa ΜΡΡσ5.6105.62.010260623−=×−=×−=（3）AC 段线应变45105.2101.05.2−×−=×−==ΕσεN-图CB 段线应变45105.6101.05.6−×−=×−==Εσε（4）总变形m 3441035.15.1105.65.1105.2−−−×=××−××−=ΑΒ∆2-2图(a)所示铆接件，板件的受力情况如图（ｂ）所示．已知：P ＝7kN ，t ＝0.15cm ，b 1＝0.4cm ，b 2=0.5cm ，b 3=0.6cml 。
试绘板件的轴力图，并计算板内的最大拉应力。
解:（2）aΜΡσ4.194101024.015.0767311=×××××=−a ΜΡσ1.311101025.015.0767322=×××××=−a ΜΡσ9.388101026.015.07673=××××=−最大拉应力aΜΡσσ9.3883max ==2-3直径为１cm 的圆杆，在拉力P ＝10kN 的作用下，试求杆内最大剪应力，以及与横截面夹角为＝30o 的斜截面上的正应力与剪应力。
α解:（1）最大剪应力a d ΜΡππΡστ66.6310101102212672241max =××××===−（2）界面上的应力°=30α()a ΜΡασσα49.952366.632cos 12=×=+=a ΜΡαστα13.5530sin 66.632sin 2=×=×=°2-4图示结构中ABC 与CD 均为刚性梁，C 与D 均为铰接，铅垂力P ＝20kN 作用在C 铰，若（1）杆的直径d 1=1cm ，（2）杆的直径d 2=2cm ，两杆的材料相同，E ＝200Gpa ，其他尺寸如图示，试求（1）两杆的应力；（2）C 点的位移。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章质点运动学（习题）
2.1.1质点的运动学方程为
I 7 -' -二’J•二 只 二 二］ 上求质点轨迹并用图表示
解：①.• — 轨迹方程为y=5
x = 2 - 3/
②3皿—1消去时间参量t得：
3y+4z-5=0
—_ ■护丄
# J
2.1.2 质点运动学方程为 ，（1 ）.求质点的轨迹；（2 ）.求自
t=-1 至t=1质点的位移
z = 2
解；①I 消去t得轨迹：xy=1,z=2
②心二已+戶了+龙 和二启+呂予+2上
至t=1质点的位移
解：①.一*:厂】::' 消去t得轨迹方程
②［二…/ =■■ ' /■ 二二一.；
2.2.1 雷达站于某瞬时测得飞机位置为
-
:
1 - _
' '"， 0.75s 后测得
- '
：
- - - •宀.
门、均在铅直平面内。 求飞机瞬时速率的近似值和飞行方向
"〔八代入数值得:
2.1.3 质点运动学方程为
r = 4凸 +(2t +3)j , (i
).求质点的轨迹;
求自t=o
(a 角)
^|= V4W03 + 4W^2x4100x4240cos4.4c
=349 385
脚)
利用正弦定理可解岀 上 ・34加
222 —小圆柱体沿抛物线轨道运动，抛物线轨道为
八■" - 11 （长度mm ）。第一次观察到圆柱体在
x=249mm处，经过时间2ms后圆柱体移到 x=234mm处。求圆柱体瞬时速度的近似值
…屈 (即 丫
V153 +36.225J
V
弟 = =
At Ai 2
=
2.2.3 一人在北京音乐厅内听音乐，离演奏者 17m。另一人在广州听同一演奏的转播，广州离
北京2320km，收听者离收音机 2m，问谁先听到声音？声速为
340m/s,电磁波传播的速度为
7 1
v«-——=
349.385
0.75
= 465.8(w/s)
—= 005(s)
340
在广州的人先听到声音
224 如果不允许你去航空公司问讯处，问你乘波音
747飞机自北京不着陆飞行到巴黎， 你能否估计大约用多少时间？如果能， 试估计一下
所需数据）。
2.2.5 火车进入弯道时减速， 最初列车向正北以 90km/h速率行驶，3min后以70km/h
北偏西二I」方向行驶。求列车的平均加速度
解,
y4 北 30**
2320xl03 2
3.0 x10s 340
= 0.0136(s)
（自己找
速率向
□ -30°
o
226 ( 1 ) ”一八 「门一 一'：：【一「- .■■''： . R 为正常数。求 t=0,
n
/2
(2 )
— 卜 2巧
jA
"-求t=0,1 时的速度和加速度(写岀正交分解式) 解：(1 )
y
= J?casX?4- +2ii,
df *
亠“
p = — = -Rsinti 4-J?cosp+ 2kr dt
a = — =
- J?cost/ - 7?sin5
当t=0 时，
v = A? +
% ■ 0*= Rrvz= 2,
ar^-R,ay-as = ^
当t= n /2 时，
v =
-Ri + 2k, a
=-取
v
x =~R,vy=0,vz
=2,
ax = 05 ay - -R. az -0
= 90/ v2 = -70 cos 60°i +70 cos30° ji
也0 =务一
R = -70 cosI5OV + (7Ocos 30°-
90))
=0.071(M/S)
913.91x0.05 sin 30° 70
sin. 6
,sin^=0.7t559^= 49.99°
时的速度和加速度
〒二 3i - 9J +1陆匸二-
9j +
36k
、
2.3.1
图中a、b和c表示质点沿直线运动三种不同情况下的 x-t 图，试说明三种运动的特 点（即速度，
计时起点时质点的坐标，位于坐标原点的时刻）。
解：a 直线的斜率为速度
r — 3ti — 4.5t2j + 6t3k,
-3i -9tj +
-dr
v -——
dt
一
dv d
—
当t=0
dt
时，
二
—9J
A A 4 A
代