菱形十字格10×12
小学奥数4-2-6 不规则图形的面积.专项练习及答案解析-精品

本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例 1】 你有什么好的方法计算所给图形的面积呢?(单位:厘米)3994399439943994图1 图2 图3 【考点】不规则图形的面积 【难度】1星 【题型】解答 【解析】 (方法一)采用分割法,可给原图分成两个长方形,(图1或图2)两个长方形的总面积就是所求的面积.图1的面积是: 4(93)9375⨯++⨯=(平方厘米).图2的面积是: (94)39475+⨯+⨯=(平方厘米). (方法二)采用补图法,如果补上一个边长是9厘米的正方形(图3),就成了一个面积是:(49)(93)156+⨯+=(平方厘米)的大长方形.因此用这个长方形的面积减去所补正方形的面积,就是要求的图形面积(49)(93)9975+⨯+-⨯=(平方厘米). 【答案】75平方厘米【巩固】如图是学校操场一角,请计算它的面积(单位:米)30203040例题精讲4-2-6.不规则图形的面积【解析】 这是一个不规则图形,怎样使它能转化为我们熟悉的基本图形呢?可以在图中添上一条辅助线,把多边形切割成上下两个长方形或左右两个长方形;也可以把多边形补充完整,成为一个长方形;302030403020304030203040图一 图二 图三方法一:如图一,3040203040120014002600⨯+⨯+=+=()(平方米) 方法二:如图二,203040203060020002600⨯+⨯+=+=()(平方米) 方法三:如图三,40302030303035009002600+⨯+-⨯=-=()()(平方米) 【答案】2600平方米【巩固】如右图所示,图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的,线段的长度如图所示(单位:厘米),求ABEFGD 的周长和面积.F【考点】不规则图形的面积 【难度】1星 【题型】解答 【解析】 方法一:如果求出长方形的宽及正方形的边长,则图形ABEFGD 的周长和面积可以求出.而正方形的边长1046GC DC DG AB DG =-=-=-=(厘米),长方形的宽1064BE CE =-=-=(厘米),所求图形的周长102624440=⨯+⨯++=(厘米) 面积1046676CEFG ABCD S S =+=⨯+⨯=正方形长方形(平方厘米)方法二:可以将线段GF 、DG 向外平移,得一个新的图形ABEH ,因为D G H F =,GF DH =,所以图形ABEH 的周长就是图形A B E F G D 的周长.而10AB BE ==(厘米),所以图形ABEH 是边长为10厘米的正方形. 所求图形的周长=正方形ABEH 的周长10440=⨯=(厘米) 面积10106476ABEH DGFH S S =-=⨯-⨯=正方形长方形(平方厘米)【总结】方法一是利用基本图形的周长及面积公式求解,因此首先要知道长方形的长、宽及正方形的边长.方法二是利用转化的思想方法,将较复杂图形转化为基本图形,图形转化前后的周长不变,面积增加了,在计算时应减去增加的面积. 【答案】76【巩固】求图中五边形的面积.6453【解析】由图可见五边形为矩形切去一角得来,把切去的角补出来,它的一条直角边长633-=,斜边等于5,所以另一直角边为4,所以矩形的长为448+=,五边形面积16843422⨯-⨯⨯=.【答案】42【例2】这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20 厘米.问,此楼梯截面的面积是多少?【考点】不规则图形的面积【难度】2星【题型】解答【关键词】华杯赛、口试【解析】如果把楼梯截面补成右图所示的长方形,那么此长方形高280厘米.宽300厘米,它的面积恰好是所求截面的2倍.所以楼梯截面面积为280300242000⨯÷=()(平方厘米).【答案】42000【巩固】如图是一个楼梯的截面图,每级台阶的宽和高都是20厘米.这楼梯的截面积是多少平方厘米?【考点】不规则图形的面积【难度】2星【题型】解答【解析】先求出大三角形的两条直角边都是208160⨯=(厘米),因此大三角形的面积为160160212800⨯÷=(平方厘米);8个小三角形的面积为2020281600⨯÷⨯=(平方厘米);因此这楼梯的截面积为12800160014400+=(平方厘米).【答案】14400【例3】有一块菜地长16米,宽8米,菜地中间留了宽2米的路,把菜地平均分成四块,每一块地的面积是多少?【考点】不规则图形的面积【难度】2星【题型】解答【解析】方法一:可以直接求出每小块菜地的长和宽,从而求出每小块菜地的面积;每一块地的面积是:[1622][822]7321-÷⨯-÷=⨯=()()(平方米)方法二:也可以求出这块地的总面积,再减去道路的面积,然后把剩余的面积四等分求出每小块菜地的面积;每一块地的面积是:[1682168222]412844421⨯-⨯+⨯-⨯÷=-÷=()()(平方米)方法三:还可以运用平移的方法,将道路移到菜地的边沿,先求出四个小长方形组成的长方形面积,再求出其中每一小块菜地的面积.如图所示:[16282]484421-⨯-÷=÷=()()(平方米) 【答案】21【例 4】 有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 通过操作,一张一张的添加,可以发现每多盖一张,遮住的面积增加21⨯平方厘米,所以这10张纸片盖住的面积是:3221924⨯+⨯⨯=(平方厘米).【答案】24【例 5】 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 所求面积等于图中阴影部分的面积,为2052082140-+⨯÷=()(平方厘米). 【答案】140【巩固】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.FBA【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 阴影部分是一个高为3厘米的直角梯形,然而它的上底与下底都不知道,因而不能直接求出它的面积.因为三角形ABC 与三角形DEF 完全相同,都减去三角形DOC 后,根据差不变性质,差应相等,即阴影部分与直角梯形OEFC 面积相等,所以求阴影部分的面积就转化为求直角梯形OEFC 的面积.直角梯形OEFC 的上底为1037-=(厘米),面积为7102217+⨯÷=()(厘米2). 所以,阴影部分的面积是17平方厘米。
万能解题模型(十五)十字架模型【2021中考数学二轮复习】答案版
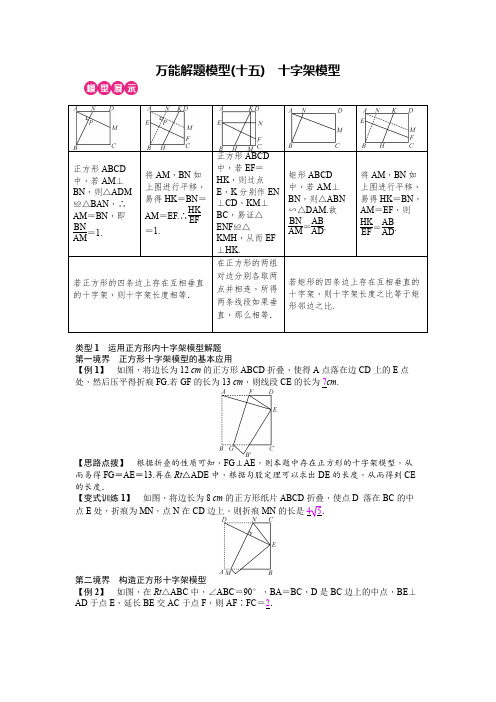
万能解题模型(十五) 十字架模型正方形ABCD 类型1 运用正方形内十字架模型解题 第一境界 正方形十字架模型的基本应用【例1】 如图,将边长为12 cm 的正方形ABCD 折叠,使得A 点落在边CD 上的E 点处,然后压平得折痕FG.若GF 的长为13 cm ,则线段CE 的长为7cm .【思路点拨】 根据折叠的性质可知,FG ⊥AE ,则本题中存在正方形的十字架模型,从而易得FG =AE =13.再在Rt △ADE 中,根据勾股定理可以求出DE 的长度,从而得到CE 的长度.【变式训练1】 如图,将边长为8 cm 的正方形纸片ABCD 折叠,使点D 落在BC 的中点E 处,折痕为MN ,点N 在CD 边上,则折痕MN 的长是第二境界 构造正方形十字架模型【例2】 如图,在Rt △ABC 中,∠ABC =90°,BA =BC ,D 是BC 边上的中点,BE ⊥AD 于点E ,延长BE 交AC 于点F ,则AF ∶FC =2.【思路点拨】 图中有一个垂直的十字架,可以考虑将十字架放在一个正方形或矩形中,运用模型解题.如图,过点C 作CG ∥AB ,过点A 作AG ∥BC ,两条直线交于点G ,则可得四边形ABCG 是正方形,延长BF 交CG 于点H.根据“正方形内十字架模型”可以得到△ABD ≌△BCH ,则CH =BD.在根据△AFB ∽△CFH ,由相似的性质可以求出AF ∶FC 的值.类型2 运用矩形内十字架模型解题 第一境界 矩形十字架模型的基本应用【例3】 如图所示,在矩形ABCD 中,EF ⊥GH ,AM ⊥BN.EF 分别交AB ,CD 于点E ,F ,点M ,N 分别在BC ,CD 上.若EF GH =79,则BN AM =79.【思路点拨】 分析出图中的十字架模型,然后根据矩形内十字架模型可以求出. 【变式训练2】 (九上北师大教材P 19第4题改编)如图,在矩形纸片ABCD 中,AB =6,BC =8,将纸片折叠,使点C 与点A 重合,折痕为EF ,则EF 的长为152.提示:∵EF ⊥AC ,∴EF AC =ABBC,即EF 10=68.∴EF =152. 第二境界 构造矩形十字架模型【例4】 如图,在▱ABCD 中,AB =2,BC =2,且∠B =45°,将▱ABCD 对折,使点B 和点D 重合,则折痕MN 3【思路点拨】 图中有垂直的十字架,补全图形将十字架放在矩形中,过点B 作BE ⊥AD于点E ,过点D 作DF ⊥BC 于点F ,则由矩形十字架型可得MN BD =BEDE.【变式训练3】 如图,在四边形ABCD 中,∠ABC =90°,AB =AD =10,BC =CD =5,AM ⊥DN ,点M ,N 分别在BC ,AB 边上,求DNAM的值.解:连接AC ,易证△ADC ≌△ABC(SSS ),∴∠ADC =∠ABC =90°. 过点D 作EF ∥AB ,过点A 作AF ⊥EF 于点F ,延长BC 交EF 于点E. 易证△DEC ∽△AFD ,且相似比为1∶2. 设CE =x ,则DF =2x ,∴DE =10-2x. ∴AF =20-4x =BE =5+x. ∴x =3.∴BE =8.根据“矩形内十字架模型”可得DN AM =BE AB =45.启示:一般情况下,当矩形、正方形、直角三角形等图形内出现“垂直”情况时,可考虑十字架结构模型,通过相似(或全等)求线段的长.1.如图,已知正方形ABCD 的边长为5,点E ,F 分别在AD ,DC 上,AE =DF =2,BE 与AF 相交于点G ,点H 为BF 的中点,连接GH ,则GH 的长为(B )A .25B .342C .42D .8532.如图,已知直线y =-12x +2分别与x 轴、y 轴交于B ,A 两点,将△AOB 沿着AB 翻折,使点O 落在点D 上.若反比例函数y =kx的图象经过点D ,则k 的值为(D )A .4B .12125C .5D .128253.(2019·张家界)如图,正方形ABCD 的边长为1,点E ,F 分别为BC ,CD 边的中点,连接AE ,BF 交于点P ,连接PD ,则tan ∠APD =2.4.(2017·安徽)已知正方形ABCD ,点M 为边AB 的中点.(1)如图1,点G 为线段CM 上的一点,且∠AGB =90°,延长AG ,BG 分别与边BC ,CD 交于点E ,F.求证: ①BE =CF ; ②BE 2=BC·CE.(2)如图2,在边BC 上取一点E ,满足BE 2=BC·CE ,连接AE 交CM 于点G ,连接BG 并延长交CD 于点F ,求tan ∠CBF 的值.解:(1)①∵四边形ABCD 是正方形, ∴AB =BC ,∠ABC =∠BCF =90°. ∴∠ABG +∠CBF =90°.∵∠AGB =90°,∴∠ABG +∠BAG =90°. ∴∠BAG =∠CBF.∴△ABE ≌△BCF(ASA ). ∴BE =CF.②∵∠AGB =90°,点M 为AB 的中点, ∴MG =MA =MB.∴∠GAM =∠AGM. 又∵∠CGE =∠AGM ,∠GAM =∠CBG , ∴∠CGE =∠CBG.又∵∠ECG =∠GCB ,∴△CGE ∽△CBG. ∴CE CG =CGBC,即CG 2=BC·CE. 由∠CFG =∠GBM =∠BGM =∠CGF 得CF =CG , 由①知BE =CF , ∴BE =CG. ∴BE 2=BC·CE.(2)延长AE ,DC 交于点N , ∵四边形ABCD 是正方形, ∴AB ∥CD.∴∠N =∠EAB. 又∵∠CEN =∠BEA , ∴△CEN ∽△BEA. ∴CE BE =CNBA,即BE·CN =AB·CE. ∵AB =BC ,BE 2=BC·CE ,∴CN =BE.∵AB ∥DN ,∴CN AM =CG GM =CFBM.∵AM =MB , ∴FC =CN =BE.设正方形的边长为1,BE =x ,由BE 2=BC·CE 可得x 2=1×(1-x),解得x 1=5-12,x 2=-5-12(舍去).∴BEBC =5-12.FC BC=BEBC=5-12.则tan∠CBF=。
小学数学《图形规律》练习题(含答案)
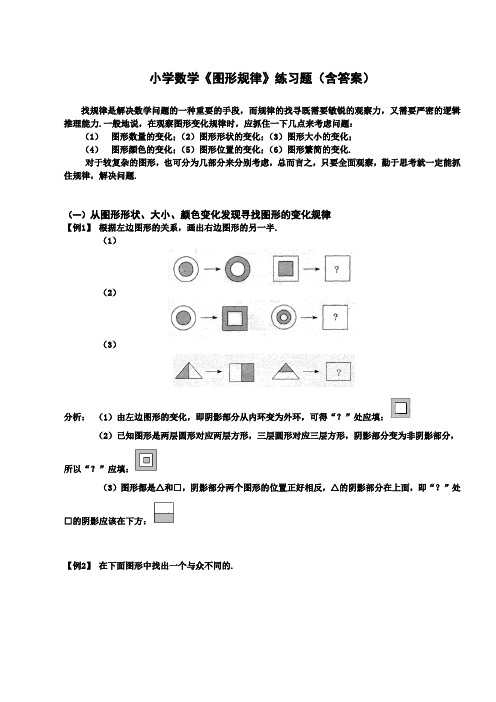
小学数学《图形规律》练习题(含答案)找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题:(1)图形数量的变化;(2)图形形状的变化;(3)图形大小的变化;(4)图形颜色的变化;(5)图形位置的变化;(6)图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.(一)从图形形状、大小、颜色变化发现寻找图形的变化规律【例1】根据左边图形的关系,画出右边图形的另一半.(1)(2)(3)分析:(1)由左边图形的变化,即阴影部分从内环变为外环,可得“?”处应填:(2)已知图形是两层圆形对应两层方形,三层圆形对应三层方形,阴影部分变为非阴影部分,所以“?”应填:(3)图形都是△和□,阴影部分两个图形的位置正好相反,△的阴影部分在上面,即“?”处□的阴影应该在下方:【例2】在下面图形中找出一个与众不同的.分析:很容易从图中看出,(1)、(3)、(4)的形状相同,只是位置和颜色不同.(1)(3),而且三角形与圆的颜色互换了一下.(1)(4),颜色没有发生变化.(2)(5),(2)和(5)是一组图形,图形的形状相同,位置和颜色发生了变化,大小两个长方形的颜色互换了.根据上面的分析,(2)与(5)配对,(1)与(3)配对,因此与众不同的图形是图10中的(4),如图:[巩固]按照下列图形的变化规律,空白处应是什么样的图形?分析:先看图中不变的部分.在整个变化过程中,图形中大小两个正方形没有变化,因此可以肯定空白处的图形一定是大小两个正方形,位置是一里一外.变化的部分可以分为两部分:(1)图形中的直线段部分,其变化规律是每次顺时针旋转90°,因此空白处图中的直线段应是如图的形状.(2)图中的阴影部分,是在小正方形的对角线的左右两边交替出现的,因此空白处图中的阴影部分应在小正方形对角线的右边.根据上面的分析,可画出空白处的图形,如图所示:【例3】如图,根据图中已知3个方格表中阴影的规律,在空白的方格表中也填上相应的阴影.分析:通过观察前三个方格表中阴影部分的规律,可以得出:把前3个方格表一列一列的看,阴影部分在一格一格的向下移动,当移到最下方时,便重新从最上面的一格重新开始循环,不难看出第4个方格表的第一列应该把最下面一个格染黑,依此可以判断出其他的3个方格,所以,答案为:[拓展]根据前三个方格表中阴影部分的变化规律,填上第(10)个方格表中阴影部分的小正方形内的几个数之和698754321......(10)(3)(2)(1)分析:由阴影部分在每一列都在一格一格下移的规律可得,每经过四次移动,阴影部分就会回到原来的位置,因为10÷4=2...2,所以,第(10)个图应该与第(2)个图相同,所以,第(10)个图为:所以方格中几个数的和是:1+2+5+9=17.【例4】 观察图形变化规律,在右边补上一幅,使它成为一个完整系列分析:观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:[小游戏]下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画出来.答案:(二)从图形数量、位置变化出发观察思考几何图形的规律【例5】 下面的图形是按一定规律排列的,请仔细观察,并在“?”处填上适当的图形. (1)第3组第1组(2)第3组第1组(3)★★★★★第3组第1组分析:(1)仔细观察可发现第1组和第2组中间的部分都是由三个小图形构成的.构成的规律是:当按照第1、第2、第3组的顺序观察时,6个小图形都在向左移动,而且移动的同时又在重新分组和组合,但排列顺序保持不变,当某一个小图形移动到了最左边时,下一步它就回到了最右边.按这个规律可知图中第3组中间“?”处是:□△0.(2)注意观察第1组和第2组,每组都是由三对小图形组成;而每对小图形都是由一个“空白”的和一个“黑色”的小图形组成;而且它俩的排列顺序都是“空白”的在左边,“黑色”的在右边.再按着第1、第2、第3组的顺序观察下去,可发现每对小图形在各组中的位置的变化规律:它们都在向左移动,当一对小图形移动到最左边后,下一步它就回到了最右边.按这个移动规律,可知第3组“?”处应填:○▲.(3)观察第1组与第2组,每组中有三种图形:★、□、■,我们把每组图形再分为三小组,将更明显的得出变化规律.第2组将第1组中的1、2小组按原顺序调至第3小组,根据这个规律,可得“?”中应填.【例6】观察下列各组图的变化规律,并在“?”处画出相关的图形.(1)(2)分析:(1)四个图形的位置是按顺时针方向旋转的.因此第四幅图右上角为三角形,右下角为半圆形,左下角为圆形,左上角是正方形.正方形的阴影部分是按逆时针方向依次旋转90°.得到的,因此第四幅图中正方形的阴影部分应在它的上方.三角形的方向是按逆时针方向依次旋转90°.得到的,所以第四幅图中三角形应向右.半圆形的方向与三角形的方向相同,第四幅图中半圆形也应向右.圆形的阴影部分是按顺时针方向依次旋转90°.得到的,因此第四幅图中圆形阴影部分应在圆形的左上角.因此,第四幅图应为:(2)观察前三幅图可以看出两个规律“一是四个小图形是按顺时针方向转动的,而且△、方形和*都没有变化,根据这条规律,可以先把这两个图形位置定下来;二是圆中间横线的方向,根据观察可以得到答案:[前铺]观察下图的变化规律,画出丙图.DC B A丙乙甲D CB A分析:(甲)图与(乙)图中,点A 、B 、C 、D 的顺序和距离都没有改变,只是每个点的位置发生了变化,如:甲图中,A 在左方;而乙图中,A 在上方,……我们把这样一种位置的变化称为图形的旋转,乙图可以看作是甲图沿顺时针方向旋转90°得到的,甲图也可以看成是乙图沿逆时针旋转90°而得到的, 同样的道理,我们可以把到的位置变化也叫做旋转,叫做沿顺时针方向旋转90°.所以丙处应填:ABCD[小结]旋转是数学中的重要概念,掌握好这个概念,可以提高观察能力,加快解题速度,对于许多问题的解决,也有事半而功倍的效果.【例7】 观察下图中的点群,请回答:(1) 方框内的点群包含多少个点?(2) 推测第10个点群中包含多少个点?(3) 前10个点群中,所有点的总数是多少?分析:(1)数一数,前4个点群包含的点数分别是:1,4,9,16.不难发现,1=1×1,4=2×2,9=3×3,16=4×4,按照这个规律,第5个点群(即方框中的点群)包含的点数是:5×5=25(个). (2)按发现的规律推出,第十个点群的点数是:10×10=100(个). (3)前十个点群,所有的点数是:[拓展]下图表示“宝塔”,它们的层数不同,但都是由一样大的小三角形摆成的.仔细观察后,请回答:(1)五层的“宝塔”的最下层包含多少个小三角形? (2)整个五层“宝塔”一共包含多少个小三角形?分析:(1)数一数“宝塔”每层包含的小三角形数:可见1,3,5,7是个奇数列,所以由这个规律猜出第五层应包含的小三角形是9个.(2)整个五层塔共包含的小三角形个数是:1+3+5+7+9=25(个).[巩固]观察下面由点组成的图形(点群),请回答:(1)方框内的点群包含多少个点?(2)第(10)个点群中包含多少个点?(3)前十个点群中,所有点的总数是多少?分析:(1)数一数可知:前四个点群中包含的点数分别是:1,4,7,10.可以看出,在每相邻的两个数中,后一个数都比前一个数大3.因为方框内应是第(5)个点群,它的点数应该是10+3=13(个).(2)列表,依次写出各点群的点数,可知第(10)个点群包含有28个点.(3)前十个点群,所有点的总数是:1+4+7+10+13+16+19+22+25+28=145(个)[数学游戏]观察下图,看看右图中哪一个图形可以代替“?”答案:E.因为1加2等于3,4加5等于6,但是相同的符号都要消掉.(三)复杂图形变化规律【例8】仔细观察下图中图形的变化规律,并在“?”处填入合适的图形.fedcba分析:显然,图(a )、(b )的变化规律对应于图(c )的变化规律;图(d )、(e )的变化规律也对应于图(f )的变化规律,我们先来观察(a )、(b )两组图形,发现在形状、位置方面都发生了变化,即把圆变为它的一半——半圆,把三角形也变为它的一半——直角三角形;同时,变化后图形的位置相当于把原图形沿顺时针方向旋转90°而得到.因此,我们很容易地就把图(c )中的直角梯形还原为等腰梯形并通过逆时针旋转而得到图(c )“?”处的图形.当我们从左到右来观察图(d )、(e )的变化规律时,我们发现,图(d )、(e )的变化规律有与图(a )、(b )相同的一面,即都是把一个图形变为自身的一半,但也有与图(a )、(b )不同的一面,即图(d )、(e )中右半部分的图形无法通过旋转原图来得到,只能通过上下翻转而获得.这样,我们就得到了这些图形的变化规律.所以图(c )中“?”处的图形应是下面甲图,图(f )中“?”处的图形应是乙图.乙甲小结:本题观察的出发点主要有三点:(1)形状变化;(2) 位置变化;(3) 颜色变化.[巩固]分析:从前两幅图可以看出,右边图形是左边图形的一半,从第二幅图看出,上边的图是由阴影部分顺时针旋转90°后去掉阴影得到的,下边的图是由左边的阴影部分旋转180°后去掉阴影得到的,所以,第三幅图形应为:【例9】 图10—1是由9个小人排列的方阵,但有一个小人没有到位,请你从下面图10—2中的6个小人中,选一位小人放到问号的位置,你认为最合适的人选是几号?分析:从图10—1中可以发现小人的排列规律:即每行每列小人的“手臂”有向上、水平、向下;“身腰”有三角形、长方形;“脚”有圆脚、方脚、平脚.因此可以知道问号处的小人应该是向上仲臂、圆脚的小人,所以最合适的人选是6号.【例10】四个小动物排座位,一开始,小鼠坐在第1号位子上,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子,第一次上下两排交换.第二次是在第一次交换后左右两列交换,第三次再上下两排交换,第四次再左右两列交换…这样一直换下去.问:第十次交换位子后,小兔坐在第几号位子上?分析:(方法1)因为题目中问的只是第十次交换位子后,小兔的位子是几.因此,我们只需考虑小兔的位子变化规律,小兔刚开始时在3号位子,记为③,则变化过程为:③一次→①二次→②三次→④四次→③→…容易看出每一次交换座位,小兔的座位按顺时针方向转动一格,每四次交换座位后,小兔又回到原处,知道了这个规律,就不难得出答案.即10次后,小兔到了第2号位子.(方法2)仔细观察示意图时会发现,开始的图沿顺时针方向旋转两格(即180°)时,恰得到第二次交换位子后的图,由此可以知道,每一次上下交换后再一次左右交换的结果就相当于把原图沿顺时针方向旋转180°,第十次交换位子后,相当于是这些小动物沿顺时针方向转了4圈半,这样,我们就得到了小兔的位子及它们的整体变化规律.但其中需注意一点的是:单独一次上下(或左右)的交换与旋转90°得到的结果是不同的.小猫、小鼠的位子变化规律是沿逆时针方向,而小猴的位子变化规律与小兔相似.所以,第十次交换位子后,小兔到了2号位子.[巩固]仔细观察下列图形的变化,请先回答:(1)在方框(4)中应画出怎样的图形?(2)再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?分析:(1)先按(1)、(2)、(3)、……的顺序仔细观察,可以发现:在(1)中,*在左上角,在(2)中它在右上角,在(3)中它在右下角,……可见它在沿顺时针方向转动.其他三个小图形,即□、△、○,也和*一样都在沿着顺时针方向转动.发现规律:因方框中的每个小图形的位置的变化都是按顺时针方向旋转,可以说,方框连同内部的小图形及整体在按顺时针方向旋转.进一步猜想,根据所发现的规律进一步推测可知,第(4)个方框中的图形的样子:(2)按(1)、(2)、(3)、……的顺序仔细观察,进一步还可发现,图形的变化是有“周期性”的,也就是说,每过4个方框后,完全同样的图形又重新出现,如第(1)、(5)、(9)个图形是完全一样的.因为2+4+4=10,所以第(10)个方框内的图形与第(2)完全相同.1.(例3)顺序观察给出图形的变化,按照这种变化规律,在空格中填上应有的图形.分析:本题与刚刚前埔中所讲题目相似但不一样,需要仔细观察,发现本题不只是箭方向上有变化,箭尾数量上也有变化,在同一行中,每旋转90°,箭尾上的“羽毛”将减少一对,依照这个规律,空格中的箭,其尾部的“羽毛”没有了,成了光秃秃的一支箭,所以空格中应填:2.(例4)根据下列图形的变化规律,接着画下去.分析:观察得知,每幅图只有四个小图形,注意因为图形是由旋转而得到的,所以其中三角形、菱形的方向随旋转而变化,作图的时候要注意到这一点,丁图中应填:3.(例5)请找出下面哪个图形与其他图形不一样(1)(2)分析:(1)这组图形主要是构图上的差异,几个图形都是大图形的内部有一个同一类型的小图形.但是(1)、(2)、(4)、(5)中的小图形都位于大图形的一个拐角上,只有(3)中的小图形位于达图形的中间,因此,第(3)个图形与其它图形不一样.(2)这组图形的共同特征是,连接各边上一点,组成一个复合图形.所不同的是,第四个图形是一个五边形,而其它几个都是四边形,这样,只有(4)与其它不一样4.(例8)观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.分析:第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:5.(例9)仔细观察下列图形的变化,请先回答:(1)在方框(4)中应画出怎样的图形?(2)再按(1)、(2)、(3)、……的顺序数下去,第(10)个方框是怎样的图形?分析:(1)观察阴影部分可得这组图形的规律,它在沿逆时针方向转动.所以第(4)个方框中的图形的样子:(2)按(1)、(2)、(3)、……的顺序仔细观察,进一步还可发现,图形的变化是有“周期性”的,也就是说,每过4个方框后,完全同样的图形又重新出现,如第(1)、(5)、(9)个图形是完全一样的.因为2+4+4=10,所以第(10)个方框内的图形与第(2)完全相同.。
【奥数题】人教版小学数学六年级上册数与形奥数思维拓展(试题))含答案与解析

数与形奥数思维拓展(试题)一.选择题(共8小题)1.像如图这样继续画,第10组应该画()个。
A.81B.100C.1212.将正方形纸片按规律拼成如下的图案,第()个图案中恰好有45张纸片。
A.3B.5C.10D.113.把边长1cm的正方形按如图所示拼成各种图形。
当图形是4层时,它的周长是16cm。
如果图形有n层,它的周长是()cm。
A.4n B.5n C.6n4.如图,在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退。
开始时骰子如图(1)那样摆放,朝上的点数是2;最后翻动到如图(2)所示的位置,此时骰子朝上的点数不可能是下列数中的()A.5B.4C.3D.15.将黑色棋子按照一定规律排列成一系列如图所示的图案,第1个图中有8枚黑棋子,第2个图中有13枚黑棋子,第3个图中有18枚黑棋子,按照此规律,第9个图中有()枚黑棋子。
A.49B.48C.47D.466.把同样的小棒按下面的方式摆放,第9个图形需要()根小棒。
A.24B.27C.307.观察下面图形的规律,其中第1个图形由4个小正方形组成,第2个图形由7个小正方形组成,第3个图形由10个小正方形组成,…按此规律排列下去,则第n个图形由()个小正方形组成。
A.4n B.2n﹣1C.3n+1D.3n﹣18.如图所示,用白色小正方形和黑色长方形按照下面的摆法,组成不同的长方形。
当摆5个黑色长方形时,四周需要摆()个白色小正方形。
A.16B.20C.26D.36二.填空题(共8小题)9.如图,用小棒摆出若干个小正方形。
照这样的规律,摆n个小正方形需要根小棒;用100根小棒可以摆个这样的正方形。
10.观察如图规律,如果一幅图中涂色正方形是6个,那么空白正方形有个。
11.观察下面的图形并填空。
利用你发现的规律直接写出下面算式的结果:1992﹣1982=12.照此规律画下去,第n个图形共有个■,个□。
刍议如何利用菱形十字格提升学生的写字水平

刍议如何利用菱形十字格提升学生的写字水平作者:孙玉红来源:《学习与科普》2019年第05期摘要:俗话说“字如其人”,字写得好坏,对学生未来第一印象有很大影响。
初中语文要让学生养成好的书写习惯,并对书写姿势要严格指导。
学生最开始学习书写对以后书写习惯养成有很大影响。
教师要空出时间,让学生去练字,并不断指导学生使用硬笔熟练地写正楷字,练就规范的行楷字,让学生书写流利、书写质量得到提高。
关键词:初中语文;菱形十字格;写字水平目前很多初中学生写字不规范、书写不正规、字体不规整、写字潦草。
大部分学生写字都有很多坏习惯,看起来字不饱满,对于学生以后考试、就业等有很坏的第一印象。
初中语文教师要在学生坏习惯还能纠正的时候,多加指导,并对学生写字重视起来,采用好的练字方法,让学生事半功倍的练好字。
一、让学生分组练习教师可以让学生自己分组进行练习,一个人学习都会有厌烦心理,毕竟总是一个人练习写字会变得枯燥无味。
教师需要对学生字体练习多加重视,并成立专门小组,设计菱形十字格的专业纸张,并用word排版,计算机老师帮忙设计各种各样的书稿,例如:钢笔稿纸、毛笔稿纸、描红稿纸。
学校自行设计的菱形十字稿,更符合本校學生的写作水平,也方便教师教学修改。
分组之后,小组之间选拔一个写字好的学生进行带领。
学生小组之间可以互帮互助,写的好的可以指点写的差的,同时写的差的可以向优秀的学习,并询问其经验。
对于喜欢写字的同学,教师可以组织学生成立学习兴趣小组,让学习写字不仅仅是一个任务,更是一个兴趣爱好,写字好的学生可以课堂展示,让被展示学生有自豪感,激发学生学习写字的兴趣,并让他们不断形成良好的书写习惯。
例如:我会把班级分成8个组,每个组选拔出一个组长。
组长的选拔首要条件必须是字写的漂亮的学生,只有写的好的学生做组长,才能起到更好的带头作用。
组长选好之后我会下达一定的任务。
如:每周每个人必须完成多少菱形十字格写字要求,组长负责督促并指导。
四十种杯垫编织方法

四十种杯垫编织方法四十种杯垫编织方法杯垫在我们的生活中有着重要的作用,它可以保护我们的桌子不被烫伤或者污渍,同时也能为我们的饮品增添一份可爱的小装饰。
如果你喜欢手工编织,那么为自己人手一份精美的杯垫也是一种非常不错的选择。
下面,我们来介绍四十种常见的杯垫编织方法。
一、十字编织法1. 基础编法:首先拿两个不同颜色的线,把它们的一端交叉在一起,把长的放在下面,短的放在上面,然后将长的线从交叉处穿过短的线的上面,再从短的线的下面穿回来,再把短的线从交叉处穿过长的线的下面,从上面穿回来,你就可以交叉编织了。
2. 十字编织法:用项链线或者毛线,起始点为交叉处的正中心点,用针尖钩住其中一根线,穿过另外一根线,形成一个三角形的空洞,注意要把针尖穿过线的下面,然后侧面再进去一次,从三角形的另外一个顶点出来,再钩住另外一根线,穿过回去,就可以形成一个十字型的编织了。
二、钩针编织法3. 钩针编织法一:使用银色或者金色的薄线,用钩针从右边往左边传线,钩一个简单的环,再在环上继续钩线,依次绕圈钩,就可以变成一个小杯垫了。
4. 钩针编织法二:准备质地柔软的卡其布条,弯曲成圆型,然后用带钩针的线穿过去,用针把布条固定住。
三、十字纹编织法5. 十字纹编织法一:先编一排钩织网,再用四色线围绕其边缘再钩一圈,接下来在每个网的边角上拧打一个靠近网的小环,在这里做一个叉款纹。
6. 十字纹编织法二:利用线、钩和固定夹子,将线固定在夹子上,一面钩一面调整编织纹路,可以编织出非常漂亮的十字花纹。
四、心形编织法7. 心形编织法一:使用线编织成一个框架,然后在框架内编织,先将一条线从左上角的交点处穿过到右下角,再从右上角穿到左下角,形成一个十字型,然后在两条线的中央用两个钩子分别在上下部分编织,形成一个心型。
8. 心形编织法二:首先把两条线交叉在一起,用钩子把线朝着同一方向钩起来,向内刚钩,继续换颜色,直到钩完一个心形杯垫。
五、八卦纹编织法9. 八卦纹编织法一:准备不同颜色的线,首先在一条线的两端分别打结,再将它们分别穿到八卦纹的边缘,从外向内循环穿过,最后再回到起始点打上一顶扣子,就可以了。
十字架表格找规律填数字

十字架表格找规律填数字1.(2021秋•洪山区期末)已知关于x的两个多项式A=x2﹣8x+3.B=ax﹣b,且整式A+B 中不含一次项和常数项.(1)求a,b的值;(2)如图是去年2021年3月份的月历,用带阴影的十字方框覆盖其中5个数字,例如:1,7,8,9,15.现在移动十字方框使其履盖的5个数之和等于9a+6b,则此时十字方框正中心的数是.【考点】一元一次方程的应用;整式的加减.【专题】计算题;整式;运算能力;应用意识.【答案】(1)a=8,b=3;(2).【分析】(1)根据题意列式合并同类项,根据整式A+B中不含一次项和常数项,列出方程,计算即可;(2)设最小的数为x,根据题意列式x+x+6+x+7+x+8+x+14=9a+6b,求出x,再根据规律求出中心数.解:(1)根据题意得,x2﹣8x+3+ax﹣b=x2+(a﹣8)x+3﹣b,∵整式A+B中不含一次项和常数项,∴a﹣8=0,3﹣b=0,∴a=8,b=3;(2)设最小的数为x,根据题意得:x+x+6+x+7+x+8+x+14=9a+6b,5x+35=9a+6b,5x=9a+6b﹣35,x=,∴十字方框正中心的数是:+7=,故答案为:.【点评】本题考查解一元一次方程的应用、整式的加减,掌握整式加减和一元一次方程的应用,理解题意列出式子是解题关键.2.(2018•竞秀区一模)如图,将连续的奇数1,3,5,7…按图1中的方式排成一个数表,用一个十字框框住5个数,这样框出的任意5个数中,四个分支上的数分别用a,b,c,d 表示,如图2所示.(1)计算:若十字框的中间数为17,则a+b+c+d=.(2)发现:移动十字框,比较a+b+c+d与中间的数.猜想:十字框中a、b、c、d的和是中间的数的;(3)验证:设中间的数为x,写出a、b、c、d的和,验证猜想的正确性;(4)应用:设M=a+b+c+d+x,判断M的值能否等于2020,请说明理由.【考点】解一元一次方程.【专题】一次方程(组)及应用.【答案】见试题解答内容【分析】(1)直接相加即得到答案;(2)根据(1)猜想a+b+c+d=4x;(3)用x表示a、b、c、d,相加后即等于4x;(4)得到方程5x=2020,求出的x不符合数表里数的特征,故不能等于2020.解:(1)5+15+19+29=68故答案为:68(2)答案为:4倍(3)a=x﹣12,b=x﹣2,c=x+2,d=x+12∴a+b+c+d=x﹣12+x﹣2+x+2+x+12=4x∴猜想正确.(4)M=a+b+c+d+x=4x+x=5x若M=5x=2020,解得:x=404但整个数表所有的数都为奇数,故不成立∴M的值不能等于2020.【点评】本题考查了一元一次方程的应用.当解得方程的解后,要观察是否满足题目和实际要求再进行取舍.3.(2014秋•新都区期中)将连续的奇数1,3,5,7…排列成如下的数表,用十字框框出5个数(如图)(1)十字框框出5个数的和与框子正中间的数19有什么关系?十字框框出5个数的和与框子正中间的数19的关系是.(2)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a 的代数式表示十字框框住的5个数和5个数之和;5个数分别表示为、、a、.5个数之和表示为.(3)十字框框住的5个数之和能等于2000吗?能等于2010吗?能等于2011吗?若能,分别写出十字框框住的5个数,并填入下图中.【考点】整式的加减;列代数式.【专题】常规题型.【答案】见试题解答内容【分析】(1)将各数相加可得出5个数的和与框子正中间的数19的关系.(2)由图标信息可得出各数的表示形式.(3)将(2)中的各数相加等于2000,组成方程,解出即可判断出答案.解:(1)十字框框出5个数的和与框子正中间的数19的关系是7+17+19+21+31=5×19.(2)5个数分别表示为a﹣12、a﹣2、a、a+2、a+12.5个数之和表示为5a.(3)当5a=2000、2010时,解得,a=400,402,与题意a为奇数不符,而2011不能被5整除,所以,不能框出.【点评】本题考查整式的加减及获取图表信息的能力,有一定难度,关键是仔细看图.4.(2021秋•滨海县校级月考)如表是2021年某月份的月历,回答下列问题:星期天星期一星期二星期三星期四星期五星期六123 45678910111213141516171819202122232425262728293031(1)小张一家外出旅游5天,这5天的日期之和是20,小张旅游的第一天是号;(2)如图,在日历上圈出5个数,呈十字框形,它们的和是40,则中间的数k是;(3)用一个长方形方框任意框出3×3个数,从左下角到右上角的“对角线上的3个数字的和为27,那么这个长方形方框中最中间的日期是号.【考点】一元一次方程的应用.【专题】数字问题;应用意识.【答案】(1)2;(2)1;(3)9.【分析】(1)设小张旅游的第一天是x号,日历中的连续两个数,后面的数比它前面的数大1,于是可列方程x+x+1+x+2+x+3+x+4=20,解方程求出x的值即可;(2)用十字框在日历中框出的五个数,下面的数比它上面相邻的数大7,可列方程k+k+6+k+7+k+8+k+14=40,解方程求出k的值即可;(3)设这个长方形方框中最中间的日期是n号,在日历中用长方形方框任意框出3×3个数,左下角到右上角三个数的特点是:右上角的数比最中间的数小6,左下角的数比最中间的数大6,于是可列方程n﹣6+n+n+6=27,解方程求出n的值即可.解:(1)设小张旅游的第一天是x号,根据题意得x+x+1+x+2+x+3+x+4=20,解得x=2,所以小张旅游的第一天是2号,故答案为:2.(2)由题意得k+k+6+k+7+k+8+k+14=40,解得k=1,所以中意的数k是1,故答案为:1.(3)设这个长方形方框中最中间的日期是n号,根据题意得n﹣6+n+n+6=27,解得n=9,所以这个长方形方框中最中间的日期是9号,故答案为:9.【点评】此题重点考查解一元一次方程、列一元一次方程解应用题等知识与方法,正确理解日历中前后两个数及上下两个数之间的关系是解题关键.5.(2018秋•沙湾区期末)2018年11月日历如图所示.(1)①小明用十字框按如图的方式框中的五个数,这五个数的和与中间数13有什么关系?②请你用同样的方式再框五个数,五个数的和与中间数的关系是否还成立?(2)请你把(1)中发现的规律写出来,并用学习的知识说明理由.(3)请你用同样的方式框五个数,使这五个数的和等于115(只需画出满足条件的十字框).【考点】一元一次方程的应用.【专题】数字问题;应用意识.【答案】(1)①这五个数的和是中间数13的5倍;②这五个数也成立,图形见解答;(2)五个数的和是中间数的5倍,理由见解答;(3)图形见解答.【分析】(1)①将5个数相加后除以13即可求解;②根据图上的数之间的关系即可求解;(2)根据发现规律,可得:中间一个为a,上面的数是a﹣7,下面的数是a+7,前面一个是a﹣1,后面一个是a+1,然后再计算这五个数的和即可求解;(3)设中间数为a,根据题意可得方程5a=115,然后可以计算出a的值即可求解.解:(1)①(6+12+13+14+20)÷13=5.故这五个数的和是中间数13的5倍;②将十字框中上下左右移动,可框住另外五个数,这五个数也成立,框数如图所示:(2)规律:五个数的和是中间数的5倍,理由如下:设中间数为x,则x+(x+1)+(x﹣1)+(x﹣7)+(x﹣7)=5x(8分)(3)设中间数为a,依题意有5a=115,解得:a=23,23﹣10=13,23+10=33,23﹣2=21,23+2=25,故中间数为23,框数略如图所示:【点评】此题主要考查了一元一次方程的应用,以及数字规律,关键是根据图上的数之间的关系,得到所框住的5个数的关系.6.(2019秋•青秀区校级月考)观察某月的月历,回答下列问题.(1)设十字框中间的数为a,求带阴影的十字框中间的5个数的和是多少?(2)小李一家外出游玩了5天,这5天的日期之和是75,小李一家是几号外出的?(3)在该月的日历上用十字框框出5个数,能使这5个数的和为100吗?如果不能,请说明理由;如果能,请求出十字框中间的数.【考点】一元一次方程的应用;列代数式.【专题】一次方程(组)及应用;应用意识.【答案】(1)带阴影的十字框中的5个数的和是5a;(2)小李一家是13号外出的;(3)20号在日历的最右侧,无法圈出5个数使20在中间.【分析】(1)根据所给数据进行计算可得答案;(2)根据图上的数之间的关系可得:设中间的数为a,上面的数是a﹣1,下面的数是a+1,前面一个是a﹣7,后面一个是a+7,然后再计算这五个数的和即可;(3)根据题意用未知数表示出框出5个数,根据这5个数的和为100列出方程解答即可.解:(1)(a﹣1)+a+(a+1)+(a﹣7)+(a+7)=5a,则带阴影的十字框中的5个数的和是5a.(2)设中间的数为a,依题意得:(a﹣2)+(a﹣1)+a+(a+1)+(a+2)=75解得:a=15,a﹣2=13答:小李一家是13号外出的.(3)不能:设十字框中间的数为a(a﹣1)+a+(a+1)+(a﹣7)+(a+7)=5a依题意得:5a=100;a=20.∴20号在日历的最右侧,无法圈出5个数使20在中间.【点评】此题考查一元一次方程的实际运用,根据日历表中的数字排列规律解决问题.。
第六章《组合图形的面积》五年级数学上册单元提优精选题汇编1版

【精品】第六章《组合图形的面积》五年级数学上册单元提优精选题汇编1北师大版一.选择题(共8小题)1.如图中阴影分的面积是()平方厘米.(单位:cm)A.60 B.108 C.120 D.1682.如图中每个小方格的面积为1cm2,五角星图(阴影部分)的面积约()1cm2.A.26~30 B.19~25 C.9~18 D.4~83.如图所示,不规则图形的面积大约是()平方厘米.(每个小正方形的面积是1平方厘米)A.16 B.22 C.35 D.634.估计一下,这个心形图案的面积约是()cm2.(每个小方格表示1cm2)A.6 B.8 C.105.中心广场的占地面积约为5公顷,()个中心广场的面积约为1平方千米.A.2 B.20 C.2006.如图,两条虚线相互平行,两条虚线间的距离为hm.从左往右,各图形中的涂色部分的总面积分别标记为①、②、③、④,则()A.①=②=③B.②=③=④C.①=②=④D.①=②=③=④=2hm27.求组合图形A的面积.不正确的方法是()A.组合图形A的面积=长方形的面积﹣梯形的面积B.组合图形A的面积=三角形的面积+梯形的面积C.组合图形A的面积=长方形的面积+梯形的面积D.组合图形A的面积=正方形的面积+三角形的面积8.以下表达正确的是()A.1平方千米=1000平方米B.100公顷=1平方千米C.1公顷=100平方米二.填空题(共8小题)9.目前亚洲最大的室外四季滑雪场﹣﹣奥森尖锋旱雪四季滑雪场的占地面积约为2公顷,个这样的四季滑雪场的占地面积约为1平方千米.10.0.25平方千米=公顷3000平方米=公顷11.估计如图各图形的面积大约是多少平方厘米.(每个小方格的面积均为1cm2)图①:cm2图②:cm2图③:cm212.估计图中的实物各有几厘米长,再量一量.估计:厘米;测量:厘米.13.如下图所示,平行四边形的面积是28cm2,阴影部分的面积是cm2.14.图中阴影部分的面积是8.5cm2,这个平行四边形的面积是cm2.15.借助方格图解决问题.(每个小方格的边长表示1cm)组合图形的面积是cm2,不规则图形的面积大约是cm216.如图是一个平行四边形被分成了三个三角形,涂色图形的面积是40cm2,没涂色的三角形的面积是cm2.三.判断题(共5小题)17.如图中阴影部分的面积占整个图形面积的12.5%.(判断对错)18.一桶水重15吨.(判断对错).19.天安门广场的面积大约是44公顷,1平方千米比2个天安门广场还要大一些.(判断对错)20.如图正方形的面积为4平方厘米,则阴影部分的面积为2平方厘米..(判断对错)21.用滴管滴100滴水大约有1毫升..(判断对错)四.计算题(共2小题)22.如图所示,下面梯形的面积280dm2,求阴影部分的面积.23.求如图阴影部分的面积.(单位:cm)五.操作题(共1小题)24.估计下列物体的长度时,你会用身体的哪一部位来测量?(连一连)六.应用题(共6小题)25.有一条宽2米的长方形小路穿过一块梯形田地,如图所示,这块田地的实际种植面积是多少平方米?26.有如图所示的一面墙,粉刷这面墙每平方米需用0.2千克涂料,一共要用多少千克涂料?27.每个小方格的面积表示1m2(不满1格的按半格计算),请你估计这个池塘的面积大约是多少平方米?28.你能想办法求出如图的面积吗?(每个小方格的边长表示1cm)29.王大伯从平行四边形菜地中划出一块三角形地种西红柿,其余地方种黄瓜(如图),这块黄瓜地的面积是多少平方米?30.国庆节到来之际,“中华人民共和国成立70周年”主题花坛亮相全国许多城市.花坛中摆放的五颜六色的花卉来自某种植基地,如果该基地中1平方米的土地能种8株花,那么1公顷的土地能种多少株花?参考答案与试题解析一.选择题(共8小题)1.解:10×12÷2=10×6=60(平方厘米)答:阴影分的面积是60平方厘米.故选:A.2.解:通过数格子来计算五角星的面积:满格子的有:4格,不足1格的有:16格,不足1格按半格计算,则面积大约为:4+16÷2=4+8=12(平方厘米)故选:C.3.解(4+8)×6÷2=12×6÷2=36(平方厘米)36平方厘米与答案C最接近答:不规则图形的面积大约是35平方厘米.故选:C.4.解:如图所示:整格6个,不满整格4个,面积约是:6×1+4÷2=6+2=8(cm2)答:这个心形图案的面积约是8cm2.故选:B.5.解:1平方千米=100公顷100÷5=20(个)答:20个中心广场的面积约为1平方千米。
