卫星轨道计算
卫星定位公式
卫星定位公式【原创版】目录1.卫星定位的基本原理2.卫星定位公式的构成3.卫星定位公式的应用4.卫星定位技术的发展正文1.卫星定位的基本原理卫星定位系统是一种利用卫星发射的信号来确定地球表面某一点的精确位置的技术。
其基本原理可以概括为：测量卫星发射的信号从卫星到达地面某一点的时间，根据光速和时间的关系，计算出该点与卫星之间的距离。
同时，通过至少三个卫星的定位，可以确定该点的三维坐标。
2.卫星定位公式的构成卫星定位公式主要包括以下三个部分：(1) 计算卫星与地面点之间的距离公式：d = c * t，其中 d 为距离，c 为光速（约为 3 * 10^8 米/秒），t 为信号传输时间。
(2) 计算卫星的轨道参数公式：T = 2 * π * sqrt(a^3 / μ)，其中 T 为卫星的周期，a 为卫星的半长轴，μ为地球的标准引力参数。
(3) 计算地面点的三维坐标公式：x = (t1 * cos(E1) - t2 * cos(E2)) * cos(A) + (t1 * sin(E1) - t2 * sin(E2)) * sin(A)，y = (t1 * cos(E1) - t2 * cos(E2)) * sin(A) - (t1 * sin(E1) - t2 * sin(E2)) * cos(A)，z = (t1 * cos(E1) + t2 * cos(E2)) * cos(I) + (t1 * sin(E1) + t2 * sin(E2)) * sin(I)，其中 x、y、z 为地面点的三维坐标，t1、t2 为卫星 1、卫星 2 的信号传输时间，E1、E2、I 分别为卫星 1、卫星 2 的倾角和地球的倾角。
3.卫星定位公式的应用卫星定位公式广泛应用于各种定位导航系统，如我国的北斗卫星导航系统、美国的 GPS 系统等。
这些系统通过卫星发射的信号，实时计算接收器与卫星之间的距离，从而实现对地球表面的精确定位。
卫星运动基础与轨道计算
卫星轨道方程：r p
讨论：
1 e cos l
e=0, r=p 即a=b, 轨道为圆
e<1， m inpp,m axp 为椭圆轨道
1e 2
1e
e1,m inp,m ax 为抛物线，卫星飞离地
球e1 ,m in2pp,m ax
1e 2
为双曲线
发射参数与轨道方程的关系
第一、二、三宇宙速度
OMEGA_0= -0.6E+01 ;//100.0/180.0* pi; 点赤经
// 参 考 时 刻 的 升 交
i0=0.958512160302E+00; //30.0/180.0*pi; //参考时刻的轨道倾角
omega_s=-0.258419417299E+01;//50.0/180.0*pi; 点角距
// 近 地
OMEGA_=-0.819426989566E-08; //升交点赤经变率
i_=-0.253939149013E-09;
//轨道倾角变率
Cuc=0.2E-06;
//改正项振幅
Cus=0.912137329578E-05 ;
Crc=0.201875E+03;
Crs=0.40625E+01;
开普勒方程求解
6.求卫星在轨道面的直角坐标系中的坐标
cos
r
sin
0
r
M
ms
近地点
开普勒方程求解
7.轨道面坐标转向升交点为轴
x0 cos
y0
r
sin
z 0 0
w
w
i 升交点
x
春分点
x0
开普勒方程求解
8.卫星在天球坐标系中位置
卫星轨道插值计算公式
卫星轨道插值计算公式卫星轨道插值计算是用来估算在两个已知轨道点之间卫星位置的技术。
轨道插值技术在航天器导航、轨道预报以及地球观测等领域中非常重要。
常用的轨道插值方法包括线性插值、三次样条插值、Kriging 插值等。
线性插值是最简单的插值方法之一，它假设卫星在两个轨道点之间的运动是匀速的。
如果已知卫星在两个不同时间点的位置\( (t_1, \mathbf{r}_1) \) 和\( (t_2, \mathbf{r}_2) \)，线性插值可以表示为：\[ \mathbf{r}(t) = \mathbf{r}_1 + \frac{t -t_1}{t_2 -t_1} \left( \mathbf{r}_2 - \mathbf{r}_1 \right) \]其中，\( \mathbf{r}(t) \) 是在时间t 处的卫星位置向量，\( \mathbf{r}_1 \) 和\( \mathbf{r}_2 \) 是已知的轨道位置，t 是插值点的时间，\( t_1 \) 和\( t_2 \) 是已知时间点。
三次样条插值则考虑了卫星轨道的曲线特性，通过对轨道数据进行样条函数拟合，得到一个连续的三次函数，该函数可以精确地通过所有的轨道点，并且具有连续的一阶和二阶导数，从而保证插值结果的平滑性。
Kriging插值是一种统计学方法，它利用了数据的变异性和空间相关性，通过计算最优权重来插值未知的数据点。
Kriging插值适用于地球科学领域中的空间数据插值，也可以用于卫星轨道数据的插值。
在实际应用中，选择哪种插值方法取决于数据的特性和所需的插值精度。
线性插值计算简单，但仅适用于线性变化的场景；三次样条插值和Kriging插值则可以更好地处理非线性变化的数据，提供更平滑的插值结果。
在卫星轨道计算中，通常会根据具体任务需求和数据特性来选择合适的插值方法。
卫星轨道计
卫星轨道计算1.轨道根数如果知道卫星的轨道根数，可以根据它们求出卫星在任一时刻的位置。
1．1 开普勒六参数卫星的轨道根数包括六个积分常数，如图1，包括，a为轨道长半轴；e为轨道偏心率；i 为卫星运动轨道面与赤道面的夹角；Ω为卫星轨道升交点N的赤道经度(自春分点算起)；ω为轨道近地点极角，即轨道平面内升交点到近地点的角度；ζ为卫星过近地点时刻1. 轨道半长轴，是椭圆长轴的一半。
2. 轨道偏心率，也就是椭圆两焦点的距离和长轴比值。
3. 轨道倾角，这个是轨道平面和地球赤道平面的夹角。
对于位于赤道上空的同步静止卫星来说，倾角就是0。
4. 升交点赤经：卫星从南半球运行到北半球时穿过赤道的那一点叫升交点。
这个点和春分点对于地心的张角称为升交点赤经。
5. 近地点幅角：这是近地点和升交点对地心的张角。
6. 过近地点时刻：卫星位置随时间的变化需要一个初值。
其中i、Ω、ω决定卫星轨道平面和长轴在空间的位置，而a、e、ζ可求出卫星在任何时刻在轨道上的位置。
1．2 TLE卫星星历TLE两行根数格式如下：AAAAAAAAAAAAAAAAAAAAAAAA1 NNNNNU NNNNNAAA NNNNN.NNNNNNNN +.NNNNNNNN +NNNNN-N +NNNNN-N N NNNNN2 NNNNN NNN.NNNN NNN.NNNN NNNNNNN NNN.NNNN NNN.NNNN NN.NNNNNNNNNNNNNN以国际空间站为例ISS (ZARYA)1 25544U 98067A 06052.34767361.00013949 00000-0 97127-4 0 39342 25544 051.6421 063.2734 0007415 308.6263 249.9177 15.74668600414901（1）第0行第0行是一个最长为24个字符的卫星通用名称，由卫星所在国籍的卫星公司命名，如SINOSAT 3。
卫星轨道参数计算
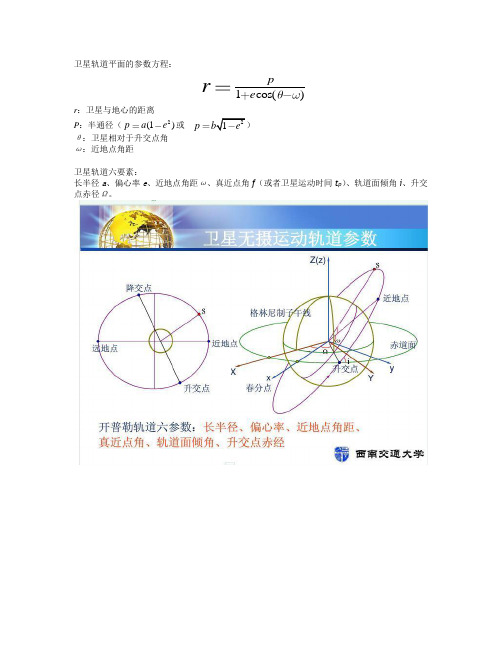
卫星轨道平面的参数方程：1cos()p e rr ：卫星与地心的距离P ：半通径（2(1)p a e 或21p b e ） θ：卫星相对于升交点角 ω：近地点角距卫星轨道六要素：长半径a 、偏心率e 、近地点角距ω、真近点角f （或者卫星运动时间t p ）、轨道面倾角i 、升交点赤径Ω。
OXYZ─赤道惯性坐标系，X轴指向春分点T ；ON─卫星轨道的节线（即轨道平面与赤道平面的交线），N为升交点；S─卫星的位置；P─卫星轨道的近地点；f─真近点角，卫星位置相对于近地点的角距；ω─近地点幅角，近地点到升交点的角距；i─轨道倾角，卫星通过升交点时，相对于赤道平面的速度方向；Ω─升交点赤经，节线ON与X轴的夹角；e─偏心率矢量，从地心指向近地点，长度等于e；W─轨道平面法线的单位矢量，沿卫星运动方向按右旋定义，它与Z轴的夹角为i；a─半长轴；α，δ─卫星在赤道惯性坐标系的赤经、赤纬。
两个坐标系：地心轨道坐标系、赤道惯性坐标系。
地心轨道坐标系Ox0y0z0：以ee1为x0轴的单位矢量，以W为z0轴的单位矢量，y0轴的单位矢量可以由x0轴的单位矢量与z0轴的单位矢量确定，它位于轨道平面内。
赤道惯性坐标系：OXYZ,X轴指向春分点。
由地心轨道坐标系到赤道惯性坐标系的转换：1.先将地心轨道坐标绕W旋转角（-ω），旋转矩阵为R Z(-ω)；2.绕节线ON旋转角（-i），旋转矩阵为R X(-i)；3.最后绕Z轴旋转角（-Ω），旋转矩阵为R Z(-Ω)；经过三次旋转后，地心轨道坐标系和赤道惯性坐标系重合。
在地心轨道坐标系中，卫星的位置坐标是：0 0 0cos sin 0x r f y r fz地心轨道坐标系到赤道惯性坐标系的转换关系是：000()()()cos cos sin cos sin sin cos cos cos sin sin sin cos =cos sincos cos sin sin sincos cos cos sin cos sin sin cos sin cos z x z x x y R R i R y z z i i i r f i i i i ii2sin 0cos sin()sin sin()cos(1)=sin cos()cos sin()cos 1cos sin()sin r f f f i a e f f ie ff i赤道惯性坐标系下的坐标确定后，可与r 、α、δ联系起来，关系式如下：1222()2arctan arctan(1)1cos 1cos y xz x y p a e re fe f若卫星六要素都已知，则可以解出α、δ。
人造地球卫星推算公式
人造地球卫星推算公式
人造地球卫星的推算公式是为了计算卫星的运动轨迹和位置而设计的。
公式的推导过程基于牛顿运动定律，考虑到地球和卫星的引力相互作用，以及卫星的质量和速度等因素。
推算公式可以分为两部分：第一部分是计算卫星的轨道半径和周期，第二部分是计算卫星在轨道上的位置。
第一部分的公式如下：
1. 计算轨道半径：
a = (GM*T^2/4π^2)^(1/3)
其中，G是万有引力常数，M是地球质量，T是卫星绕地周期，a 是轨道半径。
2. 计算轨道周期：
T = 2π*(a^3/GM)^(1/2)
其中，G、M和a的含义同上，T是卫星绕地周期。
第二部分的公式如下：
1. 计算卫星在轨道上的位置：
x = a*cos(E) - ae
y = a*(1-e^2)^(1/2)*sin(E)
其中，a是轨道半径，e是轨道离心率，E是偏近点角，x和y是卫星在轨道上的坐标，ae是轨道的长半径。
2. 计算偏近点角E：
M = n*t + M0
E - e*sin(E) = M
其中，n是卫星的平均角速度，t是时间，M是平近点角，M0是
平近点角在某一时刻的值。
以上公式是人造地球卫星推算公式的基本内容，可以通过数值计算的方式得到卫星的运动轨迹和位置信息。
这些信息对于卫星的设计、控制和应用都具有重要的意义。
卫星轨道计算
④ 离
⑤ 卫星与地球质心的几何距离为：
3.卫星轨道计算
3.2 开普勒方程
① 开普勒第三定律可表示为：
② 假定为 点角：
卫星通过近地点A的时刻，对应t 时刻的平近
3.卫星轨道计算
3.2 开普勒方程
③ 对应任意t 时刻的开普勒方程可描述为：
④ 于是，可得到真近点角f 可表示为：
4.卫星坐标计算算法步骤
4.2 重要MATLAB函数说明
（三）计算卫星位置模块 （1）读观测值文件（*.o文件）函数 在求解卫星位置时，第一需要利用o文件中每个历元 的历元时刻t。在计算某时刻卫星位置时，这里的某时刻便 是o文件历元时刻t。第二需要利用读取的每个历元不同的
卫星PRN号。根据PRN号和历元时刻 t 在广播星历n文件中
单位为弧度，是由于摄动力而引起的改正项。
4.卫星坐标计算算法步骤
4.1 算法
① 计算卫星运行的平均角速度 n
② 计算归化时间
4.卫星坐标计算算法步骤
4.1 算法
③ 观测时刻卫星平近点角 的计算
④ 计算偏近点角
⑤ 真近点角
的计算
4.卫星坐标计算算法步骤
4.1 算法
⑥ 升交距角 的计算
⑦ 摄动改正项
计算卫星位置。
4.卫星坐标计算算法步骤
4.2 重要MATLAB函数说明
（3）dt = check_t(time) time—儒略日； 返回值—修复后的儒略日。 （4）X = satpos(tx_GPS, Eph(:,k)) tx_GPS—上节所述的归化时间，用儒略日表示的； Eph(:,k)—Eph星历矩阵中的某一列数据； 返回值—卫星在地心地固坐标系中坐标。
1.开普勒定律
卫星速度公式
卫星速度公式
卫星速度公式是描述卫星在轨道上运动速度与轨道参数之间关系的公式。
在研究卫星轨道、卫星通信、卫星导航等领域具有重要的意义。
本文将详细介绍卫星速度公式，包括其推导和应用。
一、卫星速度公式简介
卫星速度公式为：
v = √(GM/r)
其中，v 代表卫星在轨道上的线速度，G 为万有引力常数，M 为地球质量，m 为卫星质量，r 为卫星轨道半径。
二、卫星速度公式推导
根据牛顿第二定律，卫星所受合力为：
F =
G * (M * m) / r
由于卫星在轨道上做圆周运动，合力提供向心力，所以有：
F = m * (v / r)
将两个公式联立，可得：
m * (v / r) = G * (M * m) / r
化简后得到卫星速度公式：
v = √(GM/r)
三、卫星速度公式应用
1.计算卫星轨道速度：根据卫星速度公式，可以计算出卫星在不同轨道上的线速度，为卫星发射、轨道设计提供参考。
2.分析卫星通信性能：卫星速度与轨道高度密切相关，通过分析卫星速度公式，可以了解卫星通信系统的性能，如覆盖范围、通信质量等。
3.优化卫星导航系统：卫星速度公式可用于优化卫星导航系统，提高导航精度，满足各类用户需求。
四、总结
卫星速度公式是描述卫星轨道运动的基本公式，对于卫星工程、卫星通信、卫星导航等领域具有重要的理论指导意义。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
几何形状参数
偏心率e：eccentricity (0 ≤ e < 1) 轨道半长轴a：semi-major axis 真近点角θ: true anomaly
14
2.2 卫星的空间定位 续4
轨道六要素
Z perigee descending node nodal line Equator plane O
卫星的在轨角速度
S 2 / T
(h Re)3
因此，最长连续服务时间为
tmax / S 1020.69s 17 min
29
2.4 轨道摄动
关于轨道公式的基本假设 卫星仅仅受到地球引力场的作用 卫星和地球都被视为点质量物体 地球是一个理想的球体
M = n· (t – t0) (3)
偏近点角(eccentric anomaly) E
18
2.2 卫星的空间定位 续8
椭圆轨道面内的卫星定位
开普勒方程
M = E - e· sin(E) (4)
高斯方程
1 e E 2 arctan( tan ) 1 e 2
(5)
19
flying direction
a C
E
r O
Orbital plane circumscribed circle
17
2.2 卫星的空间定位 续7
椭圆轨道面内的卫星定位
定义 平均近点角(mean anomaly) M : 假设卫星在t0通 过近地点，它以其平均角速度n绕椭圆轨道的外 接圆移动，到时刻t所经过的大圆弧长
地心角随着仰角El的减小而增大, 随着卫星半俯角β 的增加而增大。 通常，最小用户仰角会作为系统参数给出。通过该 参数可以计算给定高度卫星的最大覆盖地心角
27
2.3 卫星覆盖计算 续4
距离计算
d Re2 (h Re)2 2 Re (h Re) cos Re2 sin 2 El 2 h Re h2 Re sin El
2.2 卫星的空间定位 续9
椭圆轨道面内的卫星定位
计算流程 1) 使用方程(1)计算卫星的平均角速度n 2) 使用方程(3)计算平均近点角M 3) 解开普勒方程(4)获得偏心近点角E 4) 使用高斯方程(5)计算真近点角θ 5) 按下式计算距离矢量r r = a(1-e· cos(E))
20
椭圆轨道卫星具有时变的在轨飞行速度
2 1 V＝ （ ） r a (km / s ) (2)
在远地点和近地点的速度分别为
Va＝
a(1 e)
a a(1 e)
rp
ara
Vp＝
a(1 e)
a a(1 e)
ra
SkyBridge (LEO)
Iridium (LEO)
1469
780
7.1272
7.4624
01/55/17.8
01/40/27.0
9
2.1 卫星运动特性 续7
例 2.1 某椭圆轨道卫星的远地点高度为4000km，近地点高 度为1000km。假设地球的平均半径为6378.137km，求该卫 星的轨道周期T 解: 根据开普勒第一定理，近地点和远地点之间的距离为 2a = 2Re+hp+ha = 2×6378.137+1000+4000=17756.274 km
s (t ) arcsin(sin i sin )
式中: λ 0是0时刻的升交点经度 ω0是地球的自转角速度 ‘+’ 对应于顺行轨道而 ‘-’对应于逆行轨道
22
2.2 卫星的空间定位 续12
卫星星下点轨迹
Hale Waihona Puke 232.3 卫星覆盖计算
卫星和用户的空间几何关系
d user El
horizon h+Re Sub- satellite point
arp
8
2.1 卫星运动特性 续6
圆轨道卫星具有恒定的运动速度
V＝
a
(km / s )
(3)
典型卫星通信系统的轨道高度、卫星速度和轨道周期如下表
卫星系统 Intelsat (GEO) NewICO (MEO) 轨道高度 (km) 在轨速度 (km/s) 轨道周期（时/分/秒 ） 35786 10355 3.0747 4.8954 23/56/04.1 05/59/01.0
11
2.2 卫星的空间定位 续1
近焦点 (Perifocal)坐标系
以轨道平面为基础平面 以地心为坐标圆点 地心-近地点方向为X轴
Z轴垂直于轨道平面
XYZ轴构成右手坐标系
12
2.2 卫星的空间定位 续2
North pole
地心坐标系
以地心为坐标圆点 以赤道平面为基础平面 地心-春分点方向为X轴
参数定义
半长轴 semi-major axis 半短轴 semi-minor axis 偏心率 eccentricity 远地点半径 apogee radius 近地点半径 perigee radius 半交弦 semi-latus rectum 真近点角 true anomaly 位置矢量 position vector a b
第二章 卫星轨道
1
第一章概要
2.1 卫星运动特性 2.2 卫星的空间定位 2.3 卫星覆盖计算 2.4 轨道摄动 2.5 轨道对通信系统性能的影响 2.6 卫星发射
参考资料 作业
2
2.1 卫星运动特性
围绕地球飞行的卫星和航天器服从与行星绕太阳飞 行的运动规律 约翰尼斯 开普勒(1571-1630)通过观察推导了行星运 动的3大定理，即开普勒3定理 艾萨克· 牛顿爵士(1642-1727)从力学原理出发证明了 开普勒定理并创立了万有引力理论 开普勒定理适用于空间任何两个物体间通过引力相 互作用的情况，即二体问题（two-body problem）
21
2.2 卫星的空间定位 续11
卫星对地的定位 —— 星下点轨迹公式
180(180 90) 经度 s (t ) 0 arctan(cos i tan ) e t 0( 90 90 ) 180(90 180) 纬度
26
2.3 卫星覆盖计算 续3
地心角的计算
arccos
Re h Re cos El El arcsin sin h Re Re
使用两点的经纬度坐标计算地心角
arccos sin(u ) sin(s ) cos(u ) cos(s ) cos(u s )
轨道位置的漂移与时间成线性关系。在t1时刻，以轨道六要 素描述的卫星位置可描述为 d di d de da d t , i t , t , e t , a t , t 0 0 0 0 0 0 式中 0 , i0 , 0 , e0 , a0 ,0 ) 是卫星在t0时刻的轨道要素，d()/dt是 t 等于(t1-t0 ) 轨道要素随时间的线性漂移， 为消除摄动的影响，在卫星的生存周期内需要进行周期性的 位置保持和校正操作。
x
Re
O
24
2.3 卫星覆盖计算 续1
定义
用户仰角(elevation angle)，El 卫星半俯角，β （卫星与用户间的）地心角(geocentric angle), α （卫星与用户间的）距离，d 覆盖区半径， X 覆盖区面积， A
25
2.3 卫星覆盖计算 续2
6
2.1 卫星运动特性 续4
开普勒第三定理 (1618)：行星/卫星轨道周期的平方 正比与椭圆轨道半长轴的立方 使用能量守恒定理和开普勒第三定理，可以推导卫 星的轨道周期T为
T 2 a3
(1)
其中：a是半长轴，开普勒常数μ=3.9861×105 km3/s2
7
2.1 卫星运动特性 续5
2 max 2 arccos
6378.137 cos10 10 53.28 1450 6378.137
398601.58 9.12 104 rad / s 0.0522 / s 3 (1450 6378.137)
e 1 (b / a)2 ra = a (1 + e) rp = a (1 - e) p = a (1 – e2)
a(1 e2 ) r 1 e cos
5
2.1 卫星运动特性 续3
开普勒第二定理 (1605)：行星/卫星和太阳/地球之 间的连线在相同时间内扫过的面积相同
O
Equator plane O
Z
Y
Z轴垂直于赤道平面
XYZ轴构成右手坐标系
X Vernal equinox Orbital plane
13
2.2 卫星的空间定位 续3
轨道六要素（或卫星参数）
方向参数
右旋升交点赤经Ω：the right ascension of ascending node (RAAN) 轨道倾角i：inclination angle 近地点幅角ω: argument of the perigee
覆盖区半径计算
X Re sin
服该区面积估算
A 2 Re2 (1 cos )
28
2.3 卫星覆盖计算 续5
例2.2：轨道高度为1450 km的为最小仰角为10°的用户提 供服务，求给卫星能够提供的最长连续服务时间。 解: 假设该卫星恰好能够从用户头顶的正上方经过，此时该 用户能够获得最长的连续服务时间。 连续服务时间段，卫星飞行轨迹所对应的地心角的大小为