2011级应用时间序列分析课程试题(A卷)
2010《时间序列分析》试卷A答案精选全文完整版
可编辑修改精选全文完整版2010—2011学年第一学期2007应用数学《时间序列分析》试卷A 答案一 （18分，每空1分）1 112211t t t t t X X X a a ϕϕθ-----=-2 偏自相关函数；自相关函数3 矩估计法、最小二乘估计法、极大似然估计法4 B51ϕ；0 6 1,1,2,i i n λ<=7 m8利用序列图进行判断；利用样本自相关函数ˆk ρ进行平稳性检验；利用单位根检验进行判断9 12222011ˆ 1.96()t l a l X G G G σ+-±+++ 10 存在 11 使得预测误差的均方値达到最小10 (1)S DB -二 （8分，每小题1分）1 错；2错；3对；4对；5 错；6 错；7 错；8对三 （12分，每小题2分）1 (1)2(10.80.5)t t X B B a =-+；(2) 21(10.5)(1 1.20.4)t t B X B B a --=-+2 (1) 稳定；（2）稳定3 （1）120.5,0.25G G ==; (2) 120.5,0G G =-=四 （4分）AR{1}（1）34321324321ˆ(1)(,,)([100.60.3],,)100.697.20.39696.12X E X X X X E X X a X X X ==+++=+⨯+⨯=；（2分）35321435321ˆ(2)(,,)([100.60.3],,)100.697.120.397.297.432X E X X X X E X X a X X X ==+++=+⨯+⨯=；（2分）36321546321ˆ(3)(,,)([100.60.3],,)100.697.4320.397.1297.5952X E X X X X E X X a X X X ==+++=+⨯+⨯= （2分）（2）010110.6G G G ϕ===221/21/2011.96() 1.966 1.3613.7144G G σ+=⨯⨯=五月份销售额的 95%的置信区间为(83.7176,111.1464) （2分）六 （50分）1 （1）AR(1)模型：10.667831t t t X X a -=+ （5分）疏系数的ARMA(1,6)模型：160.5578970.47526t t t t X X a a --=++ （5分）（2）上边AR(1)模型的AIC 值为-0.804969，第二个模型的AIC 值为-0.876542，根据AIC 准则可知，第二个模型拟合效果更好。
时间序列考试A卷——答案 2
一、单项选择题1. t X 的k 阶差分是 【 C 】（A ）k t t t k X X X -∇=- （B ）11k k k t t t k X X X ---∇=∇-∇ （C ）111k k k t t t X X X ---∇=∇-∇ （D ）1112k k k t t t X X X ----∇=∇-∇ 2. MA(2)模型121.10.24t t t t X εεε--=-+，则移动平均部分的特征根是 【 A 】 （A ）10.8λ=，20.3λ= （B ）10.8λ=-，20.3λ= （C ）10.8λ=-，20.3λ=- （D ）10.8λ=-，20.2λ= 3.关于差分121.30.40t t t X X X ---+=，其通解是 【 D 】 （A ）1(0.80.3)t t C + （B ） 1(0.80.5)t t C + （C ） 120.80.3t t C C + （D ）120.80.5t t C C +4. AR(2)模型121.10.24t t t t X X X ε--=-+，其中0.04t D ε=，则t t EX ε=【 B 】 （A ）0 （B ） 0.04 （C ） 0.14 （D ）0.25. ARMA(2,1)模型1210.240.8t t t t t X X X εε-----=-，其延迟表达式为【 A 】（A ）2(10.24)(10.8)t t B B X B ε--=- （B ） 2(0.24)(0.8)t t B B X B ε--=- （C ）2(0.24)0.8t t B B X ε--=∇ （D ）2(10.24)t t B B X ε--=∇三、（15分）已知MA(2)模型为120.60.5t t t t X εεε--=-+，其中0.04t D ε=， （1）计算前3个逆函数，,1,2,3j I j =；----------------（8分） （2）计算()t Var X ；-----------------------------------（7分）解答：（1）t X 的逆转形式为：1t jt j t j X IX ε+∞-==+∑，或0()t j t j j I X ε+∞-==-∑------------（1分）将其代入原模型得：2212(10.60.5)(1)t t X B B I B I B X =-+----------（1分）比较B 的同次幂系数得：11:0.600.6B I I --=⇒=-———（2分）2212:0.60.500.14B I I I -++=⇒=———（2分） 33213:0.60.500.384B I I I I -++=⇒=———（2分）（2）12(0.60.5)0t t t t EX E εεε--=-+=———（1分）21212[(0.60.5)(0.60.5)]t t t t t t t EX E εεεεεε----=-+-+，———（2分）因为20,0.04,t s t s E t sεεεσ≠⎧=⎨==⎩———（2分） 所以：222()(10.60.5)0.040.0644t t Var X EX ==++⨯=———（2分） 四、（15分）已知AR(2)模型为(10.5)(10.3)t tB B X ε--=，20.5t D εεσ==。
统计学考试试卷A及答案
统计学考试试卷A及答案6. 下面的哪一个图形最适合于描述结构性问题（）2012—2013 学年第二学期闽江学院考试试卷A. 条形图B. 饼图C. 雷达图D. 直方图考试课程：统计学7. 对于大批量的数据, 最适合描述其分布的图形是( )A. 条形图B. 茎叶图C. 直方图D. 饼图试卷类别：A卷□√ B 卷□考试形式：闭卷□√开卷□8. 将某企业职工的月收入依次分为2000元以下、2000元~3000元，3000元~4000适用专业年级：2011 级金融学、国际贸易学、保险学专业元、4000 元~5000元、5000 元以上几个组。
最后一组的组中值近似为( )注明：试卷答案请做在答题纸上。
A.5000B.7500C.5500D.6500一、单选题（每题1分，共30分，30%）9. 下列关于众数的叙述，不正确的是（）A.一组数据可能存在多个众数B. 众数主要适用于分类数据C.一组数据的众数是唯一的D. 众数不熟极端值的影响1. 下列不属于描述统计问题的是（）10. 一组数据的最大值与最小值之差称为（）A根据样本信息对总体进行的推断B了解数据分布的特征A. 平均数B. 规范差C. 极差D. 四分位差C分析感兴趣的总体特征D利用图，表或其他数据汇总工具分析数据11. 如果一组数据不是对称分布的，根据切比雪夫不等式，对于k ＝3, 其意义是2. 根据样本计算的用于推断总体特征的概括性度量值称作（）（）A．参数 B. 总体C．样本 D. 统计量A.至少有75%的数据落在平均数加减 3 个规范差的范围之内3. 通过调查或观测而收集到的数据称为（）B. 至少有89%的数据落在平均数加减 3 个规范差的范围之内A．观测数据 B. 实验数据C．至少有94%的数据落在平均数加减3 个规范差的范围之内C．时间序列数据 D. 截面数据D. 至少有99%的数据落在平均数加减 3 个规范差的范围之内4. 从总体中抽取一个元素后，把这个元素放回到总体中再抽取第二个元素，直12. 下列不是次序统计量的是（）。
10-11上学期时间序列分析A卷及答案
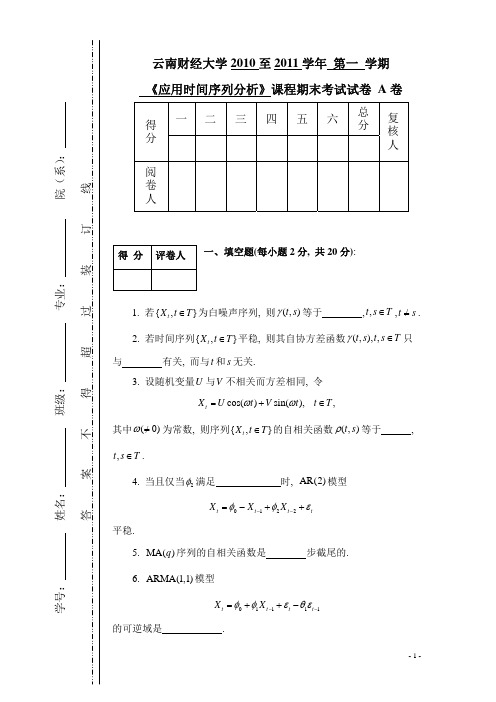
1. 若 { X t , t T } 为白噪声序列, 则 (t , s) 等于 0 , t , s T , t s. 2. 若时间序列 { X t , t T } 平稳, 则其自协方差函数 (t , s ), t , s T 只与 t s 有关, 而
ˆ (l ) 的均方误差为 的 MA(q) 序列, 则已知 X t , X t 1 , X t 2 , 时, X t l 的最佳线性预测 X t
2 (1 12 l21 ) , l 1, , q .
二、选择题(每小题 2 分, 共 20 分):
1. 对于正态序列来说, 其严平稳性与(宽)平稳性是 a a.等价的, b.不等价的.
1.试求模型的传递形式. 2.试求模型的逆转形式. 3.试求满足模型的 ARMA(1,1) 序列 { X t , t 0, 1, 2,} 的均值和自协方差函数.
-3-
-4-
得 分
评卷人
四、计算题(每小题 5 分, 共 15 分) 设 { X t , t 0, 1, 2,} 是满足 AR(2) 模型
.
2. 为了度量序列中两个随机变量之间真实的相关程度, 应该使用 b . a.自相关函数, b.偏相关函数. .
3. 平稳序列的偏相关函数 p 步截尾是其为 AR( p) 序列的 b a.充分条件, 4. 若一序列严平稳, 则其 a.一定, b b.充要条件.
是(宽)平稳的.
b.不一定. .
5. 满足平稳 ARMA 模型的 ARMA 序列有 a a.一个, b.无穷多个. .
中, 用白噪声序列 { t , t 0, 1, 2,} 线性地表示 ARMA( p, q) 序列称为模型的 a
统计学考试试卷A及答案
2012—2013学年第二学期闽江学院考试试卷考试课程： 统计学试卷类别：A 卷□√ B 卷□ 考试形式：闭卷□√ 开卷□ 适用专业年级：2011级金融学、国际贸易学、保险学专业 注明：试题答案请做在答题纸上。
一、单选题（每题1分，共30分，30%）1. 下列不属于描述统计问题的是（ ）A 根据样本信息对总体进行的推断B 了解数据分布的特征C 分析感兴趣的总体特征D 利用图，表或其他数据汇总工具分析数据 2. 根据样本计算的用于推断总体特征的概括性度量值称作（ ） A ． 参数 B. 总体 C ．样本 D. 统计量 3. 通过调查或观测而收集到的数据称为（ ）A ． 观测数据 B. 实验数据 C ． 时间序列数据 D. 截面数据 4. 从总体中抽取一个元素后，把这个元素放回到总体中再抽取第二个元素，直至抽取n 个元素为止，这样的抽样方法称为（ ）。
A.重复抽样 B.不重复抽样 C.分层抽样 D.整群抽样5. 调查时首先选择一组调查单位，对其实施调查之后，再请他们提供另外一些属于研究总体的调查对象，调查人员根据所提供的线索，进行此后的调查。
这样的调查方式称为（ ）。
A 系统抽样B 整群抽样C 滚雪球抽样D 判断抽样 6. 下面的哪一个图形最适合于描述结构性问题（ ）A.条形图B.饼图C.雷达图D. 直方图 7. 对于大批量的数据,最适合描述其分布的图形是( )A.条形图B.茎叶图C.直方图D.饼图8. 将某企业职工的月收入依次分为2000元以下、2000元~3000元，3000元~4000元、4000元~5000元、5000元以上几个组。
最后一组的组中值近似为( ) A.5000 B.7500 C.5500 D.6500 9. 下列关于众数的叙述，不正确的是（ ）A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不熟极端值的影响 10. 一组数据的最大值与最小值之差称为（ ） A. 平均数 B.标准差 C.极差 D.四分位差11.如果一组数据不是对称分布的，根据切比雪夫不等式，对于k ＝3,其意义是（ ）A.至少有75%的数据落在平均数加减3个标准差的范围之内B. 至少有89%的数据落在平均数加减3个标准差的范围之内 C ．至少有94%的数据落在平均数加减3个标准差的范围之内 D. 至少有99%的数据落在平均数加减3个标准差的范围之内 12. 下列不是次序统计量的是（）。
中级经济师经济基础 第二十七章 时间序列分析
中级经济师经济基础第二十七章时间序列分析一、单项选择题1、以下关于发展水平的说法中，错误的是（）。
A、在绝对数时间序列中，发展水平是绝对数B、在相对数时间序列中，发展水平表现为相对数C、发展水平是时间序列中对应于具体时间的指标数值D、平均数时间序列中，发展水平表现为绝对数2、（）也称序时平均数或动态平均数，是对时间序列中各时期发展水平计算的平均数，它可以概括性描述现象在一段时期内所达到的一般水平。
A、发展水平B、发展速度C、平均发展水平D、平均发展速度我国2005—2017年平均每年第三产业就业人数是（）万人。
A、12 480B、12 918C、14 000D、14 4124、环比发展速度等于（）。
A、逐期增长量与其前一期水平之比B、累计增长量与最初水平之比C、报告期水平与最初水平之比D、报告期水平与其前一期水平之比5、已知一个序列的环比发展速度为102%、103%、105%，则该序列的定基发展速度为（）。
A、103%B、105%C、110%D、112%6、以相对数形式表示的两个不同时期发展水平的比值是（）。
A、增长量B、发展水平C、增长速度D、发展速度7、已知某地区2012-2016年社会消费品零售总额的环比增长速度分别为5%、7%、10%、11%，则这一时期该地区社会消费品零售总额的定基增长速度为（）。
A、5%×7%×10%×11%B、（5%×7%×10%×11%）+1C、105%×107%×110%×111%D、（105%×107%×110%×111%）-18、甲企业某种商品前11个月的实际销售量如下表所示。
采用移动平均数法预测，取k＝3，则第A、303B、350C、384D、3949、目前计算平均发展速度通常采用（）。
A、众数B、几何平均法C、算术平均法D、增长1%的绝对值法10、某企业2010年—2016年销售收入的年平均增长速度是27.6%，这期间相应的年平均发展速度是（）。
统计学考试试卷A及答案
2012—2013学年第二学期闽江学院考试试卷考试课程：统计学试卷类别：A卷B卷□考试形式：闭卷开卷□适用专业年级：2011级金融学、国际贸易学、保险学专业注明：试题答案请做在答题纸上。
一、单选题（每题1分，共30分，30%）1.下列不属于描述统计问题的是（）A根据样本信息对总体进行的推断B了解数据分布的特征C分析感兴趣的总体特征D 利用图，表或其他数据汇总工具分析数据2.根据样本计算的用于推断总体特征的概括性度量值称作（）A．参数B.总体C．样本D.统计量3.通过调查或观测而收集到的数据称为（）A．观测数据B.实验数据C．时间序列数据D.截面数据4.从总体中抽取一个元素后，把这个元素放回到总体中再抽取第二个元素，直至抽取n 个元素为止，这样的抽样方法称为（）。
A.重复抽样B.不重复抽样C.分层抽样D.整群抽样5.调查时首先选择一组调查单位，对其实施调查之后，再请他们提供另外一些属于研究总体的调查对象，调查人员根据所提供的线索，进行此后的调查。
这样的调查方式称为（）。
A系统抽样B整群抽样C滚雪球抽样D判断抽样6.下面的哪一个图形最适合于描述结构性问题（）A.条形图B.饼图C.雷达图D.直方图7.对于大批量的数据,最适合描述其分布的图形是()A.条形图B.茎叶图C.直方图D.饼图8.将某企业职工的月收入依次分为2000元以下、2000元~3000元，3000元~4000元、4000元~5000元、5000元以上几个组。
最后一组的组中值近似为().7500 C下列关于众数的叙述，不正确的是（）A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不熟极端值的影响10.一组数据的最大值与最小值之差称为（）A.平均数B.标准差C.极差D.四分位差11.如果一组数据不是对称分布的，根据切比雪夫不等式，对于k＝3,其意义是（）A.至少有75%的数据落在平均数加减3个标准差的范围之内B.至少有89%的数据落在平均数加减3个标准差的范围之内C．至少有94%的数据落在平均数加减3个标准差的范围之内D.至少有99%的数据落在平均数加减3个标准差的范围之内12.下列不是次序统计量的是（）。
2011级练习题
《金融时间序列分析》练习题 判断题：（ F ）1、某项投资分为4个周期，每个周期的收益率不同，用Ri ，i=1,…，4表示，那么该项投资与投资期4个周期，每个周期收益率都是441∑=i iR 的投资是等价的。
（ T ）2、 如果以t 分布作为对照分布画出的Q-Q 图是直线说明该组数据服从t 分布。
（根据t 分布计算理论上的分位数标在纵轴上，根据数据计算出的样本分位数画在横轴上） （ F ）3、 使用JB 检验判断数据的分布是否是正态分布，如果检验的p －值等于0.78，说明该组数据不服从正态分布。
（ T ）4、自回归过程t t t t t y y y y ε++−=−−−3217.04.11.0的偏自相关系数*4ρ等于0。
（ T ）5 、Q 检验的缺陷是经常把不是白噪声的残差误认为是白噪声过程。
（ F ）6、 如果某银行宣布该银行1－天内，99％置信水平下，风险价值等于30（百万），说明该银行有1％的可能性1天内的损失会小于30（百万）。
（ F ）7、假设半年支付利率一次，周期利率5％（以半年为一个周期），那么年简单收益率是10％，年复利收益率是10.25%，年连续复利收益率9.89%（ T ）8、 对某模型的残差的平方进行检验，发现存在自相关，所以应该对残差建立ARCH 类模型。
（ T ）9、对MA(1)模型16.04.0−++=t t t y εε的3－步预测值等于0.4。
（ T ）10、 白噪声过程和ARCH 过程都是平稳随机过程。
（ F ）11、 如果某组数据的偏度大于0，说明该组数据的分布是非对称的，并且有一个较长的左尾。
（ F ）12 如果1年支付利息一次，那么一年内连续复利收益率大于复利收益率大于简单收益率。
（ T ）13、 如果建立回归模型遗漏掉一个重要解释变量，并且该解释变量与模型中其它解释变量相关系数不等于0，那么会造成遗漏变量偏差。
（ T ）14、 ARMA(1,1)-GARCH(1,1)过程的条件均值和条件方差都随着时间的变化而变化，但是无条件均值和无条件方差仍然是常数。
时间序列练习题
时间序列练习题时间序列分析是一种用于研究以时间为顺序的数据变动规律的方法。
它可以帮助我们理解和预测未来的趋势，对于决策和规划具有重要的意义。
本文将通过一些时间序列练习题，帮助读者更好地理解和应用时间序列分析。
练习题一：季度销售数据分析某公司的销售数据按照季度记录如下：季度销售额Q1 100Q2 200Q3 300Q4 400请你根据这些数据，进行以下的分析和预测：1. 绘制季度销售额的时间序列图。
2. 计算季度销售额的平均值。
3. 判断季度销售额是否存在趋势性，并进行趋势线的拟合。
4. 判断季度销售额是否存在季节性，如果存在，请进行季节性分解。
5. 使用你认为最适合的模型进行未来一年季度销售额的预测，并给出预测结果。
练习题二：月度股票收益率分析某股票连续12个月的收益率数据如下：月份收益率1 0.032 0.053 -0.024 0.025 -0.016 0.047 -0.038 0.019 0.0210 -0.0511 0.0112 0.03请你根据这些数据，进行以下的分析和预测：1. 绘制月度股票收益率的时间序列图。
2. 计算月度收益率的平均值和标准差。
3. 判断股票收益率是否存在趋势性，并进行趋势线的拟合。
4. 判断股票收益率是否存在季节性，如果存在，请进行季节性分解。
5. 使用你认为最适合的模型进行未来三个月股票收益率的预测，并给出预测结果。
练习题三：年度气温分析某城市过去10年（2011年至2020年）的年度平均气温数据如下：年份平均气温（摄氏度）2011 192012 212013 202014 182015 172016 182017 202018 222019 232020 21请你根据这些数据，进行以下的分析和预测：1. 绘制年度平均气温的时间序列图。
2. 计算年度平均气温的平均值、中位数和极差。
3. 判断气温是否存在趋势性，并进行趋势线的拟合。
4. 判断气温是否存在季节性，如果存在，请进行季节性分解。
时间序列分析期末题库试题及答案
时间序列分析期末题库试题及答案（以下是一个范例，您可以根据需要进行修改和调整）时间序列分析期末题库试题及答案时间序列分析是一门研究随时间变化的数据模式和规律的统计学方法，广泛应用于物理学、经济学、环境科学等领域。
在进行时间序列分析时，掌握相关的试题及其答案是提高分析能力和应对考试的重要途径。
本文将为您提供一份时间序列分析期末题库试题及答案，希望能帮助您更好地掌握这门学科。
一、简答题1. 请解释什么是时间序列分析。
答：时间序列分析是一种统计学方法，用于研究随时间变化的数据。
它可以揭示出数据内在的趋势、季节性和周期性等模式，帮助我们进行预测和决策。
2. 时间序列分析的主要步骤有哪些？答：时间序列分析的主要步骤包括：数据收集和整理、数据可视化、确定模型、模型识别和拟合、模型检验和评估、模型预测和应用。
3. 请解释平稳时间序列的概念。
答：平稳时间序列是指其数学期望、方差和自协方差不随时间的变化而发生显著变化的时间序列。
平稳时间序列的均值和方差不依赖于时间，具有稳定的趋势和季节性。
4. 如何进行时间序列的平稳性检验？答：常见的平稳性检验方法包括ADF检验、KPSS检验和单位根检验。
这些方法可以通过检验时间序列数据的单位根是否存在来判断其是否平稳。
5. 时间序列分析中的自相关和偏自相关函数有什么作用？答：自相关函数（ACF）和偏自相关函数（PACF）用于分析时间序列数据的相关性。
ACF可以帮助确定数据的季节性和周期性，而PACF可以帮助确定数据的自回归阶数。
二、计算题请根据以下时间序列数据，回答下面的问题：年份 | 销售额（万元）-----------------------2015 | 2002016 | 2302017 | 2502018 | 2802019 | 3002020 | 3201. 请绘制销售额的时间序列图。
答：（在此插入相应的时间序列图）2. 根据观察的时间序列图，总结该时间序列的趋势和季节性。
应用时间序列分析习题答案解析
第二章习题答案2.1（1）非平稳（2）0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376（3）典型的具有单调趋势的时间序列样本自相关图2.2（1）非平稳，时序图如下（2）- （3）样本自相关系数及自相关图如下：典型的同时具有周期和趋势序列的样本自相关图2.3（1） 自相关系数0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 --0.034 0.206 -0.010 0.080 0.1182）平稳序列3）白噪声序列 2.4LB=4.83 ，LB 统计量对应的分位点为 0.9634 ，P 值为 0.0363 。
显著性水平 =0.05，序列不能视为纯随机序列。
2.51）时序图与样本自相关图如下2) 非平稳3)非纯随机2.6(1)平稳，非纯随机序列(拟合模型参考： ARMA(1,2) )(2)差分序列平稳，非纯随机 第三章习题答案 3.1 解：E(x t ) 0.7 E(x t1) E( t )3.2解：对于 AR (2)模型：1 1 02 1 1 2 10.52 1 121 1 20.3解得：17/152 1/153.3解：根据该 AR(2)模型的形式，易得： E(x t ) 0原模型可变为： x t 0.8x t 1 0.15x t 2t(1 0.7B) x ttx t (1 10.7B) 1t 22(1 0.7B 0.72B 2)Var(x t ) 1 22 2 1.9608 21 0.492 210 0.49 22 0(1 0.7)E(x t )E(x t ) 0Var ( x t )12(1 2)(1 1 2)(1 1 2 )(1 0.15)(1 0.15)(1 0.8 0.15)(1 0.80.15)22=1.98231 1 /(12 ) 0.69572 1 1 2 0 0.40663 1 2 2 1 0.2209 11 122 2330.69570.153.4 解：原模型可变形为： 2(1 B cB 2)x tt由其平稳域判别条件知：当 | 2 | 1， 21 且2 1 1时， 模型平稳。
统计学考试试卷A及答案
2012—2013学年第二学期闽江学院考试试卷考试课程：统计学试卷类别：A卷□√B卷□考试形式：闭卷□√开卷□适用专业年级：2011级金融学、国际贸易学、保险学专业注明：试题答案请做在答题纸上。
一、单选题（每题1分，共30分，30%）1. 下列不属于描述统计问题的是（）A根据样本信息对总体进行的推断 B了解数据分布的特征C分析感兴趣的总体特征 D利用图，表或其他数据汇总工具分析数据2. 根据样本计算的用于推断总体特征的概括性度量值称作（）A．参数 B. 总体 C．样本 D. 统计量3. 通过调查或观测而收集到的数据称为（）A．观测数据 B. 实验数据C．时间序列数据 D. 截面数据4. 从总体中抽取一个元素后，把这个元素放回到总体中再抽取第二个元素，直至抽取n个元素为止，这样的抽样方法称为（）。
A.重复抽样B.不重复抽样C.分层抽样D.整群抽样5. 调查时首先选择一组调查单位，对其实施调查之后，再请他们提供另外一些属于研究总体的调查对象，调查人员根据所提供的线索，进行此后的调查。
这样的调查方式称为（）。
A 系统抽样B 整群抽样C 滚雪球抽样D 判断抽样6. 下面的哪一个图形最适合于描述结构性问题（）A.条形图B.饼图C.雷达图D. 直方图7. 对于大批量的数据,最适合描述其分布的图形是( ) A.条形图 B.茎叶图 C.直方图 D.饼图8. 将某企业职工的月收入依次分为2000元以下、2000元~3000元，3000元~4000元、4000元~5000元、5000元以上几个组。
最后一组的组中值近似为( )A.5000B.7500C.5500D.65009. 下列关于众数的叙述，不正确的是（）A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不熟极端值的影响10. 一组数据的最大值与最小值之差称为（）A.平均数B.标准差C.极差D.四分位差11.如果一组数据不是对称分布的，根据切比雪夫不等式，对于k＝3,其意义是（）A.至少有75%的数据落在平均数加减3个标准差的范围之内B. 至少有89%的数据落在平均数加减3个标准差的范围之内C．至少有94%的数据落在平均数加减3个标准差的范围之内D. 至少有99%的数据落在平均数加减3个标准差的范围之内12. 下列不是次序统计量的是（）。
2011时间序列分析与预测习题答案
ˆ T
2006年 年一季度 二季度 Nhomakorabea三季度 四季度
4.5（1）移动平均法消除季节变动计算表
2007年 年 一季度 二季度 三季度 四季度 2008年 年 一季度 二季度 三季度 四季度 14.6 17.5 16 18.2 18.4 20 16.9 18 14.775 16.575 17.525 18.15 18.375 18.325 13.9875 15.675 17.05 17.8375 18.2625 18.35
yt = 8.69 + 0.64×t 4.5（4）根据模型 趋势剔除法季节比例计算表（1）
年别 2005年 年 季别 一季度 二季度 三季度 四季度 2006年 年 一季度 二季度 三季度 四季度 2007年 年 一季度 二季度 三季度 四季度 2008年 年 一季度 二季度 三季度 四季度 时间序列号t 时间序列号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 鲜蛋销售量 Y=TCSI 13.1 13.9 7.9 8.6 10.8 11.5 9.7 11 14.6 17.5 16 18.2 18.4 20 16.9 18 鲜蛋销售量T 预测 鲜蛋销售量 9.33 9.97 10.61 11.25 11.89 12.53 13.17 13.81 14.45 15.091 15.73 16.37 17.01 17.65 18.29 18.93 趋势剔除值 Y/T=CSI 1.40 1.39 0.74 0.76 0.91 0.92 0.74 0.80 1.01 1.16 1.02 1.11 1.08 1.13 0.92 0.95
思考题4解
上例的问题很常见，复利下计算平均年 利率用几何平均法，单利下计算用简单 算术平均法，目前我国银行基本采用的 是单利计算。再看本题，在已知条件不 具备下，可以用解法一，即用简单算术 平均法。这似乎与相对数时间数列计算 平均数的原则相矛盾，但在缺少必要资 料的条件下 ，这样计算有实际意义。
应用时间序列习题(含答案)
应用时间序列习题(含答案)一、单项选择题1．时间数列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值大小排列的C 前者是根据时间顺序排列的，后者是根据变量值大小排列的D 前者是根据变量值大小排列的，后者是根据时间顺序排列的 2．时间数列中，数值大小与时间长短有直接关系的是( )A 平均数时间数列B 时期数列C 时点数列D 相对数时间数列3．发展速度属于( )A 比例相对数B 比较相对数C 动态相对数D 强度相对数4．计算发展速度的分母是( )A 报告期水平B 基期水平C 实际水平D 计划水平5．某车间月初工人人数资料如下：则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6．某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为( )A150万人 B150．2万人 C150．1万人 D 无法确定 7．由一个9项的时间数列可以计算的环比发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 8．采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度 9．某企业的产值2005年比2000年增长了58．6％，则该企业2001—2005年间产值的平均发展速度为( )A 5%6.58B 5%6.158C 6%6.58 D6%6.158 10．根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是( )A 简单平均法B 几何平均法C 加权序时平均法D 首末折半法11、时间序列在一年内重复出现的周期性波动称为（ ）A 、长期趋势B 、季节变动C 、循环变动D 、随机变动1．C 2．B 3．C 4．B 5．C 6．C 7．A 8．A 9．B 10．D 11、B二、多项选择题1．对于时间数列，下列说法正确的有( )A 数列是按数值大小顺序排列的B 数列是按时间顺序排列的C 数列中的数值都有可加性D 数列是进行动态分析的基础E 编制时应注意数值间的可比性 2．时点数列的特点有( )A 数值大小与间隔长短有关B 数值大小与间隔长短无关C 数值相加有实际意义D 数值相加没有实际意义E 数值是连续登记得到的 3．下列说法正确的有( )A 平均增长速度大于平均发展速度B 平均增长速度小于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有( )A%100⨯=基期水平增长量增长速度 B %100⨯=报告期水平增长量增长速度C 增长速度= 发展速度—100％D %100⨯-=基期水平基期水平报告期水平增长速度E %100⨯=基期水平报告期水平增长速度5．采用几何平均法计算平均发展速度的公式有( )A1231201-⨯⨯⨯⨯=n n a a a a a a a a nx K B 0a a n x n =C1a a nx n= D n R x = En x x ∑=6．某公司连续五年的销售额资料如下：根据上述资料计算的下列数据正确的有( )A第二年的环比增长速度=定基增长速度=10％B第三年的累计增长量=逐期增长量=200万元C第四年的定基发展速度为135％D第五年增长1％绝对值为14万元E第五年增长1％绝对值为13．5万元7．下列关系正确的有( )A环比发展速度的连乘积等于相应的定基发展速度B定基发展速度的连乘积等于相应的环比发展速度C环比增长速度的连乘积等于相应的定基增长速度D环比发展速度的连乘积等于相应的定基增长速度E平均增长速度=平均发展速度-18．测定长期趋势的方法主要有( )A时距扩大法 B方程法 C最小平方法 D移动平均法 E几何平均法9．关于季节变动的测定，下列说法正确的是( )A目的在于掌握事物变动的季节周期性B常用的方法是按月(季)平均法C需要计算季节比率D按月计算的季节比率之和应等于400％E季节比率越大，说明事物的变动越处于淡季10．时间数列的可比性原则主要指( )A时间长度要一致 B经济内容要一致 C计算方法要一致 D总体范围要一致E计算价格和单位要一致1．BDE 2．BD 3．BC 4．ACD 5．ABD 6．ACE 7．AE 8．ACD 9．ABC 10．ABCDE三、判断题1．时间数列中的发展水平都是统计绝对数。
数字信号处理试卷和答案
北京信息科技大学2010 ~2011 学年第一学期《数字信号处理》课程期末考试试卷（A）一、填空题（本题满分30分，共含4道小题，每空2分）1.两个有限长序列x1(n)，0≤n≤33和x2(n)，0≤n≤36，做线性卷积后结果的长度是，若对这两个序列做64点圆周卷积，则圆周卷积结果中n= 至为线性卷积结果。
2.DFT是利用nkW的、和三个固有特性来实现FFT快速运算的。
N3.IIR数字滤波器设计指标一般由、、和等四项组成。
4.FIR数字滤波器有和两种设计方法，其结构有、和等多种结构。
二、判断题（本题满分16分，共含8道小题，每小题2分，正确打√，错误打×）1.相同的Z变换表达式一定对应相同的时间序列。
（）2.Chirp-Z变换的频率采样点数M可以不等于时域采样点数N。
（）3.按频率抽取基2 FFT首先将序列x(n)分成奇数序列和偶数序列。
（）4.冲激响应不变法不适于设计数字带阻滤波器。
（）5.双线性变换法的模拟角频率Ω与数字角频率ω成线性关系。
（）6.巴特沃思滤波器的幅度特性必在一个频带中（通带或阻带）具有等波纹特性。
（）7.只有FIR滤波器才能做到线性相位，对于IIR滤波器做不到线性相位。
（）8.在只要求相同的幅频特性时，用IIR滤波器实现其阶数一定低于FIR阶数。
（）三、综合题（本题满分18分，每小问6分）若x (n)= {3，2，1，2，1，2 }，0≤n≤5，1) 求序列x(n)的6点DFT，X (k)=？2) 若)()]([)(26k X W n g DFT k G k ==，试确定6点序列g(n)=? 3) 若y(n) =x(n)⑨x(n)，求y(n)=？四、IIR 滤波器设计（本题满分20分，每小问5分）设计一个数字低通滤波器，要求3dB 的截止频率f c =1/π Hz ，抽样频率f s =2 Hz 。
1. 导出归一化的二阶巴特沃思低通滤波器的系统函数H an (s)。
2011-2012学年第一学期统计学试卷A及答案
4.为检验广告媒体和广告方案对产品销售量的影响，一家营销公司做了一项实
验，考察三种广告方案和两种广告媒体，获得的销售量数据如下：
A
广告方案
B
C
报纸 10 12 22 15 12 20
广告媒体
电视 12 10 26 28 20 16
（1）写出检验广告方案和广告媒体及其交互作用的假设。
（2）完成下面的方差分析表。
0.405285 96 141 237
22148 120
2.一种汽车配件的长度要求为12厘米，高于或低于改标准均被认为是不合格 的汽车生产企业在购进配件时，通常经过招标，然后对中标的配件提供商提供的 样品进行检验，以决定是否采购，现对一个配件提供商提供的10个样本进行检验， 结果如下（单位：厘米）。
A. 由于x与y之间的线性关系引起的y的变化部分
B. 除了x对y的线性影响之外的其他因素对y变差的影响
C. 由于x与y之间的非线性关系引起的y的变化部分
D. 由于x与y之间的函数关系引起的y的变化部分
17.已知回归平方和SSR=4863，残差平方和SSE=282，则判定系数R2=（
）。
A.94.52%
的有关结果：
方差分析表
df
SS
MS
F
回归分析
残差
2196005
—
总计
19 18221598 —
—
Significance F 1.05354E-09 — —
Intercept X Variable 1
参数估计表 Coefficients 标准误差
268.5646259 127.479726 5.194491112 0.45322762
2012 年 1 月 5 日
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2011级应用时间序列分析课程试题（A卷）
合分人：
一、简述题（共30分）
1.简述投影定理。
2.简述均方收敛和Cauchy收敛准则。
3.简述(),()
AR p MA q和(,)
ARMA p q过程自相关函数和偏自相关函数的性质。
4. 写出()AR p 过程的一步预测方程、两步预测方程及其均方误差。
5.简述ARCH 和GARCH 过程的定义。
二、 判断下列过程的可逆性和因果性。
（10分） 1. 1152
t t t t X X X Z ---+= 2. 112
71
1212
t t t t t X X X Z Z ----+=-
三.计算题（20分）
设1121.20.352,(0,4)t t t t t t X X X Z Z Z WN ----+=-:，求 （1）{}t X 的自相关函数; （2）{}t X 的谱密度函数； （3）写出{}t X 的因果可逆表示式。
四．证明题。
（25分）
1. 设{}t X 是均值为0，协方差函数为()⋅γ的平稳时间序列， ||1φ<。
证明：级数 1
j
t j j X φ
∞
-=∑均方收敛。
（10分）
2. 设{}t X 是均值为0，协方差函数为()⋅γ的平稳时间序列，满足：()0q ≠γ，且
当||h q >时()0h =γ。
证明：{}t X 是一个MA(q)过程，即存在一个
{}
2(0,)t Z WN σ 使
1122.t t t t q t q X Z Z Z Z ---=+++
+θθθ （15分）
1．设math是一个时间序列，则
（1）写出对math建立一个均值为0的ARIMA(2,1,2)过程的程序。
（2）写出（1）中建立的ARIMA(2,1,2)过程向前5步预测的程序.
2.下面是某个程序运行的结果：
Call:
arima(x = math, order = c(3, 0, 0))
Coefficients:
ar1 ar2 ar3 intercept
0.64 -0.06 -0.42 2.3931
s.e. 0.14 0.17 0.14 0.0963
sigma^2 estimated as 0.1787: log likelihood = -27.09, aic = 62.18
(1)写出估计方程；
(2)说明估计系数的显著性；
(3)试写出修正的估计程序（即删除不显著的系数）。