时间序列分析试题(卷)与答案解析
8章时间序列分析练习题参考答案

8章时间序列分析练习题参考答案第⼋章时间数列分析⼀、单项选择题1.时间序列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值⼤⼩排列的C 前者是根据时间顺序排列的,后者是根据变量值⼤⼩排列的D 前者是根据变量值⼤⼩排列的,后者是根据时间顺序排列的 C2.时间序列中,数值⼤⼩与时间长短有直接关系的是( )A 平均数时间序列B 时期序列C 时点序列D 相对数时间序列 B3.发展速度属于( )A ⽐例相对数B ⽐较相对数C 动态相对数D 强度相对数 C4.计算发展速度的分母是( )A 报告期⽔平B 基期⽔平C 实际⽔平D 计划⽔平 B5.某车间⽉初⼯⼈⼈数资料如下:则该车间上半年的平均⼈数约为( )A 296⼈B 292⼈C 295 ⼈D 300⼈ C6.某地区某年9⽉末的⼈⼝数为150万⼈,10⽉末的⼈⼝数为150.2万⼈,该地区10⽉的⼈⼝平均数为( )A 150万⼈B 150.2万⼈C 150.1万⼈D ⽆法确定 C7.由⼀个9项的时间序列可以计算的环⽐发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 A8.采⽤⼏何平均法计算平均发展速度的依据是( )A 各年环⽐发展速度之积等于总速度B 各年环⽐发展速度之和等于总速度C 各年环⽐增长速度之积等于总速度D 各年环⽐增长速度之和等于总速度 A9.某企业的科技投⼊,2010年⽐2005年增长了58.6%,则该企业2006—2010年间科技投⼊的平均发展速度为( ) A5%6.58 B 5%6.158 C6%6.58 D 6%6.158B10.根据牧区每个⽉初的牲畜存栏数计算全牧区半年的牲畜平均存栏数,采⽤的公式是( ) A 简单平均法 B ⼏何平均法 C 加权序时平均法 D ⾸末折半法 D11.在测定长期趋势的⽅法中,可以形成数学模型的是( )A 时距扩⼤法B 移动平均法C 最⼩平⽅法D 季节指数法12.动态数列中,每个指标数值相加有意义的是()。
2010《时间序列分析》试卷A答案精选全文完整版

可编辑修改精选全文完整版2010—2011学年第一学期2007应用数学《时间序列分析》试卷A 答案一 (18分,每空1分)1 112211t t t t t X X X a a ϕϕθ-----=-2 偏自相关函数;自相关函数3 矩估计法、最小二乘估计法、极大似然估计法4 B51ϕ;0 6 1,1,2,i i n λ<=7 m8利用序列图进行判断;利用样本自相关函数ˆk ρ进行平稳性检验;利用单位根检验进行判断9 12222011ˆ 1.96()t l a l X G G G σ+-±+++ 10 存在 11 使得预测误差的均方値达到最小10 (1)S DB -二 (8分,每小题1分)1 错;2错;3对;4对;5 错;6 错;7 错;8对三 (12分,每小题2分)1 (1)2(10.80.5)t t X B B a =-+;(2) 21(10.5)(1 1.20.4)t t B X B B a --=-+2 (1) 稳定;(2)稳定3 (1)120.5,0.25G G ==; (2) 120.5,0G G =-=四 (4分)AR{1}(1)34321324321ˆ(1)(,,)([100.60.3],,)100.697.20.39696.12X E X X X X E X X a X X X ==+++=+⨯+⨯=;(2分)35321435321ˆ(2)(,,)([100.60.3],,)100.697.120.397.297.432X E X X X X E X X a X X X ==+++=+⨯+⨯=;(2分)36321546321ˆ(3)(,,)([100.60.3],,)100.697.4320.397.1297.5952X E X X X X E X X a X X X ==+++=+⨯+⨯= (2分)(2)010110.6G G G ϕ===221/21/2011.96() 1.966 1.3613.7144G G σ+=⨯⨯=五月份销售额的 95%的置信区间为(83.7176,111.1464) (2分)六 (50分)1 (1)AR(1)模型:10.667831t t t X X a -=+ (5分)疏系数的ARMA(1,6)模型:160.5578970.47526t t t t X X a a --=++ (5分)(2)上边AR(1)模型的AIC 值为-0.804969,第二个模型的AIC 值为-0.876542,根据AIC 准则可知,第二个模型拟合效果更好。
时间序列分析试题

第九章 时间序列分析一、单项选择题1、乘法模型是分析时间序列最常用的理论模型。
这种模型将时间序列按构成分解为( ) 等四种成分,各种成分之间( ),要测定某种成分的变动,只须从原时间序列中( )。
A. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;除去其他影响成分的变动D.长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;除去其他影响成分的变动答案:C2、加法模型是分析时间序列的一种理论模型。
这种模型将时间序列按构成分解为( )等四种成分,各种成分之间( ),要测定某种成分的变动,只须从原时间序列中( )。
A. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;减去其他影响成分的变动B. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;减去其他影响成分的变动C. 长期趋势、季节变动、循环波动和不规则波动;保持着相互依存的关系;除去其他影响成分的变动D.. 长期趋势、季节变动、循环波动和不规则波动;缺少相互作用的影响力量;除去其他影响成分的变动答案:B3、利用最小二乘法求解趋势方程最基本的数学要求是( )。
A.∑=-任意值2)ˆ(t Y Y B. ∑=-min )ˆ(2t Y Y C. ∑=-max )ˆ(2t Y Y D. 0)ˆ(2∑=-t Y Y 答案:B4、从下列趋势方程t Y t86.0125ˆ-=可以得出( )。
A. 时间每增加一个单位,Y 增加0.86个单位B. 时间每增加一个单位,Y 减少0.86个单位C. 时间每增加一个单位,Y 平均增加0.86个单位D. 时间每增加一个单位,Y 平均减少0.86个单位答案:D.5、时间序列中的发展水平( )。
时间序列期末试题及答案

时间序列期末试题及答案1. 试题考试时间:3小时考试形式:闭卷注意:请将答案写在答题纸上,不要在试卷上直接作答。
题目一:简答题(每题10分)1. 什么是时间序列分析?时间序列分析具有哪些应用领域?2. 请解释平稳时间序列的概念,并提供一个平稳时间序列的例子。
3. 什么是季节性、趋势性和周期性?请分别举一个例子。
4. 时间序列分析的步骤是什么?5. 请解释自相关函数(ACF)和偏自相关函数(PACF)的概念,并说明它们在时间序列分析中的作用。
题目二:计算题(每题20分)1. 从某超市取得了一组销售额数据,包括2004年到2019年的年度销售额。
请计算该时间序列的移动平均值,并绘制移动平均图。
2. 下表是某公司2005年到2019年每个季度的销售额数据,请利用季节性指数法预测2020年第一季度的销售额。
| 年份 | 第一季度销售额 ||-------|--------------|| 2005 | 100 || 2006 | 120 || 2007 | 140 || 2008 | 160 || 2009 | 180 || 2010 | 200 || 2011 | 220 || 2012 | 240 || 2013 | 260 || 2014 | 280 || 2015 | 300 || 2016 | 320 || 2017 | 340 || 2018 | 360 || 2019 | 380 |3. 通过对某股票每周收益率进行分析,发现其自相关系数和偏自相关系数都在95%置信区间之外。
该时间序列数据是否呈现ARCH效应?请解释原因。
4. 将某商品销售额数据建模为自回归移动平均模型(ARMA),请给出该模型的阶数,并解释原因。
2. 答案题目一:简答题1. 时间序列分析是一种研究时间相关数据的统计方法,通过对时间序列的特征进行分析,揭示其随时间变化的规律和趋势。
时间序列分析广泛应用于经济学、金融学、气象学、社会学等领域。
(完整word版)时间序列分析考试卷及答案
考核课程 时间序列分析(B 卷)考核方式 闭卷 考核时间 120 分钟注:B 为延迟算子,使得1-=t t Y BY ;∇为差分算子,1--=∇t t t Y Y Y 。
一、单项选择题(每小题3 分,共24 分。
)1。
若零均值平稳序列{}t X ,其样本ACF 和样本PACF 都呈现拖尾性,则对{}t X 可能建立( B )模型。
A. MA(2)B.ARMA(1,1) C 。
AR (2) D 。
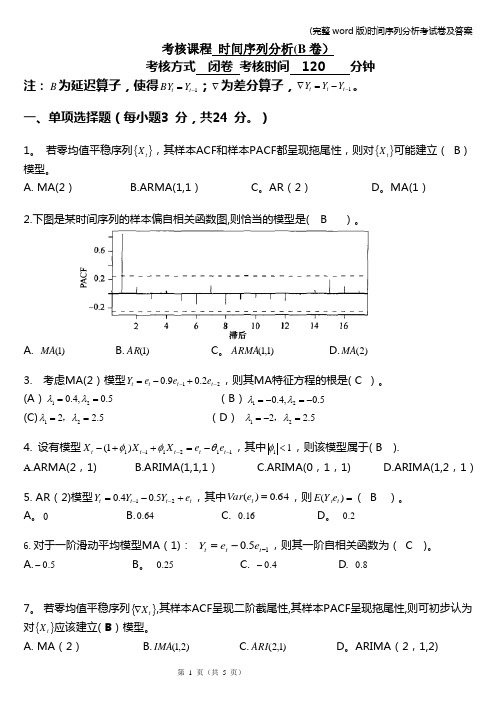
MA(1)2.下图是某时间序列的样本偏自相关函数图,则恰当的模型是( B )。
A. )1(MAB.)1(AR C 。
)1,1(ARMA D.)2(MA3. 考虑MA(2)模型212.09.0--+-=t t t t e e e Y ,则其MA 特征方程的根是( C )。
(A )5.0,4.021==λλ (B )5.0,4.021-=-=λλ (C)5.2221==λλ, (D ) 5.2221=-=λλ,4. 设有模型112111)1(----=++-t t t t t e e X X X θφφ,其中11<φ,则该模型属于( B ).A.ARMA(2,1)B.ARIMA(1,1,1)C.ARIMA(0,1,1)D.ARIMA(1,2,1)5. AR (2)模型t t t t e Y Y Y +-=--215.04.0,其中64.0)(=t e Var ,则=)(t t e Y E ( B )。
A 。
0 B.64.0 C. 16.0 D 。
2.06.对于一阶滑动平均模型MA (1): 15.0--=t t t e e Y ,则其一阶自相关函数为( C )。
A.5.0- B 。
25.0 C. 4.0- D. 8.07。
若零均值平稳序列{}t X ∇,其样本ACF 呈现二阶截尾性,其样本PACF 呈现拖尾性,则可初步认为对{}t X 应该建立( B )模型。
A. MA (2)B.)2,1(IMAC.)1,2(ARI D 。
8章-时间序列分析练习题参考答案

第八章 时间数列分析一、单项选择题1.时间序列与变量数列( )A 都是根据时间顺序排列的B 都是根据变量值大小排列的C 前者是根据时间顺序排列的,后者是根据变量值大小排列的D 前者是根据变量值大小排列的,后者是根据时间顺序排列的 C2.时间序列中,数值大小与时间长短有直接关系的是( )A 平均数时间序列B 时期序列C 时点序列D 相对数时间序列 B3.发展速度属于( )A 比例相对数B 比较相对数C 动态相对数D 强度相对数 C4.计算发展速度的分母是( )A 报告期水平B 基期水平C 实际水平D 计划水平 B5.某车间月初工人人数资料如下:则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人 C6.某地区某年9月末的人口数为150万人,10月末的人口数为150.2万人,该地区10月的人口平均数为( )A 150万人B 150.2万人C 150.1万人D 无法确定 C7.由一个9项的时间序列可以计算的环比发展速度( ) A 有8个 B 有9个 C 有10个 D 有7个 A8.采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度 A9.某企业的科技投入,2010年比2005年增长了58.6%,则该企业2006—2010年间科技投入的平均发展速度为( ) A5%6.58 B 5%6.158 C6%6.58 D 6%6.158B10.根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数,采用的公式是( ) A 简单平均法 B 几何平均法 C 加权序时平均法 D 首末折半法 D11.在测定长期趋势的方法中,可以形成数学模型的是( )A 时距扩大法B 移动平均法C 最小平方法D 季节指数法12.动态数列中,每个指标数值相加有意义的是()。
A.时期数列B.时点数列C.相对数数列D.平均数数列A13.按几何平均法计算的平均发展速度侧重于考察现象的()A.期末发展水平B.期初发展水平C.中间各项发展水平D.整个时期各发展水平的总和A14.累计增长量与其相应的各逐期增长量的关系表现为()A.累计增长量等于相应各逐期增长量之和B.累计增长量等于相应各逐期增长量之差C.累计增长量等于相应各逐期增长量之积D.累计增长量等于相应各逐期增长量之商A15.已知某地区2010年的粮食产量比2000年增长了1倍,比2005年增长了0.5倍,那么2005年粮食产量比2000年增长了()。
时间序列练习题答案

时间序列练习题答案一、选择题1. 时间序列分析中的自回归模型(AR)是指:A. 模型中的误差项B. 模型预测值依赖于自身过去的值C. 模型预测值依赖于其他变量的值D. 模型预测值依赖于未来的值2. 移动平均模型(MA)的主要特征是:A. 预测值依赖于过去的误差项B. 预测值依赖于过去的观测值C. 预测值依赖于未来的误差项D. 预测值依赖于未来的观测值3. 以下哪个不是时间序列分析中的平稳性检验方法?A. 单位根检验B. 协整检验C. KPSS检验D. 方差比检验4. 时间序列的差分操作通常用于:A. 消除季节性效应B. 消除趋势C. 消除周期性变化D. 消除随机波动5. 季节性调整的目的是:A. 消除随机波动B. 消除季节性效应C. 消除长期趋势D. 消除周期性变化二、简答题1. 简述自回归积分滑动平均模型(ARIMA)的基本组成部分。
2. 解释什么是时间序列的平稳性,并说明为什么在时间序列分析中需要考虑平稳性。
3. 描述季节性时间序列的特点,并说明如何识别和处理季节性效应。
三、计算题1. 给定以下时间序列数据:\[ y_t = \{10, 15, 20, 25, 30, 35, 40, 45, 50, 55\} \] 假设这是一个一阶自回归模型AR(1),其中自回归系数φ=0.8。
请计算下一个时间点的预测值。
2. 假设一个时间序列模型的ACF(自相关函数)在滞后1时显著不为0,而在滞后2及以后时显著为0。
根据这个信息,推测该时间序列可能属于哪种类型的模型?四、案例分析题1. 某公司销售数据呈现明显的季节性变化,如何在时间序列分析中对数据进行季节性调整?2. 一个时间序列模型的ADF(Augmented Dickey-Fuller)检验结果表明存在单位根,这意味着什么?如何对数据进行处理以消除单位根?五、论述题1. 论述时间序列分析在金融领域中的应用,并举例说明。
2. 讨论时间序列分析中的因果关系检验方法,并说明在实际应用中如何选择合适的方法。
(完整word版)《时间序列》试卷

《时间序列分析》试卷注意:请将答案直接写在试卷上一、填空题(1分*20空=20分)1. 德国药剂师、业余天文学家施瓦尔发现太阳黑子的活动具有11年周期依靠的是 时序分析方法。
2. 时间序列预处理包括 和 。
3. 平稳时间序列有两种定义,根据限制条件的严格程度,分为和 。
使用序列的特征统计量来定义的平稳性属于 。
4. 统计时序分析方法分为 和 。
5. 为了判断一个平稳的序列中是否含有信息,即是否可以继续分析,需对该序列进行 检验,该检验用到的统计量服从 分布;原假设和备择假设分别是 和 。
6. 图1为2000年1月——2007年12月中国社会消费品零售总额时间序列图,据此判断,该序列{}t X 是否平稳(填“是”或者“否”) ;要使其平稳化,应该对原序列进行 和 差分处理。
用Eviews 软件对该序列做差分运算的表达式是 。
7. ARIMA 模型的实质 是和的结合。
8. 差分运算的实质是使用的方式提取确定性信息。
9. 用延迟算子表示中心化的AR(P)模型是 。
二、不定项选择题(下列每小题至少有一个答案是正确的,请将正确答班级 姓名 学号50010001500200025003000350040009394959697989900图1案代码填入相应括号内,2分*5题=10分)1.下列属于白噪声序列{}t ε所满足的条件的是( )A. 任取T t ∈,有με=)(t E (μ为常数)B. 任取T t ∈,有0)(=t E εC.)(0),(s t Cov s t ≠∀=εεD. 2)(εσε=t Var (2εσ为常数) 2.使用n 期中心移动平均法对序列{}t x 进行平滑时,下列表达式正确的是( )A.n x x x x x n x n t n t t n t n t t ),(1~2112112121-+--++----++++++=ΛΛ为奇数;B. n x x x x x n x n t n t t n t n t t ),(1~212122+-++--++++++=ΛΛ为偶数;C. )(1~11+--+++=n t t t t x x x n x Λ; D. n x x x x x n x n t n t t n t n t t ),2121(1~212122+-++--++++++=ΛΛ为偶数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间序列分析试卷1一、 填空题(每小题2分,共计20分)1. ARMA(p, q)模型_________________________________,其中模型参数为____________________。
2. 设时间序列{}t X ,则其一阶差分为_________________________。
3. 设ARMA (2, 1):1210.50.40.3t t t t t X X X εε---=++-则所对应的特征方程为_______________________。
4. 对于一阶自回归模型AR(1): 110t t t X X φε-=++,其特征根为_________,平稳域是_______________________。
5. 设ARMA(2, 1):1210.50.1t t t t t X X aX εε---=++-,当a 满足_________时,模型平稳。
6. 对于一阶自回归模型MA(1):10.3t t t X εε-=-,其自相关函数为______________________。
7. 对于二阶自回归模型AR(2):120.50.2t t t t X X X ε--=++则模型所满足的Yule-Walker 方程是______________________。
8. 设时间序列{}t X 为来自ARMA(p,q)模型:1111t t p t p t t q t q X X X φφεθεθε----=++++++则预测方差为___________________。
9. 对于时间序列{}t X ,如果___________________,则()~t X I d 。
10. 设时间序列{}t X 为来自GARCH(p ,q)模型,则其模型结构可写为_____________。
二、(10分)设时间序列{}t X 来自()2,1ARMA 过程,满足()()210.510.4ttB B X B ε-+=+,其中{}t ε是白噪声序列,并且()()2t t 0,E Var εεσ==。
(1) 判断()2,1ARMA 模型的平稳性。
(5分)(2) 利用递推法计算前三个格林函数012,,G G G 。
(5分)三、(20分)某国1961年1月—2002年8月的16~19岁失业女性的月度数据经过一阶差分后平稳(N =500),经过计算样本其样本自相关系数ˆ{}k ρ及样本偏相关系数ˆ{}kkφ的前10个数值如下表(1) 利用所学知识,对}{t X 所属的模型进行初步的模型识别。
(10分) (2) 对所识别的模型参数和白噪声方差2σ给出其矩估计。
(10分) 四、(20分)设}{t X 服从ARMA(1, 1)模型:110.80.6t t t t X X εε--=+-其中1001000.3,0.01X ε==。
(1) 给出未来3期的预测值;(10分)(2) 给出未来3期的预测值的95%的预测区间(0.975 1.96u =)。
(10分) 五、(10分)设时间序列}{t X 服从AR(1)模型:1t t t X X φε-=+,其中{}t ε为白噪声序列,()()2t t 0,E Var εεσ==,1212,()x x x x ≠为来自上述模型的样本观测值,试求模型参数2,φσ的极大似然估计。
六、(20分)证明下列两题:(1) 设时间序列{}t x 来自()1,1ARMA 过程,满足110.50.25t t t t x x εε---=-,其中()2t ~0,WN εσ, 证明其自相关系数为11,00.2710.52k k k k k ρρ-=⎧⎪==⎨⎪≥⎩(10分) (2) 若t X ~I(0),t Y ~I(0),且{}t X 和{}t Y 不相关,即(,)0,,r s cov X Y r s =∀。
试证明对于任意非零实数a 与b ,有~(0)t t t Z aX bY I =+。
(10分)时间序列分析试卷2七、填空题(每小题2分,共计20分)1. 设时间序列{}t X ,当__________________________序列{}t X 为严平稳。
2. AR(p)模型为_____________________________,其中自回归参数为______________。
3. ARMA(p,q)模型_________________________________,其中模型参数为____________________。
4. 设时间序列{}t X ,则其一阶差分为_________________________。
5. 一阶自回归模型AR(1)所对应的特征方程为_______________________。
6. 对于一阶自回归模型AR(1),其特征根为_________,平稳域是_______________________。
7. 对于一阶自回归模型MA(1),其自相关函数为______________________。
8. 对于二阶自回归模型AR(2):1122t t t t X X X φφε--=++,其模型所满足的Y ule-Walker 方程是___________________________。
9. 设时间序列{}t X 为来自ARMA(p,q)模型:1111t t p t p t t q t qX X X φφεθεθε----=++++++,则预测方差为___________________。
10. 设时间序列{}t X 为来自GARCH(p, q)模型,则其模型结构可写为_____________。
八、(20分)设{}t X 是二阶移动平均模型MA(2),即满足t t t-2X εθε=+,其中{}t ε是白噪声序列,并且()()2t 0,t E Varεεσ== (1) 当1θ=0.8时,试求{}t X 的自协方差函数和自相关函数。
(2) 当1θ=0.8时,计算样本均值1234(X X X X )4+++的方差。
九、(20分)设}{t X 的长度为10的样本值为0.8,0.2,0.9,0.74,0.82,0.92,0.78,0.86,0.72,0.84,试求(1) 样本均值x 。
(2) 样本的自协方差函数值21ˆ,ˆγγ和自相关函数值21ˆ,ˆρρ。
(3) 对AR(2)模型参数给出其矩估计,并且写出模型的表达式。
十、(20分)设}{t X 服从ARMA(1, 1)模型:110.80.6t t t t X X εε--=+-其中1001000.3,0.01X ε==。
(1) 给出未来3期的预测值;(2) 给出未来3期的预测值的95%的预测区间。
十一、 (20分)设平稳时间序列}{t X 服从AR(1)模型:11t t t X X φε-=+,其中{}t ε为白噪声,()()2t 0,t E Var εεσ==,证明:221()1t Var X σφ=-时间序列分析试卷3十二、 单项选择题(每小题4分,共计20分)11. t X 的d 阶差分为(a )=d t t t k X X X -∇- (b )11=d d d t t t k X X X ---∇∇-∇ (c )111=d d d t t t X X X ---∇∇-∇ (d )11-12=d d d t t t X X X ---∇∇-∇12. 记B 是延迟算子,则下列错误的是(a )01B = (b )()1=t t t B c X c BX c X -⋅⋅=⋅ (c )()11=t t t t B X Y X Y --±± (d )()=1ddt t d t X X B X -∇-=-13. 关于差分方程1244t t t X X X --=-,其通解形式为(a )1222t t c c + (b )()122tc c t +(c )()122tc c - (d )2tc ⋅14. 下列哪些不是MA 模型的统计性质(a )()t E X μ= (b )()()22111q t Var X θθσ=+++(c )()(),,0t t t E X E με∀≠≠ (d )1,,0q θθ≠15. 上面左图为自相关系数,右图为偏自相关系数,由此给出初步的模型识别(a )MA (1) (b )ARMA (1, 1) (c )AR (2) (d )ARMA (2, 1)十三、 填空题(每小题2分,共计20分)1. 在下列表中填上选择的的模型类别得分2. 时间序列模型建立后,将要对模型进行显著性检验,那么检验的对象为___________,检验的假设是___________。
3. 时间序列模型参数的显著性检验的目的是____________________。
4. 根据下表,利用AIC 和BIC 准则评判两个模型的相对优劣,你认为______模型优于______模型。
_______检验和_______检验。
十四、 (10分)设{}t ε为正态白噪声序列,()()2t t 0,E Var εεσ==,时间序列}{t X 来自110.8t t t t X X εε--=+-问模型是否平稳?为什么? 十五、 (20分)设}{t X 服从ARMA(1, 1)模型:110.80.6t t t t X X εε--=+-其中1001000.3,0.01X ε==。
(3) 给出未来3期的预测值;(10分)(4) 给出未来3期的预测值的95%的预测区间(0.975 1.96u =)。
(10分) 十六、 (20分)下列样本的自相关系数和偏自相关系数是基于零均值的平稳序列样本量为500计算得到的(样本方差为2.997)ACF: 0:340; 0:321; 0:370; 0:106; 0:139; 0:171; 0:081; 0:049; 0:124; 0:088; 0:009; 0:077 PACF: 0:340; 0:494; 0:058; 0:086; 0:040; 0:008; 0:063; 0:025; 0:030; 0:032; 0:038; 0:030根据所给的信息,给出模型的初步确定,并且根据自己得到的模型给出相应的参数估计,要求写出计算过程。
得分得分得分1121t t t t X X X ααε--=++其中{}t ε为正态白噪声序列,()()2t t 0,E Var εεσ==,假设模型是平稳的,证明其偏自相关系数满足223kk k k αφ=⎧=⎨≥⎩。
