2020届江苏省苏锡常镇四市2017级高三一调考试数学试题(含附加题)及答案
【数学】江苏省苏锡常镇四市2020届高三第一次教学情况调研试题(解析版)

【解析】由题意,可得所得到的几何体是由一个圆柱挖去两个半球而成;其中,圆柱的底面半径为1,母线长为2;体积为 ;两个半球的半径都为1,则两个半球的体积为 ;则所求几何体的体积为
.
12.在△ABC中,( )⊥ ( >1),若角A的最大值为 ,则实数 的值是_______.
【答案】3
【解析】
,解得 =3.
故答案为:3.
13.若函数 (a>0且a≠1)在定义域[m,n]上的值域是[m2,n2](1<m<n),则a的取值范围是_______.
【答案】(1, )
【解析】由题意知: 与 的图像在(1, )上恰有两个交点
考查临界情形: 与 切于 ,
.
故答案为: .
14.如图,在△ABC中,AB=4,D是AB的中点,E在边AC上,AE=2EC,CD与BE交于点O,若OB= OC,则△ABC面积的最大值为_______.
(1)求A;
(2)已知a=2 ,B= ,求△ABC的面积.
解:(1)∵bcosA﹣ asinB=0.
∴由正弦定理可得:sinBcosA﹣ sinAsinB=0,
∵sinB>0,
∴cosA= sinA,
∴tanA= ,
∵A∈(0,π),
∴A= ;
(2)∵a=2 ,B= ,A= ,
∴C= ,根据正弦定理得到
【解析】由题意A B中有且只有一个元素,所以 ,即 .
故答案为: .
3.已知一组数据1.6,1.8,2,2.2,2.4,则该组数据的方差是_______.
【答案】0.08
【解析】首先求得 ,
.ቤተ መጻሕፍቲ ባይዱ
故答案为:0.08.
4.在平面直角坐标系xOy中,已知双曲线 (a>0)的一条渐近线方程为 ,则a=_______.
江苏省苏锡常镇四市2020届高三数学第一次教学情况调研试卷
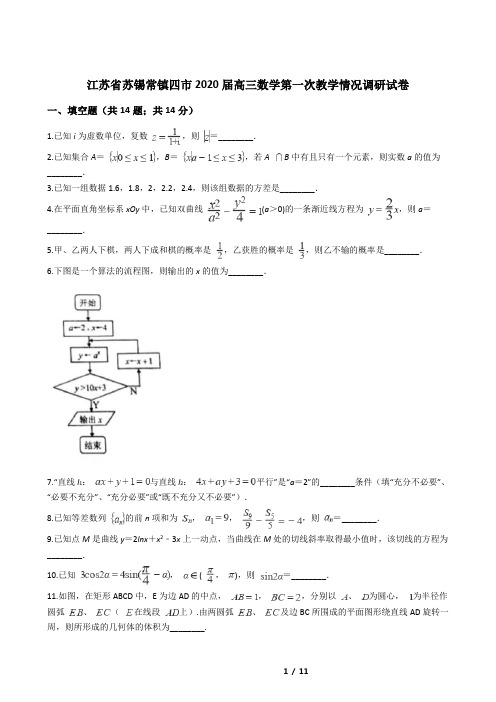
江苏省苏锡常镇四市2020届高三数学第一次教学情况调研试卷一、填空题(共14题;共14分)1.已知i为虚数单位,复数,则=________.2.已知集合A=,B=,若A B中有且只有一个元素,则实数a的值为________.3.已知一组数据1.6,1.8,2,2.2,2.4,则该组数据的方差是________.4.在平面直角坐标系xOy中,已知双曲线(a>0)的一条渐近线方程为,则a=________.5.甲、乙两人下棋,两人下成和棋的概率是,乙获胜的概率是,则乙不输的概率是________.6.下图是一个算法的流程图,则输出的x的值为________.7.“直线l1:与直线l2:平行”是“a=2”的________条件(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分又不必要”).8.已知等差数列的前n项和为,,,则=________.9.已知点M是曲线y=2lnx+x2﹣3x上一动点,当曲线在M处的切线斜率取得最小值时,该切线的方程为________.10.已知,( ,),则=________.11.如图,在矩形ABCD中,E为边AD的中点,,,分别以、为圆心,为半径作圆弧、(在线段上).由两圆弧、及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的体积为________.12.在△ABC中,( )⊥( >1),若角A的最大值为,则实数的值是________.13.若函数(a>0且a≠1)在定义域[m,n]上的值域是[m2,n2](1<m<n),则a的取值范围是________.14.如图,在△ABC中,AB=4,D是AB的中点,E在边AC上,AE=2EC,CD与BE交于点O,若OB=OC,则△ABC面积的最大值为________.二、解答题(共11题;共100分)15.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足bcosA﹣asinB=0.(1)求A;(2)已知a=2 ,B=,求△ABC的面积.16.如图,在四棱锥P—ABCD中,四边形ABCD为平行四边形,BD⊥DC,△PCD为正三角形,平面PCD⊥平面ABCD,E为PC的中点.(1)证明:AP∥平面EBD;(2)证明:BE⊥PC.17.某地为改善旅游环境进行景点改造.如图,将两条平行观光道l1和l2通过一段抛物线形状的栈道AB连通(道路不计宽度),l1和l2所在直线的距离为0.5(百米),对岸堤岸线l3平行于观光道且与l2相距1.5(百米)(其中A为抛物线的顶点,抛物线的对称轴垂直于l3,且交l3于M),在堤岸线l3上的E,F两处建造建筑物,其中E,F到M的距离为1 (百米),且F恰在B的正对岸(即BF⊥l3).(1)在图②中建立适当的平面直角坐标系,并求栈道AB的方程;(2)游客(视为点P)在栈道AB的何处时,观测EF的视角(∠EPF)最大?请在(1)的坐标系中,写出观测点P的坐标.18.如图,在平面直角坐标系xOy中,已知椭圆C:(a>b>0)的离心率为.且经过点(1,),A,B分别为椭圆C的左、右顶点,过左焦点F的直线l交椭圆C于D,E两点(其中D在x轴上方).(1)求椭圆C的标准方程;(2)若△AEF与△BDF的面积之比为1:7,求直线l的方程.19.已知函数(m R)的导函数为.(1)若函数存在极值,求m的取值范围;(2)设函数(其中e为自然对数的底数),对任意m R,若关于x的不等式在(0,)上恒成立,求正整数k的取值集合.20.已知数列,,数列满足,n.(1)若,,求数列的前2n项和;(2)若数列为等差数列,且对任意n,恒成立.①当数列为等差数列时,求证:数列,的公差相等;②数列能否为等比数列?若能,请写出所有满足条件的数列;若不能,请说明理由.21.已知矩阵,且二阶矩阵M满足AM=B,求M的特征值及属于各特征值的一个特征向量.22.在平面直角坐标系xOy中,曲线l的参数方程为(为参数),以原点O为极点,x轴非负半轴为极轴建立极坐标系,曲线C的极坐标方程为r=4sin q.(1)求曲线C的普通方程;(2)求曲线l和曲线C的公共点的极坐标.23.已知正数x,y,z满足x+y+z=t(t为常数),且的最小值为,求实数t的值.24.某商店举行促销反馈活动,顾客购物每满200元,有一次抽奖机会(即满200元可以抽奖一次,满400元可以抽奖两次,依次类推).抽奖的规则如下:在一个不透明口袋中装有编号分别为1,2,3,4,5的5个完全相同的小球,顾客每次从口袋中摸出一个小球,共摸三次,每次摸出的小球均不放回口袋,若摸得的小球编号一次比一次大(如1,2,5),则获得一等奖,奖金40元;若摸得的小球编号一次比一次小(如5,3,1),则获得二等奖,奖金20元;其余情况获得三等奖,奖金10元.(1)某人抽奖一次,求其获奖金额X的概率分布和数学期望;(2)赵四购物恰好满600元,假设他不放弃每次抽奖机会,求他获得的奖金恰好为60元的概率.25.已知抛物线C:x2=4py(p为大于2的质数)的焦点为F,过点F且斜率为k(k¹0)的直线交C于A,B 两点,线段AB的垂直平分线交y轴于点E,抛物线C在点A,B处的切线相交于点G.记四边形AEBG 的面积为S.(1)求点G的轨迹方程;(2)当点G的横坐标为整数时,S是否为整数?若是,请求出所有满足条件的S的值;若不是,请说明理由.答案解析部分一、填空题1.【答案】2.【答案】23.【答案】0.084.【答案】35.【答案】6.【答案】67.【答案】必要不充分8.【答案】-2n+19.【答案】y=x-310.【答案】11.【答案】12.【答案】313.【答案】(1,)14.【答案】二、解答题15.【答案】(1)解:∵b cos A﹣a sin B=0.∴由正弦定理可得:sin B cos A﹣sin A sin B=0,∵sin B>0,∴cos A=sin A,∴tan A=,∵A∈(0,π),∴A=(2)解:∵a=2 ,B=,A=,∴C=,根据正弦定理得到∴b=6,∴S△ABC=ab==616.【答案】(1)证明:连结AC交BD于点O,连结OE因为四边形ABCD为平行四边形∴O为AC中点,又E为PC中点,故AP∥OE,又AP平面EBD,OE平面EBD所以AP∥平面EBD(2)证明:∵△PCD为正三角形,E为PC中点所以PC⊥DE因为平面PCD⊥平面ABCD,平面PCD平面ABCD=CD,又BD平面ABCD,BD⊥CD∴BD⊥平面PCD又PC平面PCD,故PC⊥BD又BD DE=D,BD平面BDE,DE平面BDE故PC⊥平面BDE又BE平面BDE,所以BE⊥PC17.【答案】(1)解:以A为原点,l1为x轴,抛物线的对称轴为y轴建系由题意知:B(1,0.5),设抛物线方程为代入点B得:p=1,故方程为,x[0,1](2)解:设P( ,),t[0,],作PQ⊥l3于Q,记∠EPQ=,∠FPQ=,,令,,则:,当且仅当即,即,即时取等号;故P( ,)时视角∠EPF最大,答:P( ,)时,视角∠EPF最大18.【答案】(1)解:设焦距为2c,由题意知:;解得,所以椭圆的方程为(2)解:由(1)知:F(﹣1,0),设l:,D( ,),E( ,),<0<①,,,②;③;由①②得:,,代入③得:,又,故,因此,直线l的方程为19.【答案】(1)解:因为,所以,所以,则,由题意可知,解得(2)解:由(1)可知,,所以因为整理得,设,则,所以单调递增,又因为,所以存在,使得,设,是关于开口向上的二次函数,则,设,则,令,则,所以单调递增,因为,所以存在,使得,即,当时,,当时,,所以在上单调递减,在上单调递增,所以,因为,所以,又由题意可知,所以,解得,所以正整数k的取值集合为{1,2}20.【答案】(1)解:因为,,所以,且,由题意可知,数列是以1为首项,2为公差的等差数列,数列是首项和公比均为4的等比数列,所以(2)解:①证明:设数列的公差为,数列的公差为,当n为奇数时,,若,则当时,,即,与题意不符,所以,当n为偶数时,,,若,则当时,,即,与题意不符,所以,综上,,原命题得证;②假设可以为等比数列,设公比为q,因为,所以,所以,,因为当时,,所以当n为偶数,且时,,即当n为偶数,且时,不成立,与题意矛盾,所以数列不能为等比数列21.【答案】解:设矩阵M=,则AM=,所以,解得,所以M=,则矩阵M的特征方程为,解得,即特征值为1,设特征值的特征向量为,则,即,解得x=0,所以属于特征值的的一个特征向量为22.【答案】(1)解:∵曲线C的极坐标方程为,∴,则,即(2)解:,∴,联立可得,(舍)或,公共点( ,3),化为极坐标(2 ,)23.【答案】解:因为即,当且仅当,,时,上述等号成立,所以,即,又x,y,z>0,所以x+y+z=t=424.【答案】(1)解:由题意知,随机变量X的可能取值为10,20,40且,,所以,即随机变量X的概率分布为X10 20 40P所以随机变量X的数学期望(2)解:由题意知,赵四有三次抽奖机会,设恰好获得60元为事件A,因为60=20×3=40+10+10,所以25.【答案】(1)解:设,则,抛物线C的方程可化为,则,所以曲线C在点A处的切线方程为,在点B处的切线方程为,因为两切线均过点G,所以,所以A,B两点均在直线上,所以直线AB的方程为,又因为直线AB过点F(0,p),所以,即G点轨迹方程为(2)解:设点G( ,),由(1)可知,直线AB的方程为,即,将直线AB的方程与抛物线联立,,整理得,所以,,解得,因为直线AB的斜率,所以,且,线段AB的中点为M ,所以直线EM的方程为:,所以E点坐标为(0,),直线AB的方程整理得,则G到AB的距离,则E到AB的距离,所以,设,因为p是质数,且为整数,所以或,当时,,是无理数,不符题意,当时,,因为当时,,即是无理数,所以不符题意,当时,是无理数,不符题意,综上,当G点横坐标为整数时,S不是整数.11 / 11。
2020届江苏省苏锡常镇四市高三第一次教学情况调研数学试题(带答案解析)
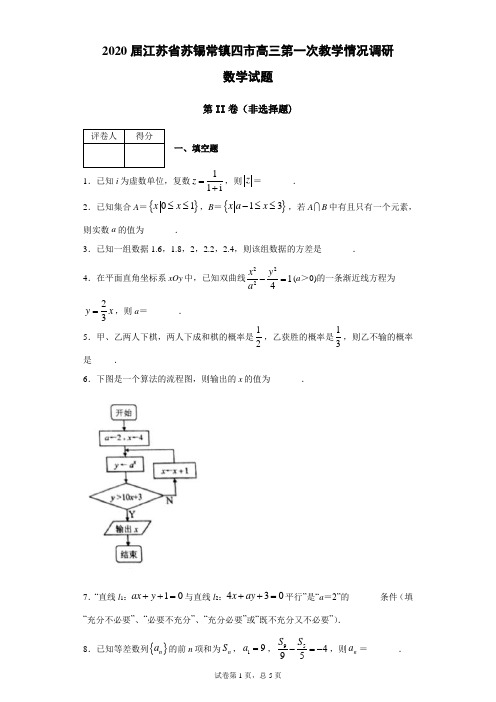
(2)赵四购物恰好满600元,假设他不放弃每次抽奖机会,求他获得的奖金恰好为60元的概率.
25.已知抛物线C:x24py(p为大于2的质数)的焦点为F,过点F且斜率为k(k0)的直线交C于A,B两点,线段AB的垂直平分线交y轴于点E,抛物线C在点A,B处的切线相交于点G.记四边形AEBG的面积为S.
评卷人
得分
二、解答题
15.在ቤተ መጻሕፍቲ ባይዱABC中,角A,B,C所对的边分别为a,b,c,且满足bcosA﹣ asinB=0.
(1)求A;
(2)已知a=2 ,B= ,求△ABC的面积.
16.如图,在四棱锥P—ABCD中,四边形ABCD为平行四边形,BD⊥DC,△PCD为正三角形,平面PCD⊥平面ABCD,E为PC的中点.
2020届江苏省苏锡常镇四市高三第一次教学情况调研
数学试题
第II卷(非选择题)
评卷人
得分
一、填空题
1.已知i为虚数单位,复数 ,则 =_______.
2.已知集合A= ,B= ,若A B中有且只有一个元素,则实数a的值为_______.
3.已知一组数据1.6,1.8,2,2.2,2.4,则该组数据的方差是_______.
(1)求椭圆C的标准方程;
(2)若△AEF与△BDF的面积之比为1:7,求直线l的方程.
19.已知函数 (m R)的导函数为 .
(1)若函数 存在极值,求m的取值范围;
(2)设函数 (其中e为自然对数的底数),对任意m R,若关于x的不等式 在(0, )上恒成立,求正整数k的取值集合.
20.已知数列 , ,数列 满足 ,n .
(1)若 , ,求数列 的前2n项和 ;
苏锡常镇四市2017年高考数学一模试卷 含解析

2017年江苏省苏锡常镇四市高考数学一模试卷一.填空题:本大題共14小败,每小題5分,共70分。
不需要写出解答过程1.已知集合U={1,2,3,4,5,6,7},M={x|x2﹣6x+5≤0,x∈Z},则∁U M= .2.若复数z满足z+i=,其中i为虚数单位,则|z|= .3.函数f(x)=的定义域为.4.如图是给出的一种算法,则该算法输出的结果是5.某高级中学共有900名学生,现用分层抽样的方法从该校学生中抽取1个容量为45的样本,其中高一年级抽20人,高三年级抽10人,则该校高二年级学生人数为.6.已知正四棱锥的底面边长是2,侧棱长是,则该正四棱锥的体积为.7.从集合{1,2,3,4}中任取两个不同的数,则这两个数的和为3的倍数的槪率为.8.在平面直角坐标系xOy中,已知抛物线y2=8x的焦点恰好是双曲线﹣=l的右焦点,则双曲线的离心率为.9.设等比数列{a n}的前n项和为S n,若S3,S9,S6成等差数列.且a2+a5=4,则a8的值为.10.在平面直角坐标系xOy中,过点M(1,0)的直线l与圆x2+y2=5交于A,B两点,其中A点在第一象限,且=2,则直线l的方程为.11.在△ABC中,已知AB=1,AC=2,∠A=60°,若点P满足=+,且•=1,则实数λ的值为.12.已知sinα=3sin(α+),则tan(α+)= .13.若函数f(x)=,则函数y=|f(x)|﹣的零点个数为.14.若正数x,y满足15x﹣y=22,则x3+y3﹣x2﹣y2的最小值为.二.解答题:本大题共6小题,共计90分15.(14分)在△ABC中,a,b,c分别为角A,B,C的对边.若acosB=3,bcosA=l,且A﹣B=(1)求边c的长;(2)求角B的大小.16.(14分)如图,在斜三梭柱ABC﹣A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1(1)求证:E是AB中点;(2)若AC1⊥A1B,求证:AC1⊥BC.17.(14分)某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)•高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l.(1)请将l表示成关于α的函数l=f(α);(2)问当α为何值时l最小?并求最小值.18.(16分)在平面直角坐标系xOy中,已知椭圆+=l (a>b >0)的焦距为2,离心率为,椭圆的右顶点为A.(1)求该椭圆的方程:(2)过点D(,﹣)作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的斜率之和为定值.。
江苏省苏锡常镇四市2020~2021学年度第二学期高三一模数学试卷(含答案)

A.辛酉年
B.辛戊年
C.壬酉年
D.壬戊年
1/15
【答案】A 【考点】文化题:等差数列的应用 【解析】由题意天干是公差为 10 的等差数列,地支为公差为 12 的等差数列,则 100 年前可 得到为辛酉年,故答案选 A. 4.(3-2x)(x+1)5 式中 x3 的系数为 A.错误!未定义书签。-15 B.-10 C.10 错误!未定义书签。D.15 【答案】C 【考点】二项式定理展开式的应用
9.函数 f (x) = sin 2x + π ,则
4
A.函数 y=f(x)的图象可由函数 y=sin2x 的图象向右平移 π4个单位得到 B.函数 y=f(x)的图象关于直线 x=π8轴对称
2/6
C.函数 y=f(x)的图象关于点 (-π8,0)中心对称
D.函数 y=x2+f(x)在 0,π 上为增函数 8
A.辛酉年
B.辛戊年
C.壬酉年
D.壬戊年
4.(3-2x)(x+1)5 式中 x3 的系数为
A.错误!未定义书签。-15 B.-10 C.10 错误!未定义书签。D.15
( ) 5.函数 f (x) = sin x ln x2 +1 − x 的图象大致是
1/6
6.过抛物线 y2=2x上一点 P 作圆 C:x2 + (y − 6)2 = 1的切线,切点为 A,B,则当四边形
(2)设数列{an}的前 n 项和为 Sn ,证明:数列{sn}中的任意连续三项按适当顺序排列后,可
以成等差数列.
4/6
19.(12 分) 如图,在四棱锥 P-ABCD 中,△PAD 是以 AD 为斜边的等腰直角三角形,BC//AD,AB⊥ AD,AD=2AB=2BC=2,PC= 2,E 为 PD 的中点. (1)求直线 PB 与平面 PAC 所成角的正弦值; (2)设 F 是 BE 的中点,判断点 F 是否在平面 PAC 内,并请证明你的结论.
2020届江苏省苏锡常镇四市高三第一次教学情况调研数学试题(学生版)

2019—2020学年度苏、锡、常、镇四市高三教学情况调查(一)数学I一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上.)1.已知i 为虚数单位,复数11i z =+,则z =_______.2.已知集合A ={}01x x ≤≤,B ={}13x a x -≤≤,若A I B 中有且只有一个元素,则实数a 的值为_______.3.已知一组数据1.6,1.8,2,2.2,2.4,则该组数据的方差是_______.4.在平面直角坐标系xOy 中,已知双曲线22214x y a -=(a >0)的一条渐近线方程为23y x =,则a =_______. 5.甲、乙两人下棋,两人下成和棋的概率是12,乙获胜的概率是13,则乙不输的概率是_____. 6.下图是一个算法的流程图,则输出的x 的值为_______.7.“直线l 1:10ax y ++=与直线l 2:430x ay ++=平行”是“a =2”的_______条件(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分又不必要”).8.已知等差数列{}n a 的前n 项和为n S ,19a =,95495S S -=-,则n a =_______. 9.已知点M 是曲线y =2lnx +x 2﹣3x 上一动点,当曲线在M 处的切线斜率取得最小值时,该切线的方程为_______.10.已知3cos 24sin()4παα=-,α∈(4π,π),则sin 2α=_______.11.如图,在矩形中,为边的中点,1AB =,2BC =,分别以A 、D 为圆心,1为半径作圆弧EB 、EC (在线段AD 上).由两圆弧EB 、EC 及边所围成的平面图形绕直线旋转一周,则所形成的几何体的体积为 .12.在△ABC 中,(AB AC λ-u u u r u u u r )⊥BC uuu r (λ>1),若角A 的最大值为6π,则实数λ的值是_______. 13.若函数()x f x a =(a >0且a ≠1)在定义域[m ,n ]上的值域是[m 2,n 2](1<m <n ),则a 的取值范围是_______.14.如图,在△ABC 中,AB =4,D 是AB 的中点,E 在边AC 上,AE =2EC ,CD 与BE 交于点O ,若OB =2OC ,则△ABC 面积的最大值为_______.二、解答题(本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.)15.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且满足bcosA 3=0.(1)求A ;(2)已知a =3B =3π,求△ABC 的面积. 16.如图,在四棱锥P —ABCD 中,四边形ABCD 为平行四边形,BD ⊥DC ,△PCD 为正三角形,平面PCD ⊥平面ABCD ,E 为PC 的中点.(1)证明:AP ∥平面EBD ;(2)证明:BE ⊥PC .17.某地为改善旅游环境进行景点改造.如图,将两条平行观光道l 1和l 2通过一段抛物线形状的栈道AB 连通(道路不计宽度),l 1和l 2所在直线的距离为0.5(百米),对岸堤岸线l 3平行于观光道且与l 2相距1.5(百米)(其中A 为抛物线的顶点,抛物线的对称轴垂直于l 3,且交l 3于M ),在堤岸线l 3上的E ,F 两处建造建筑物,其中E ,F 到M 的距离为1 (百米),且F 恰在B 的正对岸(即BF ⊥l 3).(1)在图②中建立适当的平面直角坐标系,并求栈道AB 的方程;(2)游客(视为点P )在栈道AB 的何处时,观测EF 的视角(∠EPF )最大?请在(1)的坐标系中,写出观测点P 的坐标.18.如图,在平面直角坐标系xOy 中,已知椭圆C :22221x y a b+=(a >b >0)的离心率为12.且经过点(1,32),A ,B 分别为椭圆C 的左、右顶点,过左焦点F 的直线l 交椭圆C 于D ,E 两点(其中D 在x 轴上方).(1)求椭圆C 的标准方程;(2)若△AEF 与△BDF 的面积之比为1:7,求直线l 的方程.19.已知函数3222()3f x x mx m x =-+(m ∈R )的导函数为()f x '. (1)若函数()()()g x f x f x =-'存在极值,求m 的取值范围;(2)设函数()(e )(ln )x h x f f x ='+'(其中e 为自然对数的底数),对任意m ∈R ,若关于x 的不等式22()h x m k ≥+在(0,+∞)上恒成立,求正整数k 的取值集合.20.已知数列{}n a ,{}n b ,数列{}n c 满足n n n a n c b n ⎧=⎨⎩,为奇数,为偶数,n N *∈.(1)若n a n =,2n n b =,求数列{}n c 的前2n 项和2n T ;(2)若数列{}n a 为等差数列,且对任意n N *∈,1n n c c +>恒成立.①当数列{}n b 为等差数列时,求证:数列{}n a ,{}n b 的公差相等;②数列{}n b 能否为等比数列?若能,请写出所有满足条件的数列{}n b ;若不能,请说明理由.第II 卷(附加题,共40分)【选做题】本题包括三小题,请选定其中两题作答,每小题10分共计20分,解答时应写出文字说明,证明过程或演算步骤.选修4—2:矩阵与变换21.已知矩阵1323,2111A B -⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦,且二阶矩阵M 满足AM =B ,求M 的特征值及属于各特征值的一个特征向量.选修4—4:坐标系与参数方程22.在平面直角坐标系xOy 中,曲线l的参数方程为22cos 2x y θθ=+⎧⎪⎨=⎪⎩(θ为参数),以原点O 为极点,x 轴非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=4sin θ.(1)求曲线C 的普通方程;(2)求曲线l 和曲线C 公共点的极坐标.选修4—5:不等式选讲23.已知正数x ,y ,z 满足x +y +z =t (t 为常数),且22249x y z ++的最小值为87,求实数t 的值.【必做题】第22题、第23题,每题10分,共计20分,解答时应写出文字说明,证明过程或演算步骤.24.某商店举行促销反馈活动,顾客购物每满200元,有一次抽奖机会(即满200元可以抽奖一次,满400元可以抽奖两次,依次类推).抽奖的规则如下:在一个不透明口袋中装有编号分别为1,2,3,4,5的5个完全相同的小球,顾客每次从口袋中摸出一个小球,共摸三次,每次摸出的小球均不放回口袋,若摸得的小球编号一次比一次大(如1,2,5),则获得一等奖,奖金40元;若摸得的小球编号一次比一次小(如5,3,1),则获得二等奖,奖金20元;其余情况获得三等奖,奖金10元.(1)某人抽奖一次,求其获奖金额X的概率分布和数学期望;(2)赵四购物恰好满600元,假设他不放弃每次抽奖机会,求他获得的奖金恰好为60元的概率.25.已知抛物线C:x2=4py(p为大于2的质数)的焦点为F,过点F且斜率为k(k≠0)的直线交C于A,B两点,.线段AB的垂直平分线交y轴于点E,抛物线C在点A,B处的切线相交于点G.记四边形AEBG的面积为S(2)当点G由.的横坐标为整数时,S是否为整数?若是,请求出所有满足条件的S的值;若不是,请说明理。
苏 苏锡常镇四市2020届高三教学情况调研(一)含答案

苏锡常镇四市2020届高三教学情况调研(一)数学Ⅰ试题参考公式:样本数据12n x x x L ,,,的方差2211()n i i s x x n ==-∑,其中11n i i x x n ==∑. 球的体积34π3V R =,其中R 表示球的半径. 柱体的体积V Sh =,其中S 表示柱体的底面积,h 表示柱体的高.一、填空题:本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上. 1.已知i 为虚数单位,复数11z i=+,则|z |= . 2.已知集合A ={x |0≤x ≤1},B ={x |a -1≤x ≤3},若A ⋂B 中有且只有一个元素,则实数a 的值为 .3.已知一组数据1.6,1.8,2,2.2,2.4,则该组数据的方差是 .4.在平面直角坐标系xOy 中,已知双曲线2221(0)4x y a a -=>的一条渐近线方程为23y x =,则a = . 5.甲乙两人下棋,两人下成和棋的概率是12,乙获胜的概率是13,则乙不输的概率是 . 6.右图是一个算法的流程图,则输出的x 的值为 .7.“直线l 1:ax +y +1=0与直线l 2:4x +ay +3=0平行”是“a =2”的 条件.(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分又不必要”) 8.已知等差数列{a n }的前n 项和为S n ,a 1=9,9595S S -=-4,则a n = .9.已知点M 是曲线y =2ln x +x 2-3x 上一动点,当曲线在M 处的切线斜率取得最小值时,该切线的方程为 .10.已知3cos2α=4sin(π4-α),α∈(π,π4),则sin2α= . 11.如图在矩形ABCD 中,E 为边AD 的中点,AB =1,BC =2.分别以A ,D 为圆心,1为半径作圆弧EB ,EC ,将两圆弧EB ,EC 及边BC 所围成的平面图形(阴影部分)绕直线AD 旋转一周,所形成的几何体的体积为 .ED CBA (第6题图) (第11题图)12.在∆ABC 中,()AB AC BC λ-⊥u u u r u u u r u u u r(1λ>),若角A 的最大值为π6,则实数λ的值是 .13.若函数f (x )=a x (a >0且a ≠1)在定义域[m ,n ]上的值域是[m 2,n 2](1<m <n ),则a 的取值范围是 . 14.如图,在∆ABC 中,AB =4,D 是AB 的中点,E 在边AC 上,AE =2EC ,CD 与BE 交于点O ,若OB=OC ,则∆ABC 面积的最大值为 .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域作答,解答时应写出文字说明、证明过程或演算步骤。
2017年江苏省苏锡常镇四市高三一模数学试卷

2017年江苏省苏锡常镇四市高三一模数学试卷一、填空题(共14小题;共70分) 1. 已知集合 U ={1,2,3,4,5,6,7},M ={x∣ x 2−6x +5≤0,x ∈Z },则 ∁U M = ______. 2. 若复数 z 满足 z +i =2+i i,其中 i 为虚数单位,则 ∣z∣= ______.3. 函数 f (x )=1ln (4x−3) 的定义域为______.4. 下面是给出的一种算法,则该算法输出的结果是______. t←1 i←2While i≤4 t←t×i i←i+1 End WhilePrint t5. 某高级中学共有 900 名学生,现用分层抽样的方法从该校学生中抽取 1 个容量为 45 的样本,其中高一年级抽 20 人,高三年级抽 10 人,则该校高二年级学生人数为______. 6. 已知正四棱锥的底面边长是 2,侧棱长是 √3,则该正四棱锥的体积为______. 7. 从集合 {1,2,3,4} 中任取两个不同的数,则这两个数的和为 3 的倍数的概率为______.8. 在平面直角坐标系 xOy 中,已知抛物线 y 2=8x 的焦点恰好是双曲线 x 2a 2−y 23=1 的右焦点,则双曲线的离心率为______.9. 设等比数列 {a n } 的前 n 项和为 S n ,若 S 3,S 9,S 6 成等差数列.且 a 2+a 5=4,则 a 8 的值为 ______.10. 在平面直角坐标系 xOy 中,过点 M (1,0) 的直线 l 与圆 x 2+y 2=5 交于 A ,B 两点,其中 A 点在第一象限,且 BM ⃗⃗⃗⃗⃗⃗ =2MA⃗⃗⃗⃗⃗⃗ ,则直线 l 的方程为______. 11. 在 △ABC 中,已知 AB =1,AC =2,∠A =60∘,若点 P 满足 AP ⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +λAC ⃗⃗⃗⃗⃗ ,且 BP ⃗⃗⃗⃗⃗ ⋅CP⃗⃗⃗⃗⃗ =1,则实数 λ 的值为______.12. 已知 sinα=3sin (α+π6),则 tan (α+π12)= ______.13. 若函数 f (x )={12x−1,x <1lnxx 2,x ≥1,则函数 y =∣f (x )∣−18的零点个数为______.14. 若正数 x ,y 满足 15x −y =22,则 x 3+y 3−x 2−y 2 的最小值为______.二、解答题(共12小题;共156分)15. 在 △ABC 中,a ,b ,c 分别为角 A ,B ,C 的对边.若 acosB =3,bcosA =1,且 A −B =π6.(1)求边 c 的长; (2)求角 B 的大小.16. 如图,在斜三梭柱 ABC −A 1B 1C 1 中,侧面 AA 1C 1C 是菱形,AC 1 与 A 1C 交于点 O ,E 是棱 AB上一点,且 OE ∥平面BCC 1B 1.(1)求证:E 是 AB 中点;(2)若 AC 1⊥A 1B ,求证:AC 1⊥BC .17. 某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门 BADC (如图),设计要求彩门的面积为 S (单位:m 2),高为 ℎ(单位:m )(S ,ℎ 为常数),彩门的下底 BC 固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为 α,不锈钢支架的长度和记为 l .(1)请将 l 表示成关于 α 的函数 l =f (α); (2)问当 α 为何值时 l 最小?并求最小值.18. 在平面直角坐标系 xOy 中,已知椭圆 x 2a 2+y 2b 2=1(a >b >0) 的焦距为 2,离心率为 √22,椭圆的右顶点为 A .(1)求该椭圆的方程:(2)过点 D(√2,−√2) 直线 PQ 交椭圆于两个不同点 P ,Q ,求证:直线 AP ,AQ 的斜率之和为定值.19. 已知函数 f (x )=(x +1)lnx −ax +a (a 为正实数,且为常数).(1)若 f (x ) 在 (0,+∞) 上单调递增,求 a 的取值范围; (2)若不等式 (x −1)f (x )≥0 恒成立,求 a 的取值范围.20. 已知 n 为正整数,数列 {a n } 满足 a n >0,4(n +1)a n 2−na n+12=0,设数列 {b n } 满足 b n =a n2t n.(1)求证:数列 {n√n } 为等比数列;(2)若数列 {b n } 是等差数列,求实数 t 的值;(3)若数列 {b n } 是等差数列,前 n 项和为 S n ,对任意的 n ∈N ∗,均存在 m ∈N ∗,使得 8a 12S n −a 14n 2=16b m 成立,求满足条件的所有整数 a 1 的值.21. 如图,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆的切线l,过A作l的垂线AD,AD分别与直线l,圆交于点D,E.求∠DAC的度数与线段AE的长.22. 已知二阶矩阵M有特征值λ=8及对应的一个特征向量e1⃗⃗⃗ =[11],并且矩阵M对应的变换将点(−1,2)变换成(−2,4).(1)求矩阵M;(2)求矩阵M的另一个特征值.23. 已知圆O1和圆O2的极坐标方程分别为ρ=2,ρ2−2√2ρcos(θ−π4)=2.(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;(2)求经过两圆交点的直线的极坐标方程.24. 已知a,b,c为正数,且a+b+c=3,求√3a+1+√3b+1+√3c+1的最大值.25. 如图,已知正四棱锥P−ABCD中,PA=AB=2,点M,N分别在PA,BD上,且PMPA =BNBD=13.(1)求异面直线MN与PC所成角的大小;(2)求二面角N−PC−B的余弦值.26. 设∣θ∣<π2,n为正整数,数列{a n}的通项公式a n=sin nπ2tan nθ,其前n项和为S n.(1)求证:当n为偶函数时,a n=0;当n为奇函数时,a n=(−1)n−12tan nθ;(2)求证:对任何正整数n,S2n=12sin2θ⋅[1+(−1)n+1tan2nθ].答案第一部分1. {6,7}2. √103. {x∣∣ x>34且x≠1}4. 245. 3006. 437. 138. 29. 210. x−y−1=011. −14或112. 2√3−413. 414. 1第二部分15. (1)因为acosB=3,bcosA=1,所以a×a 2+c2−b22ac=3,b×b2+c2−a22bc=1,化为:a2+c2−b2=6c,b2+c2−a2=2c.相加可得:2c2=8c,解得c=4.(2)由(1)可得:a2−b2=8.由正弦定理可得:asinA =bsinB=4sinC,又A−B=π6,所以A=B+π6,C=π−(A+B)=π−(2B+π6),可得sinC=sin(2B+π6).所以a=4sin(B+π6)sin(2B+π6),b=4sinBsin(2B+π6).所以16sin2(B+π6)−16sin2B=8sin2(2B+π6),所以1−cos(2B+π3)−(1−cos2B)=sin2(2B+π6),即cos2B−cos(2B+π3)=sin2(2B+π6),所以−2sin(2B+π6)sin(−π6)=sin2(2B+π6),所以sin(2B+π6)=0或sin(2B+π6)=1,B∈(0,5π12).解得:B=π6.16. (1) 连接 BC 1,取 AB 中点 Eʹ, AA 1C 1C 是菱形,AC 1 与 A 1C 交于点 O , 所以 O 为 AC 1 的中点, 因为 Eʹ 是 AB 的中点, 所以 OEʹ∥BC 1;因为 OEʹ⊄平面BCC 1B 1,BC 1⊂平面BCC 1B 1, 所以 OEʹ∥平面BCC 1B 1, 因为 OE ∥平面BCC 1B 1, 所以 E ,Eʹ 重合, 所以 E 是 AB 中点.(2) 因为侧面 AA 1C 1C 是菱形, 所以 AC 1⊥A 1C ,因为 AC 1⊥A 1B ,A 1C ∩A 1B =A 1,A 1C ⊂平面A 1BC ,A 1B ⊂平面A 1BC , 所以 AC 1⊥平面A 1BC , 因为 BC ⊂平面A 1BC , 所以 AC 1⊥BC .17. (1) 设上底长为 a ,则 S =(a+a+2ℎtanα)ℎ2,所以 a =Sℎ−ℎtanα, 所以 l =Sℎ−ℎtanα+2ℎsinα(0<α<π2). (2) lʹ=ℎ⋅1−2cosαsin 2α,所以 0<α<π3,lʹ<0,π3<α<π2,lʹ>0, 所以 α=π3 时,l 取得最小值 Sℎ+√3ℎ m .18. (1) 由题意可知:椭圆 x 2a 2+y 2b 2=1(a >b >0),焦点在 x 轴上,2c =1,c =1, 椭圆的离心率 e =c a=√22,则 a =√2,b 2=a 2−c 2=1,则椭圆的标准方程:x 22+y 2=1.(2) 设 P (x 1,y 1),Q (x 2,y 2),A(√2,0), 由题意 PQ 的方程:y =k(x −√2)−√2, 则 {y =k(x −√2)−√2,x 22+y 2=1,整理得:(2k 2+1)x 2−(4√2k 2+4√2k)x +4k 2+8k +2=0, 由韦达定理可知:x 1+x 2=4√2k 2+4√2k2k 2+1,x 1x 2=4k 2+8k+22k 2+1,则 y 1+y 2=k (x 1+x 2)−2√2k −2√2=−2√2−2√2k2k 2+1,则 k AP +k AQ =1x−√2+2x −√2=1221√2(12x x −√2(x +x )+2,由y 1x 2+y 2x 1=[k(x 1−√2)−√2]x 2+[k(x 2−√2)−√2]x 1=2kx 1x 2−(√2k +√2)(x 1+x 2)=−4k2k 2+1,k AP +k AQ =1221√2(12x x −√2(x +x )+2=−4k 2k 2+1−√2×−2√2−2√2k2k 2+14k 2+8k+22k 2+1−√2×4√2k 2+4√2k2k 2+1+2=1,所以直线 AP ,AQ 的斜率之和为定值 1.19. (1) f (x )=(x +1)lnx −ax +a ,fʹ(x )=lnx +1x +1−a ,若 f (x ) 在 (0,+∞) 上单调递增,则 a ≤lnx +1x +1 在 (0,+∞) 恒成立,(a >0), 令 g (x )=lnx +1x +1,(x >0),gʹ(x )=x−1x 2,令 gʹ(x )>0,解得:x >1,令 gʹ(x )<0,解得:0<x <1,故 g (x ) 在 (0,1) 递减,在 (1,+∞) 递增,故 g (x )min =g (1)=2,故 0<a ≤2. (2) 若不等式 (x −1)f (x )≥0 恒成立,即 (x −1)[(x +1)lnx −a ]≥0 恒成立,① x ≥1 时,只需 a ≤(x +1)lnx 恒成立,令 m (x )=(x +1)lnx ,(x ≥1),则 mʹ(x )=lnx +1x +1, 由(1)得:mʹ(x )≥2,故 m (x ) 在 [1,+∞) 递增,m (x )≥m (1)=0, 故 a ≤0,而 a 为正实数,故 a ≤0 不合题意; ② 0<x <1 时,只需 a ≥(x +1)lnx ,令 n (x )=(x +1)lnx ,(0<x <1),则 nʹ(x )=lnx +1x +1,由(1)nʹ(x ) 在 (0,1) 递减,故 nʹ(x )>n (1)=2,故 n (x ) 在 (0,1) 递增,故 n (x )<n (1)=0,故 a ≥0, 而 a 为正实数,故 a >0.20. (1) 数列 {a n } 满足 a n >0,4(n +1)a n 2−na n+12=0,所以 2√n +1a n =√na n+1n+1√n+1=n √n,所以数列 {n √n} 是以 a 1 为首项,以 2 为公比的等比数列. (2) 由(1)可得:n√n=a 1×2n−1, 所以 a n 2=na 12⋅4n−1.因为 b n =a n2t n,所以 b 1=a 12t,b 2=a 22t 2,b 3=a 32t 3,因为数列 {b n } 是等差数列, 所以 2×a 22t 2=a 12t+a 32t 3, 所以2×2a 12×4t=a 12+3a 12×42t 2,化为:16t =t 2+48,解得 t =12或4.(3) 数列 {b n } 是等差数列,由(2)可得:t =12或4. ① t =12 时,b n =na 12⋅4n−112n=na 124×3n,S n =n(a 1212+na 124×3n)2,因为对任意的 n ∈N ∗,均存在 m ∈N ∗,使得 8a 12S n −a 14n 2=16b m 成立,所以 8a 12×n(a 1212+na 124×3n)2−a 14n 2=16×ma 124×3m,所以 a 12(n 3+n 23n −n 2)=4m3m ,n =1 时,化为:−13a 12=4m 3m>0,无解,舍去.② t =4 时,b n =na 12⋅4n−14n=na 124,S n =n(a 124+na 124)2,对任意的 n ∈N ∗,均存在 m ∈N ∗,使得 8a 12S n−a 14n 2=16bm 成立,所以 8a 12×n(a 124+na 124)2−a 14n2=16×ma 124,所以 na 12=4m ,所以 a 1=2√mn . 因为 a 1 为正整数, 所以 √mn=12k ,k ∈N ∗.所以满足条件的所有整数 a 1 的值为 {a 1∣ a 1=2√m n ,n ∈N ∗,m ∈N ∗,且√m n =12k,k ∈N ∗}.21. 如图,连接 OC , BC =OB =OC =3, 因此 ∠CBO =60∘. 由于 ∠DCA =∠CBO ,所以 ∠DCA =60∘,又 AD ⊥DC 得 ∠DAC =30∘. 又因为 ∠ACB =90∘,得 ∠CAB =30∘,那么 ∠EAB =60∘,从而 ∠ABE =30∘, 于是 AE =12AB =3.22. (1) 设矩阵 A =[a bc d ],这里 a,b,c,d ∈R ,则 [a b c d ][11]=8[11]=[88],故 {a +b =8,c +d =8,由于矩阵 M 对应的变换将点 (−1,2) 换成 (−2,4). 则 [a b c d ][−12]=[−24],故 {−a +2b =−2,−c +2d =4,联立以上两方程组解得 a =6,b =2,c =4,d =4,故 M =[6244].(2) 由(1)知,矩阵 M 的特征多项式为 f (λ)=(λ−6)(λ−4)−8=λ2−10λ+16,故矩阵 M 的另一个特征值为 2. 23. (1) 由 ρ=2 知 ρ2=4,故圆 O 1 的直角坐标方程为 x 2+y 2=4. 因为 ρ2−2√2ρcos (θ−π4)=2,所以 ρ2−2√2ρ(cosθcos π4+sinθsin π4)=2,故圆 O 2 的直角坐标方程为 x 2+y 2−2x −2y −2=0. (2) 将两圆的直角坐标方程相减, 得经过两圆交点的直线方程为 x +y =1. 化为极坐标方程为 ρcosθ−ρsinθ=1, 即 ρsin (θ+π4)=√22. 24. 由柯西不等式可得(√3a +1+√3b +1+√3c +1)2≤[12+12+12][(√3a +1)2+(√3b +1)2+(√(3c +1))2]=3×12,所以 √3a +1+√3b +1+√3c +1≤6,当且仅当 √3a +1=√3b +1=√3c +1 时取等号. 所以 √3a +1+√3b +1+√3c +1 的最大值为 6. 25. (1) 设 AC 与 BD 的交点为 O ,AB =PA =2.以点 O 为坐标原点,DA ⃗⃗⃗⃗⃗ ,DC ⃗⃗⃗⃗⃗ ,OP ⃗⃗⃗⃗⃗ 方向分别是 x 轴,y 轴,z 轴正方向,建立空间直角坐标系 O −xyz .A (1,−1,0),B (1,1,0),C (−1,1,0),D (−1,−1,0), 设 P (0,0,p ),则 AP ⃗⃗⃗⃗⃗ =(−1,1,p ), 又 AP =2,所以 1+1+p 2=4,所以 p =√2,因为 OM ⃗⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +AM ⃗⃗⃗⃗⃗⃗ =OA ⃗⃗⃗⃗⃗ +23AP ⃗⃗⃗⃗⃗ =(13,−13,2√23),ON ⃗⃗⃗⃗⃗⃗ =13OB ⃗⃗⃗⃗⃗ =(13,13,0),所以 PC ⃗⃗⃗⃗⃗ =(−1,1,−√2),MN ⃗⃗⃗⃗⃗⃗⃗ =(0,23,−2√23), 设异面直线 MN 与 PC 所成角为 θ, 则 cosθ=∣MN⃗⃗⃗⃗⃗⃗⃗ ⋅CP ⃗⃗⃗⃗⃗ ∣∣MN⃗⃗⃗⃗⃗⃗⃗ ∣⋅∣PC ⃗⃗⃗⃗⃗ ∣=23+432√49+89=√32. θ=30∘,所以异面直线 MN 与 PC 所成角为 30∘.(2) PC ⃗⃗⃗⃗⃗ =(−1,1,−√2),PB ⃗⃗⃗⃗⃗ =(1,1,−√2),PN ⃗⃗⃗⃗⃗⃗ =(13,13,−√2), 设平面 PBC 的法向量 n ⃗ =(x,y,z ), 则 {n ⃗ ⋅PB⃗⃗⃗⃗⃗ =x +y −√2z =0,n ⃗ ⋅PC ⃗⃗⃗⃗⃗ =−x +y −√2z =0,取 z =1,得 n ⃗ =(0,√2,1), 设平面 PNC 的法向量 m ⃗⃗ =(a,b,c ), 则 {m ⃗⃗ ⋅PN⃗⃗⃗⃗⃗⃗ =13a +13b −√2c =0,m ⃗⃗ ⋅PC ⃗⃗⃗⃗⃗ =−a +b −√2c =0, 取 c =1,得 m ⃗⃗ =(√2,2√2,1), 设二面角 N −PC −B 的平面角为 θ,则cosθ=∣m⃗⃗⃗ ⋅n⃗ ∣∣m⃗⃗⃗ ∣⋅∣n⃗ ∣=√3⋅√11=5√3333.所以二面角N−PC−B的余弦值为5√3333.26. (1)a n=sin nπ2tan nθ,当n=2k(k∈N∗)为偶数时,a n=sinkπ⋅tan nθ=0;当n=2k−1为奇函数时,a n=sin2k−12πtan nθ=(−1)k−1tan nθ=(−1)n−12tan nθ.(2)a2k−1+a2k=(−1)n−12tan nθ.所以奇数项成等比数列,首项为tanθ,公比为−tan2θ.所以S2n=tanθ[1−(−1)n tan2nθ]1−(−tan2θ)=12sin2θ⋅[1+(−1)n+1tan2nθ].。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020届江苏省苏锡常镇四市2017级高三一调考试
数学试题
数学Ⅰ试题
一、填空题:本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请把答案直接填写在答题卡相应位置上。
1.已知i 为虚数单位,复数11z i =+,则|z |=
2.已知集合A ={x |0≤x ≤1},B ={x |a -1≤x ≤3},若A ⋂B 中有且只有一个元素,则实数a 的值为
3.已知一组数据1.6,1.8,2,2.2,2.4,则该组数据的方差是
4.在平面直角坐标系xOy 中,已知双曲线22
21(0)4x y a a -=>的一条渐近线 方程为23
y x =,则a = 5.甲乙两人下棋,两人下成和棋的概率是
12,乙获胜的概率是13,则乙不输的概率是 6.右图是一个算法的流程图,则输出的x 的值为
7.“直线l 1:ax +y +1=0与直线l 2:4x +ay +3=0平行”是“a =2”的 条件.(填“充分不必要”、“必要不充分”、“充分必要”或“既不充分又不必要”)
8.已知等差数列{a n }的前n 项和为Sn ,a 1=9,9595
S S -=-4,则a n = 9.已知点M 是曲线y =2ln x +x 2-3x 上一动点,当曲线在M 处的切线斜率取得最小值时,该切线的方程为
10.已知3cos2α=4sin(4π-α),α∈(,4ππ),则sin2α= 11.如图在矩形ABCD 中,E 为边AD 的中点,AB =1,BC =2.分别以A ,D 为圆心,1为半径作圆弧EB ,EC ,将两圆弧EB ,EC 及边BC 所围成的平面图形(阴影部分)绕直线AD 旋转一周,所形成的几何体的体积为
12.在∆ABC 中,,若角A 的最大值为6
π,则实数λ的值是 13.若函数f (x )=a x (a >0且a ≠1)在定义域[m ,n ]上的值域是[m 2,n 2](1<m <n ),则a 的取值范围是
14.如图,在∆ABC 中,AB =4,D 是AB 的中点,E 在边AC 上,AE =2EC ,CD 与BE 交于点O ,若OB =2OC ,则∆ABC 面积的最大值为
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域作答,解答时应写出文字说明、证明过程或演算步骤。
15.(本小题满分14分)
在∆ABC 中,角A ,B ,C 所对应的边分别是a ,b ,c ,且满足b cos A 3sin B =0
(1)求A ;
(2)已知a =3B =
3π,求∆ABC 的面积.。
