双肢墙计算
双肢剪力墙计算时,整体系数的大小对结构的影响规律

双肢剪力墙是一种常用的建筑结构形式,其在建筑工程中承担着重要的抗震作用。
双肢剪力墙的设计和计算是建筑工程中的重要环节,而整体系数的大小对结构的影响规律是设计中需要考虑的重要因素。
1. 双肢剪力墙的作用双肢剪力墙是指在建筑结构中设置的两个相邻的剪力墙,通过其对地震力的吸收和抵抗,来保护建筑物免受地震破坏。
双肢剪力墙的设计和计算必须符合相应的规范和标准,以确保结构的安全可靠。
2. 整体系数的定义整体系数是用于描述结构的整体受力性能的一个参数,它综合考虑了结构的受力性能和受力体系的作用。
整体系数的大小直接影响着结构的抗震性能,因此在双肢剪力墙的设计和计算中,整体系数的选择非常重要。
3. 整体系数的大小对结构的影响规律整体系数的大小对结构的抗震性能和受力性能有着重要的影响。
一般来说,整体系数越大,结构的抗震性能越好,但相应的造价也会增加。
在实际的设计中,需要权衡整体系数的大小与结构的经济性和安全性。
4. 整体系数的选择原则在双肢剪力墙的设计和计算中,选择合适的整体系数是非常重要的。
一般来说,根据建筑结构的重要性、地震区的地震烈度、结构的高度和材料的强度等因素来确定整体系数的大小。
对于重要性较高的建筑结构,可以适当提高整体系数,以提高结构的抗震性能;对于一般性建筑结构,可以适当降低整体系数,以降低结构的造价。
5. 整体系数的调整方法在实际的设计中,可以通过对结构的材料、尺寸、截面形状等参数进行调整,来间接影响整体系数的大小。
采用高强度的材料、增加墙体的厚度、改变墙体的截面形状等方式,都可以影响整体系数的大小。
需要注意的是,调整整体系数的还需要考虑结构的稳定性、变形性能和承载能力,以确保整体结构的安全可靠。
6. 结论整体系数的大小对双肢剪力墙结构的影响规律是一个复杂的问题,需要综合考虑结构的抗震性能、经济性和安全性。
在实际的设计中,需要根据具体的工程条件和要求,合理选择整体系数的大小,并通过对结构的参数进行调整,来达到设计要求。
双肢墙解题思路
I Ib /(1 3EIb / GAb a )
0 b 2
——连梁截面折算惯性矩 I b Ab ——连梁截面惯性矩和面积 a——连梁截面计算跨度一半,设连梁净跨为2a0 a a h / 4 0 b c——洞口两侧墙肢轴线距离一半
I
0 b
D I c /a
0 2 b
3
连梁刚度系数
M pj——水平荷载在j层截 面处总的倾覆力矩 墙肢弯矩分配系数
1i
2i
I1 I1 I 2
I2 I1 I 2
6
2014-12-29
⑤墙肢内力(墙肢水平位移相等) 剪力
I V1 j 0 V pj 0 I1 I 2
V2 j
0 I2 0 V pj 0 I1 I 2
⑤墙肢内力(墙肢转角相等) 弯矩
M1 j ( x) ห้องสมุดไป่ตู้ 2 j ( x) M pj ( x) 2cN j ( x) M p ( x) m j
j
n
n I1 M1 j (M pj m j ) I1 I 2 j
M2 j
n I2 ( M pj m j ) I1 I 2 j
②整体系数
H
Th I i
6
D
h——层高(各层不等时可取沿高度的加权平均值) ——整体系数 H——剪力墙总高度 T——轴向变形影响系数 判断剪力墙类型
③连梁约束弯矩函数 ( , ) m( )
、 x / H ,查图表得 根据:荷载形式、
m( ) V0T ( , )
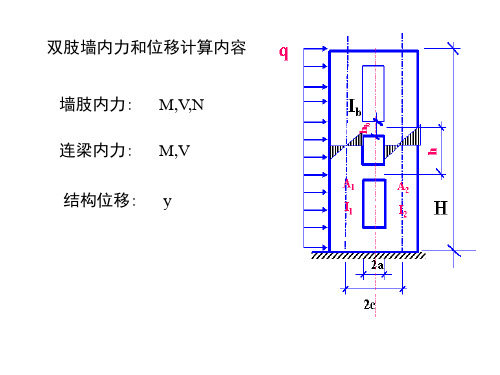
双肢墙内力和位移计算内容
墙肢内力:
连梁内力: 结构位移:
M,V,N
M,V y
双肢剪力墙内力的计算方法及荷载与抗力的统计特征探究

双肢剪力墙内力的计算方法及荷载与抗力的统计特征探究作者:艾进贵来源:《科技视界》2012年第30期【摘要】国内外对双肢剪力墙的弹塑性研究表明,连梁的延性是影响双肢剪力墙极限承载力的一个重要因素。
然而用在中高层建筑的RC连梁剪力墙,在一次地震反复作用下,剪力和变形由连梁来满足,由于跨高比较小,就要求连梁配筋很复杂,势必增加施工时间和成本。
普通混凝土连梁的抗剪能力有限,导致设计出来的梁很高,往往对施工来说是不切实际的。
上世纪90年代起美国辛辛那提大学和加拿大麦吉尔大学的研究人员提出来用钢梁来代替RC连梁,将梁端嵌入钢筋混凝土剪力墙墙肢内形成了一种更高效的抗侧力结构体系,从而来实现结构的抗震设计目标。
我们把这种双肢剪力墙就称为带钢连梁混合双肢剪力墙,简称HCW。
从国内外代表性研究成果来看,双肢剪力墙结构研究主要是探索一个高性能连梁的过程,使它能保证结构整体有着良好抗震性能,而且要求其本身具有良好延性,同时也是从普通钢筋混凝土双肢剪力墙到混合双肢剪力墙的探索过程。
【关键词】双肢剪力墙;内力组合;统计特征;延性破坏;地震作用;随机变量0 引言剪力墙结构是指纵横向主要承重构件全部为结构墙的结构。
当墙体处于建筑物中合适的位置时,他们能形成一种有效抵抗水平作用的结构体系,同时,又能起到对空间的分割作用。
近年来,由于住宅需求的增加和用于建造住宅的土地供应紧张,高层住宅的建造成为众多开发商的首选,推动了剪力墙结构的广泛应用。
1 内力的计算方法1.1 地震作用双肢剪力墙是多自由度超静定平面结构。
对于多自由度弹性体系的水平地震作用一般采用底部剪力法和振型分解法求得。
对于高度不超过40m、以剪切变形为主且质量和刚度沿高度分布比较均匀的结构,以及近似于单质点体系的结构可采用底部剪力法。
但双肢剪力墙的变形以弯曲变形为主,根据《高层建筑混凝土结构技术规程》JGJ3-2002中3.3.4的规定:高层建筑结构宜采用振型分解反应谱法。
连续化方法计算联肢剪力墙简介

5.3.3.2 连续连杆法的基本方程及求解
令G=0.42E,矩形截面连梁剪应力不均匀系数µ=1.2,则 连梁折算惯性矩可近似为:
(5-14)
5.3.3.3 联肢剪力墙的内力
(1) 第一种方法:
mi
Vbi
h
(i )
h
VbiM biFra biblioteka0m(i )
( ) M 1i
( )
M 2i
(a) 连杆内力;(b) 连梁剪力、弯矩;(c) 墙肢轴力及弯矩 图5-28
(5-13)
式中,s为联肢墙洞口列数;s+1为墙肢列数;2ai和2ci分别 为第i个洞口的净宽及相邻墙肢重心到重心的距离。多肢墙 中计算墙肢轴向变形影响比较困难,T常近似:3~4肢时取 0.8,5~7肢时取0.85,8肢及以上时取0.9。
5.3.3.2 连续连杆法的基本方程及求解
整体系数a只与联肢剪力墙的几何尺寸有关。a愈大表示 连梁刚度与墙肢刚度的相对比值愈大,连梁刚度与墙肢刚度 的相对比值对联肢墙内力分布和位移的影响很大,是一个重 要的几何参数。
5.3.3.2 连续连杆法的基本方程及求解
(c) 连梁弯曲及剪切变形 图5-25 墙肢和连梁的变形
5.3.3.2 连续连杆法的基本方程及求解
的计算式见下:
(5-5)
位移协调方程: 对x求导一次:
5.3.3.2 连续连杆法的基本方程及求解
将式(5-5)代入式(5-4),并微分两次,可得位移协调方程如下:
5.3.3 连续化方法计算联肢剪力墙
5.3.3.1 基本方法与假定
(a) 结构尺寸 (b) 计算简图
(c) 基本体系
图5-24 连续化方法计算简图及基本体系
双肢剪力墙耦合比计算方法及其应用研究

双肢剪力墙耦合比计算方法及其应用研究一、引言双肢剪力墙是一种常见的结构形式,具有良好的承载性能和抗震性能。
而双肢剪力墙的耦合比则是评价其结构性能的重要指标之一。
本文将围绕双肢剪力墙耦合比的计算方法和应用研究展开讨论。
二、双肢剪力墙耦合比的定义双肢剪力墙的耦合比是指剪力墙两侧受压纵筋与受拉纵筋的配筋比值,通常用ρ表示。
在实际工程中,双肢剪力墙的耦合比直接影响其抗震性能和承载性能,因此对其进行准确的计算至关重要。
三、双肢剪力墙耦合比的计算方法1. 经验公式法通过对历史工程案例的总结和分析,人们提出了一些经验公式来计算双肢剪力墙的耦合比。
这种方法简单易行,适用范围广,但精度相对较低。
2. 极限承载力法利用受压区混凝土和受拉区钢筋的极限承载力来计算双肢剪力墙的耦合比。
这种方法需要考虑更多的因素,计算结果相对精确。
3. 非线性有限元法借助有限元分析软件,采用非线性有限元法来模拟双肢剪力墙的受力和变形情况,从而得到更加精确的耦合比计算结果。
以上三种方法各有优劣,工程设计中可以根据实际情况选择合适的方法进行计算。
四、双肢剪力墙耦合比的应用研究1. 结构设计双肢剪力墙的结构设计中,耦合比是关键的设计参数之一。
合理的耦合比设计可以提高结构的承载性能和抗震性能,减小裂缝的发展,提高结构的整体稳定性。
2. 工程施工在双肢剪力墙的施工过程中,合理的耦合比设计可以降低施工难度,减小施工变形,提高工程施工效率。
3. 结构监测与维护通过对双肢剪力墙结构的实时监测,可以及时发现结构变形和裂缝情况,从而采取相应的维护措施,保障结构的安全和稳定。
五、个人观点和理解双肢剪力墙作为一种重要的结构形式,其耦合比的计算和应用是结构设计和工程实践中需要重点关注的问题。
合理的耦合比设计可以提高结构的整体性能,促进工程的安全可靠。
需要加强对双肢剪力墙耦合比计算方法和应用研究的深入理解和实践探索。
六、总结回顾本文对双肢剪力墙耦合比的定义、计算方法和应用研究进行了全面的介绍和探讨,旨在帮助读者更好地理解和应用这一重要的结构参数。
剪力墙结构内力与位移计算(多肢墙)

宽度小的墙肢不易满足JA/J≤Zi,需要对Mi进行修 正。
墙肢有反弯点,假定反弯点在中点。修正后:
M i M i (x) Vi (x) h2 / 2
连梁剪力可以由上下层轴力之差求得,再由剪力计算 连梁端部弯矩。
顶点位移公式为P61(4-6)乘上1.2的修正系数
1
V0H 3
i 1
1 4 2 T T
k 1
E Ii
i 1
1 3 2 T T
Φ(ξ )及 m(ξ )由表4.4~表4.6查出,约束弯矩系数Φ(ξ ),
倒三角形分布荷载
均布荷载
顶点集中荷载
m(
)
V0
12 2
(
)
4、计算连梁内力 首先计算多肢墙连梁约束弯矩分配系数,双肢墙无需计算
Ii
j j
i 1
j层第i墙肢剪力:
Vij
Ii0
k 1
VPj
其中,
Ii0
i 1
7、计算顶点位移
1
V0H 3
60 EIeq
1 8
V0H 3 EIeq
1 3
V0H 3 EIeq
倒三角形分布荷载 均布荷载 顶点集中荷载
Ii0
Ii
1
12 EIi GAi h 2
连梁计算跨度:
ai
ai0
hbi 4
连梁刚度:
Di
I b0i ci2 ai3
其中:ai0——连梁净跨的一半;hbi——连梁高度
梁、墙刚度比参数:12
双肢剪力墙内力和位移分析
α1为连梁与墙
肢刚度比
α 为剪力墙的整
体工作系数
双肢墙的基本微分方程:
4、第四步:引入约束弯矩表述的微分方程 m ( m (z) 1 z) (z) (z) 2
P
H
(z) (z)
a1 a2
z
m (z) m ( m ( a ( z ) 1 z) 2 z)
3.3 微分方程的求解
3.2 微分方程的建立
1、第一步:根据基本体系在连梁切口处的变形连续条件,建立微分方程: 将连续化后的连梁沿反弯点处切开,可得力法求解时的基本体系。 切开后的截面上有剪力集度τ(z ) 和轴力集度σ(z ),取τ(z )为多余未知力。 根据变形连续条件,切口处沿未知力τ(z ) 方向上的相对位移应为零,建 立微分方程。
1
●
2
3
0
d2y EI 2 M dz
微分方程的建立
补充条件
●
微分方程的求解 求解内力
求解二阶常系数非齐次线性微分方程 微分关系求解内力
●
将连杆离散 化 ,均匀分布
(z) (z)
求解两个未知 力的超静定结 构
受力平衡方 程求解内力
(z) 多余未知力
3.1 基本假定
1)每一楼层处的连梁简化为沿该楼层均匀连续分布的连杆。 2)忽略连梁轴向变形,两墙肢同一标高水平位移相等。转角和曲率亦相同。 3)每层连梁的反弯点在梁的跨度中央。 4)沿竖向墙肢和连梁的刚度及层高均不变。当有变化时,可取几何平均值。
y N M
4 壁式框架的内力和位移计算
由于墙肢和连梁的截面高度较大,节点区也较大,故计算时应将节点 视为墙肢和连梁的刚域,按带刚域的框架(即壁式框架)进行分析。
4剪力墙结构内力与位移计算2(双肢墙)
图4-6c是双肢墙的基本体系,沿梁中点切开,切开后连杆弯矩为0(假定反弯点在中 点),连杆剪力τ(x)是多余未知力,是一个连续函数。未知轴力σ(x)虽然存在, 但与求解τ(x)无关,不必解出其值。 由切开处的变形连续条件建立τ(x)的微分方程,求解微分方程可得连杆剪力τ(x)。 将—个楼层高度范围内各点剪力积分,还原成一根连梁中的剪力。各层连梁中的剪 力求出后,所有墙肢及连梁内力都可相继求出.这就是连续连杆法的基本思路。
令
m( x) 2c ( x)
6H 2 D 12 h S 2c
2
可以得到
12 x 2 V [ 1 ( 1 ) ] 2 0 H H2 2 x m( x) 2 m( x) 12 V0 H H H2 1 V 2 0 H
y ym yv
1
1
dy d 2 ym v d d d 2 1 d d
d 2 ym 1 M ( ) m( )d 0 P d 2 E ( J1 J 2 )
dyv VP ( ) d G ( A1 A2 )
一、双肢墙计算
基本假定: 1、忽略连梁轴向变形,假定两墙肢水平位移完全相同。 2、两墙肢各截面转角与曲率相等,故连梁两端转角相等,连梁反弯点在梁中点。 3、各个墙肢、连梁截面以及层高等几何尺寸沿着双肢墙全高相同。 适用范围: 开洞比较规则,由下到上墙厚度以及层高都不变的联肢墙。 实际工程如果变化不多,取各楼层平均值计算,很不规则剪力墙,本方法不适用。 结构层数愈多本方法计算结果愈好。对于低层和多层结构中的墙,计算误差较大。 基本思路和方程:
每一楼层处连梁假设为均匀分布在该楼层高度内的连续连杆。
第十六讲 双肢剪力墙结构的内力和位移计算
• 令Ib为计及剪切变形影响后的连系梁折算惯性矩,即 :
• 则有:
• 根据连系梁切口处的变形协调条件有 • δ 1+ δ 2 +δ3 =0 将式(a)、(b)、(c)代入上式即得 :
1 1 1 hl a 1 dzdz 0 E A1 A2 0 z 12 EI b
2.建立微分方程
• 将连续化后的连系梁在跨中切开(图15-21c),由于 假定跨中为反弯点,故切开后在截面上只有剪力集度。 沿连系梁切口处,在外荷载和切口处剪力的共同作用下, 沿未知力方向上的竖向相对位移应为零。此竖向相对位 移由图15-22所示三部分组成. (1)由墙肢弯曲变形所引起的竖向相对位移 δ1 如图15 - 22 (a)所示,基本体系在外荷载和切口处剪力 的共同作用下发生弯曲变形。由于弯曲变形,使切口处 产生竖向相对位移 δ1 δ1 =-aθ1 (a) 式中 :θ1 —由于墙肢的弯曲变形所产生的转角; a—洞口两侧墙肢轴线间的距离。
(2)由墙肢的轴向变形所引起的竖向相对位移δ 2 • 如图15-22(b)所示,基本体系在外荷载和切口处剪力共同 作用下使墙肢发生轴向变形。自两墙肢底到z标高处的轴向变形 差,就是切口处的竖向相对位移。 •
• (3)由连系梁的弯曲和剪切变形所引起的竖向相对位移δ 3 • 如图15-22(C)所示,由于连系梁切口处剪力τh的作用,连系 梁将产生弯曲变形与剪切变形。
2 1
(15-19)
• 4·内力计算
由式(15-18)可求得在任意高度ξ 处Φ (ξ )的值。 又由式(15-19)可求得连续栅片切口处的分布剪力 τ (ξ ),这样,便可求得连续栅片对墙肢的约束弯矩为 2 • (15-20a) 1 m V0 2 • j层连系梁的剪力: • (15-20b) Vbj h •
双肢和多肢剪力墙内力和位移计算中假定
双肢和多肢剪力墙内力和位移计算中假定1. 前言在结构工程领域,双肢和多肢剪力墙是常见的结构形式,其内力和位移计算是工程设计中的重要环节。
在进行内力和位移计算时,通常需要进行一些理想化假定,以简化计算过程并尽可能准确地反映结构的实际行为。
2. 理想化假定的意义在进行双肢和多肢剪力墙内力和位移计算时,我们经常会使用一些理想化假定,这是为了方便计算和分析结构的受力情况,同时也可以更好地指导结构设计和施工。
然而,我们也要明白这些假定的局限性,不能够盲目地追求简化而忽视了实际的复杂情况。
3. 理想化假定的具体内容3.1 假定墙体为刚性在进行双肢和多肢剪力墙内力和位移计算时,常常假定墙体为刚性体,这是为了简化计算过程。
然而,实际上墙体存在一定的变形和柔度,特别是在地震等外部荷载作用下,墙体的柔度会对结构的整体性能产生重要影响。
3.2 忽略非线性效应在实际工程中,由于结构本身的非线性和荷载的不确定性,双肢和多肢剪力墙的内力和位移计算常常会忽略一些非线性效应,如材料的非线性、连接件的非线性等。
这可能会导致计算结果与实际情况存在一定的偏差,需要在设计中进行合理的修正。
3.3 假定荷载作用为静力作用在进行内力和位移计算时,常常假定荷载作用为静力作用,而忽略了动力荷载的作用。
然而,在地震等自然灾害作用下,荷载作用会是具有动力特性的,这就需要结构在动力荷载作用下的内力和位移进行特殊考虑。
4. 对双肢和多肢剪力墙内力和位移计算假定的个人观点和理解从我个人的观点来看,理想化假定在双肢和多肢剪力墙内力和位移计算中是必不可少的。
它为我们简化了复杂的计算过程,使得我们能够更加方便地进行分析和设计。
然而,我们也要清醒地认识到这些假定的局限性,不能够盲目地追求简化而忽视了结构实际的复杂情况。
在实际工程中,我们需要根据具体的情况对假定进行合理的修正,并结合实际的监测数据进行验证,以保证结构的安全性和可靠性。
5. 总结与回顾通过本文的探讨,我们对双肢和多肢剪力墙内力和位移计算中的理想化假定有了更加清晰的认识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6章 剪力墙结构分析与设计
[例题] 某12层双肢剪力墙,墙肢和连梁尺寸如图6.4.6所示。
混凝土强度等级为C20,承受图示倒三角形荷载,试计算此双肢墙的侧移和内力。
[解] (1)墙肢和连梁的几何特征计算
墙肢1:2
1m 813.008.516.0=⨯=A
4
31m 748.108.516.0121
=⨯⨯=I
4
22
1111m 171.09.2813.0748
.12.1301748.1301=⨯⨯⨯+=+
='h A I I I μ
墙肢2:2
2m 627.092.316.0=⨯=A
432m 803.092.316.0121
=⨯⨯=I
4
22
2222m 124.09.2672.0803
.02.1301803
.0301=⨯⨯⨯+=+
='h A I I I
连梁:m
60.128
.02.120=+=+=b b h l l m
70.52.1)92.308.5(21
=++=a 3
301083.68.016.0121
-⨯=⨯⨯=b I
4
32
33
2
00m
1090.360.18.016.01083.62.13011083.6301---⨯=⨯⨯⨯⨯⨯+⨯=+=b b b b b l A I I I
33
323b
b
2m 0619.060
.11090.370.52l I a 2D =⨯⨯⨯==
- (2)基本参数计算
32121m 018.2627
.0813.0627.0813.070.5A A A aA S =+⨯⨯=+=
80.60)
803.0748.1(9.20619.08.346)I I (h D H 6a 221221
=+⨯⨯⨯=+= 28.7470
.5018.29.20619
.08.34680.60hSa D H 62221
2
=⨯⨯⨯⨯+=+=αα
62.8=α
()()()()
0044062708130834803074812152A A H I I 522212212.........=+⨯+⨯⨯=++=μγ
818028748060221...===α
ατ
图6.4.6 双肢剪力墙
27m kN 10552E ⨯=.,由式(6.4.38)可求得0360a .=ψ,则等效刚度为 ()
()()
()2872
2110×862=0044
0×643+10360×8180+18030+7481×10×552=643+1+1+=
m kN .........I I E EI a eq ——γ
ψτ
(3)连梁内力计算
双肢墙的底部剪力为kN 780V 0=,由式(6.4.26)可求得第i 层连梁的约束弯矩为
()()()ξΦξΦα
αξΦ501851902780287480
60h V m 0221i ....=⨯⨯==
由式(6.4.27)和(6.4.28)可求得第i 层连梁的剪力和梁端弯矩分别为
()()ξΦξΦ82324705501851a m V i bi ...===
()()ξΦξΦ862592
6
1823242l V M b bi bi ...=⨯==
根据连梁位置可得连梁的相对高度ξ,由式(6.4.24)可求得()ξΦ,由此可计算求得各层连梁的
内力,各层连梁剪力如图6.4.7(a)所示,计算结果从略。
(4)墙肢内力计算
由式(6.4.29)—(6.4.31)可求得两墙肢的内力分别为
()()⎪⎪⎭⎫
⎝⎛
-⨯=⎪⎪⎭⎫ ⎝⎛-+=
∑
∑n
i
i p n
i i p 2
11
1i m M 6850m M I I I M ξξ. ()()⎪⎪⎭
⎫ ⎝⎛-⨯=⎪⎪⎭⎫ ⎝⎛
-+=∑
∑n
i
i p n
i i p 2122i m M 3150m M I I I M ξξ. ()()ξξp p 2
11
1i V 5800V I I I V ⨯=+=.'
'' ()()ξξp p 2
122i V 4200V I I I V ⨯=+=
.'''
∑=
-=n
i
bi
2i 1i V
N N
根据外荷载产生的弯矩()ξp M 和剪力()ξp V ,及连梁的约束弯矩i m 可求得各墙肢的内力,墙肢1的剪力、轴力和弯矩分别如图6.4.7(b)、(c)、(d)所示,计算结果从略, (5)顶点位移计算
m 606.01086.28.347806011EI H V 6011u 8
3eq 30=⨯⨯⨯==
(a ) (b ) (c ) (d )
图6.4.7 双肢墙连梁剪力及墙肢1内力图
[例题]某12层钢筋混凝土整体小开口剪力墙,如图6.6.3所示,混凝土强度等级为C25,承受倒三角形水平荷载。
试计算其顶点位移和底层各墙肢的内力。
[解] 首先计算各墙肢的几何参数,见表6.6.1。
表6.6.1 各墙肢的几何参数计算
组合截面的形心轴坐标为
m 574296
1925
5A
x A x j
j
j 0
...==
=
∑∑ 组合截面的惯性矩为各墙肢对组合截面形心轴的惯性矩之和,
即
底层总弯矩和总剪力分别为m kN 646761M i ⋅=.,kN 45291V i .=。
根据整体小开口墙的内力计算公式,可求得各墙肢的内力,见表6.6.2。
由于墙肢3较细小,其弯矩还按式(6.6.6)计算了附加弯矩。
表中负值表示受压墙肢。
表6.6.2 各墙肢底层的内力分配
剪力墙混凝土强度等级为C25,m kN 10802E 7⨯=.,故等效刚度为
272
72eq m kN 10976218342961521102191521
101080280AH I 91EI 80EI ⋅⨯=⨯⨯⨯+
⨯⨯⨯=+=.........μ
可求得顶点位移为
m 010201097621834452916011EI H V 6011u 7
3eq 30....=⨯⨯==
图6.6.3 整体小开口墙
∑∑
=+=+=42521
.1010.9421.1m y A I I j j j。
