第一章 Ⅱ 微专题二 (二)
第一篇 专题二 微专题2 板块模型的综合分析

微专题2板块模型的综合分析命题规律 1.命题角度:(1)牛顿运动定律在板块模型中的应用;(2)动量定理及动量守恒定律在板块模型中的应用;(3)能量观点在板块模型中的应用.2.常用方法:假设法、整体法与隔离法.3.常考题型:选择题、计算题.1.用动力学解决板块模型问题的思路2.滑块和木板组成的系统所受的合外力为零时,优先选用动量守恒定律解题;若地面不光滑或受其他外力时,需选用动力学观点解题.3.应注意区分滑块、木板各自相对地面的位移和它们的相对位移.用运动学公式或动能定理列式时位移指相对地面的位移;求系统摩擦生热时用相对位移(或相对路程).例1(2022·广东省模拟)如图甲所示,一右端固定有竖直挡板的质量M=2 kg的木板静置于光滑的水平面上,另一质量m=1 kg的物块以v0=6 m/s的水平初速度从木板的最左端P点冲上木板,最终物块在木板上Q点(图甲中未画出)与木板保持相对静止,物块和木板的运动速度随时间变化的关系图像如图乙所示.物块可视为质点.求:(1)图乙中v1、v2和v3的大小;(2)整个过程物块与木板之间因摩擦产生的热量.答案(1)4 m/s 3 m/s 2 m/s(2)12 J解析(1)根据题意可知,题图乙中图线a表示碰撞前物块的减速运动过程,图线b表示碰撞前木板的加速过程,图线c表示碰撞后木板的减速过程,图线d表示碰撞后物块的加速过程.物块与挡板碰撞前瞬间,物块的速度大小为v 1,此时木板速度大小v 木=1 m/s 从物块滑上木板到物块与挡板碰撞前瞬间的过程,根据系统动量守恒有 m v 0=m v 1+M v 木 解得v 1=4 m/s物块与挡板碰撞后瞬间,物块的速度为0,木板速度大小为v 2,从物块滑上木板到物块与挡板碰撞后瞬间的过程,根据系统动量守恒有 m v 0=M v 2 解得v 2=3 m/s2 s 末物块与木板共同运动的速度大小为v 3,从物块滑上木板到最终共同匀速运动的过程,根据系统动量守恒有 m v 0=(m +M )v3 解得v 3=2 m/s(2)物块与挡板碰撞前瞬间,系统的动能 E k1=12m v 12+12M v 木2=9 J物块与挡板碰撞后瞬间,系统的动能 E k2=12M v 22=9 J故碰撞过程系统没有机械能损失,物块滑上木板时系统的动能 E k0=12m v 02=18 J最终相对静止时系统的动能 E k3=12(m +M )v 32=6 J所以系统产生的热量 Q =E k0-E k3=12 J.例2 (2022·甘肃金昌市月考)如图所示,一质量M =3 kg 的小车由水平部分AB 和14光滑圆轨道BC 组成,圆弧BC 的半径R =0.4 m 且与水平部分相切于B 点,小物块Q 与AB 段之间的动摩擦因数μ=0.2,小车静止时左端与固定的光滑曲面轨道MN 相切,一质量为m 1=0.5 kg的小物块P 从距离轨道MN 底端高为h =1.8 m 处由静止滑下,并与静止在小车左端的质量为m 2=1 kg 的小物块Q (两物块均可视为质点)发生弹性碰撞,碰撞时间极短.已知除了小车AB 段粗糙外,其余所有接触面均光滑,重力加速度g =10 m/s 2.(1)求碰撞后瞬间物块Q 的速度;(2)求物块Q 在小车上运动1 s 时相对于小车运动的距离(此时Q 未到B 点且速度大于小车的速度);(3)要使物块Q 既可以到达B 点又不会从小车上掉下来,求小车左侧水平长度AB 的取值范围. 答案 (1)4 m/s ,方向水平向右 (2)83m (3)1.5 m ≤L ≤3 m解析 (1)物块P 沿MN 滑下,设末速度为v 0,由机械能守恒定律得m 1gh =12m 1v 02解得v 0=6 m/s物块P 、Q 碰撞,取向右为正方向,设碰后瞬间P 、Q 速度分别为v 1、v 2,由动量守恒定律得m 1v 0=m 1v 1+m 2v 2 由机械能守恒定律得 12m 1v 02=12m 1v 12+12m 2v 22 解得v 1=-2 m/s , v 2=4 m/s故碰撞后瞬间物块Q 的速度为4 m/s ,方向水平向右(2)物块Q 与小车相对运动,可由牛顿第二定律求得两者的加速度 a 2=-μm 2g m 2=-2 m/s 2,a 3=μm 2g M =23m/s 2物块Q 的位移x 2=v 2t +12a 2t 2=3 m小车的位移x 3=12a 3t 2=13 m解得s =x 2-x 3=83m(3)物块Q 刚好到达B 点时就与木板共速时AB 段最长,根据动量守恒定律有 m 2v 2=(m 2+M )v 3 可得共同速度为v 3=1 m/s由能量守恒定律得12m 2v 22=12(m 2+M )v 32+μm 2gL 1解得L 1=3 m物块Q 刚好回到A 点时与木板共速时,AB 段最短根据动量守恒定律可得共同速度仍为v 3= 1 m/s由能量守恒定律得12m 2v 22=12(m 2+M )v 32+2μm 2gL 2解得L 2=1.5 m当AB 段最短时需要验证物块Q 在圆弧上共速时上升高度是否超过R ,由能量守恒定律得 12m 2v 22=12(m 2+M )v 32+μm 2gL 2+m 2gH 解得H =0.3 m<R =0.4 m所以不会从圆弧轨道上滑出,则AB 段的长度范围为1.5 m ≤L ≤3 m.(2022·广东湛江市模拟)在光滑水平面上有一质量为2m 、足够长的小车,小车左端锁定着一块质量为m 的木板,两者一起以v 03的速度匀速向右运动.现有一颗质量也为m 的子弹以v 0的水平初速度从同一方向射入木板.若子弹在木板运动过程中所受到的阻力为恒力且等于其自身重力,重力加速度取g .(1)子弹恰好不从木板中穿出,则木板的长度L 为多少?(2)取木板的长度为5v 0236g ,解除对木板的锁定,如果子弹在木板内运动过程中,木板相对小车发生滑动,要使子弹不能从木板中射出,则木板与小车间的动摩擦因数μ应满足什么条件? 答案 (1)v 026g(2)μ≤0.2解析 (1)木板锁定在车上,子弹在穿入木板的过程,子弹、木板和小车组成的系统动量守恒, 有m v 0+(m +2m )v 03=(m +m +2m )v根据能量守恒F f L =12m v 02+12(m +2m )(v 03)2-12(m +m +2m )v 2又F f =mg 联立解得L =v 026g(2)木板和小车间有相对运动,则对木板和子弹受力分析,由牛顿第二定律得 a 木=F f -2μmg m =(1-2μ)ga 子=F f m =mg m=g故木板向右做匀加速直线运动,子弹向右做匀减速直线运动.子弹恰好不穿出木板,则子弹最终与木板共速且两者相对位移等于木板长度,设子弹与木板共速时的速度为v , 有v -v 03a 木=v 0-v a 子联立解得v =23-μ1-μv 0子弹位移x 子=v 02-v 22g木板位移x 木=v 2-(v 03)22(1-2μ)g ,x 子-x 木=5v 0236g联立以上各式解得μ=0.5或μ=0.2 当μ=0.5时,2μmg =F f木板与小车不会发生相对滑动,舍去.因动摩擦因数越小越难穿出木块,故满足子弹不穿出木板条件为μ≤0.2.专题强化练1.(多选)(2022·河北武安市第一中学高三检测)如图甲所示,小车B 紧靠平台边缘静止在光滑水平面上,物体A (可视为质点)以初速度v 0从光滑的平台水平滑到与平台等高的小车上(未冲出),物体和小车的v -t 图像如图乙所示,取重力加速度g =10 m/s 2,则以下说法正确的是( )A .物体A 与小车B 间的动摩擦因数为0.3 B .物体A 与小车B 的质量之比为1∶2C .小车B 的最小长度为2 mD .如果仅增大物体A 的质量,物体A 有可能冲出去 答案 AC解析 物体A 滑上小车B 后做匀减速直线运动,对物体A 分析有μm A g =m A a A ,由v -t 图像可得a A =Δv 1Δt =⎪⎪⎪⎪⎪⎪1-41 m/s 2=3 m/s 2,联立解得μ=0.3,所以A 正确;对小车B 分析有μm A g=m B a B ,由v -t 图像可得a B =Δv 2Δt =⎪⎪⎪⎪⎪⎪1-01 m/s 2=1 m/s 2,联立解得m A m B =13,所以B 错误;小车B 的最小长度为物体A 在小车B 上的最大相对滑动位移,则有L min =x A -x B =4+12×1 m-0+12×1 m =2 m ,所以C 正确;如果仅增大物体A 的质量,物体A 的加速度保持不变,但是小车B 的加速度增大,所以两者达到共速的时间减小了,则物体A 与小车B 的相对滑动位移减小,所以物体A 不可能冲出去,所以D 错误.2.(多选)(2022·福建福州市高三检测)如图所示,质量为M 的长木板A 以速度v 0在光滑水平面上向左匀速运动,质量为m 的小滑块B 轻放在木板左端,经过一段时间恰好从木板的右端滑出,小滑块与木板间动摩擦因数为μ,下列说法中正确的是( )A .若只增大m ,则小滑块不能滑离木板B .若只增大M ,则小滑块在木板上运动的时间变短C .若只增大v 0,则小滑块离开木板的速度变大D.若只减小μ,则小滑块滑离木板过程中小滑块相对地面的位移变大答案AB解析若只增大滑块质量,滑块的加速度大小保持不变,但木板的加速度增大,所以两者达到共速的时间减少了,则滑块在木板上的相对滑动位移减小,所以滑块不能滑离木板,A正确;若只增大长木板质量,木板的加速度减小,以木板为参考系,滑块运动的平均速度变大,即滑块在木板上的运动时间变短,B正确;若只增大木板初速度,滑块的受力不变,滑块的加速度不变,滑块相对木板的平均速度变大,滑块在木板上的运动时间变短,所以滑块离开木板的速度变小,C错误;若只减小动摩擦因数,那么滑块和木板的加速度均减小,相对位移不变,滑块相对木板的平均速度变大,滑块滑离木板的过程所用时间变短,木板相对地面的位移变小,滑块滑离木板过程中滑块相对地面的位移为板长加木板对地位移,故减小,D 错误.3.(多选)(2022·内蒙古海拉尔第二中学高三期末)如图甲所示,粗糙的水平地面上有一块长木板P,小滑块Q放置于长木板上的最右端.现将一个水平向右的力F作用在长木板的右端,让长木板从静止开始运动,一段时间后撤去力F的作用.滑块、长木板的v-t图像如图乙所示,已知滑块与长木板的质量相等,滑块Q始终没有从长木板P上滑下.重力加速度g=10 m/s2.则下列说法正确的是()A.t=9 s时长木板P停下来B.长木板P的长度至少是7.5 mC.滑块Q与长木板P之间的动摩擦因数是0.5D.滑块Q在长木板P上滑行的相对位移为12 m答案AB解析由题图乙可知,力F在t1=5 s时撤去,此时长木板P的速度v1=5 m/s,t2=6 s时两者速度相同,共同速度为v2=3 m/s,t2=6 s前长木板P的速度大于滑块Q的速度,t2=6 s 后长木板P的速度小于滑块Q的速度,0~6 s过程中,以滑块Q为研究对象,由题图乙知a1=0.5 m/s2,由牛顿第二定律得μ1mg=ma1,解得μ1=0.05,5~6 s过程中,以长木板P为研究对象,由题图乙知a2=2 m/s2,由牛顿第二定律得μ2(2m)g+μ1mg=ma2,解得μ2=0.075,从6 s 末到长木板停下来的过程中,由牛顿第二定律得μ2(2m )g -μ1mg =ma 3,解得a 3=1 m/s 2,这段时间Δt 1=v 2a 3=3 s ,所以t =9 s 时长木板P 停下来,故A 正确,C 错误;长木板P 的长度至少是前6 s 过程中滑块Q 在长木板P 上滑行的距离Δx 1=12×5×5 m +12×(5+3)×1 m -12×3×6 m =7.5 m ,故B 正确;在从6 s 末到滑块停下来的过程中,由牛顿第二定律得μ1mg =ma 4,解得a 4=0.5 m/s 2,这段时间Δt 1=v 2a 4=6 s ,所以t 3=12 s 时滑块Q 停下来,6 s 后滑块Q 在长木板P 上滑行的距离Δx 2=12×6×3 m -12×3×3 m =4.5 m ,前6 s 长木板P 速度更大,后6 s 滑块Q 速度更大,则滑块Q 在长木板P 上滑行的相对位移为Δx =Δx 1-Δx 2=3 m ,故D 错误.4.(2022·四川成都市月考)如图,长为L 的矩形长木板静置于光滑水平面上,一质量为m 的滑块以水平向右的初速度v 0滑上木板左端.①若木板固定,则滑块离开木板时的速度大小为v 03;②若木板不固定,则滑块恰好不离开木板.滑块可视为质点,重力加速度大小为g .求:(1)滑块与木板间的动摩擦因数μ; (2)木板的质量M ;(3)两种情况下,滑块从木板左端滑到右端的过程中,摩擦力对滑块的冲量大小之比I 1∶I 2. 答案 (1)4v 029gL(2)8m (3)3∶4解析 (1)木板固定时,滑块做匀减速直线运动,所受摩擦力大小为F f =μmg 由动能定理有-F f L =12m (v 03)2-12m v 02解得μ=4v 029gL.(2)木板不固定时,木板和滑块系统在相互作用过程中动量守恒,设两者共速时的速度为v ,由能量守恒定律有 μmgL =12m v 02-12(m +M )v 2由动量守恒定律有m v 0=(m +M )v 联立两式解得M =8m .(3)规定水平向右的方向为正方向,木板固定时,对滑块由动量定理有 I 1=m (v 03)-m v 0=-23m v 0木板不固定时滑块末速度由(2)知 v =m v 0m +M =v 09由动量定理有I 2=m v -m v 0=m (v 09)-m v 0=-89m v 0解得I 1∶I 2=3∶4.5.(2022·云南省玉溪第一中学高三检测)如图所示,质量M =0.9 kg 的木板A 静止在粗糙的水平地面上,质量m =1 kg 、可视为质点的物块B 静止放在木板的右端,t =0时刻一质量为m 0=0.1 kg 的子弹以速度v 0=50 m/s 水平射入并留在木板A 内(此过程时间极短).已知物块B 与木板A 间的动摩擦因数μ1=0.20,木板A 与地面间的动摩擦因数μ2=0.30,各接触面间的最大静摩擦力等于滑动摩擦力,且物块始终在木板上.取重力加速度大小g =10 m/s 2,求:(1)子弹射入木板过程中系统损失的机械能;(2)子弹“停”在木板内之后瞬间A 和B 的加速度大小; (3)最终物块B 停止运动时距离木板A 右端的距离. 答案 (1)112.5 J (2)8 m/s 2 2 m/s 2 (3)1.125 m解析 (1)子弹射中木板A 的过程动量守恒,有m 0v 0=(m 0+M )v 1 由能量守恒可知,子弹射入木板过程中系统损失的机械能为 ΔE =12m 0v 02-12(m 0+M )v 12解得v 1=5 m/s ,ΔE =112.5 J ;(2)子弹“停”在木板内之后瞬间对B 应用牛顿第二定律可得μ1mg =ma B ,对子弹与A 组成的整体应用牛顿第二定律可得μ1mg +μ2(m +m 0+M )g =(m 0+M )a A , 解得a A =8 m/s 2,a B =2 m/s 2;(3)子弹停在木板A 内之后,A 、B 发生相对滑动,A 减速,B 加速, 设经过时间t 1二者共速,有v 1-a A t 1=a B t 1 解得t 1=0.5 s ,此时二者速度为v2=a B t1=1 m/s,故此过程A与B相对地面的位移分别为x A=v1t1-12a A t12,x B=12a B t12,共速后,因为μ1<μ2,故二者分别做匀减速运动,对子弹与A组成的整体应用牛顿第二定律可得μ2(m+m0+M)g-μ1mg=(m0+M)a A′,对B应用牛顿第二定律可得μ1mg=ma B′,解得a A′=4 m/s2,a B′=2 m/s2,共速后A、B继续滑行的距离分别为x A′=v222a A′,x B′=v222a B′,故最终物块B停止运动时距离木板A右端的距离为Δx=(x A+x A′)-(x B+x B′),联立可得Δx=1.125 m.6.(2022·山西晋中市高三期末)如图所示,在水平地面上静置一质量为M=3 kg的木板A,在木板A的上面右侧放置一质量为m=1 kg的木块B(可视为质点).木块B与木板A之间的动摩擦因数μ1=0.1,木板A与地面之间的动摩擦因数μ2=0.2.一个底面光滑、质量也为M=3 kg 的木块C以速度v0=2 m/s与木板A发生弹性碰撞.重力加速度g取10 m/s2.(1)求碰后瞬间木板A获得的速度大小;(2)在木块B与木板A相对运动的过程中,若要保证木块B不从木板A上滑下,求木板A的最小长度.答案(1)2 m/s(2)0.5 m解析(1)设木块C与木板A碰后瞬间速度分别为v1、v2,木块C与木板A发生弹性碰撞,有M v0=M v1+M v212M v02=12M v12+12M v22代入数据解得v 1=0,v 2=v 0=2 m/s(2)碰后木板A 做减速运动,其加速度a 1=-μ1mg +μ2(m +M )g M=-3 m/s 2 木块B 做加速运动,其加速度a 2=μ1mg m=μ1g =1 m/s 2 设二者速度相同时速度为v ,有v -v 2a 1=v a 2解得v =0.5 m/s此过程中木板A 的位移为x 1=v 2-v 222a 1=58m 木块B 的位移为x 2=v 22a 2=18m 二者速度相同后,木板A 继续减速,假设B 相对A 向右滑动,则A 的加速度为a 3=μ1mg -μ2(m +M )g M =-73m/s 2 木块B 向右做减速运动,其加速度a 4=-μ1mg m=-μ1g =-1 m/s 2 因为|a 3|>|a 4|,假设成立.所以速度相同后,木块B 相对木板A 将向右运动,直至停止.A 向右减速到零的位移x 3=0-v 22a 3=356m A 减速到零时,由于μ1mg <μ2(m +M )g ,故保持静止.B 向右减速到零的位移为x 4=0-v 22a 4=18m 即B 先相对A 向左移动了x 1-x 2=0.5 m ,后相对A 向右移动了x 4-x 3=114m , 则要保证木块B 不从木板A 上滑下,木板A 的最小长度为L =x 1-x 2=0.5 m.7.(2022·山东省模拟)如图所示,一倾角为θ=37°的足够长斜面体固定在水平地面上,一质量为M =2 kg 的长木板B 沿着斜面以速度v 0=9 m/s 匀速下滑,现把一质量为m =1 kg 的铁块A轻轻放在长木板B 的左端,铁块恰好没有从长木板右端滑下,A 与B 间、B 与斜面间的动摩擦因数相等,最大静摩擦力等于滑动摩擦力,g =10 m/s 2,sin 37°=0.6,cos 37°=0.8,求:(1)铁块A 和长木板B 共速后的速度大小;(2)长木板的长度;(3)请用数值验证,铁块刚放上长木板左端时与达到共速时系统的总能量相等.答案 (1)6 m/s (2)2.25 m (3)见解析解析 (1)根据动量守恒定律有M v 0=(M +m )v解得v =6 m/s(2)根据题意可知μ=tan θ=0.75对铁块A 受力分析有mg sin θ+μmg cos θ=ma 1解得a 1=12 m/s 2对长木板受力分析有Mg sin θ-μmg cos θ-μ(M +m )g cos θ=Ma 2解得a 2=-6 m/s 2经过时间t 速度相等,有v =v 0+a 2t =a 1t铁块运动位移x 1=v 2t =1.5 m 长木板运动位移x 2=v 0+v 2t =3.75 m 长木板的长度l =x 2-x 1=2.25 m(3)系统动能的变化量ΔE k =12(M +m )v 2-12M v 02=-27 J 铁块重力势能的变化量ΔE p1=-mgx 1sin θ=-9 J长木板重力势能的变化量ΔE p2=-Mgx2sin θ=-45 J长木板与斜面之间摩擦产生的热量Q1=μ(M+m)gx2cos θ=67.5 J铁块与长木板之间摩擦产生的热量Q2=μmgl cos θ=13.5 J因为ΔE k+ΔE p1+ΔE p2+Q1+Q2=0 故系统能量守恒.。
微专题2 二次不等式恒成立与能成立问题

微专题2 二次不等式恒成立与能成立问题
视角 1 在R上恒成立问题
1 若 关 于 x 的 不 等 式 x2 - mx + m + 1 > 0 恒 成 立 , 则 实 数 m 的 取 值 范 围 为 ____________________.
变式 已知f(x)=ax2+x-a,a∈R,若不等式f(x)>-2x2-3x+1-2a对一切实数x
B.0,47 D.47,+∞
()
3.若存在实数 x,使得 mx2-(m-2)x+m<0 成立,则实数 m 的取值范围为( )
A.(-∞,2) C.-∞,23
B.(-∞,0]∪13,32 D.(-∞,1)
4.若不等式x2+px>4x+p-3,当0≤p≤4时恒成立,则x的取值范围是 ( )
A.[-1,3]
3 (1) 若 关 于 x 的 不 等 式 ax2 + 2x + 1 < 0 有 实 数 解 , 则 实 数 a 的 取 值 范 围 是 _____________.
(2)若关于x的不等式x2-6x+2-a>0在区间[0,5]内有解,则实数a的取值范围是 _____________.
变式 已知关于x的不等式mx2-6x+3m<0在(0,2]上有解,那么实数m的取值范
6.(多选)命题“∀x∈R,2kx2+kx-38<0”为真命题的一个充分不必要条件是
A.-3<k<0
B.-3<k≤0
()
C.-3<k<-1
D.k>-3
7.已知关于x的不等式x2-ax+1≥0在区间[1,2]上有解,则实数a的取值范围为
___________.
8 . 若 不 等 式 kx2 + 2kx - 1 < 0 对 一 切 实 数 x 都 成 立 , 则 实 数 k 的 取 值 范 围 为
高考二轮复习专题二微专题(二)提高农作物产量的措施课件(22张)

作物 株高(cm) 光饱和点(μmol·m-2·h-1)
甲
乙 丙丁
170 65 59 165
1 200 1 180 560 623
4.某研究小组的实验:在某些因素的作用和影响下可以获得不同产量的 春黑麦。实验结果如下图所示,请据图回答下列问题:
(1)据图可知影响春黑麦产量的因素有_光__照__强__度__、__土__壤__湿__度__和__施__肥__情__况__。
(1)在绿色植物细胞光合作用过程中,RuBP羧化酶(Rubisco)催化暗反应中 _C_O__2_的__固__定__,在光反应提供的_A_T__P_和__N_A__D_P_H__作用下,生成有机物。
(2)据图分析可知,在光呼吸过程中,Rubisco催化__O__2__与RuBP反应, 生成的_C_2_(_乙__醇__酸__)_经一系列反应,最终分解为CO2。光呼吸被冠以“呼 吸”二字,你认为理由是_光__呼__吸__过__程__中__消__耗__O_2_并__生__成__C_O__2_,__与__有__氧__呼__吸__ _过__程__相__似__(提示:从与有氧呼吸进行比较的角度回答)。
(5)除图所示的因素外,若要进一步提高春黑麦的产量,还可以采取哪些 措施?(答出两点)_合__理__密__植__;__适__当__提__高__C_O__2浓__度__;__温__度__要__适__宜__等___。
5.(2021·山 东 高 三 三 模 ) 光 呼 吸 是 在光的驱动下将有机物氧化生成 CO2和水的一个高耗能反应,据估 计光呼吸可损耗掉1/4的光合产物, 降低光呼吸,成为提高作物产量的 研究方向之一。我国科学家通过转基因技术,将相关基因导入水稻细胞并 将其定位在叶绿体中,成功构建了一条新的光呼吸支路,使光呼吸产生的 部分乙醇酸在叶绿体内完全分解为CO2,所获得的新型转基因水稻的光合 效率和产量均大幅提高。绿色植物细胞中光合作用和光呼吸的过程如上图 所示。据图分析回答:
第一章 微专题2 匀变速直线运动推论及应用

微专题2 匀变速直线运动推论及应用1.凡问题中涉及位移及发生这段位移所用时间或一段运动过程的初、末速度时,要尝试运用平均速度公式.2.若问题中涉及两段相等时间内的位移或相等Δv 的运动时可尝试运用Δx =aT 2.3.若从静止开始的匀加速直线运动,涉及相等时间或相等位移时,则尝试应用初速度为零的比例式.1.如图所示,一汽车在平直公路上做匀变速直线运动,依次经过A 、B 、C 、D 四棵树,已知汽车经过AB 段、BC 段和CD 段所需的时间分别为t 、2t 、3t ,在AB 段和CD 段发生的位移分别为x 1和x 2,则该汽车运动的加速度为( )A.x 2-x 1t 2B.x 2-x 16t 2C.x 2-3x 112t 2D.x 2-3x 118t 2答案 C解析 设汽车的加速度为a ,根据“匀变速直线运动中间时刻的速度等于这段时间内的平均速度”这一推论,AB 段中间时刻的速度v 1=x 1t ,CD 段中间时刻的速度v 2=x 23t ,结合加速度的定义,有a =v 2-v 1t 2+2t +3t 2,联立解得a =x 2-3x 112t 2,C 正确.2.一辆公共汽车进站后开始刹车,做匀减速直线运动,开始刹车后的第1 s 内和第2 s 内位移大小依次为8 m 和6 m ,则( ) A .公共汽车的加速度大小为3 m/s 2 B .第2 s 末的速度大小为7 m/s C .刹车后6 s 内的位移大小为18 m D .公共汽车的初速度大小为9 m/s 答案 D解析 根据Δx =aT 2得,汽车刹车的加速度a =6-81 m/s 2=-2 m/s 2,即公共汽车的加速度大小为2 m/s 2,故A 错误;根据x 1=v 0t 1+12at 12,代入数据解得v 0=9 m/s ,则第2 s 末的速度大小为v 2=v 0+at =(9-2×2) m/s =5 m/s ,故B 错误,D 正确;汽车开始刹车到停下的时间t 0=0-v 0a =4.5 s ,刹车后6 s 内的位移大小等于前4.5 s 内的位移,即x =v 02t 0=92×4.5 m =20.25 m ,故C 错误.3.(多选)小辉是一名体育特长生,特长为100米短跑,假设百米训练中,前6 s 内做匀加速直线运动,其中第2 s 内的位移是2.5 m ,第5 s 内的位移是7.5 m ,则下列说法正确的是( ) A .前6 s 内加速度为53 m/s 2B .第3 s 末速度为5 m/sC .第2 s 内平均速度为1.25 m/sD .第3 s 初至第4 s 末,这两秒内位移为10 m 答案 ABD解析 根据x 5-x 2=3aT 2,可求得加速度为a =53 m/s 2,故A 正确;第2 s 内平均速度v 2=x 2T =2.5 m/s ,故C 错误;第1.5 s 末速度与第2 s 内平均速度相同,则由速度时间关系式可得第3 s 末速度为x 3=2.5 m/s +53×1.5 m/s =5 m/s ,故B 正确;第3 s 初至第4 s 末,这两秒内平均速度为第3 s 末速度5 m/s ,所以这两秒内位移为10 m ,故D 正确.4.如图所示,一小滑块沿足够长的斜面以初速度v 向上做匀减速直线运动,依次经A 、B 、C 、D 到达最高点E ,已知AB =BD =6 m ,BC =1 m ,滑块从A 到C 和从C 到D 所用的时间都是2 s .设滑块经C 时的速度为v C ,则( )A .滑块上滑过程中加速度的大小为0.5 m/s 2B .vC =6 m/s C .DE =3 mD .从D 到E 所用时间为2 s 答案 A解析 由题意知,AC =7 m ,CD =5 m ,根据Δx =aT 2得加速度为a =Δx T 2=5-722 m/s 2=-0.5 m/s 2,故A 正确;C 点的速度等于AD 段的平均速度,则有v C =x AC +x CD 2T =7+54m/s=3 m/s ,故B 错误;根据速度位移公式得,CE 间的距离为CE =0-v C 22a =0-322×(-0.5) m=9 m ,则DE =9 m -5 m =4 m ,故C 错误; 采用逆向思维,根据x DE =12at 2,得t =2x DE a=2×40.5s =4 s ,故D 错误. 5.蹦极是一项刺激的户外休闲活动,可以使蹦极者在空中体验几秒钟的“自由落体”.如图所示,蹦极者站在高塔顶端,将一端固定的弹性长绳系在腰上,然后双臂伸开,双腿并拢,头朝下跳离高塔.设弹性绳的原长为L ,蹦极者下落第一个L5时速度的增加量为Δv 1,下落第五个L5时速度的增加量为Δv 2,把蹦极者视为质点,蹦极者离开塔顶时的速度为零,不计空气阻力,则Δv 1Δv 2满足( )A .1<Δv 1Δv 2<2B .2<Δv 1Δv 2<3C .3<Δv 1Δv 2<4D .4<Δv 1Δv 2<5答案 D解析 蹦极者下落高度L 的过程为初速度为零的匀加速直线运动,通过连续相等位移的时间之比为1∶(2-1)∶(3-2)∶(2-3)∶(5-2)∶…,可知t 1t 2=15-2=5+2,即4<t 1t 2<5,根据Δv =gt ,可得4<Δv 1Δv 2<5,故D 正确,A 、B 、C 错误.6.(2023·重庆市高三质检)钢架雪车也被称为俯式冰橇,是北京冬奥会的比赛项目之一.运动员需要俯身平贴在雪橇上,以俯卧姿态滑行.比赛线路由起跑区、出发区、滑行区及减速区组成.若某次运动员练习时,恰好在终点停下来,且在减速区间的运动视为匀减速直线运动.运动员通过减速区时间为t ,其中第一个t 4时间内的位移为x 1,第四个t4时间内的位移为x 2,则x 2∶x 1等于( ) A .1∶16 B .1∶7 C .1∶5 D .1∶3 答案 B解析 由题意知,在减速区间的运动视为匀减速直线运动,且最终减为零,将此减速过程由逆向思维,可看作初速度为零的匀加速直线运动,则根据初速度为零的匀加速直线运动在连续相等时间内位移之比为1∶3∶5∶…可知,x 2∶x 1之比即为初速度为零的匀加速直线中第一个t 4时间内的位移与第四个t4时间内的位移之比,即x 2∶x 1=1∶7,故选B. 7.一个物体做末速度为零的匀减速直线运动,关于该物体在减速运动的倒数第3 m 、倒数第2 m 、最后1 m 内的运动,下列说法中正确的是( ) A .经历的时间之比是1∶2∶3 B .平均速度之比是3∶2∶1C .平均速度之比是1∶(2-1)∶(3-2)D .平均速度之比是(3+2)∶(2+1)∶1 答案 D解析 将物体所做末速度为零的匀减速直线运动看成反方向的初速度为零的匀加速直线运动,根据初速度为零的匀加速直线运动的推论可知,经历的时间之比是(3-2)∶(2-1)∶1,A 错误;平均速度公式为v =xt ,x 都是1 m ,则得,平均速度与时间成反比,则有平均速度之比是(3+2)∶(2+1)∶1,D 正确,B 、C 错误.8.一辆汽车以6 m/s 的速度沿平直公路匀速行驶,突然发现前方有障碍物,立即刹车,汽车以大小2 m/s 2的加速度做匀减速直线运动,则下面说法正确的是( ) A .第1 s 内与第3 s 内的位移之差3 m B .刹车的整个过程平均速度大小为3 m/sC .刹车后1 s 内与刹车后4 s 内汽车通过的位移之比为5∶8D .刹车的第1 s 内、第2 s 内、第3 s 内的位移之比为3∶2∶1 答案 B解析 汽车从刹车到停止的时间为t 0=v 0a =3 s ,则从刹车到停止的位移为x =v 022a =9 m ,刹车的整个过程平均速度大小为v =93 m/s =3 m/s ,由逆向思维,汽车反向做初速度为零的匀加速直线运动,可得刹车的第1 s 内、第2 s 内、第3 s 内的位移之比为5∶3∶1,则刹车后第1 s 内的位移为5 m ,第2 s 内的位移为3 m ,第3 s 内的位移为1 m ,可得第1 s 内与第3 s 内的位移之差4 m ,汽车刹车后1 s 内与刹车后4 s 内汽车通过的位移之比为5∶9.故选B.。
2022年高考化学二轮复习第一篇 专题2 微专题2 一定物质的量浓度溶液的配制

2.(高考题组合)配制一定物质的量浓度的溶液在科研领域有着广泛的应用。 下列说法正确 的是( ) A.(2019·江苏高考)将 4.0 g NaOH 固体置于 100 mL 容量瓶中,加水至刻度,配制 1.000 mol·L-1 NaOH 溶液 B.(2019·天津高考改编)配制一定浓度溶液时的定容实验操作如图所示: C.(2018·浙江选考)容量瓶洗净后须用酒精灯加热干燥 D.(2018·全国卷Ⅱ)配制 250 mL 0.400 0 mol·L-1 NaOH 溶液的实验过程:称取 4.00 g 固体 NaOH 于烧杯中,加入少量蒸馏水溶解,冷却后转移至 250 mL 容量瓶中定容 【解析】选 D。配制一定物质的量浓度溶液时,固体不能直接在容量瓶中溶解,A 项错误; 配制一定浓度的溶液定容时,胶头滴管不能伸入容量瓶中,B 项错误;容量瓶洗净后不需 要进行干燥处理,可直接使用,C 项错误。
(2)注意事项 ①容量瓶使用前必须检漏、洗涤,但不能润洗; ②只能配制一定体积的溶液,即不能配制任意体积的一定物质的量浓度的溶液; ③转移溶液时,溶液的温度应为室温,玻璃棒要靠在瓶颈刻度线以下。 2.容量瓶的使用 (1)查漏操作
(2)容量瓶使用时的注意事项 ①不能将固体或浓溶液直接在容量瓶中溶解或稀释; ②不能作为反应容器或用来长期贮存溶液; ③不能配制任意体积的溶液,只能配制容量瓶上规定容积的溶液。 3.容量瓶读数误差的图示分析:
一定物质的量浓度溶液的配制中的误差分析 3.(2021·山东省实验中学高三 3 月份月考)利用碳酸钠晶体(Na2CO3·10H2O)来配制 0.5 mol·L-1 的碳酸钠溶液 1 000 mL,假如其他操作均是准确无误的,下列情况会引起配制 溶液的浓度偏高的是( ) A.称取碳酸钠晶体质量 100 g B.定容时俯视刻度线 C.移液时,没有对用于溶解碳酸钠晶体的烧杯进行冲洗 D.定容、摇匀、静置后发现液面低于刻度线,于是又加入少量水至刻度线 【解析】选 B。配制 0.5 mol·L-1 的碳酸钠溶液 1 000 mL,需称取 Na2CO3·10H2O 质量 143 g, 称取 100 g 碳酸钠晶体,浓度偏低;定容时俯视刻度线,会造成所配溶液的体积偏小,浓度 偏高,B 符合题意;未冲洗溶解碳酸钠晶体的烧杯,会造成碳酸钠损失,浓度偏低;发现 液面低于刻度线,又加少量水导致浓度偏低。
第(1)章 微专题2 氧化还原反应中的基本规律课件高一上学期化学人教版

(3)歧化规律 氧化还原反应中,有原子化合价升高,必然有原子化合价降低。某物质发 生歧化反应时,中间价态―→高价态+低价态。
3.强弱规律 还原剂+氧化剂===氧化产物 + 还原产物 (强还原性)(强氧化性) (弱氧化性)(弱还原性) 还原性:还原剂>还原产物;氧化性:氧化剂>氧化产物。即“强制弱” 或“前强后弱”。 应用:物质间氧化性(或还原性)强弱的比较或判断氧化剂(或还原剂)和有还 原性(或氧化性)的物质在一定条件下能否发生反应。
【 跟 踪 训 练 3 】 已 知 在 热 的 碱 性 溶 液 中 , NaClO 发 生 如 下 反 应 :
3NaClO===2NaCl + NaClO3 。 在 相 同 条 件 下 NaClO2 也 能 发 生 类 似 的 反 应,其最终产物是( B )
A.NaCl、NaClO
B.NaCl、NaClO3
(3)判断I2与FeCl2能否共存?__能__(填“能”或“否”)。 【解析】 由反应①知氧化性:FeCl3>I2,还原性:KI>FeCl2;由反应 ② 知 氧 化 性 : Cl2 > FeCl3 , 还 原 性 : FeCl2 > Cl - ; 由 反 应 ③ 知 氧 化 性 : KMnO4 > Cl2 , 还 原 性 : Cl - > Mn2 + 。 由 此 推 知 : 氧 化 性 强 弱 顺 序 为 KMnO4>Cl2>FeCl3>I2。(3)氧化性:FeCl3>I2,I2与FeCl2不反应,能共 存。
(2)已知氮元素有多种可变化合价,常见的有-3、+2、+3、+4、+5价 等。某同学写出以下三个化学方程式(未配平): ①NO+HNO3―→N2O3+H2O ②NH3+NO―→HNO2+H2O ③N2O4+H2O―→HNO3+HNO2
根据价态规律,判断上述反应是否有可能实现,说明判断的理由。 【答案】 ①可能,反应物中的氮元素为+2价、+5价,生成物中为+3 价,符合归中反应规律。 ②不可能,反应物中的氮元素为-3价、+2价,生成物中为+3价,N元素 的化合价只升不降。 ③可能,反应物中的氮元素为+4价,生成物中为+3价、+5价,符合歧 化反应规律。
高中地理选择性必修一 练透试卷 第一章 第二节 微专题2 太阳视运动
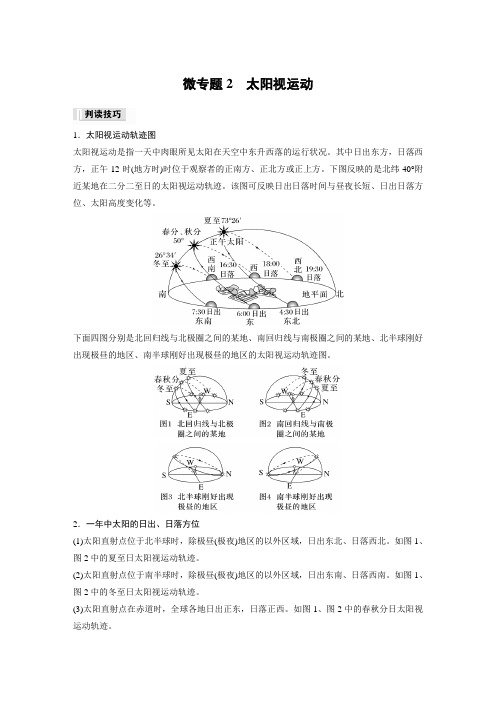
微专题2太阳视运动1.太阳视运动轨迹图太阳视运动是指一天中肉眼所见太阳在天空中东升西落的运行状况。
其中日出东方,日落西方,正午12时(地方时)时位于观察者的正南方、正北方或正上方。
下图反映的是北纬40°附近某地在二分二至日的太阳视运动轨迹。
该图可反映日出日落时间与昼夜长短、日出日落方位、太阳高度变化等。
下面四图分别是北回归线与北极圈之间的某地、南回归线与南极圈之间的某地、北半球刚好出现极昼的地区、南半球刚好出现极昼的地区的太阳视运动轨迹图。
2.一年中太阳的日出、日落方位(1)太阳直射点位于北半球时,除极昼(极夜)地区的以外区域,日出东北、日落西北。
如图1、图2中的夏至日太阳视运动轨迹。
(2)太阳直射点位于南半球时,除极昼(极夜)地区的以外区域,日出东南、日落西南。
如图1、图2中的冬至日太阳视运动轨迹。
(3)太阳直射点在赤道时,全球各地日出正东,日落正西。
如图1、图2中的春秋分日太阳视运动轨迹。
(4)北半球刚好出现极昼的地区:日出正北、日落正北。
如图3中的太阳视运动轨迹。
(5)南半球刚好出现极昼的地区:日出正南、日落正南。
如图4中的太阳视运动轨迹。
3.正午太阳的方位(极昼与极夜地区除外)(1)直射点以北地区:太阳始终位于正南。
如图1中二分二至日的太阳视运动轨迹,图3中的太阳视运动轨迹。
(2)直射点以南地区:太阳始终位于正北。
如图2中二分二至日的太阳视运动轨迹,图4中的太阳视运动轨迹。
(3)在直射点上:太阳始终位于正上方。
4.一天中太阳方位的变化(以北半球为例,极昼、极夜地区除外)(1)春、秋分:正东→东南→正南→西南→正西。
(2)直射点在北半球,且位于直射点以北的地区:东北→正东→东南→正南→西南→正西→西北。
(3)直射点在北半球,且直射的地区:东北→正上方→西北。
(4)直射点在北半球,且位于直射点以南的地区:东北→正北→西北。
(5)直射点在南半球:东南→正南→西南。
5.昼长与日出日落时间在北半球,昼越长,日出越早,日落越晚,日出日落的位置越偏北,太阳视运动的弧度越大;反之,在北半球,昼越短,日出越晚,日落越早,日出日落位置越偏南,太阳视运动的弧度越小。
高考物理一轮复习 第一章 微专题2 匀变速直线运动规律——推论公式法练习(含解析)教科版-教科版高三

微专题2 匀变速直线运动规律——推论公式法方法点拨1.凡问题中涉与位移与发生这段位移所用时间或一段运动过程的初末速度时,要尝试平均速度公式.2.假设问题中涉与两段相等时间内的位移,或相等Δv的运动时可尝试运用Δx=aT2. 1.(2020·河北武邑中学月考)做匀加速直线运动的质点在第一个3s内的平均速度比它在第一个5s内的平均速度小3m/s.如此质点的加速度大小为( )A.1m/s2B.2m/s2C.3m/s2D.4m/s22.(2019·四川成都市高新区模拟)一小球沿斜面匀加速滑下,依次经过A、B、C三点,AB =6m,BC=10m,小球经过AB和BC两段所用的时间均为2s,如此小球经过A、B、C三点时的速度大小分别是( )A.2m/s,3m/s,4m/sB.2m/s,4m/s,6m/sC.3m/s,4m/s,5m/sD.3m/s,5m/s,7m/s3.(2019·福建省六校联考)假设一位同学在某星球上完成自由落体运动实验:让一个质量为2kg的物体从一定的高度自由下落,测得在第5s内的位移是18m(未落地),如此( ) A.物体在2s末的速度大小是20m/sB.物体在第5s内的平均速度大小是3.6m/sC.物体在前2s内的位移大小是20mD.物体在5s内的位移大小是50m4.(2019·安徽蚌埠市第二次质检)图1中ae为港珠澳大桥上四段110m的等跨钢箱连续梁桥,假设汽车从a点由静止开始做匀加速直线运动,通过ab段的时间为t,如此通过ce段的时间为( )图1A.t B.2t C.(2-2)t D.(2+2)t5.(多项选择)一物体在粗糙地面上以一定的初速度匀减速滑动.假设物体在第1s 内位移为 8.0m ,在第3s 内位移为0.5m .如此如下说法正确的答案是( ) A .物体的加速度大小一定为4.0m/s 2B .物体的加速度大小一定为3.75m/s 2C .物体在第0.5s 末速度一定为8.0m/sD .物体在第2.5s 末速度一定为0.5m/s6.(多项选择)如图2,一长为L 的长方体木块可在倾角为α的斜面上以加速度a 匀加速下滑,1、2两点间的距离大于L ,木块经过1、2两点所用的时间分别为t 1和t 2,如此如下说法正确的答案是( )图2A .木块前端从点1到点2所用时间为t 1-t 22+L a ·⎝ ⎛⎭⎪⎫1t 2-1t 1 B .木块前端从点1到点2所用时间为L a ⎝ ⎛⎭⎪⎫1t 2-1t 1C .木块通过点2的平均速度为L t 2D .1、2两点间的距离是L 22a ⎝ ⎛⎭⎪⎫1t 22-1t 127.(2020·宁夏银川市检测)一质点做匀加速直线运动时,速度变化Δv 时发生位移x 1,紧接着速度变化同样的Δv 时发生位移x 2,如此该质点的加速度为( )A .(Δv )2⎝ ⎛⎭⎪⎫1x 1+1x 2B .2Δv 2x 2-x 1C .(Δv )2⎝ ⎛⎭⎪⎫1x 1-1x 2D.Δv 2x 2-x 1答案精析1.C [根据匀变速直线运动的规律可知,第一个3s 内的平均速度为第1.5s 末的速度;第一个5s 内的平均速度为第2.5s 末的速度.如此由a =Δv Δt 可得a =31m/s 2=3m/s 2,应当选C.]2.B [根据物体做匀加速直线运动的特点,两点之间的平均速度等于中间时刻的瞬时速度,故B 点的速度就是AC 段的平均速度,v B =AB +BC2t=4m/s ;又因为两个连续相等时间间隔内的位移之差等于恒量,即Δx =at 2,如此由Δx =BC -AB =at 2,解得a =1m/s 2;再由速度公式v t =v 0+at ,解得v A =2m/s ,v C =6m/s ,应当选项B 正确.]3.D [设该星球外表的重力加速度为g ,由自由下落在第5s 内的位移是18m ,可得12g ×(5s)2-12g ×(4s)2=18m ,如此g =4m/s 2.所以物体在2s 末的速度大小为8m/s ,选项A 错误;物体在第5s 内的平均速度大小为18m/s ,选项B 错误;物体在前2s 内的位移大小是12g ×(2s)2=8m ,选项C 错误;物体在5s 内的位移大小是12g ×(5s)2=50m ,选项D 正确.]4.C [设汽车的加速度为a ,经过bc 段、ce 段的时间分别为t 1、t 2,x ab =12at 2,x ac =12a (t+t 1)2,x ae =12a (t +t 1+t 2)2,解得:t 2=(2-2)t ,应当选C.]5.AC [假设物体一直做匀减速直线运动,在第3s 末未停下来,根据匀变速直线运动规律可知,某段时间内的平均速度等于该段时间的中间时刻的瞬时速度,故t 1=0.5s 时刻的瞬时速度v 1=8.0m/s ,t 2=2.5s 时刻的瞬时速度为v 2=0.5m/s ,根据加速度的定义式可得加速度大小为a 1=v 1-v 2t 2-t 1=3.75m/s 2,如此物体从0.5s 时刻开始到停下来所用时间为t =v 1a 1=3215s ,即物体整个运动时间为0.5s +3215s <3s ,故假设不成立,v 2并非2.5s 时刻的瞬时速度,物体一定在3s 时刻之前停止运动.设物体在2s 时刻后再运动t 0时间停下,如此v 1=a (1.5s +t 0),2s 时刻物体的速度为v 2′=v 1-a ×1.5s,从2s 时刻开始到物体停下来的这段时间内,即t 0时间内物体运动的位移x =v 2′t 0-12at 02=0.5m ,解得t 0=0.5s ,a =4m/s 2,故物体实际上在2.5s 时刻停止运动,此后静止,选项A 、C 正确,B 、D 错误.]6.AC [设木块前端通过点1后t 12时刻的速度为v 1′,通过点2后t 22时刻的速度为v 2′,由匀变速直线运动平均速度的推论有v 1′=Lt 1,v 2′=L t 2,木块前端从点1到点2所用时间t =v 2′-v 1′a +t 12-t 22=t 1-t 22+L a ⎝ ⎛⎭⎪⎫1t 2-1t 1,故A 正确,B 错误;木块通过点2的时间为t 2,经历的位移为L ,如此木块通过点2的平均速度为Lt 2,故C 正确;木块前端经过点1的速度v 1=L t 1-a t 12,木块前端经过点2的速度v 2=L t 2-a t 22,如此1、2两点间的距离x =v 22-v 122a ≠L 22a ⎝ ⎛⎭⎪⎫1t 22-1t 12,故D 错误.] 7.D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[示例]
咏柳(贺知章)
碧玉妆成一树高,
万条垂下绿丝绦。
不知细叶谁裁出,
二月春风似剪刀。
[赏析] 诗人由柳枝的纷披下垂、婀娜多姿联想到翠绿的丝带,运用巧妙
的比喻,塑造出一个别具浪漫色彩的新颖形象。
[表现手法] 想 象
[说明] 在已有材料和观念的基础上,经过联想、推断、分析、综合,
创造出新的观念的思维过程。
[示例]
秋思(张籍) 洛阳城里见秋风,
欲作家书意万重。
复恐匆匆说不尽,
行人临发又开封。
[赏析] “行人临发又开封”这个细节显示出诗人对家书的重视和对亲 人的深切思念——千言万语,唯恐遗漏了一句。
注 ①描写是古诗最常用的表达方式之一,它有许多方法与表现手法有 重合之处。除这里介绍的白描、虚实结合、动静结合、正侧结合、细节 描写外,描写还有观察角度多变、声形色描写及多种感官描写等。②借 景抒情、托物言志既是抒情方式,又是表现手法,两者重合,参见前面 “古诗常见抒情方式”。
[赏析] 该联俯仰所见所闻,一连出现六个特写镜头,渲染秋江景物的 特点。
[表现手法] 白 描
[说明] 用最朴素、最简练的笔墨,抓住所写对象的特征,如实地勾勒出
人物、事物与景物的情态面貌。
[示例]
田家(聂夷中)
父耕原上田,
子 山下荒。
六月禾未秀,
官家已修仓。
[赏析] 描绘了一幅父子辛勤劳作、官家修筑粮仓的画面,表现了封建统
返回
练一练
1.阅读下面这首诗,然后回答问题。 水村闲望 俞紫芝①
画桡两两枕汀沙,隔岸烟芜一望赊。 翡翠②闲居眠藕叶,鹭鸶别业在芦花。 溪云淡淡迷渔屋,野旆翩翩露酒家。 可惜一绷③真水墨,无人写得寄京华。 注 ①俞紫芝:笃信佛教,仕途失意后终身不娶不仕。②翡翠:翠鸟。 ③绷:布幅。
本诗颔联和王维的“月出惊山鸟,时鸣春涧中”(《鸟鸣涧》)都是写鸟, 但在内容和手法上有何不同? 答案 俞诗写翠鸟和鹭鸶的“闲”居,刻画鸟栖宿的状态,是静景;王 诗写月下鸟鸣,着意于写声,是动景。俞诗用鸟“闲”居来衬托诗人的 “闲”望,是正衬(或“以静衬静”);王诗用鸟鸣来衬托春山月夜的幽静, 是反衬(或“以动衬静”)。
实景空余桃花,以虚衬实,意境凄美。
[表现手法] 动静结合
[说明] 对事物、景物作动态、静态的描写,两者相互映衬,构成一种
Hale Waihona Puke 情趣。[示例]漫成一首(杜甫)
沙头宿鹭联拳静,
船尾跳鱼拨剌鸣。
[赏析] 第二句鱼跳的“动”更衬托出前一句景物的“静”。
[表现手法] 正侧结合
[说明] 对描写对象进行正面的直接的描写是正面描写。描写周围的事
答案
返回
物,使描写对象更鲜明、突出的是侧面描写。
[示例]
梦游天姥吟留别(李白)
天姥连天向天横,
势拔五岳掩赤城。
天台四万八千丈,
对此欲倒东南倾。
[赏析] 前两句主要是运用正面描写,表现天姥山的高峻奇伟之势;后两
句则是用侧面描写烘托天姥山的高峻奇伟。
[表现手法] 细节描写
[说明] 用极细腻的笔法,精细地描绘人或事。
[赏析] 前三句描写昔日繁荣和最后一句描写今日冷落凄凉形成强烈的 对比,使读者感受特别深切,其中蕴涵着诗人深沉的历史思考。
[表现手法] 象 征
[说明] 通过特定的、容易引起联想的具体形象,表现与之有相似或相近
特点的概念、思想和感情。
[示例]
登崖州城作(李德裕) 青山似欲留人住,
百匝千遭绕郡城。 [赏析] 这两句描写青山环绕、层峦叠嶂,自己所处的郡城正处在严密 封锁、重重阻隔之中。象征了自己被政敌迫害的景况,抒写了思归不得
答案
2.阅读下面这首唐诗,然后回答问题。 访秋[注] 李商隐
酒薄吹还醒,楼危望已穷。 江皋当落日,帆席见归风。 烟带龙潭白,霞分鸟道红。 殷勤报秋意,只是有丹枫。 注 此诗为诗人客居桂林时所作。
颈联与尾联运用了哪些表现手法?请简要分析其表达效果。 答案 ①色彩(视觉)描写。烟白、霞红,秋色正丽,色彩对比鲜明。 ②寓情于景。诗人危楼远眺,寻找桂林秋意,字里行间,寄寓着异域思 乡之情。[颈联有比喻,尾联有拟人;两联有衬托(反衬)或乐景写哀情]faq
[赏析] 要塑造的人物形象是周瑜,却从“千古风流人物”写起,由此 引出赤壁之战时的“多少豪杰”,最后才集中为周瑜一人,突出了周瑜 在词人心中的主要地位。
[表现手法] 对比对照 [说明] 把两种不同的事物或情形作对照,互相比较,突出强调。
[示例]
越中览古(李白) 越王勾践破吴归, 战士还家尽锦衣。 宫女如花满春殿, 只今惟有鹧鸪飞。
第一章 核心知识再强化 Ⅱ 阅读核心知识再强化
微专题二 熟读古诗鉴赏核心知识
(二)古诗常用表现手法
栏目索引
一、读一读 二、练一练
读一读
古诗常用表现手法一览表
[表现手法] 衬托烘托
[说明] 指的是以乙托甲,使甲的特点或特质更加突出。有正衬和反衬两种。
[示例]
念奴娇·赤壁怀古(苏轼)
大江东去,浪淘尽,千古风流人物。故垒西边,人道是,三国周郎赤壁。
治者剥削、压榨农民的深刻主题。
[表现手法] 虚实结合
[说明] 是指现实的景事与想象(回忆)的景事互相映衬,交织在一起表达
感情,拓展意境,表情更为深远。
[示例]
题都城南庄(崔护)
去年今日此门中,
人面桃花相映红。
人面不知何处去,
桃花依旧笑春风。
[赏析] “去年今日”是虚景,“今年今日”是实景,虚景有花有人,
[示例]
望洞庭(刘禹锡)
湖光秋月两相和,
潭面无风镜未磨。
遥望洞庭山水色,
白银盘里一青螺。
[赏析] 这首诗选择月夜遥望的角度,通过极富想象力的描写,将洞庭
的湖光山色别出心裁地再现于纸上。
[表现手法] 渲 染 [说明] 对环境、景物作多方面的描写形容,以突出形象,加强艺术效果。
[示例]
登高(杜甫) 风急天高猿啸哀, 渚清沙白鸟飞回。
的忧伤。
[表现手法] 起 兴 [说明] 兴,先言他物以引起所咏之辞。
[示例]
关雎(《诗经》) 关关雎鸠,在河之洲。 窈窕淑女,君子好逑。
[赏析] 借雎鸟一声声的互相和鸣起兴,引起男子无限的情思。
[表现手法] 联 想
[说明] 由一事物联系到与之有关的另一事物,或把事物中类似的特点联
系起来造成一个典型。
