2.7 弧长及扇形的面积
弧长与扇形面积知识点总结

弧长与扇形面积知识点总结圆是数学中常见的几何图形之一,而与圆相关的知识点也是我们学习数学不可或缺的一部分。
其中,弧长和扇形面积是圆的两个重要概念。
本文将对弧长和扇形面积这两个知识点进行总结,并介绍其计算公式和应用。
一、弧长弧长是指圆周的一部分长度,它与圆的半径和圆心角有关。
圆心角是以圆心为顶点的角,其对应的弧称为弧度。
下面是计算弧长的公式:弧长 = 弧度 ×半径其中,弧度是以弧长与圆心角所对应的弧度数。
要计算弧度,可以使用以下公式:弧度 = 圆心角/360° × 2π在计算弧长时,需要注意圆心角的单位应与弧度的单位一致,如都是弧度或都是角度。
二、扇形面积扇形是圆中的一部分,由圆心角和两条半径所围成。
扇形的面积是扇形所占的圆的面积。
为了方便计算扇形面积,我们需要了解如下公式:扇形面积 = 扇形的圆心角/360° × πr²其中,r是扇形的半径,π是一个近似值,约等于3.14。
计算扇形面积时,需要将圆心角的单位与面积的单位保持一致。
三、应用案例1. 弧长应用假设一辆车以10m/s的速度绕一个半径为20m的圆形跑道做匀速圆周运动,问车在15秒内行驶的弧长是多少?解:首先,我们需要计算圆心角:圆周长= 2πr = 2π × 20 = 40π m车在15秒内行驶的弧长 = 10m/s × 15s = 150m2. 扇形面积应用一块土地位于一个半径为10m的花圃内,其夹角为60°,问这块土地的面积是多少?解:首先,计算扇形的面积:扇形面积= 60°/360° × π×10² = 1/6 × π × 100 ≈ 52.36m²四、总结弧长和扇形面积是圆的重要概念,它们的计算可以帮助我们解决各种实际问题。
在计算弧长时,需要了解弧度的概念,并注意圆心角的单位。
弧长和扇形面积的计算

弧长和扇形面积的计算弧长和扇形面积是圆的基本性质,在几何学和数学运算中经常使用。
本文将介绍如何计算弧长和扇形面积,并提供示例以便更好地理解。
一、弧长的计算弧长是圆上一段弧的长度。
要计算弧长,需要知道弧所对应的圆的半径(r)和弧的夹角(θ)。
公式:L = 2πr × (θ/360°)其中,L表示弧长,r表示半径,θ表示夹角。
示例1:如果半径为5 cm的圆的夹角为60°,则弧长可以通过以下计算得到:L = 2π × 5 cm × (60°/360°) = 10π/3 cm ≈ 10.47 cm示例2:如果半径为8 m的圆的夹角为120°,则弧长计算如下:L = 2π × 8 m × (120°/360°) = 16π/3 m ≈ 16.76 m二、扇形面积的计算扇形面积是圆的一部分,由弧与两个半径所围成。
要计算扇形面积,需要知道扇形所对应的圆的半径(r)和扇形的夹角(θ)。
公式:A = πr² × (θ/360°)其中,A表示扇形面积,r表示半径,θ表示夹角。
示例3:如果半径为10 cm的圆的夹角为90°,则扇形面积计算如下:A = π × (10 cm)² × (90°/360°) = 25π cm² ≈ 78.54 cm²示例4:如果半径为6 m的圆的夹角为150°,则扇形面积可以通过以下计算得到:A = π × (6 m)² × (150°/360°) = 9π m² ≈ 28.27 m²通过上述示例,我们可以看到如何计算弧长和扇形面积。
这两个计算都使用了圆周率(π),在具体计算时,可以使用3.14或根据需要的精度使用更多位小数。
弧长和扇形面积公式

弧长和扇形面积公式在几何学中,弧长和扇形面积是与圆形和圆的扇形相关的重要概念和计算方法。
这些公式可以用于解决许多几何问题,例如计算圆的周长、计算弧长和扇形的面积等。
本文将详细介绍关于弧长和扇形面积的公式及其推导过程。
首先,我们先来介绍一下什么是圆和圆的扇形。
圆是一个平面上所有点到一个固定点的距离都相等的图形。
而圆的扇形则是由半径为r的圆上的一段弧和两条半径所围成的图形。
1.弧长公式:弧长是圆上一段弧的长度,由于圆在数学上具有无限个点,所以我们可以定义一个角度来度量弧长。
我们知道圆的一周是360度,因此弧长的度量可以用度数或弧度来表示。
当我们用度数来度量弧长时,弧长和弧度的关系可以由以下公式得到:弧长=弧度×半径该公式是通过比较整个圆的周长与360度的比例得到的。
当我们用弧度来度量弧长时,弧度的定义是:圆的半径等于半径所对应的弧长的度数。
因此,当我们用弧度来度量弧长时,直接使用半径和弧度的乘积即可表示弧长。
2.扇形面积公式:扇形是由圆心、圆上一段弧和两条半径所围成的图形。
扇形的面积就是扇形所覆盖的圆的面积。
扇形面积可以由以下公式得到:扇形面积=(弧度÷2π)×πr²该公式是通过将圆的面积与圆的周长的比例乘以扇形所对应的弧长所得到的。
推导过程如下:假设圆的半径为r,圆心角为θ度,则该圆心角所对应的弧长为:弧长=(θ÷360)×2πr由于扇形是由半径为r的圆上一段弧和两条半径所围成的,所以扇形的面积可以表示为:扇形面积=(θ÷360)×πr²化简得到:扇形面积=(θ÷2π)×πr²将弧度用θ表示,得到最终的扇形面积公式:扇形面积=(弧度÷2π)×πr²需要注意的是,使用上述公式计算扇形面积时,角度必须使用弧度表示。
如果给出的是度数,则需将角度转换为弧度后再进行计算。
沪科版数学九年级下册《24.7 弧长与扇形面积》教学设计1

沪科版数学九年级下册《24.7 弧长与扇形面积》教学设计1一. 教材分析《24.7 弧长与扇形面积》是沪科版数学九年级下册的教学内容。
这部分内容主要包括弧长的计算公式、扇形面积的计算公式以及弧长和扇形面积在实际问题中的应用。
教材通过实例引入弧长和扇形面积的概念,然后引导学生通过观察、思考、探索,得出弧长和扇形面积的计算公式。
这部分内容是圆相关知识的重要组成部分,对于学生理解和掌握圆的相关概念和计算方法具有重要意义。
二. 学情分析九年级的学生已经学习了平面几何的基本知识,对图形的性质和计算方法有一定的了解。
但是,对于弧长和扇形面积的计算,学生可能还比较陌生。
因此,在教学过程中,需要引导学生通过观察、思考、探索,自己发现弧长和扇形面积的计算公式。
同时,学生需要具备一定的逻辑思维能力和空间想象力,能够将实际问题抽象为数学问题,并运用所学知识解决实际问题。
三. 教学目标1.理解弧长和扇形面积的概念,掌握弧长和扇形面积的计算公式。
2.能够将实际问题抽象为数学问题,运用弧长和扇形面积的计算公式解决实际问题。
3.培养学生的观察能力、思考能力和探索能力,提高学生的逻辑思维能力和空间想象力。
四. 教学重难点1.弧长和扇形面积的概念理解。
2.弧长和扇形面积的计算公式的推导和应用。
3.将实际问题抽象为数学问题,并运用所学知识解决实际问题。
五. 教学方法1.引导观察法:通过观察实例,引导学生发现弧长和扇形面积的计算规律。
2.探索法:引导学生通过思考、探索,自己得出弧长和扇形面积的计算公式。
3.实例教学法:通过实际问题,引导学生将所学知识应用于解决实际问题。
4.小组合作学习法:引导学生分组讨论,共同解决问题,提高学生的合作能力。
六. 教学准备1.教学课件:制作课件,展示实例和计算公式的推导过程。
2.教学素材:准备一些实际问题,用于引导学生运用所学知识解决实际问题。
3.计算器:为学生提供计算器,方便他们进行计算。
七. 教学过程1.导入(5分钟)通过展示一些与圆相关的实例,如自行车轮子、地球仪等,引导学生观察和思考这些实例中圆的弧长和面积的计算方法。
弧长公式及扇形面积公式
知识点1、弧长公式因为360°的圆心角所对的弧长就是圆周长C=2R,所以1°的圆心角所对的弧长是,于是可得半径为R的圆中,n°的圆心角所对的弧长l的计算公式:,说明:(1)在弧长公式中,n表示1°的圆心角的倍数,n和180都不带单位“度”,例如,圆的半径R=10,计算20°的圆心角所对的弧长l时,不要错写成。
(2)在弧长公式中,已知l,n,R中的任意两个量,都可以求出第三个量。
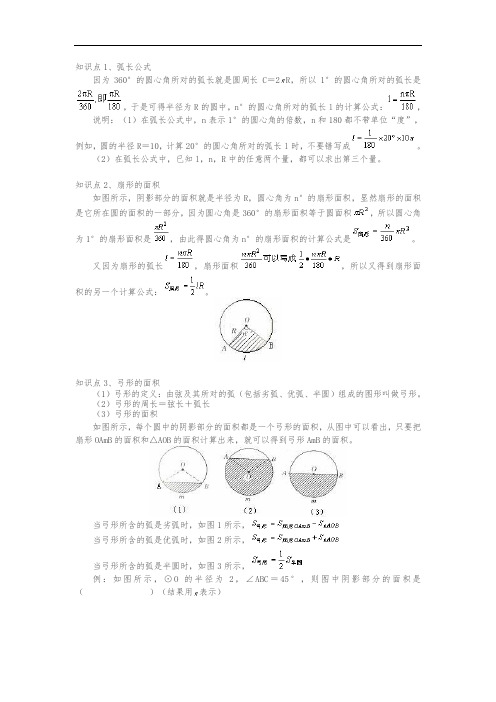
知识点2、扇形的面积如图所示,阴影部分的面积就是半径为R,圆心角为n°的扇形面积,显然扇形的面积是它所在圆的面积的一部分,因为圆心角是360°的扇形面积等于圆面积,所以圆心角为1°的扇形面积是,由此得圆心角为n°的扇形面积的计算公式是。
又因为扇形的弧长,扇形面积,所以又得到扇形面积的另一个计算公式:。
知识点3、弓形的面积(1)弓形的定义:由弦及其所对的弧(包括劣弧、优弧、半圆)组成的图形叫做弓形。
(2)弓形的周长=弦长+弧长(3)弓形的面积如图所示,每个圆中的阴影部分的面积都是一个弓形的面积,从图中可以看出,只要把扇形OAmB的面积和△AOB的面积计算出来,就可以得到弓形AmB的面积。
当弓形所含的弧是劣弧时,如图1所示,当弓形所含的弧是优弧时,如图2所示,当弓形所含的弧是半圆时,如图3所示,例:如图所示,⊙O的半径为2,∠ABC=45°,则图中阴影部分的面积是()(结果用表示)分析:由图可知由圆周角定理可知∠ABC=∠AOC,所以∠AOC=2∠ABC=90°,所以△OAC是直角三角形,所以,所以注意:(1)圆周长、弧长、圆面积、扇形面积的计算公式。
圆周长弧长圆面积扇形面积公式(2)扇形与弓形的联系与区别图示面积。
扇形面积公式和弧长公式

扇形面积公式和弧长公式
扇形所对应的弧长公式为:L=n2πR/360。
扇形面积计算公式:S=nπR/360或S=LR/2。
扇形面积公式描述了扇形面积和圆心角(顶角)、半径、所对弧长的关系。
推导过程:由定理“等半径的两个扇形的面积之比等于它们的弧长之比”,将圆看作扇形,利用弧长公式和圆的面积公式即可。
简介:组成部分:1、圆上A、B两点之间的的部分叫做“圆弧”简称“弧”,读作“圆弧AB”或“弧AB”。
2、以圆心为中心点的角叫做“圆心角”。
3、有一种统计图就是“扇形统计图。
”曲线的弧长也称曲线的长度,是曲线的特征之一。
不是所有的曲线都能定义长度,能够定义长度的曲线称为可求长曲线。
最早研究的曲线弧长是圆弧的长度,所以狭义上,特指圆弧的长度。
半径为R的圆中,n°的圆心角所对圆弧的弧长为nπR/180°。
六年级扇形面积和弧长公式

六年级扇形面积和弧长公式
扇形的面积公式
(1)扇形面积S=l×r/2,其中l为扇形的弧长,r为扇形的半径。
(2)扇形面积S=圆心角的角度×π×r²/360°。
(3)扇形面积S=圆心弧度绝对值|a|×r²/2。
扇形的弧长公式
(1)弧长l=(n÷180)×π×r,其中l是弧长,n是扇形圆心角,π是圆周率,r是扇形半径。
(2)弧长l=|α|×r,l是弧长,其中|α|是弧l所对的圆心角的弧度数的绝对值,r是半径。
扇形的周长公式
周长C=2r+(n÷360)πd,其中n为扇形所对的圆心角的度数,d为扇形的直径。
周长C=2r+(n÷180)πr,其中n为扇形所对的圆心角的度数,r为扇形的半径。
扇形简介
一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形。
显然,它是由圆周的一部分与它所对应的圆心角围成。
圆上A、B两点之间的的部分叫做“圆弧”简称“弧”,读作“圆弧AB”或“弧AB”。
以圆心为中心点的角叫做“圆心角”。
计算扇形面积的公式

扇形面积公式扇形面积S=弧长L×半径/ 2推导过程:S=πR²×L/2πR=LR/2扇形面积S=圆周率π3.14 ×半径r²×弧长L/ 2×圆周率π3.14×半径=弧长L×半径/ 2(L=│α│·R)(弧度制)循环链条扇形面积计算公式:扇形面积S=圆心弧度绝对值|a|×半径r²/ 2圆心弧度绝对值|a| =扇形面积S×2 /半径r²弧长L=圆心弧度绝对值|a|×半径r扇形面积S=弧长L×半径r / 2扇形(符号:⌔),是圆的一部分,由两个半径和和一段弧围成,在较小的区域被称为道小扇形,较大的区域被称为大扇形。
在右图版中,θ是扇形的角弧度,r是圆的半径,L是小扇形的弧长。
圆弧为180°的扇形称为半圆。
其他圆弧角的扇形有时给予其特别的名字,其中包括象限角(90°)、六分角(60°)以及八分角(45°),它们分别是整圆权的1/4、1/6、1/8。
练习:1.如图,扇形AOB中,OA=2,C为上的一点,连接AC,BC,如果四边形AOBC 为平行四边形,则图中阴影部分的面积为()A.B.C.D.2.如图,在扇形AOB中,∠AOB=90°,OA=2,点D在OA上,连接BD,点C 在AB上,且点C,O关于直线BD对称,连接CD,则图中阴影部分的面积是()A.﹣B.π﹣C.﹣D.﹣3.如图,在圆心角为90°的扇形OAB中,半径OA=2,C为的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为()A.πB.C.D.4.如图,在Rt△ABC中,∠C=90°,CA=CB=4,分别以A、B、C为圆心,以AC 为半径画弧,三条弧与边AB所围成的阴影部分的面积是()A.8﹣4πB.8﹣πC.16﹣2πD.8﹣2π5.如图,扇形AOB的圆心角是60°,半径是,点C为弧AB的中点,过点C作CD∥OB交DA于点D,过点B作BE∥OA交DC延长线于点E,则图中阴影部分面积为()A.B.C.D.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课堂总结
1.弧长、扇形面积公式; 2.不规则图形的面积的求法:用规则的图 形的面积来表示; 3.数学思想转化的应用: ①转化思想;②整体思想.
2.7 弧长及扇形的面积
课后作业
课本P85第1、2、3、4.
2.7 弧长及扇形的面积
cm
50 答:此圆弧的长度为 cm 3
2.7 弧长及扇形的面积
请你练一练
(1)已知圆弧的半径为24,所对的圆心角为
60°,它的弧长为__________.
(2)已知一弧长为12πcm,此弧所对的圆心
角为240°,则此弧所在圆的半径为_________.
回顾
如下图,由组成圆心角的两条半径 和圆心角所对的弧围成的图形是扇形。
1 lr 2
在这两个公式中,弧长和扇形面积都和圆心 角n°、半径r有关系,因此l 和S之间也有一 定的关系,你能得出吗?
2.7 弧长及扇形的面积
请你想一想
(1)一个扇形的弧长为20πcm,半径为24cm,
则该扇形的面积为_______. (2)扇形的圆心角为60°,半径为5cm,则这 个扇形的弧长为_______, 这个扇形的面积为 ______. (3)已知扇形的圆心角为120°,弧长为20π, 扇形的面积为 .
4
问题探究
上面求的是的圆心角900所对的弧长,若圆心角 为n0,如何计算它所对的弧长呢?
思考:
请同学们计算半径为 r,圆心角分别为1800、900、 450、n0所对的弧长。
图 23.3.2
圆心角占整个周角的
1800
所对弧长是
180 360 90 360 45 360 n 360
180 2r 360 90 2r 360 45 2r 360
2.7 弧长及扇形的面积
典型例题
例1 如图,△ABC是⊙O的内接三角形,
∠BAC=60°.设⊙O的半径为2,求
长.
⌒ BC
的
2.7 弧长及扇形的面积
典型例题
例2 如图,折扇完全打开后,OA、OB的 夹角为120°,OA的长为30cm,AC的长为20cm, 求图中阴影部分的面积S.
2.7 弧长及扇形的面积
B 弧 O 圆心角 A O A B
扇形
1.圆心角是3600的扇形面积是多少?
2.圆心角是1800的扇形面积是多少? 3.圆心角是900的扇形面积是多少? 4.圆心角是2700的扇形面积是多少? 1 1个圆面 个圆面积 1个圆面积 3 个圆面积 积 2 4 4
圆心角是10的扇形面积是多少?
圆心角是10的扇形面积是圆面积的
1 360
圆心角为n0的扇形面积是多少?
圆心角是n0的扇形面积是圆面积的
n 360
如果用字母 S 表示扇形的面积, n表示圆心角的度数,r 表示圆半径, 那么扇形面积的计算公式是: n n 2 S扇形= 360 S圆 = 360 πr
l
n 弧=180 πr
n S扇形= 360
nr r πr2 = 180 2
拓展提升
如图,半圆的直径AB=40,C、D是半圆 的3等分点.求弦AC、AD与 ⌒ CD 围成的阴 影部分的面积.
1.如图,⊙A、⊙B、⊙C、⊙D相互外离,它们的 半径都是1,顺次连接四个圆心得到四边形 ABCD,则图形中四个扇形(阴影部分)的面积之 和是___________.
●
●
●
ห้องสมุดไป่ตู้
●
2.7 弧长及扇形的面积
初中数学 九年级(上册)
2.7 弧长及扇形的面积
作 者:吴正龙 安丰初中
知识回顾
圆的周长公式 o
r
p
C=2πr
圆的面积公式
2 S=πr
问题情景:
如图是圆弧形状的铁轨示意图,其中铁轨的半径 为100米,圆心角为90°.你能求出这段铁轨的 长度吗? 解:∵圆心角900
1 ∴铁轨长度是圆周长的 图 23.3.1 4 1 2 100 50米 则铁轨长是
900
450
n0
n 2r 360
结论:
如果弧长为l,圆心角度数为n,圆的半径为r,那 么,弧长的计算公式为:
n nr l 2r 360 180
练一练:
已知圆弧的半径为50厘米,圆心角为60°,求此 圆弧的长度。 n nr 2r 解:l 360 180
50 = 3
