基于ARMA_GARCH模型的股市量价动态关系研究
基于ARMA—GARCH模型的股票价格分析及预测

的时间序列 ( 见图 1 ) ,可以看 出差分序列 已经呈现相对平稳
若A R多项式 有单位根 1 ,则 A R MA模 型就变成了 A R I .
MA模型 ,则单位根是非平稳 的。处理单 位根非 平稳性 的惯
的趋势 ,只是在第 1 1 0天前后有较 大的波动 。为 了验证观 察 出的结果 ,我们分别对差分前后的序列做平稳性检验。
动平均的阶数 ,它们 都是 非负整 数。A R和 M A模 型是 A R - MA ( P ,q )的特殊情形 。如 果特征 方程所 有根 的绝对值 都
小于 1 ,则该 A R M A模型是弱平稳的 。这时 ,模型 的无 条件 均值为 E ( r ) =机/ ( 1 一 一 . - ) 。
个 A R C H ( m)模 型。
和J B 分别称为 A R C H 参 数 和
G A R C H参数。
2 A R MA ( p ,q )模型的建立
2 . 1 数据选取
的预测方法 ,能够 为投 资者 的决 策提供一些帮助 。 1 . 2 A R MA ( P ,q )模 型简介
一
t =( r l l , = 0 +2 t 一 ‘ +2 c r ‘ - j ‘
i= l J=1
其中 { 8 }是均值 为 0 、方差为 1的独立 同分布 随机变
3 . 0 5 8 4 , 检 验 的 P值 是 0 . 0 3 3 9 1 ,表 明拒 绝 单 位 根 检验 假 设 ,
对 3月最后 三个交 易 日的收盘价进行预测 ,预测值与真 实值 非常接近 ,能够为有关该只股票的决策提供 一定的帮助。
[ 关键词 ]股票价格预测 ;A R MA模型 ;G A R C H模 型 ;条件异方差
基于ARMA—EGARCH—M模型的沪深股市波动性分析

J1 07 u .2 0
基 于 ARMA— GARCH— 模 型 的 E M 沪深 股 市 波动 性 分 析
何 帮强 , 惠 军
200) 3 0 9 ( 肥工业 大学 理学院 ,安徽 合肥 合
摘Leabharlann 要: 文章讨论 了 AR H模 型族 的拟合 波动性 的优缺点 , C 建立 A RMAE RC M 模 型 , — GA H— 简要说 明 了此模 AE - GAR H— 模 型进行 拟合分析 , C M 结果表 明该模 型能更有 效地拟 合我 国沪深股市 的波动
HE a g qa g, HUIJ n B n - in u
( h o fS in e ,H ee ie st fTe h lgy,H ee 3 0 9,Chn ) c s o lo ce c s fiUnv riy o c noo fi2 0 0 ia
Ab ta t I iw ft ea v n a ea d d a a k o h a i fARCH d l i ua ig t ev l- sr c :n ve o h d a t g n r wb c ft efm l o y mo esi sm lt h oa n n
Ke r s ARCH d l ywod : mo e ;GARCH d l mo e ;DGARCH o e ;ARM A — m dl EGARCH— d l ee o c — M mo e ;h t r s e
d sii a tct y
0 引
言
峰厚 尾性 的影 响 , 它 却 难 以很好 地 处 理 收 益 率 但 分布 的有 偏性 , 该 模 型 对 系 数 的非 负 性 约 束 太 且
tl y o ia ca ak t 。h i t ff n il r e s t eARM A— i n m EGARCH — o e ul a disa v n a ee p an d b if . M m d l sb i n d a t g x lie re l i t t y
沪市股票市场效率的分析_基于ARMA_GARCH模型

现代商业MODERN BUSINESS56资本市场的发展目标是形成一个高效率、资源合理配置的的市场。
而衡量市场的效率与资源配置的合理性的一个重要标志就是资本市场的有效性。
只有资本市场有效,信息在价格中才能得到充分的反映,才能实现资本的有效配置。
股票市场作为我国经济体制的重要部分,已经运行了二十年,为我国的经济发展助送了鲜活的血液。
但其作为资本配置的市场,对我国的经济资源是否实现了合理有效的配置,不仅是政府部门所关心的问题,对各经济主体筹资与投资的决策也有着巨大深远的影响。
所以对股票市场有效性的研究无疑有着巨大的意义。
一、ARMA-GARCH模型的介绍ARMA是用于描述随机过程既具有自回归过程的特性又具有移动平均过程的特性。
模型ARMA(p,q)的一般表达式为但人们在实践中发现,ε之间并非满足独立同分布的假定,反而具有很强的聚类相关性,而且值的分布也呈尖峰厚尾的特征,与假设有一定的差异。
为了更真实的反映现实的情况,于是提出了GARCH模型,对ARMA模型进行改进,从而更好地描述金融时间序列中出现的条件方差时变、波动集束和宽尾现象。
为了描述波动的非对称性,人们又对GARCH模型进行修正,提出了非对称波动的TGARCH模型,EGARCH模型,PARCH模型等。
此处仅以TGARCH为例,另几种模型与其类似。
二、ARMA-GARCH模型的应用方法运用ARMA-GARCH模型分析股票市场效率/应该按照以下几个步骤进行。
1.划分市场有效性检验市场的有效性,首先应对市场的有效性程度进行划分。
现在被普遍接受的是Fama提出的市场有效性假说(EfficientMarketHypothesis,简称EMH)。
根据获得信息的不同,EMH将有效的市场分为三种形式:弱式有效、半强式有效和强式有效。
在弱式有效假设的市场里,价格只包括以往价格的信息集;在半强式有效假设的市场里,价格包括以往价格信息和其他共享的信息;在强式有效假设的市场里,价格包括了市场子集独享的信息以及所有可共享的信息。
基于GARCH族模型的我国股市的波动性及联动性实证研究的开题报告

基于GARCH族模型的我国股市的波动性及联动性实证研究的开题报告一、研究背景和意义股市波动性及联动性作为风险管理的重要研究领域,一直备受关注。
在全球化的背景下,股市波动性和联动性越来越受到国内外研究者的关注,而GARCH族模型具有广泛的应用价值,可用于量化分析金融市场中的波动性并进行风险管理。
因此,对于我国股市的波动性及联动性进行实证研究,对于有效预测市场风险、提高资产的配置效率等具有重要的实际意义。
二、研究内容和方法本研究将选取我国股市中的代表性指数作为研究对象,采用GARCH 族模型,对股市中存在的波动性和联动性进行深入研究。
具体来讲,研究将从以下几个方面展开:1. 对我国股市中代表性指数的波动性进行测算,并探究其波动性的特点和趋势变化。
2. 基于GARCH族模型,对我国股市中不同指数的波动性进行建模,探究其模型参数的变化规律。
3. 将建立的模型应用于风险管理领域,探究其对于风险的预测和分析的能力;4. 基于GARCH族模型,分析我国股市中不同指数之间的联动性,探究其联动关系及波动性的传染效应。
三、研究预期成果通过本研究,预期可以得到以下成果:1. 揭示我国股市中存在的波动性和联动性特点和趋势变化,并探究其背后的原因和机制。
2. 建立GARCH族模型,并对我国股市中不同指数的波动性进行模型拟合,对风险进行预测和分析,为风险管理提供一定的支持和帮助。
3. 基于GARCH族模型,探究我国股市中不同指数之间的联动关系,为投资者提供合理的资产配置建议。
四、研究的实施计划本研究从2022年2月开始,预计在2023年底完成。
具体的实施计划如下:1. 第一年:调研前沿文献,整理参考资料,初步构建研究框架,并制定实验方案和数据采集计划,进行资料的搜集和整理,学习量化分析理论和工具。
2. 第二年:对股市中代表性指数的波动性进行实证研究,开展波动性的特征分析与测算,并对GARCH族模型进行建模。
3. 第三年:对股市中不同指数的波动性进行建模,并对风险进行预测和分析,探究其对于风险管理的作用,并对联动关系进行研究和分析,撰写论文,完成毕业论文。
基于ARIMA-GARCH模型的股票价格预测研究

基于ARIMA-GARCH模型的股票价格猜测探究一、引言股票市场是金融市场中最重要和最具活力的组成部分之一。
准确猜测股票价格对投资者和股票来往者来说至关重要。
浩繁探究者使用不同的方法和模型来猜测股票价格,其中ARIMA-GARCH模型已被证明在猜测股票价格方面具有很高的准确性和可靠性。
本文将对ARIMA-GARCH模型的股票价格猜测方法进行探究和探讨。
二、ARIMA模型ARIMA模型是指自回归挪动平均模型,它是通过对时间序列数据进行拟合和猜测的一种方法。
ARIMA模型包括差分整合自回归挪动平均模型。
差分是指对时间序列数据进行差分来消除数据的非平稳性,整合是指将差分后的时间序列数据转化为平稳序列,自回归是指使用过去时间点的数据进行拟合和猜测,挪动平均是指使用过去时间点的误差项进行拟合和猜测。
三、GARCH模型GARCH模型是指广义自回归条件异方差模型,它是ARIMA模型的一个扩展,用于建模和猜测时间序列数据的波动率。
GARCH 模型包括ARCH模型和GARCH模型。
ARCH模型用于描述时间序列数据的条件异方差性,GARCH模型在ARCH模型的基础上引入了过去时间点的波动率信息,可以更准确地猜测时间序列数据的波动。
四、ARIMA-GARCH模型ARIMA-GARCH模型是将ARIMA模型和GARCH模型相结合的一种方法,用于猜测股票价格。
ARIMA-GARCH模型可以有效地处理时间序列数据的非平稳性和波动性,并提供准确的股票价格猜测结果。
ARIMA-GARCH模型起首使用ARIMA模型对时间序列数据进行差分和拟合,然后使用GARCH模型对拟合后的序列数据的波动性进行建模和猜测。
最后,将ARIMA模型和GARCH模型的猜测结果结合起来,得到最终的股票价格猜测结果。
五、实证探究为了验证ARIMA-GARCH模型在股票价格猜测中的有效性,我们选择了某股票的历史价格数据作为样本数据,分别使用ARIMA模型、GARCH模型和ARIMA-GARCH模型进行猜测,并比较它们的猜测结果。
GARCH模型对研究股市交易量与股价关系的作用

GARCH模型对研究股市交易量与股价关系的作用本文运用Granger因果检验和扩展GARCH模型实证研究了深圳A股市场交易量与股价之间的关系。
得到了如下结论:交易量变量和收益率、波动率存在双向Granger因果关系;交易量只能在有限程度内解释波动率的持续性,深圳股市还存在其他影响波动率持续性的因素。
标签:交易量波动性Granger因果关系GARCH模型一、引言证券市场中的量价关系是指证券价格的波动与交易量之间的关系,对量价关系的研究近年来日益受到金融界的重视。
通过量价关系的研究,能够帮助了解金融市场的微观结构,揭示价格波动产生的根源。
Clark首次提出了混合分布假说(the Mixture Distribution Hypothesis, 简称MDH)。
在而后的发展中,Tauchen 和Pitts建立了量价关系的二元混合模型(Bivarite Mixture model),Andersen对模型进行改进,他在Glosten和Milgrom的理论框架的基础上, 形成了修正的混合分布模型(MMM)。
Andersen认为信息的不对称和流动性的需求是产生信息到达的交易量的原因。
Lamoureux 和Lastrapes 把交易量变量加入到GARCH模型的条件方差方程,证实了把交易量作为信息流的替代指标对价格波动具有很强的解释能力。
二、研究方法和模型选择首先,本文对深圳股市中成交量是否对收益率、波动性产生影响进行了检验。
如果成交量对收益率和波动性有影响,则成交量和收益率、波动性两两之间应存在Granger因果关系。
反之,则说明成交量对收益率和波动性没有影响。
其次,本文分析了交易量能在多大程度上解释收益波动率的GARCH效应。
如果金融资产的收益服从混合分布理论,每日信息到达的不同会导致不同的资产收益波动, 而GARCH模型正好刻画了每日到达信息的相关性。
因此,若引入交易量变量后能解释股价波动的GARCH效应,则说明交易量可以作为信息到达的替代变量。
基于GARCH_M模型的中国股市量价关系研究
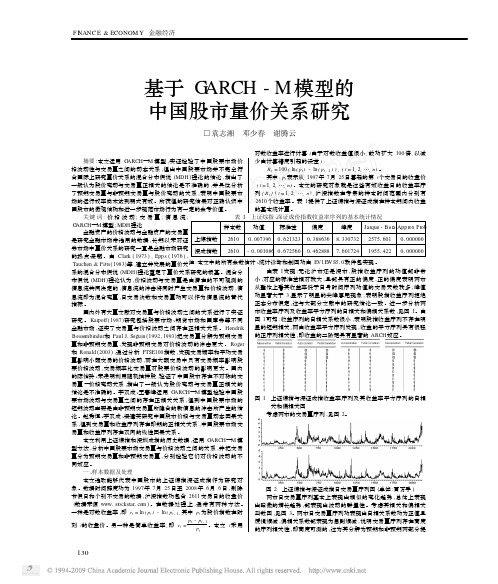
F I N ANC E &ECONOM Y 金融经济基于G ARCH -M 模型的中国股市量价关系研究□袁志湘 邓少春 谢腾云表1 上证综指、深证成份指数收益率序列的基本统计情况样本数均值标准差偏度峰度Jarque -Bera App r ox Pr ob上综指数2610010073960162132301388636813307322575160101000000深成指数2610-010010860167256001462888716017241955142201000000注:本文中的所有参数估计、统计诊断和制图均由EV1E W S510软件包实现。
摘要:本文运用G ARCH —M 模型,实证检验了中国股票市场价格波动性与交易量之间的动态关系,得出中国股票市场并不完全符合国际上研究量价关系的混合分布假说(MDH )理论的结论,指出了一般认为股价变动与交易量正相关的结论是不准确的,并具体分析了预期交易量与非预期交易量与股价变动的关系,表明中国股票市场的运行效率尚未达到弱式有效。
所获得的研究结果对正确认识中国股市的微观结构和进一步规范市场行为有一定的参考价值。
关键词:价格波动;交易量;信息流;G ARCH —M 模型;MDH 理论金融资产的价格波动与金融资产的交易量是研究金融市场常选用的数据,长期以来对证券市场中量价关系的研究一直是金融市场研究的热点课题。
由Clark (1973),Epp s (1976),Tauchen &Pitts (1983)等,建立并发展的量价关系的混合分布假说(MDH )理论奠定了量价关系研究的根基。
混合分布假说(MDH )理论认为,价格波动与交易量是由潜在的不可观测的信息流共同决定的,信息流的冲击将同时产生交易量和价格波动,信息流即为混合变量,日交易次数和交易量均可以作为信息流的替代指标。
国内外有大量文献对交易量与价格波动之间的关系进行了实证研究。
基于ARIMA-GARCH模型的股票价格预测研究

基于ARIMA-GARCH模型的股票价格预测研究基于ARIMA-GARCH模型的股票价格预测研究摘要:股票价格的预测是金融市场中的重要研究领域,对投资者和决策者都有重要的意义。
本文通过引入时间序列分析中的ARIMA模型和GARCH模型,构建了ARIMA-GARCH模型用于股票价格预测。
利用该模型对一家上市公司的股票价格进行预测,研究结果表明ARIMA-GARCH模型能够较准确地预测股票价格的变动趋势,有一定的实用价值。
一、引言股票价格的预测是金融市场中重要的研究领域之一,对投资者和决策者都有重要的意义。
股票价格的波动受多种因素的影响,如公司业绩、宏观经济因素、政策变化等。
因此,通过各种模型和方法进行股票价格的预测,能够提供一定的决策依据。
本文旨在研究基于ARIMA-GARCH模型的股票价格预测方法。
二、ARIMA模型ARIMA模型是时间序列分析中常用的模型之一,它基于时间序列的自相关和移动平均来进行预测。
ARIMA模型根据时间序列的平稳性分为AR模型、MA模型和ARMA模型。
AR模型是自相关模型,表示当前的数值与过去一段时间的数值有关;MA模型是移动平均模型,表示当前的数值与过去一段时间的误差项有关;ARMA模型是AR模型和MA模型的组合。
三、GARCH模型GARCH模型是对时间序列的波动进行建模的方法,它能够描述时间序列的条件异方差性。
GARCH模型可以分为GARCH(p,q)模型和EGARCH模型等。
其中,GARCH(p,q)模型建立了波动的自回归关系,用来捕捉时间序列波动的长期影响,而EGARCH模型通过引入对称与非对称杠杆效应,以更好地解释波动。
在本文的研究中,我们选取GARCH(1,1)模型。
四、ARIMA-GARCH模型ARIMA-GARCH模型是将ARIMA模型和GARCH模型相结合,用于预测时间序列的股票价格。
首先,利用ARIMA模型对时间序列数据进行建模,得到其残差项;然后,对ARIMA模型的残差项进行GARCH模型拟合,得到条件异方差项;最后,将AR模型和GARCH模型的结果进行组合,得到ARIMA-GARCH模型预测的股票价格。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SC 确定。
表3
ARMA 模型残差检验
项目
股价方程残差 股价方程残差平方 成交量方程残差 成交量方程残差平方
统计量
Q(12)
LM(10)(T*R2 )
12.669(0.394)
306.17(0.000)
144.09995(0.000)
16.176(0.095)
110.69(0.000)
78.43215(0.000)
统计与决策 2011 年第 4 期(总第 328 期) 145
财经论坛
而且 α+β 接近于 1,表明波动具有显著的持续性。 2.2 ARMA-GARCH 组合预测模型的估算结果
Jarque-Bera 显示检验残差不服从正态分布, 采 用 拟 极 大似然估计,得到 DCC-GARCH 的估计结果,如表 6 所示。
ADF 单位根检验
变量 检验形式(C,T,L)
T 统计量
1%临 界 值
SRt
(C,0,0)
-34.70795 -3.432948
VLt
(C,0,3)
-31.45917 -3.43295
结论 平稳 平稳
注 :检 验 形 式 中 C、T、L 分 别 表 示 常 数 项 、趋 势 项 和 滞 后 阶 数 ,L 值 由 AIC 及
表4
GARCH(1,1)模 型 估 计 结 果
ω(t 值)
αi (t 值)
βi(t 值)
αi+βi
股价 3.66E-06(5.536518) 0.106238(6.8287) 0.887731(99.93969) 0.993969
成交量 0.000244(2.7072) 0.031919(9.306932) 0.963939(248.982) 0.995848
财经论坛
基于 ARMA- GARCH 模型的 股市量价动态关系研究
李 丽 1,2
(深圳信息职业技术学院 信息经济系,广东 深圳 518029)
摘 要:文章以 GARCH 模型为基础,纳 入 ARMA 结 构 的 均 值 方 程 形 式 ,建 立 了 描 述 股 价 和 成
交量之间内在关系的 ARMA-GARCH 组合预测模型。 基于股价和成交量的历史高频交易数据,对
改进。 由上述检验可知,序列均存在序列相关,本文在建立单
变量 GARCH 模型的均值方程时,采用 ARMA 结构。 经过多
次比较,最后得到均值方程形式为:
SRt=0.064*SRt-4+0.0435*SRt-11+0.0489*SRt-13-0.0435*SRt-19
(3.094) (2.103)
(2.357)
(0.302)
Jarque-Bera 445.4885 (0.000) 725.9862 (0.000)
表6
参数 α* β*
DCC 模型估计结果
估计值 0.006313249 0.990420479
对数似然比
标准差 0.004444331 0.008024539 19712.37
Z 统计量 1.42052 123.42456
T
Σ L=-
1 2
t
=
T -1
[nlog(2π)+2log|Dt|+log|Rt|+εt Rt εt]
1
(6)
T
εt 是 从 第 一 阶 段 一 元 GARCH 模 型 估 计 得 到 的 经 过 标
准化后的残差, 它是 均 值 为 零 , 方 差 为 Rt 的 独 立 同 分 布 序
列。 因此,方差矩阵也是初始零均值收益序列的相关系数矩
对数据建模之前,为防止出现设定错误,有必要大致判 断一下数据的统计特征,对数据的描述性检验结果如表 1 所 示。
从 表 1 可 知 ,SRt 与 VLt 的 Jarque-Bera 统 计 量 均 拒 绝 服 从正态分布,而且具有“尖峰厚尾”性,因为它们的峰度均大 于 3。 对 SRt 和 VLt 滞后 6 阶和 12 阶的 Ljung-Box 检验拒绝 了白噪声的零假设,表明存在序列相关,而 SRt 和 VLt 平方的 Ljung-box 检验则表明序列存在 ARCH 效应。 高波动性时期
SRt 0.000323 0.017367 -0.064433 6.798548 15.78(p=0.0015) 24.245(p=0.019) 1546.912SRt 平方 196.41(p=0) 348.76(p=0)
注:LB(n)表示 n 阶滞后的自相关显著性的 Ljung-Box 检验。
表2
本文选择 2001 年 1 月 4 日至 2009 年 9 月 16 日上证 综
指日收盘价与成交量数据, 数据来源于清华金融数据库,剔
作者简介:李 丽(1982-),女,湖北荆州人,博士后,讲师,研究方向:经济计量分析与预测等。
144 统计与决策 2011 年第 4 期(总第 328 期)
财经论坛
表1
统计量 均值
标准差 偏度 峰度 LB(6) LB(12) JB LB(6) LB(12)
序列的描述性统计
VLt 0.001191 0.260225 0.799367 6.727003 160.12(p=0.00) 166.37(p=0.00) 1605.59Vt 平方 161.66(p=0) 206.42(p=0)
rt,εt~N(0,Rt)。 其动态相关结构设定为:
*-1
*-1
Rt=Qt QtQt
(4)
*
*
*
T
*
Qt=(1-Σαm -Σβn )Q+Σαm (εt-m-εt-m )+Σβn Qt-n
(5)
m
n
m
n
*
这 里 Qt 是 包 含 Qt 的 对 角 元 素 平 方 根 的 对 角 矩 阵 ,Qt 是
由第一阶段估计得到的条件方差-协方差矩阵。 Q軍是从 Qt 计
(-2.109)
(0.002) (0.036)
(0.018)
(0.035)
+0.0569*SRt-22 (2.742)
(0.006)
-0.0352*SRt-33+0.0611*SRt-34+0.0471*SRt-35+0.000178+εt
(-1.7)
(2.95)
(2.27)
(0.501)
(0.0896) (0.0032) (0.023)
Ljung-Box 检 验 发 现 ,残 差 不 存 在 自 相 关 ,ARCH-LM 检 验 表
明 残 差 序 列 存 在 显 著 的 ARCH 效 应 , 因 此 可 以 进 一 步 建 立
GARCH 模型进行分析。
按 照 上 面 确 定 的 均 值 方 程 ,用 GARCH(1,1)模 型 对 收 益
2 ARMA- GARCH 组合预测模型的构建及 估算结果
2.1 ARMA-GARCH 组合预测模型的构建
估 计 DCC-GARCH, 首 先 要 估 计 各 个 收 益 率 的 单 变 量
GARCH 过程,然后用获 得 的 条 件 方 差 hit 去 除 残 差 得 到 标 准 化残差 εit,用此标准化残差估计动态相关结构的参数。 为了 提高模型的拟合 优 度 ,下 面 对 GARCH 基 本 模 型 的 形 式 进 行
该模型进行了参数估计和检验,同时对我国股市量价动态关系进行了实证分析。 研究结果显示,股价
与成交量之间的动态条件相关关系并非常数,而是具有时变性。 在整个样本区间,动态条件相关系数
均为正,而且随着进出市场的信息流呈现出很强的波动性特征。
关键词:AR性
中 图 分 类 号 :F830.92
条件相关性结合起来的方法[14]。 与 GARCH 类模型对条件波
动建模一样,条件相关的当前值与其滞后值和滞后平方差有
关。 DCC-GARCH 模型的条件方差-协方差矩阵为:
茗
rt|准t-1 N(0,Ht)
(1)
Ht=DtRtDt
(2)
其 中 ,rt 是 一 个 n×n 向 量 ,Ht 是 条 件 协 方 差 矩 阵 ,Rt={ρij}t
算 得 到 的 加 权 平 均 矩 阵 , 是 标 准 差 的 非 条 件 协 方 差 矩 阵 ;εt-m,
T
εt-m 是标准化残差的滞后 值 ;Qt-n 是 条 件 协 方 差 的 滞 后 值 。 这
*
*
个模型需要估计额外两个参数:αm 和 βn 。 DCC-GARCH 模型
可以运用(拟)极大似然法估计,对数似然式可以表示为:
表5
GARCH 模型残差检验
项目
股价 GARCH 残差 股价 GARCH 残差平方 成交量 GARCH 残差 成交量 GARCH 残差平方
Q(12) 22.44(0.033) 6.5633(0.885) 10.119(0.43) 12.307(0.265)
统计量 LM(10)(T*R2)
4.539024 (0.919773) 11.75186
阵。 DCC 模型通过两阶段来估计。 首先估计每一资产的单变
量 GARCH 过程,然后 用 获 得 的 条 件 方 差 去 除 残 差 得 到 标 准
残差,然后以此标准残差利用极大似然法估计相关结构的参
数,通过两阶段得到的 DCC 估计量具有一致性和有效性。
1.2 DCC-GARCH 基本模型的计量经济学检验
是条件相关性矩阵。 Dt=diag{ 姨hi,t }是从一元 GARCH 模型得 到的 n×n 对角时变标准差矩阵。 Dt 的元素服从一元 GARCH (p, q)过程:
pi
θi
Σ Σ 2
hit=ωi+ αipεit-p + βiphit-p ,坌i=1,2,…,n
