股票价格的期权定价模型分析
期权定价二叉树模型
9 e
0.10.25
8.78
• 这也应该是期初用于投资组合的资金，由 此得：
1 30 C 8.78, C 10 8.78 1.22 3 • 买入期权的价格应该定为1.22元
三、期权定价的二项式公式
符号: S 0 股票在期初的价格, S X 期权确定的执行价格, u 股票价格在单个时间阶段内的上升因子 d 股票价格在单个时间阶段内的下降因子(-) Ru 期权在股票价格上升状态下的收益 Rd 期权在股票价格下降状态下的收益 r 年无风险收益率 T 期权的期限
7.14 qu max{ S 0 (1 u ) 3 (1 d ) S X ,0} q d max{ S 0 (1 u ) 2 (1 d ) 2 S X ,0}
0.33 qu max{ S 0 (1 u ) 2 (1 d ) 2 S X ,0} q d max{ S 0 (1 u )(1 d ) 3 S X ,0}
n n i i n i i C i qu q d max{ S 0 (1 u ) (1 d ) S X ,0} i 0
n
n n! n (n 1) (n i 1) , n 0,1, i (i 1) 1 i (n i )!i !
0 qu max{ S 0 (1 u ) 3 (1 d ) S X ,0} qd max{ S 0 (1 d ) 4 S X ,0}
对于第2阶段各状态期权价值有
2 13.7 qu 18.03 q d 7.14 qu max{ S 0 (1 u ) 4 S X ,0}
计算相关数据
u (e rT 1) ud 0.1 (e 0.05 1) 0.1 0.05 0.324859
期权定价模型
二、期权价值评估的方法（一）期权估价原理1、复制原理基本思想复制原理的基本思想是：构造一个股票和贷款的适当组合，使得无论股价如何变动投资组合的损益都与期权相同，那么创建该投资组合的成本就是期权的价值。
基本公式每份期权价格（买价）＝借钱买若干股股票的投资支出＝购买股票支出－借款额计算步骤（1）确定可能的到期日股票价格Su和Sd上行股价Su=股票现价S×上行乘数u下行股价Sd=股票现价S×下行乘数d（2）根据执行价格计算确定到期日期权价值Cu和Cd：股价上行时期权到期日价值Cu=上行股价-执行价格股价下行时期权到期日价值Cd=0（3）计算套期保值率：套期保值比率H=期权价值变化/股价变化=(CU-Cd)/(SU-Sd)（4）计算投资组合的成本（期权价值）=购买股票支出-借款数额购买股票支出=套期保值率×股票现价＝H×S0借款数额=价格下行时股票收入的现值＝（到期日下行股价×套期保值率）/（1+r）= H×Sd/（1+r）2、风险中性原理基本思想假设投资者对待风险的态度是中性的，所有证券的预期收益率都应当是无风险利率；假设股票不派发红利，股票价格的上升百分比就是股票投资的收益率。
因此：期望报酬率（无风险收益率）＝（上行概率×股价上升时股价变动百分比）+（下行概率×股价下降时股价变动百分比）＝p×股价上升时股价变动百分比+（1-p）×股价下降时股价变动百分比计算步骤（1）确定可能的到期日股票价格Su和Sd（同复制原理）（2）根据执行价格计算确定到期日期权价值Cu和Cd（同复制原理）（3）计算上行概率和下行概率期望报酬率＝（上行概率×股价上升百分比）+（下行概率×股价下降百分比）（4）计算期权价值期权价值＝(上行概率×Cu+下行概率×Cd)/（1+r）（二）二叉树期权定价模型1、单期二叉树定价模型基本原理风险中性原理的应用计算公式（1）教材公式期权价格＝U=股价上行乘数＝1＋股价上升百分比d=股价下行乘数＝1－股价下降百分比（2）理解公式：（与风险中性原理完全一样）2、两期二叉树模型基本原理把到期时间分成两期，由单期模型向两期模型的扩展，实际上就是单期模型的两次应用。
期权定价的二叉树模型
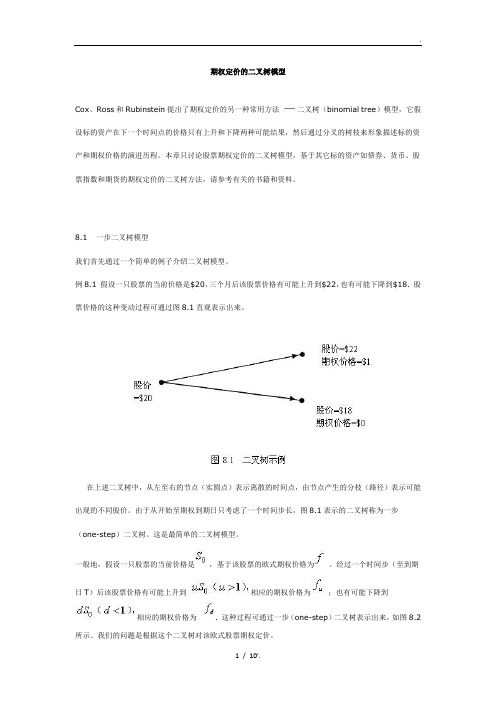
期权定价的二叉树模型Cox、Ross和Rubinstein提出了期权定价的另一种常用方法二叉树（binomial tree）模型，它假设标的资产在下一个时间点的价格只有上升和下降两种可能结果，然后通过分叉的树枝来形象描述标的资产和期权价格的演进历程。
本章只讨论股票期权定价的二叉树模型，基于其它标的资产如债券、货币、股票指数和期货的期权定价的二叉树方法，请参考有关的书籍和资料。
8.1 一步二叉树模型我们首先通过一个简单的例子介绍二叉树模型。
例8.1 假设一只股票的当前价格是$20，三个月后该股票价格有可能上升到$22，也有可能下降到$18. 股票价格的这种变动过程可通过图8.1直观表示出来。
在上述二叉树中，从左至右的节点（实圆点）表示离散的时间点，由节点产生的分枝（路径）表示可能出现的不同股价。
由于从开始至期权到期日只考虑了一个时间步长，图8.1表示的二叉树称为一步（one-step）二叉树。
这是最简单的二叉树模型。
一般地，假设一只股票的当前价格是，基于该股票的欧式期权价格为。
经过一个时间步（至到期日T）后该股票价格有可能上升到相应的期权价格为；也有可能下降到相应的期权价格为. 这种过程可通过一步（one-step）二叉树表示出来，如图8.2所示。
我们的问题是根据这个二叉树对该欧式股票期权定价。
为了对该欧式股票期权定价，我们采用无套利（no arbitrage）假设，即市场上无套利机会存在。
构造一个该股票和期权的组合（portfolio），组合中有股的多头股票和1股空头期权。
如果该股票价格上升到，则该组合在期权到期日的价值为；如果该股票价格下降到，则该组合在期权到期日的价值为。
根据无套利假设，该组合在股票上升和下降两种状态下的价值应该相等，即有由此可得(8.1)上式意味着是两个节点之间的期权价格增量与股价增量之比率。
在这种情况下，该组合是无风险的。
以表示无风险利率，则该组合的现值（the present value）为,又注意到该组合的当前价值是，故有即将(8.1)代入上式，可得基于一步二叉树模型的期权定价公式为(8.2)(8.3)需要指出的是，由于我们是在无套利（no arbitrage）假设下讨论欧式股票期权的定价，因此无风险利率应该满足： .现在回到前面的例子中，假设相应的期权是一个敲定价为$21，到期日为三个月的欧式看涨权，无风险的年利率为12%，求该期权的当前价值。
期权定价的二叉树模型
03
二叉树模型在期权定价中 的应用
二叉树模型在欧式期权定价中的应用
欧式期权定义
二叉树模型原理
欧式期权是一种只能在到期日行权的期权。
二叉树模型是一种离散时间模型，通过构造 一个二叉树来模拟股票价格的演变过程。
模型参数
定价过程
包括无风险利率、股票波动率、期权行权价 等。
从到期日逆推至起始时间，考虑各种可能的 价格路径，计算期权的预期收益，并使用无 风险利率折现至起始时间。
与其他理论的结合
二叉树模型与其它金融理论的结合也是理论研究的一个重要方向，如将二叉 树模型与随机过程理论、博弈论等相结合，以提供更深入、更全面的分析框 架。
二叉树模型的应用研究进展
扩展到其他金融衍生品
二叉树模型在期权定价方面的应用已经非常成熟，研究者们正在将其应用于其他金融衍生品的定价，如期货、 掉期等。
案例一：某公司股票期权定价
背景介绍
某上市公司股票期权激励计划需要为期权定价，以确定向员工发 放的期权数量和行权价格。
模型应用
根据二叉树模型，预测股票价格的上涨和下跌幅度，并计算期权 的内在价值和时间价值。
结论分析
根据计算结果，确定期权的行权价格和数量，实现了员工激励与公 司发展的双赢。
案例二：某交易所债券期权定价
调整利率和波动率
根据市场数据和实际情况，调整利率和波动率的参数，可以提 高模型的拟合度。
模型的选择与比较
1 2
基于误差
比较不同模型的预测误差，选择误差最小的模 型。
基于风险
比较不同模型的风险指标，选择风险最小的模 型。
3
基于解释性
选择更具有解释性的模型，以便更好地理解市 场行为和风险。
05
期权定价的二叉树模型介绍
计算期权的价值
计算期权的现值
根据预期收益和折现率，我们可以计算出期权的现值。 看涨期权的现值是每个节点的股票价格与执行价格的差 值与风险中性概率的乘积之和；看跌期权的现值是每个 节点的执行价格与股票价格的差值与风险中性概率的乘 积之和。
校准二叉树模型参数
为了使模型的预测结果与实际期权价格一致，我们需要 校准模型参数。通常，我们使用历史数据来估计参数， 例如股票价格的波动率和无风险利率。
建立二叉树
以时间步长为单位，从最后一个时间步长开始，依 次向前建立二叉树，每个节点代表一个时间步长。
确定初始股票价格
确定股票的当前价格
通常以市场价格为基础确定初始股票价格 。
考虑股息
如果股票在期权有效期内发放股息，需要 在每个时间步长上调整股票价格。
确定无风险利率与时间步长
要点一
确定无风险利率
无风险利率是投资者在相同风险水平下可以获得的最低 回报率。
05
二叉树模型的结果分析
模拟结果展示
假设一个股票价格变动模型，通过二叉树模型模拟股 票价格的涨跌情况，并计算期权的价值。
根据不同的利率和波动率等参数设置，模拟不同的股 票价格路径，从而得到期权价格的模拟结果。
结果分析与比较
将模拟结果与实际期权价格进行比较，分析二叉树模型 定价的准确性。
对比不同参数设置下的模拟结果，分析利率和波动率等 因素对期权价格的影响。
期权定价的二叉树模型介绍
2023-11-06
目 录
• 引言 • 二叉树模型基本原理 • 构建二叉树模型 • 计算期权价值 • 二叉树模型的结果分析 • 二叉树模型在金融实践中的应用 • 结论与展望
01
引言
研究背景与意义
对期权定价模型的偏微分方程分析--Black-Scholes期权定价模型
对期权定价模型的偏微分方程分析--Black-Scholes期权定
价模型
Black-Scholes（BS）期权定价模型是20世纪70年代由Fisher Black、Myron Scholes和Robert Merton独立发明和发展的。
BS模型将期权定价问题转化为偏微分方程问题，并提供了一种通过经济因素来解决期权定价的方法。
BS模型假设股票价格服从几何布朗运动，并使用随机微分方程来描述它们的漂移和随机波动性。
该模型还假定期权的价格服从Black-Scholes PDE：
$$\\frac{\\partial V}{\\partial
t}+\\frac{1}{2}\\sigma^2S^2\\frac{\\partial^2 V}{\\partial S^2}+rS\\frac{\\partial V}{\\partial S}-rV=0$$
其中，$V(S,t)$是期权价格，$S$是标的资产价格，
$\\sigma$是波动率，$r$是无风险利率，$t$是时间。
该方程可以被解释为投资组合在动态套利环境中的漂移和随机波动性，其中投资组合由一单股票和一个期权组成。
该方程的求解需要使用特殊函数，如Black-Scholes方程的解析解。
这个解析解有助于我们理解期权价格如何受到各种因素的影响，例如股票价格、波动率、时间和无风险利率。
总之，BS模型的偏微分方程分析提供了一种方法，使我们能够根据标的资产价格、波动率、时间和无风险利率来定价期权。
第四讲 BS期权定价模型
第四讲BS期权定价模型统计与管理学院第四讲BS期权定价模型第一节BS期权定价模型的基本思路第二节BS期权定价公式第三节BS期权定价公式的精确度评价与拓展第一节BS期权定价模型的基本思路股票价格服从的随机过程由It ô引理可得期权价格相应服从的随机过程dS Sdt SdWm s =+222212f f f fdf S S dt SdWS t S S m s s æö¶¶¶¶÷ç÷=+++ç÷ç÷綶¶¶èø第一节BS期权定价模型的基本思路BS微分方程BS期权定价公式222212f f frS S rft S S s ¶¶¶++=¶¶¶()()()12r T t c SN d Xe N d --=-第二节BS期权定价公式一、模型基本假设二、BS方程的推导三、风险中性定价原理四、BS期权定价公式的推导五、BS期权定价公式的参数估计一、假设证券价格遵循几何布朗运动，即µ和σ为常数 允许卖空标的证券没有交易费用和税收，所有证券都完全可分 衍生证券有效期内标的证券没有现金收益支付 不存在无风险套利机会证券交易是连续的，价格变动也是连续的衍生证券有效期内，无风险利率r为常数二、BS微分方程的推导由于假设股票价格S遵循几何布朗运动，因此在一个小的时间间隔∆t中，S的变化值∆S为dS Sdt SdWm s =+S S t S Wm s D =D +D二、BS微分方程的推导设f是依赖于S的衍生证券的价格，则f一定是S 和t的函数，根据伊藤引理可得：在一个小的时间间隔∆t中，f的变化值∆f满足：222212f f f f df S S dt SdW S t S S m s s æö¶¶¶¶÷ç÷=+++ç÷ç÷綶¶¶èø222212f f f f f S S t S W S t S S m s s æö¶¶¶¶÷ç÷D =++D +D ç÷ç÷綶¶¶èø二、BS微分方程的推导为了消除风险源∆W，可以构建一个包括一单位衍生证券空头和单位标的证券多头的组合。
B-S期权定价模型解析
没有交易费用或税收，即无摩擦的市场假设，且所 有证券都是高度可分的。
在期权的有效期内无风险利率和金融资产收益的变 量恒定。
不存在无风险套利机会。 证券交易是连续的，即不存在股票价格的跳跃行为。
投资者能够以相同的无风险利率借款或贷款，无风 险利率r为常数且对所有到期日都相同。
该期权是欧式期权
( f t
1 2
2 f S 2
2S 2 )dt
价值变动仅与时间 dt 有关，因此该组合
成功消除了 dz 带来的不确定性 12
根据无套利定价原理，组合收益率应 等于无风险利率 r (无套利机会)：
d rdt
( f t
1 2
2 f S 2
2S 2 )dt
r(- f
f S
S )dt
f rS f t S
1、股票价格的运动过程
dS dt dz, dz dt
S
dS ：股票的瞬间收益率
S
：股票的期望瞬间收益率
：股价收益率的瞬间标准差
4
波动率估计
1 观测证券价格的历史数据S0 、 S1 、…… 、 Sn ， 观测时间间隔为t（以年为单位）
2 计算每期以复利计算的回报率
ui＝Ln(Si / Si-1 ), i=1,……,n 3 计算回报率的标准差s
10
（3）B-S微分方程的推导
股票及衍生品的运动过程分别为：
dS Sdt Sdz
df
f S
S f
t
பைடு நூலகம்
1 2
2 S
f
2
2S
2
dt＋
f S
Sdz
为消除不确定性，构造投资组合：
衍生品：－1；股票：＋ f S
布莱克-舒尔斯-默顿期权定价模型
5
12.1 布莱克-舒尔斯-默顿期权定价模型的 基本思路
• 式（12. 1)的两边同吋乘上 着买入 ，并将两式相减消去dz,实际上意味
单位的股票，并卖空1单位的期权，可以构造出一个短期
内没有不确定性的投资组合。而在一个无套利的市场中，一个没 有不确定性的投资组合必然只能获得无风险利率的收益。这样在 数学上，就可以从（12. 1)和（12. 2)的联立方程组中解出一个 期权价格所满足的偏微分方程，求解这一方程，就得到了期权价 格的最终公式。 • 以上就是斯权定价模型推导过程的基本思路，理解这一思路，将 有助于在下面看似无关的数学推导中不会迷失方向。
(12.2)
4
12.1 布莱克-舒尔斯-默顿期权定价模型的 基本思路
• 观察式（12. 2)会发现影响期权价格的随机因素也完全体现 在等式右边的第二项中的dz上.这与我们的直觉是一致的： 股票价格及其衍生产品——期权价格都只受到同一种不确定 性的影响，其区别只是在于随机因素dz前面的系数不同,也 就是对随机因素变化的反应程度不同。 • 如果式（12. 1)两边同时乘以 并与式（12. 2)相减,则可 ∂S 以消去dz项。
•
• •
dz = ε
dt
(12. 4)
10
标准布朗运动
� 那么为什么采用维纳过程来描述股票价格变化中的随机 因素呢？ � 首先，维纳过程中用 ε 即标准正态分布的随机变量来反 映变量变化的随机特征。 现实生活中很多变量的分布都 近似于正态分布，加上其在数学上的易于处理,使得正 态分布成为最常见和最重要的分布假设之一。金融市场 也不例外，经验事实证明，股票价格的连续复利收益率 近似地服从正态分布。
(12.1)
等式右边的第二项中的dz完全捕捉了影响股票价格变化的随机因 素。根据数学家伊藤（K. Ito)提出的伊藤引理（Ito Lemma)可 知，当股票价格服从式 (12. 1)时，作为股票衍生产品的期权价 格将服从
布莱克-舒尔斯期权定价模型
第二节 布莱克-舒尔斯期权定价模型
一、布莱克-舒尔斯微分方程
假设： ❖ 证券价格遵循几何布朗运动，即 和 为常数 ❖ 允许卖空标的证券 ❖ 没有交易费用和税收，所有证券都是完全可分的 ❖ 在衍生证券有效期内标的证券没有现金收益支付 ❖ 不存在无风险套利机会 ❖ 证券交易是连续的，价格变动也是连续的 ❖ 在衍生证券有效期内，无风险利率r为常数
❖ 假设：在对衍生证券定价时，所有投资者都是风险中性的。
❖ 风险中性定价的一般程序：
所有资产的预期收益率都等于无风险利率 确定衍生工具的边界条件，计算到期日的期望值 把期望值按无风险利率贴现
第二节 布莱克-舒尔斯期权定价模型
一、布莱克-舒尔斯微分方程 风险中性定价原理在远期合约定价中的应用：
S
(m, s) 表示均值为m ，标准差为s的正态分布
第一节 证券价格的变化过程
四、证券价格的变化过程
对几何布朗运动的理解：
❖
但是，在一个较长的时间T后，
S S
不再具有正态分
布的性质：这是百分比多期收益率的乘积问题。
❖ 因此，尽管 t 是短期内股票价格百分比收益率 的标准差，但是在任意时间长度T后，这个收益率 的标准差却不再是 T 。
❖ 在任意时间长度T后，x值的变化也具有正态分布特 征，其均值为aT，方差为 b2T ，标准差b T 。
❖ 标准布朗运动的漂移率a为0，方差率为1。
第一节 证券价格的变化过程
三、伊藤过程 伊藤过程 ( Ito Process )
❖ 假设变量x的漂移率和方差率是变量x和时间t的函数
dx adt bdz
率进行贴现后的现值，即：
布莱克-舒尔斯期权定价模型
布莱克-舒尔斯期权定价模型布莱克-舒尔斯期权定价模型是一种用于计算欧式期权的理论定价模型。
该模型于1973年由费舍尔·布莱克和麦伦·舒尔斯提出，并且在同年被罗伯特·默顿-米勒进一步完善和发展。
布莱克-舒尔斯期权定价模型的基本原理是通过建立股票和债券的投资组合，获得一个无风险的合成证券，该合成证券与欧式期权具有相同的收益率。
该模型的关键假设包括资产价格满足几何布朗运动、市场无摩擦、无交易成本和无道德风险等。
根据这些假设，布莱克-舒尔斯期权定价模型的基本公式可以表示为：C = S*N(d1) - X*e^(-rt)*N(d2)，其中C表示期权的价格，S是标的资产（如股票）的当前价格，X是期权的行权价格，r是无风险利率，t是期权的剩余期限，e是自然常数（约等于2.71828），N(d1)和N(d2)分别表示标准正态分布的累积分布函数。
在该公式中，d1=(ln(S/X) + (r+σ^2/2)t) / (σ*√t)，d2=d1-σ*√t。
其中σ是标的资产的波动率，它衡量标的资产的波动程度。
布莱克-舒尔斯期权定价模型的优点是可以较为准确地计算欧式期权的理论定价，并且可以用于不同类型的期权，如看涨期权、看跌期权等。
它在金融市场中得到了广泛的应用，并为投资者和金融机构提供了重要的参考依据。
然而，布莱克-舒尔斯期权定价模型也存在一些限制。
首先，该模型基于一系列假设，不一定适用于所有市场和资产。
其次，该模型仅适用于欧式期权，而不适用于美式期权等其他类型的期权。
最后，该模型假设市场无摩擦和无道德风险，这在实际市场中并不总是成立。
综上所述，布莱克-舒尔斯期权定价模型为计算欧式期权的理论价格提供了一个重要的工具，但在实际应用中需要对假设进行谨慎评估，并结合其他方法进行综合分析和决策。
布莱克-舒尔斯期权定价模型是金融领域中非常重要且广泛应用的一种定价模型。
它的提出对于金融市场的发展和期权的交易产生了巨大的影响。
期权定价模型介绍
期权定价模型介绍期权是指其中一方在合约规定的时间内，以合约规定的价格购买（或出售）一定数量的标的资产的权利。
期权作为一种金融衍生品，其价格可以由期权定价模型来确定。
期权定价模型的目标是为了找出一个公平的价格，使买方和卖方在交易中没有不利的地位。
最早的期权定价模型是1973年由Black、Scholes和Merton提出的Black-Scholes-Merton模型（BSM模型）。
该模型假设市场中不存在无风险套利的机会，并且标的资产的价格满足几何布朗运动。
BSM模型使用了随机微分方程与偏微分方程的方法，利用股票价格、期权执行价格、无风险利率、标的资产波动率以及到期时间等变量来计算期权的价格。
BSM模型的基本原理是将期权的价值分解为两个部分：delta和vega。
Delta表明期权价格对标的资产价格的变动的敏感度，而vega则表明期权价格对波动率的变动的敏感度。
BSM模型通过动态对冲策略来调整delta的大小，并通过对冲操作来避免无风险套利的机会。
BSM模型的假设条件是非常严格的，因此它并不适用于所有的情况。
后续的研究对BSM模型进行了改进和扩展，提出了多种不同的期权定价模型。
其中比较有代表性的是二叉树模型、蒙特卡洛模型和波动率曲面模型等。
二叉树模型使用一个二叉树来模拟标的资产价格的随机过程。
从根节点开始，每一步向上或向下移动，直到到达期权到期日。
通过计算每一步的价格和概率，可以得到到期时期权的价值。
二叉树模型相对于BSM模型的优势是更加灵活，可以处理更加复杂的市场情况。
蒙特卡洛模型通过模拟大量的随机路径来估计期权的价格。
在每一个时间步骤上，生成一个随机数，根据随机数和标的资产价格的变动方程计算出未来的价格。
重复这一过程，最终可以得到到期时期权的价值的分布。
蒙特卡洛模型的优势是可以处理更加复杂的市场情况，但计算量较大。
波动率曲面模型使用波动率曲面来刻画标的资产价格波动率与期限之间的关系。
该模型认为波动率并不是恒定的，而是根据期限的不同而变化的。
浅析经理人股票期权定价模型
。 Ｏ 州 Ｍ Ｃ Ｃ Ｅ Ｏ Ｒ Ｃ Ｕ Ｉ Ｎ Ａ Ｔ Ｌ Ｉ Ｎ Ｇ
口黄
莹（ 上 海大 学 上海 ２ ０ ０ ４ ４ ４ ）
摘 要： 经理人股票期权是指上 市公 司授予经理人在未来一定期限 内以预先确定的价格和条件购买本公司
一
定 数量 股份 的权 利 。 其 价 值 计 量 一 直 是 会 计 计 量 的 难 题 。布 莱 克 一 斯 科 尔斯 模 型 （ Ｂ— Ｓ模 型 ） 符合 Ｆ ＡＳ Ｂ
炎键 ｝ 国： 经理计 准则 第 １ １号—— 股 份 支付 准则 》 （ 以下 简称 Ｃ ＡＳ Ｎ Ｏ ． １ １ ） 规定 对 于存 在 活 跃市 场 的权 益 工具 ， 应 当按 照 活跃 市场 中的报 价确 定其 公允 价值 ：对 于不 能在金 融 市场 自由转让 和交 易 的经 理人 股票 期权 ，由于不存 在其 市 场价 格 的情 况 ，企 业 只 能采 用期 权 定 价模 型 确定 其 公允 价 值 。 Ｃ ＡＳ Ｎ Ｏ． １ １并 未指 出具 体 的经 理 人 股 票期 权 定 价模 型 ． 但 认 为定价 模 型应 至少 考虑 以下 因素 ： （ １ ） 期 权行 权 价格 ； （ ２ ） 期权 有效 期 ； （ ３ ）标 的股 票的现 行价 格 ； （ ４ ）股 价 预计 波动 率； （ ５ ） 预 计股 利率 ； （ ６ ） 期 权有 效期 内的无 风险利 率 。 此外， ２ ０ １ １ 年 财政 部发 布 的“ ２ ０ １ ０年 上市 公 司执 行会 计 准则 情况 分 析报告 ”对 运用 期权 定 价模 型计量 经理 人股 票期 权 价值 提 出 了新 的要 求 ：各企 业应 结 合经理 人股 票期 权 的特 点改 进 期权定 价模 型 ，使定 价模 型 的计量 结果 公允 反 映经 理人 股 票期权 的价值 。 为 进 一 步 分 析 经 理 人 股 票 期权 定 价模 型 ，本 文 根 据
期权及期权定价模型(pdf 115页)
随着有效期的增加，欧式看涨期权和欧式看跌期权的价值 并不一定增加。
考虑同一个股票的两个欧式看涨期权，一个到期期限为1 个月，另一个到期期限为2个月。假定预计在6周以后将支 付大量的红利，红利会使股票的价格下降，这就有可能使 有效期短的期权的价值超过有效期长的期权的价值
波动率volatility
股票的现价S 执行价格，X; 到期期限，T 股票价格的波动率σ； 无风险利率r 期权有效期内预计max(ST-X,0) 看跌期权 max(X- ST,0)
到期期限 当期权的到期期限增加时，美式看跌期权和看涨 期权的价值都会增加。因为有效期长的期权不仅 包含了有效期短的那个期权的所有执行机会，而 且他的获利机会会更多。因此有效期长的期权价 值总是大于或等于有效期短的期权价值。
主要讨论影响股票期权价格的一些因素。我们探讨欧式期 权价格、美式期权价格和标的资产价格之间的关系。这些 关系中最重要的是看涨期权-看跌期权的平价关系。
讨论美式看涨期权是否应该提前执行。我们可以证明提前 执行不付红利股票美式看涨期权决不是最佳选择，即不分 红股票的美式买权不可能提前执行。
一 影响期权价值的因素：
期权市场机制
期权市场的历史 交易:做市商,场内会员经纪人,指令登记员
期权市场的历史
早在18世纪，欧洲和美国开始了首批看涨期权和看跌期权 的交易。
20世纪的前几年，一些公司成立了经纪人与交易者协会 (Put and Call Brokers and Dealers Association).—— 柜台交易(over-the-counter market).
期权式单边风险工具，它只保护价格向一个方向变 化
期权的风险特征（续）
ST X
金融市场的股票定价模型
金融市场的股票定价模型在金融市场中，股票定价模型是投资者和分析师用来估计股票价格的一个重要工具。
通过研究股票的基本面和市场环境，运用股票定价模型可以帮助我们确定一个合理的股票价格，并作出相应的投资决策。
本文将介绍几种常用的股票定价模型，并对其原理和应用进行分析。
一、股票定价模型的作用股票定价模型是在分析资本资产定价模型（CAPM）的基础上发展起来的。
它的主要作用是帮助投资者预测股票的未来价格，并根据这一预测做出相应的买入或卖出决策。
股票定价模型的核心思想是通过分析股票的风险和回报之间的关系，来确定股票的合理价格。
二、常用的股票定价模型1. 价值投资模型价值投资模型是根据股票的内在价值来进行估值的一种方法。
其核心思想是通过研究公司的财务数据和经营状况，确定公司的真实价值，然后根据市场价格与真实价值之间的差异来决定买入或卖出股票。
著名的价值投资者沃伦·巴菲特就是运用这种模型来选择股票的。
2. 相对估值模型相对估值模型是将股票的价值与同行业或同类资产进行比较，从而确定股票的相对价值。
常用的方法包括市盈率、市净率等。
例如，如果某个公司的市盈率较同行业低，那么可以认为该股票的相对价值较高，有投资价值。
3. 期权定价模型期权定价模型是用来确定股票期权合理价格的一种方法。
该模型主要用于衍生品市场中，通过考虑时间价值、波动率等因素，计算出股票期权的合理价格。
著名的期权定价模型包括布莱克-斯科尔斯模型等。
三、股票定价模型的应用股票定价模型广泛应用于金融市场中的投资分析和风险管理中。
投资者可以根据股票定价模型提供的合理价格，进行股票选择和买卖决策。
同时，金融机构和分析师也可以利用股票定价模型进行投资组合管理和风险分析，帮助他们做出明智的投资策略。
四、股票定价模型的局限性股票定价模型虽然在投资分析中起到重要作用，但也存在一些局限性。
首先，股票定价模型往往基于一些假设，如市场有效性假设等，这些假设在实际市场中可能并不成立。
第六章 black-schols期权定价模型
的值
相互独立。
考察变量z在一段较长时间T中的变化情形，我们可得:
（6.2）
N
z(T ) z(0) i t i 1
T i
(6.2)式t均值0为0，方差为
（ 是相互独立的 ）
当
时d，z我们就可dt以得到极限的标准布朗运动:
（6.3）
2.普通布朗运动
我们先引入两个概念: 漂移率和方差率。
标准布朗运动的漂移率为0，方差率为1.0。
( f t
1 2
2 f S 2
2S 2 )t
r( f
f S
S )t
布莱克——舒尔斯微分分程
化简为:
f rS f t S
1 2S2
2
2 f S 2
rf
(6.18)
这就是著名的布莱克——舒尔斯微分分程，它 适用于其价格取决于标的证券价格S的所有衍生 证券的定价。
（二）风险中性定价原理
假设所有投资者都是风险中性的, 那么所有现金流量都可以通过无 风险利率进行贴现求得现值。
我们令漂移率的期望值为a,方差率的期望值为b2，就可得到变量x 的 普通布朗运动:
dx adt bdz
其中，a和b均为常数，dz遵循标准布朗运动。
（6.4）
(三)伊藤过程 普通布朗运动假定漂移率和方差率为常数，若
把变量x的漂移率和方差率当作变量x和时间t的
函数，dx我们a可(以x,从t )公dt式(b6(.x4), 得t )d到z伊藤过程
S f
t
1 2
2 f S 2
2S
2
)dt
f S
Sdz
(6.10)
根据伊藤引理，衍生证券的价格 f 应遵循如
伊藤引理证明:
布莱克斯克尔斯期权定价模型
布莱克斯克尔斯期权定价模型汇报人：日期:目录CATALOGUE•引言•布莱克斯克尔斯模型原理•模型应用•模型优势与局限•布莱克斯克尔斯模型与其他模型的比较•未来展望与研究方向01 CATALOGUE引言1背景介绍23布莱克斯克尔斯模型起源于1973年，由费雪·布莱克斯克尔斯（Fischer Black）和迈伦·斯科尔斯（Myron Scholes）提出。
当时，该模型是为了解决金融衍生品，特别是期权定价的问题而建立的。
金融衍生品是一种金融合约，其价值取决于其他金融资产或指标。
模型发展历程布莱克斯克尔斯模型的发展得益于许多重要的突破，其中包括无套利原则：模型利用无套利原则，这意味着在市场上不能通过买卖资产来赚取无风险利润。
欧式期权定价：该模型适用于欧式期权，即只能在到期日行使的期权。
随机过程：模型运用随机过程来描述股票价格的变化。
模型应用领域布莱克斯克尔斯模型被广泛应用于金融衍生品市场，包括期权：该模型用于定价欧式和美式期权。
互换：该模型用于定价利率互换和其他类型的互换合约。
其他衍生品：该模型还可用于定价其他金融衍生品，如期货、认股权证等。
02CATALOGUE布莱克斯克尔斯模型原理基础概念布莱克斯克尔斯模型是一种用于定价欧式期权的数学模型，该模型基于随机过程，并使用偏微分方程来描述。
在该模型中，期权价格被表示为时间t和股票价格S的函数，用C(t,S)表示。
股票价格服从几何布朗运动，即dS = μSdt + σSdwt，其中μ是股票的预期收益率，σ是股票的波动率，wt是威纳过程。
布莱克斯克尔斯模型的期权定价公式为：C(t, S) = SN(d1) - Ke^(-r)(T-t)N(d2)，其中N是正态分布函数，d1和d2是由模型参数确定的公式。
d2 = d1 - σ√(T - t)K 是期权的执行价格，r 是无风险利率，T 是到期时间，t 是当前时间，σ是股票的波动率。
d1 = (ln(S/K) + (r + 0.5σ^2)(T - t)) / (σ√(T - t))期权定价公式参数确定方法参数σ（波动率）通常由历史数据估计得出，也可以使用市场波动率作为其近似值。
增发股票的期权定价模型分析
ｍｏ ｅ ａ ｅ ｐ ｎ Ｂ－ ｄ ｌｔ ｅ ｔ ｈ ｈ ￣ ｇ ｆｔ ｄｔ ｎ ｐ ｉｉｇ ｍｏ ｅ ． ｅ ａ ｓ Ｓ ｍｏ ｅ ｏ ｎ ｔｃ ｎ ａｎ ｄ ｌ ｓ ｄ ｕ ｏ Ｓ ｍｏ ｅ ｏ ｓ ｔ ｅ ｔ ｅ ｓ ｏ ａ ｅ ｏ ｒ ｉ ｏ ｒ ｎ ｄ １ Ｂ ｃ ｕ ｅ Ｂ— ｄ ｌｄ ｏ ｏ ｔ ｉ ｂ ｌ ａ ｉ ｃ
Ｋｅ ｒ ｓ： ｓ ａ ｏ ｅ ｑ ｉｙｏ ｅ ｎ ｓ；ｏ ｔｏ ｙ ｗｏ ｄ ｅ ｓ ｎ ｄ ｅ ｕ ｔ ｆ ｒ ｇ ｉ ｐ ｉｎ；Ｂ－ ｄ ｌ Ｓ ｍｏ 的焦点之一 。 早
期的股利折现模型 （ Ｄ 模型 ） 股票 的价格定义 为 ＤＭ 把 未来红利的总收 入的折 现之 和 。到 了 ２ ０世纪 ５ — ０ ０ ６ 年代 马柯威 茨的均 值—— 方差模 型和夏 普 的 Ｃ Ｐ ＡＭ 模 型的提 出 ， 标志 着股票定价理论 的完 整建立 。进 入 ２ ０世纪 ８ Ｏ年代 ， 在努力 寻求一个 性状 良好 的均衡定 价模 型而进展甚微 时 ， 一部分学者 又将 兴趣转移 到股 票定价理论初 建时对微 观主体 即投 资者 行为 的考察 上来 了 ， 通过实证分 析方法考察信息 与股价变 动的关 系 ，然后 由此 总结 出一个 有关 投 资者行 为 的一般 结
ｖ ｒａｉｎ ｉ ｓ ｒ ｆ ｒｉ ｇ ｏ ｖ ｓｏ ， ｏ ｎ ｔｅ ｔ ｔ ａｎｉｇ ｒ ｔ ｆｉ ｖ ｓｏ ｎ ｎ ｓｏ ｍｐ ｎ ． ａ ｔ ｎ ｒ ｋ ｐ ｅｅ ｒｎ ｆｉ ｅ ｔｒ ｗｅｄ ｏ ｓｉ ｅｅ ｒ ｎ ａｉ ｏ ｅ ｔｒａ ｄ Ｂｏ ｕ ｆＣｏ ａ ｙ ｉ ｏ ｉ ｎ ｍａ ｏ ｎ
维普资讯
２ ０ 第 ５期 ０ ７年 （ 总第 ４ ５期）
科 技 与 管 理
Ｓ ｉ ｅ ｈ ｏｏ ｙ ａ ｄ ｃ－ ｃ ｎ ｌｇ ｎ Ｍａ ａ ｅ Ｔ ｎ ｇ ｍｅ ｔ ｎ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
*股票价格的期权定价模型分析李啸宇（南京信息工程大学数学与统计学院南京 210044）摘要：在2000年之后，证券交易在世界范围内得到良好发展，随之产生期权问题，投资消费相关情况开始得到我国专家和学者的关注，对此领域进行高效科学的分析，是目前高效管理且避免风险的重要方式，是金融衍生证券正常运作和长久发展的核心。
期权定价的分析主要是在大量衍生证券定价模型中进行，现实因素是：（1）期权定价简单易行。
（2）若干期权合约就可以构建成新的证券组合，通过对期权定价，可以更容易对证券组合定价。
（3）对于多种证券来说，定价原理本质重点相同，所以，利用分析期权定价，也许可以寻找到证券定价的一般性结果。
本文对若干期权定价问题进行研究，试图得到一些实用的数学结论，此外可以表现出数学与金融两者间的紧密关系：第一，前者是后者分析活动的主要方式，第二，后者促进前者理论领域的进步。
论文共分为三章:第一章叙述期权定价理论发展与主要使用的方式：第二章叙述股票具体定价方式；第三章是对全文的总结。
关键词:股票期权定价证券组合Option pricing model of stock price analysisLi Xiao-YuCollege of Mathematics and Statistics, NUIST, Nanjing 210044, ChinaAbstract:Since 2000, on a global scale to obtain rapid development of stock exchange, the subsequent rights as scheduled, investment spending more and more cause the attention of domestic mathematicians and financial economists, a reasonable valuation, financial derivatives accurately is the precondition of effective management and risk aversion, a reasonable existence and healthy development of financial derivatives.The study of option pricing is the most widely studied in the pricing model of many derivative securities, because:(1) option pricing is simple and easy.(2) a number of options contracts can be built into a new portfolio, which can be more easily priced through the pricing of options.(3) for all kinds of securities, the pricing principle is the one that changes from one to another. Therefore, by studying the pricing of options, it is possible to find the general conclusion of securities pricing.In this paper, the number of option pricing problem is studied,trying to get some practical mathematical conclusion, and be able to show the dialectical relationship between mathematics and finance: on the one hand, mathematics is a powerful tool of financial research,on the other hand, the financial practice to promote the development of mathematics itself. The thesis is divided into three chapters: chapter one introduces the development of option pricing theory and the basic method of pricing: the second chapter introduces the pricing method of stock options. The third chapter is the summary of the full text. Keywords:Stock Option pricing Portfolio第一章 课题背景与相关理论1.1 课题背景与意义改革开放使得在中国大陆上沉寂了20年之久的证券市场重新崛起，随着90年代上海交易所与深圳交易所的成立以及邓小平同志的南巡，中国股市开始迅速扩张，这是中国金融市场新的开始。
然而,随着金融行业的不断扩张，金融事件如经济危机，泡沫经济等也都在给全球的经济带来难以估量的伤害。
可以说，股价的合理性对国家的经济繁荣尤为重要，也牵扯到平民百姓的损益。
这是本论文的出发点——希望借以分析股票的期权定价模型来探索股市的规律性。
1.2 早期模型1.2.1 期权的含义期权，简单地说就是一个订货合同，我们用一个例子来说明。
甲希望在一年以后购得某品牌新上市的手机A ，甲认为该手机新上市时会以8000元出售，超过了甲的承受范围，同时，有乙认为，该手机新上市时会以6000元出售，那么这时甲乙同意签署一份合同（即期权），且甲向乙支付期权费用，该合同规定，当手机上市时，甲有权利以7000元的价格从乙处购买手机A ，但是甲不具备买入的义务。
这是最简单的期权模型，我们也可以规定将“买入”改为“卖出”，不变的只是支付期权费用的人是有权利而无义务的。
1.2.2 期权定价模型的发展股市有风险，投资需谨慎。
正是这种风险显示了期权的价格，长久以来，人们一直致力于研究如何用各种不确定因素估计标的资产的风险。
早在20世纪初，法国数学家路易斯在他的《投机理论》中就提出了对绝对的布朗运动的股票价格[2]（股价的变动也是一个随机过程，其变化过程可以用布朗运动来模拟）的估值模型，站在买方的角度上进行统计，其期权价值主要是：⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-Φ-⎪⎭⎫ ⎝⎛-Φ=τσϕτστστσXS X S X X S S V (1-1)()dx e 21y 2x -y-2⎰∞=πφ , ()2y -2e 21y πϕ=因为理论并未关注到正值货币的时间价值，投资者对风险的接受程度，所以该理论也只能作为定价模型的基石。
1964年，波内斯提出了在固定对数分布下的股票收益，给出了以下定价公式：()()⎪⎪⎪⎪⎭⎫⎝⎛-+Φ-⎪⎪⎪⎪⎭⎫⎝⎛++Φ=-τστσατστσαατ)21(/ln e )21(/ln 22X S X X S S V (1-2) 此处，α表示股票预期收益率。
二十世纪中期，萨缪尔森寻找到欧式买方期权[17]的定价方式，思考到需要具备较高预期收益率β，此主要公式为：()()()⎪⎪⎪⎪⎭⎫⎝⎛-+Φ-⎪⎪⎪⎪⎭⎫⎝⎛++Φ=-τστσατστσαβττβα)21(/ln e )21(/ln e 22-X S X X S S V (1-3) 通过观察（1-2）（1-3）可知，波内斯模型就是萨缪尔森模型在 α=β 时的特殊情况[3-7,11]。
这些理论,为Black -Scholes 定价理论的发展寻找到正确方向,还对日后的各项定价理论的发展起到了决定性的作用。
第二章 现代期权定价模型2.1 Black-Scholes 模型二十世纪七十年代，Black 等专家指出Black -Scholes 模型[15] (此后叫做B -S 模型），另外，Merton [8]在很多方面做出了重要推广。
上述学者在股价服从对数正态分布的假设基础上，使用相关观点知识，推测得到不需要红利的欧式期权定价模型： ()()2-r 1d Xe -d ΦΦ=τS V(2-1)其中：()τστσ⎪⎭⎫⎝⎛++=2121r /ln d X S()τστστσ-d 21-r /ln d 122=⎪⎭⎫ ⎝⎛+=X S我们已经知道，在清算日，买入期权的支付为()X S C T T -=,0m ax ，我们只要求出T C 的期望，我们就可以通过利率贴现，求出现在的期权价格，即：()()()T t T r C E e t S c --=,(2-2)因此突破口在于计算出()T C E 。
取P 是X S T >的概率，那么，()[]{}()01|⨯-+->•=P X X S S E P C E T T T ,即()[]{}X X S S E P C E T T T ->•=|(2-3)该问题最终归结为求解P 和[]X S S E P T T >•|。
接下来我们来求解这两个量。
（1）求P 。
因为0>>X S T ,有X S T ln ln >和S X S S T ln ln ln ln ->-，()()S X S S T /ln /ln >， 故有()()()()S X S S ob X S ob P T T /ln /ln Pr Pr >=>=(2-4)在风险中性基础上，r =μ，基于上述假定我们就可以知道，()S S T /ln 服从正态分布，此外其期望与方差主要是：τσ⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛221ln r S S E T 及 τσ2ln =⎪⎭⎫⎝⎛S S D T其中t T -=τ()⎪⎪⎪⎪⎭⎫⎝⎛⎪⎭⎫⎝⎛-->⎪⎭⎫ ⎝⎛--=>=τστστστσ2221ln 21lnPr rob r S X r S S ob X S P P T T (2-5)如果记()τστσ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛++=2121ln r X S d , τσ-=12d d 。
()()()()()221121121ln Pr d d d d r S S ob P T Φ=-Φ-=+-Φ-=⎭⎬⎫⎩⎨⎧+->⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--=τστστστσ (2-6)由于⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=T T e r S S τστσ221ex p 服从对数正态分布。