材料力学(第五版)扭转切应力页PPT文档
合集下载
材料力学-扭转1ppt课件

横截面上 —
max
T IP
max
IP
T
max
T WP
Ip—截面的极惯性矩,单位:m4 , mm 4
WP
Ip
max
WP —抗扭截面模量,单位:m3, mm3.
整个圆轴上——等直杆:
max
Tm a x WP
三、公式的使用条件: 1、等直的圆轴, 2、弹性范围内工作。
30
四、圆截面的极惯性矩 Ip 和抗扭截面系数Wp
d
dx
d / dx-扭转角变化率
二)物理关系:
弹性范围内 max P
G → G
G
d
dx
方向垂直于半径。
28
三)静力关系:
T A dA
T A dA
G d 2dA dx A
I p
2dA
A
Ip
横截面对形心的极惯性矩
T
GI p
d
dxp
29
二、圆轴中τmax的确定
结论:
横截面上 0, 0 0 0
根据对称性可知剪应力沿圆周均匀分布;
t D, 可认为剪应力沿壁厚均匀分布,
且方向垂直于其半径方向。
t
D
20
3、剪应力的计算公式:
T
AdA.r0
2 0
r0
2td
r02t2
d
T
2r0 2t
薄壁圆筒横截面上的剪应力计算式
21
二、关于剪应力的若干重要性质
例题: 1、一传动轴作200r/min的匀速转动,轴上装有五个轮子。 主动轮2输入的功率为60kW,从动轮1、3、4、5依次输出的 功率为18kW、12kW、22kW和8kW。试作出该轴的扭矩图。
材料力学-扭转ppt课件

´
a
b
dy
´
c
d
T
①无正应力 dx
②横截面上各点处只产生垂直于半径
的均匀分布的剪应力 ,沿周向大小
不变,. 方向与该截面的扭矩方向一19 致。
二、薄壁圆筒剪应力
根据实验观测的结果,圆轴截面
上应力应该如右图分布:
且扭矩T应该是截面上所有剪切
力对圆心的矩的总和。因此有
T
AdAr0 T
r0 AdAr02r0tT
由 m 0 x
m2 1 m3 2
T1
A1 B2
m1 3 m4
x
C 3D
分别有
T1m2 0 T1m2 4.78kNm
.
13
②求扭矩(扭矩按正方向设)
利用截面法: 分别用1-1 , m2
2-2 , 3-3截面将AB , BC与CD段截开,选研究 对象,画受力图:
由 m 0 x
A
m3 2 m1
T2
.
21
四、薄壁圆筒扭转变形
L
A
A'
在圆轴截面上 AA' R
在圆轴表面上 AA' L
RL
.
22
五、剪切虎克定律:
T=m
T ( 2A0t) ( LR)
剪切虎克定律:当剪应力不超过材料的剪切比例极限 时(τ ≤τp),剪应力与剪应变成正比关系:
.
23
G
式中:G是材料的一个弹性常数,称为剪切弹性模量,因 无 量纲,故G的量纲与 相同,不同材料的G值可通过实验确定,钢
薄壁圆筒横截面
T T 2 r02 t 2A0 t
扭转剪应力的计
算公式
其中A0:平均半径所作.圆的面积。
材料力学-扭转课件

dz z B dx C
At
D
n
t
t
Bt C
扭转试验和破坏分析
利用截面法和静力衡,
F x 0 d A c o s td A sin td A x 0 y F y 0 d A sin td A c o s td A y 0
注意到:
dAx=dAsin dAy=dAcos
得: t sin2 t t cos2
MD
T1=MB=3.5103 N·m
1
2
3
T2=MB+ MC =7103 N·m T3= -MD= -4.68103 N·m
MB
T1
若扭矩为正,表明
与所设方向相同(扭矩 MB MC
MD
的正向);若为负,表
T2
明扭矩与所设方向相反
T3
外力偶矩、扭矩和扭矩图
绘制扭矩图。 最大扭矩产生
在CA段上,其值为
B
C
A
主动轮 D
外力偶矩、扭矩和扭矩图
解 主动轮和从动轮的外力偶矩分别为
MA
9549PA n
11.68103
N m
MB
MC
9549PB n
3.50103
N m
MD
9549PD n
4.68103
方向如图所示
N m
MB
MC
MA
MD
外力偶矩、扭矩和扭矩图
各段的扭矩为
MB 1 MC 2
MA 3
圆轴扭转强度条件
45o
受扭轴的破坏标志仍为屈服和断裂 屈服时横截面上的最大切应力称为扭转
屈服应力,记为ts
断裂时横截面上的最大切应力称为扭转
强度极限,记为tb 它们统称为扭转极限应力,记为tu
材料力学(扭转) PPT课件

y
3、斜截面上的 应力分析
x
n
x
z
t
Fn 0 dA zdAcos sin dAsin cos 0
Ft 0 dA dAcos cos dAsin sin 0
sin 2
讨论:
外力偶矩的计算、扭矩和扭矩图
功率、转速和外力偶矩之间的关系
ω = 2π n /60 ,1 kW = 1000 N•m/s
功率:P 角速度: 转速:n 外力偶矩:T 功率、转速和外力偶矩之间的关系:
T P P 2n
若功率P的单位为千瓦,转速n的单位为转/分:
T 9549 P ( N m) n
T
第三章 扭转
§3-2 外力偶矩、扭矩和扭矩图
例4-1 NA=19kW,NB=44kW,
TA
NC=25kW, n=150rpm
求:作图示传动轴的扭矩图
解:1. 求外力偶
TA
TA= 9549 19 =1210Nm
150
同样 TB=2800Nm, TC=1590Nm
TA
Mn
2.截面法求内力( 设正法)
Mn IPFra bibliotek变形
Mnl GI p
强度条件 max
Mn Wp
刚度条件 d Mn 180
dx G I p
第三章的基本要求
1.掌握根据轴的传递功率和转速计算外力偶矩;
2.掌握扭转时内力(即扭矩)的计算以及扭矩图的画 法;
3.掌握扭转切应力的计算方法;
45
第三章 扭转
材料力学扭转PPT课件

方向如图所示
Nm
MB
MC
MA
MD
14
材
料 力
外力偶矩、扭矩和扭矩图
学
Mechanics of Materials
各段的扭矩为
MB 1 MC 2
MA 3
MD
T1=MB=3.5103 N·m
1
2
3
T2=MB+ MC =7103 N·m T3= -MD= -4.68103 N·m
MB
T1
若扭矩为正,表明
B
C
A
主动轮 D
13
材 料 力 学
Mechanics of Materials
外力偶矩、扭矩和扭矩图
解 主动轮和从动轮的外力偶矩分别为
MA
9549 PA n
11.68 103
Nm
MB
MC
9549 PB n
3.50 103
Nm
MD
9549 PD n
4.68 103
材 料 力 学
Mechanics of Materials
第四章 扭转
1
材 料 力 学
Mechanics of Materials
引言-概念
工程实例
2
材 料 力 学
Mechanics of Materials
引言-概念
受力特点:两个等值反向的 力偶矩分别作用在杆件两端 垂直于轴线的平面内
变形特点:杆件的各横截面 绕杆的轴线发生相对转动
12
材 料 力 学
Mechanics of Materials
外力偶矩、扭矩和扭矩图
例 如图所示的传动轴的转速n=300转 /分,主动轮的输入功率PA=367kW,从动 轮B、C及D的输出功率分别为 PB=PC=110kW,PD=147kW,绘制该轴 的扭矩图,并确定最大扭矩Tmax及其所在位
材料力学-第4章 扭转 ppt课件

dA
T
O
dA
23
材料力学-第4章 扭转
圆轴扭转横截面上的应力
A dA T
代入:
G
G
d dx
得到:
G d 2dA T dx A
记: IP -2dA称为圆截面的极惯性矩
A
则:圆轴扭转角的变化率 d T
dx GIP
圆截面切应力
采用右手螺旋法则,如果用四指表示扭矩的转向, 拇指的指向与截面的外法线n的方向相同时,该扭矩为 正;反之,规定扭矩为负
正扭矩
负扭矩
——保证了无论从哪一段计算,扭矩的大小和符号 都相同
12
材料力学-第4章 扭转
扭力偶矩计算与扭矩
讨论:如图受扭圆轴,m-m截面上扭矩为多少?
Me
m
2M e
m m
T Me
17
材料力学-第4章 扭转
圆轴扭转横截面上的应力
几何变形:
1. 横截面绕圆轴的轴线转动
?
主要
2. 圆轴中段的横截面缩小 几何变形特征
有剪切应变 rz 次要
3. 圆轴的长度略有增长
有轴向应变 z 次要
– 变形后,横截面仍保持为平面,其形状和大小均不
改变,半径仍为直线
– 变形后,相邻横截面的间距保持不变,相邻横截面 绕圆轴轴线转动一定的角度
外力偶矩的计算
• 工程中的传动轴,通常给出传动轴所传递的功率和转 速,而不直接给出外力偶矩的数值
• 设外力偶矩为Me,传动轴的功率为P,角速度为w,则
有(理论力学)
Me
P
w
外力偶矩Me 单位:N·m (牛顿·米) 功率为P 单位:J (焦耳)
材料力学扭转(共56张PPT)

例题: :空心轴和实心轴材料相同,面积相同, α= 0.5。试比较空心轴和实心轴的强度和刚度情况。
解: 1〕确定两轴尺寸关系
面积相同 (1)校核空心轴及实心轴的强度〔不考虑键槽的影响〕;
扭转角单位:弧度〔rad〕 在B、C轮处分别负载N2=75kW,N3=75kW。
D1 d1
D d 2 2可G、I见P扭—在矩—载计抗荷算扭相1、2刚同符度的号。条规件定下和,扭空矩2心图轴绘的制重量仅为实2心轴的31% 。
1、扭转杆件的内力〔截面法〕
m
m
左段:
mx 0, T m 0
T m
右段:
m x
0,
mT 0
T m
m
Tx
T
m
x
内力偶矩——扭矩 T
2、扭矩的符号规定:按右手螺旋法那么判断。
+
T
T
-
3、内力图〔扭矩图〕
扭矩图作法:同轴力图:
例题: 1、一传动轴作200r/min的匀速转动,轴上装有五个轮子。主动轮 2输入的功率为60kW,从动轮1、3、4、5依次输出的功率为18kW、 12kW、22kW和8kW。试作出该轴的扭矩图。
二、 扭转杆的变形计算
1、扭转变形:〔相对扭转角〕
d T
dx GI P
扭转变形与内力计算式
d T dx
GIP
T dx
L GIP
1) 扭矩不变的等直轴
Tl GI p
扭转角单位:弧度〔rad〕 GIP——抗扭刚度。
2)各段扭矩为不同值的阶梯轴
Tili GI pi
3)变截面轴
T (x) dx l GI p (x)
2)、设计截面尺寸:
T
Ip
材料力学课件:扭转应力
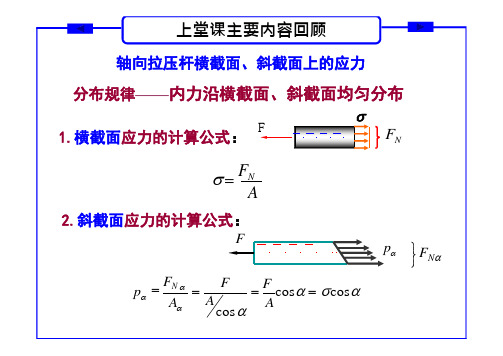
上堂课主要内容回顾
轴向拉压杆横截面、斜截面上的应力
分布规律——内力沿横截面、斜截面均匀分布
1.横截面应力的计算公式: F
FN
FN
A
2.斜截面应力的计算公式:
F
p FN
p
FN A
F A
cos
F cos cos
A
上堂课主要内容回顾 1.横截面应力的计算公式: F
FN
FN
A 2.斜截面应力的计算公式:
结论: 横截面上 e= 0
s =0
g¹
t ¹0
t
根据对称性切应力沿0 圆周均匀分布
r0
t r0, 可认为切应力沿壁厚均匀分布
方向垂直于其半径方向 ???
§ 4 . 3 扭转
3. 横截面上切应力的计算公式
dA
r0
d
r0 dA T
A
2
dA t r0d
r0 t r0d T
0
r0 2 r0t T
试校核支架强度.
解: 1.内力分析
FN
F
sin
32 22 2
50 90.1kN(压)
BC
FN AB FNBC cos
3
90.1 75kN
32 22
(拉)
2.强度条件
木
FN BC a2
90.1103
0.12
9.01MPa [ ]木
钢
FN AB
d2 /4
75103 4
0.0252
dx dx
tg dd d
dx dx
§ 4 . 3 扭转
d
dx
d dx-扭转角变化率
2)物理条件:由应变的变化规律→应力的分布规律
轴向拉压杆横截面、斜截面上的应力
分布规律——内力沿横截面、斜截面均匀分布
1.横截面应力的计算公式: F
FN
FN
A
2.斜截面应力的计算公式:
F
p FN
p
FN A
F A
cos
F cos cos
A
上堂课主要内容回顾 1.横截面应力的计算公式: F
FN
FN
A 2.斜截面应力的计算公式:
结论: 横截面上 e= 0
s =0
g¹
t ¹0
t
根据对称性切应力沿0 圆周均匀分布
r0
t r0, 可认为切应力沿壁厚均匀分布
方向垂直于其半径方向 ???
§ 4 . 3 扭转
3. 横截面上切应力的计算公式
dA
r0
d
r0 dA T
A
2
dA t r0d
r0 t r0d T
0
r0 2 r0t T
试校核支架强度.
解: 1.内力分析
FN
F
sin
32 22 2
50 90.1kN(压)
BC
FN AB FNBC cos
3
90.1 75kN
32 22
(拉)
2.强度条件
木
FN BC a2
90.1103
0.12
9.01MPa [ ]木
钢
FN AB
d2 /4
75103 4
0.0252
dx dx
tg dd d
dx dx
§ 4 . 3 扭转
d
dx
d dx-扭转角变化率
2)物理条件:由应变的变化规律→应力的分布规律
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
代入: dA dd
IP
3dd
A
2d R3d
0
0
R4 D4
2 32
dA
O
实心圆轴的极惯性矩 I P
D 4
I P 32
O
空心圆轴的极惯性矩 I P
D
IP
D4 d4 32
Ip
πD4 1α4 32
d
O
式中: d
c’
Me
d’
a’
c’
b’
Me
b’
pq
切应变 γ :直角的改变量
φ 圆筒两端面的相对扭转角
r
l
对于线弹性材料,
或者对于 p 时,有
剪切胡克定律
G
G – 材料的剪切弹性模量 钢材的 G = 80GPa
pq
d’
a’
c’
b’
φ
pq
d’
γ
τ
a’
c’
τ
b’
到目前为止,已经学到三个材料的弹性常量: E,,G
pq
薄壁圆筒由于壁很薄,表 面变形即为内部变形。
Me
d’
a’
c’
b’
Me
圆轴无此结论
必须对内部变形作进一步分析
pq
2、平面假设
变形前的横截面,变形后仍为平面,且 形状、大小不变,原先的半径仍为半径。
φ 圆轴两端面的
相对扭转角
Me
qq平面相对于pp的相对扭转角
为:d
圆轴表面的切应变γ 为:
aaR dRd
A
mB36kN m d 2
mC14kNm
mA
T (kNm)
解:作轴的扭矩图
对AB段和BC段的 强度要分别计算
B
mB
22
C
d1 mC
14
AB段: TAB 22kN m
A
d2
mA
T (kNm)
W pAB 1 d3 2611 2 3 6 0 1 0 9
B
mB
22
C
d1 mC
14
33.3 91 06m 3
( m) a A x BW T P A A BB 32 .3 3 2 1 1 9 3 0 6 0 6.8 4 M P a
BC段: TBC14kN m
A
d2
mA
T (kNm)
W pB
d3 21030 1 0 9
Mx 0
TA(dA)r
dA
T
d
T 2rdr 0
r
得到:
T
2r2
T
2A0
圆筒壁厚
A0
圆筒考虑圆筒中的微元体abcd
Me
dx
d
a dy
c
b
Me
Mz 0 (dy )d x(dx )dy
C 16
16
B
mB
22
C
d1 mC
14
19.3 61 0 6m 3
( m) a B xC W T p B B C C 11 9 .3 4 1 1 6 3 0 6 0 7.3 1 M P a
轴的强度符合要求
例题
已知:P=7.5kW,n = 100r/min,许用切应力=
ad dx dx
Rd (a)
dx
pq
d’
a’
c’
b’
Me
φ
pq
p
q
R
d
a
ρ
c
a b
b
p
q
现研究圆轴内部的切应变
圆轴内部的切应变
R
d
ae
ρ
e
c
a e’ b
e’
b
d
dx
(b)
圆轴内部任意一点的切应变
与该点到圆心的距离ρ成正比
二、物理关系
Me
d
dx
max
Tmax Wp
例题
A
d2 mA
B
mB
C
d1 mC
已知:阶梯轴尺寸如图 m A 2 k 2 m ,N m B 3 k 6 m ,N m C 1 k 4 m N d 1 12 m 0 ,d m 2 1m 00m
80MPa
要求:计算轴的强度
m A22kN m
§3-3 薄壁圆筒的扭转,纯剪切
一、薄壁圆筒的扭转应力
变形观察:
Me
圆周线不变(大小、 间距都不变)
纵向线倾斜, 倾斜角相同
表面矩形变成
Me
平行四边形
pq
d
a
Me
c
b
pq
pq
d’
a’
Me
c’
b’
pq
横截面上扭转应力分布 规律的分析:
1、横截面上仅有切应力 M e
没有正应力,切应力方 向与圆周线相切。
令:
IP
2dA
A
得: d T
dx GI P
极惯性矩
T
dA
O
四、圆轴扭转切应力计算公式
Gd
dx
(c)
Me
d T
dx GI P
由上述两个方程最终解得
圆轴扭转时横截面上的 切应力计算公式为:
T
IP
dA
O
圆轴的极惯性矩 I P
IP
2dA
pq
d’
a’
Me
c’
b’
pq
因为各圆周线大小、形状、间距都不变
2、沿同一圆周线上的切应力
大小相等
Me
因为各纵向线倾斜角相同
T
3、沿壁厚方向切应力 大小相等
因为薄壁圆筒
Me T
T
薄壁圆筒的扭转时
横截面上扭转应 力分布规律为:
在整个横截面均匀分布,方向 沿圆周线的切线,与T的转向相同。
扭转应力的大小:
得:
pq
da
Me
cb
pq
pq
d’
a’
Me
c’
b’
pq
切应力互等定理
切应力互等定理
d
c
a
d
b
c
a
b
在相互垂直的两个截面上,切应力 必然成对出现,且大小相等,方向为共 同指向或共同背离两个截面的交线。
二、剪切胡克定律
d
a
Me
c
b
d’
γ
a’
pq
da
Me
cb
pq pq
D
D
圆轴扭转最大切应力
max
|R
TR IP
令:
Wp
IP R
抗扭截面系数
圆轴扭转最大切应力为:
max
T Wp
实心圆轴的抗扭截面系数为:
Wp
D 3 16
空心圆轴的抗扭截面系数为:
W pD311 64
五、圆轴扭转时的强度条件
圆轴扭转时的最大切应力不能超过 材料的许用切应力
E 拉压弹性模量
泊松比
G
剪切弹性模量
三个弹性常量之间有如下关系:
G
E
21
对于钢材: G212 0 0.20580 GPa
§3-4 圆轴扭转时的应力
一、变形几何条件
1、变形观察:
pq
圆周线不变(大小、
间距都不变)
Me
纵向线倾斜, 倾斜角相同
d
a
Me
c
b
pq
表面矩形变成 平行四边形
(b)
由剪切胡克定律
G
圆轴内部到圆心的距离为ρ 的任意一点的切应力为:
圆轴内部任意一点的切应力
与该点到圆心的距离ρ成正比
Gd
dx
(c)
0
0
R maxGRddx
三、静力关系
Me
TA(dA )
代入:
Gd
dx
(c)
得: TGd 2dA dx A
代入: dA dd
IP
3dd
A
2d R3d
0
0
R4 D4
2 32
dA
O
实心圆轴的极惯性矩 I P
D 4
I P 32
O
空心圆轴的极惯性矩 I P
D
IP
D4 d4 32
Ip
πD4 1α4 32
d
O
式中: d
c’
Me
d’
a’
c’
b’
Me
b’
pq
切应变 γ :直角的改变量
φ 圆筒两端面的相对扭转角
r
l
对于线弹性材料,
或者对于 p 时,有
剪切胡克定律
G
G – 材料的剪切弹性模量 钢材的 G = 80GPa
pq
d’
a’
c’
b’
φ
pq
d’
γ
τ
a’
c’
τ
b’
到目前为止,已经学到三个材料的弹性常量: E,,G
pq
薄壁圆筒由于壁很薄,表 面变形即为内部变形。
Me
d’
a’
c’
b’
Me
圆轴无此结论
必须对内部变形作进一步分析
pq
2、平面假设
变形前的横截面,变形后仍为平面,且 形状、大小不变,原先的半径仍为半径。
φ 圆轴两端面的
相对扭转角
Me
qq平面相对于pp的相对扭转角
为:d
圆轴表面的切应变γ 为:
aaR dRd
A
mB36kN m d 2
mC14kNm
mA
T (kNm)
解:作轴的扭矩图
对AB段和BC段的 强度要分别计算
B
mB
22
C
d1 mC
14
AB段: TAB 22kN m
A
d2
mA
T (kNm)
W pAB 1 d3 2611 2 3 6 0 1 0 9
B
mB
22
C
d1 mC
14
33.3 91 06m 3
( m) a A x BW T P A A BB 32 .3 3 2 1 1 9 3 0 6 0 6.8 4 M P a
BC段: TBC14kN m
A
d2
mA
T (kNm)
W pB
d3 21030 1 0 9
Mx 0
TA(dA)r
dA
T
d
T 2rdr 0
r
得到:
T
2r2
T
2A0
圆筒壁厚
A0
圆筒考虑圆筒中的微元体abcd
Me
dx
d
a dy
c
b
Me
Mz 0 (dy )d x(dx )dy
C 16
16
B
mB
22
C
d1 mC
14
19.3 61 0 6m 3
( m) a B xC W T p B B C C 11 9 .3 4 1 1 6 3 0 6 0 7.3 1 M P a
轴的强度符合要求
例题
已知:P=7.5kW,n = 100r/min,许用切应力=
ad dx dx
Rd (a)
dx
pq
d’
a’
c’
b’
Me
φ
pq
p
q
R
d
a
ρ
c
a b
b
p
q
现研究圆轴内部的切应变
圆轴内部的切应变
R
d
ae
ρ
e
c
a e’ b
e’
b
d
dx
(b)
圆轴内部任意一点的切应变
与该点到圆心的距离ρ成正比
二、物理关系
Me
d
dx
max
Tmax Wp
例题
A
d2 mA
B
mB
C
d1 mC
已知:阶梯轴尺寸如图 m A 2 k 2 m ,N m B 3 k 6 m ,N m C 1 k 4 m N d 1 12 m 0 ,d m 2 1m 00m
80MPa
要求:计算轴的强度
m A22kN m
§3-3 薄壁圆筒的扭转,纯剪切
一、薄壁圆筒的扭转应力
变形观察:
Me
圆周线不变(大小、 间距都不变)
纵向线倾斜, 倾斜角相同
表面矩形变成
Me
平行四边形
pq
d
a
Me
c
b
pq
pq
d’
a’
Me
c’
b’
pq
横截面上扭转应力分布 规律的分析:
1、横截面上仅有切应力 M e
没有正应力,切应力方 向与圆周线相切。
令:
IP
2dA
A
得: d T
dx GI P
极惯性矩
T
dA
O
四、圆轴扭转切应力计算公式
Gd
dx
(c)
Me
d T
dx GI P
由上述两个方程最终解得
圆轴扭转时横截面上的 切应力计算公式为:
T
IP
dA
O
圆轴的极惯性矩 I P
IP
2dA
pq
d’
a’
Me
c’
b’
pq
因为各圆周线大小、形状、间距都不变
2、沿同一圆周线上的切应力
大小相等
Me
因为各纵向线倾斜角相同
T
3、沿壁厚方向切应力 大小相等
因为薄壁圆筒
Me T
T
薄壁圆筒的扭转时
横截面上扭转应 力分布规律为:
在整个横截面均匀分布,方向 沿圆周线的切线,与T的转向相同。
扭转应力的大小:
得:
pq
da
Me
cb
pq
pq
d’
a’
Me
c’
b’
pq
切应力互等定理
切应力互等定理
d
c
a
d
b
c
a
b
在相互垂直的两个截面上,切应力 必然成对出现,且大小相等,方向为共 同指向或共同背离两个截面的交线。
二、剪切胡克定律
d
a
Me
c
b
d’
γ
a’
pq
da
Me
cb
pq pq
D
D
圆轴扭转最大切应力
max
|R
TR IP
令:
Wp
IP R
抗扭截面系数
圆轴扭转最大切应力为:
max
T Wp
实心圆轴的抗扭截面系数为:
Wp
D 3 16
空心圆轴的抗扭截面系数为:
W pD311 64
五、圆轴扭转时的强度条件
圆轴扭转时的最大切应力不能超过 材料的许用切应力
E 拉压弹性模量
泊松比
G
剪切弹性模量
三个弹性常量之间有如下关系:
G
E
21
对于钢材: G212 0 0.20580 GPa
§3-4 圆轴扭转时的应力
一、变形几何条件
1、变形观察:
pq
圆周线不变(大小、
间距都不变)
Me
纵向线倾斜, 倾斜角相同
d
a
Me
c
b
pq
表面矩形变成 平行四边形
(b)
由剪切胡克定律
G
圆轴内部到圆心的距离为ρ 的任意一点的切应力为:
圆轴内部任意一点的切应力
与该点到圆心的距离ρ成正比
Gd
dx
(c)
0
0
R maxGRddx
三、静力关系
Me
TA(dA )
代入:
Gd
dx
(c)
得: TGd 2dA dx A
