Excel线性内插值计算实例
Excel实现绘制复杂曲线与插值计算
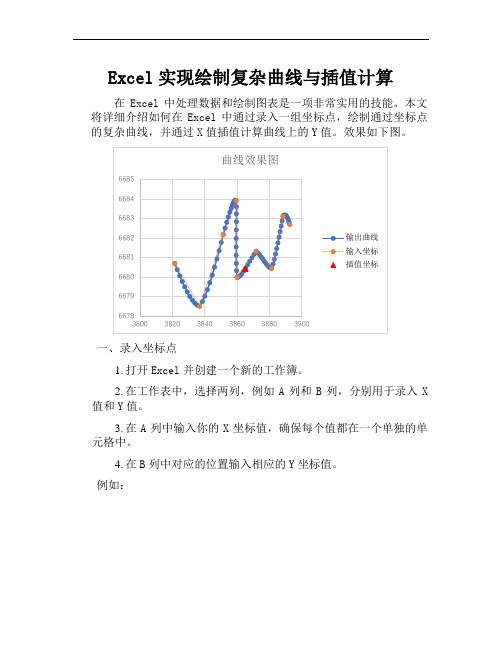
Excel实现绘制复杂曲线与插值计算在Excel中处理数据和绘制图表是一项非常实用的技能。
本文将详细介绍如何在Excel中通过录入一组坐标点,绘制通过坐标点的复杂曲线,并通过X值插值计算曲线上的Y值。
效果如下图。
一、录入坐标点1.打开Excel并创建一个新的工作簿。
2.在工作表中,选择两列,例如A列和B列,分别用于录入X 值和Y值。
3.在A列中输入你的X坐标值,确保每个值都在一个单独的单元格中。
4.在B列中对应的位置输入相应的Y坐标值。
例如:二、录入公式1.在x列和y列后面继续录入 xa,xb,xc,xd,ya,yb,yc,yd,t,ia,ib,ic,id 等列。
2.t列录入从0开始序列值0,1,2,3等。
ia列录入“=K2^3”,ib列录入“=K2^2”,ic列录入“=K2”,id列录入数值“1”。
3.在xa~xd列录入矩阵公式“=TRANSPOSE(MMULT(MINVERSE(L2:O5),A2:A5))”。
在ya~yd列录入矩阵公式“=TRANSPOSE(MMULT(MINVERSE(L2:O5),B2:B5))”。
如下图:4.单元格A2标黄区域录入公式“=2*A3-A4”,B2复制A2。
曲线延长端引入一段直线。
5.上述公式全部录入之后曲线系数就计算完成。
为了查看效果,再新建区域录入公式“=$C3*(P$2+$K3)^3+$D3*(P$2+$K3)^2+$E3*(P$2+$K3)+$F3”,为后续插入图表显示曲线效果计算插值。
三、绘制曲线1.分别选择x值插值与y值插值。
也可以新建区域赋值粘贴转置,得到新的两列数据AJ列与AK列,选中AJ列与AK列中的所有数据。
2.在Excel的菜单栏中,点击“插入”选项卡。
3.在“插入”选项卡中,找到“图表”区域,选择“散点图”或“折线图”。
4.选择你喜欢的图表样式,Excel将自动生成包含你所录入坐标点的曲线图。
三、通过X值计算曲线上的Y值1.在EXCEL表中新的区域布局如下:2.在单元格P13中录入“=VLOOKUP($P$12,$A$2:$J$9,3)”。
excel内插法计算公式举例

excel内插法计算公式举例好嘞,以下是为您创作的关于“excel 内插法计算公式举例”的文章:在我们日常的工作和学习中,Excel 可是个超级实用的工具。
而内插法计算公式,更是能在很多场景下帮我们解决大问题。
比如说,咱们来假设这么一个情况。
小李是一家公司的销售经理,他负责统计每个月的销售数据。
有一个月,他发现销售业绩的增长呈现出了一种有趣的趋势。
从 1 月到 5 月,销售额分别是 10 万、15 万、20 万、25 万、30 万。
现在他想预测一下 3 月中旬的销售额大概是多少。
这时候,内插法计算公式就派上用场啦!在 Excel 中,内插法的基本原理就是通过已知的数据点,来估算中间未知的数据点。
那具体咋操作呢?先来说说线性内插法。
假设我们有两个已知点 (x1, y1) 和 (x2, y2),要估算位于 x1 和 x2 之间的 x 所对应的 y 值。
计算公式就是:y = y1 + ((x - x1) * (y2 - y1) / (x2 - x1))咱们就拿小李的销售数据来举例。
1 月销售额 10 万(x1=1,y1=10),2 月销售额 15 万(x2=2,y2=15),现在要估算 1.5 月(x=1.5)的销售额 y。
y = 10 + ((1.5 - 1) * (15 - 10) / (2 - 1)) = 10 + (0.5 * 5) = 12.5 万这就得出 1.5 月大概的销售额是 12.5 万。
再来说说多项式内插法。
假如已知三个点 (1, 2)、(2, 5)、(3, 10),要估算 x = 2.5 时的值。
我们先设多项式函数为 y = a*x^2 + b*x + c ,然后把三个已知点代入,得到方程组:2 = a + b + c5 = 4a + 2b + c10 = 9a + 3b + c解这个方程组,得出 a = 1.5,b = -1.5,c = 2所以多项式函数就是 y = 1.5*x^2 - 1.5*x + 2当 x = 2.5 时,y = 1.5 * 2.5^2 - 1.5 * 2.5 + 2 = 8.125通过这些例子,您是不是对内插法的计算公式有点儿感觉啦?回到小李这,他后来发现,用内插法估算出来的销售额,和实际情况虽然不能完全一样,但也能给他提供一个很有参考价值的大概数字,帮助他提前做好一些销售策略的调整。
Excel线性内插值计算实例

Excel线性内插值计算实例excel插值,通常通过函数公式完成。
如果手工计算插值,N多烦琐。
excel插值函数有trend和forecast函数。
通过这两个excel插值函数来写相关的插值公式。
下面是两个相关excel 插值资料和案例,供学习者使用。
第一:线性内插值计算实例excel附件中包括四个工作表:一维插值、二维插值(1)、二维插值(2)、三维插值。
第二:Excel画平滑曲线散点图excel附件详细说明了Excel画平滑曲线散点图的算法,并提供了一个自定义函数BezierInt() ,让用户可以随时查找曲线上任意点的坐标(函数值)。
附件的.mht文件,是一个简单介绍贝塞尔三次插值的文档,可以用IE打开,更多贝塞尔插值的算法,可以用搜索引擎插值。
附件的.xls文件,打开以后,会看见三个工作表,分别演示了:找一个数值在曲线上的一组对应点,找一个数值在曲线上的所有对应点,和贝塞尔曲线是怎样在通过每两个节点的(每一对输入的X-Y数值代表平面坐标系的一个点,称为节点,Excel的平滑曲线通过每一个节点)。
如果需要在其他Excel文档使用BezireInt() 函数,需要按Alt+F11,双击模块一复制所有代码,然后打开其他Excel文档按Alt+F11,插入-模块,然后粘贴代码。
自定义函数的使用方法是:在空白单元格输入=BezierInt(X坐标的范围,Y坐标的范围,待查的数值),函数就会返回一个包含六个元素的数组,分别是三个点的X,Y坐标。
如:根据a1:a4的数值作为X值,b2:b4的数值作为Y值,画了一个平滑线散点图。
想查找c1的数值是不是在这条曲线上。
可以输入:=Index( BezierInt(a1:a4,b1:b4,c1) ,1,1) 得到曲线上第一个X值=C1数值的点的X坐标=Index( BezierInt(a1:a4,b1:b4,c1) ,1,2) 得到曲线上第一个X值=C1数值的点的Y坐标=Index( BezierInt(a1:a4,b1:b4,c1) ,1,3) 得到第2个X值=C1数值的点的X坐标=Index( BezierInt(a1:a4,b1:b4,c1) ,1,4) 得到第2个X值=C1数值的点的Y坐标=Index( BezierInt(a1:a4,b1:b4,c1) ,1,5) 得到第3个X值=C1数值的点的X坐标=Index( BezierInt(a1:a4,b1:b4,c1) ,1,6) 得到第3个X值=C1数值的点的Y坐标如果有多段曲线上的点包含C1的数值,那么可以增加输入参数,指定从哪个节点开始查找。
Excel应用大全如何计算插值?
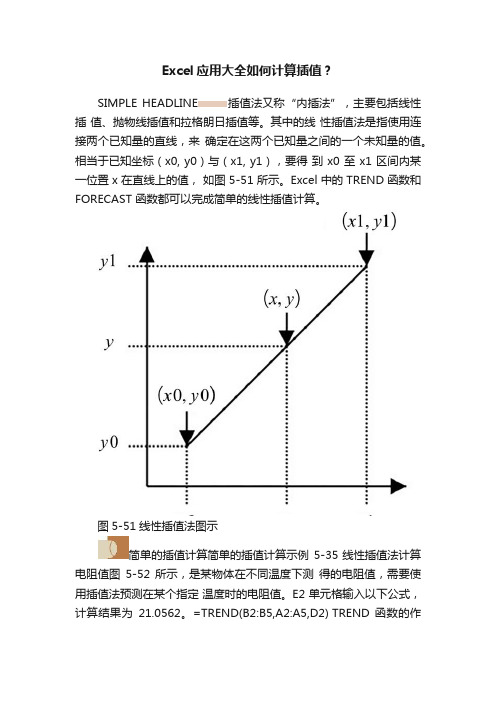
Excel应用大全如何计算插值?SIMPLE HEADLINE插值法又称“内插法”,主要包括线性插值、抛物线插值和拉格朗日插值等。
其中的线性插值法是指使用连接两个已知量的直线,来确定在这两个已知量之间的一个未知量的值。
相当于已知坐标(x0, y0)与(x1, y1),要得到 x0 至 x1 区间内某一位置 x 在直线上的值,如图 5-51 所示。
Excel 中的 TREND 函数和FORECAST 函数都可以完成简单的线性插值计算。
图5-51线性插值法图示简单的插值计算简单的插值计算示例5-35线性插值法计算电阻值图5-52 所示,是某物体在不同温度下测得的电阻值,需要使用插值法预测在某个指定温度时的电阻值。
E2 单元格输入以下公式,计算结果为21.0562。
=TREND(B2:B5,A2:A5,D2) TREND 函数的作用是根据已知x 序列的值和y 序列的值,构造线性回归直线方程,然后根据构造好的直线方程,计算x 值序列对应的y 值序列。
函数语法为:TREND(known_y's,[known_x's],[new_x's],[const]) 第一参数指定已知关系y=mx+b 中的y 值集合。
第二参数指定已知关系y=mx+b 中的 x 值集合。
第三参数指定需要函数 TREND 返回对应 y 值的新 x 值。
第四参数是一个逻辑值,如果为 TRUE 或省略,b 将按正常计算。
如果为 FALSE,b 将被设为 0(零)。
图5-52插值法计算电阻值本例中,TREND 函数的 y 值集合为 B2:B5 单元格区域的电阻值,x 值集合为 A2:A5 单元格区域中的温度值,新 x 值为 D2 单元格中的温度值。
TREND 函数省略第四参数,最终以线性插值法计算出温度为-194 度时对应的电阻值。
使用以下公式也可实现相同的计算。
=FORECAST(D2,B2:B5,A2:A5) FORECAST 函数的作用是根据现有的x 值和 y 值,根据给定的 x 值通过线性回归来预测新的 y 值。
内插法计算例子范文

内插法计算例子范文内插法(Interpolation)是一种在给定数据点之间估计未知数据点的方法。
在数学和统计学中,内插法被广泛应用于近似函数、构建曲线,或者从有限数量的数据点中恢复缺失的数据。
此外,内插法还可以用于数据平滑、滤波和信号处理等应用。
内插法的主要思想是根据已知数据点之间的函数关系,通过插值公式计算出未知数据点的值。
最常用的内插法包括线性内插法、拉格朗日插值法、牛顿插值法等。
下面将以线性内插法和拉格朗日插值法为例,详细介绍内插法的计算步骤和应用。
一、线性内插法线性内插法是最简单且常用的内插法之一,适用于已知两个数据点之间的线性关系。
具体步骤如下:1.给定两个已知数据点:(x1,y1)和(x2,y2),其中x1<x22.计算未知数据点x0的纵坐标y0:y0=y1+(x0-x1)*(y2-y1)/(x2-x1)线性内插法的计算过程非常简单,适用于需要快速估计未知数据点的值的情况。
然而,线性内插法对数据点之间的关系要求较高,如果数据点之间存在非线性的关系,则线性内插法的精度可能较低。
二、拉格朗日插值法拉格朗日插值法是通过构造一个多项式函数来估计未知数据点的值。
具体步骤如下:1. 给定 n+1 个已知数据点:(x0, y0),(x1, y1),...,(xn, yn)。
2.构造n次多项式函数L(x):L(x) = y0 * l0(x) + y1 * l1(x) + ... + yn * ln(x)其中 li(x) = (x - x0) * (x - x1) * ... * (x - xi-1) * (x -xi+1) * ... * (x - xn) / ((xi - x0) * (xi - x1) * ... * (xi -xi-1) * (xi - xi+1) * ... * (xi - xn))3.计算未知数据点x的纵坐标y:y=L(x)拉格朗日插值法通过构造一个满足已知数据点条件的多项式函数来进行插值计算,可以适应各种不同的数据分布和函数形态。
excel线性回归涉及的两个函数:trend和forecast函数,同时也可以使用四种运算。。。

excel线性回归涉及的两个函数:trend和forecast函数,同时也可以使⽤四种运算。
excel线性回归相对来说⽤得⽐较少,但对于做统计和建筑分析预测的朋友来说,有时会涉及到。
下⾯讲讲excel线性回归的具体⽤法,可以使⽤四种运算和Excel内置函数:trend和forecast函数来完成。
⽐如下⾯所⽰Excel⼯作表,就是⼀个典型的线性内插值的实例。
已知两点确定⼀条直线,通过斜率相等求出对应的Y值。
分别使⽤了forecast函数和TREND函数完成。
⽤Excel线性回归计算出4对应的值为 5.8。
第三种⽅法,就是纯粹的四则运算,借助EXCEL的⾃动计算功能完成结果。
forecast函数的帮助说明:根据已有的数值计算或预测未来值。
此预测值为基于给定的 x 值推导出的 y 值。
已知的数值为已有的 x 值和 y 值,再利⽤线性回归对新值进⾏预测。
可以使⽤该函数对未来销售额、库存需求或消费趋势进⾏预测。
forecast函数语法为:FORECAST(x, known_y's, known_x's) X 必需。
需要进⾏值预测的数据点。
Known_y's 必需。
因变量数组或数据区域。
Known_x's 必需。
⾃变量数组或数据区域。
TREND函数的帮助说明:返回⼀条线性回归拟合线的值。
即找到适合已知数组 known_y's和 known_x's 的直线(⽤最⼩⼆乘法),并返回指定数组 new_x's 在直线上对应的 y 值。
TREND函数的语法:TREND(known_y's, [known_x's], [new_x's], [const]) trend和forecast函数区别,都可以完成Excel线性回归分析,它们都是返回沿线性趋势的值。
两个都是根据已知的两列数据,得到线性回归⽅程,并根据给定的新的X值,得到相应的预测值。
excel内插法公式
在财务成本管理中,计算到期收益率、内含报酬率、股权成本、年金现值系数时,都要用到内插法。
表弟表妹们,你会编制内插法的公式吗?内插法基本原理:内插法一般是指数学上的直线内插,它是利用等比关系,用一组已知的未知函数的自变量的值和与它对应的函数值来求一种未知函数其它值的近似计算方法,是一种求未知函数,数值逼近求法。
比如已经两个点,其坐标为(x1,y1),(x2,y2)现已知他们两者之间某个点的X值,要计算该点对应的Y值,使用内插法,其公式如下图所示:内插法应用案例1手动计算法已知容积率4.8和5的修正系数,现要计算容积率为4.9的修正系数,使用内插法手动计算,其公式为:半自动计算法我们也可以使用TREND函数来计算=TREND(B3:C3,B2:C2,C6)或者使用FORECAST函数=FORECAST(C6,B3:C3,B2:C2)关于TREND函数的解释及用法,请参见以前的文章:内插法应用案例2全自动求插值的公式上面的方法只适用于在确定的两个数值之间求插值,如果是已知一系列X、Y值,要计算某个数值对应的插值,上面的公式就不太适用了。
比如下表第二行为容积率,第三行为不同容积率对应的修正系数现随机给出一个容积率,要使用内插法计算对应的修正系数公式1:使用LOOKUP函数使用LOOKUP函数做数组运算,就可轻松搞定=LOOKUP(C6,$B2:$P2,$B3:$P3+(C6-$B2:$P2)*($C3:$Q3-$B3:$P3)/($C2:$Q2-$B2:$P2))公式2:使用TREND函数还是使用TREND函数。
只是TREND函数的第一第二参数需要使用OFFSET函数,结合MATCH函数来取相应单元格的值。
TREND函数的第一第二参数分别为:OFFSET($A$3,0,MATCH(C$6,$B$2:$Q$2,1),1,2)OFFSET($A$2,0,MATCH(C$6,$B$2:$Q$2,1),1,2)扩展阅读:行列交叉查询公式汇总及解释行列交叉查询公式汇总及解释(二)【文末赠书】行列交叉查询公式汇总及解释(三)只能用VLOOKUP匹配数据?还有更多的公式(查找引用公式集锦)将其代入TREND函数的第一第二参数,公式为=TREND(OFFSET($A$3,0,MATCH(C$6,$B$2:$Q$2,1),1,2),OFFSET($A$2,0,MATCH(C $6,$B$2:$Q$2,1),1,2),C$6)上面的公式在容积率为5时会出错,需要加一层IF外套:当容积率为5时,修正系数为5,否则为内插法求得的值:=IF(C6=5,$Q$3,TREND(OFFSET($A$3,0,MATCH(C$6,$B$2:$Q$2,1),1,2),OFFSET($A $2,0,MATCH(C$6,$B$2:$Q$2,1),1,2),C$6))公式3:使用FORECAST函数=IF(C6=5,$Q$3,FORECAST(C$6,OFFSET($A$3,0,MATCH(C$6,$B$2:$Q$2,1),1,2),OF FSET($A$2,0,MATCH(C$6,$B$2:$Q$2,1),1,2)))上面介绍的公式都是使用的直线内插法,这样得出的结果并不够准确。
用excel的线性规划计算 9、16、25宫格
0 0 0 0 0 x5 x6 0 0 0 0 0 x7 x8 x9 0 0 x7 0 0
x5
0 0 x8 0 0 x6 0 0 x9 x5 0 0 0 x9 x5 0 x7 0 0
这个目标函数按道理来说就是刚才所说的从19个自然数中挑选数字填到矩阵的各个元素位置上但是我们做不到将这个汉语直接翻译成代数式刚才我们也用了4个约束条件只满足了这个语文句子的前半句
用 excel 的线性规划计算 9、16、25 宫格 Statist3927 暨南大学经济学硕士 前阵子外甥女突然问我,“姨酱,你会填 9 宫格吗?就是 9 个格子分别填入 1-9 这 9 个 数字,使得每一行,每一竖排,对角线加起来都等于 15?” 这个问题真难倒我了,因为我想 起了高中那会儿给化学方程式配平, 总是按下葫芦浮起瓢, 填好这个系数那个系数又不平衡 了。不过后来我还是用线性代数+R 语言后搞定了这一心中遗憾。于是我脑海里灵光一闪: 会不会用线性代数的方法也可以解出这个问题呢?我觉得这个思路还是靠谱的。 为什么这么 说呢? 我们看,九宫格其实就相当于一个 3×3 的矩阵,要求每个矩阵的元素按照特定的方向 求和后,代数和为相等的一个值,也就是 15。
的范式,直接代入到 excel 你是无法计算的。究竟怎么转变呢?其实不难 首先要有个目标函数。这个目标函数按道理来说就是刚才所说的“从 1-9 这 9 个自然 数中挑选数字填到矩阵的各个元素位置上” ,但是我们做不到将这个汉语直接翻译成代数 式,刚才我们也用了 4 个约束条件,只满足了这个语文句子的前半句。因此,我们必须转 变一下思路:将目标函数设定的简单一些,然后把约束条件加多一些,这样就可以间接实 现了。请看如下操作 目标函数:
内插值计算
内插值计算在工程中有广泛的应用,在其他行业也有应用,如财务管理中的利率查表等。
为理解内插值计算的含义,举个简单例子:图中可见:整个数据区连起来后是一条曲线,但每两个点之间都可以近似看作一段(如果连这样的误差也需要考虑减小的话,看本文的后面其他更进一步的按照这个思路,我们就可以直接转换为用公式计算的方法:12B=243.538(注:这里的计算范围为>=0,<80)公式为: =LOOKUP(B37,A8:B24)+(INDEX($A$8:$B$24,W+1,2)-LOO其中定义名称 W =MATCH(内插值计算!$B$37,内这是一个最“原始”的算法,完全模拟了手工计算。
当然还有其他的公式写法,但实际上,EXCEL已经提供了计算线性插值的函数。
这就是TREND()内插值计算计算方法1格式为:TREND (known_y's ,known_x's,new_x's,const)其中第一和第二参数为已知y值和已知x值,分别对应于上表中的B列和A列 而第三参数则为需要求插值的数值,对应于上面的A=12函数更详细的说明见帮助文件。
使用这个函数时,我们要注意:如果我们按帮助文件中的举例来作,把公式写成:TREND(B8:B24,A8:A24,12)将得不原因在于:TREND是求一条线性回归拟合线的值,而我们表一并不是线性关系,图一所以我们必须仍然按照上面的思路把曲线分割成若干直线段来计算B=243.538公式: =TREND(INDIRECT("B"&W+7&":"&"B"&W+8),INDIRECT("A这是不是简单多了?上面说到,由于图一不是直线,所以我们采用分段计算。
如果是直线,怎么样?看下例:当数据是线性相关时,可以取整个数据区,否则应分段计算我们注意到图二是一条直线,那么我们自然就想到:能不能写出这条直线的解析式?有了解析式,问题肯定简单得多!我们知道,直线的解析式是 y=ax+b,怎么求a,b?这就要用到excel函数的另一个函数:LINEST()格式为:LINEST (known_y's ,known_x's,const,stats)其中后两个参数省略的情况下,即可返对于表二的数据,我们有以下的计算:有这样一个温度-电阻的表达式,计算不就太简单了吗!计算方法2计算方法3LINEST函数TREND函数-18226.1886-18126.6163-18027.044那么,对于不是直线的表一、图一,还能用类似办法吗?能!我们用表一数据来说明:计算方法4图三35030025020015010050020*********图四表四计算结果系数A B 上面的这个图表中给出的公式,即可用来计算0211.99212.022218.47218.46-8.78744E-103221.5221.47 2.47137E-075227.16227.12-2.86078E-058234.78234.780.001830558其中的系数也可以用公式法来求,这样计算方10239.41239.43-0.07852947215249.73249.80 3.368981529公式及计算结果见左侧表四。
如何利用EXCEL进行线性插值
如何利用EXCEL进行线性插值EXCEL表格使用中,我们常常会遇到线性插值的问题,其中,比较有代表性的就是在水温密度和比容的取值方面。
以下内容就以水温的密度和比容来说明如何利用EXCEL进行线性插值。
上图是水温密度和比容的取值计算的excel计算的截图,其中红色部分为输入的温度值,蓝色部分为计算的结果,具体的计算公式及说明见下表计算公式 说明温度 25 -/- 输入温度值温度范围(下限) 20 =INDEX(A2:A12,MATCH(H2,A2:A12,1)) 找到输入的温度值的计算范围(下限)温度范围(上限) 30 =INDEX(A2:A12,MATCH(H2,A2:A12,1)+1) 找到输入的温度值的计算范围(上限)温度范围(下限)对应的密度 998.2 =INDEX(B2:B12,MATCH(H2,A2:A12,1)) / 温度范围(上限)对应的密度 995.7 =INDEX(B2:B12,MATCH(H2,A2:A12,1)+1) / 温度范围(下限)对应的比容 4.183 =INDEX(C2:C12,MATCH(H2,A2:A12,1)) / 温度范围(上限)对应的比容 4.174 =INDEX(C2:C12,MATCH(H2,A2:A12,1)+1) /密度 996.95 =TREND(H5:H6,H3:H4,H2) 通过线性拟合函数求解密度比容 4.1785 =TREND(H7:H8,H3:H4,H2) 通过线性拟合函数求解比容相关的excel函数说明如下:(1)INDEX函数函数名称:INDEX主要功能:返回列表或数组中的元素值,此元素由行序号和列序号的索引值进行确定。
使用格式:INDEX(array,row_num,column_num)参数说明:Array代表单元格区域或数组常量;Row_num表示指定的行序号(如果省略row_num,则必须有 column_num);Column_num表示指定的列序号(如果省略column_num,则必须有 row_num)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Excel线性内插值计算实例
excel插值,通常通过函数公式完成。
如果手工计算插值,N多烦琐。
excel插值函数有trend和forecast函数。
通过这两个excel插值函数来写相关的插值公式。
下面是两个相关excel 插值资料和案例,供学习者使用。
第一:线性内插值计算实例
excel附件中包括四个工作表:一维插值、二维插值(1)、二维插值(2)、三维插值。
第二:Excel画平滑曲线散点图
excel附件详细说明了Excel画平滑曲线散点图的算法,并提供了一个自定义函数BezierInt() ,让用户可以随时查找曲线上任意点的坐标(函数值)。
附件的.mht文件,是一个简单介绍贝塞尔三次插值的文档,可以用IE打开,更多贝塞尔插值的算法,可以用搜索引擎插值。
附件的.xls文件,打开以后,会看见三个工作表,分别演示了:找一个数值在曲线上的一组对应点,找一个数值在曲线上的所有对应点,和贝塞尔曲线是怎样在通过每两个节点的(每一对输入的X-Y数值代表平面坐标系的一个点,称为节点,Excel的平滑曲线通过每一个节点)。
如果需要在其他Excel文档使用BezireInt() 函数,需要按Alt+F11,双击模块一复制所有代码,然后打开其他Excel文档按Alt+F11,插入-模块,然后粘贴代码。
自定义函数的使用方法是:在空白单元格输入=BezierInt(X坐标的范围,Y坐标的范围,待查的数值),函数就会返回一个包含六个元素的数组,分别是三个点的X,Y坐标。
如:根据a1:a4的数值作为X值,b2:b4的数值作为Y值,画了一个平滑线散点图。
想查找c1的数值是不是在这条曲线上。
可以输入:
=Index( BezierInt(a1:a4,b1:b4,c1) ,1,1) 得到曲线上第一个X值=C1数值的点的X坐标=Index( BezierInt(a1:a4,b1:b4,c1) ,1,2) 得到曲线上第一个X值=C1数值的点的Y坐标=Index( BezierInt(a1:a4,b1:b4,c1) ,1,3) 得到第2个X值=C1数值的点的X坐标
=Index( BezierInt(a1:a4,b1:b4,c1) ,1,4) 得到第2个X值=C1数值的点的Y坐标
=Index( BezierInt(a1:a4,b1:b4,c1) ,1,5) 得到第3个X值=C1数值的点的X坐标
=Index( BezierInt(a1:a4,b1:b4,c1) ,1,6) 得到第3个X值=C1数值的点的Y坐标
如果有多段曲线上的点包含C1的数值,那么可以增加输入参数,指定从哪个节点开始查找。
=Index( BezierInt(a1:a4,b1:b4,c1,3),1,1) 得到从第三组X-Y数据开始查找,返回第一个符合C1数值的点的X坐标=Index( BezierInt(a1:a4,b1:b4,c1,3),1,2) 得到从第三组X-Y数据开始查找,返回第一个符合C1数值的点的Y坐标。
函数默认输入数值是X值,要根据Y值找点的话,还可以增加输入参数,指定输入的是Y 值=Index( BezierInt(a1:a4,b1:b4,c1,1,"Y"),1,1) 得到返回曲线上第一个Y值=C1数值的点的X 坐标。
