深圳市南山区2014届高三上学期期末考试数学(文)
深圳市宝安区2014届上学期末高三调研测试文科数学试卷

深圳市宝安区2014高三上学期调研测试数学(文科)一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合},2,1,0,1,2{},1|1||{--=>+=B x x A 则=B A C R )( ( ). A. }2{- B. }1,2{- C. }1,0{ D. }0,1,2{--2.下列函数中,既是偶函数又在区间),0(+∞上是单调递减函数的是( ).A. x x f 1)(=B. 1)(2+-=x x f C. |21|)(x x f = D. ||lg )(x x f =3.设i 是虚数单位,若复数iai --310是实数,则a 的值为( ).A.3-B. 1-C. 3D. 14.等差数列}{n a 中,,26,2491321=-=++a a a a 则此数列}{n a 前20项和等于( ). A.220 B. 200 C. 180 D. 1605.已知向量),,2(),,1(m b m a =-=若1=⋅b a ,则实数=m ( ). A. ,1或1- B. 1- C. 0 D. 2-6.若点(,)x y 位于曲线2||y x =与2y =所围成的封闭区域,则2x y -的最小值为( ).A.4-B.6-C. 0D. 17.将函数)32cos(2π+=x y 的图像向右平移)0(>m m 个单位长度后,所得到的图像关于y 轴对称,则y x -2的最小值为( ).A. 2πB. 3πC. 6πD. 12π8.椭圆)0(122>=+m m y x 的离心率大于21的充分必要条件是( ). A. 41<m B. 3443<<m C. 43>mD. 340<<m ,或43>m9.阅读如图所示的程序框图,运行相应的程序.若输入m 的值为2,则 输出的结果为=i ( ).A. 3B. 4C. 5D. 610.给出下列关于互不相同的直线n l m ,,和平面βα,的四个命题: ①若,,A l m =⊂αα 点m A ∉,则l 与m 不共面;②若l m ,是异面直线,αα//,//m l ,且m n l m ⊥⊥,,则α⊥n ; ③若βαβα//,//,//m l ,则m l //;④若,//,//,,,ββααm l A m l m l =⊂⊂ ,则βα//.其中为假命题的是( ).A. ①B. ②C.④D. ③二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分否是 输出i 结束A B <A A m =⨯ 开始 1,1,0AB i ===1i i =+ 输入mB B i =⨯(一)必做题(9—13题)11.右图中的三个直角三角形是一个体积为20cm 3的几何体的三视图, 则h=______cm.12.据统计,高三年级男生人数占该年级学生人数60%.在上次考试中, 男、女生数学平均分数分别为115,120,则这次考试该年级学生平均 分数为_________.13.设常数0>a ,若192+≥+a xa x 对一切正实数x 成立,则a 的取值范围为_________.(二)选做题(14、15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图,在Rt ABC 中, 90,30,C A ∠=∠= 圆O 经过B 、C ,且与AB 、AC分别相交于C 、D 。
【精选高中试题】广东省深圳市南山区高三上学期期末教学质量监测数学(文)试题Word版含答案

高三教学质量监测数学(文科注意:本试卷分选择题和非选择题两部分,共150分,考试时间120分钟.1.答卷前,考生填、涂好学校、班级、姓名及座位号。
2.选择题用2B 铅笔作答;非选择题必须用黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,并将答题卡交回。
参考公式:锥体的体积公式13V Sh =,其中S 为锥体的底面积,h 为锥体的高.一组数据12,,,n x x x 的标准差s =其中x 表示这组数据的平均数.第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,在每一小题给出的四个选项中,只有一项是符合题目要求的。
1. 集合()(){}041/<-+=x x x A ,{}ln 1B x x =<,则 A .A B φ= B .A B A =C .A B A =D .以上都不对2. 设i 为虚数单位,则复数34ii-= A .43i -- B .43i -+ C .i 4+3 D .i 4-3 3. 若p 是真命题,q 是假命题,则 A .p q ∧是真命题 B .p q ∨是假命题 C .p ⌝是真命题D .q ⌝是真命题4.在ABC ∆中,若15,,sin 43b B A π=∠==,则a = A .325 B .335C .33D .533 5.下列函数为偶函数的是A .sin y x =B.)ln y x =C .x y e =D.y =6. 函数y =sin (2x +3π)•cos (x ﹣6π)+cos (2x +3π)•sin (6π﹣x )的图象的一条对称轴方程是 A .x =4π B .x =2π C .x =π D .x =23π 7.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n 的样本进行调查,其中从丙车间的产品中抽取了3件,则n=. A .9B .10C .12D .138.设m 、n 是两条不同的直线,α、β是两个不同的平面,则以下结论正确的是A .若m ∥α,n ∥α,则m ∥nB .若m ∥α,m ∥β,则α∥βC .若m ∥n ,m ⊥α,则n ⊥αD .若m ∥α,α⊥β,则m ⊥β 9.如图所示,程序据图(算法流程图)的输出结果为A .43B .61C .1211D .2425 10.设,x y 满足约束条件 ,则6+4+x y 的取值范围是A .B .C .D . 11.已知F 1(﹣3,0)、F 2(3,0)是椭圆ny m x 22+=1的两个焦点,P 是椭圆上的点,当∠F 1PF 2=32π时,△F 1PF 2的面积最大,则有 A .m =12,n =3B .m =24,n =6C .m =6,n =23D .m =12,n =6 12.设函数()f x 的定义域为D ,若满足条件:存在[,]a b D ⊆,使()f x 在[,]a b上的值域202300x y x y x y --≤⎧⎪-+≥⎨⎪+≤⎩3[3,]7-[3,1]-[4,1]-(,3][1,)-∞-+∞为[,]22a b,则称()f x 为“倍缩函数”.若函数()ln f x x t =+为“倍缩函数”,则实数t 的取值范围是A .(﹣∞,ln2﹣1)B .(﹣∞,l n 2﹣1]C .(1﹣l n 2,+∞)D .[1﹣l n 2,+∞)第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答,第22~第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分。
广东省中山市2014届高三上学期期末数学文试卷Word版含答案

中山市高三级2013—2014学年度第一学期期末统一考试数学试卷(文科)本试卷共4页,20小题,满分150分.考试用时120分钟.注意事项:1、答卷前,考生务必将自己的姓名、统考考号、座位号、考试科目用铅笔涂写在答题卡上。
2、每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题上。
3、不可以使用计算器。
4、考试结束,将答题卡交回,试卷不用上交。
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.设复数113i z =-,21i z =-,则12z z +在复平面内对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限2.设全集U 是实数集,R {}22,M x x =-≤≤,{}2430N x x x =-+>,则M N ⋂=( ) A .{|21}x x -≤< B .{|22}x x -≤≤ C .{|12}x x <≤D .{|2}x x <3.已知平面向量()21=,a ,()2x =-,b ,若a ∥b ,则a +b 等于( ) A .()2,1--B .()2,1C .()3,1-D .()3,1-4.已知数列{}n a 为等差数列,若23a =,1612a a +=,则789a a a ++=A .36B .42C .45D .635.在某次测量中得到的A 样本数据如下:82, 84, 84, 86, 86, 86, 88, 88, 88, 88.若B 样本数据恰好是A 样本数据都加2后所得数据,则A ,B 两样本的下列数字特征对应相同的是( ) A .众数B .平均数C .中位数D .标准差6.如图,设A 、B 两点在河的两岸,一测量者在A 的同侧所在的河岸边选定一点C ,测出AC 的距离为50m , 105,45=∠=∠CAB ACB 后, 就可以计算出A 、B 两点的距离为( ) A.m 2225B .m 225C .m 250D .m 3507.如图,定义某种运算a S b =⊗,运算原理如右图所示,则式子131100lg ln )45tan 2(-⎪⎭⎫⎝⎛⊗+⊗e π的值为( )A .11B .13C .8D .48.若一个底面为正三角形、侧棱与底面垂直的棱柱 的三视图如下图所示,则该棱柱的体积为( )A .B .C .D .69.已知函数)(x f y =)(R x ∈满足(2)2()f x f x +=,且[1,1]x ∈-时,()1f x x =-+,则当(0,10]x ∈时,)(x f y =与4()log g x x =的图象的交点个数为( ) A .11B .10C .9D .810.对a ∀、b R ∈,运算“⊕”、“⊗”定义为:a b ⊕=,().()a a b b a b <⎧⎨≥⎩,a b ⊗=,().()a ab b a b ≥⎧⎨<⎩,则下列各式其中不恒成立的是( ) ⑴a b a b a b =+⊗+⊕ ⑵a b a b a b =-⊗-⊕ ⑶[][]a b a b a b =⋅⊗⋅⊕ ⑷[][]a b a b a b =÷⊗÷⊕ A .⑴、⑶B .⑵、⑷C .⑴、⑵、⑶D .⑴、⑵、⑶、⑷二、填空题(本大题共4小题,每小题5分,满分20分。
南山区2013-2014学年高一上期末考试数学试卷

高一期末考试数学2014-01-8本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟.注意事项:1、答卷前,考生首先检查答题卡是否整洁无缺损.之后务必用黑色签字笔在答题卡指定位置填写自己的学校、班级、姓名及座位号,在右上角的信息栏填写自己的考号,并用2B 铅笔填涂相应的信息点.2、选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.不按要求填涂的,答案无效.3、非选择题必须用黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,请注意每题答题空间,预先合理安排、如需改动,先划掉原来的答案,然后再写上新的答案、不准使用铅笔和涂改液.不按以上要求作答的答案无效.4、考生必须保持答题卡的整洁,不折叠,不破损、考试结束后,将答题卡交回.5、考试不可以使用计算器.第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的编号用铅笔涂在答...............题卡上....1、设集合M={-1,0,1},N={x|x2=x},则M∩N=()A、{-1,0,1}B、{0,1}C、{1}D、{0}2、下列函数中,与函数y=x相同的函数是()A、2xy=xB、2y=C、2log xy=2D、y=lg10x3、已知a,b是异面直线,直线c∥a,那么直线c与b()A、一定是相交直线B、一定是异面直线C、不可能是相交直线D、不可能是平行直线4、幂函数y=f(x)的图像经过点(4,0.5),则f(0.25)的值为()A、1B、2C、3D、45、已知m ,n 是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的是( ) A 、若α∥β,m ⊂α,n ⊂β,则m ∥n B 、若α⊥β,m ⊂α,则m ⊥β C 、若m ⊥n ,m ⊂α,则n ⊥α D 、若m ⊥α,m ∥β,则α⊥β6、若4a =25b =10,则11+a b=( ) A 、1 B 、2 C 、3 D 、47的等边三角形,侧棱长都为2,则侧棱与底面所成角的大小为( )A 、30oB 、45oC 、60oD 、90o8、若当x ∈R 时,函数f (x )=a |x |(a >0且a ≠1)满足f (x )≤1,则函数y =log a (x +1)的图像大致为( )9、已知f (x )是R 上的奇函数,对于x ∈R ,都有f (x +4)=f (x )+f (2)成立,若f (1)=2,则f (2013)等于( )A 、0B 、2C 、2014D 、-2 10、对于不重合的两个平面α与β,给定下列条件:①存在平面γ,使得α,β都垂直于γ;②存在平面γ,使得α,β都平行于γ; ③α内有不共线的三点到β的距离相等;④存在异面直线l ,m ,使得l ∥α,l ∥β,m ∥α,m ∥β、 其中,可以判定α与β平行的条件有( )A 、1个B 、2个C 、3个D 、4个第Ⅱ卷(非选择题共100分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.......... (一)必做题:(11~13题)11、若集合A ={x |-1≤x ≤2},B ={x |x ≤a },A ∩B =A ,则实数a 的取值范围是_______. 12、如果一个几何体的三视图如图所示(单位长度:cm ),则此几何体的表面积是_______.13、把函数y =log a x (a >0,且a ≠1)的图像上所有的点向左平移2个单位长度,再向下平移1个单位长度后得到函数y =f (x )的图像,已知函数y =f (x )的图像经过定点A (m ,n ).若方程kx 2+mx +n =0有且仅有一个零点,则实数k 的值为________.(二)必做题:(14~15题只选做一题)14、如果执行下图程序框图,那么输出的S =_____. 15、已知两点A (-3,-4),B (6,3)到直线l :ax +y +1=0的距离相等,则实数a 的值等于______.三、解答题:本大题共6小题,共80分,解答应写出文字说明或演算步骤、 16、(本小题满分12分)已知集合U =R ,A ={x |0.5<2x <4},B ={x |log 3x ≤2}. (1)求A ∩B ; (2)求∁U (A ∪B ).左视图17、(本小题满分12分)已知函数222(0)()0(0)2(0)x x x f x x x x x ⎧-+>⎪==⎨⎪+<⎩,,,. (1)求证函数y =f (x )是奇函数;(2)试作出函数y =f (x )是的图像; (3)若函数y =f (x )在区间[-1,a -2]上单调递增,求实数a 的取值范围.18、(本小题满分14分)如图,在三棱锥A -BOC 中,∠OAB =30o ,AO ⊥平面BOC ,AB =4,∠BOC =90o ,BO =CO ,D 是AB 的中点.(1)求证:CO ⊥平面AOB ;(2)求异面直线AO 与CD 所成角的正切值.ABCDO已知函数f(x)=log a(2x+2),g(x)=log a(2x-2)(a>0,且a≠1).(1)求函数h(x)=f(x)-g(x)的定义域;(2)判断函数h(x)=f(x)-g(x)在x∈(1,+∞)内的单调性,并用定义给予证明;(3)当a=2时,若对[3,5]上的任意x都有h(x)<2x+m成立,求m的取值范围.20、(本小题满分14分)如图,菱形ABCD的边长为4,∠BAD=60o,AC∩BD=O,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,且DM=求证:OM//平面ABD;(2)求证:平面DOM⊥平面ABC;(3)求点B到平面DOM的距离.ABCDOABCDOM已知函数f(x)=ax2+bx+c满足:f(0)=0,对任意x∈R,都有f(x)≥x且f(x)的对称轴为x=-0.5,令g(x)=f(x)-|tx-1|(t>0).(1)求函数f(x)的表达式;(2)当t=1时,求函数g(x)的最小值;(3)求函数g(x)的单调区间.高一数学参考答案及评分标准 2014.1.8一、选择题:(10×5'=50')二、填空题:(4×5′=20′)11、a ≥2; 12、(20+cm 2; 13、0或14-;14、94 ;15、79-或13-.三、解答题:(80′) 16、(本小题满分12分)解:(1) ∵A ={x |0.5<2x <4}={x |-1<x <2}, ……2分 B ={x |log 3x ≤2}={x |0<x ≤9}, ……4分 ∴A ∩B ={x |0<x <2}. ……6分 (2) A ∪B ={x |-1<x ≤9}, ……9分 ∁U (A ∪B ) ={x | x ≤-1或x > 9}. ……12分 17、(本小题满分12分) 解:(1)∀x <0,则-x >0,所以f (-x )=-(-x )2+2(-x )=-x 2-2x =-f (x ); ……2分 又∀x >0,则-x <0,所以f (-x )=-(-x )2+2(-x )=-x 2-2x =-f (x ); ……3分 且f (0)=0,所以f (-x )=-f (x ). ……4分∴f (x )为奇函数. ……5分(2)图像如右上图. ……9分(3)要使f (x )在[-1,a -2]上单调递增,结合f (x )的图象知,a 21a 21->-⎧⎨-≤⎩,所以1<x ≤3,故实数a 的取值范围是(1,3]. ……12分 18、 (本小题满分14分)O CADBE解:(1)由题意,∵AO ⊥平面BOC ,又CO ⊂平面COB ,∴CO ⊥AO , ……3分 ∴∠BOC =90o , ∴CO ⊥BO , ……4分 又∵AO ∩B 0=O ,∴CO ⊥平面AOB . ……6分 (2)作DE ⊥OB ,垂足为E ,连结CE (如图), 则DE ∥AO ,∴∠CDE 是异面直线AO 与CD 所成的角. ……8分 在Rt △COE 中,CO =BO =2,OE =0.5BO =1,∴CE == ……10分又1DE =AO =2∴在Rt △CDE中,CE tan CDE ===DE 3∠. …13分 ∴异面直线AO 与CD所成角的正切值为3. ……14分 19、(本小题满分14分)解:(1)由题意可知,h (x )=f (x )-g (x )= log a (2x +2)-log a (2x -2),……1分 由2x +2>02x 2>0⎧⎨-⎩解得x >1,所以h (x )的定义域为(1,+∞). ……2分(2) h (x )=f (x )-g (x )= log a (2x +2)-log a (2x -2)aa2x +2x +1=log =log 2x 2x 1--, ……3分 令x +1k(x)=x 1-,设x 1,x 2∈(1,+∞),且x 1<x 2,那么12211212121+x 1+x 2(x x )k(x )k(x )==x 1x 1(x 1)(x 1)------- , ……5分 因为x 1,x 2∈(1,+∞),且x 1<x 2,所以x 1-x 2<0,x 1-1>0,x 2-1>0,所以2112122(x x )k(x )k(x )=>0(x 1)(x 1)----,k (x )在区间(1,+∞)上为减函数. ……7分 ∴a >1时,y =h (x )在区间(1,+∞)上为减函数.0<a <1时,y =h (x )在区间(1,+∞)上为增函数, ……9分 (3)由题意知,m >h (x )-2x ,对∀ x ∈[3,5]恒成立, ∴m >[h (x )-2x ]max , ……11分又当a =2时,h (x )与y =-2x 在x ∈[3,5]都是减函数, ……12分 ∴m >[h (x )-2x ]max =-7,∴m ∈(-7,+∞). ……14分 20、(本小题满分14分)(2)因为在菱形ABCD 中,OD ⊥AC , 所以在三棱锥B -ACD 中,OD ⊥AC .在菱形ABCD 中,AB =AD =4,∠BAD =60o,所以BD =4.因为O 为BD 的中点,所以OD =0.5BD =2.因为O 为AC 的中点,M 为BC 的中点,所以OM =0.5AB =2. .……6分因为OD 2+OM 2=8=DM 2,所以∠DOM =90o ,即OD ⊥OM .因为AC ⊂平面ABC ,OM ⊂平面ABC ,AC ∩OM =O ,所以OD ⊥平面ABC . 因为OD ⊂平面DOM ,所以平面DOM ⊥平面ABC . ……9分 (3)由(2)得,OD ⊥平面BOM ,所以OD 是三棱锥D -BOM 的高. 设点B 到面DOM 距离为h ,因为OD =2,ABDOM21、(本小题满分14分)解:(1)由f (0)=0,得c =0,且对任意x ∈R ,都有f (x )≥x 恒成立, 即ax 2+(b -1)x ≥0恒成立, ……2分 可得b =1,又f (x )的对称轴为x =-0.5,即b 1=2a 2--,得a =1, 所以f (x )=x 2+x . ……4分(2) g (x )= x 2+x .-|x -1|=22x +1x 1x +2x 1x <1⎧≥⎨-⎩,, ……5分当x ≥1时,g (x )的最小值为g (1)=2;当x <1时,g (x )的最小值为g (-1)=-2, 所以g (x )的最小值为-2. ……8分(3) g (x )=f (x )-|tx -1|=221x +(1t)x +1x t 1x +(1+t)x 1x <t ⎧-≥⎪⎪⎨⎪-⎪⎩,,, ……9分①当1x t≥时,g (x )的对称轴为t 1x 2-=,t 112t-≤,即0<t ≤2时, g (x )在1[)t +∞,上单调增,t 112t ->,即t >2时,g (x )在t 1()2-+∞,上单调增,在1t 1()t 2-,上单调减. ……11分②当1x t<时,g (x )的对称轴为t 1x 2+=-,因为t >0,则t 112t+-<, 所以g (x )在t 11()2t +-,上单调递增,在t 1()2+-∞-,上单调递减.……13分综上所述:0<t≤2时,g(x)在t1()2+-+∞,单调递增,在t1()2+-∞-,单调减;t>2时,g(x)在t11()2t+-,,t1()2-+∞,单调递增,在t1()2+-∞-,,1t1()t2-,单调递减. ……14分。
2013-2014学年广东省深圳市南山区高一下学期期末统考数学试卷(带解析)
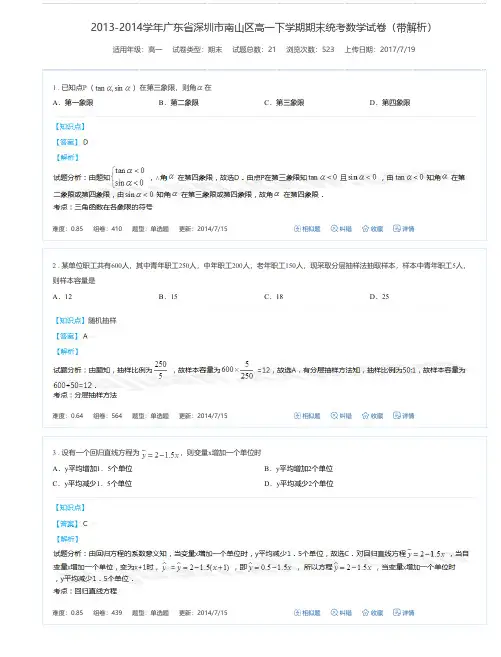
, B.矩形
【知识点】平面向量的数量积
,则该四边形是 C.直角梯形
D.正方形
难度:0.85 组卷:466 题型:单选题 更新:2014/7/15
相似题 纠错 收藏 详情
11 . 直线
与圆
【知识点】直线与圆的位置关系
的位置关系是 (填相交、相切、相离)
难度:0.85 组卷:579 题型:填空题 更新:2014/7/15
相似题 纠错 收藏 详情
14 . 直线 【知识点】直线的方程
在 轴和 轴上的截距相等,则 的值是______
难度:0.64 组卷:958 题型:填空题 更新:2011/2/24
相似题 纠错 收藏 详情
15 . 如图给出的是计算
的值的一个程序框图,判断框中应该填入的条件是 .
【知识点】算法与程序框图
相似题 纠错 收藏 详情
2 . 某单位职工共有600人,其中青年职工250人,中年职工200人,老年职工150人,现采取分层抽样法抽取样本,样本中青年职工5人,
则样本容量是
A.12
B.15
C.18
D.25
【知识点】随机抽样
难度:0.64 组卷:564 题型:单选题 更新:2014/7/15
相似题 纠错 收藏 详情
12 . 若点P
在直线
上,则
【知识点】三角函数的图象与性质
相似题 纠错 收藏 详情
难度:0.64 组卷:561 题型:填空题 更新:2014/7/15
相似题 纠错 收藏 详情
13 . 已知
,
,则向量 与向量 的夹角的余弦值为
【知识点】平面向量的数量积
难度:0.85 组卷:342 题型:填空题 更新:2014/7/15
广东省深圳市南山区2014年七年级上学期期末统考数学试题

七 年 级 期 末 考 试数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页,满分100分,考试时间90分钟。
注意事项:1.答卷前,考生首先检查答题卡是否整洁无缺损,之后务必用黑色签字笔在答题卡指定位置填写自己的学校、班级、姓名及座位号,在右上角的信息栏填写自己的考号,并用2B 铅笔填涂相应的信息点.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上,不按要求填涂的,答案无效.3.非选择题必须用黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,请注意每题答题空间,预先合理安排,如需改动,先划掉原来的答案,然后再写上新的答案.不准使用铅笔和涂改液,不按以上要求作答的答案无效. 4.考生必须保持答题卡的整洁,不折叠,不破损.考试结束后,将答题卡交回.第Ⅰ卷 选择题一、选择题(本题有10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确的....选项..用铅笔涂在答题卡上..........) 1.下列调查方式的选取不合适的是A .为了解全市初中生每周“阳光体育”的时间,采取抽样调查的方式B .对“嫦娥三号”卫星零部件的检查,采取抽样调查的方式C .为了解人们保护水资源的意识,采取抽样调查的方式D .为了解全班同学的睡眠状况,采用普查的方式2.嫦娥三号于2013年12月2日1时30分由长征三号乙运载火箭从西昌卫星发射中心发射升空.截至12月2日16时,嫦娥三号卫星距地面高度约为14万千米,则14万用科学记数法表示为A .41014⨯ B .4104.1⨯ C .51014⨯ D .5104.1⨯2014.1.3.若单项式y x 232-的系数是m ,次数是n ,则mn 的值为 A .2-B .6-C .4-D .43-4.下列运算中,正确的是A .()()326-=-÷-B .94322=⎪⎭⎫⎝⎛-C .ab b a 532=+D .23=-a a 5.以下四个语句中,错误的是A .两点确定一条直线B .'305.0=C .数轴是一条直线D .射线AB 也可以写作射线BA6.为确保信息安全,信息需要加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).已知加密规则为:明文a 、b 、c 对应的密文1+a ,42+b ,93+c .例如明文1,2,3,对应的密文为2,8 ,18.如果接收方收到密文7,18,15,则解密得到的明文为A .6,5,2;B .6,5,7;C .6,7,2D .6,7,6;7.某学校七年级(3)班共有50名学生,老师对学生最喜欢的一种球类运动进行了调查,并根据调查的结果制作了如图扇形统计图(不完整),请你根据扇形统计图中提供的信息判断下列说法错误的是.A .最喜欢足球的人数最多,达到了15人;B .最喜欢羽毛球的人数比例最少,只有10%;C .图中表示排球的扇形的圆心角为50°;D .最喜欢乒乓球的人数比最喜欢篮球的人数多6人.8.已知a 、b 在数轴上对应点的位置如图所示,则下列结论中正确的是A .0>-b aB .0>-b aC .0>+b aD .0>ab9.一个长方形的周长是26cm ,若这个长方形的长减少 1cm ,宽增加2cm ,就可以成为一 个正方形,则此正方形的边长是A .5cmB .6cmC .7cmD .8cm10.已知O 为圆锥的顶点,M 为底面圆周上一点,点P 在OM 上,一只蚂蚁从点P 出发绕圆锥侧面爬行回到点P 时所经过的最短路径的痕迹如右图,若沿OM 将圆锥侧面剪开并展平,所得侧面展开图是第Ⅱ卷 非选择题二、填空题:本题有5小题,每小题3分,共15分.把答案填在答题卡上.......... 11.如果□02=+,那么“□”内应填的实数是__________. 12. 已知321y x m 与n xy 2-是同类项,则m n +=__________. 13. 若1=-b a ,则代数式221a b -+的值是__________. 14.若1=x 是关于x 的方程032=+k x 的解,则=k __________.15.填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m 的值是_________.三、解答题(本大题有7题,其中16题12分,17题6分,18题8分,19题8分,20题8分,21题7分,22题6分,共55分)16.(12分)计算与化简 (1)()()5312-+-- (2)()()3116248⎛⎫÷---⨯- ⎪⎝⎭(3)化简:22247583x x x x -++--(4)先化简,再求值:211(428)(2)42a a a -+---,其中12a =.17.(6分)解下列方程(1) x x -=-1)1(4 (2) 3122413--=+y y18.(8分)按要求完成下列视图问题(1)如图(一),它是由6个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?(2)如图(二),请你借助虚线网格画出该几何体的俯视图.(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助虚线网格画出该几何体的主视图.(4)如图(四),它是由8个大小相同的正方体组成的几何体的主视图和俯视图,请你借助虚线网格画出该几何体的左视图.19.(8分)2013年4月23日是第18个世界读书日,《南山教育》记者就南山区中小学教师阅读状况进行了一次问卷调查,并根据调查结果绘制了教师每年阅读书籍数量的统计图(不完整).设x 表示阅读书籍的数量(x 为正整数,单位:本).其中A :31≤≤x ; B :64≤≤x ; C :97≤≤x ;D :10≥x .请你根据两幅图提供的信息解答下列问题:(1)本次共调查了多少名教师?(2)补全条形统计图;(3)计算扇形统计图中扇形D 的圆心角的度数.(4)若南山区中小学教师共有6000人,则一年读书不少于10本的教师约有多少人?20.(8分)计算与说理(1)如图线段AB ,C 是线段AB 的中点,点D 在CB 上,且cm AD 5.6=,(2)如图,O 为直线AB 上一点,50=∠AOC °,OD 平分AOC ∠,90=∠DOE °①求出BOD ∠的度数;②OE 是BOC ∠的平分线吗?为什么?21.(7分)小张自主创业开了一家服装店,因为进货时没有进行市场调查,在换季时积压了一类服装.为了缓解资金压力,小张决定将这类服装打折销售.若每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元. (1)请你算一算每件服装的标价和进价各是多少元?(2)该服装改款后,小张又以同样的进价进货500件,若标价不变,按标价销售了300件后,剩下的进行甩卖,为了尽快减少库存,又要保证盈利2万元,请你告诉小张最低能打几折?22.(6分)结合数轴与绝对值的知识回答下列问题: (1)探究:①数轴上表示5和2的两点之间的距离是 ; ②数轴上表示2-和6-的两点之间的距离是 ; ③数轴上表示4-和3的两点之间的距离是 ; (2)归纳:一般地,数轴上表示数m 和数n 的两点之间的距离等于n m -. (3)应用:①如果表示数a 和3的两点之间的距离是7,则可记为:37a -=,那么a = ; ②若数轴上表示数a 的点位于4-与3之间,求++4a 3-a 的值;③当a 取何值时,++4a +-1a 3-a 的值最小,最小值是多少?请说明理由.七年级数学试卷参考答案及评分标准(2014.1)三、解答题(本大题有7题,其中16题12分,17题6分,18题8分,19题8分,20题8分,21题7分,22题6分,共55分)16.(1)()()5312-+--1235=+- ………………………2分=10 ………………………3分(2)()()3116248⎛⎫÷---⨯- ⎪⎝⎭()11682=÷--………………………1分 122=-- ………………………2分52=- ………………………3分(3)解:22247583x x x x -++--22234578x x x x =--++- ………………………1分 21x x =-+- ………………………3分 (4)解:原式2112222a a a =-+--+……………………1分 2a =- ……………………2分 当12a =时,上式41--212==⎪⎭⎫ ⎝⎛ ……………………3分17.(1)x x -=-1)1(4解:441x x -=- ………………………1分414x x +=+55x =1x = ………………………3分(2)3122413--=+y y 解:()()33124421y y +=-- ………………………1分932484y y +=-+ 1725y = 2517x =………………………3分 18.(1)解:左视图………………………2分 (2)………………………4分(3)………………………6分(4)………………………8分19.解:(1)3819%200÷=人 ………………………2分(2)………………………4分(3)4036072200⨯=° ………………………6分 (4)4060001200200⨯= ………………………8分20.(1)2.5cm ………………2分(2)①∵50AOC ∠=°,且OD 平分∠AOC ∴∠1=115022AOC ∠=⨯°=25°……………………3分 ∴∠BOD=180°—25°=155°……………………5分②由①知∠2=∠1=25° ∵∠DOE=90°∴∠3=∠DOE-∠2=90°-25°=65°……………………6分∠4=180°-∠1-∠DOE =180°-25°-90°=65° ……………………7分∴∠3=∠4的平分线……………………8分∴OE是BOC21.解:(1)设标价是x元,由题意得,50%•x+20=80%•x-40,……………………2分解得:x=200,即每件服装的标价是200元;……………………3分进价为50%•x+20=50%•200+20=120元……………………4分(2)设小张最多能打x折,由题意得,300×(200-120)+(500-300)×(200×0.1x-120)=20000,……6分解得:x=5,即小张最多能打5折.……………………7分22. (1)探究① 3 ……………………1分② 4 ……………………2分③ 7 ……………………3分(3)应用①—4或10 ……………………4分②因为|a+4|+|a-3|表示数轴上数a和-4,3之间距离的和.又因为数a位于-4与3之间,所以|a+4|+|a-3|=7;……………………5分③根据|a+4|+|a-1|+|a-3|表示一点到-4,1,3三点的距离的和.所以当a=1时,式子的值最小,此时|a+4|+|a-1|+|a-3|的最小值是7.……………………6分。
【数学】广东省深圳市南山区2013-2014学年高一上学期期末考试.docx
高 一 期末 考 试数 学 2014-01-8本试卷分第Ⅰ卷 ( 选择题 ) 和第Ⅱ卷 ( 非选择题 ) 两部分,共 150 分,考试时间 120 分钟 .第Ⅰ卷 ( 选择题共 50 分 ) 一、选择题 :本大题共 10 小题,每小题 5 分,共 50 分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的编号用铅笔涂在答题卡上 ...................1、设集合 M={- 1,0, 1} , N={x|x 2=x} ,则 M ∩ N=A 、 { - 1, 0, 1}B 、 {0 ,1}C 、 {1}D 、 {0}2、下列函数中,与函数 y=x 相同的函数是A 、 y = x 2 B、 y = ( x) 2 C 、 y = 2log 2 x D 、y=lg10 xx3、已知 a , b 是异面直线,直线 c ∥ a ,那么直线 c 与 bA 、一定是相交直线B 、一定是异面直线C 、不可能是相交直线D 、不可能是平行直线 4、幂函数 y=f(x) 的图像经过点 (4 , 0.5) ,则 f(0.25) 的值为 A 、 1 B 、 2 C 、 3 D 、 45、已知 m , n 是两条不同的直线, α ,β 是两个不同的平面,则下列命题中正确的是 A 、若 α ∥β , m α , n β,则 m ∥n B、若 α ⊥ β, m α ,则 m ⊥ β C 、若 m ⊥n , m α ,则 n ⊥ αD、若 m ⊥ α ,m ∥ β ,则 α ⊥ β6、若 4a=25b=10,则 1 +1a bA 、 1B 、 2C、 3 D、 47、已知三棱锥的底面是边长为 3 的等边三角形, 侧棱长都为 2,则侧棱与底面所成角的大小为A 、 30o B、45oC、 60oD、 90o8、若当 x ∈ R 时,函数 f(x)=a |x|(a>0 且 a ≠1) 满足 f(x) ≤ 1,则函数 y=log a (x+1) 的图像大致为题yyyyO 1 2 x O 1 2x O 12 x O 1 2xABCD9、已知 f(x) 是 R 上的奇函数,对于 x ∈ R ,都有 f(x+4)=f(x)+f(2)成立,若 f(1)=2 ,则 f(2013)等于A 、 0B 、 2C 、 2014D 、- 2 10、对于不重合的两个平面 α 与 β ,给定下列条件:①存在平面 γ ,使得 α , β 都垂直于 γ ;②存在平面 γ ,使得 α, β 都平行于 γ ; ③α 内有不共线的三点到 β 的距离相等; ④存在异面直线 l ,m ,使得 l ∥ α , l ∥ β , m ∥α , m ∥ β 、其中,可以判定 α 与 β 平行的条件有A 、 1 个B、 2 个C、 3 个D 、 4 个第Ⅱ卷 ( 非选择题共 100 分 )二、填空题:本大题共4 小题,每小题5 分,共 20 分.把答案填在答题卡上 ..........( 一 ) 必做题 :(11 ~ 13 题 )11、若集合 A={x| -1≤x≤2} ,B={x|x ≤a} ,A∩B=A,则实数 a 的取值范围是 _______.1 12、如果一个几何体的三视图如右图所示( 单位长度: cm),则此几何体的表面积是_______.113、把函数 y=log a x(a>0 ,且 a≠1) 的图像上所有的点向左2平移 2 个单位长度,再向下平移 1 个单位长度后得到函数主视图y=f(x) 的图像,已知函数 y=f(x)的图像经过定点A(m, n).若方程 kx 2+mx+n=0有且仅有一个零点,则实数k 的值为 ________.2( 二 ) 必做题:(14 ~ 15 题只选做一题 )俯视图14、如果执行下图程序框图,那么输出的S=_____.开始i=1 , S=1i=i+1S=2(S+1)是输出 S结束i>5否15、已知两点A( - 3,- 4) ,B(6 , 3) 到直线l:ax+y+1=0 的距离相等,则实数______.三、解答题:本大题共6 小题,共80 分,解答应写出文字说明或演算步骤、16、 ( 本小题满分12 分 )已知集合U=R, A={x|0.5<2x<4},B={x|log3x≤2}.(1) 求 A∩B;(2)求?U(A∪ B).左视图a的值等于x2 + 2x ,(x0)17、 ( 本小题满分12 分 ) 已知函数f(x) =0,(x0).x 2+ 2x, (x0)(1)求证函数 y=f(x) 是奇函数; (2) 试作出函数 y=f(x) 是的图像;(3) 若函数 y=f(x)在区间[-1,a-2]上单调递增,求实数 a 的取值范围 .y321-3 -2 -1O 1 2 3x-1-2-318、 ( 本小题满分14 分 )如图,在三棱锥o oA-BOC中,∠ OAB=30,AO⊥平面BOC,AB=4,∠ BOC=90,BO=CO,D 是 AB的中点 .(1)求证: CO⊥平面 AOB; (2) 求异面直线 AO与 CD所成角的正切值 .ADOBC19、 ( 本小题满分14 分 )已知函数f(x)=log a(2x+2),g(x)=log a(2x-2)(a>0,且a≠1) .(1)求函数 h(x)=f(x) - g(x) 的定义域;(2)判断函数 h(x)=f(x) - g(x) 在 x∈ (1 , +∞ ) 内的单调性,并用定义给予证明;(3)当 a=2 时,若对 [3 , 5] 上的任意 x 都有 h(x)<2 x +m成立,求 m的取值范围 .20、 ( 本小题满分14 分 )如图,菱形ABCD的边长为 4,∠ BAD=60o, AC∩ BD=O,将菱形 ABCD沿对角线 AC折起,得到三棱锥 B-ACD,点 M是棱 BC的中点,且DM = 2 2 . (1)求证:OM//平面ABD;(2)求证:平面 DOM⊥平面 ABC; (3) 求点 B 到平面 DOM的距离 .BB MA O C AO CD D21、 ( 本小题满分14 分 )已知函数f(x)=ax2+bx+c满足:f(0)=0,对任意x∈R,都有f(x)≥ x且f(x)的对称轴为x=-0.5 ,令 g(x)=f(x)-|tx-1|(t>0).(1)求函数 f(x) 的表达式; (2) 当 t=1 时,求函数 g(x) 的最小值;(3)求函数 g(x) 的单调区间 .高一数学参考答案及评分标准2014.1.8一、:( 10×5'=50')号12345678910答案B D D B D B C C B B二、填空:(4 ×5′=20′)11、a≥2; 12、 (20 4 2) cm2;13、 0 或1; 14、 94 ;15 、7或1.493三、解答:(8 0′)16、 ( 本小分12 分 )解: (1)∵A={x|0.5<2x<4}={x|- 1<x<2} ,⋯⋯2分B={x|log x≤2}={x|0<x≤9} ,⋯⋯4 分3∴A∩B={x|0<x<2}.⋯⋯6分(2) A ∪B={x| -1<x≤9} ,⋯⋯9 分? (A∪B) ={x| x≤- 1 或 x> 9}.⋯⋯ 12 分U17、 ( 本小分12 分 )解: (1) ? x<0,- x>0,y所以 f(- x)= - ( - x) 2+2( - x)= -x2- 2x3=- f(x);⋯⋯2分2又? x>0,- x<0,1所以 f(- x)= - ( - x) 2+2( - x)= -x2- 2x-3 -2 -1 O 123x=- f(x);⋯⋯3分-1且 f(0)=0 ,所以 f( - x)= -f(x).⋯⋯4 分-2f(x) 奇函数 .⋯⋯5分-3(2) 像如右上 .⋯⋯9分(3) 要使 f(x)在 [ - 1, a- 2] 上增,合a21 f(x) 的象知,2,a1所以 1<x≤3,故数 a 的取范是(1 ,3].18、 ( 本小分 14 分 )解: (1)由意,∵ AO⊥平面 BOC,又 CO平面 COB,∴ CO⊥AO,⋯⋯ 3 分o⋯⋯ 4 分∴∠ BOC=90,∴CO⊥ BO,又∵ AO∩ B0=O,∴ CO⊥平面 AOB.⋯⋯ 6 分(2)作 DE⊥OB,垂足 E, CE(如 ) ,DE∥ AO,⋯⋯ 12 分ADOEB C∴∠ CDE是异面直AO与 CD所成的角 .⋯⋯8分在Rt △ COE中, CO=BO=2, OE=0.5BO=1,∴ CE = CO2 +OE 2 = 5 .⋯⋯ 10 分又 DE = 1AO = 3 . 2∴在 Rt △ CDE中,tan CDE =CE= 5 =15.⋯ 13 分DE3315∴异面直AO与 CD所成角的正切.⋯⋯14分319、 ( 本小分14 分 )解: (1)由意可知, h(x)=f(x) - g(x)= log (2x+2)- log(2x - 2) ,⋯⋯1 分a a由 2x + 2> 0解得 x>1,所以 h(x) 的定域 (1 ,+∞).⋯⋯2 分2x2> 0(2) h(x)=f(x)- g(x)= log a(2x+2) - log a(2x - 2)= log a2x+ 2= log a x +1 ,⋯⋯3分2x2x 1令k(x) = x +1,x1,x2∈(1,+∞),且x1<x2,x 1那么 k(x 1) k(x 2 ) = 1+ x11+ x2 =2(x 2 x 1),⋯⋯5分x1 1x 2 1(x1 1)(x 21)因 x1, x2∈ (1 ,+∞) ,且 x1<x2,所以 x1- x2<0,x1- 1>0, x2- 1>0,2(x2x1)> 0 ,所以 k(x 1) k(x 2 ) =(x1 1)(x 21)k(x) 在区 (1 ,+∞) 上减函数 .∴a>1 , y=h(x) 在区 (1 ,+∞) 上减函数 . 0<a<1 ,y=h(x) 在区 (1 ,+∞) 上增函数,(3)由意知, m>h(x) - 2x, ? x ∈ [3 ,5] 恒成立,∴m>[h(x) - 2x] max,⋯⋯11分又当 a=2 , h(x) 与 y=- 2x在 x∈ [3 , 5] 都是减函数,∴m>[h(x) - 2x] max=- 7,∴ m∈ ( - 7,+∞).20、 ( 本小分 14 分 )解: (1)) 因 O AC的中点, M BC的中点,所以 OM∥ AB.⋯⋯2分因 OM ?平面 ABD,AB平面 ABD,A所以 OM∥平面 ABD.⋯⋯4 分(2)因在菱形 ABCD中, OD⊥AC,⋯⋯7 分⋯⋯9分⋯⋯12 分⋯⋯14 分BMOC所以在三棱B-ACD中, OD⊥AC.o D在菱形 ABCD中, AB=AD=4,∠ BAD=60,所以 BD=4.因 O BD的中点,所以 OD=0.5BD=2.因 O AC的中点, M BC的中点,所以 OM=0.5AB=2.⋯⋯6分222o因 OD+OM=8=DM,所以∠ DOM=90,即 OD⊥ OM.因 AC平面 ABC, OM 平面 ABC,AC∩OM=O,所以 OD⊥平面 ABC.因 OD平面 DOM,所以平面 DOM 平面 ABC.⋯⋯9分(3) 由 (2)得, OD⊥平面 BOM,所以 OD是三棱 D-BOM的高 .ABMOCD点 B 到面 DOM 距离 h ,因 OD=2,SSBOMDOM= 1 OB BM sin600= 12 233 ,22 2= 1OD OM = 2 ,⋯⋯ 11分2因 V B-DOM =V D-BOM ,所以1S DOM h = 1 S BOM OD ,解得 h = 3 .⋯⋯ 14 分3 321、 ( 本小 分 14 分 )解: (1) 由 f(0)=0,得 c=0,且 任意 x ∈ R ,都有 f(x)≥x 恒成立,即 ax 2+(b - 1)x ≥ 0 恒成立, ⋯⋯ 2 分可得 b=1,又 f(x)的 称x=- 0.5 ,即所以 f(x)=x 2+x.b1 =,得 a=1,2a2⋯⋯ 4 分(2) g(x)= x2+x. - |x -1|=x 2,x 1 ⋯⋯5 分+1x 2+ 2x ,1 x < 1当 x ≥ 1 , g(x) 的最小 g(1)=2 ;当 x<1 , g(x) 的最小 g( - 1)= -2,所以 g(x) 的最小 - 2.⋯⋯8分x 2 , 1+ (1 t)x +1 xt ,(3) g(x)=f(x)- |tx - 1|=⋯⋯9分x 2,1 + (1+ t)x 1 x <t①当 x1, g(x)的 称xt 1 t 11 t2 ,2,即 0<t ≤2 ,tg(x) 在 [1,) 上 增,t1 1 ,即 t>2 ,g(x) 在 ( t1, ) 上 增,在 (1,t 1)t2 t2t 2 上 减 .⋯⋯ 11 分②当 x1 , g(x)的 称 xt 1 ,因 t>0 ,t 1< 1 ,t22 t所以 g(x) 在 (t 1,1) 上 增,在( ,t1) 上 减 .2t2⋯⋯ 13 分上所述: 0<t ≤2 , g(x) 在 (t 1) 增,在(t 1 ,,) 减; t>2 ,22g(x) 在 (t1,1) , (t1, ) 增,在 (,t21) , (1,t1)2t2t2减. ⋯⋯ 14 分。
广东省深圳南山区高三上期末考试数学文试题
高 三 教 学 质 量 监 测数 学(文科)注意:本试卷分选择题和非选择题两部分,共150分,考试时间120分钟. 1.答卷前,考生填、涂好学校、班级、姓名及座位号。
2.选择题用2B 铅笔作答;非选择题必须用黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,并将答题卡交回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的编号用铅笔涂在答题卡上..................。
1.已知集合A ={|x y =,集合{}2≥=x x B ,A B =A. ]3,0[ B .]3,2[C .),2[+∞D .),3[+∞2.若复数z 满足,i z i 43)34(-=+,则z 的虚部为 A. 53-B .45- C .i 53- D .i 54- 3.椭圆125922=+y x 上一点P 到椭圆一个焦点的距离为2,则P 到另一焦点的距离为 A. 3B .5C .7D .84.已知数列}{n a 为等差数列,若21062π=++a a a ,则)tan(93a a +的值为A. 0 B .33C .1D .35.设a ,b 是非零向量,“a b a b ⋅=”是“//a b ”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件6.已知()f x 是定义在R 上的奇函数,当0x ≥时,2()2f x x x =-,则函数()()1g x f x =+的零点的个数是A. 1B. 2C. 3D. 4 7.已知正三棱柱111ABC A B C -的底面边长为cm 2,高为cm 4,则一质点自点A 出发,沿着三棱柱的侧面,绕行两周到达点1A 的最短路线的长为 A. cm 104 B. cm 312 C. cm 132D. cm 138. 已知ABC ∆中,a ,b ,c 分别为内角C B A ,,所对的边长,且2,1==b a ,1tan =C ,则ABC ∆外接圆面积为 A.π21 B. π31C . π D.π39.一个几何体的三视图如图所示,则这个几何体外接球的表面积为 A. 8π B. 16π C. 32π D. 64π10.如图所示,输出的n 为A. 10B. 11C. 12D. 1311.椭圆)0(1:2222>>=+b a by a x C 的左焦点为F ,若F 关于直线03=+y x 的对称点A 是椭圆C 上的点,则椭圆C 的离心率为A.1-2 B. 13-C.25- D. 2-612.已知函数⎩⎨⎧>+≤+-=0,20),1ln()(2x x x x x x f ,若0)1()(≥+-x m x f ,则实数m 的取值范围是A. ]0-,(∞B. ]1,1[-C. ]2,0[D. ),2[+∞二、填空题:本大题共4小题,每小题5分,共20分,把答案填在答题卷上.........。
华附、省实、广雅、深中四校2014届高三上学期期末联考数学文
俯视图正视图侧视图211 1S=S -T结束输出S T=T+S开始T ≥0是否T=0,S =1l 3l 2l 1y xOA (m ,n )5π12-π32Oy x2014届高三上学期期末华附、省实、广雅、深中四校联考文科数学命题学校:深圳中学本试卷分选择题和非选择题两部分,共4页,满分150分,考试用时120分钟.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项符合要求.1.已知i 是虚数单位,11iz =+,则z =A . 0B . 1C . 2D . 22.若向量(1,2),(4,5)BA CA ==,则BC =A . (5,7)B . (3,3)--C . ()3,3D . ()5,7--3.若集合{}21,A m=,{}2,4B =,则“2m =”是“{}4A B = ”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.执行如图所示的程序框图,输出的S 值为A .1B . 1-C . 2-D . 05.已知12log 1a >,112b⎛⎫> ⎪⎝⎭,23c=,则A . a b c >>B . c a b >>C . a c b >>D . c b a >>6.函数()2sin()(,0,||f x x x ωϕωϕ=+∈><R π)2的部分图象如图所示,则,ωϕ的值分别是A .π2,3-B . π2,6-C . π4,6-D . π4,37.下列函数在定义域内为奇函数,且有最小值的是 A . 1y x x =+B . sin y x x =C . (1)y x x =-D . πcos()2y x =- 8.某几何体的三视图如图所示,其中正(主)视图与侧(左)图的边界均为直角三角形,俯视图的边界为直角梯形,则该几何体的体积是A .13 B . 12C . 1D . 3 9.已知约束条件对应的平面区域D 如图所示,其中123,,l l l 对应的直线方程分别为:112233,,y k x b y k x b y k x b =+=+=+,若目标函数z kx y =-+ 仅.在点(,)A m n 处取到最大值,则有 A .12k k k << B . 13k k k << C . 13k k k ≤≤ D . 1k k <或3k k > 10.已知圆C :2221()()64x a y a -+-=(a ∈R),则下列命题:①圆C 上的点到()1,0的最短距离的最小值为78;②圆C 上有且只有一点P 到点1,08⎛⎫ ⎪⎝⎭的距离与到直线38x =-的距离相等;③已知3,08A ⎛⎫ ⎪⎝⎭,在圆C 上有且只有一点P ,使得以AP 为直径的圆与直线18x =相切.真命题的个数为A .0B . 1C . 2D . 3DBCOA频率/组距寿命(h)0.0020.004O1002003004005006000.001y 0二、填空题:本大题共4小题,每小题5分,共20分.11. 不等式111x >-的解集为 . 12. 与双曲线221x y -=过一、三象限的渐近线平行且距离为2的直线方程为 .13. 已知数列{}n a 中,121,2a a ==,且*21()N n n n a a a n ++⋅=∈,则2014a 的值为 . 选做题(请考生在以下两小题中任选一题做答,若两小题都做,则按第14题记分) 14.(几何证明选讲选做题)如图,过点C 作ABC ∆的外接圆O 的 切线交BA 的延长线于点D .若3CD =,2AB AC ==, 则BC = .15.(坐标系与参数方程选做题)在极坐标系(0,02π)O ρθρθ≥≤< 中,点(2,)2A π关于直线:cos 1l ρθ=的对称点的极坐标为 .三、解答题:本大题6小题,共80分,解答应写出必要的文字说明、证明过程或演算步骤. 16. (本小题满分12分)在ABC ∆中,角,,A B C 所对的边为,,a b c ,角A 为锐角,若6(sin,)23=A m ,3(cos ,)23=-A n 且⊥m n .(1)求cos A 的大小;(2)若1,2a b c =+=,求ABC ∆的面积S .17. (本小题满分12分)对某电子元件进行寿命追踪调查,所得情况如右 频率分布直方图.(1)图中纵坐标0y 处刻度不清,根据图表所提供的数据还原0y ;(2)根据图表的数据按分层抽样,抽取20个元件,寿命为100~300之间的应抽取几个;(3)从(2)中抽出的寿命落在100~300之间的元 件中任取2个元件,求事件“恰好有一个寿命为 100~200,一个寿命为200~300”的概率.O 1DCBC 1A 1D 1B 1A18. (本小题满分14分) 已知长方体1111ABCD A BC D -,点1O 为11B D 的中点. (1)求证:1//AB 面11AO D ; (2)若123AB AA =,试问在线段1BB 上是否存在点E 使得1AC ⊥AE ,若存在求出1BEBB ,若不存在,说明理由.19. (本小题满分14分)数列{}n a ,{}n b 满足12212nn a a na b n++⋅⋅⋅+=++⋅⋅⋅+()N n *∈.(1)若{}n b 是等差数列,求证:{}n a 为等差数列;(2)若2n n a =,求数列(1)21nnb n ⎧⎫⎨⎬-⋅+⎩⎭的前n 项和n S .20. (本小题满分14分)已知椭圆1C :22221x y a b +=的离心率为32e =且与双曲线2C :22221+1x y b b -=有共同焦点.(1)求椭圆1C 的方程;(2)在椭圆1C 落在第一象限的图像上任取一点作1C 的切线l ,求l 与坐标轴围成的三角形的面积的最小值;(3)设椭圆1C 的左、右顶点分别为,A B ,过椭圆1C 上的一点D 作x 轴的垂线交x 轴于点E ,若C 点满足AB BC ⊥ ,//AD OC,连结AC 交DE 于点P ,求证:PD PE =.21. (本小题满分14分)已知函数2()(266)e x f x x x a =-++⋅(e 为自然对数的底数). (1)求函数()f x 在(0,)+∞上的单调区间;(2)设函数()()(24)e x g x f x x a =+--⋅,是否存在区间[](),1,m n ⊆+∞,使得当[],x m n ∈时函数()g x 的值域为[]2,2m n ,若存在求出,m n ,若不存在说明理由.2014届高三上学期期末华附、省实、广雅、深中四校联考参考答案与评分标准文科数学 2014-01-16说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分数.一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项符合要求.题号1 2 3 4 5 6 7 8 9 10 答案C B AD B A D C B D 1.【解析】1i 2z z =-⇒=2.【解析】()3,3BC BA AC =+=--3.【解析】{}244 2.A B m m =⇔=⇔=± 4.【解析】0,11,01,1T S T S T S ==⇒==⇒==- 0,11,0.T S T S ⇒==-⇒=-=5.【解析】121log 102a a >⇒<<, 1102bb ⎛⎫>⇒< ⎪⎝⎭,12123222cc =>=⇒>c a b ∴>>6.【解析】由图知()f x 在5π12x =时取到最大值2,且最小正周期T 满足 35ππ+.4123T =故2,A =32π3π,2,4ωω⨯==5π2sin(2)212θ⨯+=,5πsin()1,6θ+= 5πππ2π,2π,623k k k θθ+=+=-∈Z .所以π2sin ()(2).3x f x -= 或由5(π)212f =逐个检验知π2sin ()(2).3x f x -=7.【解析】πcos()sin 2y x y x =-⇒=,()sin sin x x -=-且[]sin 1,1x ∈-8.【解析】由三视图可知该几何体是一个四棱锥,根据“正侧等高,正俯等长,侧俯等宽”的规则,其体积为11(12)21 1.32V =⨯+⨯⨯=9.【解析】A 是1l 与3l 的交点,目标函数z kx y =-+仅.在点A 处取到最大值,所以直线 y kx z =+的倾斜角比1l 的要大,比3l 的要小,即有13k k k <<10.【解析】已知动圆C 的圆心的轨迹方程为:2y x =,所以动圆C 构成的轨迹为夹在抛物线218y x =-和BA (2,π2)O抛物线218y x =+之间的部分(包括边界),所以①②③都满足题意 二、填空题:本大题共4小题,每小题5分,共20分. 11. {}|12x x <<; 12. 20x y -±=; 13. 1; 14. 23; 15. (22,)4π11.【解析】1210(1)(2)01211x x x x x x ->⇒>⇒--<⇒<<-- 12.【解析】双曲线221x y -=过一、三象限的渐近线方程为:0x y -=设直线方程为:0x y b -+=所以22b=,解得2b =±13.【解析】*21()N n n n a a a n ++⋅=∈ 由121,2a a ==,得32a =,由232,2a a ==得41a =,由342,1a a ==得512a =,由4511,2a a ==得612a =,由5611,22a a ==得71a =,671,12a a ==得82a =由此推理可得{}n a 是一个周期为6的数列,所以201441a a ==14. 【解析】由2()CD DA DB DA DA AB =⨯=⨯+知 2230DA DA +-=,解得1, 3.DA DB == 由DAC DCB 得AC CD BC BD =,即2 3.AC BDBC CD⨯== 15. 【解析】如图,在极坐标系(0,02π)O ρθρθ≥≤<中,设(2,)2A π关于 直线:cos 1l ρθ=的对称点为(,),B ρθ则2OA AB ==,且.OA AB ⊥从而π22,,4OB AOB =∠=即πππ22,.244ρθ==-= 三、解答题:本大题共6小题,共80分,解答应写出必要的文字说明、证明过程或演算步骤. 16. 解:(1)由⊥m n 可得0⋅=m n 即2sincos 223A A ⋅=…………………………………………1分 22sin 3A ∴=…………………………………3分 22sin cos 1A A += 21cos 9A ∴=………………………………5分π0,2A ⎛⎫∈ ⎪⎝⎭1cos 3A ∴=………………………………6分(2)222cos 2b c a A bc+-= 由(1)知1cos 3A =,()22232bc b c a ∴=+-………………………………8分()()223988bc b c a ∴=+-=………………………………10分G O 1DCBC 1A1D 1B 1AMEO 1DCBC 1A1D 1B 1A132sin 28S bc A ∴==………………………………12分 17. 解(1)根据题意:00.00110021000.0021000.0041001y ⨯+⨯+⨯+⨯=解得00.0015y =………………………………3分(2)设在寿命为100~300之间的应抽取x 个,根据分层抽样有:()0.0010.001510020x=+⨯………………………5分 解得:5x =所以应在寿命为100~300之间的应抽取5个………………………………7分 (3)记“恰好有一个寿命为100~200,一个寿命为200~300”为事件A ,由(2)知寿命落在100~200之间的元件有2个分别记12,a a ,落在200~300之间的元件有3个分别记为:123,,b b b ,从中任取2个球,有如下基本事件:()()()()12111213,,,,,,,a a a b a b a b()()()212223,,,,,a b a b a b ,()()()121323,,,,,b b b b b b ,共有10个基本事件………9分事件A “恰好有一个寿命为100~200,一个寿命为200~300”有:()()()111213,,,,,a b a b a b ,()()()212223,,,,,a b a b a b 共有6个基本事件………10分63()105P A ∴==……………………………11分 答:事件“恰好有一个寿命为100~200,另一个寿命为200~300”的概率为35.12分 18. (1)证明:连结1AD 交1A D 于点G ,所以G 为1AD 的中点,连结1O G在11AB D ∆中,1O 为11B D 的中点11//O G AB ∴……………………………4分 1O G ⊂面11AO D 且1AB ⊄面11AO D ∴1//AB 面11AO D ……………………………7分 (2)若在线段1BB 上存在点E 得1AC ⊥AE ,连结1A B 交AE 于点M BC ⊥ 面11ABB A 且AE ⊂面11ABB ABC AE ∴⊥ 又1AC BC C = 且1,AC BC ⊂面1A BC AE ∴⊥面1A BC 1A B ⊂ 面1A BC1AE A B ∴⊥……………………………10分在AMB ∆和ABE ∆中有:90,90BAM ABM BAM BEA ∠+∠=︒∠+∠=︒ ABM BEA ∴∠=∠同理:1BAE AA B ∠=∠1Rt Rt ABE A AB ∴∆∆ ……………………………12分 1BE ABAB AA ∴=123AB AA =12439BE AB BB ∴==即在线段1BB 上存在点E 有149BE BB =…………14分19. (1)证明:由题{}n b 是等差数列,设{}n b 的公差为d12212nn a a na b n++⋅⋅⋅+=++⋅⋅⋅+()12122n n n b a a na ∴++⋅⋅⋅+=++⋅⋅⋅+①;∴有()()()112112121n n n n b a a na n a ++++⋅⋅⋅++=++⋅⋅⋅+++②…………3分∴②-①可得:()()()()11121122n n n n n n n bb n a +++++-=+即()1122n n n n b nb a +++-=()()1112n n n n b n b a -+--∴=…………5分()()()()11111321222n n n n n n a a n b b n b b d ++-∴-=+----={}n a ∴是公差为32d 的等差数列…………7分(2)记122n n T a a na =++⋅⋅⋅+,2n n a =22222n n T n ∴=+⋅+⋅⋅⋅+⋅① 23122222n n T n +∴=+⋅+⋅⋅⋅+⋅②①-②得:2112(12)2222212n nn n n T n n ++--=++⋅⋅⋅+-⋅=-⋅-()1122n n T n +∴=-⋅+,12224((1)21)12(1)(1)n n n n a a na T n b n n n n n ++⋅⋅⋅+-+∴===++⋅⋅⋅+++…………11分 4114()(1)21(1)1n n b n n n n n ∴==--⋅+++…………13分 11111144()4122311n S n n n ∴=-+-+⋅⋅⋅+-=-++…………14分20. 解:(1)由32e =可得:32c a =即2234c a =22234a b a -∴=224a b ∴=①………………………2分 又2221c b =+ 即22221a b b -=+ ②联立①②解得:224,1a b ==∴椭圆1C 的方程为:2214x y +=……………………3分(2) l 与椭圆1C 相切于第一象限内的一点,∴直线l 的斜率必存在且为负 设直线l 的方程为:y kx m =+(0)k <联立2214y kx m x y =+⎧⎪⎨+=⎪⎩消去y 整理可得: 22212104k x kmx m ⎛⎫+++-= ⎪⎝⎭③,………………4分根据题意可得方程③只有一实根,()222124()(1)04km k m ∆∴=-+-=整理可得:2241m k =+④………………6分直线l 与两坐标轴的交点分别为(),0,0,m m k ⎛⎫- ⎪⎝⎭且0k <………………7分∴l 与坐标轴围成的三角形的面积212m S k =⋅-⑤,………………8分 ④代入⑤可得:()1222S k k =-+≥-(当且仅当12k =-时取等号)…………9分 (3)由(1)得(2,0),(2,0)A B -,设000(,)(,0)D x y E x ∴, AB BC ⊥ ,∴可设1(2,)C y ,∴001(2,),(2,)AD x y OC y =+=由//AD OC 可得:010(2)2x y y +=即01022y y x =+…………11分∴直线AC 的方程为:002242y x y x +=+整理得:()0022(2)y y x x =++ 点P 在DE 上,令0x x =代入直线AC 的方程可得:02yy =,…………13分即点P 的坐标为00,2y x ⎛⎫ ⎪⎝⎭∴P 为DE 的中点∴PD PE =…………14分21. 解:(1)2211()(22)e 2()e 22xx f x x x a x a ⎡⎤'=-+⋅=-+-⋅⎢⎥⎣⎦…………1分①当12a ≥时,由()0f x '≥恒成立,()f x ∴在),0(+∞上单调递增…………2分②当12a <时,()0f x '>解得11222b x -<-或11222bx ->+(ⅰ)若0a ≤,则1120(0,)22b --≤∉+∞,1121(0,)22b-+≥∈+∞,()f x ∴在112(0,)22b-+上单调递减,在112,22b ⎡⎫-++∞⎪⎢⎪⎣⎭上单调递增…………4分 (ⅱ)若102a <<,则11211202222b b--+>-> ()f x ∴在1120,22b ⎛⎤-- ⎥ ⎝⎦和112,22b⎡⎫-++∞⎪⎢⎪⎣⎭上单调递增,在112112,2222b b ⎛⎫---+ ⎪ ⎪⎝⎭上单调递减…………6分 综上所述:当0a ≤时,()f x 的单调递减区间为:112(0,)22b-+, 单调递增区间为:112,22b ⎡⎫-++∞⎪⎢⎪⎣⎭; 当102a <<时,()f x 的单调递减区间为:112112,2222b b ⎛⎫---+ ⎪ ⎪⎝⎭单调递增区间为:1120,22b ⎛⎤-- ⎥ ⎝⎦和112,22b⎡⎫-++∞⎪⎢⎪⎣⎭; 当12a ≥时,单调递增区间为:),0(+∞.…………7分(2)由题意2()(242)e x g x x x =-+⋅,2()2(1)e x g x x '∴=-⋅…………8分假设存在区间[](),1,m n ⊆+∞,使得当[],x m n ∈时函数()g x 的值域为[]2,2m n ,即1n m >>,当[],x m n ∈时2()2(1)e 0x g x x '=-⋅>,()g x 在区间[],m n 单调递增………9分()2()2g m mg n n=⎧∴⎨=⎩,即方程()2g x x =有两个大于1的相异实根…………10分 设2()()2(242)e 2x h x g x x x x x =-=-+⋅-(1)x >, 2()(22)e 2x h x x '∴=-⋅-…………11分设2()()(22)e 2x x h x x ϕ'==-⋅-2()(242)e x x x x ϕ'∴=+-⋅1x > ,()0x ϕ'∴>,()x ϕ∴在(1,)+∞上单调增,又2(1)20,(2)6e 20ϕϕ=-<=->,即存在唯一的012x <<使()00x ϕ=.………12分当()01,x x ∈时,()00x ϕ<,()h x 为减函数;当()0,x x ∈+∞时,()00x ϕ>,()h x 为增函数;()h x ∴在0x 处取到极小值.又2(1)20,(2)2e 40h h =-<=-> ………13分()h x ∴在()1,+∞只存在一个零点,与方程()2g x x =有两个大于1的相异实根相矛盾,所以假设不成立,所以不存在,m n 符合题意. …………………………14分。
广东省华附、省实、广雅、深中四校2014届高三数学上学期期末联考试题 文(含解析)新人教A版
广东省华附、省实、广雅、深中四校2014届高三上学期期末联考数学文第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 是虚数单位,11iz =+,则z =A. 0B. 1C. 2D. 22.若向量(1,2),(4,5)BA CA ==,则BC =A. (5,7)B. (3,3)--C. ()3,3D. ()5,7--【结束】 3.若集合{}21,A m =,{}2,4B =,则“2m =”是“{}4A B =”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 【答案】A【解析】 试题分析:{}244 2.AB m m =⇔=⇔=±考点:集合的运算、充分条件、必要条件. 【结束】4.执行如图所示的程序框图,输出的S 值为 A .1 B. 1- C. 2- D. 0【结束】5.已知12log 1a >,112b⎛⎫> ⎪⎝⎭,23c=A. a b c >>B. c a b >>C. a c b >>D. c b a >> 【答案】B 【解析】试题分析:121log 102a a >⇒<<, 1102bb ⎛⎫>⇒< ⎪⎝⎭,12123222cc =>=⇒>c a b ∴>>考点:指数函数和对数函数的性质. 【结束】6.函数()2sin()(,0,||f x x x ωϕωϕ=+∈><R π)2的部分图象如图所示,则,ωϕ的值分别是 A .π2,3- B. π2,6- C. π4,6- D. π4,3【答案】A【结束】7.下列函数在定义域内为奇函数,且有最小值的是 A. 1y x x =+ B. sin y x x = C. (1)y x x =- D. πcos()2y x =- 【答案】D【解析】试题分析:πcos()sin 2y x y x =-⇒=,()sin sin x x -=-且[]sin 1,1x ∈-考点:函数的奇偶性和值域. 【结束】8.某几何体的三视图如图所示,其中正(主)视图与侧(左) 视图的边界均为直角三角形,俯视图的边界为直角梯形, 则该几何体的体积是 A.13 B. 12C. 1D. 3【结束】9.已知约束条件对应的平面区域D 如图所示,其中123,,l l l 对应的 直线方程分别为:112233,,y k x b y k x b y k x b =+=+=+,若目 标函数z kx y =-+仅.在点(,)A m n 处取到最大值,则有 A .12k k k << B. 13k k k << C. 13k k k ≤≤ D. 1k k <或3k k >【答案】B 【解析】试题分析: A 是1l 与3l 的交点,目标函数z kx y =-+仅.在点A 处取到最大值,所以直线 y kx z =+的倾斜角比1l 的要大,比3l 的要小,即有13k k k <<考点:线性规划和最优解 【结束】10.已知圆C :2221()()64x a y a -+-=(a ∈R),则下列命题:①圆C 上的点到()1,0的最短距离的最小值为78;②圆C 上有且只有一点P 到点1,08⎛⎫⎪⎝⎭的距离与到直线38x =-的距离相等;③已知3,08A ⎛⎫ ⎪⎝⎭,在圆C 上有且只有一点P ,使得以AP 为直径的圆与直线18x =相切.真命题的个数为 A .0 B. 1 C. 2 D. 3第Ⅱ卷(共90分)二、填空题(每题4分,满分16分,将答案填在答题纸上) 11. 不等式111x >-的解集为 .【答案】{}|12x x <<; 【解析】 试题分析:1210(1)(2)01211x x x x x x ->⇒>⇒--<⇒<<-- 考点:分式不等式的解法. 【结束】12. 与双曲线221x y -=过一、三象限的渐近线平行且距离为2的直线方程为 . 【答案】20x y -±=; 【解析】试题分析:双曲线221x y -=过一、三象限的渐近线方程为:0x y -= 设直线方程为:0x y b -+=所以22b =,解得2b =±考点:双曲线的性质、直线方程和两平行直线减的距离. 【结束】13. 已知数列{}n a 中,121,2a a ==,且*21()N n n n a a a n ++⋅=∈,则2014a 的值为 .【结束】14.(几何证明选讲选做题)如图,过点C 作ABC ∆的外接圆O 的 切线交BA 的延长线于点D .若3CD =2AB AC ==, 则BC = .【答案】23; 【解析】试题分析:由2()CD DA DB DA DA AB =⨯=⨯+知 2230DA DA +-=,解得1, 3.DA DB == 由DACDCB 得AC CD BC BD =,即2 3.AC BDBC CD⨯== 考点:圆的切线长定理、弦切角定理、相似三角形的判断和性质. 【结束】【结束】【结束】三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.) 16.(本小题满分12分)在ABC ∆中,角,,A B C 所对的边为,,a b c ,角A 为锐角,若(sin2=A m ,(cos,)23=-A n 且⊥m n . (1)求cos A 的大小;(2)若1,2a b c =+=,求ABC ∆的面积S .【答案】(1)13 (2) 8【解析】17.(本小题满分12分)对某电子元件进行寿命追踪调查,所得情况如下频率分布直方图. (1)图中纵坐标0y 处刻度不清,根据图表所提供的数据还原0y ;(2)根据图表的数据按分层抽样,抽取20个元件,寿命为100~300之间的应抽取几个; (3)从(2)中抽出的寿命落在100~300之间的元件中任取2个元件,求事件“恰好有一个寿命为100~200,一个寿命为200~300”的概率.【答案】(1)0.0015 (2)5 (3)35解得00.0015y =………………………………3分(2)设在寿命为100~300之间的应抽取x 个,根据分层抽样有:()0.0010.001510020x=+⨯………………………5分 解得:5x =所以应在寿命为100~300之间的应抽取5个………………………………7分(3)记“恰好有一个寿命为100~200,一个寿命为200~300”为事件A ,由(2)知寿命落在100~200之间的元件有2个分别记12,a a ,落在200~300之间的元件有3个分别记为:123,,b b b ,从中任取2个球,有如下基本事件:()()()()12111213,,,,,,,a a a b a b a b()()()212223,,,,,a b a b a b ,()()()121323,,,,,b b b b b b ,共有10个基本事件………9分事件A “恰好有一个寿命为100~200,一个寿命为200~300”有:()()()111213,,,,,a b a b a b ,()()()212223,,,,,a b a b a b 共有6个基本事件………10分63()105P A ∴==……………………………11分 答:事件“恰好有一个寿命为100~200,另一个寿命为200~300”的概率为35 (12)分考点:1.数据频率分布直方图;2.随机事件的概率.【结束】18.(本小题满分14分)已知长方体1111ABCD A BC D -,点1O 为11B D 的中点.(1)求证:1//AB 面11AO D ;(2)若123AB AA =,试问在线段1BB 上是否存在点E 使得1AC ⊥AE ,若存在求出1BE BB ,若不存在,说明理由.(2)若在线段1BB 上存在点E 得1AC ⊥AE ,连结1A B 交AE 于点M BC ⊥面11ABB A 且AE ⊂面11ABB A BC AE ∴⊥又1AC BC C =且1,AC BC ⊂面1A BCAE ∴⊥面1A BC1A B ⊂面1A BC1AE A B ∴⊥……………………………10分在AMB ∆和ABE ∆中有:90,90BAM ABM BAM BEA ∠+∠=︒∠+∠=︒ABM BEA ∴∠=∠同理:1BAE AA B ∠=∠1Rt Rt ABEA AB ∴∆∆……………………………12分 1BE AB AB AA ∴= 123AB AA = 12439BE AB BB ∴==即在线段1BB 上存在点E 有149BE BB =…………14分考点:1. 直线与平面平行的判定定理;2. 直线与平面垂直的判定和性质定理;3.三角形相似和相似三角形的性质.【结束】19.(本小题满分14分)数列{}n a ,{}n b 满足12212n n a a na b n++⋅⋅⋅+=++⋅⋅⋅+()N n *∈. (1)若{}n b 是等差数列,求证:{}n a 为等差数列;(2)若2n n a =,求数列(1)21n n b n ⎧⎫⎨⎬-⋅+⎩⎭的前n 项和n S . 【答案】(1)证明详见解析.(2)441n -+. 【解析】试题分析:(1)由12212n n a a na b n ++⋅⋅⋅+=++⋅⋅⋅+得12(123...)2...n n n b a a na ++++=+++,1121(123...)[2...(1)]n n n n b a a na n b ++++++=+++++,相减得()()()()11121122n n n n n n n b b n a +++++-=+,再求出1,n n a a +,最后根据等差数列的定义求证即可. (2)记122n n T a a na =++⋅⋅⋅+,2n n a =22222n n T n ∴=+⋅+⋅⋅⋅+⋅① 23122222n n T n +∴=+⋅+⋅⋅⋅+⋅②①-②得:2112(12)2222212n n n n n T n n ++--=++⋅⋅⋅+-⋅=-⋅- ()1122n n T n +∴=-⋅+, 12224((1)21)12(1)(1)n n n n a a na T n b n n n n n ++⋅⋅⋅+-+∴===++⋅⋅⋅+++…………11分 4114()(1)21(1)1n n b n n n n n ∴==--⋅+++…………13分 11111144()4122311n S n n n ∴=-+-+⋅⋅⋅+-=-++…………14分考点:1.数列的递推公式和等差数列的判定;2.数列前n 项和的求法.【结束】20.(本小题满分14分)已知椭圆1C :22221x y a b +=的离心率为32e =且与双曲线2C :22221+1x y b b -=有共同焦点. (1)求椭圆1C 的方程;(2)在椭圆1C 落在第一象限的图像上任取一点作1C 的切线l ,求l 与坐标轴围成的三角形的面积的最小值;(3)设椭圆1C 的左、右顶点分别为,A B ,过椭圆1C 上的一点D 作x 轴的垂线交x 轴于点E ,若C 点满足AB BC ⊥,//AD OC ,连结AC 交DE 于点P ,求证:PD PE =.(3)(2,0),(2,0)A B -,设1(2,)C y ,000(,)(,0)D x y E x ∴,求出,AD OC 的坐标,由向量平行的充要条件可得01022y y x =+,在求出直线AC 的方程,整理得()0022(2)y y x x =++,然后求出P 点坐标即可. 试题解析:(1)由3e =3c a =即2234c a =22234a b a -∴=224a b ∴=①………………………2分 又2221c b =+即22221a b b -=+②联立①②解得:224,1a b ==∴椭圆1C 的方程为:2214x y +=……………………3分(3)由(1)得(2,0),(2,0)A B -,设000(,)(,0)D x y E x ∴,AB BC ⊥,∴可设1(2,)C y ,∴001(2,),(2,)AD x y OC y =+=由//AD OC 可得:010(2)2x y y +=即01022y y x =+…………11分【结束】21.(本小题满分14分)已知函数2()(266)e x f x x x a =-++⋅(e 为自然对数的底数).(1)求函数()f x 在(0,)+∞上的单调区间;(2)设函数()()(24)e xg x f x x a =+--⋅,是否存在区间[](),1,m n ⊆+∞,使得当[],x m n ∈时函数()g x 的值域为[]2,2m n ,若存在求出,m n ,若不存在说明理由.(ⅱ)若102a <<,则112112022b b --+>> ()f x ∴在1120,2b ⎛- ⎝⎦和1122b ⎡⎫-+∞⎪⎢⎪⎣⎭上单调递增, 在11211222b b ⎛---+ ⎝⎭上单调递减…………6分 综上所述:当0a ≤时,()f x 的单调递减区间为:112(0,22b -+, 单调递增区间为:11222b ⎡⎫-++∞⎪⎢⎪⎣⎭; 当102a <<时,()f x 的单调递减区间为:1121122222b b ⎛---+ ⎝⎭单调递增区间为:1120,2b ⎛-- ⎝⎦和1122b ⎡⎫-++∞⎪⎢⎪⎣⎭;当12a≥时,单调递增区间为:),0(+∞.…………7分【结束】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南山区高 三 期 末 考 试文 科 数 学 2014.01.08本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟. 注意事项:1、答卷前,考生首先检查答题卡是否整洁无缺损.之后务必用黑色签字笔在答题卡指定位置填写自己的学校、班级、姓名及座位号,在右上角的信息栏填写自己的考号,并用2B 铅笔填涂相应的信息点.2、选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上.不按要求填涂的,答案无效.3、非选择题必须用黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上,请注意每题答题空间,预先合理安排、如需改动,先划掉原来的答案,然后再写上新的答案、不准使用铅笔和涂改液.不按以上要求作答的答案无效.4、考生必须保持答题卡的整洁,不折叠,不破损、考试结束后,将答题卡交回.5、考试不可以使用计算器.参考公式:独立性检验中的随机变量:22n(ad bc)K =(a +b)(c +d)(a +c)(b +d)-,其中n=a+b+c+d 为样本容量;参考数据:P(K ≥k 0) 0.10 0.05 0.025 0.010 k 0 2.706 3.841 5.024 6.635第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案的编号用铅笔涂在答题卡上................... 1、已知全集U=R ,集合P={x|x 2≤1},那么∁U P=A 、(-∞,-1)B 、(1,+∞)C 、(-1,1)D 、(-∞,-1)∪(1,+∞)2、计算:2(2i)(1i)12i+-=-A 、2B 、-2C 、2iD 、-2i 3、下列函数中是偶函数,且又在区间(-∞,0)上是增函数的是A 、y=x 2B 、y=x -2C 、|x|1y ()4-= D 、653y log x =4、下列命题中的假命题是A 、∃x ∈R ,x 3<0B 、“a>0”是“|a|>0”的充分不必要条件C 、∀x ∈R ,2x >0D 、“x<2”是“|x|<2”的充分不必要条件5、已知a (12)= ,,b (x 1)= ,,且(a 2b)//(2a b)+-,则x 的值为 A 、1 B 、2 C 、13 D 、126、已知a ,b ,c 分别是△ABC 中角A ,B ,C 的对边,且A=60o ,c=3b ,则ac的值为 A 、35BCD7、已知x ,y 满足x 32y x 3x 2y 63y x 9≤⎧⎪≥⎪⎨+≥⎪⎪≤+⎩,则z=2x -y 的最大值是A 、152B 、92C 、94D 、28、点P 是抛物线y 2=4x 上一动点,则点P 到点A(0,-1)的距离与到直线x=-1的距离和的最小值是ABC 、2 D9、若对任意a ,b ∈A ,均有a+b ∈A ,且a -b ∈A ,则称集合A 为闭集合,下面正确的是 A 、集合{-4,-2,0,2,4}为闭集合 B 、集合{n|n=3k ,k ∈Z}为闭集合C 、若集合A 1,A 2为闭集合,则A 1∪A 2为闭集合D 、闭集合A 至少有两个元素10、双曲线2222x y 1a b-=(a>0,b>0)的左、右焦点分别是F 1,F 2,以过F 1作倾斜角为30o 的直线交双曲线的右支与M 点,若MF 2垂直于x 轴,则双曲线的离心率为 ABC 、53D第Ⅱ卷(非选择题共100分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.......... (一)必做题:(11~13题):11、已知数列{a n }的前n 项和为S n =n 2+n ,(n ∈N*),则a n =______. 12、如果执行右图程序框图,那么输出的S=______.13、命题“若空间两条直线a ,b 分别垂直平面α,则a ∥b ”,学生小夏这样证明:设a ,b 与平面α相交于A ,B ,连结A 、B ,∵a ⊥α,b ⊥α,AB ⊂α,…… ① ∴a ⊥AB ,b ⊥AB , ……② ∴a ∥b. ……③这里的证明有两个推理,即①⇒②和②⇒③,老师评改认为小夏的证明推理不正确,这两个推理中不正确的是_________.(二)选做题:(14~15题,考生只能从中选做一题):14、(坐标系与参数方程选做题)在直角坐标系xOy 中,曲线C 的参数方程为x cos y 1sin =α⎧⎨=+α⎩(α为参数),以O 为极点,x 轴的正半轴为极轴建立极坐标系,则曲线C 的极坐标方程为________________.15、(几何证明选讲选做题)如图,在四边形ABCD 中,EF ∥BC ,FG ∥AD ,则EF FG BC AD+=__________. 三、解答题:本大题共6小题,共80分,解答应写出文字说明或演算步骤. 16、(本小题满分12分)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现在采用分层抽样方法(层内采用不放回的简单随机抽样)从甲、乙两组中共抽取3人进行考核. (1)求甲、乙两组各抽取的人数;(2)求从甲组抽取的工人中恰有又1名女工的概率;(3)令X 表示抽取的3名工人中男工人的人数,求X 的分布列及数学期望.A如图所示,设A 、B 是单位圆O 上的动点,且A 、B 分别在第一、第二象限. C 是圆O 与x 轴正半轴的交点,△ABC 为等边三角形.记以Ox 轴正半轴为始边,射线OA 为终边的角为θ.(1)若点A 的坐标为34()55,,求22sin sin 2cos cos 2θ+θθ+θ的值; (2)设2f ()|BC |θ= ,求函数f(θ)的解析式和值域.18、(本小题满分14分)如图所示,已知斜三棱柱(侧棱不垂直底面)A 1ACC与底面ABC 垂直, BC=2,AC =AB =11AA A C ==(1)求侧棱B 1B 在平面A 1ACC 1上的正投影的长度; (2)设AC 的中点为D ,证明:A 1D ⊥底面ABC ; (3)求侧面A 1ABB 1与底面ABC 所成二面角的余弦值.19、(本小题满分14分)已知椭圆C :2222x y 1a b+=(a>b>0)的离心率为2,其左焦点为F(0). (1)求椭圆C 的方程;(2)已知点D(1,0),直线l :y=kx+m(k≠0)与椭圆C 交于A ,B 两点,若 △DAB 是以AB 为底边的等腰三角形,试求k 的取值范围.A BCD A 1B 1C 1已知函数xf (x)1x=+(x>0),数列{a n }满足a 1=0.5,a n+1=f(a n )(n ∈N*). (1)求a 2,a 3的值; (2)证明数列n1{}a 是等差数列并求出数列{a n }的通项公式; (3)设n n n 1b 1(1)(2)a a 4=11--+(n ∈N*),求证:b 1+b 2+……+ b n <5.21、(本小题满分14分) 已知函数xf (x)k ln x=+(k 为常数,e=2.71828是自然对数的底数). (1)求函数f(x)的单调区间;(2)探究函数ln xg(x)f (x)x=-)在x ∈(1,+∞)上的零点个数(只要求写出结果); (3)若函数22kf (x)e h(x)f (x)+= (k>2,x>1),求函数h(x)的最小值.高三数学(文)参考答案及评分标准2014.1.8一、选择题:(8×5′=40′)题号1 2 3 4 5 6 7 8 答案D A B D B C A B 二、填空题:(6×5′=30′)9、2n ; 10、94; 11、②⇒③; 12、0.5 ;1314、ρ=2sin θ; 15、1. 三、解答题:(80′) 16、(本题满分12分) 解:(1)310=215⨯ ,3×5=115, 答:从甲组抽取2名,从乙组抽取1名. ……2分(2)从甲组抽取的工人中恰有1名女工的概率为11146521105C C C 8=C C 15. ……6分(3)X 可取值:0,1,2,3,214321105C C 2P(X =0)==C C 25, 111126432421105C C C +C C 28P(X =1)==C C 75, 211116326421105C C +C C C 31P(X =2)==C C 75,216221105C C 2P(X =3)==C C 15, X 的分布列为:X 0 12 3P 2252875 3175 215……10分2283128E(X)0123257575155=⨯+⨯+⨯+⨯=. ……12分17、(本题满分12分)解:(1)因为点A 的坐标为34()55,,故4sin 5θ=,3cos 5θ=,……3分所以22222sin θ+sin2θsin θ+2sin θcos θ==20cos θ+cos2θ2cos θsin θ-. ……6分 (2)因为以OA 为终边的角是θ,且△AOB 为等边三角形,所以以OB 为终边的角为πθ+3,所以点B 的坐标是ππ(cos(θ+)sin(θ+))33,.……8分而C(1,0).所以222ππf(θ)=|BC |=[cos(θ+)1]+sin (θ+)33-π=22cos(θ+)3-. ……10分因为点A 、B 分别在第一、二象限,所以ππθ(2k π+2k π+)62∈,,k ∈z ,所以ππ5π(θ+)(2k π+2k π+)326∈,,k ∈z . ……11分所以πcos(θ+)3的值域为(0),所以2|BC |(22+∈,. ……13分因此函数πf(θ)=22cos(θ+)3=-,f(θ)的值域是(22+,. ……14分18、(本题满分14分)解:(方法一)(1)∵ABC-A1B1C1是斜三棱柱,∴BB1∥平面A1ACC1,故侧棱B1B在平面A1ACC1上的正投影的长度等于侧棱B1B的长度. (2)分又11BB=AA=故侧棱B1B在平面A1ACC1. ……3分(2)证明:∵AC=11AA=A C=∴AC2= A1A2+ C1A2,∴三角形AA1C是等腰直角三角形,……5分又D是斜边AC的中点,∴A1D⊥AC,……6分∵平面A1ACC1⊥平面ABC,∴A1D⊥底面ABC,……7分(3)作DE⊥AB,垂足为E,连A1E,∵A1D⊥面ABC,得A1D⊥AB.∴AB⊥平面A1ED,……8分从而有A1E⊥AB,∴∠A1ED是面A ABB与面ABC所成二面角的平面角.……9分∵BC=2,AC=AB=AC2=BC2+AB2,∴三角形ABC是直角三角形,AB⊥BC,……10分∴ED∥BC ,又D是AC的中点,BC=2,AC=……11分∴DE=1,1A D=AD=,1A E==2,……12分∴11DE1cos A ED==A E2∠,……13分即侧面A1 ABB1与底面ABC所成二面角的余弦值为0.5. ……14分(方法二)(1)同方法一;(2)同方法一.(3)∵BC=2,AC=AB=AC2=BC2+AB2,∴三角形ABC是直角三角形,过B作AC的垂线BE,垂足为E,则AB BCBE===AC⋅EC===∴DE=CD EC==33-,……8分以D为原点,A1D所在的直线为z轴,DC所在的直线为y标系,如图所示,则A(00),,1A(00,0),1A A(0=,,1A B=,设平面A1ABB1的法向量为n=(x y z),,,则11n A A=0n A B=0⎧⋅⎪⎨⋅⎪⎩,ABCDEA1B1C1即=0x +y =033⎧⎪⎨⎪⎩,化简得z =y+y 3z =0-⎧⎪⎨-⎪⎩令x =y=-1,z=1,所以p =11)-,是平面A 1ABB 1的一个法向量. ……11分由(1)得A 1D ⊥面ABC ,所以设平面ABC 的一个法向量为q =(001),,, ……12分设向量p 和q 所成角为θ,则p q 1cos θ===p q2⋅, ……13分 即侧面A 1 ABB 1 与底面ABC 所成二面角的余弦值为0.5. ……14分 19、(本题满分14分)解:(1)由题意知,c =a 2,c =,∴a=2,b=1, ……1分 所以,椭圆C 的方程为22x +y =14. ……4分(2)设A(x 1,y 1),B(x 2,y 2),AB 的中点M(x 0,y 0),由22y =kx +m x +y =14⎧⎪⎨⎪⎩,得(4k 2+1)x 2+8kmx+4(m 2-1)=0, ……6分 据△>0,得4k 2+1>m 2 (※), ……7分有128km +x =2(4k +1)-228km x =2(4k +1)-1228kmx +x =4k +1-, ∴024km x =4k +1-,02my =4k +1, ……10分又由题意知,DM 垂直平分AB ,则DM 的方程为:x=-ky+1,……11分将点M 的坐标代入,得24k +1m =3k -, (☆) ……12分由(※),(☆)得,222(4k +1)4k +1>9k,解得k (U (+)55∈-∞-∞,所求. ……14分 20、(本题满分14分)解:(1)易求得21a =3,31a =4. ……2分 (2)∵xf(x)=(x 0)1+x>,则n n+1n n a a =f(a )=1+a , ……3分得n+1n 11=1a a +, ……5分 即n+1n11=1a a -, ……6分 ∴数列n1{}a 是首项为2,公差为1的等差数列, ……7分∴n 1=n +1a , 即n 1a =n +1. ……9分 (3)由(2)知,b 1=4, ……10分n 1111b ==1n(n 1)n 1nn(n 1)+4≤----(n≥2), ……12分则 123n 11111b +b +b ++b <4+(1)+()+...+()223n 1n---- (1)=5<5n-,故b 1+b 2+b 3+…+b n <5. ……14分 21、(本题满分14分)解:(1)已知f(x)的定义域为(0,1)∪(1,+∞),2lnx 1f(x) =(lnx)-. ……2分 令f ′ (x)>0,得x ∈(e ,+∞),f ′ (x)<0,得x ∈(0,1)、(1,e), ……3分 ∴f(x)的单调增区间为(e ,+∞);单调减区间为(0,1)、(1,e). ……5分 (2)①当1k >e e -时,g(x)没有零点;②当1k =e e-时,g(x)有一个零点; ③当1k <e e-时,g(x)有两个零点. ……8分 (3)设F(k)=e k -e -k(k ≥2),则F ′(k)=e k -1>0,∴F(k)在[2,+∞]上单调递增,∴当k>2时,F(k)= F(2)= e 2-e-2>0,即当k>2时,e k >e+k ,……10分由(1)知,当x>1时,f(x)≥f(e)=e+k , ……11分22k 2kk f (x)+e e h(x)==f(x)+=2e f(x)f(x)≥, ……13分当且仅当f(x)= e k 时取等号,∴h(x)最小值为2e k . 三、解答题:(80′)16、(本题满分12分) 解:(1)依题意得2π2π1==T 6π3ω=,∴x πf(x)=Asin(+)36, ……2分由f(2π)=2,得2ππAsin(+)=236,即5πAsin=26,∴A=4, ……4分 ∴x πf(x)=4sin(+)36. ……5分(2)由16f(3α+π)=5,得1π164sin[(3α+π)+)]=365,即π164sin(α+)=25,∴4cos 5α=, ……6分又∵πα[0]2∈,,∴3sin 5α=, ……7分由5π20f(3+)=213β-,得15ππ204sin[(3+)+)]=32613β-,即5sin(+π)=13β-,∴5sin β13=, ……9分又∵πβ[0]2∈,,∴12cos β13=, ……10分cos(α-β)= cosαcosβ+ sinαsinβ412356351351365=⨯+⨯=. ……12分 17、(本题满分12分) 解:(1)总计 甲班55乙班 20 30 50 合计 30 75 105……3分(2)根据列联表中的数据,得到2105(10302045)k = 6.109 3.84155503075⨯-⨯≈>⨯⨯⨯, ……5分因此有95%的把握认为“成绩与班级有关系”. ……6分(3)设“抽到6或10号”为事件A ,先后两次抛掷一枚均匀的骰子,出现的点数为(x ,y). 所有的基本事件有(1,1)、(1,2)、(1,3)、(1,4)、(1,5)、(1,6)、(2,1)、(2,2)、(2,3)、(2,4)、(2,5)、(2,6)、(3,1)、(3,2)、(3,3)、(3,4)、(3,5)、(3,6)、(4,1)、(4,2)、(4,3)、(4,4)、(4,5)、(4,6)、(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6)、(6,1)、(6,2)、(6,3)、(6,4)、(6,5)、(6,6),共36个. ……8分事件A 包含的基本事件有:(1,5)、(2,4)、(3,3)、(4,2)、(4,6)、 (5,1)、(5,5)、(6,4),共8个, ……10分 ∴82P(A)399==, ……11分 故抽到6或10号的概率是29. ……12分 18、(本题满分12分)解:(1)取线段A 1B 1中点M ,连结C 1M ,∵C 1A 1=C 1B 1,点M 为线段A 1B 1中点, ∴C 1M ⊥A 1B.又三棱柱ABC-A 1B 1C 1为直三棱柱, ∴A 1A ⊥平面C 1A 1B 1,∴A 1A ⊥C 1M ,∵A 1A ∩A 1B 1= A 1,∴C 1M ⊥平面ADB 1A 1,……2分 ∴1113C -ADB A 1(2a +a)2aV ==32⨯⨯. ……5分(2)连结BC 1,B 1C 交于点E , 则点E 是B 1C 的中点,连结DE ,因为D 点为AB 的中点,所以DE 是△ABC 1的中位线,所以AC 1∥DE , ……7分 因为DE ⊂平面CDB 1,AC 1 ⊄平面CDB 1, 所以AC 1∥平面CDB 1. ……9分 (3)因为AC 1∥DE , 所以∠EDB 1是异面直线AC 1与DB 1所成的角, ……10分 因为棱长为2a ,所以1DE =EB =,1DB =,取DB 1的中点F ,连接EF ,则EF ⊥DB 1,且DE =, ……12分 所以1DF cos EDB ==DE ∠, 即异面直线AC 1与DB 1 ……14分 19、(本题满分14分) 解:(1)由题意知,c =a c =,∴a=2,b=1, ……1分 1 C AB C D A 1 B 1C 1M所以,椭圆C 的方程为22x +y =14. ……4分(2)设A(x 1,y 1),B(x 2,y 2),AB 的中点M(x 0,y 0),由22y =kx +m x +y =14⎧⎪⎨⎪⎩,得(4k 2+1)x 2+8kmx+4(m 2-1)=0, ……6分 据△>0,得4k 2+1>m 2 (※), ……7分有1x =2x =1228kmx +x =4k +1-, ∴024km x =4k +1-,02my =4k +1, ……10分 又由题意知,DM 垂直平分AB ,则DM 的方程为:x=-ky+1,……11分将点M 的坐标代入,得24k +1m =3k -, (☆) ……12分由(※),(☆)得,222(4k +1)4k +1>9k,解得k (U +)∈-∞∞,所求. ……14分 20、(本题满分14分)解:(1)易求得21a =3,31a =4. ……2分 (2)∵xf(x)=(x 0)1+x>,则n n+1n n a a =f(a )=1+a , ……3分得n+1n 11=1a a +, ……5分 即n+1n11=1a a -, ……6分 ∴数列n1{}a 是首项为2,公差为1的等差数列, ……7分∴n 1=n +1a , 即n 1a =n +1. ……9分 (3) ∵21[f(x)]'=(1+x), ……10分 ∴函数f(x)在点(n ,f(n))(n ∈N*)处的切线方程为:2n 1y =(x n)1+n (1+x)--, ……11分 令x=0,得2n 22n n n b ==1+n (1+n)(1+n)-. ……12分 ∴222n 2n n b λλn +λ(n +1)=(n +)+λa a 24λ+=-, 仅当n=5时取得最小值,只需9λ11222<-<,解得-11<λ<-9,故λ的取值范围为(-11,-9). ……14分21、(本题满分12分) 解:(1)当1a =2时,f(x)的定义域为1()2,+∞, ……1分11又'12(x +)(x 1)12f (x)=2x =11x x 22----- ……2分 ∴1x (1)2,∈时,f ′(x)>0;x ∈(1,+∞)时,f ′(x)<0. ……3分 所以f(x)的递增区间为1(1)2,,递减区间为(1,+∞). ……4分 (2)当x ∈[1,2]时,x -a>0恒成立,即a<1; ……5分 当x ∈[1,2]时,'1f (x)=2x 0x a -≤-恒成立,即1a x 2x≤-恒成立, ……6分 又x ∈[1,2]时,min 110(x )2x 2≤-=, ……8分 所以1a 2≤. ……9分 (3)设切点为(x 0,y 0),则00'000y =x f (x )=1y =f(x )⎧⎪⎨⎪⎩, ……10分所以ln(x 0-a)-x 02=x 0,且001=1+2x x a -,即001x a 1x -=+. 所以20001ln x =x 1+2x -,所以2000x +x +ln(1+2x )=0 ……11分 设g(x)=x 2+x+ln(1+2x),1x >2-,则2'(1+2x)+1g (x)=>01+2x , 所以g(x)在1()2,-+∞上为增函数,又g(0)=0, ……13分 所以g(x)=0有唯一解x=0,故x 0=0,于是a=-1. ……14分。
