高中数学一轮复习基础知识手册第八编概率与统计.doc
(完整版)高考数学概率和统计知识点,推荐文档

ξ、η 等表示.
②随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量. ③随机变量可以取某区间内的一切值,这样的随机变量叫做连续型随机变量.
2.离散型随机变量的分布列
①离散型随机变量的分布列的概念和性质
一般地,设离散型随机变量 可能取的值为 x1, x2 ,……, xi ,……, 取每一个值 xi (
所以商家拒收这批产品的概率为 95 . 例 12.
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即
432
被淘汰. 已知某选手能正确回答第一、二、三轮的问题的概率分别为 5 、 5 、 5 ,且各轮问 题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为 ,求随机变量 的分布列与数学期望. (注:本小题结果可用分数表示)
(1) 二项分布
n 次独立重复试验中,事件 A 发生的次数 是一个随机变量,其所有可能的取值为
P P( k ) Ck pk qnk
q 1 p
0,1,2,…n,并且 k
n
,其中0 k n,
,随机变量 的分布列
如下:
0
1
…
k
…
n
P
C 0 p 0 qn n
C1 p1qn1 n
…
Ck pk qnk n
及推理和运算能力.
[解答提示]至少有 3 人出现发热反应的概率为
C3 0.803 0.202 C 4 0.804 0.20 C5 0.805 0.94
5
5
5
.
故填 0.94.
离散型随机变量的分布列
1.随机变量及相关概念
①随机试验的结果可以用一个变量来表示,这样的变量叫做随机变量,常用希腊字母
高中数学概率与统计知识点.docx

实用标准高中数学之概率与统计求等可能性事件、互斥事件和相互独立事件的概率解此类题目常应用以下知识:card ( A)m(1)等可能性事件 (古典概型 )的概率: P(A) =card ( I )=n;等可能事件概率的计算步骤:计算一次试验的基本事件总数n ;设所求事件 A ,并计算事件 A 包含的基本事件的个数m ;mP( A)依公式n求值 ;答,即给问题一个明确的答复.(2) 互斥事件有一个发生的概率:P(A + B)= P(A) + P(B);特例:对立事件的概率:P(A) +P( A )= P(A +A )= 1.(3) 相互独立事件同时发生的概率:P(A ·B)= P(A) ·P(B);特例:独立重复试验的概率:Pn(k)=Cnkp k(1p)n k .其中 P 为事件 A 在一次试验中发生的概率,此式为二项式 [(1-P)+P]n展开的第 k+1项.(4) 解决概率问题要注意“四个步骤,一个结合”:求概率的步骤是:第一步,确定事件性质等可能事件互斥事件独立事件n次独立重复试验即所给的问题归结为四类事件中的某一种.第二步,判断事件的运算和事件积事件即是至少有一个发生,还是同时发生,分别运用相加或相乘事件.等可能事件 :P( A)mn互斥事件: P( A B )P( A) P(B )独立事件: P ( A B ) P(A) P(B)第三步,运用公式n 次独立重复试验: P n (k ) C n k p k (1 p )n k求解第四步,答,即给提出的问题有一个明确的答复 .例 1 .在五个数字1,2,3,4,5中,若随机取出三个数字,则剩下两个数字都是奇数的概率是(结果用数值表示) .PC 13 3 3C 535 4 .10[ 解答过程 ]0.3 提示 :2例 2 .一个总体含有100 个个体,以简单随机抽样方式从该总体中抽取一个容量为5 的样本,则指定的某个个体被抽到的概率为.1 .P5 1 . [解答过程 ]20提示 :10020例 3.接种某疫苗后,出现发热反应的概率为 0.80. 现有 5 人接种该疫苗,至少有 3 人出现发热反应的概率为 __________(.精确到 0.01 )[ 考查目的 ] 本题主要考查运用组合、概率的基本知识和分类计数原理解决问题的能力,以 及推理和运算能力 .[ 解答提示 ]至少有 3 人出现发热反应的概率为3324455C 5 0.80 0.20C 5 0.80 0.20 C 5 0.800.94 .故填 0.94.离散型随机变量的分布列1.随机变量及相关概念①随机试验的结果可以用一个变量来表示,这样的变量叫做随机变量,常用希腊字母ξ、η等表示 .②随机量可能取的,可以按一定次序一一列出,的随机量叫做离散型随机量.③随机量可以取某区内的一切,的随机量叫做型随机量.2.离散型随机量的分布列①离散型随机量的分布列的概念和性一般地,离散型随机量可能取的x1 ,x2 ,⋯⋯,xi,⋯⋯,取每一个xi(i1 ,2 ,⋯⋯)的概率P(x i) =P i,称下表 .x1x2⋯x i⋯P P1P2⋯P i⋯随机量的概率分布,称的分布列.由概率的性可知,任一离散型随机量的分布列都具有下述两个性:(1)Pi0 ,i1,2,⋯;(2)P1P2⋯=1.②常的离散型随机量的分布列:(1 )二分布n次独立重复中,事件 A 生的次数是一个随机量,其所有可能的取 0,1 ,2 ,⋯n ,并且Pk P(k ) C n k p k q n k,其中0k n ,q 1p,随机量的分布列如下:01⋯k⋯nP C n0 p0 q n C n1 p 1q n 1⋯ C n k p k q n k C n n p n q 0称随机量服从二分布,作~ B(n , p),其中n、p参数,并:C n k p k q n k b( k ; n , p) .(2 )几何分布在独立重复中,某事件第一次生所作的的次数是一个取正整数的离散型随机量,“k”表示在第k 次独立重复事件第一次生.随机量的概率分布:123⋯k⋯P p qp q 2 p⋯q k 1 p⋯例 1 .厂家在品出厂前,需品做,厂家将一批品商家,商家按合同定也需随机抽取一定数量的品做,以决定是否接收批品 .(Ⅰ)若厂家房中的每件品合格的概率0.8, 从中任意取出 4 件行 ,求至少有 1件是合格的概率;(Ⅱ)若厂家商家 20件品中 ,其中有 3 件不合格 ,按合同定商家从中任取 2 件.都行 ,只有 2件都合格才接收批品.否拒收 ,求出商家出不合格品数的分布列及期望E,并求出商家拒收批品的概率.[ 解答程 ](Ⅰ)“厂家任取4件品,其中至少有 1 件是合格品” 事件A用立事件 A 来算,有P4A 1 P A 1 0.20.9984(Ⅱ)可能的取0,1,2.P0C172136 C2190,20P1C31C17151C 202190 ,C23P23C202190012P136513190190190E013615123319019019010 .记“商家任取 2 件产品检验,都合格”为事件B,则商家拒收这批产品的概率P1P B11362719095 .27所以商家拒收这批产品的概率为95.例 12.某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被432淘汰 . 已知某选手能正确回答第一、二、三轮的问题的概率分别为5、5、5,且各轮问题能否正确回答互不影响.(Ⅰ)求该选手被淘汰的概率;(Ⅱ)该选手在选拔中回答问题的个数记为,求随机变量的分布列与数学期望.(注:本小题结果可用分数表示)[ 解答过程 ]解法一:(Ⅰ)记“该选手能正确回答第i轮的问题”的事件为A i (i 1,2,3) ,则43P( A3)2P( A1)P(A2)5 ,5 , 5 ,该选手被淘汰的概率P P(A1A1 A2A2 A2 A3 ) P(A1 )P( A1 )P(A2 ) P( A1 )P(A2 ) P( A3 ) 142433101555555125 .P(1)1 P(A1)(Ⅱ)的可能值为12,,3, 5 ,P (2) P(A1A2) P( A1)P( A2 )4285525 ,P(3) P( A1A2 ) P( A1) P( A2 )4312525 .5的分布列为123P 1812 52525E1128312575252525 .4i的”的事件A i(i1,2,3)P(A1)解法二:(Ⅰ)“ 手能正确回答第, 5 ,P(A2)3P(A3)25 , 5 .P 1 P( A1A2A3) 1 P( A1)P(A2) P( A3)1432101手被淘汰的概率555125 .(Ⅱ)同解法一.离散型随机量的期望与方差随机量的数学期望和方差(1) 离散型随机量的数学期望:E x1 p1 x2 p2⋯;期望反映随机量取的平均水平.⑵离散型随机量的方差:D(x1 E )2 p1 ( x2 E )2 p2⋯(x n E )2 pn⋯;方差反映随机量取的定与波,集中与离散的程度.⑶基本性:E(a b)aE b ; D (a b) a2 D .(4) 若~ B(n , p) ,E np;D=npq (里 q=1-p) ;g(k , p) ,E1q如果随机量服从几何分布,P (k)p, D= p 2其中 q=1-p.例 1 .甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,所得次品数分ε、η,ε和η的分布列如下:ε012η012P613P532 101010101010比两名工人的技水平的高低.思路:一是要比两名工人在加工零件数相等的条件下出次品数的平均,即期望;二是要看出次品数的波情况,即方差的大小.E0611230.7101010,D(00.7) 26(10.7) 21(2 0.7) 230.891101010;工人乙生产出次品数η的期望和方差分别为:E0513220 .7D(0 0.7)25(1 0.7) 23(2 0.7)220.664 101010,101010由 Eε=E η知,两人出次品的平均数相同,技术水平相当,但 D ε>D η,可见乙的技术比较稳定.小结:期望反映随机变量取值的平均水平;方差反映随机变量取值的稳定与波动,集中与离散的程度 .例 2.某商场经销某商品,根据以往资料统计,顾客采用的付款期数的分布列为12345P0.40.20.20.10.1商场经销一件该商品,采用 1期付款,其利润为 200元;分 2期或 3 期付款,其利润为 250元;分 4 期或 5 期付款,其利润为300 元.表示经销一件该商品的利润.(Ⅰ)求事件 A :“购买该商品的3位顾客中,至少有 1 位采用 1 期付款”的概率P(A) ;(Ⅱ)求的分布列及期望E.[ 解答过程 ](Ⅰ)由A表示事件“购买该商品的3位顾客中至少有 1 位采用 1 期付款”.知A表示事件“购买该商品的 3 位顾客中无人采用 1 期付款”P( A)(10.4)20.216 , P( A) 1 P( A) 10.2160.784 .(Ⅱ)的可能取值为200元,250元,300元.P(200)P(1)0.4 ,P(250)P(2)P(3)0.2 0.20.4 ,P(300) 1 P(200) P(250) 1 0.4 0.4 0.2 .的分布列为200250300P0.40.40.2E200 0.4 250 0.4 300 0.2240(元).抽样方法与总体分布的估计抽样方法1 .简单随机抽样:设一个总体的个数为N ,如果通过逐个抽取的方法从中抽取一个样本,且每次抽取时各个个体被抽到的概率相等,就称这样的抽样为简单随机抽样.常用抽签法和随机数表法 .2.系统抽样:当总体中的个数较多时,可将总体分成均衡的几个部分,然后按照预先定出的规则,从每一部分抽取 1 个个体,得到所需要的样本,这种抽样叫做系统抽样(也称为机械抽样) .3.分层抽样:当已知总体由差异明显的几部分组成时,常将总体分成几部分,然后按照各部分所占的比进行抽样,这种抽样叫做分层抽样.总体分布的估计由于总体分布通常不易知道,我们往往用样本的频率分布去估计总体的分布,一般地,样本容量越大,这种估计就越精确.总体分布:总体取值的概率分布规律通常称为总体分布.当总体中的个体取不同数值很少时,其频率分布表由所取样本的不同数值及相应的频率表示,几何表示就是相应的条形图.当总体中的个体取值在某个区间上时用频率分布直方图来表示相应样本的频率分布.总体密度曲线:当样本容量无限增大,分组的组距无限缩小,那么频率分布直方图就会无限接近于一条光滑曲 ,即 体密度曲 .典型例例 1.某工厂生 A 、B 、C 三种不同型号的 品, 品数量之比依次 2:3:5. 用分 抽方法抽出一个容量n 的 本, 本中 A 种型号 品有16 件 .那么此 本的容量 n=.21080解答 程: A 种型号的 体是16.10, 本容量 n=2例 2 .一个 体中有100 个个体,随机 号 0 ,1 ,2 ,⋯,99 ,依 号 序平均分成 10 个小 , 号依次 1,2 ,3 ,⋯,10. 用系 抽 方法抽取一个容量 10 的 本, 定如果在第 1 随机抽取的号 m,那么在第k中抽取的号 个位数字与mk的个位数字相同,若m6, 在第 7 中抽取的号 是.解答 程:第K 的号(k1)10 , (k 1)101,⋯,( k 1)10 9,当 m=6 ,第 k 抽取的号的个位数字 m+k 的个位数字,所以第 7 中抽取的号 的个位数字 3 ,所以抽取号 63 .正态分布与线性回归1.正态分布的概念及主要性质(1 )正 分布的概念1 ( x) 2f ( x)e 22R如果 型随机 量的概率密度函数2, x其中、> 0 , 称 服从正 分布, ~ N (2常数,并且,).(2 )期望 E= μ,方差D2.(3 )正 分布的性正 曲 具有下列性:①曲 在 x 上方,并且关于直 x =μ 称 .③曲的称位置由μ确定;曲的形状由确定,越大,曲越“矮胖”;反之越“高瘦” .三σ原即数分布在(μ—σ ,μ+ σ)中的概率 0.6526数分布在(μ— 2 σ,μ+2σ)中的概率 0.9544数分布在(μ— 3 σ,μ+3σ)中的概率 0.9974(4 )准正分布当 =0 , =1服从准的正分布,作~ N(0,1)(5 )两个重要的公式① ( x) 1 (x) ,② P( a b)(b) (a) .(6) N( , 2)与 N(0,1)二者系.若~N( ,2),~ N (0,1);②若~ N(, 2 ) ,P(ab) (b) (a) .2.性回的,性回就是理量与量之的性关系的一种数学方法.量和量之的关系大致可分两种型:确定性的函数关系和不确定的函数关系.不确定性的两个量之往往仍有律可循.回分析就是理量之的相关关系的一种数量方法 .它可以提供量之相关关系的公式.具体来,n 个本数据(x1, y1),(x2, y2),⋯,(xn, yn),其回直方程,或公式nx i y i n xyb i 1, a y b x,n2: y? bx a.其中x i n(x)2i 1,其中x, y分 |xi |、 |yi |的平均数 .例 1.如果随机量ξ~ N (μ,σ2 ),且 Eξ=3 , Dξ=1 , P(- 1 <ξ≤1 =等于 ()A.2 Φ(1 )- 1B.Φ(4 )-Φ( 2 )C.Φ(2 )-Φ( 4 )D.Φ(- 4 )-Φ(- 2 )解答过程:对正态分布,μ=E ξ=3 ,σ2=D ξ=1 ,故 P(- 1 <ξ≤1 ) = Φ(1 - 3)-Φ(- 1-3 )= Φ(- 2 )-Φ(- 4) = Φ(4)-Φ( 2 ) .答案: B例 2. 将温度调节器放置在贮存着某种液体的容器内,调节器设定在 d ℃,液体的温度ξ(单位:℃)是一个随机变量,且ξ~N ( d ,0.52 ) .(1)若 d=90 °,则ξ<89 的概率为;(2)若要保持液体的温度至少为80℃的概率不低于 0.99,则 d 至少是?(其中若η~N ( 0 , 1 ),则Φ( 2 ) =P (η<2 ) =0.9772,Φ(- 2.327) =P (η< - 2.327) =0.01 ) .8990解答过程:( 1 )P(ξ<89 )=F( 89 )= Φ(0.5)= Φ(- 2 )=1 -Φ( 2 )=1 -0.9772=0.0228.(2)由已知 d 满足 0.99 ≤P(ξ≥80 ),即 1 - P(ξ<80 )≥1 - 0.01 ,∴P(ξ<80 )≤0.01.80 d∴Φ(0.5)≤0.01=Φ(-2.327).80 d∴0.5≤-2.327.∴d ≤81.1635.故 d 至少为 81.1635.小结:( 1 )若ξ~N ( 0 ,1),则η=~N(0,1).(2)标准正态分布的密度函数f( x)是偶函数, x<0 时, f( x)为增函数, x>0 时, f ( x)为减函数 .1、分加法数原理新知:完成一件事情,有n 法,在第 1 法中有m1种不同的方法,在第 2 法中有m2种不同的方法,⋯,在第n 法中有m n种不同的方法 .文档那么完成件事共有N m1m2m n种不同的方法.(也称加法原理)分加法数原理特点:分加法数原理的是“分” ,完成一件事的法要分若干,各的法法相互独立,各法中的各种方法也相独立,用任何一法中的任何一种方法都可以独完成件事 .分步乘法数原理:完成一件事情,需要分成n 个步,做第 1 步有m1种不同的方法,做第 2 步有m2种不同的方法⋯⋯做第 n 步有m n种不同的方法 .那么完成件事共有 N m1m2m n种不同的方法.(也称乘法原理)分步乘法数原理的特点:分步数原理的是“分步” ,完成一件事要分若干步,各个步相互依存,完成任何其中的一步都不能完成件事,只有当各个步都完成后,才算完成件事 .思考:分加法数原理与分步乘法数原理有什么异同点?要注意什么?相同点:它都是研究完成一件事情, 共有多少种不同的方法;不同点:分加法数原理分完成一件事,任何一法中的任何一个方法都能完成件事;分步乘法数原理分步完成一件事,些方法需要分步,各个步次相依 ,且每一步都完成了 ,才能完成件事情。
高考数学概率与统计部分知识点梳理(DOC)
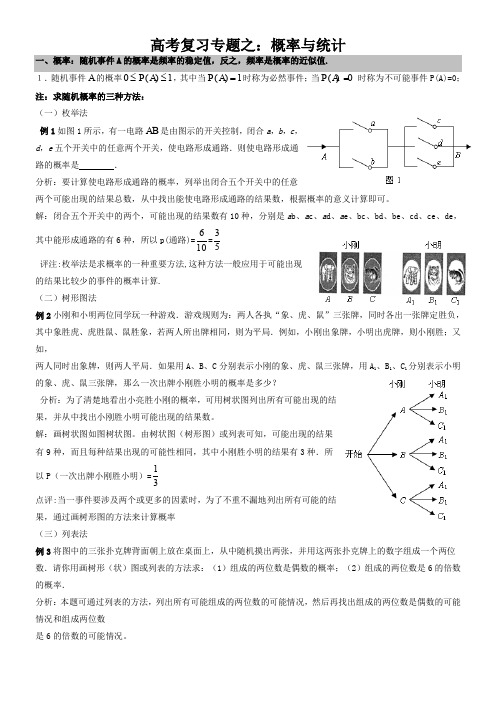
高考复习专题之:概率与统计一、概率:随机事件A 的概率是频率的稳定值,反之,频率是概率的近似值.1.随机事件A 的概率0()1P A ≤≤,其中当()1P A =时称为必然事件;当()0P A =时称为不可能事件P(A)=0; 注:求随机概率的三种方法: (一)枚举法例1如图1所示,有一电路AB 是由图示的开关控制,闭合a ,b ,c ,d ,e 五个开关中的任意两个开关,使电路形成通路.则使电路形成通路的概率是 .分析:要计算使电路形成通路的概率,列举出闭合五个开关中的任意两个可能出现的结果总数,从中找出能使电路形成通路的结果数,根据概率的意义计算即可。
解:闭合五个开关中的两个,可能出现的结果数有10种,分别是a b 、a c 、a d 、a e 、bc 、bd 、be 、cd 、ce 、de ,其中能形成通路的有6种,所以p(通路)=106=53评注:枚举法是求概率的一种重要方法,这种方法一般应用于可能出现的结果比较少的事件的概率计算. (二)树形图法例2小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局.如果用A 、B 、C 分别表示小刚的象、虎、鼠三张牌,用A 1、B 1、C 1分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?分析:为了清楚地看出小亮胜小刚的概率,可用树状图列出所有可能出现的结果,并从中找出小刚胜小明可能出现的结果数。
解:画树状图如图树状图。
由树状图(树形图)或列表可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种.所以P (一次出牌小刚胜小明)=31点评:当一事件要涉及两个或更多的因素时,为了不重不漏地列出所有可能的结果,通过画树形图的方法来计算概率 (三)列表法例3将图中的三张扑克牌背面朝上放在桌面上,从中随机摸出两张,并用这两张扑克牌上的数字组成一个两位数.请你用画树形(状)图或列表的方法求:(1)组成的两位数是偶数的概率;(2)组成的两位数是6的倍数的概率.分析:本题可通过列表的方法,列出所有可能组成的两位数的可能情况,然后再找出组成的两位数是偶数的可能情况和组成两位数 是6的倍数的可能情况。
高中数学统计与概率知识点(原稿).doc

高中数学统计与概率知识点(文)第一部分:统计一、什么是众数。
一组数据中出现次数最多的那个数据,叫做这组数据的众数。
众数的特点。
①众数在一组数据中出现的次数最多;②众数反映了一组数据的集中趋势,当众数出现的次数越多,它就越能代表这组数据的整体状况,并且它能比较直观地了解到一组数据的大致情况。
但是,当一组数据大小不同,差异又很大时,就很难判断众数的准确值了。
此外,当一组数据的那个众数出现的次数不具明显优势时,用它来反映一组数据的典型水平是不大可靠的。
3.众数与平均数的区别。
众数表示一组数据中出现次数最多的那个数据;平均数是一组数据中表示平均每份的数量。
二、.中位数的概念。
一组数据按大小顺序排列,位于最中间的一个数据(当有偶数个数据时,为最中间两个数据的平均数)叫做这组数据的中位数。
三 .众数、中位数及平均数的求法。
①众数由所给数据可直接求出;②求中位数时,首先要先排序(从小到大或从大到小),然后根据数据的个数,当数据为奇数个时,最中间的一个数就是中位数;当数据为偶数个时,最中间两个数的平均数就是中位数。
③求平均数时,就用各数据的总和除以数据的个数,得数就是这组数据的平均数。
四、中位数与众数的特点。
⑴中位数是一组数据中唯一的,可能是这组数据中的数据,也可能不是这组数据中的数据;⑵求中位数时,先将数据有小到大顺序排列,若这组数据是奇数个,则中间的数据是中位数;若这组数据是偶数个时,则中间的两个数据的平均数是中位数;⑶中位数的单位与数据的单位相同;⑷众数考察的是一组数据中出现的频数;⑸众数的大小只与这组数的个别数据有关,它一定是一组数据中的某个数据,其单位与数据的单位相同;(6)众数可能是一个或多个甚至没有;(7)平均数、众数和中位数都是描述一组数据集中趋势的量。
五.平均数、中位数与众数的异同:⑴平均数、众数和中位数都是描述一组数据集中趋势的量; ⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据。
高中数学教案:概率与统计的基础知识

高中数学教案:概率与统计的基础知识概率与统计是高中数学中重要的内容之一,是数学与现实生活相结合的重要领域之一。
在概率与统计的教学中,我们需要让学生掌握一些基础知识,如概率的定义和性质、随机事件的概率计算、统计数据的收集和整理等。
本文将介绍概率与统计的基础知识,并结合实例进行详细解析,以帮助教师设计高效的教案。
一、概率的基础知识1.1 概率的定义和性质概率是描述事件发生可能性的一种数值,通常用从0到1的实数表示。
学生需要掌握概率的基本定义和性质,如概率的非负性、必然事件概率为1、互斥事件概率相加等。
教师可以通过简单的例子,如抛硬币、掷骰子等,让学生感受概率的概念和性质。
1.2 随机事件的概率计算学生需要学习如何计算随机事件的概率。
对于等可能事件,其概率可以通过事件发生的次数与总次数的比值得到。
对于不等可能事件,需要将事件的可能数转化为较简单的问题,如组合数的计算等。
二、统计的基础知识2.1 数据的收集和整理统计是指通过对数据的收集、整理和分析,从中获取有关事物的定量信息的过程。
学生需要学习如何进行数据的收集和整理。
教师可以引导学生参与实际调查,并借助电子表格、统计软件等工具进行数据的整理和分析。
同时,学生还需学习如何进行数据图表的绘制,以直观地展示数据的特征。
2.2 统计指标的计算与解释统计指标是对数据进行概括和度量的方法,包括均值、中位数、众数、标准差等。
学生需要学习如何计算这些统计指标,并能够解释其意义。
教师可以通过实际例子引导学生计算和解释统计指标,帮助学生深入理解数据的特征和规律。
三、概率与统计的实际应用概率与统计的知识在现实生活中有着广泛的应用。
教师可以通过引入实际应用例子,帮助学生认识到概率与统计的重要性,并激发学生的学习兴趣。
3.1 概率在游戏中的应用概率在游戏中的应用是概率教学中常用的实例之一。
教师可以通过分析各种游戏的规则和背后的概率原理,让学生理解游戏胜负的概率,并通过游戏的规则设计,让学生具体计算相关概率。
高中数学《统计》与《概率》知识点

第二章统计一、简单随机抽样1.总体和样本在统计学中 , 把研究对象的全体叫做总体.把每个研究对象叫做个体.把总体中个体的总数叫做总体容量.为了研究总体的有关性质,一般从总体中随机抽取一部分:,,,研究,我们称它为样本.其中个体的个数称为样本容量.2.简单随机抽样,就是从总体中不加任何分组、划类、排队等,完全随机地抽取调查单位。
特点是:每个样本单位被抽中的可能性相同(概率相等),样本的每个单位完全独立,彼此间无一定的关联性和排斥性。
简单随机抽样是其它各种抽样形式的基础。
通常只是在总体单位之间差异程度较小和数目较少时,才采用这种方法。
3.简单随机抽样常用的方法:(1)抽签法;⑵随机数表法;⑶计算机模拟法4.抽签法:(1)给调查对象群体中的每一个对象编号;(2)准备抽签的工具,实施抽签(3)对样本中的每一个个体进行测量或调查5.随机数表法:例:利用随机数表在所在的班级中抽取10位同学参加某项活动。
二、系统抽样1.系统抽样(也叫等距离抽样):把总体的单位进行排序,再计算出抽样距离,然后按照这一固定的抽样距离抽取样本。
第一个样本采用简单随机抽样的办法抽取。
K(抽样距离)=N(总体)/n(样本个数)前提条件:总体中个体的排列对于研究的变量来说,应是随机的,即不存在某种与研究变量相关的规则分布。
可以在调查允许的条件下,从不同的样本开始抽样,对比几次样本的特点。
如果有明显差别,说明样本在总体中的分布有某种循环性规律,且这种循环和抽样距离重合。
2.系统抽样是实际中最为常用的抽样方法之一。
因为它对抽样框的要求较低,实施也比较简单。
三、分层抽样1.分层抽样:先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次,然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本,最后,将这些子样本合起来构成总体的样本。
两种方法:1.先以分层变量将总体划分为若干层,再按照各层在总体中的比例从各层中抽取。
高中数学第8章统计与概率章末小结讲义含解析湘教版选修

第8章 统计与概率1.离散型随机变量的概率分布 (1)X 的概率分布离散型随机变量X 的所有不同取值为x 1,x 2,…,x n ,X 取每一个值x i (i =1,2,…,n )的概率P (X =x i )=p i ,则称以下表格为随机变量X 的概率分布列,简称为分布列.离散型随机变量具有如下性质:①p i ≥0,i =1,2,…,n ;② i =1np i =1.(2)两点分布:两点分布也叫0~1分布,它只有两个试验结果0和1,其分布列为(3)二项分布:在n 次独立重复试验中,事件A 发生的次数为X ,在每次试验中事件A 发生的概率为p ,那么在n 次独立重复试验中,事件A 恰好发生k 次的概率为P (X =k )=C k n p k·(1-p )n -k,k=0,1,2,…,n .这时称X 服从二项分布,记为X ~B (n ,p ).(4)超几何分布N 件产品中M 件次品,从中随机抽取n 件,因X 表示这n 件中的次品数,则X 服从超几何分布H (N ,M ,n ),即P (X =M )=C m M C n -mN -MC n N ,m =0,1,…,n2.离散型随机变量的均值和方差 (1)均值和方差随机变量X 的分布列是P (X =x i )=p i ,i =1,2,…,n ,则称E (X )=x 1p 1+x 2p 2+…+x n p n为X 的均值或数学期望;D (X )=[x 1-E (X )]2×p 1+[x 2-E (X )]2×p 2+…+[x n -E (X )]2×p n 为随机变量X 的方差.(2)均值与方差的性质: ①E (ax +b )=aE (X )+b ;②D (ax +b )=a 2D (X ).(3)两点分布与二项分布的均值与方差:①若X 服从两点分布,则E (X )=p ,D (X )=p (1-p ). ②若X ~B (n ,p ),则E (X )=np ,D (X )=np (1-p ). 3.条件概率及事件的相互独立性 (1)事件A 发生的条件下事件B 发生的概率P (B |A )=P A ∩B P A =n A ∩Bn A(P (A )>0).(2)若事件A 与事件B 相互独立, 则P (A ∩B )=P (A )P (B ). 4.正态分布若X ~N (μ,σ2),则P (μ-σ<X ≤μ+σ)=68.3%,P (μ-2σ<X ≤μ+2σ)=95.4%, P (μ-3σ<X ≤μ+3σ)=99.7%.5.线性回归方程对于一组具有线性相关关系的数据(x 1,y 1),(x 2,y 2),…,(x n ,y n ),其线性回归直线方程为y ^=bx +a .其中b =s xy s 2x,a =y --b x -. 6.相关系数r xy 与随机变量χ2(1)相关系数r xy相关系数r xy 是用来刻画回归模型的回归效果的,其值越大,残差平方和越小,模型的拟合效果越好.(2)随机变量χ2随机变量χ2是用来判断两个分类变量在多大程度上相关的变量.独立性检验即计算χ2的观测值,并与教材中所给表格中的数值进行比较,从而得到两个分类变量在多大程度上相关.[例1] 坛子里放着3个是绿皮的,2个是白皮的.如果不放回地依次拿出2个鸭蛋,求:(1)第1次拿出绿皮鸭蛋的概率;(2)第1次和第2次都拿到绿皮鸭蛋的概率;(3)在第1次拿出绿皮鸭蛋的条件下,第2次拿出绿皮鸭蛋的概率.[解] 设第1次拿出绿皮鸭蛋为事件A ,第2次拿出绿皮鸭蛋为事件B ,则第1次和第2次都拿出绿皮鸭蛋为事件A ∩B .(1)从5个鸭蛋中不放回地依次拿出2个的事件数为n (Ω)=A 25=20.根据分步乘法计数原理,n (A )=A 13×A 14=12. 于是P (A )=n An Ω=1220=35. (2)因为n (A ∩B )=A 23=6,所以P (A ∩B )=n A ∩B n Ω=620=310.(3)法一:由(1)(2)可得,在第1次拿出绿皮鸭蛋的条件下,第2次拿出绿皮鸭蛋的概率为P (B |A )=P A ∩BP A =31035=12.法二:因为n (A ∩B )=6,n (A )=12,所以P (B |A )=n A ∩B n A =612=12.求条件概率时,P (B |A )=n A ∩B n A =P A ∩BP A是常用的方法,解题时一定要分清谁是前提条件.1.设某种动物活到20岁以上的概率为0.7,活到25岁以上的概率为0.4,求现龄为20的这种动物能活到25岁以上的概率.解:设这种动物活到20岁以上的事件为A ,活到25岁以上的事件为B ,则P (A )=0.7,而A ∩B =B ,即P (A ∩B )=P (B )=0.4.故事件A 发生条件下B 发生的条件概率为P (B |A )=P A ∩B P A =0.40.7=47.2.掷两枚均匀的骰子,已知点数不同,求至少有一个是6点的概率.解:法一:设两枚骰子出现的点数分别为x ,y ,事件A :“两枚骰子出现的点数不同,即x ≠y ”,事件B :“x 、y 中有且只有一个是6点”;事件C :“x =y =6”,则P (B |A )=P A ∩BP A =10363036=13,P (C |A )=P A ∩CP A =0363036=0.∴至少有一个是6点的概率为P (B ∪C |A )=P (B |A )+P (C |A )=13+0=13.法二:也可用古典概型来求解,“至少有一个是6点”包含的结果数是10个,故所求的概率为P (D )=1030=13.(由于两枚骰子点数不同,故基本事件空间中包含30个结果)[例2] 格”,两部分考核都“合格”,则该课程考核“合格”.甲、乙、丙三人在理论考核中合格的概率分别为0.9、0.8、0.7;在实验考核中合格的概率分别为0.8、0.7、0.9.所有考核是否合格相互之间没有影响.(1)求甲、乙、丙三人在理论考核中至少有两人合格的概率; (2)求这三人该课程考核都合格的概率.(结果保留三位小数) [解] 记“甲理论考核合格”为事件A 1,记A 1为A 1的对立事件; 记“乙理论考核合格”为事件A 2,记A 2为A 2的对立事件; 记“丙理论考核合格”为事件A 3,记A 3为A 3的对立事件;记“甲实验考核合格”为事件B 1,“乙实验考核合格”为事件B 2,“丙实验考核合格”为事件B 3.(1)记“理论考核中至少有两人合格”为事件C ,记C 为C 的对立事件. 法一:P (C )=P [(A 1∩A 2∩A 3)∪(A 1∩A 2∩A 3)∪(A 1∩A 2∩A 3)∪(A 1∩A 2∩A 3)]=P (A 1∩A 2∩A 3)+P (A 1∩A 2∩A 3)+P (A 1∩A 2∩A 3)+P (A 1∩A 2∩A 3)=0.9×0.8×0.3+0.9×0.2×0.7+0.1×0.8×0.7+0.9×0.8×0.7=0.902. 法二:P (C )=1-P (C )=1-P [(A 1 ∩A 2 ∩A 3 )∪(A 1∩A 2∩ A 3)∪(A 1∩A 2∩A 3)∪(A 1 ∩A 2∩A 3)]=1-[P (A 1∩ A 2∩ A 3)+P (A 1 ∩A 2∩ A 3)+P (A 1∩A 2 ∩A 3)+P (A 1∩ A 2∩A 3)]=1-(0.1×0.2×0.3+0.9×0.2×0.3+0.1×0.8×0.3+0.1×0.2×0.7)=1-0.098=0.902.所以,理论考核中至少有两人合格的概率为0.902. (2)记“三人该课程考核都合格”为事件D .P (D )=P [(A 1∩B 1)∩(A 2∩B 2)∩(A 3∩B 3)]=P (A 1∩B 1)P (A 2∩B 2)P (A 3∩B 3) =P (A 1)P (B 1)P (A 2)P (B 2)P (A 3)P (B 3) =0.9×0.8×0.8×0.7×0.7×0.9 =0.254 016≈0.254.所以这三人该课程考核都合格的概率约为0.254.此类题目主要是融互斥事件与相互独立事件于一体,重在分析各事件间的关系,解答此类题目时,应先分析待求事件由几部分基本事件组成,如果彼此互斥,则利用公式P (A ∪B )=P (A )+P (B ),然后就每部分事件A 、B 借助于相互独立事件的定义求解.3.有三种灯泡,合格率分别为0.90,0.95,0.95,现各抽取一件进行检验. 求:(1)恰有一件不合格的概率; (2)至少有两件不合格的概率.解:设P (A )=0.90,P (B )=0.95,P (C )=0.95, (1)恰有一件不合格的概率为P (A BC +A B C +AB C )=0.10×0.952+0.90×0.05×0.95+0.90×0.95×0.05=0.175 75.(2)至少有两件不合格的概率为P (A -B -C +A -BC -+AB -C -+A -B -C -)=0.10×0.05×0.95+0.10×0.95×0.05+0.90×0.052+0.10×0.052=0.012.4.某射手进行射击训练,假设每次射击击中目标的概率为35,且各次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答); (2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答).解:(1)记“射手射击1次,击中目标”为事件A ,则在3次射击中至少有两次连续击中目标的概率P 1=P (A ∩A ∩A )+P (A ∩A ∩A )+P (A ∩A ∩A )=35×35×25+25×35×35+35×35×35=63125. (2)射手第3次击中目标时,恰好射击了4次的概率P 2=C 23×⎝ ⎛⎭⎪⎫352×25×35=162625.[例3] 中国男子篮球职业联赛总决赛采用七场四胜制(即先胜四场者获胜),进入总决赛的甲乙两队中,若每一场比赛甲队获胜的概率为23,乙队获胜的概率为13,假设每场比赛的结果互相独立,现已赛完两场,乙队以2∶0暂时领先.(1)求甲队获得这次比赛胜利的概率;(2)设比赛结束时两队比赛的场数为随机变量X ,求随机变量X 的分布列和数学期望. [解] (1)设甲队获胜为事件A ,则甲队获胜包括甲队以4∶2获胜和甲队以4∶3获胜两种情况.设甲队以4∶2获胜为事件A 1,则P (A 1)=⎝ ⎛⎭⎪⎫234=1681,设甲队以4∶3获胜为事件A 2, 则P (A 2)=C 14×13×⎝ ⎛⎭⎪⎫233×23=64243,P (A )=P (A 1)+P (A 2)=1681+64243=112243.(2)随机变量X 可能的取值为4,5,6,7,P (X =4)=⎝ ⎛⎭⎪⎫132=19;P (X =5)=C 12×13×23×13=427; P (X =6)=C 13×13×⎝ ⎛⎭⎪⎫232×13+⎝ ⎛⎭⎪⎫234=2881; P (X =7)=C 14×13×⎝ ⎛⎭⎪⎫233=3281. 所以X 的分布列为E (X )=4×19+5×427+6×81+7×81=81.求离散型随机变量的分布列,关键是找出随机变量的取值,求出相应的概率,计算时可能会用到等可能事件、互斥事件、相互独立事件的概率公式等.5.一个袋子中装有大小相同的3个红球和2个黄球,从中同时取出2个,试求所含红球个数的数学期望.解:若记红球个数为X ,X 的所有可能取值为0,1,2. P (X =0)=C 03C 22C 25=110,P (X =1)=C 13C 12C 25=35,P (X =2)=C 23C 02C 25=310.故X 的分布列为:E (X )=0×110+1×35+2×310=1.2.6.某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是13,每次测试时间间隔恰当.每次测试通过与否互相独立.(1)求该学生考上大学的概率;(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为X ,求X 的分布列及X 的数学期望.解:(1)记“该生考上大学”为事件A ,其对立事件为A ,则P (A )=C 15⎝ ⎛⎭⎪⎫13⎝ ⎛⎭⎪⎫234+⎝ ⎛⎭⎪⎫235.∴P (A )=1-⎣⎢⎡⎦⎥⎤C 15⎝ ⎛⎭⎪⎫13⎝ ⎛⎭⎪⎫234+⎝ ⎛⎭⎪⎫235=131243.(2)参加测试次数X 的可能取值为2,3,4,5,P (X =2)=⎝ ⎛⎭⎪⎫132=19,P (X =3)=C 12·13·23·13=427, P (X =4)=C 13·13·⎝ ⎛⎭⎪⎫232·13=427, P (X =5)=C 14·13·⎝ ⎛⎭⎪⎫233+⎝ ⎛⎭⎪⎫234=1627. 故X 的分布列为:E (X )=2×19+3×427+4×427+5×1627=389.答:该生考上大学的概率为131243;所求数学期望是389.[例4](1)作出散点图; (2)求出线性回归方程; (3)作出残差图; (4)计算r xy ;(5)试预测该运动员训练47次及55次的成绩.[解] (1)作出该运动员训练次数x 与成绩y 之间的散点图,如图所示,由散点图可知,它们之间具有线性相关关系.(2)可求得x =39.25,y =40.875,∑i =18x 2i =12 656,∑i =18y 2i =13 731,∑i =18x i y i =13 180,∴b =∑i =18x i -xy i -y∑i =18x i -x2=∑i =18x i y i -8x -y-∑i =18x 2i -8x 2≈1.0 415,a =y -b x =-0.003 875.∴线性回归方程为y ^=1.041 5x -0.003 875. (3)残差分析作残差图如图所示,由图可知,残差点比较均匀地分布在水平带状区域中,说明选用的模型比较合适.(4)计算相关系数r xy . 计算相关系数r xy ≈0.985 5.说明了该运动员的成绩的差异有98.55%是由训练次数引起的. (5)作出预报由上述分析可知,我们可用回归方程y =1.0 415x -0.003 875作为该运动员成绩的预报值.将x =47和x =55分别代入该方程可得y ≈49和y ≈57. 故预测运动员训练47次和55次的成绩分别为49和57.回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法,其步骤是先画出散点图,并对样本点进行相关性检验,在此基础上选择适合的函数模型去拟合样本数据,从而建立较好的回归方程,并且用该方程对变量值进行分析;有时回归模型可能会有多种选择(如非线性回归模型),此时可通过残差分析或利用相关系数r xy 来检查模型的拟合效果,从而得到最佳模型.7.对一质点的运动过程观测了4次,得到如表所示的数据,则刻画y 与x 的关系的线性回归方程为____________.解析:由表可知x =1+2+3+44=2.5,y =1+3+5+64=154, b =∑i =14x i y i -4x -y-∑i =14x 2i -4x 2=+2×3+3×5+-4×2.5×1542+22+32+42-2=1.7,a =y -b x =154-1.7×2.5=-0.5.故所求线性回归方程为y =1.7x -0.5. 答案:y =1.7x -0.58.随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:(1)求y 关于t 的回归方程y =b t +a ;(2)用所求回归方程预测该地区2019年(t =6)的人民币储蓄存款.附:回归方程y ^=b ^t +a ^中,b ^=∑i =1nt i y i -n t y∑i =1nt 2i -n t 2,a ^=y -b ^t .解:(1)列表计算如下:这里n =5,t =1n ∑i =1nt i =155=3,y =1n ∑i =1n y i =365=7.2.又∑i =1nt 2i -n t 2=55-5×32=10,∑i =1nt i y i -n ty =120-5×3×7.2=12,从而b ^=1210=1.2,a ^=y -b ^t =7.2-1.2×3=3.6,故所求回归方程为y ^=1.2t +3.6.(2)将t =6代入回归方程可预测该地区2019年的人民币储蓄存款为y ^=1.2×6+3.6=10.8(千亿元).[例5] 现统计数据如下:质量监督员甲在现场时,990件产品中合格品有982件,次品有8件,甲不在现场时,510件产品中, 合格品有493件,次品有17件.试分别用列联表、独立性检验的方法对数据进行分析.[解] (1)2×2列联表如下:由列联表看出|ac-bd|=|982×17-493×8|=12 750,相差较大,可在某种程度上认为“甲在不在场与产品质量有关”.(2)由2×2列联表中数据,计算χ2的值χ2=-2 1 475×25×510×990≈13.097>10.828.所以,在犯错误的概率不超过0.001的前提下认为“质量监督员甲在不在现场与产品质量有关系”.独立性检验是对两个分类变量间是否存在相关关系的一种案例分析方法.利用假设检验求随机变量χ2的值能更精确地判断两个分类变量间的相关关系.9.在一次天气恶劣的飞机航程中,有关人员调查了男女乘客在飞机上晕机的情况:男乘客晕机的有24人,不晕机的有31人;女乘客晕机的有8人,不晕机的有26人.请你根据所给数据判定:能否以90%的把握认为在天气恶劣的飞机航程中,男乘客比女乘客更容易晕机?解:根据题意,列出2×2列联表如下:由列联表中的数据,得χ2的值为χ2=-255×34×32×57≈3.689>2.706,因此,能以90%的把握认为在天气恶劣的飞机航程中,男乘客比女乘客更容易晕机.(时间120分钟,满分150分)一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知随机变量X服从正态分布N(2,σ2),P(X≤4)=0.84,则P(X≤0)=( )A .0.16B .0.32C .0.68D .0.84解析:选A 由正态分布的特征得P (X ≤0)=1-P (X ≤4)=1-0.84=0.16.2.甲袋中装有2个白球,2个黑球,乙袋中装有2个白球,4个黑球,从甲、乙两袋中各取一球均为白球的概率为( )A.16B.25C.215D.56解析:选A 记“从甲袋中任取一球为白球”为事件A ,“从乙袋中任取一球为白球”为事件B ,则由题意知,事件A 、B 是相互独立事件,故P (A ∩B )=P (A )P (B )=24×26=16.3.设随机变量X 的分布列为P (X =i )=a ⎝ ⎛⎭⎪⎫13i(i =1,2,3),则a 的值为( )A .1 B.913 C.1113D.2713解析:选D 因为P (X =1)=a 3,P (X =2)=a9,P (X =3)=a27,所以a 3+a 9+a 27=1,所以a =2713.4.对有线性相关关系的两个变量建立的回归直线方程y ^=a +bx 中,回归系数b ( ) A .可以小于0 B .大于0 C .能等于0D .只能小于0解析:选A ∵b =0时,则r =0,这时不具有线性相关关系,但b 可以大于0也可以小于0.5.某种型号的印刷机在一小时内不需要工人照看的概率为0.8,现有四台这种型号的印刷机,且同时各自独立工作,则在一小时内至多有2台需要照看的概率为( )A .0.153 6B .0.180 8C .0.563 2D .0.972 8解析:选D “一小时内至多有2台印刷机需要照看”的事件包括有0,1,2台需要照看三种可能.因此,所求概率为C 04·0.20·0.84+C 14·0.21·0.83+C 24·0.22·0.82=0.972 8.6.为考察数学成绩与物理成绩的关系,在高二随机抽取了300名学生.得到下面列联表:现判断数学成绩与物理成绩有关系,则判断的出错率为( ) A .0.5% B .1% C .2%D .5%解析:选D 代入公式得 χ2=-272×228×122×178≈4.514>3.841查表可得犯错误的概率不超过5%.7.已知X ~B (n ,p ),且E (X )=7,D (X )=6,则p 等于( ) A.17 B.16 C.15D.14解析:选A 由题易知,E (X )=np =7,D (X )=np (1-p )=6,所以p =17.8.张家的3个鸡仔钻进了李家装有3个鸡仔的鸡笼里,现打开笼门,让鸡仔一个一个地走出来,若第一个走出来的是张家的鸡仔,那么第二个走出的也是张家的鸡仔的概率是( )A.25B.23C.15D.35解析:选A 设“第一个走出的是张家的鸡仔”为事件A ,“第二个走出的是张家的鸡仔”为事件B ,则P (B |A )=P A ∩BP A =A 23A 26A 13A 16=25.9.若同时抛掷两枚骰子,当至少有5点或6点出现时,就说这次试验成功,则在3次试验中至少有1次成功的概率是( )A.125729B.80243C.665729D.100243解析:选C 一次试验中,至少有5点或6点出现的概率为1-⎝ ⎛⎭⎪⎫1-13×⎝ ⎛⎭⎪⎫1-13=1-49=59,设X 为3次试验中成功的次数,则X ~B ⎝ ⎛⎭⎪⎫3,59,故所求概率P (X ≥1)=1-P (X =0)=1-C 03×⎝ ⎛⎭⎪⎫590×⎝ ⎛⎭⎪⎫493=665729.10.一袋中装有5个白球和3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了X 次球,则P (X =12)等于( )A .C 1012×⎝ ⎛⎭⎪⎫3810×⎝ ⎛⎭⎪⎫582B .C 911×⎝ ⎛⎭⎪⎫389×⎝ ⎛⎭⎪⎫582×38C .C 911×⎝ ⎛⎭⎪⎫589×⎝ ⎛⎭⎪⎫382D .C 911×⎝ ⎛⎭⎪⎫389×⎝ ⎛⎭⎪⎫582解析:选B X =12表示第12次取到红球,前11次中有9次取到红球,从而P (X =12)=C 911×⎝ ⎛⎭⎪⎫389×⎝ ⎛⎭⎪⎫582×38.11.一个篮球运动员投篮一次得3分的概率为a ,得2分的概率为b ,不得分的概率为c [a 、b 、c ∈(0,1)],已知他投篮一次得分的数学期望为1(不计其他得分情况),则ab 的最大值为( )A.148B.124C.112D.16解析:选B 由已知3a +2b +0×c =1,即3a +2b =1.∴ab =16×3a ×2b ≤16×⎝ ⎛⎭⎪⎫3a +2b 22=16×⎝ ⎛⎭⎪⎫122=124.当且仅当3a =2b =12,即a =16,b =14时取“等号”.12.设由“0”、“1”组成的三位数组中,若用A 表示“第二位数字为‘0’的事件”,用B 表示“第一位数字为‘0’的事件”,则P (A |B )=( )A.25B.34C.12D.18解析:选C ∵P (B )=1×2×22×2×2=12,P (A ∩B )=1×1×22×2×2=14,∴P (A |B )=P A ∩B P B =12.二、填空题(本大题共4小题,每小题5分,满分20分.把答案填写在题中的横线上) 13.甲、乙两名同学通过英语听力测试的概率分别为12和13,两人同时参加测试,恰有一人通过的概率是__________.解析:解析:恰有一人通过有两种可能:恰好甲通过或恰好乙通过,故其概率为12×⎝ ⎛⎭⎪⎫1-13+13×⎝ ⎛⎭⎪⎫1-12=12. 答案:1214.对于P (χ2≥ x 0),当x 0>2.706时,就有________的把握认为“x 与y 有关系”. 解析:由k >2.706,可知P (χ2≥2.706)≈0.10,即若k >2.706,此时则有90%的把握认为“x 与y 有关系”.答案:90%15.若100件零件中包含10件废品,现从中任取两件,已知取出的两件中有废品,则两件都是废品的概率为________.解析:设事件A 为“取出的两件中有废品”,事件B 为“取出的两件都是废品”,由题意,显然,A ∩B =B ,而P (A )=C 110·C 190+C 210C 2100,P (B )=C 210C 2100, 故P (B |A )=P B P A =C 210C 210+C 110·C 190=121. 答案:12116.某种种子每粒发芽的概率都为0.9,现播种了1 000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X ,则X 的数学期望为________.解析:记“不发芽的种子数为X ”,则ε~B (1 000,0.1),所以E (ε)=1 000×0.1=100,而X =2ε,故E (X )=E (2ε)=2E (ε)=200.答案:200三、解答题(本大题共有6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分10分)某人从某城市的南郊乘公交车前往北区火车站,由于交通拥挤,所需时间X (单位:分钟)服从正态分布N (50,102),求他在时间段(30,70]内赶到火车站的概率.解:由X ~N (50,102)知μ=50,σ=10,所以P (30<X ≤70)=P (50-2×10<X ≤50+2×10)=95.4%,所以所求概率为95.4%. 18.(本小题满分12分)某班有6名班干部,其中男生4人,女生2人,任选3人参加学校的义务劳动.(1)设所选3人中女生人数为X ,求X 的分布列; (2)求男生甲或女生乙被选中的概率;(3)设“男生甲被选中”为事件A ,“女生乙被选中”为事件B ,求P (B )和P (B |A ). 解:(1)X 的所有可能取值为0,1,2,依题意得 P (X =0)=C 34C 36=15,P (X =1)=C 24C 12C 36=35.P (X =2)=C 14C 22C 36=15.∴X 的分布列为(2)则P (C )=C 34C 36=15;∴所求概率为P (C )=1-P (C )=1-15=45.(3)P (B )=C 25C 36=1020=12.P (B |A )=P A ∩BP A =C 14C 36C 25C 36=410=25.19.(本小题满分12分)有两个分类变量x 与y ,其一组观测值如下面的2×2列联表所示:其中a,15-a 均为大于5的整数,则a 取何值时,在犯错误的概率不超过0.1的前提下认为x 与y 之间有关系?解:查表可知,要使在犯错误的概率不超过0.1的前提下认为x 与y 之间有关系,则χ2≥2.706,而χ2=65×[a +a --a -a220×45×15×50=a -220×45×15×50=a -260×90.由χ2≥2.706得a ≥7.19或a ≤2.04. 又a >5且15-a >5,a ∈Z ,即a =8,9.故a 为8或9时,在犯错误的概率不超过0.1的前提下认为x 与y 之间有关系. 20.(本小题满分12分)某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽数之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天100颗种子中的发芽数,得到如下资料:2组数据用于回归方程检验.(1)若选取12月1日和12月5日这两日的数据进行检验,请根据12月2日至12月4日的数据,求出y 关于x 的线性回归方程y ^=b ^x +a ^;(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的.试问(1)中所得到的线性回归方程是否可靠?若可靠,请预测温差为14 ℃时的发芽数.解:(1)由数据,求得x =12,y =27, 由公式,求得b ^=52,a ^=y -b ^x =-3,所以y 关于x 的线性回归方程为y ^=52x -3.(2)当x =10时,y ^=52×10-3=22,|22-23|<2;当x =8时,y ^=52×8-3=17,|17-16|<2.因此得到的线性回归方程是可靠的. 当x =14时,y ^=52×14-3=35-3=32,所以预测温差为14 ℃时的发芽数为32颗.21.(2017·天津高考)(本小题满分12分)从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为12,13,14.(1)记X 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量X 的分布列和数学期望; (2)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率. 解:(1)随机变量X 的所有可能取值为0,1,2,3.P (X =0)=⎝⎛⎭⎪⎫1-12×⎝⎛⎭⎪⎫1-13×⎝⎛⎭⎪⎫1-14=14,P (X =1)=12×⎝⎛⎭⎪⎫1-13×⎝⎛⎭⎪⎫1-14+⎝ ⎛⎭⎪⎫1-12×13×⎝⎛⎭⎪⎫1-14+⎝⎛⎭⎪⎫1-12×⎝⎛⎭⎪⎫1-13×14=1124,P (X =2)=⎝⎛⎭⎪⎫1-12×13×14+12×⎝ ⎛⎭⎪⎫1-13×14+12×13×⎝ ⎛⎭⎪⎫1-14=14,P (X =3)=12×13×14=124.所以随机变量X 的分布列为:随机变量X 的数学期望E (X )=0×4+1×24+2×4+3×24=1312.(2)设Y 表示第一辆车遇到红灯的个数,Z 表示第二辆车遇到红灯的个数,则所求事件的概率为P (Y +Z =1)=P (Y =0,Z =1)+P (Y =1,Z =0)=P (Y =0)P (Z =1)+P (Y =1)P (Z =0) =14×1124+1124×14=1148. 所以这2辆车共遇到1个红灯的概率为1148.22.(本小题满分12分)已知一个口袋中装有n 个红球(n ≥1且n ∈N *)和2个白球,从中有放回地连续摸三次,每次摸出两个球,若两个球颜色不同则为中奖,否则不中奖.(1)当n =3时,设三次摸球中(每次摸球后放回)中奖的次数为X ,求X 的分布列; (2)记三次摸球中(每次摸球后放回)恰有两次中奖的概率为P ,当n 取多少时,P 最大? 解:(1)当n =3时,每次摸出两个球,中奖的概率P =3×2C 25=35.P (X =0)=C 03⎝ ⎛⎭⎪⎫253=8125; P (X =1)=C 13·35·⎝ ⎛⎭⎪⎫252=36125;P (X =2)=C 23⎝ ⎛⎭⎪⎫352·25=54125; P (X =3)=C 33·⎝ ⎛⎭⎪⎫353=27125. 所以X 的分布列为(2)P =C 23·p 2·(1-p )=-3p 3+3p 2,0<p <1,P ′=-9p 2+6p =-3p (3p -2),知在⎝ ⎛⎭⎪⎫0,23上P 为增函数,在⎝ ⎛⎭⎪⎫23,1上P 为减函数,当p =23时,P 取得最大值.所以p =C 1n C 12C 2n +2=23,即n 2-3n +2=0,解得n =1或n =2.故当n =1或n =2时,P 最大.。
高考数学一轮复习知识点与练习随机事件的概率.doc

1.概率和频率(1) 在相同的条件S 下重复 n 次试验,观察某一事件 A 是否出现,称n 次试验中事件 A 出现的次数n A为事件 A 出现的频数,称事件 A 出现的比例 f n(A)=nn A为事件 A 出现的频率.(2) 对于给定的随机事件A,在相同条件下,随着试验次数的增加,事件 A 发生的频率会在某个常数附近摆动并趋于稳定,我们可以用这个常数来刻画随机事件 A 发生的可能性大小,并把这个常数称为随机事件 A 的概率,记作P(A).2.事件的关系与运算定义符号表示包含关系如果事件 A 发生,则事件 B 一定发生,这时称事件B? A( 或 A? B) B 包含事件 A(或称事件 A 包含于事件 B)相等关系若 B? A 且 A? B A=B并事件若某事件发生当且仅当事件 A 发生或事件 B 发生,A∪ B( 或 A+ B) (和事件 ) 称此事件为事件 A 与事件 B 的并事件 (或和事件 )交事件若某事件发生当且仅当事件 A 发生且事件 B 发生,A∩B(或 AB) (积事件 ) 则称此事件为事件 A 与事件 B 的交事件 (或积事件 )互斥事件若 A∩ B 为不可能事件 (A∩ B= ?),则称事件 A 与事A∩B= ? 件 B 互斥对立事件若 A∩ B 为不可能事件, A∪ B 为必然事件,那么称P(A)+P(B)= 1 事件 A 与事件 B 互为对立事件(1)概率的取值范围: 0≤P(A)≤ 1.(2)必然事件的概率 P(E)=1.(3)不可能事件的概率 P( F)= 0.(4)概率的加法公式如果事件 A 与事件 B 互斥,则P(A∪ B)= P(A)+ P(B).(5)对立事件的概率若事件 A 与事件 B 互为对立事件,则P(A) = 1- P(B).【知识拓展】互斥事件与对立事件的区别与联系互斥事件与对立事件都是两个事件的关系,互斥事件是不可能同时发生的两个事件,而对立事件除要求这两个事件不同时发生外,还要求二者之一必须有一个发生,因此,对立事件是互斥事件的特殊情况,而互斥事件未必是对立事件.【思考辨析】判断下面结论是否正确 (请在括号中打“√”或“×”)(1) 事件发生频率与概率是相同的.( )(2) 随机事件和随机试验是一回事.( )(3) 在大量重复试验中,概率是频率的稳定值.( )(4) 两个事件的和事件是指两个事件都得发生.( )(5) 对立事件一定是互斥事件,互斥事件不一定是对立事件.()(6) 两互斥事件的概率和为 1.( )1.一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是________.①至多有一次中靶②两次都中靶③只有一次中靶④两次都不中靶2.从某班学生中任意找出一人,如果该同学的身高小于160 cm 的概率为0.2,该同学的身高在[160,175]( 单位: cm)内的概率为0.5,那么该同学的身高超过175 cm 的概率为 ________.3. (2015 ·北改编湖 )我国古代数学名著《数书九章》有“米谷粒分”题:粮仓开仓收粮,有人送来米 14.给出下列三个命题,其中正确的命题有________个.①有一大批产品,已知次品率为10%,从中任取100 件,必有10 件是次品;②做7 次抛硬币的试验,结果 3 次出现正面,因此正面出现的概率是37;③随机事件发生的频率就是这个随机事件发生的概率.5. (教材改编 ) 袋中装有9 个白球, 2 个红球,从中任取 3 个球,则①恰有 1 个红球和全是白球;②至少有 1 个红球和全是白球;③至少有 1 个红球和至少有 2 个白球;④至少有 1 个白球和至少有 1 个红球.在上述事件中,是对立事件的为________.题型一事件关系的判断例 1某城市有甲、乙两种报纸供居民订阅,记事件 A 为“只订甲报纸”,事件 B 为“至少订一种报纸”,事件 C 为“至多订一种报纸”,事件 D 为“不订甲报纸”,事件 E 为“一种报纸也不订”.判断下列每对事件是不是互斥事件;如果是,再判断它们是不是对立事件.思维升华对互斥事件要把握住不能同时发生,而对于对立事件除不能同时发生外,其并事件应为必然事件.这些也可类比集合进行理解,具体应用时,可把所有试验结果写出来,看所求事件包含哪几个试验结果,从而判定所给事件的关系.判断下列各对事件是不是互斥事件或对立事件:某小组有 3 名男生和 2 名女生,从中任选2 名同学去参加演讲比赛,其中①恰有1 名男生和恰有2 名男生;②至少有 1 名男生和至少有 1 名女生;③至少有 1 名男生和全是女生.题型二随机事件的频率与概率例2 (2015 ·北京 ) 某超市随机选取 1 000 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整商品甲乙丙丁顾客人数100 √×√√217 ×√×√200 √√√×300 √×√×85 √×××98 ×√××(1)估计顾客同时购买乙和丙的概率;(2)估计顾客在甲、乙、丙、丁中同时购买3 种商品的概率;(3)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中哪种商品的可能性最大?思维升华(1) 概率与频率的关系:频率反映了一个随机事件出现的频繁程度,频率是随机的,而概率是一个确定的值,通常用概率来反映随机事件发生的可能性的大小,有时也用频率来作为随机事件概率的估计值.(2)随机事件概率的求法:利用概率的统计定义求事件的概率,即通过大量的重复试验,事件发生的频率会逐渐趋近于某一个常数,这个常数就是概率.某企业生产的乒乓球被奥运会指定为乒乓球比赛专用球,目前有关部门对某批产品进行了抽样检测,检查结果如下表所示:抽取球数 n 50 100 200 500 1 000 2 000优等品数 m 45 92 194 470 954 1 902m优等品频率n(1) 计算表中乒乓球优等品的频率;(2) 从这批乒乓球产品中任取一个,质量检查为优等品的概率是多少?(结果保留到小数点后三位)题型三互斥事件、对立事件的概率命题点 1 互斥事件的概率1,得例 3 袋中有 12 个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率是35 ,得到黄球或绿球的概率也是 5 ,试求得到黑球、黄球到黑球或黄球的概率是和绿球的概率各是多1212少?命题点 2对立事件的概率例 4某商场有奖销售中,购满100元商品得 1 张奖券,多购多得 .1 000 张奖券为一个开奖单位,设特等奖 1 个,一等奖10 个,二等奖50 个.设 1 张奖券中特等奖、一等奖、二等奖的事件分别为A、 B、C,求:(1) P(A),P(B), P(C);(2)1 张奖券的中奖概率;(3)1 张奖券不中特等奖且不中一等奖的概率.思维升华求复杂的互斥事件的概率一般有两种方法:一是直接求解法,将所求事件的概率分解为一些彼此互斥的事件的概率的和;二是间接法,先求该事件的对立事件的概率,再由P(A)= 1- P( A )求解.当题目涉及“ 至多”“ 至少” 型问题时,多考虑间接法.国家射击队的队员为在射击世锦赛上取得优异成绩,正在加紧备战,经过近期训练,某队员射击一次命中7~ 10 环的概率如下表所示:命中环数10 环9 环8 环7 环概率0.320.280.180.12求该射击队员射击一次:(1)射中 9 环或 10 环的概率;(2)命中不足 8 环的概率.21.用正难则反思想求互斥事件的概率专注·专业·口碑·极致- 5 -物的 100 位顾客的相关数据,如下表所示 .一次购物量 1 至 4 件 5 至 8 件9 至 12 件13 至 16 件17 件及以上顾客数 (人 ) x 30 25 y 10 结算时间 (分钟 / 人 ) 1 1.5 2 2.5 3已知这 100 位顾客中一次购物量超过8 件的顾客占 55%.(1)确定 x, y 的值,并估计顾客一次购物的结算时间的平均值;(2) 求一位顾客一次购物的结算时间不超过 2 分钟的概率.(将频率视为概率)...思维点拨若某一事件包含的基本事件多,而它的对立事件包含的基本事件少,则可用“ 正难则反”思想求解.温馨提醒(1) 要准确理解题意,善于从图表信息中提炼数据关系,明确数字特征含义.(2)正确判定事件间的关系,善于将 A 转化为互斥事件的和或对立事件,切忌盲目代入概率加法公式.易错提示 (1) 对统计表的信息不理解,错求 x, y,难以用样本平均数估计总体.(2)不能正确地把事件 A 转化为几个互斥事件的和或对立事件,导致计算错误.[方法与技巧 ]1.对于给定的随机事件 A,由于事件 A 发生的频率 f n(A)随着试验次数的增加稳定于概率P(A),因此可以用频率 f n (A)来估计概率 P(A).2.从集合角度理解互斥事件和对立事件从集合的角度看,几个事件彼此互斥,是指由各个事件所含的结果组成的集合彼此的交集为空集,事件 A 的对立事件 A 所含的结果组成的集合,是全集中由事件 A 所含的结果组成的集合的补集.[失误与防范 ]1.正确认识互斥事件与对立事件的关系:对立事件是互斥事件,是互斥事件中的特殊情况,但互斥事件不一定是对立事件,“互斥”是“对立”的必要不充分条件.2.需准确理解题意,特别留心“ 至多,,”“至少,,”“不少于,,”等语句的含义.A 组专项基础训练( 时间: 45 分钟 )则事件 M 与 N 互为对立事件;②若事件 A 与 B 互为对立事件,则事件 A 与 B 为互斥事件;③若事件A 与B 为互斥事件,则事件 A 与 B 互为对立事件;④若事件 A 与 B 互为对立事件,则事件A∪ B 为必然事件,其中,真命题是________.112 2.围棋盒子中有多粒黑子和白子,已知从中取出 2 粒都是黑子的概率为7,都是白子的概率是35,则从中任意取出 2 粒恰好是同一色的概率是________.3.从一箱产品中随机地抽取一件,设事件 A= { 抽到一等品 } ,事件 B= { 抽到二等品 } ,事件 C= { 抽到三等品 } ,且已知 P(A)= 0.65, P(B)= 0.2 , P(C)= 0.1,则事件“抽到的产品不是一等品”的概率为__________ .4.从存放的号码分别为1,2,3 , , , 10 的卡片的盒子中,有放回地取100 次,每次取一张卡片并记下号码,统计结果如下:卡片号码 1 2 3 4 5 6 7 8 9 10取到次数13 8 5 7 6 13 18 10 11 9则取到号码为奇数的卡片的频率是________.5.对一批产品的长度(单位:毫米 )进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25) 上的为一等品,在区间 [15,20) 和[25,30) 上的为二等品,在区间 [10,15) 和 [30,35) 上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为________.6.在 200 件产品中,有192 件一级品, 8 件二级品,则下列事件:①在这 200 件产品中任意选出9 件,全部是一级品;②在这 200 件产品中任意选出9 件,全部是二级品;③在这 200 件产品中任意选出9 件,不全是二级品.其中 ________是必然事件;________是不可能事件;________是随机事件.7.已知某运每次投命中的概率都40%,采用随机模的方法估运三次投恰有两次命中的概率:先由算器生0 到 9 之取整数的随机数,指定1,2,3,4 表示命中, 5,6,7,8,9,0 表示不命中;再以每三个随机数一,代表三次投的果.随机模生了如下20 随机数:907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估,运三次投恰有两次命中的概率________.8.若随机事件A,B 互斥, A, B 生的概率均不等于0,且 P(A) =2- a, P(B)= 4a- 5,数 a 的取范是 _____________.9.(2014 ·西 )某保公司利用随机抽方法,投保行抽,本中每的付果如下:付金 (元 ) 0 1 000 2 000 3 000 4 000数 ( ) 500 130 100 150 120(1)若每的投保金均 2 800 元,估付金大于投保金的概率;(2)在本中,主是新司机的占10%,在付金 4 000 元的本中,主是新司机的占20%,估在已投保中,新司机金 4 000 元的概率.10.从某学校的800 名男生中随机抽取50 名量其身高,被学生身高全部介于155 cm 和 195 cm 之,将量果按如下方式分:第一[155,160) ,第二 [160,165) ,⋯,第八 [190,195] ,如是按上述分方法得到的率分布直方的一部分,已知第一与第八人数相同,第六的人数 4.(1)求第七组的频率;(2) 估计该校的 800 名男生的身高的中位数以及身高在180 cm 以上 (含 180 cm)的人数;(3) 若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x, y,事件 E ={| x- y|≤5} ,事件 F = {| x- y|>15} ,求 P(E∪ F).B 组专项能力提升( 时间: 25 分钟 )11.在一次随机试验中,彼此互斥的事件A, B,C, D 的概率分别是0.2,0.2,0.3,0.3,则下列说法正确的是 ______________.①A+ B 与 C 是互斥事件,也是对立事件;② B+ C 与 D 是互斥事件,也是对立事件;③ A+ C 与 B+ D 是互斥事件,但不是对立事件;④ A 与 B+ C+ D 是互斥事件,也是对立事件.12.如图所示,茎叶图表示的是甲、乙两人在 5 次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为________.13.若 A,B 互为对立事件,其概率分别为P(A)=4,P( B)=1,且 x>0 ,y>0,则 x+y 的最小值为 ________.x y14.如图, A 地到火车站共有两条路径L1和 L 2,现随机抽取 100 位从 A 地到达火车站的人进行调查,调查结果如下:所用时间 /分钟10~ 20 20~30 30~ 40 40~50 50~ 60选择 L 1的人数 6 12 18 12 12选择 L 2的人数0 4 16 16 4(1)试估计 40 分钟内不能赶到火车站的概率;(2)分别求通过路径 L 1和 L 2所用时间落在上表中各时间段内的频率;(3)现甲、乙两人分别有 40 分钟和 50 分钟时间用于赶往火车站,为了尽最大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径.15. (2015 ·西陕 ) 随机抽取一个年份,对西安市该年 4 月份的天气情况进行统计,结果如下:日期123456789101112131415 天气晴雨阴阴阴雨阴晴晴晴阴晴晴晴晴日期161718192021222324252627282930 天气晴阴雨阴阴晴阴晴晴晴阴晴晴晴雨(1)在 4 月份任取一天,估计西安市在该天不下雨的概率;(2) 西安市某学校拟从4月份的一个晴天开始举行连续 2 天的运动会,估计运动会期间不下雨的概率.专注·专业·口碑·极致- 10 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八编概率与统计1.计数原理(1)理解分类加法计数原理和分步乘法计数原理,能正确区分“类”和“步”,并能利用两个原理解决一些简单的实际问题.(2)挪排列的概念及排列数公式,并能利用公式解决一些简单的实际问题.(3)理解组合的概念及组合数公式,并能利用公式解决一些简单的实际问题.(4)会用二项式定理解决与二项展开式有关的简单问题.2.事件与概率(1)了解随机事件发生的不确定性和频率的稳定性,了解概率的意义以及频率与概率的区别.(2)了解两个事件的概率加法公式.3.古典概型(1)理解古細型及概率计算公式.(2)会计算一些随机事件所含的基本事件紐事件发生的概率.4.随机数与儿何概型(1)了解随机数的意义,能运用模拟方法估计概率.(2)了解几何概型的意义.5.概率与统计(1)理解取有限个值的离散型随机变量及其分布列的概念,认识分布列刻画随机现象的重要性,会求某些取有限个值的离散型随机变量的分布列.(2)了解超几何分布,并能进行简单的应用(3)了解条件概率的概念,了解两个事件相互独立的概念,理解斤次独立重复试验模型及二项分布,并能解决一些简单的实际问题.(4)理解取有限个值的离散型随机变量的均值、方差的概念,会求简单离散型随机变量的均值、方差,并能利用离散型随机变量的均值、方差解决一些简单问题.(5)借助直方图认识正态分布曲线的特点及曲线所表示的意义.第一讲排列、组合、二项式定理知识能力解读知能解读(一)分类加法计数原理与分步乘法计数原理1分类如法计数原理完成一件事有7?类不同方案,在第1类方案中有㈣种不同的方法,在第2类方案中有加2 种不同的方法……在第n类方案中有叫种不同的方法,那么完成这件事共有N = m} +勒+••• +叫种不同的方法。
2分步乘法计数原理完成一件事需要"个步骤,做第一步有风种不同的方法,做第二步有血2种不同的方法做第"步有叫种不同的方法,那么完成这件事共有N = m A x m2x• • • x m n种不同的方法.3区别如果任何一类方案中的任何一种方法都能完成这件事,那么选用分类加法计数原理,即类与类之间是相互独立的,即“分类完成”;如果只有当斤个步骤都做完,这件事才能完成, 那么选用分步乘法计数原理,即步与步之间是相互依存的、连续的,即“分步完成”。
说明要正确把握“完成一件事”这句话的意义。
运用分类计数时,做到不重、不漏;运用分步计数时,要确定好次序,且每一步独立、互不干扰,对于复杂问题,可同时运用两个基本原理或借助列表画图帮助分析。
知能解读(二)排列与组合1.排列、组合都是研究从一些不同元素中取出〃个元素的问题,这是两个既有联系又完全不同的概念。
本质区别在于:前者有顺序,而后者无顺序.2. 区分某一问题是排列问题还是组合问题,关键是看所选出的元素与顺序是否有关,若 交换某两个元素的位置对结果产生影响,则是排列问题,否则是组合问题。
知能解读(三)排列数、组合数n!1. 排列数公式:A ; = =-——(m,n G N"且m < n )。
.(n-m)!排列数性质:(1)=(2) A : = mA ;;: + A ;:/ (以上加,M N*且加5/t)。
说明性质(1 ):从zr 个不同的元素中取出个元素,分两个步骤完成:第一步从〃 个元素中选出1个排在一个位置上,第二步从余下的(/1-1)个元去中选出(m-l)个元素排 在余下的(m-l)个位置上,就得到A :=吩;同理:A :; =S-1)A :営, A 驚=(—2)A ;J …。
实际上也可以分三步完成:A ;: = A : • A 〉• A ;:拧。
性质(2):从并个不同的元素中取出m(m</7)个元素,不分步,用分类的方法解决也 可以,此类问题,无非分两类情况:第一类:加个元素中含有元素分两步完成: ① 将d 排在某一位置上,有加种不同的方法.② 从其余(Z2-1)个元素屮収出(m-l)个排在其他(m-l)个位置上,有A ::;种方法, 即有血4:穿种不同的方法;第二类:加个元素屮不含有元素a ,从(斤-1)个元素屮取出m 个元素排在加个位置上, 有A 二种方法. 即共有mA^ + AZ 种方法,故A: = mA :匸+鹉。
2.组合数公式:C :"=詁一 '八 丿')C m 厂H-m z r> \ cm cm .厂加一1H =c n ;(2)C n = C n _} + C n _,;c ;: = c;;: + c^+c :;+・・・+c;;;1(5) C,;JC ;"C ;n+CjC_+…+ C :c :7+C ;cn (以上加,朋 N*且加S)。
说明性质(1):这个性质可以由组合数的定义得出,从斤个不同元素中取出加个元素后, 剩下-m)个元素,也就是说,从〃个不同元素中取出加个元素的每一个组合,都对应于从/?个不同元素中取出(71-m)个元素的唯一的一个组合;反过来一样,因此有C : = C :T"。
性质(2):分两类完成:第一类:含元素a,有C :,种方法;第二类:不含元素G ,有CS 种方法,即 C : = C 貯+殆o 性质(3):分两步完成: 第一步:先选出1个元素;第二步:再从余下的(H-1)个元素中取111 (m-l)个元素,但这样取有重复,如先选出 G|,再选111n\mim < n )o (1)(4)Cl2 ,。
3,…,匕”组成子集A,或先选出。
2,再选出Q|,。
3,…,4“得到的子集是相同的,且同一个集合重复了加次,因此C;:=W) + m, B|J C; = - C;;1'1 o' m 性质(4):在计算C;时,分(H-m + 1)类.第一类:含q,为C:7种;第二类:不含q,含色,为C:写种;第三类:不含坷,勺,含冬,为Gt种;・•・© = C:冒 + + C舄• •• +C:: (m<n)o性质(5 ):将含斤个元素的集合人二佃宀宀,…,。
”}分成两个子集={d],°2,…,色},B2 ={%+]4+2,・・・,d“} {r>m,n-r>rn),则可以这样来取;B冲取加个元素,中不取,为W;B冲取(m-1)个元素,中取1个元素,为CT'C\_r;冋中不取,坊中取加个元素,为C;C:J ,即C: = C;U + CjC» + ・・CC貯 + C;C;J o知能解读(四)排列、组合的应用解排列、组合应用题时应主要抓住是排列问题还是组合问题,其次要搞清需要分类,还是需要分步.排列、组合应用问题主要有三类:不带限制条件的排列或组合问题;带限制条件的排列或组合问题;排列、组合的综合性问题.具体而言,解排列、组合的应用问题,通常有以下途径:(1)以元素为主,即先满足特殊元素的要求,再考虑其他元素一一特殊元素法;(2)以位置为主,即先满足特殊位置的要求,再考虑其他位置一一特殊位置法;(3)先不考虑附加条件,计算出排列或组合数再减去不符合要求的排列数或组合数一—间接法;(4)当计算数目不是很大时,可采用列举法。
知能解读(五)二项式定理1二项式定理(° + b)H = C仙"+ C]tl a,l-l b + …+ C r n a n-r b r+ …+ C;:b"(处N*),这个公式所表示的规律叫做二项式定理。
说明二项式中a, b用“ + ”连接,共中C;(r = 0,l,2,…丿)叫做展开式的二项式系数,且二项展开式共有S + 1)项。
2二项展开式的通项公式T t.+l = C n a n-r b r(0 < r < /i, r € N, n G N^:) o说明(1) 7;+]表示二项展开式的任意项,只要斤与厂确定,该项也随之确定;(2)公式表示的第(r+l)项,而不是第厂项;(3)公式中a,方的位置不能颠倒,它们的指数和一定为/? ; (4)展开式中的第(r+l)项的二项式系数C;与第(r+l)项的系数是不同的概念。
知能解读(六)二项式系数的性质(1)对称性:二项展开式中,与首末两端“等距离”的两项的二项式系数相等,即c 加 一(2)最值:二项展开式中,中间的一项和两项的二项式系数相等并且最大: (n 、 即当77为偶数时,第-+ 1项的二项式系数最大,为Cf ;(2丿/2 4-1I 2(3) 二项展开式屮所有项的二项式系数之和等于2",即C : + C ; + C ;+・・・ + C ;=2"。
(4) 二项展开式中,奇数项的二项式系数Z 和与偶数项的二项式系数之和相等,即 c :+c ;+c :+・・Y+c ;+c :+…=2 叫知能解读(七)@ +方+ c )"展开式中a p b q c r的系数求法(p,q,rwN 且〃 + q +厂二〃) (a + b+c )"=[(a + S + c]",将此多项式按c 的升幕排列,得"C ;; • C 角• C" • M = C : • C 歸0 〃 心 0 英系数为C : •陷,化简为:n-rq!(n_r_q )!r!•c ;。
解题方法荟萃1 .数学思想方法思想方法(一)转化与化归思想 思想方法(二)分类讨论思想 点评'本题主要考查分类加法计算原理、排列知识以及分类讨论的数学思想。
思想方法 思想方法 思想方法 思想方法 说明 木题采用解法叫构造法,即在问题涉及代数或儿何元素及其关系时,构造出与问题相关 的代数模型或儿何模型,而使问题得以简捷、顺畅解决的一种解题方法。
II 解题规律技巧规律技巧(一)特殊元素(或位置)优先考虑对于存在特殊元素或特殊位置的排列组合问题,我们可以从这些“特殊”入手,先满足 特殊元素或特殊位置,再去满足其他元素或其他位置,这种解法叫特殊元素(或位置)优先法。
规律技巧(二)相邻问题捆绑法解决某些元素相邻(要求在一起)问题常用捆绑法:把相邻元素看成一个整体,再与其 他元素一起排列,同时注意捆绑元素的问题排列。
规律技巧(三)不相邻问题插空法解决不相邻问题常用插空法:先考虑不受限制的元素的排列,再将不相邻的元素插在已 排列元素的空档中。
说明(1)不相邻问题常用插空法,要先排不相邻元素以外的其他元索,然后再用不相邻元fl-1Z/+1当”为奇数时’第罗项及 + 1项的二项式系数相等且最大,为C“2 =c n 2 on\n\ 对称法 间接法 赋值法 构造法(三)(四) (五素去插空。
(2)本题也可用间接法,即(甲、乙相邻的排法)=3600 (种)。
说明不熄灭的灯不用排,熄灭的灯选“空”后不用排。
