哈工大2014年春MATLAB 大作业
MATLAB大作业

M A T L A B大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
不要抄袭复制,可以参考网上、文献资料的内容,但要理解,要变成自己的语言,按自己的思路组织内容。
(4)从给出的问题中至少选择一题(多做不限,但必须独立完成,严禁抄袭)。
(5)大作业占过程考核的20%,从完成情况、工作量、作业文档方面评分。
第一类:绘制图形。
(B级)问题一:斐波那契(Fibonacci)螺旋线,也称黄金螺旋线(Golden spiral),是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。
斐波那契螺旋线,以斐波那契数为边的正方形拼成的长方形,然后在正方形里面画一个90度的扇形,连起来的弧线就是斐波那契螺旋线,如图所示。
问题二:绘制谢尔宾斯基三角形(Sierpinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。
其生成过程为:取一个实心的三角形(通常使用等边三角形),沿三边中点的连线,将它分成四个小三角形,然后去掉中间的那一个小三角形。
接下来对其余三个小三角形重复上述操作,如图所示。
问题三:其他分形曲线或图形。
分形曲线还有很多,教材介绍了科赫曲线,其他还有皮亚诺曲线、分形树、康托(G. Cantor)三分集、Julia集、曼德布罗集合(Mandelbrot set),等等。
这方面的资料很多(如),请分析构图原理并用MATLAB 实现。
问题四:模拟掷骰子游戏:掷1000次骰子,统计骰子各个点出现的次数,将结果以下表的形式显示,并绘制出直方图。
哈工大MATLAB选修课第二次matlab作业
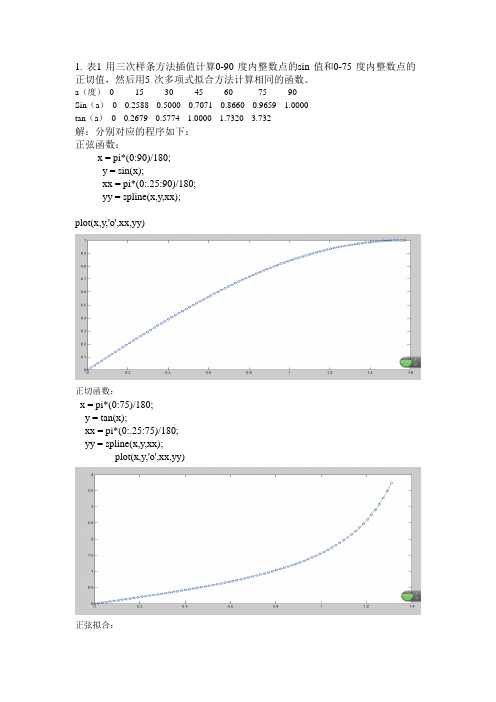
1. 表1 用三次样条方法插值计算0-90 度内整数点的sin 值和0-75 度内整数点的正切值,然后用5 次多项式拟合方法计算相同的函数。
a(度)0 15 30 45 60 75 90Sin(a)0 0.2588 0.5000 0.7071 0.8660 0.9659 1.0000tan(a)0 0.2679 0.5774 1.0000 1.7320 3.732解:分别对应的程序如下:正弦函数:x = pi*(0:90)/180;y = sin(x);xx = pi*(0:.25:90)/180;yy = spline(x,y,xx);plot(x,y,'o',xx,yy)正切函数:x = pi*(0:75)/180;y = tan(x);xx = pi*(0:.25:75)/180;yy = spline(x,y,xx);plot(x,y,'o',xx,yy)正弦拟合:figurex=pi*(0:15:90)/180;y=[0,0.2588,0.5,0.7071,0.866,0.9659,1.0]; xx=pi*(1:0.05:90)/180;p2=polyfit(x,y,5);yy=polyval(p2,xx);plot(x,y,'-ro',xx,yy);正切拟合:figurex=pi*(0:15:75)/180;y=[0,0.2679,0.5774,1,1.732,3.732];xx=pi*(1:0.05:75)/180;p2=polyfit(x,y,5);yy=polyval(p2,xx);plot(x,y,'-ro',xx,yy);legend('描点显示','五次拟合')2. 采用最近点法、线性法和3 次样条法插值计算1-100 整数间平方根n 1 4 9 16 25 36 49 64 81 100Sqtr(n)1 2 3 4 5 6 7 8 9 10解:程序如下:x=[1,4,9,16,25,36,49,64,81,100];y=[1,2,3,4,5,6,7,8,9,10];xx=1:100;yy=interp1(x,y,xx)subplot(2,2,1)plot(x,y,'-ro',xx,yy,'dr');title('线性法');subplot(2,2,2);y2=interp1(x,y,xx,'nearest');plot(x,y,'-ro',xx,y2,'dr');title('最近点法')subplot(2,2,3);y3=interp1(x,y,xx,'spline');plot(x,y,'-ro',xx,y3,'dr');title('3次样条法')仿真的结果:3. 已知p(x)=2x^4-3x^3+5x+13,求p(x)的全部根,由方程p(x)=0 的根构造一个多项式f(x),并和p(x)比较。
哈工大机械原理大作业

H a r b i n I n s t i t u t e o f T e c h n o l o g y大作业设计说明书课程名称:机械原理设计题目:凸轮机构院系:机电学院班级:姓名:学号:指导教师:丁刚设计时间:2014.5.29哈尔滨工业大学1.设计题目第31题:升程/mm 升程运动角/。
升程运动规律升程许用压力角/。
回程运动角/。
回程运动规律回程许用压力角/。
远休止角/。
近休止角/。
150 90 等加等减速40 80 余弦加速度70 40 1502.运动方程式及运动线图由题目要求凸轮逆时针旋转(1)确定凸轮机构推杆升程、回程运动方程,并绘制推杆位移、速度、加速度线图。
升程第一段:(0 <φ< pi /4)φ0=pi/2;s1 = 73*φ^2;v1=146*w*φ;a1 = 146*w^2;升程第二段:(pi/4 <φ< pi /2)s2 =90-73*(pi/2-φ)^2;v2=146*w*( pi/2-φ);a2 =-146*w.^2;远休止程:(pi/2 <φ< 10*pi/9)s3 = 90;v3 = 0;a3 = 0;回程:(10*pi/9)< φ< ( 14*pi/9)s4 =45*(1+cos(9/4*(φ-10*pi/9)));v4 =-101.25*w*sin(9/4*(φ-10*pi/9)) ;a4 =-227.8*w^2* cos(9/4*(φ-10*pi/9)); 近休止程:(14*pi/9)< φ < ( 2*pi);s5 =0;v5 =0;a5 =0;1.由上述公式通过编程得到位移、速度、加速度曲线如下:(编程见附录).基圆半径为r0 = (50^2+100^2)0.5=112mm,偏距e = 50mm。
3.凸轮实际轮廓,理论轮廓,基圆,偏距圆绘制4.整体图像附录1.求位移、速度、加速度的程序(matlab)w = input('请输入W=');x = 0:(pi/1000):(pi/4);s1 = 73*x.^2;v1=146*w*x;a1 = 146*w.^2;y = (pi/4):(pi/1000):(pi/2);s2 =90-73*(pi/2-y).^2;v2=146*w*( pi/2-y);a2 =-146*w.^2;z = (pi/2 ):(pi/1000):(10*pi/9);s3 = 90;v3 = 0;a3 = 0;c = (10*pi/9):(pi/1000):( 14*pi/9);s4 =45*(1+cos(9/4*(c-10*pi/9)));v4 =-101.25*w*sin(9/4*( c-10*pi/9)) ;a4 =-227.8*w.^2* cos(9/4*(c-10*pi/9));d=(14*pi/9):(pi/1000):( 2*pi);s5 =0; v5 =0; a5 =0;subplot (2,2,1)plot(x,s1,'b',y,s2,'b',z,s3,'b',c,s4,'b', d,s5,'b');xlabel('转角/rad')ylabel('位移/(mm/s)')title('位移与转角曲线')grid onsubplot (2,2,2)plot(x,v1,'g',y,v2,'g',z,v3,'g ',c,v4,'g', d,v5,'g')ds4 =45*9/4*sin(9/4*(c-10*pi/9));d=(14*pi/9):(pi/1000):( 2*pi);s5 =0;ds5 =0;plot(ds1,s1,'b',ds2,s2,'b',ds3,s3,'b',ds4,s4,'b',ds5,s5,'b'); xlabel('ds/dp');ylabel('(位移s/mm)')title('ds/dp 与位移s曲线')grid onhold onx3=-150:0.001:0;y3 = 0.577*x3;plot (x3,y3,'r');hold onx1=-150:0.001:150;for i=1:1:250;k1=(s1(i+1)-s1(i))/ (ds1(i+1)-ds1(i));if(k1>=-1.733 && k1<=-1.731)y1=k1*(x1-ds1(i))+s1(i);plot (x1,y1,'r');end3.确定滚子半径(1)先求凸轮理论轮廓曲线,程序如下:Clc;clear;w = input('请输入w=');s0 = 100;s = 90;e = 50; x = 0:(pi/100):(pi/4);x1 = (s + s0)*cos(x)-e*sin(x);y1 = (s0 + s)*sin(x) - e*cos(x);y = (pi/4):(pi/100):(pi/2);x2 = (s + s0)*cos(y)-e*sin(y);y2 = (s0 + s)*sin(y) - e*cos(y);z = (pi/2 ):(pi/100):(10*pi/9);x3 = (s + s0)*cos(z)-e*sin(z);y3 = (s0 + s)*sin(z) - e*cos(z);c = (10*pi/9):(pi/1000):( 14*pi/9);x4 = (s + s0)*cos(c)-e*sin(c);y4 = (s0 + s)*sin(c) - e*cos(c);d=(14*pi/9):(pi/1000):( 2*pi);x5 = (s + s0)*cos(d)-e*sin(d);y5 = (s0 + s)*sin(d) - e*cos(d);plot(x1,y1,'b',x2,y2,'b',x3,y3,'b',x4,y4,'b',x5,y5,'b');xlabel('x/mm')ylabel('y/mm')title('理论轮廓曲线')grid on(2)理论轮廓线最小曲率半径编程代码:由下程序结果可知pmin =81.6667这里滚子半径为 r r < pmin-ΔΔ=3~5mm;取r r=10mm;clear;clc;v=[];syms x1 x2 x3 x4 x5s0 = 100;e = 50;s1 = 73*x1.^2;t1 = (s1 + s0)*cos(x1)-e*sin(x1);y1 = (s0 + s1)*sin(x1) - e*cos(x1);tx1=diff(t1,x1);txx1=diff(t1,x1,2);yx1=diff(y1,x1);yxx1=diff(y1,x1,2);for xx1= 0:(pi/100):(pi/4);k1=subs(abs((tx1*yxx1-txx1*yx1)/(tx1^2+yx1^2)^1.5),{x1},{xx1}); v=[v,1/k1];ends2 =90-73*(pi/2-x2).^2;t2 = (s2 + s0)*cos(x2)-e*sin(x2);y2 = (s0 + s2)*sin(x2) - e*cos(x2);tx2=diff(t2,x2);txx2=diff(t2,x2,2);yx2=diff(y2,x2);yxx2=diff(y2,x2,2);for xx2=(pi/4):(pi/100):(pi/2);k2=subs(abs((tx2*yxx2-txx2*yx2)/(tx2^2+yx2^2)^1.5),{x2},{xx2});k4=subs(abs((tx4*yxx4-txx4*yx4)/(tx4^2+yx4^2)^1.5),{x4},{xx4}); v=[v,1/k4];ends5 =0;t5 = (s5 + s0)*cos(x5)-e*sin(x5);y5 = (s0 + s5)*sin(x5) - e*cos(x5);tx5=diff(t5,x5);txx5=diff(t5,x5,2);yx5=diff(y5,x5);yxx5=diff(y5,x5,2);for xx5=(10*pi/9):(pi/100):( 4*pi/3);k5=subs(abs((tx5*yxx5-txx5*yx5)/(tx5^2+yx5^2)^1.5),{x5},{xx5}); v=[v,1/k5];endpmin=min(v)4.绘制凸轮轮廓曲线clear ;clc;syms x y z c dw= input('请输入w=');n3 = diff(x3);m3 = diff(y3);xt3= subs(x3 + (r*m3)./sqrt(m3.^2+n3.^2),z,zz);yt3 = subs(y3 - (r*n3)./sqrt(m3.^2+n3.^2),z,zz);cc= (10*pi/9):(pi/1000):( 14*pi/9);s4 =45*(1+cos(9/4*(c-10*pi/9)));x4 = (s4 + s0).*cos(c)-e*sin(c);y4 = (s0 +s4).*sin(c) - e*cos(c);n4 = diff(x4);m4 = diff(y4);xt4= subs(x4 + (r*m4)./sqrt(m4.^2+n4.^2),c,cc);yt4 =subs( y4 - (r*n4)./sqrt(m4.^2+n4.^2),c,cc);dd=(14*pi/9):(pi/1000):( 2*pi);s5 =0;x5 = (s5 + s0).*cos(d)-e*sin(d);y5 = (s0 +s5).*sin(d) - e*cos(d);n5 = diff(x5);m5 = diff(y5);xt5= subs(x5 + (r*m5)./sqrt(m5.^2+n5.^2),d,dd);yt5 =subs( y5 - (r*n5)./sqrt(m5.^2+n5.^2),d,dd);plot(xt1,yt1,'b',xt2,yt2,'b',xt3,yt3,'b',xt4,yt4,'b',xt5,yt5,'b')for i=1:3601if yy(1,i)<=y0/2s(1,i)=2*h*(yy(i)./y0).^2;v(1,i)=4*h*w*yy(i)./(y0.^2);a(1,i)=4*h*w.^2./(y0.^2);elseif yy(1,i)>y0/2 && yy(1,i)<y0s(1,i)=h-2*h./y0.^2.*(y0-yy(i)).^2;v(1,i)=4*h*w*(y0-yy(i))./(y0.^2);a(1,i)=-4*h*w.^2./(y0.^2);elseif yy(1,i)>=y0 && yy(1,i)<y0+yss(1,i)=h;v(1,i)=0;a(1,i)=0;elseif yy(1,i)>=y0+ys && yy(1,i)<y0+ys+y01s(1,i)=h/2*(1+cos(pi/y01*(yy(1,i)-y0-ys)));v(1,i)=-pi*h*w/2/y01*sin(pi/y01*(yy(1,i)-y0-ys));a(1,i)=-pi^2*h*w^2/2/y01^2*cos(pi/y01*(yy(1,i)-y0-ys)); elseif yy(1,i)>=y0+ys+y01 && yy(1,i)<=360s(1,i)=0;v(1,i)=0;a(1,i)=0;subplot(2,3,5) ;plot(x,y,'r',xt,yt,eex,eey,'g',r0x,r0y,'k')%画图title('实际理论轮廓线')axis equal%使坐标轴比例相等grid on%画网格线。
MATLAB大作业

MATLAB⼤作业MATLAB⼤作业班级:姓名:学号:2014年4⽉24⽇MATLAB⼤作业——实现傅⾥叶级数的Gibbs现象⼀、要解决的问题及意义⽤MATLAB实现傅⾥叶级数的Gibbs现象,更为直观、具体、形象地认识并更为深⼊地了解Gibbs现象。
⼆、Gibbs现象的简单介绍Gibbs现象的来由⾃从法国数学家傅⾥叶(Fourier)发明了傅⾥叶级数,关于级数理论的研究随即⾛向了⼀个新时代的⾥程碑,傅⾥叶级数在纯粹数学、应⽤数学、物理,乃⾄⼯业应⽤上都取得了辉煌的成就,其优点是光滑性好,收敛条件要求低(尤其是⼤范围⼀致收敛⽐幂级数要求低得多),但是它也并不是完美⽆缺的。
19世纪末,美国数学家J.W.Gibbs在研究⼀个函数的三⾓级数展开时,发现了这种级数展开的缺点,即不只在被展开函数的不连续点处,甚⾄在该点附近,其傅⾥叶级数也不收敛到该函数,这就是著名的Gibbs(吉布斯)现象。
Gibbs 现象(⼜叫吉布斯效应)⼀般来说,将周期信号分解得到的三⾓函数形式的傅⾥叶级数的项数是⽆限的。
也就是说,通常只有⽆穷项的傅⾥叶级数才能与原函数精确相等。
但在实际应⽤中,显然⽆法取⾄⽆穷多项,⽽只能采⽤有限项级数来逼近⽆穷项级数。
⽽且,所取项数越多,有限项级数就越逼近原函数,原函数与有限项级数间的⽅均误差就越⼩,⽽且低次谐波分量的系数不会因为所取项数的增加⽽变化。
将具有不连续点的周期函数(如矩形脉冲)进⾏傅⽴叶级数展开后,选取有限项进⾏合成,当选取的项数越多,在所合成的波形中出现的峰起越靠近原信号的不连续点。
当选取的项数很⼤时,该峰起值趋于⼀个常数,⼤约等于总跳变值的9%。
这种现象称为吉布斯现象。
三、数学⽅法求解连续时间周期信号的傅⾥叶级数频域分析法即傅⾥叶分析法,它是变换域分析法的基⽯。
其中,傅⾥叶级数是变换域分析法的理论基础,傅⾥叶变换作为频域分析法的重要数学⼯具,具有明确的物理意义,在不同的领域得到⼴泛的应⽤。
哈工大matlab期末考试题试题及答案(95分)分解

春季学期MATLAB期末作业学院:机电工程学院专业:机械制造设计及其自动化学号:班号:姓名:2013年春季学期MATLAB 课程考查题姓名:学号:学院:机电学院专业:机械制造一、必答题:1.matlab常见的数据类型有哪些?各有什么特点?常量:具体不变的数字变量:会根据已知条件变化的数字字符串:由单引号括起来的简单文本复数:含有复数的数据2.MATLAB中有几种帮助的途径?(1)帮助浏览器:选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器;(2)help命令:在命令窗口键入“help”命令可以列出帮助主题,键入“help 函数名”可以得到指定函数的在线帮助信息;(3)lookfor命令:在命令窗口键入“lookfor 关键词”可以搜索出一系列与给定关键词相关的命令和函数(4)模糊查询:输入命令的前几个字母,然后按Tab键,就可以列出所有以这几个字母开始的命令和函数。
注意:lookfor和模糊查询查到的不是详细信息,通常还需要在确定了具体函数名称后用help命令显示详细信息。
3.Matlab常见的哪三种程序控制结构及包括的相应的语句?1.顺序结构:数据输入A=input(提示信息,选项)数据输出disp(X)数据输出fprintf(fid,format,variables)暂停pause 或pause(n)2.选择结构:If语句:if expression (条件)statements1(语句组1)elsestatements2(语句组2)EndSwitch 语句:switch expression (表达式)case value1 (表达式1)statement1(语句组1)case value2 (表达式2)statement2(语句组2)... ...case valuem (表达式m)statementm(语句组m)otherwisestatement (语句组)end3.循环结构:For循环:for variable=expression(循环变量)statement(循环体)endWhile循环:while expression (条件<循环判断语句>)statement(循环体)end4.命令文件与函数文件的主要区别是什么?命令文件:不接受输入参数,没有返回值,基于工作空间中的数据进行操作,自动完成需要花费很多时间的多步操作时使用。
matlab大作业实验报告

matlab大作业学号姓名:年级:专业:1、产生一个10 10的随机矩阵A,要求A中元素均为整数,范围[1,50]。
1)求出A中所有元素之和S,平均值M。
2)找到所有小于平均值,且能被3整除的元素。
3)绘制出A的二维纵向柱状图,横坐标为[8 5 9 1 2 3 4 7 10 13],条形宽度为0.7的“stacked”样式。
代码如下:clc,clear all,close allA=round(rand(10,10)*50);disp(A)S=sum(sum(A));P=mean(mean(A));disp(S)disp(P)disp('所有小于平均数且能被三整除的元素')XPS=H((mod(H,3)==0)&(H<P));disp(XPS')subplot(1,1,1),bar(A,0.7,'stacked'),title('ygh');set(gca,'XTickLabel',{'8','5','9','1','2','3','4','7','10','13'})2、产生一个随机四位密码。
用户用“input”进行输入对比。
猜错提示“WRONG”,正确提示“RIGHT”同时退出程序,最多五次机会。
代码如下:clc,clear all,close alldisp('请输入密码')A=round(8999*rand(1,1))+1000;m=1;while m<=5N=input('请输入一个四位数:');if A==N;disp('RIGHT');breakelsedisp('WRONG');endm=m+1;enddisp('密码是:')disp(A)disp('输入结束')3、按照脚本文件的编程风格,用for和while循环嵌套输出如下的乘法口诀表。
2014自写版Matlab 作业

1.利用循环语句,计算数列5,5,5,…的极限,要求误差小于10-8。
>> a=5;>> a1=sqrt(5);>> while((a-a1)>=10^(-8)) a=a1;a1=sqrt(a1); n=n+1; end>> vpa(a1,15) ans =1.00000000599562 >> n n =画图:>> n=1:1:29; >> x=n;>> y=5.^(0.5.^n); >> plot(x,y)2.利用级数⋯++=71-5131-14π可计算出无理数π的近似值。
由于交错数级的部分和数列S N 在级数的和上下摆动,截断误差将小于第一个被舍弃的项1+n a 的绝对值。
试分析,若要使截断误差小于10-4或10-8,应取多少项求和?计算π的近似值。
误差为10的-8次方:>> n=1;>> anspi=0;>> while((1/(1+2*(n-1)))>= (10^(-8)))anspi = anspi - 4*((-1)^n)*(1/(2*n-1));n=n+1;end>> vpa(anspi,8)ans =3.1415926>> nn =50000001舍去第50000001项,可使级数误差小于10的-8次方此时π有效值为3.1415926 误差为10的-4次方时:>> n=1;>> anspi=0;>> while((1/(1+2*(n-1)))>= (10^(-4)))anspi = anspi - 4*((-1)^n)*(1/(2*n-1));n=n+1;end>> vpa(anspi,8)ans =3.141>> nn =5001舍去第5001项,可使级数误差小于10的-4次方此时π有效值为3.141画图:>> n=1;>> anspi=0;>> while((1/(1+2*(n-1)))>= (10^(-4)))anspi = anspi - 4*((-1)^n)*(1/(2*n-1));plot(n,anspi);hold on;n=n+1;end;>>3.考虑梯形电阻电路的设计,电路如下:其中电路中的各个电流{i,2i,…,8i}须满足下列线性方程组:1R V i i =- 22 21 0 252321=-+-i i i 0 252 432=-+-i i i 0 252 543=-+-i i i 0 252 654=-+-i i i 0 252 765=-+-i i i 0 252 876=-+-i i i 052 87=+-i i这是一个三对角方程组。
MATLAB大作业

M A T L A B大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
90问题五:利用MATLAB软件绘制一朵鲜花,实现一定的仿真效果。
提示:二维/三维绘图,对花瓣、花蕊、叶片、花杆等的形状和颜色进行详细设置。
第二类:插值与拟合。
(B级)问题一:有人对汽车进行了一次实验,具体过程是,在行驶过程中先加速,然后再保持匀速行驶一段时间,接着再加速,然后再保持匀速,如此交替。
注意,整个实验过程中从未减速。
在一组时间段50个时间点的速度。
(2)绘制插值图形并标注样本点。
问题二:估算矩形平板各个位置的温度。
已知平板长为5m,宽为3m,平板上3×5栅格点上的温度值为44,25,20,24,30;42,21,20,23,38;25,23,19,27,40。
(1)分别使用最近点插值、线性插值和三次样条插值进行计算。
(2)用杆图标注样本点。
(3)绘制平板温度分布图。
对a,b,c,d的值。
提示:曲线拟合并绘图分析第三类:定积分问题。
(B级)问题一:地球密度随着离中心(r=0)距离的变化而变化,不同半径处的密度如表所示,试估问题二:河道平均流量Q(m3/s)可使用速度和深度的乘积的积分来计算(河道横截面不规则),公式如下。
其中V(x)是离岸x(m)距离处的水速(m/s),H(x)是离岸x距离处的水深(m)。
根据收集到过5(1(2(3(Q,单位是m(1(2(1(2(3)将节点1的力改为方向向上,计算这种改变对H2和V2的影响。
(4)将节点1的力撤销,而在节点1和2处施加1500N的水平外力,求节点3处垂直反作用力(V3)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年春季学期MATLAB 课程考查题姓名:学号:学院:专业:一.必答题(80分)1.如何设置当前目录和搜索路径,在当前目录上的文件和在搜索路径上的文件有何区别?(2)方法一:在MATLAB命令窗口中输入editpath或pathtool命令或通过【File】/|【SetPath】菜单,进入“设置搜索路径”对话框,通过该对话框编辑搜索路径。
方法二:在命令窗口执行“path(path,…D:\Study‟)”,然后通过“设置搜索路径”对话查看“D:\Study”是否在搜索路径中。
方法三:在命令窗口执行“addpathD:\Study-end”,将新的目录加到整个搜索路径的末尾。
如果将end改为begin,可以将新的目录加到整个搜索路径的开始。
区别:当前文件目录是正在运行的文件的目录,显示文件及文件夹的详细信息,且只有将文件设置为当前目录才能直接调用。
搜索路径中的文件可以来自多个不同目录,在调用时不用将其都设置为当前目录,为同时调用多个文件提供方便。
2.创建符号变量和符号表达式有哪几种方法?(4)(1)创建符号变量①单个符号变量函数symx = sym(‘x’) 创建x为符号变量,默认复数区域x = sym(‘x’, ‘real’) 创建实数的符号变量xx = (‘x’, ‘positive’) 创建正数的符号变量xx = sym('x', 'clear')创建一个没有额外属性的纯形式上的符号变量xs=sym(‘ab’,’flag’) 创建flag数域(复数,实数,正数)符号变量名s,内容ab②多个符号变量函数symssyms arg1 arg2 ...syms arg1 arg2 ... realsyms arg1 arg2 ... clearsyms arg1 arg2 ... positive 用这种格式定义符号变量时不要在变量名上加字符串分界符(‘),变量间用空格而不要用逗号分隔。
(2)创建符号表达式①直接法:x=sym('x');②整体定义法:f=sym(‘expression’)③字符串符号表达式:f=‘expression’3. GUIDE提供哪些常用的控件工具,各有什么功能?(5分)①按钮(Push Buttons):执行某种预定的功能或操作;②开关按钮(T oggle Button):产生一个动作并指示一个二进制状态(开或关),当鼠标点击它时按钮将下陷,并执行callback(回调函数)中指定的内容,再次点击,按钮复原,并再次执行callback 中的内容;③单选框(Radio Button):单个的单选框用来在两种状态之间切换,多个单选框组成一个单选框组时,用户只能在一组状态中选择单一的状态,或称为单选项;④复选框(Check Boxes):单个的复选框用来在两种状态之间切换,多个复选框组成一个复选框组时,可使用户在一组状态中作组合式的选择,或称为多选项;⑤文本编辑器(Editable T exts):用来使用键盘输入字符串的值,可以对编辑框中的内容进行编辑、删除和替换等操作;⑥静态文本框(Static T exts):仅用于显示单行的说明文字;⑦滚动条(Slider):可输入指定范围的数量值;⑧边框(Frames):在图形窗口圈出一块区域;⑨列表框(List Boxes):在其中定义一系列可供选择的字符串;⑩弹出式菜单(Popup Menus):让用户从一列菜单项中选择一项作为参数输入;⑩坐标轴(Axes):用于显示图形和图象。
4. 建立不同数据类型的变量:包括双精度的数值型(numeric)、符号型(sym)、结构体(structure)、单元型(cell)、字符串型(char),函数句柄(function handle)、逻辑型(logical),并且采用whos列出各变量名,变量的数组维数,占用字节数,变量的类别。
(4分)>> a=2*pia =6.2832>> whos aName Size Bytes Class Attributesa 1x1 8 double>> para=sym('para')para =para>> whos paraName Size Bytes Class Attributespara 1x1 112 sym>> b=[1,2;3,2]b =1 23 2>> whos bName Size Bytes Class Attributesb 2x2 32 doublec={pi,2,3*9}c =[3.1416] [2] [27]>> whos cName Size Bytes Class Attributesc 1x3 360 cell>> d='matlab class'd =matlab class>> whos dName Size Bytes Class Attributesd 1x12 24 charA.a1='asdw';>> A.a2=[1,2,2];>> A.a3=rand(2)A =a1: 'asdw'a2: [1 2 2]a3: [2x2 double]>> whos AName Size Bytes Class AttributesA 1x1 592 struct>> e=@(x)x+1e =@(x)x+1>> whos eName Size Bytes Class Attributes e 1x1 32 function_handle>> f=b.^2<5f =1 1 0 1 >> whos fName Size Bytes Class Attributes f 2x2 4 logical5. 求⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=728365219a 矩阵的秩,迹,特征值和特征向量,并且对矩阵进行LU 分解、QR 分解及Chollesky 分解(3分)。
>> a=[9,1,2;5,6,3;8,2,7] a =9 1 2 5 6 3 8 2 7 >> rank(a) ans = 3 >> trace(a) ans = 22 >> eig(a) ans = 13.5482 4.8303 3.6216 >> [V ,D]=eig(a) V =-0.4330 -0.2543 -0.1744 -0.5657 0.9660 -0.6091 -0.7018 0.0472 0.7736 D =13.5482 0 00 4.8303 00 0 3.6216 >> [L,U,P]=lu(a)L =1.0000 0 00.5556 1.0000 00.8889 0.2041 1.0000 U =9.0000 1.0000 2.00000 5.4444 1.88890 0 4.8367 P =1 0 00 1 00 0 1>> [Q,R,E]=qr(a)Q =-0.6903 0.3969 -0.6050-0.3835 -0.9097 -0.1592-0.6136 0.1221 0.7801 R =-13.0384 -4.2183 -6.82600 -4.8172 -1.08070 0 3.7733E =1 0 00 1 00 0 1>> R=chol(a)R =3.0000 0.3333 0.6667 0 2.4267 1.1447 0 0 2.2903 6. 执行矩阵A 和B⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321,136782078451220124B A 下列的运算:A+5*cos(B)、A.*B 、 A*B 、A./B 、B.\A 、A/B, B\A ,分别解释数组运算和矩阵运算的区别。
(4分) A=[4,12,20;12,45,78;20,78,136]; >> B=[1,2,3;4,5,6;7,8,9]; c=A+5*B c =9 22 35 32 70 108 55 118 181 >> d=A.*B d =4 24 60 48 225 468 140 624 1224 >> e=A*B e =192 228 264 738 873 1008 1284 1518 1752 >> A./B ans =4.0000 6.0000 6.6667 3.0000 9.0000 13.00002.8571 9.7500 15.1111>> B.\Aans =4.0000 6.0000 6.66673.0000 9.0000 13.00002.8571 9.7500 15.1111>> A/Bans =8.6667 0 -0.66674.5000 64.0000 -35.5000128.3333 -128.0000 57.6667>> B\Aans =11.3333 24.5000 65.6667-18.6667 -28.0000 -93.333310.0000 14.5000 47.0000区别:运算符功能运算符功能+ 相加- 相减* 矩阵相乘. * 数组相乘^ 矩阵乘方.^ 数组乘方\ 矩阵左除.\ 数组左除/ 矩阵右除./ 数组右除7.求半径为r的圆的面积和周长,分别采用脚本文件和函数文件进行编写, r值由input指令从键盘给出,数据的输出采用disp指令;并且说明脚本式文件和函数文件的特点。
(5分)脚本文件:clear;r=input('Please enter the r=:');s=pi*r*r;l=2*pi*r;a=[s,l];disp(['area= ',num2str(a(1)),'parameter=',num2str(a(2))]); 函数文件:function [s,p]=fcircle(r)%CIRCLE calculate the area and perimeter of a circle of radii r%r 圆半径 %s 圆面积 %p 圆周长 s=pi*r*r; p=2*pi*r; end 特点:脚本式M 文件不接受输入参数,没有返回值。
基于matlab 基本工作空间中的数据进行操作,存储在工作空间,属于全局变量。
