柳钉-材料非线性分析
铆钉有限元分析
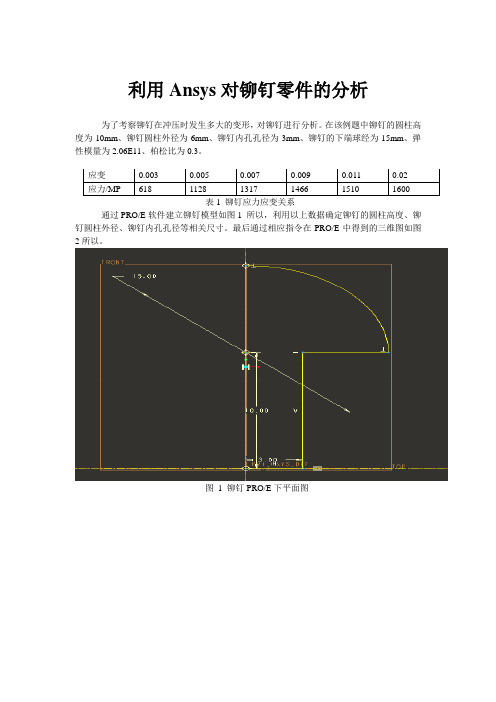
利用Ansys 对铆钉零件的分析 为了考察铆钉在冲压时发生多大的变形,对铆钉进行分析。
在该例题中铆钉的圆柱高度为10mm 、铆钉圆柱外径为6mm 、铆钉内孔孔径为3mm 、铆钉的下端球经为15mm 、弹性模量为2.06E11、柏松比为0.3。
表1 铆钉应力应变关系通过PRO/E 软件建立铆钉模型如图1 所以,利用以上数据确定铆钉的圆柱高度、铆钉圆柱外径、铆钉内孔孔径等相关尺寸。
最后通过相应指令在PRO/E 中得到的三维图如图2所以。
图 1 铆钉PRO/E 下平面图 应变0.003 0.005 0.007 0.009 0.011 0.02 应力/MP 618 1128 1317 1466 1510 1600图2 铆钉PRO/E下三维图在这里铆钉的PRO/E模型就已经建立好了,接下来需要把铆钉模型导入到Ansys中,为了实现利用ANSYS对PRO/E生成的铆钉实体模型进行模态分析,需要将PRO/E生成的模型导入ANSYS,把PRO/E的PART文件转换为ANSYS可识别的文件最常用的方法主要有以下2种。
第一种利用IGES格式文件进行数据交换,IGES是由ANSI.美国国家标准局公布为美国标准的,它以ASCII或二进制的形式存储图像,可以在不同的CAD系统间进行数据交换。
作为一种中间标准格式,IGES目前已经得到广泛的应用。
Ansys软件本身就设置了IGES转换过滤器,它支持IGES格式的数据文件输入。
而在PRO/E中也可以很方便的将建立的PART文件保存为IGES的格式。
因此通过IGES格式进行这两个软件之间的数据转换是比较常用的方法,而且比较容易实现。
虽然IGES作为一种常用的数据交换形式已经得到大部分人的认可,但是也存在一些问题,对于一些PRO/E生成的简单模型利用IGES格式可以很方便的导人到ANSYS中去,并且不会发生丢失线、面的失真现象,但是对于一些复杂的模型,利用这种格式导入后就容易丢失线、面而出现失真现象,继而影响分析结果。
柳钉-材料非线性分析

ANSYS工程软件课程设计—————柳钉-材料非线性分析姓名:韩晓宇班级:工程力学10-01班学号:100107020002指导教师:杜国君学院:建筑工程与力学学院【引言】塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力-应变关系是线性的。
另外,大多数材料在其应力低于屈服点时,表现为弹性行为,也就是说,当移走载荷时,其应变也会完全消失。
由于材料的屈服点和比例极限相差很小,因此ANSYS程序中,假定它们相同。
在应力-应变的曲线中,低于屈服点的叫做弹性部分,超过屈服点的叫做塑性部分,也叫做应变强化部分。
塑性分析中考虑了塑性区域的材料特性。
当材料中的应力超过屈服点时,塑性被激活。
本例通过对柳钉的冲压进行应力分析,来介绍ANSYS塑性问题的分析过程。
【问题分析】为了考查柳钉在冲压时,发生多大的变形,对柳钉进行分析。
柳钉如图2-1所示:柳钉圆柱高:10mm柳钉圆柱外径:6 mm柳钉内孔直径:3 mm柳钉下端球径:15 mm弹性模量:2.06E11图2-1泊松比:0.3柳钉材料的应力应变关系如表2-2所示:表2-2应力应变关系【GUI操作】1:设定分析作业名和标题:输入文件名liuding,工作标题为plastic analysis of a part。
2:定义单元类型:选用实体、八节点四面体单元SOLID45>Brick 8node 45。
3:定义实常数:选用三维的SOLID45单元,不需要设置实常数。
中必须定义材料的应力应变关系,首先要定义材料属性,选择结构线弹性各向同性,EX=2.06e11,PRXY=0.3。
再打开定义材料应力应变对话框,将条件中的应力应变关系输入进去,如图2-3为显示的材料的曲线关系。
5:建立实体模型,划分网格:如图2-4为模型图,2-2为化分的网格图。
图2-4柳钉模型图图2-5柳钉划分网格图6:定义边界条件并求解:本例中,载荷为上圆环形表面的位移载荷,位移边界条件是下半球面上所有方向的位移固定。
工程力学中的非线性分析方法有哪些?

工程力学中的非线性分析方法有哪些?在工程力学领域,非线性问题的研究至关重要。
与线性问题相比,非线性问题更加复杂,需要采用专门的分析方法来准确描述和解决。
下面我们就来探讨一下工程力学中常见的非线性分析方法。
首先要提到的是有限元法。
这是一种非常强大且广泛应用的数值分析方法。
在处理非线性问题时,它能够有效地模拟材料的非线性行为,比如塑性、蠕变等。
通过将复杂的结构离散为有限个单元,并对每个单元进行分析,最终得到整个结构的响应。
对于几何非线性问题,如大变形、大转动等,有限元法能够通过更新坐标和刚度矩阵来准确捕捉结构的变化。
而对于材料非线性,如弹塑性问题,通过定义合适的本构关系,可以精确地模拟材料在不同应力状态下的行为。
再来看看边界元法。
它是另一种有效的数值方法,特别适用于处理无限域或半无限域问题。
在非线性分析中,边界元法可以结合迭代算法来求解非线性边界条件或非线性材料特性。
与有限元法相比,边界元法通常只需要对边界进行离散,从而降低了问题的维数,减少了计算量。
但在处理复杂的非线性问题时,其数学推导和编程实现可能会相对复杂。
还有一种方法是摄动法。
这是一种基于微扰理论的分析方法。
对于弱非线性问题,通过将非线性项视为对线性问题的小扰动,将问题的解表示为一个级数形式。
通过求解这个级数的各项,可以逐步逼近非线性问题的精确解。
摄动法在处理一些简单的非线性问题时非常有效,但对于强非线性问题,其精度可能会受到限制。
接下来是增量法。
在处理非线性问题时,将加载过程或变形过程分成一系列的小增量。
在每个增量步内,将问题近似为线性问题进行求解,然后逐步累加得到最终的结果。
这种方法适用于各种非线性问题,尤其是在考虑加载历史和路径相关性的情况下。
非线性有限差分法也是常用的手段之一。
它直接对控制方程进行离散,通过差分近似来表示导数项。
在处理非线性问题时,可以采用迭代的方式求解离散后的方程组。
这种方法对于简单的几何形状和边界条件的问题较为适用,但对于复杂的结构可能会面临网格划分和精度控制的挑战。
材料力学的非线性行为分析

材料力学的非线性行为分析材料力学是研究材料在外力作用下的变形和破坏行为的科学,非线性行为是指材料在受力作用时呈现出的非线性特性,即力与应变不成比例关系。
在许多工程和科学领域中,对材料力学的非线性行为进行准确和全面的分析具有重要意义。
本文将着重讨论非线性行为的基本概念、常见的非线性模型以及分析方法。
一、非线性行为的基本概念在材料力学中,强度、刚度、屈服点等参数通常被用来描述材料的特性。
然而,当外力增大到一定程度时,材料的性质将不再呈现线性关系,这时就出现了非线性行为。
非线性行为主要包括弹性-塑性行为、接触-分离行为以及材料的损伤和断裂等。
二、非线性模型的选择1. 弹塑性模型弹塑性模型是描述材料弹性和塑性变形的常用模型。
其中,最经典的是von Mises屈服准则,常用于金属的塑性变形分析。
2. 黏弹性模型黏弹性模型主要用于描述粘弹性材料的非线性行为,包括粘性和弹性两个部分。
常见的黏弹性模型有Kelvin模型和Maxwell模型。
3. 损伤模型损伤模型用于描述材料在加载过程中的损伤积累和破坏行为。
常用的损伤模型有弹塑性损伤模型、粘弹性损伤模型以及断裂力学模型等。
三、非线性行为的分析方法1. 实验测试实验测试是分析材料非线性行为最直接的方法之一。
通过应力-应变测试、拉伸试验等,可以获得材料在不同应力下的应变,进而建立非线性模型。
2. 数值计算数值计算是通过数学方法对材料力学进行模拟和计算的重要手段。
常用的数值计算方法有有限元法、边界元法、网格法等。
通过设定材料的非线性模型及边界条件,可以得到材料的应力分布和变形情况。
非线性分析的结果可用于工程设计、材料选用以及破坏预测等方面。
但是在进行非线性分析时,需要注意模型的参数选择、模型的适用性以及计算误差等因素。
总之,非线性行为是材料力学中重要的研究内容,对于理解材料的变形和破坏行为具有重要意义。
通过选择合适的非线性模型和分析方法,我们可以准确地描述和预测材料的非线性行为,为工程实践和科学研究提供有力支持。
多钉剪力连接件非线性有限元分析

WANQingyun,XUEDongyan ,PANZhihong,MAWengang
(SchoolofCivilEngineeringandArchitecture,JiangsuUniversityofScienceandTechnology,Zhenjiang212003,China)
数模型公式:P=Pu(1-e-αs)β,其中:Pu 为极限 承 载力,s为相对滑移,α和 β分别是试验拟合的参 数.该类函数能较好地模拟推出试验的结果,因而
收稿日期:2018-01-08 修回日期:2018-05-09 作者简介:宛青云(1991—),男,硕士研究生 通信作者:薛东焱(1976—),男,博士,高级工程师,研究方向为组合结构桥梁.Email:dyxue2008@163.com 引文格式:宛青云,薛东焱,潘志宏,等.多钉剪力连接件非线性有限元分析[J].江苏科技大学学报(自然科学版),2019,33(5):104-109.
剪力连接件是钢 -混凝土组合结构的关键构 造,是确保组合结构协同工作的重要保障.焊钉连 接件由于受力各向同性、构造简单、施工方便而应 用广泛.焊钉连接件的力学性能主要通过推出试验 获得,国内外学者针对焊钉推出试验做了大量的研
究工作. 文献[1]根 据 Fra bibliotek 验 结 果 提 出 了 焊 钉 承 载 力 指
DOI:10.11917/j.issn.1673-4807.2019.05.016.
第 5期 宛青云,等:多钉剪力连接件非线性有限元分析
105
获得广泛采用.文献[2]针对焊钉不同间距的情况 进行了推出试验研究,得出分别适用于单钉和多钉 的荷载 -滑移关系表达式.文献[3]运用 ABAQUS 软件进行有限元分析,焊钉和混凝土之间采用绑定 连接的方式,较好地模拟了推出试验的结果.文献 [4]对推出试验施加横向力情况下,进行了试验和 有限元分析,该种情况下焊钉的抗剪承载力有所提 高,但对滑移 影 响 很 小.文 献 [5]在 试 验 的 基 础 上 对混凝土等级、焊钉的直径和配筋率等参数的影响 进行了模拟分析,得到影响抗剪承载力的因素,其 中混凝土等级,焊钉屈服强度,焊钉直径等影响较 大.
有限元第七章材料非线性问题的有限元

第七章 材料非线性问题的有限元法7.1 引 言前面各章所讲述的问题,都属于线性变形体系。
所谓线性变形体系是指位移与载荷呈线性关系的体系,而且当载荷全部撤除后,体系将完全恢复原始状态。
这种体系也称为线性弹性体系,它需满足下列条件:(1)材料的应力与应变关系满足虎克定律:(2)位移是微小的;(3)所有约束均为理想约束。
在分析线性弹性体系时,可以按照体系变形前的几何位置和形状建立平衡方程,并且可以应用叠加原理。
根据这种理论建立起来的方程是线性的,对于小应变和小位移的情形这种分析是适用的。
实际结构的位移与载荷可以不呈线性关系,这样的体系称为非线性变形体系。
如果体系的非线性是由于材料应力与应变关系的非线性引起的,则称为材料非线性,如材料的弹塑性性质、松驰、徐变等。
如果结构的变位使体系的受力发生了显著的变化,以至不能采用线性体系的分析方法时就称为几何非线性,如结构的大变形、大挠度的问题等。
还有一类非线性问题是边界条件非线性,或状态非线性,如各种接触问题等。
但本书只讨论前两类非线性问题的有限元解法,即材料非线性和几何非线性问题的有限元解法,对接触问题的有限元解法,读者可参考其它书籍。
材料非线性问题的处理相对比较简单,通常不必修改整个问题的表达式,而只需将应力—应变关系线性化,求解一系列的线性问题,并通过某种校正方法,最终将材料特性调整到满足给定的木构关系,从而获得了问题的解。
对于几何非线性问题,那就需要对公式进行根本的修改,这个问题将在后面详细讨论,不过应该指出,用于求解材料非线性问题的基本迭代方法也同样适用于几何非线性问题的求解。
事实上,有些工程结构问题同时具有这两类非线性性质,它们可以统一地加以处理。
本章将首先介绍用有限元方法处理非线问题的一般方法,然后讨论这些方法在非线性弹性、弹塑性和蠕变问题中的应用。
在介绍弹塑性问题的处理方法前,为便于讨论,需扼要叙述一下Mises 屈服准则和Prandtl-Reuss 塑性流动理论,并据此写出弹塑性矩阵表达式。
结构设计知识:钢结构的非线性分析与设计

结构设计知识:钢结构的非线性分析与设计钢结构在建筑设计中广泛应用,具有较高的承载能力和抗震性能。
然而,在极端荷载作用下,其受力性能会发生非线性变化,需要进行
非线性分析与设计,以保证结构的安全可靠性。
钢结构的非线性分析主要包括几何非线性、材料非线性和接触非
线性。
其中,几何非线性是指在大变形情况下,结构的剪切、变形、
轻度扭曲等非线性变化;材料非线性是指在材料受到荷载作用后出现
的弹塑性行为,包括本构关系非线性和材料应力应变非线性;接触非
线性是指结构中存在的各种接触面,如焊接连接点、螺栓连接点等,
在荷载作用下出现的非线性变化。
在进行非线性分析时,需要先进行静力分析,确定结构的初始状态,并对荷载进行合理的分析与计算。
随后,对结构进行荷载施加,
观察结构的变形情况,并根据实际情况进行修正和调整,直到得出结
构的稳定状态和极限承载能力。
钢结构的非线性设计需要考虑多种因素,包括荷载的类型、结构的材料和几何形状、结构的初始状态等。
在考虑这些因素时,需要采用合理的数学模型和计算方法,以确保结构的安全可靠性。
值得注意的是,钢结构的非线性分析和设计对于结构的构造和安装也有一定的要求。
必须确保结构的零件尺寸、零件精度和装配质量符合标准要求,以最大程度地保证结构的承载能力和安全性。
综上所述,钢结构的非线性分析和设计是保障结构安全性和承载能力的一项重要工作。
其核心在于充分考虑各种非线性因素,并采用合理的方法和模型进行分析和计算。
只有真正做到了这些,才能够确保钢结构的安全可靠性。
AnsysWorkbench工程应用之——结构非线性(中):材料非线性(1)弹塑篇

AnsysWorkbench工程应用之——结构非线性(中):材料非线性(1)弹塑篇本文结合材料知识与工程应用,从理论到实践,从书本到实操、从动脑到动手,保姆式手把手介绍非线性材料本构使用方法!这也可能是您在网上能找到的关于Ansys Workbench非线性材料蕞啰嗦(xiangxi)的一篇基础性文章。
材料的应力应变关系一般用材料本构来表示,本构模型又称材料的力学本构方程,或材料的应力-应变模型,是描述材料的力学特性(应力-应变-强度-时间关系)的数学表达式。
Ansys Workbench提供了丰富的非线性材料本构,用户也可基于试验数据定义自己的非线性材料。
材料的响应与载荷或变形施加的速率无关的材料称为率不相关材料,如弹塑性、超弹性(橡胶等)、混凝土等材料,大多数金属在低温(≤30%左右的熔点)和低应变速率时,为率无关材料,通常所说的塑性也就是率无关塑性。
材料的响应与载荷或变形施加的速率相关的材料称为率相关材料,如蠕变、黏弹性材料等。
材料的应力应变曲线也称为材料的响应曲线,是通过材料试验得到的,主要材料试验有单轴试验、等双轴试验、平面剪切试验、体积试验、松散试验等。
最常见的为单轴试验,可以测试拉伸也可以测试压缩,下图为某些塑形材料单轴拉伸试验的工程应力应变曲线。
1 率无关塑形1.1 基本理论1.1.1 比例极限与屈服极限结构的塑性响应基于单轴实验结果获得。
通过单轴应力-应变实验,可以得到材料的比例极限、屈服极限(或弹性极限)、应变强化。
对于塑形材料,当应力小于比例极限时,材料呈现线性; 当应力小于屈服点时,材料呈弹性,载荷卸除后,所有应变可以完全恢复;当应力大于屈服点时,材料呈塑性,载荷卸除后,应变不能完全恢复。
由于比例极限和屈服点非常接近,有限元软件假设两者值相等。
1.1.2 应力应变的工程曲线与真实曲线您一定很好奇,为什么材料力学课本中的塑形材料σ-ε曲线有下降段,而有限元分析软件中设置塑形材料不定义下降段,这不是因为忽然误差,而是因为材料力学课本上使用的是工程σ-ε曲线,也称名义应力-应变曲线,而有限元计算中往往使用切线斜率直线代替真实σ-ε曲线,他们的关系如下图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ANSYS工程软件课程设计
—————柳钉-材料非线性分析
姓名:韩晓宇
班级:工程力学10-01班
学号:100107020002
指导教师:杜国君
学院:建筑工程与力学学院
【引言】塑性是一种在某种给定载荷下,材料产生永久变形的材料特性,对大多的工程材料来说,当其应力低于比例极限时,应力-应变关系是线性的。
另外,大多数材料在其应力低于屈服点时,表现为弹性行为,也就是说,当移走载荷时,其应变也会完全消失。
由于材料的屈服点和比例极限相差很小,因此ANSYS程序中,假定它们相同。
在应力-应变的曲线中,低于屈服点的叫做弹性部分,超过屈服点的叫做塑性部分,也叫做应变强化部分。
塑性分析中考虑了塑性区域的材料特性。
当材料中的应力超过屈服点时,塑性被激活。
本例通过对柳钉的冲压进行应力分析,来介绍ANSYS塑性问题的分析过程。
【问题分析】
为了考查柳钉在冲压时,发生多大的变形,对柳钉进行分析。
柳
钉如图2-1所示:
柳钉圆柱高:10mm
柳钉圆柱外径:6 mm
柳钉内孔直径:3 mm
柳钉下端球径:15 mm
弹性模量:2.06E11图2-1
泊松比:0.3柳钉材料的应力应变关系如表2-2所示:
表2-2应力应变关系
【GUI操作】
1:设定分析作业名和标题:输入文件名liuding,工作标题为plastic analysis of a part。
2:定义单元类型:选用实体、八节点四面体单元SOLID45>Brick 8node 45。
3:定义实常数:选用三维的SOLID45单元,不需要设置实常数。
中必须定义材料的应力应变关
系,首先要定义材料属性,选择
结构线弹性各向同性,
EX=2.06e11,PRXY=0.3。
再打开定义材料应力应变对话框,将条件中的应力应变关系输入进去,如图2-3为显示的材料的曲线关系。
5:建立实体模型,划分网格:如图2-4为模型图,2-2为化分的
网格图。
图2-4柳钉模型图图2-5柳钉划分网格图6:定义边界条件并求解:本例中,载荷为上圆环形表面的位移载荷,位移边界条件是下半球面上所有方向的位移固定。
【查看结果】
图2-6Y 方向变形图 图2-7von mises 应变分析图。
