chapter05 一室开放模型:口服吸收的药动学
《药物动力学概述》PPT课件

二、发展概况
• 1913年,Michaelis和Menten首先提出了药物在生 物体内随时间而变化的动力学问题。
• 1919年,Widmark利用数学公式对体内药物的动态 变化数据进行了相应分析,并于1924年与Tandbery 共同构建了动力学模型的雏形,提出了开放式单室 动力学模型。
• 1937年,生理学家Torsten Teorell提出了二室模型 假设,并用数学公式详细描述了二室模型动力学规 律,发表了“物质进入机体的分布动力学”论文, 更为明确地分析了药物在生物体内的动力学过程, 初步奠定了药物动力学研究的理论基础和基本方法。
• 建立药物动力学模型 • 预测不同给药方案下的血浆、组织和尿液的药物浓度 • 探讨药物浓度与药物疗效或毒性之间的关系 • 估算药物和/或代谢物的可能蓄积 • 探讨药物结构与药动学及药效学之间的关系 • 探讨药物剂型因素与药物动力学规律的关系,开发新
型给药系统 • 根据药物动力学参数进行临床药物治疗方案的制定 • 以药物动力学观点和方法进行药物质量的认识和评价 • 新药的生物利用度和生物等效性研究
• 表观分布容积(apparent distribution volume, Vd)
• 体内药量与血药浓度间相互关系的一个比 例常数
• 假设体内的药物按血浆浓度分布时,所需 要体液的理论容积
• Vd = A(总药量)/ C0(初始血药浓度)
• Vd不是机体中真正的容积数值,只是一种 比例因素
血浆3L
第三节 药物动力学的基本概念
一、药动学模型
(一)房室模型 compartment model
整个机体视为一个系统,并将该系统按动 力学特征划分为若干个房室,把机体看成 是由若干个房室组成的一个完整的系统, 称为房室模型。
药动力学与给药问题的建模(一室模型和二室模型) 数学专业毕业论文

摘要随着社会的发展和人民生活水平的提高,医药卫生水平逐渐成了反映民生的一个重要指标,对临床上用药的要求也越来越高.大量研究表明,药物在完整的机体中,随着时间变化不断地进行着吸收、分布、转化和排泄,而且始终都处在一种动态变化的过程中.在临床上为了提高疗效,避免毒副作用,必然要求对这种动态变化的过程进行准确的刻画,而给药模型的建立就是为了解决这一问题,所以给药问题模型的建立、求解与分析有重要的理论与应用价值.本文首先介绍了药物动力学的基本概念,并根据药物的动力学原理建立了一室模型、两室模型,并对模型进行了分析与求解,求出了反映药物动力变化的主要参数值,然后根据计算结果给出了给药方案.最后本文详细的阐述了多次血管外重复给药模型的建立与求解,并根据卡那霉素肌注实验结果,继而把实验测得值与模型求得的理论值进行比较,从而来验证模型的正确性与可靠性.关键词:给药;建模;临床;模拟;验证AbstractWith the development of society and the improvement of people's living standard, medicine and health gradually became an important index which reflects people's livelihood, and the requirements for clinical medicine become much higher. A mass of research indicate that drugs in the whole body is carrying on the absorption, distribution, transformation and excretion as the time by, and always in a dynamic state. It is generally difficult for us to accurately describe the dynamic changes of the process. In clinic in order to improve the curative effect, avoid toxic effect. It is must to accurately describe the dynamic changes of the process and the establishment of dosing model is to solve this problem, so establishment and solution and analysis of give medicine model have important theory and application value.This paper firstly introduces the basic concept of pharmacokinetics, and according to the principle of dynamics drugs established one compartment model, two compartment model , then we do some analyzes and solving on the model, and get the main parameter value which reflect the dynamic changes of drugs ,then according to the calculation result gives dosing. Finally the paper expatiates outside blood-vessel many times repeat administration model establishment and solving, and according to kanamycin muscle note experimental results, and the experimental measurement value and the theoretical model for comparison, thus to validate the accuracy and reliability of the model.Keywords: Give medicine modeling; Clinical; Simulation; Application; Development摘要 (I)Abstract (II)引言 (1)1 药动力学的基本知识 (2)1.1药物浓度变化 (2)1.2药物的消除类型在体内的代谢方式 (2)1.3房室模型的基本概念 (3)1.4药物代谢动力学的主要参数 (3)1.5表观分布容积 (5)1.6半衰期 (5)1.7清除率 (6)1.8多次给药的时间-药物浓度曲线和稳态浓度 (6)2 给药模型 (7)2.1一室模型的单剂量给药方案 (7)2.1.1单次快速静脉注射给药 (7)2.1.2恒速静脉注射给药 (9)2.2两室模型 (13)2.2.1 两室模型药物静脉注射给药 (13)2.2.2 各种动力学参数的计算 (15)3 多次血管外给药方案 (17)3.1一室开放模型的药代动力学 (17)3.2二室开放模型药代动力学 (19)3.3卡那霉素肌注给药方案的制定 (21)结束语 (24)参考文献 (25)致谢 (26)建模是研究很多实际问题重要手段和前提.凡是用模型描述事物的因果关系或相互关系的过程都属于建模.由于临床上人体内的血药浓度随人体的代谢呈动态变化,所以我们一般通过模型来模拟人体血药浓度的变化.通过对药物代谢规律的分析,根据药物代谢的机理来建模;也可以通过实验或统计数据的处理,并根据我们已有的知识和经验来建模.在当代随着医药水平的提高,药物品种日益增加,但临床上滥用和不合理用药亦日益增多,临床药物治疗水平在某些方面并没有随着药品品种的增加而有较大提高,由于滥用或不合理用药,临床不断出现严重的医疗事故或引起药源性疾病.在建模和医药的共同发展下,一门新的学科药动力学产生了, 我国药动学较系统的研究始于陈琼华教授1963年对单味中药大黄的体内过程的研究其发展经历3个阶段:一阶段( 1949-1970年) ,主要进行活性成分的体内过程研究,但未应用现代药动学理论,对实验数据作动力学分析;二阶段(1970-990年) ,药动学迅速发展,相关论文大幅增加,更多高灵敏的现代分析仪器和测定方法的应用,在有效成分的药动学研究中动力学模型理论广泛开展,如丹参、人参、银杏叶等的药动学研究资料已在文献中有阐述.新药审评办法对新药药动学研究要求的提高促进药动学发展;三阶段(1990年至今) ,药动学作为一门新兴学科正在形成.新理论、新学说如证治药动学嘲、辨证药动学、复方散弹理论等涌现,极大丰富了中药药动学研究.药物动力学是定量研究药物在生物体内吸收、分布、排泄和代谢随时间变化的过程的一门学科,它的发展对药物评价,新药设计,药物剂型改进,临床指导合理用药,以及优化给药方案等具有重大的实用价值.药物动力学模型是为了定量研究药物体内过程的速度规律而建立的模拟数学模型,常用的有房室模型和生理药动学模型.通过房室模型可以分析药物在人身体的运行情况,得到药物在血液中的浓度变化(即血药浓度),从而给出最佳给药方式及血药浓度的峰值时间.这样就可以选择最佳治疗方案.而生理药动学模型则主要用于预测药物在器官组织中药物浓度及代经时过程和药物处置在动物间的外推.本文主要是根据药动力学原理进行数学建模,进而对模型进行求解,再根据求解结果,设计出合理的给药方案.1 药动力学的基本知识大量研究表明,药物在完整的机体中,随着时间变化不断地进行着吸收、分布、转化和排泄,而且始终都处在一种动态变化的过程中.我们一般很难准确地描述这种动态变化的过程,因此常借用时间-药物浓度曲线图的测定,并选定数学模型,用特定的数学公式或计算机程序软件测算出一系列药代动力学参数,通过这些参数既可从各个侧面反映药物在体内变化的动态过程,还可借以指导临床设计或调整给药方案(如确定给药的剂量、给药的途径以及给药的间隔时间等),真正做到合理用药.现将药代动力学的一些基本概念和主要药代动力学参数介绍如下:1.1 药物浓度变化用药后,药物在体内是不断地吸收、分布、转化和排泄的,血药浓度随着时间的推移也不断发生着变化,刚开始主要以吸收为主,与此同时,分布及少量的代谢和排泄也已开始进行;当代谢和排泄过程逐渐占主要地位后,药物浓度就开始下降.由此可见药物的吸收、分布、转化和排泄其实并没有严格的分界线,只是在某段时间内以哪一过程为主而已.一般我们通过药物浓度的测定,画出近似的时间-浓度曲线,我们可采用计算机程序测算出一系列药代动力学参数,以反映药物在体内吸收、分布、转化与排泄的规律和特点.1.2 药物的消除类型在体内的代谢方式药物消除类型药物在体内的消除方式,按其速率可归纳为以下三种类型:(1)一级消除动力学(first-order elimination kinetics )又称恒比消除,即单位时间内,药物总是按血药浓度的恒定比例进行消除,其消除速率总是与血药浓度成正比.大多数药物的消除都属于一级动力学消除.而且药物吸收、分布中的被药物运动,也是按照一级动力学方式进行的.一级动力学的方程式:01/C K C K dt dc e e -=-=.式中,dt dc /表示药物消除速率,e K 为一级消除速率常数(即恒定比例),负号表示药物浓度下降,0C 为消除初始时药物浓度.(2)零级消除动力学(zero-order elimination kinetics ) 又称恒量消除,即单位时间内,药物始终以一个恒定的数量进行消除,其消除与血药浓度无关.完全属于零级动力学消除的药物甚少,但药物吸收、分布中的主动转运及易化扩散则多是按零级动力学方式进行的.零级动力学的方程式:000K C K dc/dt -=-=.式中,dtK为零级消除速率常数,因为C的指数为零,所以消dc/表示药物消除速率,除与血药浓度无关.(3)米氏消除动力学(Michaelis-Menten elimination kinetics)是指包括零级和一级动力学消除在内的混合型消除方式.如当药物剂量急剧增加或患者有某些疾病(如肝、肾功能不全),或与其他药物配伍使用等情况时,药物在体内达到一定浓度后,会出现饱和现象(肝药酶代谢药物的能力达到饱和),消除方式则可从一级动力学消除转变为零级动力学消除,苯妥英钠、普萘洛尔、苯海拉明、保泰松、乙醇等少数药物的消除就可出现这种情况.如当乙醇在血液中浓度ml.0<时,按一级动力学消除;但当05mg/.005>时,则可转成按零级动力学消除.零级消除动力学和米氏消除动力学又合mg/ml称非线性消除动力学(nonlinear elimination kinetics).1.3房室模型的基本概念为预测药物在体内的动力学过程,我们可以从数学的角度把机体概念化为一个系统,并按动力学的特点将系统分为若干房室(compartments)来进行研究,称为房室模型.这个房室只是从数学的角度提出的一个抽象概念,与生理学上实际的体液房室概念不同.根据房室数目组成的不同,又可将其分为一室开放模型和多室开放模型.我们可根据不同的模型类型,采用不同的计算式或计算机程序包来估算出特定的药代动力学参数,供临床用药参考.对于一个具体药物的研究来说,准确地判定和选择模型类型是进行药代动力学分析的关键,因为不同类型的模型,将采用不同的计算式来估算其特定的药代动力学参数.下面仅介绍一室开放模型和二室开放模型的基本概念:(1)一室开放模型(one open-compartment model)是假定机体是由一个房室组成,且药物在其中的消除速率也始终一致的模型.如一个药物单次快速静脉注射给药后,可见该药迅速均匀分布到机体各部位,并迅即达到动态平衡,同时药物的消除速率也始终一致,我们就认为该药物的体内动力学过程属一室开放模型.(2)二室开放模型(two open-compartment model)是假定机体是由两个房室组成(即中央室与周边室),并有二种速率消除的模型.如一个药物单次快速静脉注射给药后,可见该药首先分布到中央室(指血液和血流供应丰富的组织,如肾、脑、心、肝等),然后再转而分布到周边室(指血流供应较少的组织,如脂肪、肌肉、皮肤、骨、软骨等),并且二者的消除速率也不一致,我们就认为该药物的体内动力学过程属二室开放模型.1.4 药物代谢动力学的主要参数根据时间-药物浓度曲线,采用相应的药代动力学计算机程序包进行数学处理,可估算出药物在体内吸收、分布、转化和排泄等相关的若干药代动力学参数(pharmacokinetic parameters ),以反映药物在体内的动力学规律和特点.常用的药代动力学参数有:(1)药峰时间(max C )和药峰浓度(max C )药峰时间(max T )是指用药以后,血药浓度达到峰值所需的时间.药峰时间短,表示药物吸收快、起效迅速,但消除也快;药峰时间长,则表明药物吸收和起效较慢,但作用持续时间也较长.药峰时间是研究药物制剂的一个重要指标. 药峰浓度(max C )又称峰值(peak value ),是指用药后所能达到的最高血药浓度.药峰浓度与药物的临床应用密切相关,药峰浓度要达到有效浓度才能显效,但若高出安全范围则可表现为毒性反应.(2)时量曲线下面积(area under the time concentration curve,AUC )又称曲线下面积,是指由坐标横轴与时间-药物浓度曲线围成的面积.它代表一段时间内,血液中的药物的相对累积量,也是研究药物制剂的一个重要指标其单位 为μg/ml.h,通常采用梯形法计算,计算公式:211)/t (t )C (C C A n n n n -⋅-=== .(3)生物利用度(bioavailability,a fraction of dose,F )生物利用度是指血管外给药时,药物吸收进入血液循环的相对数量.生物利用度也是评价药物制剂质量的一个十分重要的指标.通常用吸收百分率表示,即给药量与吸收进入体循环的药量的比值(见式①):%100F ⨯=给药量吸收进入体循环的药量(生物利用度) , ① 生物利用度也可用C A 参数表示,其计算公式如式②:(绝对生物利用度)(血管内给药)(血管外给药)(生物利用度)%100C A C A F ⨯= . ② 生物利用度还可提供试品的C A 与标准品的C A 的比值表示,叫做生物利用度(见式③):(相对生物利用度)(标准品)(供试药)(生物利用度)%100C A C A F ⨯= , ③相对F 是评价厂家产品质量的重要标准之一.如果制剂质量不合格,生物利用度低,临床疗效肯定差.一般药典上都规定药厂生产的制剂,生物利用度的差距不应超过±10%.1.5 表观分布容积表观分布容积(apparent volume of distribution,d V )是指药物在理论上应占有的体液容积量(以L 或L/kg 为单位).是一个计算所得的理论数值,而并非指药物在体内所实际占有的体液真正容积,也不代表某个特定的生理空间,故称为表观分布容积.d V 值的大小可反映药物在体内分布的广泛程度,它常用体内药物总量与血药浓度的比值来表示:其计算公式:)/(/)(L mg C mg A V d =.其中A 为体内药物的总量,C 为血药浓度.一般来说,d V 值的大小除可反映药物在体内分布的广泛程度,还可间接反映药物排泄的快慢和在体内存留时间的长短.我们还可以利用d V 值和血浆药物浓度,来推算体内药物的总量或求得为达到某血药浓度所需药物的总量.1.6 半衰期根据药物的体内过程不同,半衰期(half life,t1/2)有吸收半衰期,分布半衰期和消除半衰期之分.一般讲半衰期就是消除半衰期,即指血浆中药物浓度下降一半所需的时间. 2/1t 是反映药物在体内消除一个重要的药代动力学参数.绝大多数药物的消除过程属于一级消除动力学参数,因此半衰期总是一个固定值,它不受血药浓度高低的影响,而取决于药物消除速率常数(K )它们的关系为:k t /693.02/1=,2/1t 因药而异,例如青霉素0.5h,吗啡3h,阿司匹林6h,地高辛36h,苯巴比妥5日,洋地黄毒苷9日.了解2/1t 有助于设计最佳给药间隔、预计停药后药物从体内消除的时间及连续给药后达到稳态血药浓度所需时间.除少数2/1t 很短、很长的药物或零级消除动力学药物外,按2/1t 设计给药间隔时间是安全、有效的给药方法.按2/1t 的长短不同可将药物分为5类:超短效,2/1t 为≤1h ;短效,2/1t 为1~4 h ;中效,2/1t 为4~8 h ;长效,2/1t 为8~24 h ;超长效,2/1t 为>24 h.1.7清除率该概念来自生理学中的肌酐清除率(clearance,CL ),是药物消除速率的另一种表示方法.CL 是指单位时间内有多少表观分布容积(d V )的药物被清除,其单位为min /ml .CL 仅表示药从血清中清除的速率,并不是被清除药物的具体量.其计算公式:k V CL d ⋅=.式中K 为消除速率常数,d V 为表观分布容积.大多数药物在体内主要是通过肝代谢和肾排泄而清除,因此,药物的总清除率相当于肝清除率和肾清除率的总和.1.8多次给药的时间- 药物浓度曲线和稳态浓度根据临床治疗的需要,大多数药物均需多次给药,属于一级动力学消除的药物如每隔一个2/1t 等量给药一次,则经过5~7个2/1t 血药浓度可达到一个稳定状态(此时给药量与消除量达到相对的动态平衡),称稳态浓度(steady state concentration, ss C )或称坪值(plateau )若能将稳态浓度的波动控制在有效治疗血药浓度范围内是最理想的状况.稳态浓度也是临床多次给药时一个非常重要的药代动力学指标,其计算公式:TV FD t T V FDt T V K FD C d d d e ss 2/1443.1693.0/2/1===. 式中,D 为每次用药剂量(mg/kg ),T ,F 为用药间隔时间,e K 为消除速率常数,F 为生物利用度.总之,药物代谢动力学的研究不仅可以帮助我们了解药物在体内的吸收、分布、转化和排泄的规律及特点,同时还可以通过时间-药物浓度曲线的定及药代动力学参数的估算,来推算给药剂量和制定最佳给药方案,为临床合理用药提供理论和实际的依据.2 给药模型下面我们以一些模型的给药方案为例做简单介绍2.1 一室模型的单剂量给药方案少数的药物如镇痛药,催眠药,麻醉药,支气管扩张药等通常只需一次给药,而药物的转运速率属于一级速度过程,故可应用下面的给药方案,通过计算又可为拟定多次给药方案打下基础.2.1.1 单次快速静脉注射给药1.血药浓度变化规律:因药物系一室模型药物,并按一级速度过程消除,所以当一次快速静脉注射给药后,药物立即迅速分布到血液及各组织,并达到动态平衡,它的消除速度可由下列微分方程表示出来:kX dtdx -=, 式中:dt dx /表示体内的药物消除速率;X 为体内药量;k 为一级消除速率常数:负号表示体内药物量X 随时间的推移不断减小.将上式进行分离变量后作不定积分⎰-=dt k dtdx , 代入初始条件(00X ,X t ==)得指数方程:kt e X X -=0,上式的血药浓度方程式:kt e C C -=0.对kt e C C -=0从0=t 至∞=t 间作定积分得曲线下面积(C A ).K C K C K e C dt e C cdt ktkt 0000000)1(0=⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-==⎰⎰∞--, 对kt e C C -=0的对数方程式为:0ln ln C Kt C +-=,亦即K..K C 69303032log =-=, 由上式可推导出21/t t =时,20/C C =则得出K.K l /t n 6930221==. 2.其它参数的求法,求及K 的值;(1)当静脉注射给药后,测得不同时间i t 的血药浓度i c (n i ⋅⋅⋅⋅⋅⋅⋅⋅=3,2,1),列表,然后用最小二乘法作直线回归,可得斜率及截距,而求出K 及0C .(2)21/t 及C A 的求法已入前述.(3)表观分布容积的求法,应用00/C X V d =式即可求得. (4)体内总清除率(TBCL )的求法,用数学式表示TBCL :C/-dtdx TBCL =, 将KX dtdx-=式代入上式为:C KX TBCL =,再将aV xC =代入上式为: a aKV V ==KXT BCL . 由上式可知药物体内的总消除率是消除速度常数与表观分布容积的乘积. 另外:因为K C C A 0=,将aV XC 00=代入上式,得 aa KV XV C A 00K X == ,将上式代入a KV TBCL =式中 则ACX TBCL 0=. 因此可求出不同形式表达的TBCL 公式,便于灵活运用.2.1.2 恒速静脉注射给药静脉滴注给药在临床上应用很广泛,特别是在危重病人抢救时,是一种有效的给药方法,另外还有许多药物如去甲肾上腺素以及抗生素等由于治疗指数小,或半衰期短,都应采用静脉滴注给药,以维持恒定的有效血药浓度. 1.药物浓度的变化规律:以剂量为0X 的药物,在T 时间内,以恒定的速率0K 静脉注射入人体内.在滴注时间T 内,体内除有消除过程外,同时还存在一个恒速增加药量的过程,只有当滴注完毕后,体内才仅有消除过程,因此这个模型包括两个方面,一方面以恒速0K 进入体内,另一方面以K 即一级速度从体内消除,因此,药物的变化速度应该是这两部分的代数和,用微分方程表示为:KX0-=K dtdx解微分方程,进行分离变量因为: )——(—K KX K K 00=有Kdt K K x dx =-0不定积分⎰⎰=--dt X dxK KK 0 得C Kt K K X ln ln 0+-=⎪⎭⎫ ⎝⎛-即kt -0Ce KK X =—(1) 当将初始条件:0,0==X t ,代入上式,求得积分常数C 为:KK C 0—= 将C 代入(1)式:kt e -00KKK K X ——= kte KK K K X --=00)e (KK X kt --=10(2) 将(2)式两端同除以V 得)e (VKK C -kt -=10(3) (3)式即为单式模型静脉滴注给药,体内血液浓度与时间t 的函数关系式. 2.静脉滴注给药时的稳态血液浓度(ss C )以血液浓度C 为纵坐标,时间t 为横坐标作图,得以静脉滴注的C---t 曲线,滴注开始后一段时间内, C 随t 的增大,急剧增大,而后一段时间增大程度越来越少,逐渐减慢,最后几乎不再增加而保持一个恒定的浓度值,此值称为“稳态血液浓度” (ss C )或称“坪浓度”,此时体内药物的消除浓度等于药物输入浓度.根据(3)式,当∞→t 时, kt e -趋于0而(kt e -—1)趋于1则可得到稳态血药浓度公式如下:VKk C ss 0=, (4) 由上式可以看出ss C 的大小与0K 成正比,与K 成反比,滴注速度愈大,稳态血药浓度将更大.恒速静脉滴注给药方案设计的主要问题是根据临床期望达到有效血药浓度算出滴注速率,由以上探讨可得:CL C ss =0K , (5) 或VK C K ss =0, (6)或214410t .VK/K K ss =. (7)3.达坪浓度某一分数所需的半衰期数本节的含义是在体内药物达到某一浓度时,通过血液浓度值,来计算所需要的半衰期方法.因为不论哪一种药物,在体内达到某一个血液浓度时,所需要的半衰期是一致的,与药物半衰期的长短无关.4.静脉滴注的负荷剂量问题临床上常将药物的有效治疗浓度决定为稳态水平,而要达到稳态的90%~99%,则需3.32~6.64个半衰期的时间,例如中等半衰期为四小时的药物达到稳态90%则需要13.3h,所以一般半衰期大于0.5h 的药物,可先由静脉注射一个剂量的药物,使血药浓度达到或接近ss C 的95%,而这个剂量叫“负荷剂量”然后立即恒速静滴,维持血药浓度,可以用以下几种方法:(1)先静脉注射,后静脉滴注给药;即先静注一个较大剂量,使血药浓度接近稳态或达到稳态浓度,随后进行恒速静滴来维持血药浓度,在先前静注的剂量即为“负荷剂量”负荷剂量可用下式计算V C X ss =*0, (8)式中*0X 为负荷剂量静脉滴注速度为VK C ss =0K (9) 同时快速静注与静脉滴注给药后体内药量应为两式之和,即)1(X 0-*0kt kte KK e X --+=. (10) 将(9)式代入(8)式,得,/K 0*0K X =再代入上式,则KKe K K e K K X kt kt 000)1(=-+=-- (11) 而血药浓度则为ss C KVK C 0==. 根据上面的方案,可使血药浓度及体内药量在整个过程中保持恒定,血药浓度一直维持在稳态血药水平.(1) 先进行快速滴注,后进行慢速滴注给药.本法为先以滴注速度01K 作快速滴注,经t 时间后,达到所需的治疗浓度,再以速度0K 作慢速滴注,维持治疗稳态水平(ss C )kte K K --=1101, (12)VK C K ss =0.(2) 简易计算负荷剂量法,达到ss C 所需的负荷剂量应为ss VC X =*0 ,KK X 0*0=, 217.02144.1/2/1693.0*0*0**00t X t X t X K X K ====.由上可知,负荷剂量静脉滴注速率与药物消除速率的比值,若负荷剂量的70%被半衰期去除.并以此量按每小时滴注,即可维持负荷量所达到的浓度,负荷量可按一次或几次快速静脉注射投予. 5.静脉滴注停止后求动力学参数(1)在0K 确定的情况下,求静脉滴注停止时的V 及K ,0K 确定时,可用VKK C ss 0=求V ,此时需先测出ss C 值, 也可用),1(0kt e VKK C --=,以C 对作图,其斜率为KV K /0,解出V 即可,用上述方法求V ,其数值理论上与0C X V =求出的相等.求K 时,先停止滴注,任其血液浓度自然下降,测出下降过程中几个不同时间的血药浓度,即的t C -log 关系直线,此线的斜率303.2K 0-=K ,所以K 即可求出, 稳态后停滴,求K V '值.当达到稳态水平而停滴后,血药浓度的变化速度可用下面的微分方程表示:kc dt dc-= 解上述微分方程,分离变量后作不定积分,并代入初始条件(0'=t ,KVc 0K =),得 kte KVK C -=0 (13) 其对数式为KVK t KC 0log '303.2log +-= (14) 式中't 为停滴后时间.根据(14)式,若计算参数K 与V 值,可在停滴后的不同时间取血样测定血药浓度,以C log 对't 作图,可得一直线,该直线的斜率为303.2K-,可求得K 值,截距为)/log(K 0KV ,若已知K ,0K 可求出V 值.a)稳态前停滴,求K V 值b)达到稳态前停止滴注,血药浓度的变化的微分方程式:kc dtdc-=, 该微分方程,初始条件为0'=t ,)1KVK-0kt e C —(=,t 为滴注时间则得下式: '-0)1KVK C kt kt e e -=—(. 其对数式为()⎥⎦⎤⎢⎣⎡-+-=-kte KVKt K C 1log '303.2log 0 (15)式't 仍为停滞后时间根据(15)式停滴后测定血药浓度,以C log 对t 作图,得一直线(AB )由斜率可求得K 值,已知0K 及t 后可由截距求出V 值. 2.2 两室模型2.2.1 两室模型药物静脉注射给药 1.血药浓度变化规律本类药物在体内分布符合两室模型,但药物的消除仅在中央室,并按一级消除速率进行如下图.药物的室间交换速率亦符合一级,这种消除包括肝代谢,肾排泄,肺呼出等途径.同时,难于灌注的组织的外周室药量p X ,按一级转运速率常数21K 返回至中央室.此时中央室c X 的静变化速率等于上述这些过程的总和,可由下列微分方程组来表示:c c p tX K X K X K dtdX 101221--=, (1)p c p X K X K dtdX 2112-=. (2)(1)式和(2)式这两个一级线性微分方程是二房室模型的基本方程,解得:βt αt c e β)(α—ββ(K X e β)()K (X X -+-∂-∂=-210210. (3) 血药浓度与中央室的药量呈比例.c V 000C V X =为中央室分布容积,代入(3)式,得:。
药代动力学

2) 达到稳态某一分数所需要的时间长短取决于半衰期,
而与滴注速率无关。当时间相当于3.32t1/2,时,血药浓度 相当于稳态浓度的90%, 当时间相当于6.64t1/2时,血药 浓度相当于稳态浓度的99%。
3)已知期望血药浓度,可以确定静脉滴注速率k0
k0 Cssk.V
6
(二)开放式二室模型
药物
Ke(k10) 中央室
如预测安替比林的清除率仅为其他外展 数据的1/7
.
29
预测方法
前提条件 1,每个种属的PK均为一级动力学过程
2,蛋白结合率相似
3,有关浓度为线性
4,消除过程为物理性
5,有足够的数据回归
.
30
至少4种动物
将70kg体重代入方程 预测人
.
31
二、生理模型法
前提条件
假定药物的组织和血浆药物浓度的比(Kp)等在动 物间是不变的
CT ,ss C A,ss
消除性组织 2)面积法
Kp
CT,ss CA,ss(1 E)
非消除性组织
Kp
AUCT AUCA
消除性组织 药物的清除率
Kp
AUCT AUCA(1E)
Cli nt
Vmax,i K.m,i
体外肝微粒体酶促反
应求算酶活性参数
(Vmax,i,Km,i)
23
四、 种属间药物代谢的比例扩大 (动物种属间比放)
符合这种条件的药物被称为肝代谢活性限速药物(capacity -limited drug)或低摄取(l.ow extraction)药物,如华法林20
低摄取 华法林
高摄取 利多卡因
肝血流对肝清除率的影响
(实线代表正常时,虚线代表肝血流量减少时。
一室模型5

分析不同给药方式下血药浓度随时间的变化摘要建立一室模型,在一次给药与多次给药的情况下,分析快速静脉注射、恒速静脉滴注与口服(或肌肉注射)这三种给药方式下中心室内血药浓度随时间变化的规律,从而确定合适的给药方案。
针对问题一,一次给药时,在三种给药方式下,药物均以一级动力学消除,建立微分方程模型,由此得出血药浓度与时间的关系。
快速静脉注射时,血药浓度逐渐减少;恒速静脉滴注与口服(或肌肉注射)时,血药浓度先增后减。
利用MATLAB作图。
针对问题二,在快速静脉注射的多次重复给药方式下,首先由问题一的结论,利用数学归纳法写出多次给药时血药浓度与时间的关系。
增大首次给药剂量,令首次给药后,血药浓度达到最高安全浓度,令稳定状态时血药浓度的最大值小于等于最高安全浓度,血药浓度的最小值大于等于最低有效浓度,确定出符合题目要求的给药方案。
利用MATLAB作图。
针对问题三,在恒速静脉注射与口服或肌肉注射的多次重复给药方式下,首先根据问题一的结论,用数学归纳法写出多次给药时血药浓度与时间的关系。
在恒速静脉滴注方式下多次给药,用与问题二中相同的方法确定出使药效最好的给药方案。
通过分析不同给药方式下中心室内血药浓度随时间变化的规律,得到药效与给药方式、给药剂量以及给药间隔之间的关系。
一室模型可推广到多室模型,更准确的描述血药浓度的变化规律。
关键词一级消除动力学;血药浓度;微分方程;一室模型;稳态一.问题的重述药物在人体内,经过吸收、分布和代谢最终排出体外。
通常情况下,血药浓度对药物疗效有着很大影响:浓度太低不能达到预期的效果,浓度太高又可能导致药物中毒、副作用太强或造成浪费。
为了维持药品的疗效和保证机体的安全,则需血药浓度控制在一定范围之内。
现有问题如下:问题一:建立一室模型([1])(只有中心室),在快速静脉注射、恒速静脉滴注(持续时间为τ)和口服或肌肉注射3种给药方式下求解血药浓度,并画出血药浓度曲线的图形.问题二:在快速静脉注射的多次重复给药方式下,写出血药浓度表达式并作图.讨论怎样确定时间间隔和给予固定剂量,使血药浓度的变化满足上述要求(实际上为了简化起见,常采取加大首次剂量给药的方式,给出这种情况下的给药方案).问题三:在恒速静脉滴注和口服(或肌肉注射)的多次重复给药方式下,给出血药浓度变化的简图,并选择一种方式讨论确定时间间隔和每次给予固定剂量的问题。
药物动力学一室模型单室模型

=1-4h,庆大霉素,利多卡因,
红霉素,氟喹喹诺酮类;
3、中等消除类
t
1 2
=4-8h,四环素类;
4、慢速消除类
t
1 2
=8-24h,丙硫咪唑;
5、极慢消除类
t
1 2
>
24h,阿维菌素类药物。
部分药物在不同动物体内的消除半衰期见表2-4。
二 、 消 除 速 率 常 数 ( Elimination rate constant,K)
图2-1 快速静脉注射一室模型示意图 其中X0为给药剂量;X为血液中药量;t为变化时间;V为表观分 布容积;k为消除速率常数。
根据一室模型准则和示意图(图2-1)给出微分方程:
dx kx
dt
(2.1)
其中dx/dt为消除速率,x为快速注射经时间t的体内药量 ,负号代表药物从体内消除,消除速率常数k的单位为时间 的倒数(h-1),将上式两边进行变换和积分:
(二)求AUC方法
1、梯形法则(trapezoidal method) 非血管内给药血药浓度时间曲线下面积示意图见图3-5。
图3-5 药时曲线下面积示意图
根据梯形法则可知:
AUC
1 2
[(C1
C0 ) t1
(C2
C1 )(t2
t1 )
(C3
C2 )(t3
t2)
(C(n)
C(n1) )(t(n)
0.3
0.693
0.5
=0.97h-1
三 、 表 观 分 布 容 积 ( Apparent
distribution Volume,Vd)
(一)表观分布容积计算公式
定义:药物在体内分布达到平衡时,体内药量和血药浓度之
药代动力学数据

对药代动力学数据随时间变化的情况进行分析,如预测未来值。
数据分析方法
数据变换
对数据进行适当的数学变换,如对数转换、标准化等,以改善数据的分布特性和可比性。
数据清洗
对原始数据进行预处理,如缺失值填充、异常值处理等,以确保数据质量。
数据分组
根据研究目的和实验设计,将数据分成不同的组别或类别。
确保实验操作符合相关规范和标准,减少误差和偏差。
定期对分析仪器进行校准和维护,确保仪器性能稳定可靠。
数据质量控制
03
CHAPTER
药代动力学数据分析
对数据进行描述性统计,如求平均值、中位数、标准差等,以了解数据的分布情况。
描述性统计分析
假设检验
回归分析
时间序列分析
通过设定假设并进行检验,判断数据是否符合预期,如比较两组数据的差异是否具有统计学显著性。
组织分布法
通过测量组织中药物的分布情况来评估药物在体内的分布和靶向性。
微生物法
通过微生物转化或代谢药物来研究药物的理
准确记录每个时间点的药物浓度或代谢产物数据,并进行整理和分析。
测定
采用适当的分析方法对处理后的样品进行药物浓度或代谢产物的测定。
样品处理
对采集的样本进行预处理,如分离血浆、尿液或组织提取物等。
解读数据间的关系
分析药代动力学数据与其他数据之间的关系,如药物浓度与疗效之间的关系。
数据分析结果解读
04
CHAPTER
药代动力学数据应用
药物研发与优化
药代动力学数据可以揭示药物在体内的代谢过程,包括代谢产物的生成和排泄,有助于优化药物的代谢特性。
药物代谢
生物药剂学与药物动力学-口服药物的吸收

是指通过细胞膜的主动变形将药物摄入细胞内
或从细胞内释放到细胞外的转运过程。
入胞作用(endocytosis) 出胞作用(exocytosis)
胞饮作用(pinocytosis): 摄取的药物为溶解 物或液体
吞噬作用(phagocytosis):摄取的物质为大分子 或颗粒状物
回肠
6.5~7.5 200~350
盲肠/右结肠 5.5~7.5 90~150
左结肠/直肠 6.1~7.5
很大 较小
转运时间 0.5~3 (hr) 6 (sec) 1.5~7(hr)
14~80 (hr)
2020/6/15
17
(一) 胃
• 胃黏膜表面虽然有许多褶壁,但由于缺乏绒毛,吸
收面积有限,酸性药物可吸收。 • 成人每天分泌约2 L胃液。胃液含有以胃蛋白酶为主
2.细胞旁路通道转运 (paracellular pathway)
-是指一些小分子物质经过细胞间连接处的微孔进入体循环的 过程。 -小分子水溶性药物可通过该通道转运吸收。
2020/6/15
6
二、药物转运机制
药物跨膜转运机制示意图
2020/6/15
7
(一)被动转运
定义:被动转运(passive transport) 是指药物的膜 转运服从浓度梯度扩散原理,即从高浓度一侧向低浓度 一侧扩散的过程。
具有流动性。
2.膜结构的不对称性 膜的蛋白质、脂类
及糖类物质分布不对称。
3.膜结构的半透性 膜结构具有半透性,某
些药物能顺利通过,另一些药物则不能通过。
2020/6/15
5
(三)膜转运途径
药理学-药物体内速率过程
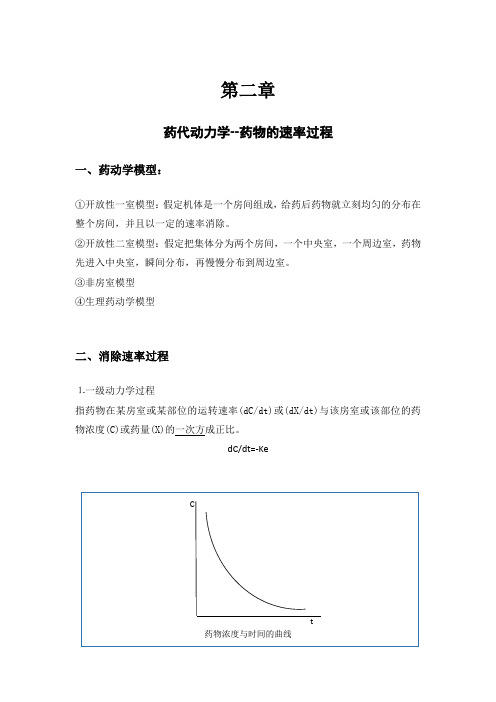
第二章药代动力学--药物的速率过程一、药动学模型:①开放性一室模型:假定机体是一个房间组成,给药后药物就立刻均匀的分布在整个房间,并且以一定的速率消除。
②开放性二室模型:假定把集体分为两个房间,一个中央室,一个周边室,药物先进入中央室,瞬间分布,再慢慢分布到周边室。
③非房室模型④生理药动学模型二、消除速率过程⒈一级动力学过程指药物在某房室或某部位的运转速率(dC/dt)或(dX/dt)与该房室或该部位的药物浓度(C)或药量(X)的一次方成正比。
dC/dt=-KeCt药物浓度与时间的曲线一级动力学过程属于被动转运,只要是按浓度梯度控制的简单扩散都符合一级动力学过程;一级动力学特点:①药物运转呈指数衰减,单位时间内运转的百分比不变,即等比运转,但单位时间内的运转量随着时间下降;②半衰期、总体清除率是恒定的,与计量和药物浓度无关;③血药浓度对时间曲线下的面积与所给的单一剂量成正比;④按相同剂量相同间隔时间给药,约经五个半衰期达到稳态浓度;约经五个半衰期,药物在体内消除接近完毕;⒉二级动力学过程 指药物自某房室或某部位的运转速率与该房室或该部位的药量或浓度的零次方成正比。
Ct药物浓度与时间的曲线C g药物浓度对数和时间曲线t斜率为-0K零级动力学过程属于主动转运,任何耗能的逆浓度梯度转运的药物,如乙醇、苯妥英钠、阿司匹林、双香豆素和丙磺舒都可以出现零级动力学过程。
零级动力学特点:①转运速度与剂量或浓度无关,按恒量转运,单位时间内运转的百分比是可变的; ②半衰期、总体清除率不恒定;加大剂量;半衰期超比例延长,总体清除率超比例减少;③血药浓度对时间曲线下的面积与剂量不成正比,剂量增加,其面积可超比例增加;⒊米-曼速率过程就是一级动力学与零级动力学互相移行的过程;此过程中高药物浓度时是零级动力学过程,低药物浓度时是一级动力学过程。
CK C V dt dC m m +-= 注:dt dC是指t 时的药物消耗速率,Vm 是该过程最大的速率常数,Km 表示消除速率达到Vm 一半时的药物浓度当药物浓度明显低于Km 时,C<<Km 时,C 可忽略不计当药物浓度明显高于Km 时,C>>Km 时,Km 可忽略不计三、药动学参数半衰期(2/1t ):血浆药物浓度下降一半时所需要的时间;是表述药物在体内消耗快慢的重要参数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dx k t Fk a x 0e a kx dt ka Fx 0 kat kt x C e e k ka
ka Fx 0 kt kat x (e e ) ka k
2014-10-10 6
将等式两边除以表观分布容积,则:
c
Cmax
ka Fx 0 kat kt C (e e ) Vd (ka k )
Ae
kt
c Ae
c
kat
log Ae
kt
kat
2.303
log A
式中 Ae kt 为外推浓度, c为实测浓度
Ae kt c 则为残数浓度(Cr)
lgCr对t是一条直线
2014-10-10
14
[例] 某单室模型药物溶液单次口服100mg,F=1,各时间 的血药浓度数据如下:
100
50 33.3 25 20
AUC
0
cdt
0
0
A e kt e kat dt
kat
A e kt e
dt
1 1 A k k a k a Fx 0 1 1 ka k Vd k ka
2014-10-10
12
ka FX 0 令A ka k Vd
C A(e
kt
e
kat
)
e kat 0
一般ka>>k 当t充分大时, 则上式变为:C
Ae
log A
kt
log c
kt
2.303
logc对t是一条直线
2014-10-10
13
残数浓度理论表达式根据上面的公式整理得到:
通常认为具有较大k值的药物不宜作为口服药品。 为了证明陡峭的曲线表示消除,必须给同一个病人做静脉注射给药,从 而得到真实的消除速度。
Ka(h-1)
0.1 0.2 0.3 0.4 0.5 0.6
K(h-1)
0.2 0.1 0.1 0.1 0.1 0.1
Tmax(h)
6.93 6.93 5.49 4.62 4.02 3.58
药物吸收和消除的模型:
X0
Xa(t)
吸收部位
ka
X(t); C; Vd
体内
k
Xa为t时吸收部位的药量 X为t时体内药量
ka为吸收速度常数
2014-10-10
3
Xa
k0
X(t); C; Vd
k
给药部位药物按照一级吸收速度过程进入体内(大 多数情况下是如此),则吸收部位,药物的吸收速 率与给药部位的药量成正比。即:
2014-10-10
11
5.4.1 残数法 残数法是药物动力学中把一条曲线分解为若干指数 成分的一种常用方法,该方法又可称为羽毛法 (feathering)或消去法(peeling)或消皮法 (stripping)及剩余法 凡是血药浓度曲线由多项指数式表示时,均可用残 数法逐个求出各指数项的参数
将上式对t求导数
dc 0 在t=Tmax时, dt
dc b 2at dt
b 2aTmax 0
Tmax
b 2a
a、b是用实验所得数据求得,取血药浓度最大值及其前后 各一个次大值,分别列出三个抛物线方程。从而求解三个 系数 用抛物线法计算Tmax,实际工作中应用是比较多的。 所得结果一般比较符合实际。
dx a k a x a F dt
xa x 0Fe
kat
2014-10-10
5
药物按照一级吸收过程进入体内,又按照一级过 程消除,且按单室分布。则:
dx k a x a kx dt
dx kat kx Fk a x 0e dt
ka Fx 0 常数:C k ka
Cmax(ug/ml) AUC(ug*h/ml)
2.50 5.00 5.77 6.29 6.69 6.99 50 100 100 100 100 100
0.3
0.3 0.3 0.3 0.3
0.1
0.2 0.3 0.4 0.5
5.49
4.05 3.33 2.88 2.55
5.77
4.44 3.68 3.16 2.79
2014-10-10 9
在已知ka、k时,将Tmax代入动力学方程中直接求得 抛物线法求出a、d、b及Tmax代入抛物线方程中可以求出
ka e kT k T k e a
C max
C max
max
e
kaT max
max
k kT e ka
max
代入
kT max k kTmax A e e k a
Fx 0 AUC kV d
CL kVd
2014-10-10 21
Ka反映的是多个个体速度过程的结果,包括药物崩 解释放、胃肠蠕动、血液流动和药物透膜传递等过 程。 根据经验选择零级或者一级吸收模型。 Ka和k用于预测多剂量给药时的峰、谷血药浓度。
什么是药物的吸收半衰期?怎样求得? 计算:两种药物A和B,口服给药500mg后具有下述 药物代谢动力学性质:A药,ka=1.0h-1,k=0.2h1,Vd=10L; B药,ka=0.2h-1,k=1h-1, Vd=20L;两种药物均符合一室模型,且100%被生 物体利用。计算两种药的达峰时间、峰值血药浓度。 药物消除依赖于剂量和药时曲线下面积,药物消除 会受药物吸收的影响吗?复习Ka与k对Tmax、 Cmax、AUC的影响。 思考:药物从静脉给药转为口服给药,最需要考虑 的事项是什么?
2014-10-10
17
有些口服制剂,服用后往往要经历一段时间才能吸 收 滞后时间是指给药开始至血液中开始出现药物的那 段时间,常用t0或Tlag表示。 考虑滞后时间以后,单室模型口服给药后血药浓度 与时间的关系式?如何求t0?
2014-10-10
18
有趣的例子:快速静注支气管扩张剂求得的k为1.72h-1,而口服给药后
ka Fx 0 ka k kT ( ) e (ka k ) Vd ka
max
C max
FX 0 kT e Vd
2014-10-10
max
10
已知某药物口服以后的生物利用度为80%, ka=1.0h-1, ke=0.1h-1, Vd=10L, 今服用该药物 剂量为250mg,试求:服药后3小时的血药浓度是 多少?设该药物在体内的最小有效浓度为10ug/ml, 问第二次服药时间最好不迟于第一次给药后几小时?
kTmax
0
ka e kT k T k e a
max
2.303 ka log ka k k
(达峰时间与ka和k有关)
2014-10-10
8
Tmax还可以用抛物线法求出,当ka、k不知时,可用实 验值求算。 对口服药时曲线,可列出以下抛物线方程
c d bt at 2
0.8
1.0
2.51
2.40
2.74
2.50
0.23
0.10
2014-10-10
16
残数法注意事项
◦ 用线性回归法,先应作散点图,确定对那些点进行回归处 理。 ◦ 用残数法求ka,必须在吸收相内测定足够的数据,至少有 三点。 ◦ 步骤:
作logc ~ t图 用消除相(曲线尾段)几个点作直线求k 直线外推得外推线,求吸收相各时间c1,c2,c3……在外推线 相应处的外推浓度C1外,C2外,C3外…… 外推浓度 — 实测浓度 = 残数浓度(cr) 作logcr ~ t图得残数线,从残数线的斜率求出ka。
t (h) c(ug/ ml) 0.2 1.65 0.4 2.33 0.6 2.55 0.8 2.51 1.0 2.40 1.5 2.00 2.5 1.27 4.0 0.66 5.0 0.39
求k、ka
2014-10-10
15
口服单室模型药物残数法数据表
时 间 (h ) 0.2 0.4 0.6 血 药 浓 度 (ug/ml) 1.65 2.33 2.55 外 推 浓 度 (ug/ml) 3.60 3.30 3.00 残 数 浓 度 (ug/ml) 1.95 0.97 0.45
这就是体内药物浓度c与t的关系
Tmax
t
上图为:口服药物血 药浓度与时间的关系
2014-10-10
7
C Ae
kt
kat
dc kat A kae ke kt 对t求导数 dt
dc 0 dt
max
在时间Tmax时,血药浓度达极大值,
kae kaT
Tmax
max
ke
算得的k只有0.7h-1,若用残数法估算ka,出乎意料ka竟为1.72h-1。
显然,用残数法求的k和ka可以互换。这个现象称为吸收和消除速度常数 的误换(flip-flop)。
大多数具有误换特性的药物是消除迅速的药物(即k>ka)。消除速度常
数大的药物(k>0.69h-1)的药物,其ka和k误换的机会要大得多。
