最新弹性力学基础(程尧舜-同济大学出版社)课后习题解答
弹性力学课后答案

弹性力学课后答案第二章习题的提示与答案2-1 是2-2 是2-3 按习题2-1分析。
2-4 按习题2-2分析。
2-5 在的条件中,将出现2、3阶微量。
当略去3阶微量后,得出的切应力互等定理完全相同。
2-6 同上题。
在平面问题中,考虑到3阶微量的精度时,所得出的平衡微分方程都相同。
其区别只是在3阶微量(即更高阶微量)上,可以略去不计。
2-7 应用的基本假定是:平衡微分方程和几何方程─连续性和小变形,物理方程─理想弹性体。
2-8 在大边界上,应分别列出两个精确的边界条件;在小边界(即次要边界)上,按照圣维南原理可列出3个积分的近似边界条件来代替。
2-9 在小边界OA边上,对于图2-15(a)、(b)问题的三个积分边界条件相同,因此,这两个问题为静力等效。
2-10 参见本章小结。
2-11 参见本章小结。
2-12 参见本章小结。
2-13 注意按应力求解时,在单连体中应力分量必须满足(1)平衡微分方程,(2)相容方程,(3)应力边界条件(假设 )。
2-14 见教科书。
2-15 2-16 见教科书。
见教科书。
2-17 取它们均满足平衡微分方程,相容方程及x=0和的应力边界条件,因此,它们是该问题的正确解答。
2-18 见教科书。
2-19 提示:求出任一点的位移分量和,及转动量,再令 ,便可得出。
第三章习题的提示与答案3-1 本题属于逆解法,已经给出了应力函数,可按逆解法步骤求解:(1)校核相容条件是否满足,(2)求应力,(3)推求出每一边上的面力从而得出这个应力函数所能解决的问题。
3-2 用逆解法求解。
由于本题中 l>>h, x=0,l 属于次要边界(小边界),可将小边界上的面力化为主矢量和主矩表示。
3-3 见3-1例题。
3-4 本题也属于逆解法的问题。
首先校核是否满足相容方程。
再由求出应力后,并求对应的面力。
本题的应力解答如习题3-10所示。
应力对应的面力是:主要边界:所以在边界上无剪切面力作用。
弹性力学教材习题及解答(供参考)
1 —1.选择题a. 下列材料中,_D_属于各向同性材料。
A. 竹材;B. 纤维增强复合材料;C. 玻璃钢;D. 沥青。
b. 关于弹性力学的正确认识是_A_。
A•计算力学在工程结构设计的中作用日益重要;B. 弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需要对问题作假设;C. 任何弹性变形材料都是弹性力学的研究对象;D. 弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析。
c. 弹性力学与材料力学的主要不同之处在于_B_。
A. 任务;B. 研究对象;C. 研究方法;D. 基本假设。
d. 所谓完全弹性体”是指_B_。
A. 材料应力应变关系满足胡克定律;B. 材料的应力应变关系与加载时间历史无关;C. 本构关系为非线性弹性关系;D. 应力应变关系满足线性弹性关系。
2—1.选择题a. 所谓应力状态”是指_B_。
A. 斜截面应力矢量与横截面应力矢量不同;B. 一点不同截面的应力随着截面方位变化而改变;C. 3个主应力作用平面相互垂直;D. 不同截面的应力不同,因此应力矢量是不可确定的。
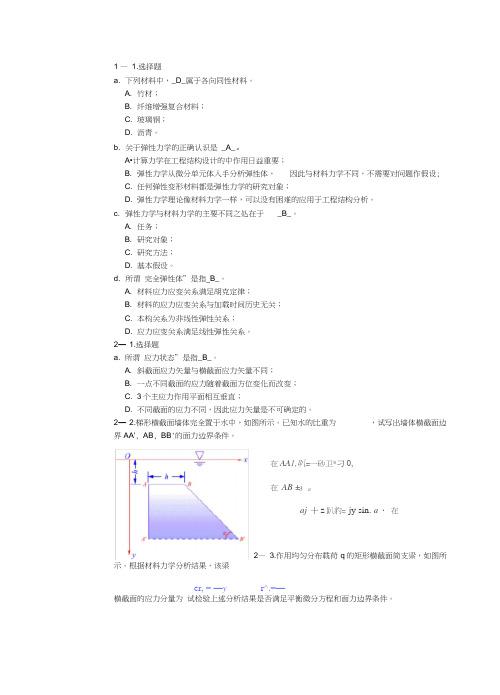
2—2.梯形横截面墙体完全置于水中,如图所示。
已知水的比重为,试写出墙体横截面边界AA', AB, BB'的面力边界条件。
在AA1,叭=一砂卫*刁0,在AB ±3 aaj十z趴豹=-jy sin. a、在2—3.作用均匀分布载荷q的矩形横截面简支梁,如图所示。
根据材料力学分析结果,该梁er, = —y r^.=—横截面的应力分量为试检验上述分析结果是否满足平衡微分方程和面力边界条件。
由此,只有当仃卩确罡.材料力学中所得轲的解答才能满足平衡方程和边界 条件’即芮満足弹性力学基本方程的解. 2 - 4.单位厚度的楔形体,材料比重为,楔形体左侧作用比重为的液体,如图所示。
试~ a x cos os - sin a,~ cos tz - tr^ sin tz y^y sin a 0 cos /? - sm 0=6 厂期cos 』一 cr 尸血厅=0.2- 5.已知球体的半径为r ,材料的密度为 1,球体在密度为 i ( 1 > 1)的液体中漂浮,如沉入複体割分 yj 面力F = -p 3g (z 0 - z ) 1边界条件为舌匕一卩”严严+ @ 一厂)% = 0-X% 十丁〔巧-51) +(z-f )r v = 0.肚迄+严疋*("尸)(务一耳)a 也来沉人液郎中的部分(珂 < 立< 2尸),边畀条件为开T ■*■尸欣斗仗一町% = °, f 十十住-尸打中=①6 +y^ 十仗“门口丁 550*写出楔形体的边界条件。
弹性力学基础(程尧舜-同济大学出版社)课后习题解答

弹性力学基础(程尧舜-同济大学出版社)课后习题解答2345(1)()T T ⨯=-⨯a A A a ,(2)()T T ⨯=-⨯A a a A 证:(1) ()()()T TT T ji i j k k ji i k jkn n A a A a e -⨯=-⊗⨯=-⊗A a e e e e e()T ji k jkn i n jn k jki i n A a e A a e =-⊗=-⊗e e e ek k jn j n a A =⨯⊗=⨯a A e e e 。
(2) ()()()T TT T i i kj j k kj i ijn n k a A A a e -⨯=-⨯⊗=-⊗a A e e e e e()nj i ijk n k nj n i jik k A a e A a e =-⊗=⊗e e e e nj n j i i A a =⊗⨯=⨯A a e e e2.10已知张量T 具有矩阵123[]456789=⎡⎤⎢⎥⎢⎥⎣⎦T求T 的对称和反对称部分及反对称部分的轴向矢量。
解:T 的对称部分具有矩阵1351([][])3572579T +=⎡⎤⎢⎥⎢⎥⎣⎦T T ,T 的反对称部分具有矩阵0121([][])1012210T ---=-⎡⎤⎢⎥⎢⎥⎣⎦T T 。
和反对称部分对应的轴向矢量为 1232=-+ωe e e 。
2.11已知二阶张量T 的矩阵为310[]130001-=-⎡⎤⎢⎥⎢⎥⎣⎦T求T 的特征值和特征矢量。
解:2310130(1)[(3)1]0001λλλλλ----=---=-由上式解得三个特征值为14λ=,22λ=,31λ=。
将求出的特征值代入书中的式(2.44),并利用式(2.45),可以求出三个特征矢量6为1121)2-a e ,121)2a e +e ,33=a e 。
2.12求下列两个二阶张量的特征值和特征矢量:αβ=+⊗A I m m ,=⊗+⊗B m n n m其中,α和β是实数,m 和n 是两个相互垂直的单位矢量。
弹性力学简明教程课后习题解答(精校版)

弹性力学简明教程(第四版)课后习题解答第一章绪论【1-1】试举例说明什么是均匀的各向异性体,什么是非均匀的各向同性体?【分析】均匀的各项异形体就是满足均匀性假定,但不满足各向同性假定;非均匀的各向异性体,就是不满足均匀性假定,但满足各向同性假定。
【解答】均匀的各项异形体如:竹材,木材。
非均匀的各向同性体如:混凝土。
【1-2】一般的混凝土构件和钢筋混凝土构件能否作为理想弹性体?一般的岩质地基和土质地基能否作为理想弹性体?【分析】能否作为理想弹性体,要判定能否满足四个假定:连续性,完全弹性,均匀性,各向同性假定。
【解答】一般的混凝土构件和土质地基可以作为理想弹性体;一般的钢筋混凝土构件和岩质地基不可以作为理想弹性体。
【1-3】五个基本假定在建立弹性力学基本方程时有什么作用?【解答】(1)连续性假定:假定物体是连续的,也就是假定整个物体的体积都被组成这个物体的介质所填满,不留下任何空隙。
引用这一假定后,物体的应力、形变和位移等物理量就可以看成是连续的。
因此,建立弹性力学的基本方程时就可以用坐标的连续函数来表示他们的变化规律。
完全弹性假定:假定物体是完全弹性的,即物体在对应形变的外力被去除后,能够完全恢复原型而无任何形变。
这一假定,还包含形变与引起形变的应力成正比的涵义,亦即两者之间是成线性关系的,即引用这一假定后,应力与形变服从胡克定律,从而使物理方程成为线性的方程,其弹性常数不随应力或形变的大小而变。
均匀性假定:假定物体是均匀的,即整个物体是由同一材料组成的,引用这一假定后整个物体的所有各部分才具有相同的弹性,所研究物体的内部各质点的物理性质都是相同的,因而物体的弹性常数不随位置坐标而变化。
各向同性假定:假定物体是各向同性的,即物体的弹性在所有各个方向都相同,引用此假定后,物体的弹性常数不随方向而变。
小变形假定:假定位移和变形是微小的。
亦即,假定物体受力以后整个物体所有各点的位移都远远小于物体原来的尺寸,而且应变和转角都远小于1。
弹性力学全程导学及习题全解

1-7 试画出题1-7图中的的矩形薄板的正的体力,面力和应力的方向。
注意:(1)无论在哪一个位置的体力,在哪一个边界面上的面力,均为沿坐标轴正方向为正,反之为负。
(2)边界面上的应力应是以在正坐标面上,方向沿坐标轴正方向为正,反之为负,在负坐标面上,方向沿坐标轴负方向为正,反之为负。
1-8 试画出题1—8图中的三角形薄板的正的面力和体力的方向.2—7 在导出平面问题的三套基本方程时,分别应用了哪些基本假设?这些方程的适用条件是什么?【解答】(1)在导出平面问题的平衡微分方程和几何方程时应用的基本假定是:物体的连续性,小变形和均匀性.在两种平面问题( 平面应力、平面应变问题)中,平衡微分方程和几何方程都适用。
(2)在导出平面问题的物理方程时应用的基本假定是:物体的连续性,完全弹性,均匀性,小变形和各向同性,即物体为小变形的理想弹性体。
在两种平面问题(平面应力、平面应变)中的物理方程不一样,如果将平面应力问题的物理方程中的E 换位21E μ-,1μμμ-换为,就得到平面应变问题的物理方程。
2-8 试列出题2-8图(a ),题2-8图(b )所示问题的全部边界条件.在其端部边界上,应用圣维南原理列出三个积分的应力边界条件。
【解】(1)对于图(a )的问题在主要边界0,x x b ==上,应精确满足下列边界条件:0(),(),x x x x b gy gy σρσρ===-=- 0()0()0xy x xy x b ττ====;。
在小边界(次要边界)y=0上,能精确满足下列边界条件:01(),y y gh σρ==-()0yx τ=。
在小边界(次要边界)2y h =上,有位移边界上条件:22()0,()0y h y h u v ====。
这两个位移边界条件可以应用圣维南原理,改用三个积分的应力边界条件来代替,当板厚1δ=时,22212000()(),()0,()0b y y h by y h byx y h dx g h h b xdx dx σρστ===⎧=-+⎪⎪=⎨⎪⎪=⎩⎰⎰⎰。
弹性理论基础答案

弹性理论基础答案【篇一:弹性力学基础习题答案nnnn1】/p> 2.1计算:(1)?pi?iq?qj?jk,(2)epqieijkajk,(3)eijpeklpbkiblj。
解:(1)?pi?iq?qj?jk(2)epqieijkajk2.2证明:若aij(3)eijpeklpbkiblj??pq?qj?jk??pj?jk??pk;?(?ik?jl??il?jk)bkiblj?biibjj?bjibij。
?(?pj?qk??pk?qj)ajk?apq?aqp;?aji,则eijkajk?0。
证:2eijkajk?eijkajk?eikjakj?eijkajk?eijkakj?eijkajk?eijkajk?0。
2.3设a、b和c是三个矢量,试证明:a?aa?ba?cb?ab?bb?c?[a,b,c]2 c?ac?bc?ca?aa?ba?caiaiaibiaicia1a2a3a1b1c12证:b?ab?bb?c?biaibibibici?b1b2b3a2b2c2?[a,b,c]。
c?ac?bc?cciaicibicicic1c2c3a3b3c32.4设a、b、c和d是四个矢量,证明:(a?b)?(c?d)?(a?c)(b?d)?(a?d)(b?c)证:(a?b)?(c?d)?aibjeijkek?cldmelmnen?aibjcldmeijkelmk ?aibjcld m(?il?jm??im?jl)?(aici)(bjdj)?(aidi)(bjcj) ?(a?c)(b?d)?(a?d)(b?c )。
2.5设有矢量u?uiei。
原坐标系绕z轴转动?系,如图2.4所示。
试求矢量u在新坐标系中的分量。
解:?1?1?cos?,?1?2?sin?,?1?3?0,?2?1??sin?,?2?2?cos ?,?2?3?0,?3?1?0,?3?2?0,?3?3?1。
u1???1?iui?u1cos??u2sin?,图2.41u2???2?iui??u1sin??u2cos?,u3???3?iui?u3。
弹性力学-答案

《弹性力学》习题答案一、单选题1、所谓“完全弹性体”是指(B)A、材料应力应变关系满足虎克定律B、材料的应力应变关系与加载时间、历史无关C、本构关系为非线性弹性关系D、应力应变关系满足线性弹性关系2、关于弹性力学的正确认识是(A )A、计算力学在工程结构设计中的作用日益重要B、弹性力学从微分单元体入手分析弹性体,因此与材料力学不同,不需要对问题作假设C、任何弹性变形材料都是弹性力学的研究对象D、弹性力学理论像材料力学一样,可以没有困难的应用于工程结构分析3、下列对象不属于弹性力学研究对象的是(D )。
A、杆件B、块体C、板壳D、质点4、弹性力学对杆件分析(C)A、无法分析B、得出近似的结果C、得出精确的结果D、需采用一些关于变形的近似假定5、图示弹性构件的应力和位移分析要用什么分析方法?(C)A、材料力学B、结构力学C、弹性力学D、塑性力学6、弹性力学与材料力学的主要不同之处在于( B )A、任务B、研究对象C、研究方法D、基本假设7、下列外力不属于体力的是(D)A、重力B、磁力C、惯性力D、静水压力8、应力不变量说明( D )。
A. 应力状态特征方程的根是不确定的B. 一点的应力分量不变C. 主应力的方向不变D. 应力随着截面方位改变,但是应力状态不变9、关于应力状态分析,(D)是正确的。
A. 应力状态特征方程的根是确定的,因此任意截面的应力分量相同B. 应力不变量表示主应力不变C. 主应力的大小是可以确定的,但是方向不是确定的D. 应力分量随着截面方位改变而变化,但是应力状态是不变的10、应力状态分析是建立在静力学基础上的,这是因为( D )。
A. 没有考虑面力边界条件B. 没有讨论多连域的变形C. 没有涉及材料本构关系D. 没有考虑材料的变形对于应力状态的影响11、下列关于几何方程的叙述,没有错误的是( C )。
A. 由于几何方程是由位移导数组成的,因此,位移的导数描述了物体的变形位移B. 几何方程建立了位移与变形的关系,因此,通过几何方程可以确定一点的位移C. 几何方程建立了位移与变形的关系,因此,通过几何方程可以确定一点的应变分量D. 几何方程是一点位移与应变分量之间的唯一关系12、平面应变问题的应力、应变和位移与那个(些)坐标无关(纵向为 z 轴方向)( C )A、 xB、 yC、 zD、 x, y, z13、平面应力问题的外力特征是(A)A 只作用在板边且平行于板中面B 垂直作用在板面C 平行中面作用在板边和板面上D 作用在板面且平行于板中面。
弹性力学基础(程尧舜_同济大学出版社)课后习题解答(完整资料).doc

【最新整理,下载后即可编辑】【最新整理,下载后即可编辑】习题解答第二章2.1计算:(1)piiqqjjkδδδδ,(2)pqi ijkjke e A ,(3)ijp klpkilje e B B 。
解:(1)piiqqjjkpqqjjkpjjkpkδδδδδδδδδδ===;(2)()pqi ijk jk pj qk pk qj jk pq qpe e A A A A δδδδ=-=-;(3)()ijp klp ki lj ik jl il jk ki lj ii jj ji ije e B B B B B B B B δδδδ=-=-。
2.2证明:若ij ji a a =,则0ijk jke a =。
证:20ijk jk jk jk ikj kj ijk jk ijk kj ijk jk ijk jki e a e a e a e a e a e a e a ==-=-=+。
2.3设a 、b 和c 是三个矢量,试证明:2[,,]⋅⋅⋅⋅⋅⋅=⋅⋅⋅a a a b a cb a b b bc a b c c a c b c c证:1231112123222123333[,,]i i i i i i i i i i i i i i i i i i a a a b a c a a a a b c b a b b b c b b b a b c c a c b c c c c c a b c ⋅⋅⋅⋅⋅⋅=⋅⋅⋅==a a a b a c b a b b b c a b c c a c b c c 。
2.4设a 、b 、c 和d 是四个矢量,证明:()()()()()()⨯⋅⨯=⋅⋅-⋅⋅a b c d a c b d a d b c证:()()ij ijkk l m lmn n i j l m ijk lmk a b ec d e a b c d e e ⨯⋅⨯=⋅=a b c d e e【最新整理,下载后即可编辑】图2.4)(jmim jl δδ-=()()()()=⋅⋅-⋅⋅a c b d a d b c 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题解答第二章2.1计算:(1)pi iq qj jk δδδδ,(2)pqi ijk jk e e A ,(3)ijp klp ki lj e e B B 。
解:(1)pi iq qj jkpq qj jk pj jk pk δδδδδδδδδδ===;(2)()pqi ijk jkpj qk pk qj jk pq qp e e A A A A δδδδ=-=-;(3)()ijp klp ki ljik jl il jk ki lj ii jj ji ij e e B B B B B B B B δδδδ=-=-。
2.2证明:若ijji a a =,则0ijk jk e a =。
证:20ijk jk jk jk ikj kj ijk jk ijk kj ijk jk ijk jk i e a e a e a e a e a e a e a ==-=-=+。
2.3设a 、b 和c 是三个矢量,试证明:2[,,]⋅⋅⋅⋅⋅⋅=⋅⋅⋅a a a b a cb a b b bc a b c c a c b c c证:1231112123222123333[,,]i i i i i i i i i i i i i i i i i i a a a b a c a a a a b c b a b b b c b b b a b c c a c b c c c c c a b c ⋅⋅⋅⋅⋅⋅=⋅⋅⋅==a a a b a c b a b b b c a b c c a c b c c 。
2.4设a 、b 、c 和d 是四个矢量,证明:()()()()()()⨯⋅⨯=⋅⋅-⋅⋅a b c d a c b d a d b c证:()()i j ijk k l m lmn n i j l m ijk lmk a b e c d e a b c d e e ⨯⋅⨯=⋅=a b c d e e ()()()()()i j l m il jm im jl i i j j i i j j a b c d a c b d a d b c δδδδ=-=- ()()()()=⋅⋅-⋅⋅a c b d a d b c 。
2.5设有矢量i i u =u e 。
原坐标系绕z 轴转动θ系,如图2.4所示。
试求矢量u 在新坐标系中的分量。
解:11cos βθ'=,12sin βθ'=,130β'=,21sin βθ'=-,22cos βθ'=,230β'=, 310β'=,320β'=,331β'=。
1112cos sin i iu u u u βθθ''==+,2212sin cos i i u u u u βθθ''==-+,333i i u u u β''==。
2.6设有二阶张量ij i j T =⊗T e e 。
当作和上题相同的坐标变换时,试求张量T 在新坐标系中的分量11T ''、12T ''、13T ''和33T ''。
解:变换系数同上题。
1122112212211111cos2sin2222i j ij T T T T T TT T ββθθ''''+-+==++, 12211221221112cos2sin2222T T T T T TT θθ''-+-=++,131323cos sin T T T θθ''=+, 3333T T ''=。
2.7设有3n个数12n i i i A ⋅⋅⋅,对任意m 阶张量12m j j j B ⋅⋅⋅,定义 12121212n mnmi i i j j j i i i j j j C A B ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=若1212n m i i i j j j C ⋅⋅⋅⋅⋅⋅为n m +阶张量,试证明12n i i i A ⋅⋅⋅是n 阶张量。
证:为书写简单起见,取2n =,2m =,则ijkl ij kl C A B =,在新坐标系中,有i j k l i j k l C A B ''''''''= (a)因为ijkl C 和kl B 是张量,所以有i j k l i i j j k k l l ijkl i i j j ij k k l l kl i i j j ij k l C C A B A B ββββββββββ''''''''''''''''===比较上式和式(a),得()0i j i i j j ij k l A A B ββ''''''-=由于B 是任意张量,故上式成立的充要条件是 i j i i j j ij A A ββ''''=即ij A 是张量。
2.8设A 为二阶张量,试证明tr ⋅=⋅I A A 。
证:=()()===tr jk j k jk i j i k jk ij ik ii i i A A A A δδ⋅=⊗⊗⋅⋅⋅⋅⋅I A A e e e e e e e e 。
2.9设a 为矢量,A 为二阶张量,试证明:(1)()T T ⨯=-⨯a A A a ,(2)()T T ⨯=-⨯A a a A证:(1) ()()()T T T T ji i j k k ji i k jkn n A a A a e -⨯=-⊗⨯=-⊗A a e e e e e ()T ji k jkn i n jn k jki i n A a e A a e =-⊗=-⊗e e e e k k jn j n a A =⨯⊗=⨯a A e e e 。
(2) ()()()T T T T i i kj j k kj i ijn n k a A A a e -⨯=-⨯⊗=-⊗a A e e e e e ()nj i ijk n k nj n i jik k A a e A a e =-⊗=⊗e e e enj n j i i A a =⊗⨯=⨯A a e e e2.10已知张量T 具有矩阵123[]456789=⎡⎤⎢⎥⎢⎥⎣⎦T求T 的对称和反对称部分及反对称部分的轴向矢量。
解:T 的对称部分具有矩阵1351([][])3572579T+=⎡⎤⎢⎥⎢⎥⎣⎦T T ,T 的反对称部分具有矩阵0121([][])1012210T ---=-⎡⎤⎢⎥⎢⎥⎣⎦T T 。
和反对称部分对应的轴向矢量为 1232=-+ωe e e 。
2.11已知二阶张量T 的矩阵为310[]130001-=-⎡⎤⎢⎥⎢⎥⎣⎦T求T 的特征值和特征矢量。
解:2310130(1)[(3)1]0001λλλλλ----=---=-由上式解得三个特征值为14λ=,22λ=,31λ=。
将求出的特征值代入书中的式(2.44),并利用式(2.45),可以求出三个特征矢量为112)-a e,12)a e +e ,33=a e 。
2.12求下列两个二阶张量的特征值和特征矢量:αβ=+⊗A I m m ,=⊗+⊗B m n n m其中,α和β是实数,m 和n 是两个相互垂直的单位矢量。
解:因为()()αβαβ⋅=+⊗⋅=+A m I m m m m ,所以m 是A 的特征矢量,αβ+ 是和其对应的特征值。
设a 是和m 垂直的任意单位矢量,则有()αβα⋅=+⊗⋅=A a I m m a a所以和m 垂直的任意单位矢量都是A 的特征矢量,相应的特征值为α,显然α是特征方程的重根。
令2)-m n e,3)+m n e ,123⨯e =e e 则有23)m e +e,23)-n e +e 上面定义的i e 是相互垂直的单位矢量。
张量B 可以表示成 1122330=⊗-⊗⊗B e e e e +e e所以,三个特征值是1、0和-1,对应的特征矢量是3e 、1e 和2e 。
2.13设a 和b 是矢量,证明:(1)2()()∇⨯∇⨯=∇∇⋅-∇a a a(2)()()()()()∇⨯⨯=⋅∇-⋅∇+∇⋅-∇⋅a b b a a b a b b a证:(1) 这一等式的证明过程和书中证明式(2.14)的过程相同,在此略。
(2) ()()()j j k k j k jkm m i iii a b a b e x x ∂∂∂∂∇⨯⨯=⨯⨯=⨯a b e e e e e ,,,,()()()j i k j k i jkm imn n j i k j k i jn ki ji kn n a b a b e e a b a b δδδδ=+=+-e e,,,,j i i j j i i j j j k k i k i k a b a b a b a b =+--e e e e ()()()()=⋅∇-⋅∇+∇⋅-∇⋅b a a b a b b a2.14设2321232x yz xz xz =-+a e e e ,求1()2=∇-∇w a a 及其轴向矢量。
解:12()=∇-∇w a a 23223211213212[(2)()(2)x z z x y z z x z =+⊗+-⊗-+⊗e e e e e e 22222331326()6]xz z x y xz -⊗+-⊗+⊗e e e e e e 由上式很容易得到轴向矢量,也可以按下面的方法计算轴向矢量222321112322[6()(2)]xz x y z z x z =∇⨯=+--+ωa e e e 。
2.15设S 是一闭曲面,r 是从原点O 到任意一点的矢径,试证明:(1)若原点O 在S 的外面,积分30S dS r⋅=⎰n r; (2)若原点O 在S 的内部,积分34SdS rπ⋅=⎰n r。
证:(1)当0r ≠时,有 33()()0i i x r x r ∂∇⋅==∂r (b) 因为原点在S 的外面,上式在S 所围的区域V 中处处成立,所以由高斯公式得 33()0S VdS dv r r ⋅=∇⋅=⎰⎰n r r 。
(2)因为原点在S 的内部,所以必定存在一个以原点为球心、半径为a 的球面S '完全在S 的内部。
用V 表示由S 和S '所围的区域,在V 中式(b)成立,所以3333()0S S S S VdS dS dS dV r r r r ''+⋅⋅⋅=+=∇⋅=⎰⎰⎰⎰n r n r n r r即33S SdS dS r r '⋅⋅=-⎰⎰n r n r 在S '上,r a =,/a =-n r ,于是 3322114S S S SdS dS dS dS r r a a π'''⋅⋅=-===⎰⎰⎰⎰n r n r 。
