小波分解与重构代码

合集下载

常用小波函数及Matlab常用指令

xd=wdencmp('gbl',x,'db3',2,thr,sorh,keepapp)
THR=wbmpen(C,L,SIGMA,ALPHA)使用penalization方法为降噪返回全局门槛THR.
STDC=wnoisest(C,L,S)返回[C,L]在尺度S上的细节系数的标准差估计
[THR,NKEEP]=wdcbm(C,L,ALPHA,M)返回各尺度上的相应门槛，存放于THR向量中，降噪一般将ALPHA设为3
y=upcoef('O',x,'wname',N) 用于一维小波分析，计算向量x向上N步的重构小波系数，N为正整数。如果O=a,对低频系数进行重构；如果O=d，对高频系数进行重构。
[thr,sorh,keepapp]=ddencmp('den','wv',x)产生信号全局默认阈值，然后利用wdencmp函数进行消除噪声的处理,thr = sqrt(2*log(n)) * s
THR=thselect(X,TPTR)使用由TPTR指定的算法计算与X相适应的门槛
D=detcoef(c,l,N) 提取N尺度的高频系数。
[nc,nl,ca]=upwlev(c,l,'wname')对小波分解结构[c,l]进行单尺度重构，返回上一尺度的分解结构并提取最后一尺度的低频分量。
x=wrcoef('type',c,l,'wname',N)对一维信号的分解结构[c,l]用指定的小波函数进行重构，当'type=a' 时对信号的低频部分进行重构，此时N可以为0.当'type=d'时，对信号的高频部分进行重构，此时N为正整数。

matlab小波分解重构高频信号

matlab小波分解重构高频信号读者可能会有的问题和困惑。

小波分解是一种遍布于各个领域，常用于信号处理、图像处理等技术的数学工具。

它基于一种名为小波变换的数学理论，可以将原始信号分解成多个频带组合，类似于频域的傅里叶变换。

在这些频带中，低频部分对应着原信号的慢变化、趋势等，而高频部分则对应着信号的短时变化、噪声等。

因此，小波分解可以用于对信号进行去噪、特征提取、边缘检测等操作，也可以用于压缩、加密等应用。

在本文中，我们将以MATLAB 为例，介绍如何使用小波分解对信号进行处理。

一、加载示例数据在MATLAB 中，可以使用wavread 函数加载音频文件作为示例数据，如下所示：matlab[x, fs] = wavread('example.wav');这里，x 是加载的音频数据，fs 是采样率。

如果需要处理的是其他类型的信号，可以使用其他载入数据的函数，如load、csvread 等。

二、进行小波分解在MATLAB 中，可以使用wavedec 函数进行小波分解，如下所示：matlab[c, l] = wavedec(x, N, wname);其中，c 是分解后的系数向量，l 是包含各个频带长度的向量，N 是分解的阶数，wname 是小波函数的名称。

这里，我们选择Daubechies-4 小波作为分析小波函数，其名称为db4。

matlab[c, l] = wavedec(x, 5, 'db4');三、获取高频信号在小波分解后的系数向量c 中，每个位置对应着一个分解出的频带。

因此，我们可以根据小波分解的原理，获取特定频带的系数，再通过逆小波变换将其重构成对应的信号。

在本文中，我们将使用高频部分作为重点介绍。

对于N 阶小波分解，l(1:N+1) 包含有N+1 个数字，分别对应着从低频到高频的各个频带长度。

其中，l(1) 对应的是最低频的长度，也就是原信号长度。

为了获取高频系数，我们需要从c 向量中抽取其中的高频部分。

小波分解与重构

%提取多尺度小波变换的高频系数
figure(2);
lev_1=lev+1;
for i=1:lev
cD=detcoef(C,L,i);
subplot(lev_1,1,i)
plot(cD);
ylabel(['cD',num2str(i)]);
Fs=1000; % 采样频率
Ts=1/Fs; % 采样间隔
N=1024; % 采样点数
t=[0:1/Fs:(N-1)/Fs]; %采样时刻
lev=5;
x=sin(2*pi*f1*t);
figure(1);
plot(t,x);
%%小波分解
[C,L]=wavedec(x,lev,'db10'); %C由[cAj,cDj,cDj-1,...,cD1]
subplot(2,2,4);
image(hd2+dd2+vd2+a1);colormap(map);
% 验证这些图像的长度都是sX
sX = size(X)
sa1 = size(a1)
shd2 = size(hd2)
norm(hd2+dd2+vd2+a1-X)
结果：
sX =
256 256
plot(A);
title('原始信号')
subplot(3,1,2);
plot(a0);
title('重构信号')
subplot(3,1,3);
plot(A-a0);
title('误差信号')
err=max(abs(A-a0))

小波图像分解和重构程序每句都带解释

小波图像分解程序：function coef=mywavedec2(x,N,wname) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 函数MYWA VEDEC2() 对输入矩阵x 进行dim 层分解，得到相应的分解系数矩阵y% 输入参数：x ——输入矩阵% N ——分解级数% wname ——分解所用的小波函数% 输出参数：coef ——分解系数矩阵，其结构如下：% coef = {cA_N;cV_N;cH_N;cD_N;cV_N-1;cH_N-1;cD_N-1;……;cV_1;cH_1;cD_1}% Copyright by Zou Yuhua ( chenyusiyuan ), original : 2007-11-10, modified: 2008-06-04 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 求出小波函数的滤波器组系数向量[Lo_D,Hi_D] = wfilters(wname,'d');% 画出原始图像imshow(x);title('Original Image');% 标明图像大小[r,c]=size(x);xlabel(['Size : ',num2str(r),'*',num2str(c)]);% 将矩阵x的数据格式转换为适合数值处理的double格式xd=double(x);coef=[];for i=1:N[cA,cV,cH,cD]=mydwt2(xd,Lo_D,Hi_D);% 第i 级小波分解xd=cA;% 将第i 级分解得到的低频系数矩阵作为第i+1 级分解的源矩阵outmp={cV;cH;cD};% 将第i 级分解得到的高频系数矩阵cV,cH,cD存入细胞矩阵outmp % 注意细胞矩阵的赋值是用大括号“{}”的，而普通矩阵赋值是用方括号“[]”% 细胞矩阵不要求其中的子矩阵的行列数都相同coef=[outmp;coef];% 将细胞矩阵outmp 存入输出矩阵coef，coef将由空矩阵变为细胞矩阵% 注意这里的方括号不能用大括号取代% 否则，使用大括号会将初始的coef空矩阵也作为细胞矩阵的子矩阵% 而且，在迭代中coef 将是一个不断嵌套的细胞矩阵，不便于后续处理和读取% 上面这个语句是一种有效的在迭代过程中保存数据的方法% 设待存数据为data，可以是单个数、向量或矩阵% 保存数据的矩阵为mat，初始为空矩阵：mat=[]% 则可按以下格式保存迭代过程产生的数据% mat=[mat;data];% 方括号内的分号“;”表示数据data 是按“列”排序的方式存入矩阵mat% mat=[mat,data];% 方括号内的逗号“,”表示数据data 是按“行”排序的方式存入矩阵mat% data 也可以在mat 前嵌入，即mat=[data;mat] 或mat=[data,mat]end% 迭代结束后，矩阵coef 中保存的是各级分解中的高频系数矩阵% 故需将迭代后得到的矩阵cA，即第dim 级低频矩阵存入矩阵coefcoef=[cA;coef];% 最后，小波系数矩阵coef 的结构如下% coef = {cA_N;cV_N;cH_N;cD_N;cV_N-1;cH_N-1;cD_N-1;……;cV_1;cH_1;cD_1}% 画出各级低频、高频系数矩阵% 首先建立一个名为“Wavelet Decomposition -- Wavelet Type: , Levels: ”的图像窗口figure('Name',['Wavelet Decomposition -- Wavelet Type: ',wname,' , Levels: ',num2str(N)]);% 图像的第1行显示低频系数，置中，左右两个subplot为空subplot(N+1,3,2);yt=uint8(coef{1});[yrow,ycol]=size(yt);imshow(yt);title( ['Approximation A',num2str(N)]);xlabel(['Size : ',num2str(yrow),'*',num2str(ycol)]);% 第2-(N+1)行显示各级高频系数titllist={['Vertical Detail V'];['Horizontal Detail H'];['Diagonal Detail D']};pn=2;% pn 是子图的显示序号for pr=1:Nfor pc=1:3subplot(N+1,3,pn+2);yt=[];% 为了使高频细节内容（轮廓、边缘）更清晰，将高频系数增加100灰度值yt=uint8(coef{pn})+100;[yrow,ycol]=size(yt);imshow(yt);title([ titllist{pc},num2str(N-pr+1)]);xlabel(['Size : ',num2str(yrow),'*',num2str(ycol)]);% 每行的第一个图像的Y轴，显示该行高频系数对应的分解级别if mod(pn+2,3)==1ylabel(['Level ',num2str(N-pr+1)]);endpn=pn+1;endendfunction [cA,cV,cH,cD]=mydwt2(x,Lo_D,Hi_D) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % 函数MYDWT2() 对输入的r*c维矩阵x 进行二维小波分解，输出四个分解系数子矩阵[LL,HL,LH,HH]% 输入参数：x ——输入矩阵，为r*c维矩阵。

仿真信号小波分解与重构程序

3仿真信号小波分解与重构程序本实验采用的初始信号为f=sin(0.03*t)，其图像如图figure（1）所示，在原信号的基础上加上噪音noissin，添加噪音后的信号的图像如figure（2）所示，然后分别对加了噪声的信号进行db3 小波降噪和sym8小波降噪，并画出了信号降噪后的图像，图像如figure（3）、figure（4）所示。

（1）仿真信号处理程序:N=1000;t=1:1000;f=sin(0.03*t);load noissin;e=noissin;figure(1);plot(t,f);xlabel('y样本序列');ylabel('原始信号幅值');grid;figure(2);plot(e);xlabel('样本序列n');ylabel('含有噪声的信号幅值');grid;s1=wden(e,'minimaxi','s','one',5,'db3');figure(3);plot(s1);xlabel('样本序列n');ylabel('db3 小波降噪后的信号幅');s2=wden(e,'heursure','s','one',5,'sym8');figure(4);plot(s2);xlabel('样本序列n');ylabel('sym8小波降噪后的信号幅');grid;%db10小波进行4层分解%一维小波分解[c,l]=wavedec(f,4,'db10');%重构第1~4层细节信号d4=wrcoef('d',c,l,'db10',4);d3=wrcoef('d',c,l,'db10',3);d2=wrcoef('d',c,l,'db10',2);d1=wrcoef('d',c,l,'db10',1);%显示细节信号figure(5);subplot(4,1,1);plot(d4, 'LineWidth',1);ylabel('d4');subplot(4,1,2);plot(d3, 'LineWidth',1);ylabel('d3');subplot(4,1,3);plot(d2,'LineWidth',1);ylabel('d2');subplot(4,1,4);plot(d1, 'LineWidth',1);ylabel('d1'); xlabel('时间t/s'); grid;（2）信号图像：Figure（1）初始信号的时域图像Figure（3）db3小波降噪后的信号幅。

小波分解和重构算法作业

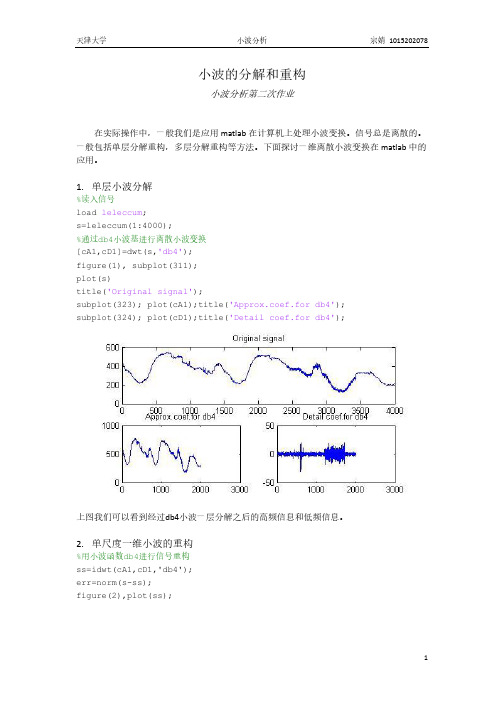
小波的分解和重构小波分析第二次作业在实际操作中，一般我们是应用matlab在计算机上处理小波变换。

信号总是离散的。

一般包括单层分解重构，多层分解重构等方法。

下面探讨一维离散小波变换在matlab中的应用。

1.单层小波分解%读入信号load leleccum;s=leleccum(1:4000);%通过db4小波基进行离散小波变换[cA1,cD1]=dwt(s,'db4');figure(1), subplot(311);plot(s)title('Original signal');subplot(323); plot(cA1);title('Approx.coef.for db4');subplot(324); plot(cD1);title('Detail coef.for db4');上图我们可以看到经过db4小波一层分解之后的高频信息和低频信息。

2.单尺度一维小波的重构%用小波函数db4进行信号重构ss=idwt(cA1,cD1,'db4');err=norm(s-ss);figure(2),plot(ss);重构完成后的误差为3.53e-10。

重构完成后的函数与分解前的函数相同，仅仅存在很小很小可以忽略为0的误差。

3.多层小波分解上文是使用单层小波分解，下面使用wavedec函数进行多层小波分解，并显示分解后的低频高频信息。

%通过db4小波基进行三尺度小波分解[c,l]=wavedec(s,3,'db4');a1=appcoef(c,l,'db4',1);%提取尺度1的低频系数a2=appcoef(c,l,'db4',2);%提取尺度2的低频系数a3=appcoef(c,l,'db4',3);%提取尺度3的低频系数figure(3);subplot(321);plot(a1);title('尺度1的低频系数');subplot(323);plot(a2);title('尺度2的低频系数');subplot(325):plot(a3):title('尺度3的低频系数');d1=detcoef(c,l,1);d2=detcoef(c,l,2);d3=detcoef(c,l,3);figure(3);subplot(322);plot(d1);title('尺度1的高频系数');figure(3);subplot(324);plot(d2);title('尺度2的高频系数');figure(3);subplot(326);plot(d2);title('尺度3的高频系数');由上图可以清晰的看出低频的信息和高频的信息。

小波分解函数和重构函数的应用和区别

小波分解函数和重构函数的应用和区别今天把有关一维小波基本函数整理了一下，也不知道在理解上是否有偏差。

小波分析基本函数可分为分解和重构两类，下面以一维小波分析为例说明小波函数的应用和相关函数的区别。

1、一维小波分解函数和系数提取函数对常用的dwt、wavedec、appcoef函数的常用格式进行举例说明。

格式：[ca, cd]=dwt(X,’wname’) %单尺度一维离散小波分解[C, L]=wavedec(X,N,’wname’) %多尺度一维小波分解（多分辨分析函数）ca=appcoef(C,L,’wname’,N) %提取一维小波变换低频系数说明：（1）小波分解函数和系数提取函数的结果都是分解系数；（2）如何理解小波系数：小波系数是信号在做小波分解时所选择的小波函数空间的投影。

我们知道，一个信号可以分解为傅里叶级数，即一组三角函数之和，而傅里叶变换对应于傅里叶级数的系数；同样，一个信号可以表示为一组小波基函数之和，小波变换系数就对应于这组小波基函数的系数。

（3）多尺度分解是按照多分辨分析理论，分解尺度越大，分解系数的长度越小（是上一个尺度的二分之一）。

我们会发现分解得到的小波低频系数的变化规律和原始信号相似，但要注意低频系数的数值和长度与原始信号以及后面重构得到的各层信号是不一样的。

举例：（为直观，把运行结果放在相应程序段后面）%载入原始信号load leleccum;s=leleccum(1:3920);ls=length(s);%单尺度一维离散小波分解函数dwt的应用[ca1,cd1]=dwt(s,'db1'); %用小波函数db1对信号s进行单尺度分解figure(1);subplot(411); plot(s); ylabel('s');title('原始信号s及单尺度分解的低频系数ca1和高频系数cd1');subplot(423); plot(ca1); ylabel('ca1');subplot(424); plot(cd1); ylabel('cd1');（注意: figure(1)中的ca1和cd1的长度都是1960，是原始信号s长度3920的一半。

几种常用小波函数对一维信号进行分解与重构MATLAB程序部分

几种常用小波函数对一维信号进行分解与重构MATLAB程序部分具体MATLAB程序如下%将十六进制转换为十进制(读入的数据为高八位第八位)function ndata=CommonToDec2(filename)s = filename;cdata = textread(s,'%2c','delimiter',' ');% for i = 1:m ;% k = 1 ;% for j = 1:n ;% if(text(i,j) ~= ' ')% cdata(i,k) = text(i,j) ;% k = k + 1 ;% end% end% end[m,n] = size (cdata) ;ndata=zeros(1,m/3);for i=0:m/3-1;k = 3*i + 1 ; %转换高八位if(cdata(k,1)>='0')&&(cdata(k,1)<='9')mdata=cdata(k,1)-48;ndata(i+1)=ndata(i+1)+mdata*16^5;elsemdata=cdata(k,1)-55;ndata(i+1)=ndata(i+1)+mdata*16^5;endif(cdata(k,2)>='0')&&(cdata(k,2)<='9')mdata=cdata(k,2)-48;ndata(i+1)=ndata(i+1)+mdata*16^4;elsemdata=cdata(k,2)-55;ndata(i+1)=ndata(i+1)+mdata*16^4;endk = 3*i + 2 ; %转换低八位if(cdata(k,1)>='0')&&(cdata(k,1)<='9')mdata=cdata(k,1)-48;ndata(i+1)=ndata(i+1)+mdata*16^3;elsemdata=cdata(k,1)-55;ndata(i+1)=ndata(i+1)+mdata*16^3;endmdata1=CommonToDec24('93.txt');[n1,m1]=size (mdata1);for i=1:m1;ldata(i)=mdata1(i)*3.3/4096;endfor i=0:m1/2-1;pdata(i+1)=(ldata(2*i+1)-ldata(2*i+2))/64;endN=m1/2;t=1:N;x=pdata;subplot(211);plot(x);[c,l]=wavedec(x,11,'haar');a2=wrcoef('a',c,l,'haar',2);subplot(212);plot(a2);title('第二层低频重构信号'); figure(2);[c,l]=wavedec(x,11,'db3');a2=wrcoef('a',c,l,'db3',2);subplot(211);plot(a2);title('第二层低频重构信号'); figure(3);[c,l]=wavedec(x,11,'sym2');a2=wrcoef('a',c,l,'sym2',2);subplot(211);plot(a2);title('第二层低频重构信号'); figure(4);[c,l]=wavedec(x,11,'Bior1.3');a2=wrcoef('a',c,l,'Bior1.3',2);subplot(211);plot(a2);title('第二层低频重构信号'); figure(5);[c,l]=wavedec(x,11,'coif2');a2=wrcoef('a',c,l,'coif2',2);subplot(211);plot(a2);title('第二层低频重构信号');结果与分析MATLAB程序运行结果如下图所示：从上到下依次为Haar小波，db小波，sym小波，CoiN小波，biorNr.Nd小波去噪结果：因为心电信号频率较低，频谱能量大都集中在低频部分，在对提取的心电信号的第二层低频信号进行重构后发现选择不同的函数，重构的信号具有不同的效果。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

load leleccum;
s = leleccum(1:3920);
% 用db1小波函数对信号进行三尺度小波分解
[C,L]=wavedec(s,2,'db1');
figure(1);
plot(s);
title('leleccum原始信号');
% 提取尺度1的低频系数
cA1 = appcoef(C,L,'db1',1); %用小波分解框架[C.L]计算1层低频系数的近似值，小波基为db1
% 提取尺度2的低频系数
cA2 = appcoef(C,L,'db1',2);
figure(2);
subplot(2,1,1);
plot(cA1);
title('尺度1的低频系数');
subplot(2,1,2);
plot(cA2);
title('尺度2的低频系数');
% 提取尺度1的高频系数
cD1 = detcoef(C,L,1); %用小波分解框架[C.L]计算1层高频系数的近似值，小波基为db1
% 提取尺度2的高频系数
cD2 = detcoef(C,L,2);
figure(3);
subplot(2,1,1);
plot(cD1);
title('尺度1的高频系数');
subplot(2,1,2);
plot(cD2);
title('尺度2的高频系数');
我给你大概标注了一下，但是你的程序有问题，
% 小波图像压缩 - RGB 图像
clear all;
close all;
% 读取图像
im = input('输入图像');%输入图像名称，要加分号
X=imread(im);
% 输入要分解的小波层数和小波
n=input('输入要分解的小波层数');%输入所要分解的层数
wname = input('输入小波名称');%输入小波名称，也要加分号
x = double(X);
NbColors = 255;
map = gray(NbColors);
x = uint8(x);
%把RGB图像转换成灰度图
% x = double(X);
% xrgb = 0.2990*x(:,:,1) + 0.5870*x(:,:,2) + 0.1140*x(:,:,3);
% colors = 255;
% x = wcodemat(xrgb,colors);
% map = pink(colors);
% x = uint8(x);
% 对图像x进行n维小波分解
x=imread(’ D:\a.jpg’);
map=x;
n=3
wname='sym5';
[c,s] = wavedec2(x,n,wname);
% 使用默认参数选择各层不同的阈值
alpha = 1.5; m = 2.7*prod(s(1,:));
[thr,nkeep] = wdcbm2(c,s,alpha,m)
% 使用上面的阈值和硬阈值处理进行图像压缩
[xd,cxd,sxd,perf0,perfl2] = wdencmp('lvd',c,s,wname,n,thr,'h');
disp('压缩效率');
disp(perf0);
% 重构（下面这个地方有问题，你这里是原始图像小波变换后进行重构，xd才是小波阀值压缩后重构的图像,cxd，sxd，是c，s经过阀值处理后得到的小波分解结构，也就是说xd=waverec2(cxd,sxd,wname);这个wdencmp函数不需要另外进行重构，你下面那些关于重构的都没用，而下面压缩后的图像才是重构后的图像，）
R = waverec2(c,s,wname);
rc = uint8(R);
% 显示原始图像和压缩图像
subplot(221), image(x);
colormap(map);
title('原始图像')
subplot(222), image(xd);
colormap(map);
title('压缩后的图像')
% 显示结果
xlab1 = ['图像压缩后保留能量百分比',num2str(perfl2)];
xlab2 = ['小波阀值压缩后置零系数百分比 ',num2str(perf0), ' %']; xlabel([xlab1 xlab2]);
subplot(223), image(rc);
colormap(map);
title('重构图像');
%计算图像大小
disp('原始图像');
imwrite(x,'original.tif');%将图像x保存为original.tif，下同imfinfo('original.tif')%显示图片original.tif详细信息，下同
disp('压缩后的图像');
imwrite(xd,'compressed.tif');
imfinfo('compressed.tif')
disp('重构后的图像');
imwrite(rc,'decompressed.tif');
imfinfo('decompressed.tif')。